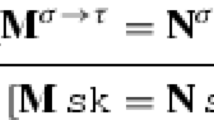Extensional Higher-Order Paramodulation in Leo-III

Abstract

Leo-III is an automated theorem prover for extensional type theory with Henkin semantics and choice. Reasoning with primitive equality is enabled by adapting paramodulation-based proof search to higher-order logic. The prover may cooperate with multiple external specialist reasoning systems such as first-order provers and SMT solvers. Leo-III is compatible with the TPTP/TSTP framework for input formats, reporting results and proofs, and standardized communication between reasoning systems, enabling, e.g., proof reconstruction from within proof assistants such as Isabelle/HOL. Leo-III supports reasoning in polymorphic first-order and higher-order logic, in many quantified normal modal logics, as well as in different deontic logics. Its development had initiated the ongoing extension of the TPTP infrastructure to reasoning within non-classical logics.

1 Introduction

Leo-III is an automated theorem prover (ATP) for classical higher-order logic (HOL) with Henkin semantics and choice. In contrast to its predecessors, LEO and LEO-II [25, 33], that were based on resolution proof search, Leo-III implements a higher-order paramodulation calculus, which aims at improved performance for equational reasoning [89]. In the tradition of the Leo prover family, Leo-III collaborates with external reasoning systems, in particular, with first-order ATP systems, such as E [85], iProver [70] and Vampire [83], and with SMT solvers such as CVC4 [14]. Cooperation is not restricted to first-order systems, and further specialized systems such as higher-order (counter)model finders may be utilized by Leo-III.

Leo-III accepts all common TPTP dialects [99] as well as their recent extensions to polymorphic types [44, 67]. During the development of Leo-III, careful attention has been paid to providing maximal compatibility with existing systems and conventions of the peer community, especially to those of the TPTP infrastructure. The prover returns results according to the standardized TPTP SZS ontology, and it additionally produces verifiable TPTP-compatible proof certificates for each proof that it finds.

The predecessor systems LEO and LEO-II pioneered the area of cooperative resolution-based theorem proving for Henkin semantics. LEO (or LEO-I) was designed as an ATP component of the proof assistant and proof planner $\Omega$MEGA [86] and hard-wired to it. Its successor, LEO-II, is a stand-alone HOL ATP system based on Resolution by Unification and Extensionality (RUE) [18], and it supports reasoning with primitive equality.

The most recent incarnation of the Leo prover family, Leo-III, comes with improved reasoning performance in particular for equational problems, and with a more flexible and effective architecture for cooperation with external specialists.¹ Reasoning in higher-order quantified non-classical logics, including many normal modal logics, and different versions of deontic logic is enabled by an integrated shallow semantical embedding approach [29]. In contrast to other HOL ATP systems, including LEO-II, for which it was necessary for the user to manually conduct the tedious and error-prone encoding procedure before passing it to the prover, Leo-III is the first ATP system to include a rich library of these embeddings, transparent to the user [59]. These broad logic competencies make Leo-III, up to the authors’ knowledge, the most widely applicable ATP system for propositional and quantified, classical and non-classical logics available to date. This work has also stimulated the currently ongoing extension of the TPTP library to non-classical reasoning.²

Leo-III is implemented in Scala and its source code, and that of related projects presented in this article, is publicly available under BSD-3 license on GitHub.³ Installing Leo-III does not require any special libraries, apart from a reasonably current version of the JDK and Scala. Also, Leo-III is readily available via the SystemOnTPTP web interface [99], and it can be called via Sledgehammer [41], from the interactive proof assistant Isabelle/HOL [79] for automatically discharging user’s proof goals.

In a recent evaluation study of 19 different first-order and higher-order ATP systems, Leo-III was found the most versatile (in terms of supported logic formalisms) and best performing ATP system overall [48].

This article presents a consolidated summary of previous conference and workshop contributions [32, 91, 93, 94, 104] as well as contributions from the first author’s Ph.D. thesis [89]. It is structured as follows: §2 briefly introduces HOL and summarizes challenging automation aspects. In §3, the basic paramodulation calculus that is extended by Leo-III is presented, and practically motivated extensions that are implemented in the prover are outlined. Subsequently, the implementation of Leo-III is described in more detail in §4, and §5 presents the technology that enables Leo-III to reason in various non-classical logics. An evaluation of Leo-III on a heterogeneous set of benchmarks, including problems in non-classical logics, is presented in §6. Finally, §7 concludes this article and sketches further work.

2 Higher-Order Theorem Proving

The term higher-order logic refers to expressive logical formalisms that allow for quantification over predicate and function variables; such a logic was first studied by Frege in the 1870s [56]. An alternative and more handy formulation was proposed by Church in the 1940s [51]. He defined a higher-order logic on top of the simply typed $\uplambda$-calculus. His particular formalism, referred to as simple type theory (STT), was later further studied and refined by Henkin [64], Andrews [2,3,4] and others [22, 77]. In the remainder, the term HOL is used synonymously to Henkin’s extensional type theory (ExTT) [26]; it constitutes the foundation of many contemporary higher-order automated reasoning systems. HOL provides lambda-notation as an elegant and useful means to denote unnamed functions, predicates and sets (by their characteristic functions), and it comes with built-in principles of Boolean and functional extensionality as well as type-restricted comprehension.

A more in-depth presentation of HOL, its historical development, metatheory and automation is provided by Benzmüller and Miller [26].

2.1 Syntax and Semantics

HOL is a typed logic; every term of HOL is associated with a fixed and unique type, written as subscript. The set $\mathcal {T}$ of simple types is freely generated from a non-empty set S of sort symbols (base types) and juxtaposition $\nu \tau$ of two types $\tau ,\nu \in \mathcal {T}$, the latter denoting the type of functions from objects of type $\tau$ to objects of type $\nu$. Function types are assumed to associate to the left and parentheses may be dropped if consistent with the intended reading. The base types are usually chosen to be $S {:=} \{\iota , o\}$, where $\iota$ and o represent the type of individuals and the type of Boolean truth values, respectively.

Let $\Sigma$ be a typed signature and let $\mathcal {V}$ denote a set of typed variable symbols such that there exist infinitely many variables for each type. Following Andrews [5], it is assumed that the only primitive logical connective is equality, denoted $=^\tau _{o\tau \tau } \in \Sigma$, for each type $\tau \in \mathcal {T}$ (called Q by Andrews). In the extensional setting of HOL, all remaining logical connectives such as disjunction $\vee _{ooo}$, conjunction $\wedge _{ooo}$ and negation $\lnot _{oo}$ can be defined in terms of them. The terms of HOL are given by the following abstract syntax (where $\tau ,\nu \in \mathcal {T}$ are types):

$$\begin{aligned} s,t :{:=} c_\tau \in \Sigma \; | \; X_\tau \in \mathcal {V}\; | \; \left( \uplambda X_\tau .\, s_\nu \right) _{\nu \tau } \; | \; \left( s_{\nu \tau } \; t_\tau \right) _\nu . \end{aligned}$$

The terms are called constants, variables, abstractions and applications, respectively. Application is assumed to associate to the left and parentheses may again be dropped whenever possible. Conventionally, vector notation $f_{\nu \tau ^n \cdots \tau ^1} \; \overline{t^i_{\tau ^i}}$ is used to abbreviate nested applications $\big (f_{\nu \tau ^n \cdots \tau ^1} \; t^1_{\tau ^1} \; \cdots \; t^n_{\tau ^n}\big )$, where f is a function term and the $t^i$, $1 \le i \le n$, are argument terms of appropriate types. The type of a term may be dropped for legibility reasons if obvious from the context. Notions such as $\alpha$-, $\beta$-, and $\eta$-conversion, denoted $\longrightarrow _\star$, for $\star \in \{\alpha , \beta , \eta \}$, free variables $\mathrm {fv}(.)$ of a term, etc., are defined as usual [13]. The notion $s\{t/X\}$ is used to denote the (capture-free) substitution of variable X by term t in s. Syntactical equality between HOL terms, denoted $\equiv _\star$, for $\star \subseteq \{\alpha , \beta , \eta \}$, is defined with respect to the assumed underlying conversion rules. Terms $s_o$ of type o are formulas, and they are sentences if they are closed. By convention, infix notation for fully applied logical connectives is used, e.g., $s_o \vee t_o$ instead of $(\vee _{ooo} \; s_o) \; t_o$.

As a consequence of Gödel’s Incompleteness Theorem, HOL with standard semantics is necessarily incomplete. In contrast, theorem proving in HOL is usually considered with respect to so-called general semantics (or Henkin semantics) in which a meaningful notion of completeness can be achieved [3, 64]. The usual notions of general model structures, validity in these structures and related notions are assumed in the following. Note that we do not assume that the general model structures validate choice. Intensional models have been described by Muskens [77] and studies of further general notions of semantics have been presented by Andrews [2] and Benzmüller et al. [22].

2.2 Challenges to HOL Automation

HOL validates functional and Boolean extensionality principles, referred to as $\mathrm {EXT}^{\nu \tau }$ and $\mathrm {EXT}^{o}$. These principles can be formulated within HOL’s term language as

$$\begin{aligned} \begin{aligned} \mathrm {EXT}^{\nu \tau }&{:}{=} \forall F_{\nu \tau }.\,\forall G_{\nu \tau }.\,(\forall X_\tau .\,F \; X =^\nu G \; X) \Rightarrow F =^{\nu \tau } G\\ \mathrm {EXT}^{o}&{:}{=} \forall P_o.\,\forall Q_o.\,(P \Leftrightarrow Q) \Rightarrow P =^o Q. \end{aligned} \end{aligned}$$

These principles state that two functions are equal if they correspond on every argument, and that two formulas are equal if they are equivalent (where $\Leftrightarrow _{ooo}$ denotes equivalence), respectively. Using these principles, one can infer that two functions such as $\uplambda P_o.\, \top$ and $\uplambda P_o.\, P \vee \lnot P$ are in fact equal (where $\top$ denotes syntactical truth), and that $\left( \uplambda P_o.\,\uplambda Q_o.\,P \vee Q\right) = \left( \uplambda P_o.\,\uplambda Q_o.\, Q \vee P\right)$ is a theorem. Boolean Extensionality, in particular, poses a considerable challenge for HOL automation: Two terms may be equal, and thus subject to generating inferences, if the equivalence of all Boolean-typed subterms can be inferred. As a consequence, a complete implementation of non-ground proof calculi that make use of higher-order unification procedures cannot simply use syntactical unification for locally deciding which inferences are to be generated. In contrast to first-order theorem proving, it is hence necessary to interleave syntactical unification and (semantical) proof search, which is more difficult to control in practice.

As a further complication, higher-order unification is only semi-decidable and not unitary [60, 65]. It is not clear how many and which unifiers produced by a higher-order unification routine should be chosen during proof search, and the unification procedure may never terminate on non-unifiable terms.

In the context of first-order logic with equality, superposition-based calculi have proven an effective basis for reasoning systems and provide a powerful notion of redundancy [9, 10, 78]. Reasoning with equality can also be addressed, e.g., by an RUE resolution approach [55] and, in the higher-order case, by reducing equality to equivalent formulas not containing the equality predicate [18], as done in LEO. The latter approaches however lack effectivity in practical applications of large-scale equality reasoning.

There are further practical challenges as there are only few implementation techniques available for efficient data structures and indexing methods. This hampers the effectivity of HOL reasoning systems and their application in practice.

2.3 HOL ATP Systems

Next to the LEO prover family [25, 33, 91], there are further HOL ATP systems available: This includes TPS [7] as one of the earliest systems, as well as Satallax [47], coqATP [37], agsyHOL [72] and the higher-order (counter)model finder Nitpick [43]. Additionally, there is ongoing work on extending the first-order theorem prover Vampire to full higher-order reasoning [38, 39], and some interactive proof assistants such as Isabelle/HOL [79] can also be used for automated reasoning in HOL. Further related systems include higher-order extensions of SMT solvers [11], and there is ongoing work to lift first-order ATP systems based on superposition to fragments of HOL, including E [85, 102] and Zipperposition [16, 53].

Further notable higher-order reasoning systems include proof assistants such as PVS [81], Isabelle/HOL, the HOL prover family including HOL4 [61], and the HOL Light system [63]. In contrast to ATP systems, proof assistants do not find proofs automatically but are rather used to formalize and verify handwritten proofs for correctness.

2.4 Applications

The expressivity of higher-order logic has been exploited for encoding various expressive non-classical logics within HOL. Semantical embeddings of, among others, higher-order modal logics [29, 59], conditional logics [20], many-valued logics [90], deontic logic [24], free logics [31] and combinations of such logics [19] can be used to automate reasoning within those logics using ATP systems for classical HOL. A prominent result from the applications of automated reasoning in non-classical logics, here in quantified modal logics, was the detection of a major flaw in Gödel’s Ontological Argument [36, 57] as well as the verification of Scott’s variant of that argument [35] using LEO-II and Isabelle/HOL. Similar and further enhanced techniques were used to assess foundational questions in metaphysics [34, 69].

Additionally, Isabelle/HOL and the Nitpick system were used to assess the correctness of concurrent C++ programs against a previously formalized memory model [45]. The higher-order proof assistant HOL Light played a key role in the verification of Kepler’s conjecture within the Flyspeck project [62].

3 Extensional Higher-Order Paramodulation

Leo-III is a refutational ATP system. The initial, possibly empty, set of axioms and the negated conjecture are transformed into an equisatisfiable set of formulas in clause normal form (CNF), which is then iteratively saturated until the empty clause is found. Leo-III extends the complete, paramodulation-based calculus EP for HOL (cf. §3.1) with practically motivated, partly heuristic inference rules. Paramodulation extends resolution by a native treatment of equality at the calculus level. In the context of first-order logic, it was developed in the late 1960s by G. Robinson and L. Wos [84] as an attempt to overcome the shortcomings of resolution-based approaches to handling equality. A paramodulation inference incorporates the principle of replacing equals by equals and can be regarded as a speculative conditional rewriting step. In the context of first-order theorem proving, superposition-based calculi [9, 10, 78] improve the naive paramodulation approach by imposing ordering restrictions on the inference rules such that only a relevant subset of all possible inferences are generated. However, due to the more complex structure of the term language of HOL, there do not exist suitable term orderings that allow a straightforward adaption of this approach to the higher-order setting.⁴ However, there is recent work to overcome this situation by relaxing restrictions on the employed orderings [15].

3.1 The EP Calculus

Higher-order paramodulation for extensional type theory was first presented by Benzmüller [17, 18]. This calculus was mainly theoretically motivated and extended a resolution calculus with a paramodulation rule instead of being based on a paramodulation rule alone. Additionally, that calculus contained a rule that expanded equality literals by their definition due to Leibniz.⁵ As Leibniz equality formulas effectively enable cut-simulation [23], the proposed calculus seems unsuited for automation. The calculus EP presented in the following, in contrast, avoids the expansion of equality predicates but adapts the use of dedicated calculus rules for extensionality principles from Benzmüller [18].

An equation, denoted $s \simeq t$, is a pair of HOL terms of the same type, where $\simeq$ is assumed to be symmetric (i.e., $s \simeq t$ represents both $s \simeq t$ and $t \simeq s$). A literal $\ell$ is a signed equation, written $[s \simeq t]^\alpha$, where $\alpha \in \{\mathfrak {t\!t},\mathfrak {f\!f}\}$ is the polarity of $\ell$. Literals of form $[s_o]^\alpha$ are shorthand for $[s_o \simeq \top ]^\alpha$, and negative literals $[s \simeq t]^\mathfrak {f\!f}$ are also referred to as unification constraints. A negative literal $\ell$ is called a flex–flex unification constraint if $\ell$ is of the form $[X \; \overline{s^i} \simeq Y \; \overline{t^j}]^\mathfrak {f\!f}$, where X, Y are variables. A clause $\mathcal {C}$ is a multiset of literals, denoting its disjunction. For brevity, if $\mathcal {C},\mathcal {D}$ are clauses and $\ell$ is a literal, $\mathcal {C} \vee \ell$ and $\mathcal {C} \vee \mathcal {D}$ denote the multi-union $\mathcal {C} \cup \{ \ell \}$ and $\mathcal {C} \cup \mathcal {D}$, respectively. $s|_\pi$ is the subterm of s at position $\pi$, and $s[r]_\pi$ denotes the term that is obtained by replacing the subterm of s at position $\pi$ by r. $\alpha$-conversion is applied implicitly to globally and consistently rename bound variables such that it can be assumed in the following, without loss of generality, that no variable capture occurs. This is always possible since there are infinitely many different variables of every type.⁶

The EP calculus can be divided into four groups of inference rules:

3.1.1 Clause normalization

The clausification rules of EP are mostly standard, cf. Fig. 1. Every non-normal clause is transformed into an equisatisfiable set of clauses in CNF. Multiple conclusions are written one below the other. Note that the clausification rules are proper inference rules rather than a dedicated meta-operation. This is due to the fact that non-CNF clauses may be generated from the application of the remaining inferences rules, hence renormalization during proof search may be necessary. In the following, we use $\mathsf {CNF}$ to refer to the entirety of the CNF rules.

Fig. 1

Extensionality and unification rules of EP

For the elimination of existential quantifiers, see rule (CNFExists) in Fig. 1, the sound Skolemization technique of Miller [75, 76] is assumed.

3.1.2 Primary inferences

The primary inference rules of EP are paramodulation (Para), equality factoring (EqFac) and primitive substitution (PS), cf. Fig. 1.

The paramodulation rule (Para) replaces subterms of literals within clauses by (potentially) equal terms given from a positive equality literal. Since the latter clause might not be a unit clause, the rewriting step can be considered conditional where the remaining literals represent the respective additional conditions. Factorization (EqFac) contracts two literals that are semantically overlapping (i.e., one is more general than the other) but not syntactically equal. This reduces the size of the clause, given that the unification of the respective two literals is successful. These two rules introduce unification constraints that are encoded as negative equality literals: A generating inference is semantically justified if the unification constraint(s) can be solved. Since higher-order unification is not decidable, these constraints are explicitly encoded into the result clause for subsequent analysis. Note that a resolution inference between clauses $\mathcal {C} \equiv \mathcal {C}^\prime \vee [p]^\mathfrak {t\!t}$ and $\mathcal {D} \equiv \mathcal {D}^\prime \vee [p]^\mathfrak {f\!f}$ can be simulated by the (Para) rule as the literals $[p]^\alpha$ are actually shorthands for $[p \simeq \top ]^\alpha$ and the clause $[\top \simeq \top ]^\mathfrak {f\!f}\vee \mathcal {C}^\prime \vee \mathcal {D}^\prime \vee [p \simeq p]^\mathfrak {f\!f}$, which eventually simplifies to $\mathcal {C}^\prime \vee \mathcal {D}^\prime$, is generated.

Moreover, note that both (Para) and (EqFac) are unordered and produce numerous redundant clauses. In practice, Leo-III tries to remedy this situation by using heuristics to restrict the number of generated clauses, including a higher-order term ordering, cf. §4. Such heuristics, e.g., prevent redundant paramodulation inferences between positive propositional literals in clauses $\mathcal {C} \vee [p]^\mathfrak {t\!t}$ and $\mathcal {D} \vee [q]^\mathfrak {t\!t}$.

Fig. 2

Primary inference rules and extensionality rules of EP

The primitive substitution inference (PS) approximates the logical structure of literals with flexible heads. In contrast to early attempts that blindly guessed a concrete instance of head variables, (PS) uses so-called general bindings, denoted $\mathcal {GB}_\tau ^{t}$ [33, §2], to step-wise approximate the instantiated term structure and hence limit the explosive growth of primitive substitution. Nevertheless, (PS) still enumerates the whole universe of terms but, in practical applications, often few applications of the rule are sufficient to find a refutation. An example where primitive substitution is necessary is the following: Consider a clause $\mathcal {C}$ given by $\mathcal {C} \equiv [P_o]^\mathfrak {t\!t}$ where P is a Boolean variable. This clause corresponds to the formula $\forall P_o.\, P$ which is clearly not a theorem. Neither (Para) nor (EqFac) or any other calculus rules presented so far or further below (except for (PS)) allow to construct a derivation to the empty clause. However, using (PS), there exists a derivation $[P]^\mathfrak {t\!t}\vdash _{\text {(PS)},\text {(Bind)}} [\lnot P^\prime ]^\mathfrak {t\!t}\vdash _{\text {CNFNeg}} [P^\prime ]^\mathfrak {f\!f}$. Note that $\{\lnot P^\prime /P\}$ is a substitution applying a general binding from $\mathcal {GB}_o^{\{\lnot , \vee \}\cup \{\Pi ^\tau , =^\tau \, | \, \tau \in \mathcal {T}\}}$ that approximates logical negation. Now, a simple refutation involving $[P]^\mathfrak {t\!t}$ and $[P^\prime ]^\mathfrak {f\!f}$ can be found.

3.1.3 Extensionality Rules

The rules (NBE) and (PBE)—for negative resp. positive Boolean extensionality—as well as (NFE) and (PFE)—for negative resp. positive functional extensionality—are the extensionality rules of EP, cf. Fig. 2.

While the functional extensionality rules gradually ground the literals to base types and provide witnesses for the (in-)equality of function symbols to the search space, the Boolean extensionality rules enable the application of clausification rules to the Boolean-typed sides of the literal, thereby lifting them into semantical proof search. These rules eliminate the need for explicit extensionality axioms in the search space, which would enable cut-simulation [23] and hence drastically hamper proof search.

3.1.4 Unification

The unification rules of EP are a variant of Huet’s unification rules and presented in Fig. 2. They can be eagerly applied to the unification constraints in clauses. In an extensional setting, syntactical search for unifiers and semantical proof search coincide, and unification transformations are regarded proper calculus rules. As a result, the unification rules might only partly solve (i.e., simplify) unification constraints and unification constraints themselves are eligible to subsequent inferences. The bundled unification rules are referred to as $\mathsf {UNI}$.

A set $\Phi$ of sentences has a refutation in EP, denoted $\Phi \vdash \square$, iff the empty clause can be derived in EP. A clause is the empty clause, written ${\square }$, if it contains no or only flex–flex unification constraints. This is motivated by the fact that flex–flex unification problems can always be solved, and hence any clause consisting of only flex–flex constraints is necessarily unsatisfiable [64].

Theorem 1

(Soundness and Completeness of $\text {EP}$) EP is sound and refutationally complete for HOL with Henkin semantics.

Proof

Soundness is guaranteed by [89, Theorem 3.8]. For completeness, the following argument is used (cf. [89, §3] for the detailed definitions and notions): By [89, Lemma 3.24], the set of sentences that cannot be refuted in EP is an abstract consistency class [89, Def. 3.11], and by [89, Lemma 3.17] this abstract consistency class can be extended to a Hintikka set. The existence of a Henkin model that satisfies this Hintikka set is guaranteed by [92, Theorem 5]. $\square$

An example for a refutation in EP is given in the following:

Example 1

(Cantor’s Theorem) Cantor’s Theorem states that, given a set A, the power set of A has a strictly greater cardinality than A itself. The core argument of the proof can be formalized as follows:

Formula C states that there exists no surjective function f from a set to its power set. A proof of C in EP makes use of functional extensionality, Boolean extensionality, primitive substitution as well as non-trivial higher-order pre-unification; it is given below.

By convention, the application of a calculus rule (or of a compound rule) is stated with the respective premise clauses enclosed in parentheses after the rule name. For rule (PS), the second argument describes which general binding was used for the instantiation, e.g., $\mathrm {PS}(\mathcal {C}, \mathcal {GB}_{\tau }^{t})$ denotes an instantiation with an approximation of term t for goal type $\tau$.⁷

The Skolem symbols $sk ^1$ and $sk ^2$ used in the above proof have type $o\iota \iota$ and $\iota (o\iota )$, respectively, and the ${X}^i$ denote fresh free variables of appropriate type. A unifier $\sigma _{\mathcal {C}_7}$ generated by $\mathsf {UNI}$ for producing $\mathcal {C}_7$ is given by (analogously for $\mathcal {C}_8$):

$$\begin{aligned} \sigma _{\mathcal {C}_7} \equiv \Big \{ sk ^2 \; \big (\uplambda Z_\iota .\, \lnot ( sk ^1 \; Z \; Z)\big )/{X}^2, \big (\uplambda Z_\iota .\, sk ^1 \; Z \; Z\big )/{X}^5 \Big \} \end{aligned}$$

Note that, together with the substitution $\sigma _{\mathcal {C}_3} \equiv \big \{\uplambda Z_\iota .\, \lnot ({X}^5 \; Z) / {X}^1\big \}$ generated by approximating $\lnot _{oo}$ via (PS) on $\mathcal {C}_3$, the free variable ${X}^1$ in $\mathcal {C}_1$ is instantiated by $\sigma _{\mathcal {C}_7} \circ \sigma _{\mathcal {C}_3}({X}^1) \equiv \uplambda Z_\iota .\, \lnot ( sk ^1 \; Z \; Z)$. Intuitively, this instantiation encodes the diagonal set of $sk ^1$, given by $\{x | x \notin sk ^1(x) \}$, as used in the traditional proofs of Cantor’s Theorem; see, e.g., Andrews [8].

The TSTP representation of Leo-III’s proof for this problem is presented in Fig. 6.

3.2 Extended Calculus

As indicated further above, Leo-III targets automation of HOL with Henkin semantics and choice. The calculus EP from §3.1, however, does not address choice. To this end, Leo-III implements several additional calculus rules that either accommodate further reasoning capabilities (e.g.,  reasoning with choice) or address the inevitable explosive growth of the search space during proof search (e.g.,  simplification routines). The latter kind of rules are practically motivated, partly heuristic, and hence primarily target technical issues that complicate effective automation in practice. Note that no completeness claims are made for the extended calculus with respect to HOL with choice. Furthermore, some of the below features of Leo-III are unsound with respect to HOL without choice. Since, however, Leo-III is designed as a prover for HOL with choice, this is not a concern here.

The additional rules address the follows aspects (cf. Steen’s monograph [89, §4.2] for details and examples):

3.2.1 Improved Clausification

Leo-III employs definitional clausification [106] to reduce the number of clauses created during clause normalization (replacing, e.g., $(a \wedge b \wedge c) \vee (d \wedge e \wedge f)$ by $(a \wedge b \wedge c) \vee r$ and $r \Rightarrow (d \wedge e \wedge f)$ obviously reduces the number of generated clauses). Moreover, miniscoping, i.e., moving quantifiers inward, is employed prior to clausification.

3.2.2 Clause Contraction

Leo-III implements equational simplification procedures, including subsumption, destructive equality resolution, heuristic rewriting and contextual unit cutting (simplify-reflect) [85]. These rules contract the search space in a satisfiability-preserving way using simplification transformations or by removing (redundant) clauses from the search space altogether.

3.2.3 Defined Equalities

Common notions of defined equality predicates (e.g., Leibniz equality and Andrews equality) are heuristically replaced with primitive equality predicates. For example, an axiom (Leibniz equation) of form $\forall P_{o\iota }. \lnot P\, a \vee P\, b$ gets replaced by $a = b$. This is motivated by the fact that formulas of the former form, but not the latter, enable cut-simulation [23] and thus significantly increase the search space.

3.2.4 Choice

Leo-III implements additional calculus rules for reasoning with choice, i.e., with statements of the form $\varepsilon P$, where $P_{o\tau }$ is a predicate on terms of some type $\tau \in \mathcal {T}$ and $\varepsilon$ is an (indefinite) choice operator. To that end, the calculus rules will insert additional clauses to the search space that instantiate the axiom of choice for the respective predicate at hand.

3.2.5 Function Synthesis

If plain unification fails for a set of unification constraints, Leo-III may try to synthesize functions that meet the specifications represented by the unification constraint. This is done using special choice instances that simulate if-then-else terms which explicitly enumerate the desired input output relation of that function. In general, this rule tremendously increases the search space, but it also enables Leo-III to solve some hard problems with TPTP rating 1.0 that were not solved by any ATP system before. As an example, function synthesis will generate the function term $\uplambda X_\iota .\,\varepsilon \big (\uplambda Z_\iota .\, ((X = a) \Rightarrow (Z = b)) \wedge ((X = b) \Rightarrow (Z = a))\big )$ for the proof problem $\exists F_{\iota \iota }.\, (F\;a = b) \wedge (F\;b = a)$; this function term witnesses the existence of a function F that returns a for argument b and vice versa, and it is then used in the proof.

3.2.6 Injective Functions

Leo-III addresses improved reasoning with injective functions by postulating the existence of left inverses for function symbols that are inferred to be injective. An exemplary application of this inference rule is depicted in Example 2.

3.2.7 Further Rules

Prior to clause normalization, Leo-III might instantiate universally quantified variables with heuristically chosen terms. This includes the exhaustive instantiation of finite types (such as o and oo) as well as partial instantiation for other interesting types (such as $o\tau$ for some type $\tau$). A universally quantified formula of form $\forall P_{oo}. P\, t$, for example, might get replaced by $(\uplambda X_o.X)\, t \wedge (\uplambda X_o.\lnot X)\, t \wedge (\uplambda X_o. \top )\, t \wedge (\uplambda X_o. \bot )\, t$. The addition of the above calculus rules to EP in Leo-III enables the system to solve various problems that can otherwise not be solved (in reasonable resource limits). An example problem that could not be solved by any higher-order ATP system before is the following, cf. [6, Problem X5309]:

Example 2

(Cantor’s Theorem, revisited) Another possibility to encode Cantor’s Theorem is by using a formulation based on injectivity:

Here, the nonexistence of an injective function from a set’s power set to the original set is postulated. This conjecture can easily be proved using Leo-III’s injectivity rule $(\mathrm {INJ})$ that, given a fact stating that some function symbol f is injective, introduces the left inverse of f, say $f^{\mathrm {inv}}$, as fresh function symbol to the search space. The advantage is that $f^{\mathrm {inv}}$ is then available to subsequent inferences and can act as an explicit evidence for the (assumed) existence of such a function which is then refuted. The full proof of C’ is as follows:

The introduced Skolem symbol $sk$ is of type $\iota (o\iota )$ and its (assumed) left inverse, denoted $sk ^{\text {inv}}$ of type $o\iota \iota$, is inferred by $(\mathrm {INJ})$ based on the injectivity specification given by clause $\mathcal {C}_0$. The inferred property of $sk ^{\text {inv}}$ is given by $\mathcal {C}_2$. The injective Cantor’s Theorem is part of the TPTP library as problem SYO037⌃1 and could not be solved by any existing HO ATP system before.

4 System Architecture and Implementation

As mentioned before, the main goal of the Leo-III prover is to achieve effective automation of reasoning in HOL, and, in particular, to address the shortcomings of resolution-based approaches when handling equality. To that end, the implementation of Leo-III uses the complete EP calculus presented in §3 as a starting point, and furthermore implements the rules from §3.2. Although EP is still unordered and Leo-III therefore generally suffers from the same drawbacks as experienced in first-order paramodulation, including state space explosions and a prolific proof search, the idea is to use EP anyway as a basis for Leo-III and to pragmatically tackle the problems with additional calculus rules (cf. §3.2), and optimizations and heuristics on the implementation level. As a further technical adjustment, the term representation data structures of Leo-III do not assume primitive equality to be the only primitive logical connective. While this is handy from a theoretical point of view, an explicit representation of further primitive logical connectives is beneficial from a practical side.

An overview of Leo-III’s top level architecture is displayed in Fig. 3. After parsing the problem statement, a symbol-based relevance filter adopted from Meng and Paulson [74] is employed for premise selection. The input formulas that pass the relevance filter are translated into polymorphically typed $\uplambda$-terms (Interpreter) and are then passed to the Proof Search component. In this component, the main top-level proof search algorithm is implemented. Subsequent to initial preprocessing, this algorithm repeatedly invokes procedures from a dedicated component, denoted Control, that acts as a facade to the concrete calculus rules, and moreover manages, selects and applies different heuristics that may restrict or guide the application of the calculus rules. These decisions are based on current features of the proof search progress and user-provided parameter values; such information is bundled in a dedicated State object. If the proof search is successful, the Proof Search component may output a proof object that is constructed by the Control module on request. Indexing data structures are employed for speeding up frequently used procedures.

Fig. 3

Schematic diagram of Leo-III’s architecture. The arrows indicate directed information flow. The external reasoners are executed asynchronously (non-blocking) as dedicated processes of the operating system

Note that the proof search procedure itself does not have direct access to the Calculus module in Fig. 3: Leo-III implements a layered multi-tier architecture in which lower tiers (e.g., the Calculus component) are only accessed through a higher tier (e.g., the Control). This allows for a modular and more flexible structure in which single components can be replaced or enriched without major changes to others. It furthermore improves maintainability as individual components implement fewer functionality (separation of concerns). Following this approach, the Calculus component merely implements the inference rules of Leo-III’s calculus but it does not specify when to apply them, nor does it provide functionality to decide whether individual calculus rules should be applied in a given situation (e.g.,  with respect to some heuristics). The functions provided by this module are low-level; invariantly, there are approximately as many functions in the Calculus module as there are inference rules. The Control component, in contrast, bundles certain inference rule applications with simplification routines, indexing data structure updates and heuristic decision procedures in single high-level procedures. These procedures are then invoked by the Proof Search which passes its current search state as an argument to the calls. The State component is then updated accordingly by the Proof Search using the results of such function calls. The Proof Search module implements a saturation loop that is discussed further below.

Leo-III makes use of external (mostly first-order) ATP systems for discharging proof obligations. If any external reasoning system finds the submitted proof obligation to be unsatisfiable, the original HOL problem is unsatisfiable as well and a proof for the original conjecture is found. Invocation, translation and utilization of the external results are also bundled by the Control module, cf. further below for details.

4.1 Proof Search

The overall proof search procedure of Leo-III consists of three consecutive phases: preprocessing, saturation and proof reconstruction.

During preprocessing, the input formulas are transformed into a fully Skolemized $\beta \eta$-normal clausal normal form. In addition, methods including definition expansion, simplification, miniscoping, replacement of defined equalities and clause renaming [106] are applied, cf. Steen’s thesis for details [89].

Saturation is organized as a sequential procedure that iteratively saturates the set of input clauses with respect to EP (and its extensions) until the empty clause is derived. The clausal search space is structured using two sets U and P of unprocessed clauses and processed clauses, respectively. Initially, P is empty and U contains all clauses generated from the input problem. Intuitively, the algorithm iteratively selects an unprocessed clause g (the given clause) from U. If g is the empty clause, the initial clause set is shown to be inconsistent and the algorithm terminates. If g is not the empty clause, all inferences involving g and (possibly) clauses in P are generated and inserted into U. The resulting invariant is that all inferences between clauses in P have already been performed. Since in most cases the number of clauses that can be generated during proof search is infinite, the saturation process is limited artificially using time resource bounds that can be configured by the user.

Leo-III employs a variant of the DISCOUNT [54] loop that has its intellectual roots in the E prover [85]. Nevertheless, some modifications are necessary to address the specific requirements of reasoning in HOL. Firstly, since formulas can occur within subterm positions and, in particular, within proper equalities, many of the generating and modifying inferences may produce non-CNF clauses albeit having proper clauses as premises. This implies that, during a proof loop iteration, potentially every clause needs to be renormalized. Secondly, since higher-order unification is undecidable, unification procedures cannot be used as an eager inference filtering mechanism (e.g., for paramodulation and factoring) nor can they be integrated as an isolated procedure on the meta-level as done in first-order procedures. As opposed to the first-order case, clauses that have unsolvable unification constraints are not discarded but nevertheless inserted into the search space. This is necessary in order to retain completeness.

If the empty clause was inferred during saturation and the user requested a proof output, a proof object is generated using backward traversal of the respective search subspace. Proofs in Leo-III are presented as TSTP refutations [97], cf. §4.4 for details.

4.2 Polymorphic Reasoning

Proof assistants such as Isabelle/HOL [79] and Coq [37] are based on type systems that extend simple types with, e.g., polymorphism, type classes, dependent types and further type concepts. Such expressive type systems allow structuring knowledge in terms of reusability and are of major importance in practice.

Leo-III supports reasoning in first-order and higher-order logic with rank-1 polymorphism. The support for polymorphism has been strongly influenced by the recent development of the TH1 format for representing problems in rank-1 polymorphic HOL [67], extending the standard THF syntax [100] for HOL. The extension of Leo-III to polymorphic reasoning does not require modifications of the general proof search process as presented further above. Also, the data structures of Leo-III are already expressive enough to represent polymorphic formulas, cf. technical details in earlier work [94].

Central to the polymorphic variant of Leo-III’s calculus is the notion of type unification. Type unification between two types $\tau$ and $\nu$ yields a substitution $\sigma$ such that $\tau \sigma \equiv \nu \sigma$, if such a substitution exists. The most general type unifier is then defined analogously to term unifiers. Since unification on rank-1 polymorphic types is essentially a first-order unification problem, it is decidable and unitary, i.e., it yields a unique most general unifier if one exists. Intuitively, whenever a calculus rule of EP requires two premises to have the same type, it then suffices in the polymorphic extension of EP to require that the types are unifiable. For a concrete inference, the type unification is then applied first to the clauses, followed by the standard inference rule itself.

Additionally, Skolemization needs to be adapted to account for free type variables in the scope of existentially quantified variables. As a consequence, Skolem constants that are introduced, e.g., during clausification are polymorphically typed symbols $\mathrm {sk}$ that are applied to the free type variables $\overline{\alpha ^i}$ followed by the free term variables $\overline{X^i}$, yielding the final Skolem term $(\mathrm {sk} \; \overline{\alpha ^i} \; \overline{X^i})$, where $\mathrm {sk}$ is the fresh Skolem constant. A similar construction is used for general bindings that are employed by primitive substitution or projection bindings during unification. A related approach is employed by Wand in the extension of the first-order ATP system SPASS to polymorphic types [103].

A full investigation of the formal properties of these calculus extensions to polymorphic HOL is further work.

4.3 External Cooperation

Leo-III’s saturation procedure periodically requests the invocation of external reasoning systems at the Control module for discharging proof obligations that originate from its current search space. Upon request the Control module checks, among other things, whether the set of processed clauses P changed significantly since the last request. If this is the case and the request is granted, the search space is enqueued for submission to external provers. If there are no external calls awaiting to be executed, the request is automatically granted. This process is visualized in Fig. 4. The invocation of an external ATP system is executed asynchronously (non-blocking), hence the internal proof search continues while awaiting the result of the external system. Furthermore, as a consequence of the non-blocking nature of external cooperation, multiple external reasoning systems (or multiple instances of the same) may be employed in parallel. To that end, a dedicated I/O driver is implemented that manages the asynchronous calls to external processes and collects the incoming results.

Fig. 4

Invocation of external reasoning systems during proof search. The solid arrows denote data flow through the respective modules of Leo-III. A dotted line indicates indirect use of auxiliary information. Postponed calls are selected by the I/O driver after termination of outstanding external calls

The use of different external reasoning systems is also challenging from a practical perspective: Different ATP systems support different logics and furthermore different syntactical fragments of these logics. This is addressed in Leo-III using an encoding module (cf. Encoder in Fig. 3 resp. Fig. 4) that translates the polymorphically typed higher-order clauses to monomorphic higher-order formulas, or to polymorphic or monomorphic typed first-order clauses. It also removes unsupported language features and replaces them with equivalent formulations. Figure 5 displays the translation pipeline of Leo-III for connecting to external ATP systems. The Control module of Leo-III will automatically select the encoding target to be the most expressive logical language that is still supported by the external system [95]. The translation process combines heuristic monomorphization [42, 46] steps with standard encodings of higher-order language features [73] in first-order logic. For some configurations, there are multiple possible approaches (e.g., either monomorphize from TH1 to TH0 and then encode to TF1, or encode directly to TF1), in these cases a default is fixed but the user may choose otherwise via command-line parameters.

While LEO-II relied on cooperation with untyped first-order provers, Leo-III aims at exploiting the relatively young support of simple types in first-order ATP systems. As a consequence, the translation of higher-order proof obligations does not require the encoding of types as terms, e.g., by type guards or type tags [42, 52]. This approach reduces clutter and hence promises more effective cooperation. Cooperation within Leo-III is by no means limited to first-order provers. Various different systems, including first-order and higher-order ATP systems and model finders, can in fact be used simultaneously, provided that they comply with some common TPTP language standard. Supported TPTP languages for external cooperation include the TPTP dialects TF0 [101], TF1 [44], TH0 [100] and TH1 [67].

Fig. 5

Translation process in the encoder module of Leo-III. Depending on the supported logic fragments of the respective external reasoner, the clause set is translated to different logic formalisms: Polymorphic HOL (TH1), monomorphic HOL (TH0), polymorphic first-order logic (TF1) or monomorphic (many-sorted) first-order logic (TF0)

4.4 Input and Output

Leo-III accepts all common TPTP dialects [99], including untyped clause normal form (CNF), untyped and typed first-order logic (FOF and TFF, respectively) and, as primary input format, monomorphic higher-order logic (THF) [100]. Additionally, Leo-III is one of the first higher-order ATP systems to support reasoning in rank-1 polymorphic variants of these logics using the TF1 [44] and TH1 [67] languages.

Leo-III rigorously implements the machine-readable TSTP result standard [97] and hence outputs appropriate SZS ontology values [98]. The use of the TSTP output format allows for simple means of communication and exchange of reasoning results between different reasoning tools and, consequently, eases the employment of Leo-III within external tools. Novel to the list of supported SZS result values for the Leo prover family is ContradictoryAxioms [98], which is reported if the input axioms were found to be inconsistent during the proof run (i.e., if the empty clause could be derived without using the conjecture even once). Using this simple approach, Leo-III identified 15 problems from the TPTP library to be inconsistent without any special setup.

Additional to the above described SZS result value, Leo-III produces machine-readable proof certificates if a proof was found and such a certificate has been requested. Proof certificates are an ASCII encoded, linearized, directed acyclic graph (DAG) of inferences that refutes the negated input conjecture by ultimately generating the empty clause. The root sources of the inference DAG are the given conjecture (if any) and all axioms that have been used in the refutation. The proof output records all intermediate inferences. The representation again follows the TSTP format and records the inferences using annotated THF formulas. Due to the fine granularity of Leo-III proofs, it is often possible to verify them step-by-step using external tools such as GDV [96]. A detailed description of Leo-III’s proof output format and the information contained therein can be found in Steen’s Ph.D. thesis [89, §4.5]. An example of such a proof output is displayed in Fig. 6.

Fig. 6

Proof output of Leo-III for the polymorphic variant (TH1 syntax) of the surjective variant of Cantor’s Theorem

4.5 Data Structures

Leo-III implements a combination of term representation techniques; term data structures are provided that admit expressive typing, efficient basic term operations and reasonable memory consumption [32]. Leo-III employs a so-called spine notation [50], which imitates first-order-like terms in a higher-order setting. Here, terms are either type abstractions, term abstractions or applications of the form $f \cdot (s_1;s_2;\ldots )$, where the head f is either a constant symbol, a bound variable or a complex term, and the spine $(s_1;s_2;\ldots )$ is a linear list of arguments that are, again, spine terms. Note that if a term is $\beta$-normal, f cannot be a complex term. This observation leads to an internal distinction between $\beta$-normal and (possibly) non-$\beta$-normal spine terms. The first kind has an optimized representation, where the head is only associated with an integer representing a constant symbol or variable.

Additionally, the term representation incorporates explicit substitutions [1]. In a setting of explicit substitutions, substitutions are part of the term language and can thus be postponed and composed before being applied to the term. This technique admits more efficient $\beta$-normalization and substitution operations as terms are traversed only once, regardless of the number of substitutions applied.

Furthermore, Leo-III implements a locally nameless representation using de Bruijn indices [49]. In the setting of polymorphism [94], types may also contain variables. Consequently, the nameless representation of variables is extended to type variables [68]. The definition of de Bruijn indices for type variables is analogous to the one for term variables. In fact, since only rank-1 polymorphism is used, type indices are much easier to manage than term indices. This is due to the fact that there are no type quantifications except for those on top level. One of the most important advantages of nameless representations over representations with explicit variable names is that $\alpha$-equivalence is reduced to syntactical equality, i.e., two terms are $\alpha$-equivalent if and only if their nameless representations are equal.

Terms are perfectly shared within Leo-III, meaning that each term is only constructed once and then reused between different occurrences. This reduces memory consumption in large knowledge bases and it allows constant time term comparison for syntactic equality using the term’s pointer to its unique physical representation. For fast basic term retrieval operations (such as access of a head symbol and subterm occurrences) terms are kept in $\beta$-normal $\eta$-long form.

A collection of basic data structures and algorithms for the implementation of higher-order reasoning systems has been isolated from the implementation of Leo-III into a dedicated framework called LeoPARD [104], which is freely available at GitHub.⁸ This framework provides many stand-alone components, including a term data structure for polymorphic $\uplambda$-terms, unification and subsumption procedures, parsers for all TPTP languages, and further utility procedures and pretty printers for TSTP compatible proof representations.

5 Reasoning in Non-classical Logics

Computer-assisted reasoning in non-classical logics (NCL) is of increasing relevance for applications in artificial intelligence, computer science, mathematics and philosophy. However, with a few exceptions, most of the available reasoning systems focus on classical logics only, including common contemporary first-order and higher-order theorem proving systems. In particular for quantified NCLs there are only very few systems available to date.

As an alternative to the development of specialized theorem proving systems, usually one for each targeted NCL, a shallow semantical embedding (SSE) approach allows for a simple adaptation of existing higher-order reasoning systems to a broad variety of expressive logics [21]. In the SSE approach, the non-classical target logic is shallowly embedded in HOL by providing a direct encoding of its semantics, typically a set theoretic or relational semantics, within the term language of HOL. As a consequence, showing validity in the target logic is reduced to higher-order reasoning and HOL ATP systems can be applied for this task. Note that this technique, in principle, also allows off-the-shelf automation even for quantified NCLs as quantification and binding mechanisms of the HOL meta-logic can be utilized. This is an interesting option in many application areas, e.g., in ethical and legal reasoning, as the respective communities do not yet agree on which logical system should actually be preferred. The resource-intensive implementation of dedicated new provers for each potential system is not an adequate option for rapid prototyping of prospective candidate logics and can be avoided using SSEs.

Leo-III is addressing this gap. In addition to its HOL reasoning capabilities, it is the first system that natively supports reasoning in a wide range of normal higher-order modal logics (HOMLs) [59]. To achieve this, Leo-III internally implements the SSE approach for quantified modal logics based on their Kripke-style semantics [28, 40].

Quantified modal logics are associated with many different notions of semantics [40]. Differences may, e.g., occur in the interaction between quantifiers and the modal operators, as expressed by the Barcan formulas [12], or regarding the interpretation of constant symbols as rigid or non-rigid. Hence, there are various subtle but meaningful variations in multiple individual facets of which many combinations yield a distinct modal logic. Since many of those variations have their particular applications, there is no reasonably small subset of generally preferred modal logics to which a theorem proving system should be restricted. This, of course, poses a major practical challenge. Leo-III, therefore, supports all quantified Kripke-complete normal modal logics [59]. In contrast, other ATP systems for (first-order) quantified modal logics such as MleanCoP [80] and MSPASS [66] only support a comparably small subset of all possible semantic variants.

Fig. 7

A corollary of Becker’s postulate formulated in modal THF, representing the formula $\forall P_{o\iota }.\,\forall F_{\iota \iota }.\,\forall X_\iota .\, \exists G_{\iota \iota }.\, (\Diamond \Box P(F(X)) \Rightarrow \Box P(G(X)))$. The first statement specifies the modal logic to be logic S5 with constant domain quantification, rigid constant symbols and a global consequence relation

Unlike in classical logic, a problem statement comprised only of axioms and a conjecture to prove does not yet fully specify a reasoning task in quantified modal logic. It is necessary to also explicitly state the intended semantical details in which the problem is to be attacked. This is realized by including a meta-logical specification entry in the header of the modal logic problem file in form of a TPTP THF formula of role logic. This formula then specifies respective details for each relevant semantic dimension, cf. [58] for more details on the specification syntax. An example is displayed in Fig. 7. The identifiers $constants, $quantification and $consequence in the given case specify that constant symbols are rigid, that the quantification semantics is constant domain, and that the consequence relation is global, respectively, and $modalities specify the properties of the modal connectives by means of fixed modal logic system names, such as S5 in the given case, or, alternatively, by listing individual names of modal axiom schemes. This logic specification approach was developed in earlier work [105] and subsequently improved and enhanced to a work-in-progress TPTP language extension proposal.⁹

When being invoked on a modal logic problem file as displayed in Fig. 7, Leo-III parses and analyses, the logic specification part, automatically selects and unfolds the corresponding definitions of the SSE approach, adds appropriate axioms and then starts reasoning in (meta-logic) HOL. This process is visualized in Fig. 8. Subsequently, Leo-III returns SZS compliant result information and, if successful, also a proof object in TSTP format. Leo-III’s proof output for the example from Fig. 7 is displayed in Appendix 1; it shows the relevant SSE definitions that have been automatically generated by Leo-III according to the given logic specification, and this file can be verified by GDV [99]. Previous experiments [30, 59] have shown that the SSE approach offers an effective automation of embedded non-classical logics for the case of quantified modal logics.

As of version 1.2, Leo-III supports, but is not limited to, first-order and higher-order extensions of the well-known modal logic cube [40]. When taking the different parameter combinations into account this amounts to more than 120 supported HOMLs. The exact number of supported logics is in fact much higher, since Leo-III also supports multi-modal logics with independent modal system specification for each modality. Also, user-defined combinations of rigid and non-rigid constants and different quantification semantics per type domain are possible. In addition to modal logic reasoning, Leo-III also integrates SSEs of deontic logics [24].

Fig. 8

Schematic structure of the embedding preprocessing procedure in Leo-III

6 Evaluation

In order to quantify the performance of Leo-III, an evaluation based on various benchmarks was conducted, cf. [91]. Three benchmark data sets were used:

• TPTP TH0 (2463 problems) is the set of all monomorphic HOL (TH0) problems from the TPTP library v7.0.0 [99] that are annotated as theorems. The TPTP library is a de facto standard for the evaluation of ATP systems.

• TPTP TH1 (442 problems) is the subset of all 666 polymorphic HOL (TH1) problems from TPTP v7.0.0 that are annotated as theorems and do not contain arithmetic. The problems mainly consist of HOL Light core exports and Sledgehammer translations of various Isabelle/HOL theories.

• QMLTP (580 problems) is the subset of all mono-modal benchmarks from the QMLTP library 1.1 [82]. The QMLTP library only contains propositional and first-order modal logic problems. Since each problem may have a different validity status for each semantic notion of modal logic, all problems are selected. The total number of tested benchmarks in this category thus is 580 (raw problems) $\times$ 5 (modal systems) $\times$ 3 (quantification semantics). QMLTP assumes rigid constant symbols and a local consequence relation; this is adopted here.

The evaluation measurements were taken on the StarExec cluster in which each compute node is a 64 bit Red Hat Linux (kernel 3.10.0) machine with 2.40 GHz quad-core processors and a main memory of 128 GB. For each problem, every prover was given a CPU time limit of 240 s. The following theorem provers were employed in one or more of the benchmark sets (indicated in parentheses): Leo-III 1.2 (TH0, TH1, QMLTP) used with E, CVC4 and iProver as external first-order ATP systems, Isabelle/HOL 2016 [79] (TH0, TH1), Satallax 3.0 [47] (TH0), Satallax 3.2 (TH0), LEO-II 1.7.0 (TH0), Zipperposition 1.1 (TH0) and MleanCoP 1.3 [80] (QMLTP).

The experimental results are discussed next; additional details on Leo-III’s performance are presented in Steen’s thesis [89].

6.1 TPTP TH0

Table 1a displays each system’s performance on the TPTP TH0 data set. For each system, the absolute number (Abs.) and relative share (Rel.) of solutions are displayed. Solution here means that a system is able to establish the SZS status Theorem and also emits a proof certificate that substantiates this claim. All results of the system, whether successful or not, are counted and categorized as THM (Theorem), CAX (ContradictoryAxioms), GUP (GaveUp) and TMO (TimeOut) for the respective SZS status of the returned result.¹⁰ Additionally, the average and sum of all CPU times and wall clock (WC) times over all solved problems are presented.

Leo-III successfully solves 2053 of 2463 problems (roughly 83.39 %) from the TPTP TH0 data set. This is 735 (35.8 %) more than Zipperposition, 264 (12.86 %) more than LEO-II and 81 (3.95 %) more than Satallax 3.0. The only ATP system that solves more problems is the most recent version of Satallax (3.2) that successfully solves 2140 problems, which is approximately 4.24 % more than Leo-III. Isabelle currently does not emit proof certificates (hence zero solutions). Even if results without explicit proofs are counted, Leo-III would still have a slightly higher number of problems solved than Satallax 3.0 and Isabelle/HOL with 25 (1.22 %) and 31 (1.51 %) additional solutions, respectively.

Leo-III, Satallax (3.2), Zipperposition and LEO-II produce 18, 17, 15 and 3 unique solutions, respectively. Evidently, Leo-III currently produces more unique solutions than any other ATP system in this setting.

Leo-III solves twelve problems that are currently not solved by any other system indexed by TPTP.¹¹

Table 1 Detailed result of the benchmark measurements

Satallax, LEO-II and Zipperposition show only small differences between their individual CPU and WC time on average and sum. A more precise measure for a system’s utilization of multiple cores is the so-called core usage. It is given by the average of the ratios of used CPU time to used wall clock time over all solved problems. The core usage of Leo-III for the TPTP TH0 data set is 2.52. This means that, on average, two to three CPU cores are used during proof search by Leo-III. Satallax (3.2), LEO-II and Zipperposition show a quite opposite behavior with core usages of 0.64, 0.56 and 0.47, respectively.

6.2 TPTP TH1

Currently, there exist only a few ATP systems that are capable of reasoning within polymorphic HOL as specified by TPTP TH1. The only exceptions are HOL(y)Hammer and Isabelle/HOL that schedule proof tactics within HOL Light and Isabelle/HOL, respectively. Unfortunately, only Isabelle/HOL was available for experimentation in a reasonably recent and stable version.

Table 1b displays the measurement results for the TPTP TH1 data set. When disregarding proof certificates, Isabelle/HOL finds 237 theorems (53.62 %) which is roughly 28.1 % more than the number of solutions founds by Leo-III. Leo-III and Isabelle/HOL produce 35 and 69 unique solutions, respectively.

Fig. 9

Comparison of Leo-III and MleanCoP on the QMLTP data set (580 problems)

6.3 QMLTP

For each semantical setting supported by MleanCoP, which is the strongest first-order modal logic prover available to date [27], the number of theorems found by both Leo-III and MleanCoP in the QMLTP data set is presented in Fig. 9.

Leo-III is fairly competitive with MleanCoP (weaker by maximal 14.05 %, minimal 2.95 % and 8.90 % on average) for all D and T variants. For all S4 variants, the gap between both systems increases (weaker by maximal 20.00 %, minimal 13.66 % and 16.18 % on average). For S5 variants, Leo-III is very effective (stronger by 1.36 % on average), and it is ahead of MleanCoP for S5/const and S5/cumul (which coincide). This is due to the encoding of the S5 accessibility relation in Leo-III 1.2 as the universal relation between possible worlds as opposed to its prior encoding as an equivalence relation [59]. Note that this technically changes the possible models, but it does not change the set of valid theorems. Leo-III contributes 199 solutions to previously unsolved problems.

6.4 On Polymorphism

The GRUNGE evaluation by Brown et al. [48] aims at comparing ATP systems across different supported logics. For this purpose, theorems from the HOL4 standard library [87] are translated into multiple different logical formalisms, including untyped first-order logic, typed first-order logic (with and without polymorphic types) and higher-order logic (with and without polymorphic types) using the different TPTP language dialects as discussed in §4.4. Of the many first-order and higher-order ATP systems that are evaluated on these data sets, Leo-III is one of the few to support polymorphic types.¹² This seems to be a major strength in the context of GRUNGE: Leo-III is identified as the most effective ATP system overall in terms of solved problems in any formalism, with approx. 19% more solutions than the next best system, and as the best ATP system in all higher-order formalisms, with up to 94% more solutions than the next best higher-order system. Remarkably, it can be seen that over 90% of all solved problems in the GRUNGE evaluation are contributed by Leo-III on the basis of the polymorphic higher-order data set, and the next best result in any other formalism is down by approx. 25%.

This suggests that reasoning in polymorphic formalisms is of particular benefit for applications in mathematics and, possibly, further domains. For systems without native support for (polymorphic) types, types are usually encoded as terms, or they are removed by monomorphization. This increases the complexity of the problem representation and decreases reasoning effectivity. Leo-III, on the other hand, handles polymorphic types natively and requires no such indirection.

7 Conclusion and Future Work

Leo-III is an ATP system for classical HOL with Henkin semantics, and it natively supports also various propositional and quantified non-classical logics. This includes typed and untyped first-order logic, polymorphic HOL and a wide range of HOMLs, which makes Leo-III, up to our knowledge, the most widely applicable theorem proving system available to date. Recent evaluations show that Leo-III is very effective (in terms of problems solved) and that in particular its extension to polymorphic HOL is practically relevant.

Future work includes extensions and specializations of Leo-III for selected deontic logics and logic combinations, with the ultimate goal to support the effective automation of normative reasoning. Additionally, stemming from the success of polymorphic reasoning in Leo-III, a polymorphic adaption of the shallow semantical embedding approach for modal logics is planned, potentially improving modal logic reasoning performance.

Leo-III Proof of Fig. 7