By their size and shape, stone tools reveal many aspects of prehistoric cultures. But size and shape of curated stone tools are not fixed properties. Instead, curated tools can be resharpened and repaired in patterns and degrees that create variation in their size and shape from first to last use. Accordingly, reduction is “an integral part of the tool itself, just like ageing is an integral part of living things” (Iovita 2010:236), and types should be characterized by the full size-form trajectories that their specimens occupy, not just their original states.

If tools experience equal proportional reduction of all segments, then the trajectory of their variation in use engages change in size but not in shape. This is isometry. If, however, different segments of tools experience different degrees of reduction for resharpening and repair, the resulting variation in their size, which can only diminish, is accompanied by variation in shape. If, for instance, segments like the tips and blades of bifaces and the bits of unifaces undergo more frequent and extensive reduction than do segments like stems, they diminish while others are little changed or unchanged. This is change in shape with change in size, i.e., allometry.

Allometry explains major patterns of biological shape variation (Klingenberg 2007:25–27). Ontogenetic allometry occurs with changing body proportions during growth; it scales with individual growth. Static allometry describes shape variation as a function of ordinary or natural differences in size of adults within age cohorts. Phylogenetic allometry is shape variation distributed along branches of a phylogeny, scaling over evolutionary time. Allometric variation in stone tools from resharpening and repair is analogous to ontogenetic allometry, yet acts in the opposite direction. That is, stone tools change in shape by reduction, not growth. This study examines allometric variation in tipped bifaces, i.e., “points.”

Reduction acts in one direction only, but allometry varies in pattern and direction. Segments of tools becoming proportionally larger as tool size declines register negative allometry, segments becoming smaller as size declines positive allometry. Because, trivially, biological growth and lithic reduction have opposite effects upon size, positive allometry in segments of stone tools means that they are larger when the tools are larger, i.e., before or early in the reduction process. Negative allometry means that they are proportionally larger when the tools are smaller.

Important of Allometry in Lithic Analysis

Some curated tools experienced damage or edge-dulling in use, then resharpening in repair. Because tool segments exposed to the greatest risk of damage (e.g., point blades and tips) probably required more resharpening or repair, than segments like stems, blades might exhibit positive allometry, at least some segments or dimensions of stems negative allometry. Dimensions of tools like maximum thickness may change little if at all during use and reduction. If so, these dimensions also should exhibit negative allometry. The reduction thesis encompasses the probability that both allometry’s cause—tool rejuvenation by resharpening—and its effects upon their size and shape characterized the life history of tools (Shott 2005). Not all stone tools were resharpened; reduction allometry probably was common, not universal.

The reduction thesis has important implications. These include typology, because specimens of a single type can vary in size and form in use in ways that may encourage the false recognition of more than one type among their variation (Prentiss et al. 2017; see Stafford and Cantin 2009:157 for resharpening that produces convergence in shape of two different early Holocene point types). Reduction also can make specimens of different types look similar (Charlin and Cardillo 2018:123). Understanding allometry’s effects upon hafted bifaces requires distinguishing segments like blade and stem; stems may change in use less than do blades. Clearly, valid typological judgments of stone tools must consider reduction effects.

The reduction thesis also has implications beyond typology. Degree of reduction is a measure of curation, a theoretical quantity of considerable importance in lithic analysis (Binford 1973; Shott 1996). Degree and pattern of reduction thus comprise characteristics of type specimens as integral as their metric dimensions (Iovita 2010:236). For instance, reduction distributions can distinguish between competing “scenarios” of Folsom hunting practices by linking the duration of biface use to different assumptions about group size and hunting rates (Hunzicker 2005:55–60). Similarly, reduction distributions are important to models of prehistoric land use and behavior. They form utility curves that can be used to test theoretical models of tool use and wider adaptive practices. Miller (2018:55-63; see also Kuhn and Miller 2015), for instance, used the marginal-value theorem to model bifaces as resource patches, relating their degree of utility extracted, and therefore reduction, to varying hunting return rates. This treatment makes reduction a behavioral variable that can be explained by, and which thereby tracks, long-term adaptive processes. In the process, it makes the form of point types’ reduction distributions (Miller 2018:Fig. 3.1)(Fig. 1) relevant to sophisticated behavioral modeling.

Fig. 1
figure 1

The marginal-value theorem applied to point production, reduction, and discard. E is the return rate in foraging models, here the expected-yield critical value where cost of continued use exceeds replacement cost. Three utility curves for time/number-of-uses, which produce three solutions t1–3 for time-in-use, approximate Weibull distributions (Shott and Seeman 2017) whose parameter β > 1, = 1, and < 1, respectively, from top to bottom. Source: Miller (2018):Fig. 3.1)

Full size image

The possibility of phylogenetic allometry among types linked by cultural transmission over long periods is yet another reason to study reduction variation in stone tools. In the past 20 years, evolutionary-development (“evo-devo”) biology has explained some evolutionary trajectories as the product of changes in timing and duration of growth processes between individuals of ancestral and descendant species. Obviously, stone-tool variation owes to nonbiological processes, but new types may emerge over time from allometric alteration of functional segments like stems. Investigating this possibility requires large datasets, the distinction between segments like blade and stem, and analytical methods that accommodate the continuous variation that inheres in stone tools (e.g., Charlin and Cardillo 2018).

Finally, the reduction thesis and the allometric patterns that contribute to it are relevant to assemblage formation. Plotting the distribution of reduction measures can be informative of accumulation rates and assemblage composition (Surovell 2009). In turn, reduction patterns calibrate discard rates (the inverse of use life) of different tool types to common scales, and implicate different causes of discard (e.g., Shott 2016). Distributions that reveal constant discard rate regardless of degree of curation suggest chance as the cause of discard; those that reveal discard rate increasing with curation implicate attrition.

Reduction measurement is method, but an important one for archaeological theory. On balance, “reduction is an important source of variation on size and shape differentiation between point assemblages” (Charlin and González-José 2018:169). Because reduction can be allometric, moreover, “major distinctions between groups of points, when measured using blade characteristics, are likely the result of differential resharpening activities” (Prentiss et al. 2017:127). Such differential patterns risk conflating allometry with original design, so analysts must avoid combining characters from areas of points that might comprise distinct segments. Prentiss et al. (2017:124 and Figs. 10-12), for instance, produced different phylogenetic results on stems and blades of points that, as they showed, might not have been discerned in analysis that combined those segments. Accordingly, reduction analysis must consider and test for the effects of modularity and allometry on the size and shape of hafted points, and exercise care in the selection of characters used in both.

A recent challenge to the reduction-allometry thesis argues not directly against it, but indirectly questions the prevalence of at least short-term curation. It opposes the “fallacy” (Dibble et al. 2017) that identifies assemblages with single occupations and all dimensions of assemblage variation with short-term behaviors involving the complex engagement of tool use and mobility. Many assemblages are indeed accumulations; methods have been developed to both reveal and exploit this quality (e.g., Lin 2017; Shott 2010; Surovell 2009). The view argues that pattern and degree of reduction of flake tools is the cumulative product of repeated occupations of stable surfaces over long periods and the opportunistic reuse there of previously discarded flakes. Its relevance to biface technology is unclear because hafted tools are subject to different use-and-abandonment criteria than are flakes (Lin 2017:1793). Also, where surfaces either are aggraded or unstable over long periods or where human occupation is comparatively recent, the probability of recurring use of previously abandoned tools over near-geological time scales is diminished. Still, this view complements more than opposes the reduction-curation thesis (see especially Surovell’s 2009 synthesis of the approaches), by identifying limiting conditions and proposing alternative scenarios.

Allometry in Hafted Bifaces

Allometry is a product of resharpening, so resharpening practices are relevant to its study. Consider, for instance, Hoffman’s (1985:Fig. 18.6; see also Miller 2018:Fig. 4.4) model of resharpening exclusively on blade and not at all on stem segment, a strictly in-haft model (Fig. 2a). As a point is used, damaged and maintained by reduction it decreases in overall size (using gross-size measures like area or mass) while the stem segment remains unchanged. In this model, the stem segment becomes proportionally larger as the point decreases in size, not by growing but by remaining constant while the blade and overall specimen size decline. Accordingly, the stem is negatively allometric, its proportion declining as point size increases. Conversely, the blade is positively allometric, being proportionally larger when the point is larger.

Fig. 2
figure 2

Point-resharpening models. a Hoffman’s in-haft model, where only blade segment (open) is reduced while stem segment (shaded) remains unchanged such that the blade is positively, the stem negatively, allometric (note: differences in stem-blade proportions deliberately exaggerated). b Ahler and Geib’s model where both blade and stem are reduced but in different proportions; the blade is negatively, the stem positively, allometric

Full size image

In Ahler and Geib’s (Ahler and Geib 2000:Fig. 7) alternative model, both blade and stem are reduced in use, the latter disproportionally. As blades are damaged or dulled, their resharpening requires removing points from the haft and incorporating portions of what originally was stem into the blade. Stems become proportionally smaller as points decline in size, blades proportionally larger (Fig. 2b). Now the stem is positively allometric—proportionally larger when the point is larger—the blade, conversely, negatively allometric.

These and other resharpening models are best viewed as hypotheses for testing. Ahler and Geib’s model was devised specifically for fluted Folsom points and assumes a particular hafting arrangement, but might apply to other lanceolate types as well. Hoffman’s model is generic.

Measuring Allometry

Allometric variation can be gauged using a common biological approach. The “Huxley-Jolicoeur” model (Klingenberg 2007:24, 2016:115; see also Buchanan 2006:190) tracks bivariate allometry between independent variable x, often a gross-size measure, and dependent y that measures a dimension or aspect usually of a segment. In ontogenetic allometry, for instance, x often is approximated by the individual’s stature or weight, while y measures size or dimensions of segments such as the head or limbs. Analysis then determines the degree to which and rate at which y may vary as a function of x. In original form, the model is:

$$ y=\mathrm{b}{x}^{\mathrm{k}} $$

where b and k are constants. Because scaling is essential to allometry, analysis must be conducted on log-transformed variables (Klingenberg 2007:30–31). Transformed (unless otherwise stated, natural logarithms “ln” are computed here), the model becomes:

$$ \ln -y=\ln -b+k\times \ln -x $$

where constant b is the intercept and constant k the slope coefficient of the regression estimate of the model. When k < 1, y is negatively allometric upon x (i.e., y declines proportionally as x increases). When k = 1 the two quantities maintain constant proportions, i.e., isometry. When k > 1 y is positively allometric upon x (i.e., y increases proportionally as x increases). All three judgments follow from the terms of the ln-ln regression model; because it is the model’s slope coefficient, when k < 1 y increases at a lower rate than x, when k = 1 y increases at unit rate with x, and when k > 1 y increases at a higher rate than x. Significant departure from k = 1 is estimated by calculating k’s 95% confidence interval (CI) as k ± 1.96 × s.e. where s.e. = the standard error of the estimate.

Because “dimensionality of morphometric variation is a prime concern of allometry” (Klingenberg 2007:28), any aspect or scale of dimensions is a legitimate subject of allometric analysis. These include simple ratios calculated between dimensions, which may vary at different rates with size (Klingenberg 2016:117). But stone-tool size and shape most often are characterized by using orthogonal dimensions like length, width, and thickness. Sometimes length is subdivided between blade and stem segments, sometimes width is measured at fixed intervals or in fixed number of locations between tip and stem, and sometimes thickness is measured separately on blade and stem or averaged among two or more separate locations.

These variables crudely reduce complex, whole-object form to a comparative handful of relevant dimensions just as stick-figures crudely caricature Leonardo’s Vitruvian Man (Shott and Trail 2010:Fig. 1). Yet they capture essential elements of size and shape that permit analysis.

Inter-landmark distances (ILDs) may be better ways to characterize size and shape of two-dimensional (2D) plan forms. Buchanan (2006) was the first to apply them to 2D outlines of stone tools. ILDs share the limitations of orthogonal dimension in reducing complex, irregular wholes to stick-figure approximations, but provide a somewhat fuller characterization of 2D size and shape. To some degree, they accommodate the complex irregularity of hand-made objects by calculating means between comparable distances computed between the plan’s two longitudinal halves. Accordingly, ILDs may be a modest improvement upon orthogonal dimensions.

Buchanan’s Study

Applying the Huxley-Jolicoeur model to ILDs, Buchanan (2006) documented clear allometric patterning in archaeological Folsom points from the North American Plains. He used point surface or plan area as gross-size measure. In bivariate analysis, most length measures were positively allometric, most width and/or stem measures negatively allometric. Only a blade-length variable was isometric, suggesting maintenance of a minimum or optimum blade length or size. Results of multivariate analysis were similar, blade length remaining isometric and all stem variables negatively allometric.

Buchanan inferred a pattern of in-haft resharpening: “blade lengths are isometric with point area, a…plausible model may be that as the length of points was reduced through resharpening, the expendable blade portion of the point was reduced accordingly” (2006:194). In this scenario, the stem is negatively allometric as found in his study (2006:Table 6) if modestly. Accordingly, the result resembles Hoffman’s more than Ahler and Geib’s model. Yet the test assumed complete independence of blade length from both total length and point area, not necessarily consistent with Ahler and Geib’s (2000:Fig. 7) model that showed non-monotonic, therefore allometric, covariation of blade and total lengths. Ahler and Geib (2000:809) proposed a test of their model that involved increasing tip angle with reduction, which geometric morphometric analysis of the current dataset supported (Shott and Otárola-Castillo 2018). Also, Buchanan measured blade length from tip to a geometric position—point of maximum edge inflection—that did not necessarily mark points’ stem-blade juncture.

Buchanan’s was a pioneering morphometric study. Its demonstration of allometric variation is worth emulation in a similar dataset characterized by similar variables, with independent experimental control over rates and patterns of resharpening allometry. Using different variables and methods, later studies documented similar allometric variation in a range of point types and contexts (e.g., Charlin and Cardillo 2018; Charlin and González-José 2018; Iovita 2011; Presnyakova et al. 2018; Suárez and Cardillo 2019).

Materials and Methods

This study involves Folsom-point replicas. Briefly, Hunzicker (2005), 2008) fired spears tipped with the points into animal carcasses to study their durability and performance. Most relevant here, points were removed from hafts after each cycle of use and damage. Repair was accomplished by resharpening in “a complex process involving simultaneous efforts to restore symmetry, reduce tip thickness, [and] improve alignment” (Hunzicker 2005:28). Most resharpening occurred on exposed blades and tips, yet stems wrapped in sinew and covered with mastic sometimes suffered damage. Whatever a point’s condition, it was removed from its haft for repair but also as an integral step of experimental design, in order to make casts of each point at each cycle; this is not in-haft resharpening. Even if stems were undamaged, blade rejuvenation could impinge upon and reduce stems. Significantly, then, stems also underwent resharpening to “restore each point to a functional state with minimal loss of length” (Hunzicker 2005:28). Accordingly, Hunzicker’s procedure was intermediate between Hoffman’s and Ahler and Geib’s models, although like the latter it could involve joint reduction of both blade and stem. Most point replicas survived the first cycle of damage and repair, and 22 of 25 experienced two or more cycles (numbered 1, 3, 5, 7 and 9 from first to last as explained in Shott and Otárola-Castillo 2018). Overall, points survived an average of about 3.3 cycles, yielding a total of 82 (25 × 3.3) versions of 25 originals.

In the same dataset analyzed here, Shott et al. (2007) studied allometry in simple ratios of size variables upon thickness, as per Klingenberg (2016:117), Shott and Otárola-Castillo (2018) in geometric morphometric analysis of three-dimensional (3D) models. This study involves the intervening case, mostly two-dimensional (2D) measures of size and shape in both bivariate and multivariate allometric analysis. It is designed with two complementary purposes in mind. First, it completes fairly comprehensive analysis of a single experimental dataset (i.e., ratios, and 2D and 3D bivariate and multivariate allometry) whose causes of allometric variation are known, and which therefore independently controls for the allometric effects examined here. Combined, these studies document allometric variation in a single dataset using various measures and methods. Second, it approximates methods used in both traditional studies and Buchanan’s (2006) pioneering study, serving partly to independently corroborate the latter.

Analysis involves 2D images of the 82 versions of the 25 Folsom replicas. For comparability to variables often used in lithic analysis, a set of common orthogonal dimensions was measured on each 2D image (Table 1). These include maximum length (ML) from tip to base on the longitudinal axis, blade length (bldlen) from tip to stem-blade juncture, stem length (stlen) from that juncture to base (bldlen + stlem = ML), stem width (BW for comparison to Buchanan’s similar variable) from edge-to-edge perpendicular to ML at the stem-blade juncture, and base length (LB). Following Buchanan, a set of ILDs then was computed (Table 1, Fig. 3). Plan area (PA, mm2, measured automatically in ScanStudio™) and maximum thickness (“thickness”) also were recorded. All linear dimensions were recorded in cm using RapidForm’s measurement tool. Supplementary Material 1 provides the data.

Table 1 A set of common orthogonal dimensions
Full size table
Fig. 3
figure 3

Inter-landmark distances: TB, mean of tip to stem corners; BL, mean of tip to stem-blade juncture, itself marked by distal extent of edge grinding; LT, mean of diagonal stem-blade juncture to base corners; BW, width at stem-blade juncture; LB, width at base. Horizontal lines extending outward from margins indicate distal extent of edge grinding which, as shown here, may not be longitudinally symmetrical. Proximal-most of these two points is taken as stem-blade juncture

Full size image

Some ILDs are identical or nearly so to Buchanan’s (2006) variables. Because ScanStudio calculates area over both faces, resulting figures were halved. Plan area calculated from 2D and 3D versions of specimens may differ slightly, variation ignored as trivial. Because ILDs were measured manually, slight errors sometimes occurred. For instance, specimen B2 was used and resharpened five times, during which of course its length diminished. Base-width LB should have declined little or remained constant but its measured value declined and then increased slightly, the latter physically impossible. Overall, LB variation spanned only 0.04 cm so this measurement error is ignored as trivial.

Obviously, the number of ILDs here is fewer than in Buchanan’s study (yet note that his analyzed distances were fewer than the distances shown on his Fig. 2, because some of them were averaged with their counterpart on the other longitudinal half of each specimen). This study omits Buchanan’s total length OL on the longitudinal axis (as largely redundant with TB), and his perimeter length EL and base boundary or perimeter length BB (as largely correlated with PA). Note also that BL here is not necessarily the same as Buchanan’s BL, which terminated at “the calculated maximum edge inflection position” (Buchanan 2006:Table 3), i.e., the greatest distance perpendicular to the long axis from the lines TB to each edge. As in Buchanan’s study (2006:Fig. 2), BL’s terminal points on the two edges may not be symmetrical; here, however, BL is treated as a measure of oblique blade length—that part of the specimen that extends beyond hafting—not merely as a particular geometric position on the point outline that corresponds to the greatest distance between the line that links tip and base corner. BW as used here is not width measured “at 1/3 total length above base landmarks” (Buchanan 2006:189) but width (measured perpendicular to ML) at the most proximal of the two not necessarily symmetrical edge points where stem grinding terminates (indicated by hash marks on right and left margins in Fig. 3). This point is treated as minimum stem length. Finally, here LT is measured from base corner to opposing edge’s stem-blade juncture wherever located, not automatically to “1/3 total length” (Buchanan 2006:Table 3). Accordingly, some ILDs here are not identical to Buchanan’s. In all cases, these dimensions measure approximately the same quantity or segment of each point’s 2D outline.

Analysis

Among other ways, allometry can be studied in regression of individual dimensions upon measures of gross size, or in simultaneous analysis of two or more dimensions as they vary with multivariate gross-size measures. These are bivariate or multivariate allometric analyses, respectively. Their “strong concordance” (Shea 1985:367) justifies a joint approach here, as in Buchanan (2006), where bivariate methods documented pairwise interactions and multivariate methods revealed broader patterns of variation “not necessarily discernible in the original data” and pairwise analysis alone (Shea 1985:369).

Bivariate Allometry

Analysis begins by consider pairwise comparisons of other variables to overall size measures. First, ln-transformed traditional orthogonal dimensions and thickness were regressed upon lnML as a model for the many datasets coded only for such dimensions. Second, following Buchanan (2006:193), ln-transformed ILDs and lnthickness were regressed upon ln√PA as gross-size measure. Some results of regression of these variables upon other gross-size measures also are reported.

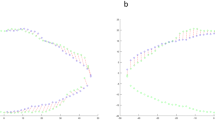
Regressing lnBL, lnLT, and lnLB separately upon ln√PA illustrates the bivariate method (Fig. 4). lnBL and lnLT correlated positively with ln√PA, hence are positively allometric. But lnBL’s regression slope is steeper (recall that this line’s slope estimates the allometric constant k), indicating higher positive allometry. Figure 4 also shows that, unlike in Buchanan’s data, lnLT consistently is greater than lnBL; here, stems usually are longer than blades. The difference may owe to Hunzicker’s experiment or to Buchanan’s definition of stems as extending a constant one-third of overall length rather than varying, as they might in empirical specimens and do in Hunzicker’s data. lnLB, however, does not correlate with ln√PA (r = .05; regression slope of lnLB upon ln√PA = − 0.03, s.e. = .064, i.e., the slope coefficient essentially = 0). Thus, some variables are allometric while others are not. This finding explains the value of ratios like length-thickness used in earlier analysis (Shott et al. 2007). It suggests the particular value of base width, perhaps even more than thickness, in future research (see Kaňáková et al. 2016:Fig. 15 for empirical documentation of variation in length variables with constancy in base width).

Fig. 4
figure 4

lnBL (solid circles), lnLT (shaded circles), and lnLB (open circles) against ln√PA. Lines are each y-variable’s least-squares regression line upon ln√PA

Full size image

Orthogonal Dimensions

In bivariate allometry using orthogonal dimensions, lnbldlen and lnstlen (ln-transformed blade and stem length, respectively) are isometric—they maintain essentially constant proportions as specimen size declines. Considering Hunzicker’s resharpening practice, results suggest that maintenance of optimal length involved roughly equal reduction of stem and blade. Yet Fig. 4 shows positive allometry in ILD equivalents of both variables, casting doubt on this interpretation. lnthickness and stem width measures lnBW and lnLB are negatively allometric, the latter highly so (Table 2). In fact, nominally lnLB has a negative slope coefficient, suggesting the rare condition of absolute, not just proportional, decline as overall size rises (Klingenberg 2007:24). But lnLB did not actually decline absolutely during each point’s use trajectory. Instead, the coefficient’s 95% CI intersects 0, so its value indicates lnLB’s near constancy regardless of overall size.

Table 2 Bivariate allometry results. Top: orthogonal dimensions regressed upon lnML. Bottom: inter-landmark distances regressed upon ln√PA. 95% CI calculated as B1 ×  ± 1.96 s.e. Values in italics significantly > 1 (positive allometry), values in bold significantly < 1 (negative allometry)
Full size table

ILDs

Results differ in bivariate allometry using ILDs regressed upon ln√PA (Table 2). Now, lnTB as a measure of overall length and lnBL as a measure of blade length are positively allometric whereas lnLT—like its orthogonal counterpart lnstlen—is isometric. Again, the latter is questionable considering the pattern exhibited between lnLT and ln√PA (Fig. 4). Again, lnBW, lnLB, and lnthickness are negatively allometric, lnLB again greatly so. These results are largely consistent with Buchanan (2006:Table 6), who reported positive allometry for lnML, lnTB, and other length and perimeter measures (but isometry for lnBL, as in analysis of orthogonal dimensions) and negative allometry for other variables. Divergence may owe to differences in resharpening between Hunzicker’s experiment and prehistoric Folsom users.

When bivariate allometry using ILDs was tested by regression upon other measures of gross size, results differed significantly. For instance, lnML used as gross-size measure yielded no regression slope or k estimates that were either positively allometric or isometric; instead, all variables returned estimates with 95% CI < 1, indicating negative allometry. Similar results were obtained in bivariate allometric tests involving regression of ILDs upon lnmass (g) and ln-centroid size (lnCS) of scanned 3D models of specimens (although in the latter case lnBL attained isometry and lnTB was modestly positively allometric). A reasonably comprehensive set of measures for segmented modules of integral wholes cannot all be negatively allometric with size variation in the whole, a physical and geometric impossibility. All can be isometric, if reduction or any other source of size variation is strictly proportional among segments, which did not occur in any permutation of analysis here. Instead, and as the reduction thesis suggests, some were positively, some negatively, allometric.

If stone-tool reduction operates as generally understood, it disproportionately diminishes some parts of the integral wholes that are points. Therefore, measures of some segments should be positively allometric, some perhaps isometric, some negatively allometric. That occurs in bivariate regression of ILDs upon ln√PA, but not upon other gross-size measures. Bivariate coefficients for each variable separately regressed upon each gross-size measure correlate significantly with one another despite difference in their magnitudes (in all pairwise tests, both r and r→1.0 and p < .01). Thus, bivariate coefficients covary strongly but do not scale similarly. Scale discrepancies between bivariate coefficients computed from variable regression upon different gross-size measures may owe to differences in the latter’s ranges.

ln√PA varies from 3.1 to 3.8, a range of 0.7. lnCS has a range of 1.0, lnML of 1.2, lnmass of 2.0. The progressive depression or reduction of B1/k estimates from ln√PA to lnmass is inversely proportional to gross-size measures’ ranges. For instance, bivariate coefficients computed from regression upon lnmass are 43–54% of coefficients computing using ln√PA. Analyzing allometry, “choice of size variable…will always affect results” (Buchanan 2006:190). In bivariate analysis here as before, plan area “was a good proxy for point size” (Buchanan 2006:193); other size measures may not be suitable. Whatever the case, magnitude of bivariate coefficients matters. When all are < 1 (as for lnmass and lnML and nearly so for lnCS), the Huxley-Jolicoeur decision rule yields the near-impossibility that all variables are negatively allometric. Only ln√PA among gross-size measures gives some bivariate coefficients < 1 and others > 1, i.e., that are consistent with the general understanding of stone-tool reduction.

Multivariate Allometry

Multivariate allometry proceeded in two steps. First, principal component analysis (PCA) was conducted in PAST v2.17 (Hammer et al. 2001) for all original variables. Again following Klingenberg (2007:30-31; see also Shea 1985:372), PCA used the variance-covariance matrix. Multivariate allometry treats the first principal component (PC1) as a general size dimension (Klingenberg 2007:28), particularly if its eigenvector explains 80%+ of total variance (Hammer 2019:236). Second, each variable’s multivariate allometric coefficient (MAC) was computed in PAST (v.2.17) (Hammer et al. 2001). MACs were estimated by dividing each original variable’s PC1 loading by the mean PC1 loading over all variables (Hammer and Harper 2006:93). Because PAST assumes that input variables are original, it automatically log-transforms them, evidently using the base-10 log. Accordingly, original untransformed variables were entered into analysis there (requiring exponentiation of lnCS). PAST bootstraps 95% confidence intervals for MACs. (Comparable PCA analysis in SPSS™ requires ln-transformation but, unlike PAST, does not compute 95% CI. SPSS and PAST results differed somewhat in values but never in significance.)

Multivariate analysis was conducted four times, each using thickness and the ILDs reported above. Each analysis, however, separately involved gross-size measures ln√PA, lnmass, lnCS, and lnML. (Results that exclude the gross-size measure upon which other variables are regressed to obtain bivariate coefficients are invalid [Shea 1985:383].) As in the bivariate case, MAC < 1 indicates negative allometry, MAC = 1 isometry, and MAC > 1 positive allometry. As in preceding analysis, bivariate coefficients computed by regressing lnthickness and ln-ILDs differed depending by gross-size measure. Unlike preceding results, however, MACs computed from different gross-size measures differed little in magnitude and never in significance (Table 3). That is, MACs for all gross-size measures (ln√PA, lnmass, lnCS, lnML) and lnTB, lnBL and lnLT were significantly greater than 1, all for lnBW, lnLB and lnthickness significantly less than 1. Indeed, the magnitudes of all MACs are so similar that ANOVA by size measure returned highly insignificant results (F = .001 p = 1.00; lowest pairwise LSD = 0.97). If ln√PA and other gross-size measures differ in bivariate analysis, they return essentially identical results in multivariate analysis. (Orthogonal dimensions regressed upon lnML returned very similar results and identical statistical decisions about each y-variable’s degree and direction of departure from 1.)

Table 3 Multivariate allometric coefficients (MACs) by variable from separate PCA analyses of ln-inter-landmark distances and lnthickness with gross-size measures ln√PA, lnmass, lnCS, and lnML. Values in italics significantly > 1 (positive allometry), values in bold significantly < 1 (negative allometry). All lnLB MACs 95% CI intersect 0—extreme negative allometry—possibly reflecting near constancy in its magnitude
Full size table

All bivariate coefficients correlated with all four of their corresponding MACs (r = .82 p < .01), and bivariate and multivariate results agreed that lnBL was positively allometric. But only bivariate coefficients upon ln√PA both patterned and scaled similarly to MACs calculated using all gross-size measures. That is, bivariate coefficients and MACs covaried strongly but only bivariate coefficients involving ln√PA and all MACs scaled similarly. Multivariate analysis gave consistent results whatever the gross-size measure but bivariate analysis gave inconsistent results, counseling the use there of ln√PA over other gross-size measures.

Besides direction of departure from critical values, magnitude of lnBL’s MAC indicated highly positive allometry; lnBL declined rapidly with point reduction. Consistently, lnLT was more modestly positive in allometry, a result also found in geometric morphometric analysis of 3D models of these data (Shott and Otárola-Castillo 2018) and that, unlike bivariate results, are consistent with Fig. 4’s patterning. They also are consistent with Hunzicker’s (2005:27-29) resharpening practices, which often reduced both blade and stem, the former disproportionally. Difference in magnitude of their MACs suggests, as did Hunzicker, that blades experienced more extensive reduction than did stems.

PCA involving ln√PA returned a single significant component, PC1, that accounted for 85.9% of total variation, and rescaled or normalized loadings that identified PC1 with overall size (Table 4). That is, area and all length measures (total, blade, and stem) loaded positively, while thickness and width at the stem-blade juncture loaded modestly negatively, and width at base practically not at all, with PC1. PCA involving other gross-size measures produced similar results. Buchanan (2006:Table 5) reported broadly similar results to Table 4’s for eigenvalues and variable loadings. In his (2006:Fig. 9) vector plot, point area PA and blade-length BL were virtually coincident with the PC1 axis, indicating not just their high loading with but also their strong contribution to PC1. Vectors for other perimeter and length variables, including TB, formed a highly covarying set that also loaded highly upon but were slightly oblique to the PC1 axis. Variables that measured stem size and shape had lower PC1 loadings and vectored more obliquely to PC1’s axis, particularly LB; stem length LT’s vector fell between other stem variables and blade and overall size ones.

Table 4 PCA summary using ln√PA as gross-size measure
Full size table

Despite the broadly similar PCA results to Buchanan’s study, here the vector plot documents some differences in data structure (Fig. 5). (PC2 does not meet conventional significance criteria, so was retained only to produce this plot.) First, Buchanan did not include lnthickness, which here loaded modestly upon and vectored, like ln√PA and lnTB, along PC1’s axis. Like them, thickness has to do with overall size. As in Buchanan’s study, ln√PA and lnBL loaded highly upon PC1; ln√PA’s vector lies almost upon the PC1 axis but lnBL’s diverged somewhat toward positive PC2 values. Oblique total length lnTB patterned near ln√PA in both loading and vector. As in Buchanan’s study, stem-blade juncture width lnBW loaded modestly on PC1 and PC2, and base-length lnLB loaded least upon and vectored farther from PC1’s axis. The greatest difference was in stem length lnLT. Here, its vector diverged sharply from other stem measures. Rather than lying between them and blade-length and overall-size variables, lnLT registered the lowest negative PC2 loading, somewhat isolating it from other variables. Overall, differences between Buchanan’s and this study occurred mostly in lnBL (isometric in Buchanan’s study, positively allometric here) and lnLT (negatively allometric in Buchanan, positively allometric here).

Fig. 5
figure 5

PCA vector plot, ln√PA as gross-size measure

Full size image

Analysis Summary

Buchanan (2006) used plan area as gross-size measure. Both here and in his study, that measured produced bivariate allometric coefficients that scaled as traditional biological analysis expects: positively allometric dimensions returned coefficients > 1, negatively allometric dimensions coefficients < 1. Here, other gross-size measures did not scale as did plan area nor yield bivariate coefficients that followed the scaling and interpretation of the Huxley-Jolicoeur model.

Here, bivariate analysis involving ln√PA and multivariate analysis of several variable sets agreed. Most length variables were positively allometric, width ones and thickness negatively allometric, base-width lnLB extremely so. lnLT provide isometric in bivariate analysis, modestly positively allometric in multivariate analysis. Figure 4 clearly shows its positive allometry, so supports multivariate over bivariate analysis.

Perhaps surprising is that length of both point segments—blade and stem—were positively allometric. That is, linear dimensions of the two segments that, combined, comprise each point’s entire 2D length both grew proportionally longer as points increased in area. The apparent paradox is explained by recalling the difference in direction between biological and lithic allometry. lnBL and lnLT do not grow; both decline as ln√PA declines (Fig. 4), but lnBL’s steeper decline matches its higher MAC. From Fig. 4 and multivariate analysis, both blade and stem decline with reduction, just at different rates. As in Buchanan’s study, analysis here documents allometric variation in reduced stone tools.

Reduction Distributions from Allometry

Allometric analysis may seem merely technical, documenting how and how much points are reduced. Whatever the value of such knowledge, allometric study extends beyond them. If, for instance, PC1 is a good multivariate size measure that incorporates allometric variation, then it can be used to test behavioral-ecology theories noted above, underscoring the higher analytical value of allometric reduction analysis. Ranks of reduction measures across specimens generate distributions of values that approximate Fig. 1’s utility curves. Models like the marginal-value theorem give different results depending not just on return-rate/abandonment-criterion E but also the form of the distributions that link E to time or number of uses. Allometric analysis specifies the forms of such distributions.

PC1 score from analysis that included ln√PA is a general reduction measure, ranging from approximately − 2.0 to 1.72. To generate distributions, specimen scores were rescaled by adding the absolute value of the lowest score to all cases (shifting the lower end of the range to 0) then dividing rescaled values by the absolute value of the range of PC1 scores (that value ≈ 3.72, the range extending from − 2.0 to 1.72) to produce a descending range from 1 to 0 that expressed both rank and relative magnitude of each specimen’s PC1 score. This is scaled multivariate PC1 (sclMVPC1). In previous analysis, simple ratios like length-thickness (L/T) also patterned with reduction (Shott et al. 2007). This ratio was rescaled similarly. This is scaled L/T (sclL/T). Other measures, including varieties of resharpening indices (e.g., Suárez and Cardillo 2019:Fig. 4), also can be used for these purposes, but consideration here is limited to the two described above.

sclMVPC1 largely sorts Folsom replicas and their resharpening stages by number of uses or reduction cycles (Fig. 6). ANOVA supports this conclusion; means decline consistently by pooled stage (F = 55.2 p < .01, all LSD < .01). Therefore, sclMVPC1 tracks size reduction and resharpening cycle and, by extension, utility extracted (Shott 1996). sclMVPC1 and sclL/T pattern somewhat differently against absolute rank (Fig. 7). sclMVPC1 patterns closely with Fig. 1’s linear model (equivalent to a Weibull model where β = 1 [Shott and Seeman 2017:732]) except at its tail, while sclL/T is modestly concave-upward and therefore trends toward Fig. 1’s lower function and a Weibull model where β < 1.

Fig. 6
figure 6

sclMVPC1 rank distribution sorted by pooled use/resharpening cycle. Solid circles = stage 1, shaded circles = stages 3 and 5, open circles = stages 7 and 9

Full size image
Fig. 7
figure 7

Rank distribution of sclMVPC1 and sclL/T. Dashed line corresponds to Fig. 1’s linear model and a Weibull model where β = 1 (Shott and Seeman 2017:732). Multifactorial rank distribution in dark grey

Full size image

Distributions derived from various reduction measures differ modestly, yet even such differences can affect solutions when inserted into models like Fig. 1’s. Multifactorial reconciliation that incorporates all measures (see Shott and Seeman 2017 for its derivation) seems the best overall measure. Accordingly, Fig. 7 also plots the distribution of a multifactorial reduction measure derived from PC1 and L/T. The multifactorial distribution lies nearest sclMVPC1’s, suggesting again that multivariate analysis produces the most robust results.

The sclMVPC1 and multifactorial distributions implicate constant attrition—chance—a Weibull model whose shape parameter β = 1, corresponding to Fig. 1’s straight-line function. In this dataset, the result is an artifact of experimental design; all iterations of size and shape from first use to last occur in the distribution in equal proportion. Because archaeological points may not be discarded equally at all reduction stages, empirical data may show different distributions of such reduction measures. When, for instance, curation rate is high (Weibull β > 1), reduction values will skew to lower sclMVPC1 range. The form of resulting cumulative distributions will be convex-upward, not linear, like Fig. 1’s top distribution. When curation rate is low (Weibull β < 1), resulting curves should be concave-upward in form and located below the straight line of constant failure.

If reduction is an integral property of curated tools then reduction distributions describe and graphically model it. If these distributions approximate the ideal utility curves of Fig. 1, they are valid measures by which to test behavioral-ecology or any theoretical models that predict pattern and degree of tool reduction. If they fit the Weibull or other failure models, theoretical explanations for the forms of utility curves also are implicated, involving processes that range from burn-in failure to chance to accelerating attrition (Shott and Seeman 2017:732).

Conclusion

Bivariate and multivariate allometric analysis in Folsom replicas substantially agree, but not in all important details. Complementary use of these methods was rare in the past (Shea 1985:368), in biology let alone archaeology. Benefits include thoroughness in analysis but especially the parsing of common and specific patterns of allometric variation that bivariate analysis documents and that multivariate analysis generalizes. Yet bivariate results are highly dependent upon the gross-size measure used, while multivariate results are robust.

Combined with earlier studies (Shott et al. 2007; Shott and Otárola-Castillo 2018), this one suggests that similar allometric signals exist in three methods applied to a single dataset. Width variables and thickness are negatively allometric, length variables positively allometric. Blades are more positively allometric than are stems. Results lend further confidence to allometric analysis of stone tools, if such is needed. In turn, allometric reduction analysis is vital to traditional archaeological concerns like typology and sophisticated behavioral models (e.g., Surovell 2009). Yet the inherent limitations of simple ratios between dimensions and the ambiguity that may inhere in bivariate allometric approaches that use different gross-size measures both suggest greater confidence in multivariate allometric results.

This and earlier studies of the present dataset involved, trivially, experimental replicas. Their advantage is foreknowledge of the sources of their variation, their disadvantage their possible departure from prehistoric norms and practices. Whatever the value of experimental data, of course the chief focus must be on archaeological data. As above, allometry and the broader reduction thesis bear upon typology, behavioral models linked to degree and pattern of reduction, to assemblage formation and, arguably, to emerging approaches in the study of point types as units of long-term change. This study has no typological implications because reduced Folsom points are unlikely to be mistaken for other types, yet might for types of very similar form and technology. Figure 7 and comparable reduction curves can test implications of behavioral-ecology models for changing return rates and land-use patterns (e.g., Miller 2018). Because greater reduction and stronger allometric pattern both relate to artifact use life, which in turn bears upon assemblage formation, degree and pattern of reduction allometry also influence assemblage size and composition in ways that can be traced and measured (e.g., Shott 2010). Where, for instance, Folsom points are more heavily resharpened, fewer will be discarded ceteris paribus. Results also bear upon assemblage quantification; typically, an unused Folsom point and a heavily reduced specimen are counted equally. Yet the former registers little to no associated tool-using behavior, the latter a great deal of such behavior. Finally, just as biological allometry contributes to organismic evolution, it may help reveal the processes of morphological transition that characterize point sequences across eastern North America. Allometric analysis at this higher level, both in time and analytical unit, requires common definitions of modules and characterization of size and shape across types, and must be linked to broader changes in the definition of theoretical units that are beyond this study’s narrow focus (e.g., Shott 2020).

Per sources cited above, many empirical datasets exhibit allometric patterns similar to those found here. As more are analyzed, one finding is especially salient: because allometry involves proportional change in size of distinct segments, analysis both requires careful variable selection and rewards approaches that parse whole objects into constituent parts. Allometry is a by-product of processes of maintenance and resharpening that play out among and between segments of tools. Any analysis of the phenomenon must define and distinguish those segments.