Introduction

The high oil yield potential of algal biofuels (Chisti 2007; Mata et al. 2010) supports their development into commercialization as a renewable, carbon-neutral energy source (Singh and Gu 2010). Recent, techno-economic analyses show that algal biofuel is currently too expensive (US$ 3.06 L−1 TAG) to replace transportation fuels, but improvements in algae productivity and lipid yield could greatly reduce the cost (Sun et al. 2011). For a competitive algal biofuel, algae cultivation must be optimized.

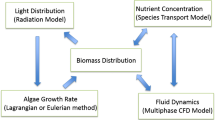
Many factors contribute to the productivity of algae cultivation. Algal photoautotrophic growth is dependent on light intensity, temperature, salinity, pH, and availability of nutrients (US-DOE 2009; James and Boriah 2010; James et al. 2013). At low irradiance levels, light is limiting and insufficient energy (for photosynthesis) hinders growth rates. Conversely, irradiance above the optimal level may lead to oxidative stress (Li et al. 2009). Further, essential nutrients (carbon dioxide (CO2), phosphate, sulfate, and nitrate) are critical to ensure that resources are available for growth and lipid production.

The temperature and pH ranges for optimal growth can be highly species/strain dependent and can vary from the low temperatures of the arctic to the high temperatures of the equatorial deserts (Lewis and Lewis 2005; Mayo 1997; Remias et al. 2005). When temperatures deviate from ideal, growth rates diminish (Eppley 1972). Salinity variations from optimal also decrease growth rates (Kirst 1989; Brock 1975; Auken and McNulty 1973; García et al. 2007; Fabregas et al. 1984; Batterton and Baalen 1971).

Large-scale bioreactor systems needed for commercial-scale biofuel production, open raceway ponds, and closed-photobioreactor systems often experience large spatiotemporal variations in environmental conditions over the course of a day, month, and year. Light conditions vary due to diurnal and annual cycles, fluctuations in cloud cover, the angle of the sun in the sky, and algae self-shading. The temperature of the bioreactor media depends on the reactor design, solar radiation, wind speed, air temperature, and evaporation. Nutrients vary due to varied consumption and delivery rates while pH depends on both extracellular (CO2 concentration) and intracellular (species-dependent H+) regulatory mechanisms (Katz et al. 1991). Salinity can vary due to evaporation and rainfall. These complex variations make it difficult to identify which parameters most affect the productivity of the culture.

A computational model that can predict the variations in the parameters affecting growth could aid in identifying which are most limiting for algae growth. Quinn et al. (2011) developed an algae growth and lipid production model of Nannochloropsis oculata for a specific design of an outdoor photobioreactor. Their model accounts for growth limitation due to light, temperature, and nitrogen. However, their model has only been validated for a single system and has not yet been applied to other bioreactor designs. Huesemann et al. (2013) developed a screening model specifically for raceway ponds. Their model accounts for light and temperature limitation but does not account for the variations in temperature within the pond nor does it predict the temperature based on meteorological data. James and Boriah (2010) developed a proof-of-concept model for algae growth in an open-channel raceway. Subsequently, James et al. (2013) verified the model against an analytical solution and then compared to experimental data. A simulation that is able to model multiple types of bioreactor systems and predict the cultivation pond conditions for locations around the globe is needed to properly optimize and design cultivation systems. Liffman et al. (2013) proposed new raceway pond geometries that reduced energy losses at the bends by 87 %.

In this work, we investigated the halophilic microalga, Nannochloropsis, that is a promising biofuel candidate (Pal et al. 2011; Boussiba et al. 1987). As with most algae strains, no complete parametric data have been published. Therefore, we must produce the data necessary to appropriately parameterize our model for the algae strain of interest. To accomplish this, we grew the algae strain at various environmental conditions in laboratory test tubes and measured growth during the exponential growth phase. With this method, we were able to vary multiple parameters (i.e., light and salinity) simultaneously to reduce the time to complete the parametric study. In addition, the small size ensured that environmental conditions were constant across the sample and reduced the amount of algae mass needed to be grown.

The numerical simulations in this work used a modified version of the US Army Corp of Engineers water quality code (CE-QUAL) (Cerco and Cole 1995; James and Boriah 2010; James et al. 2013) to simulate algal growth kinetics in well-mixed photobioreactor-type systems. The model allows the flexibility to manipulate a host of variables associated with algal growth such as temperature, pH, light intensity, and nutrient availability. Salinity of the medium is another important operational parameter governing algal growth; the effects of salinity were added to the model to expand its capabilities to marine algae. To populate the model’s empirical parameters, we conducted a parametric growth rate measurement of Nannochloropsis salina at different temperatures, light intensities, and salinities. The effect of pH was not investigated in this study due to the desire to have consistent CO2 levels for each of the conditions. The computational fluid dynamics code ANSYS FLUENT (Fluent 2012) was used to model the heat transfer and algae transport. The model was then validated by comparing predictions from the lab-scale parameterized model to experimental results from both a greenhouse pond and outdoor, open-channel raceway. We showed that our model has excellent agreement for multiple bioreactor systems and can effectively predict the pond temperature based on meteorological data.

Materials and methods

We cultivated two similar strains of Nannochloropsis: Nannochloropsis salina CCMP 1776 and Nannochloropsis granulata LRB-MP-0209. Both were grown in f/2 medium (Guillard and Ryther 1962). We grew N. salina at Sandia National Laboratories in a 25 × 115 mm2 quartz test tube at the Livermore, California, USA site to parameterize the model and in greenhouse tanks at the Albuquerque, New Mexico site. N. granulata was grown in an outdoor raceway at the Arizona Center for Algae Technology and Innovation at Arizona State University in Mesa, Arizona.

Light absorptivity

Light utilization by algae depends on the optical properties of photosynthetic pigment within the cell. While the absorptivity of pigments is generally known in select organic solvents, light extinction is undoubtedly different in vivo. Therefore, we developed a quantitative relationship between pigment optical depth from the fluid surface (as a function of wavelength) and dry cell weight for N. salina, thus, identifying the absorptivity at all wavelengths.

In brief, duplicate scatter-free absorbance measurements across six different sample concentrations of N. salina were obtained using a 60-mm integrating sphere attached to a PerkinElmer, Lambda 950 spectrophotometer. An integrating sphere was used to remove the contribution of scatter from the algal and detritus in the sample. In parallel, cell counts were used to determine the concentrations of these samples (concentrations ranged from 3.75 × 106 to 7.5 × 107 cells mL−1). Classical least squares (CLS) was used to project these concentrations onto the spectral data to obtain the pure component spectral estimate that represents the absorptivity of Nannochloropsis. This calculation was conducted with MATLAB (2013) and consisted of multiplying the pseudo-inverse of the concentrations by the measured spectra to obtain this pure component estimate. Further details of this CLS method can be found elsewhere (Haaland et al. 1985).

Lab-scale model parameterization

N. salina was grown in f/2 media in a laboratory incubator with a diurnal cycle of 16:8 (light/dark). We adapted the cultures to light conditions, NaCl concentrations, and temperatures. Algae were grown in 25-mm test tubes with air bubbled through a plastic tube submerged to the bottom of the test tube to provide CO2 and mixing. The pH was monitored daily for each sample with a submersible, calibrated meter (Omega Engineering, Inc/PHB21) and was consistently between 7.5 and 8.0. This range is within the optimal pH range for N. salina between 7.5 and 9.0 (Bartley et al. 2013; Boussiba et al. 1987). Changes in cell concentration were estimated using a calibrated digital fluorometer (Turner Designs/10-AU) to measure the chlorophyll a fluorescence in vivo. The fluorometer transmits an excitation beam of light in the 440-nm range and detects light emitted from the sample in the 680-nm range. The measurements were calibrated to initial culture cell counts at each light intensity and the fluorescence was measured daily to produce growth curves for each offset of experimental conditions. To compare with the model, the fluorescence measurements are converted to cell counts based on the initial calibration and then converted to biomass concentration based on the measured cell mass of 2.7 pg cell−1. Although chlorophyll fluorescence is not an appropriate method for measuring a quantitative biomass concentration, the change in fluorescence over time of a given sample during the exponential growth phase estimates the rate of change of the sample concentration or growth rate (Mayer et al. 1997; Serôdio et al. 2001; Torzillo et al. 1996; Samuelsson and Öquist 2006; Sukenik et al. 2009; Masojidek et al. 2010; Vyhnalek et al. 1993). Growth rates were calculated from data measured in triplicate at three light conditions (10.5, 27, and 58 W m−2), four NaCl concentrations (0.35, 0.5, 0.75, and 1 M), and four temperatures (18, 22, 26, 30 °C). The concentration over time during the exponential growth phase is represented by the equation C chla (t) = C 0exp(μt), where C chla is the chlorophyll a concentration, C 0 is the initial chlorophyll a concentration, t is the time, and μ is the exponential growth rate. The growth rates are calculated by linear curve fits to data from the exponential growth phase to ln(C chla ) = μt + ln(C 0) and averaged over the triplicate samples for each growth condition.

Greenhouse tanks experiment

A 40-L culture of laboratory-grown N. salina in f/2 media was used to inoculate two circular tanks continuously mixed by a jet system enclosed in a greenhouse located in Albuquerque, NM. Each vessel had a radius of 0.9 m and a medium depth of 0.211 m. The initial nitrate and phosphate concentrations were 54.7 and 3.1 g m−3. The two tanks were operated at different CO2 levels. The first tank was bubbled with CO2 levels elevated at 85 L h−1 with the other tank at ambient CO2 levels. Temperature and pH were monitored with a submersible, calibrated meter (YSI Inc.). The pH remained between 8.0 and 8.5 for the ambient tank and between 7.4 and 7.8 for the elevated CO2 tank during the course of the measurements. The pH was only briefly below 7.5 during the first days of the elevated-CO2 tank measurement. Again, these values are within the range for ideal growth. Irradiance was monitored with a calibrated spectroradiometer (Ocean Optics). Biomass was estimated by comparing the optical density at 750 nm of each cultivation condition to a standard curve of biomass versus optical density generated for N. salina.

Open-channel raceway experiment

A 12-m3 open raceway pond with a 20-cm culture depth was inoculated with nutrients ten times the standard f/2 media. A filtered ambient air/CO2 mixture (1.5–2.0 % CO2) is bubbled intermittently into the raceway pond through an airstone sparger to provide CO2 to the algae culture for the purpose of maintaining a fairly constant pH between 7.8 and 7.9. To determine the algae concentration, dry weight and ash-free dry weight values were measured daily (Laurens et al. 2012). The pond temperature was measured and recorded at 15-min intervals using a Yellow Springs Instruments YSI 5200A-DC Multiparameter Water Quality Monitoring Unit approximately 10 cm below the surface. Light intensity was measured with the same calibrated spectroradiometer described above.

Algae growth model

The governing equation for algal biomass growth in CE-QUAL is (Cerco and Cole 1995):

$$ \frac{\partial B}{\partial t}=\left(P-{B}_{\mathrm{M}}-{P}_{\mathrm{R}}\right)B+\frac{\partial }{\partial z}\left({w}_{\mathrm{s}}B\right)+\frac{B_{\mathrm{L}}}{V} $$
(1)

where B is the biomass, t is time, P is the production (growth) rate, B M is the basal metabolic rate, P R is the predation rate, w s is the settling velocity, B L represent external loads such as deposition or sources, and V is the model cell volume. Biomass production rates are determined by the availability of nutrients (including CO2), the intensity of light, local temperature, pH, and salinity. For this work, the effects of salinity are considered while the effects of pH are neglected. The effect of each is considered to be multiplicative and decoupled (Cerco and Cole 1995):

$$ P={P}_{\mathrm{M}}f\left(\nu \right)g(I)h(T)i(S)j\left(\mathrm{pH}\right) $$
(2)

Here, P M is the maximum instantaneous growth rate under optimal conditions; f(ν) is the effect of non-optimal nutrients, which includes CO2 limitation (0 ≤ f(ν) ≤ 1); g(I) is the effect of non-optimal illumination (0 ≤ g(I) ≤ 1); h(T) is the effect of non-optimal temperature (0 ≤ h(T) ≤ 1); i(S) is the effect of non-optimal salinity (0 ≤ i(S) ≤ 1); and j(pH) is the effect of non-optimal pH (0 ≤ j(pH) ≤ 1). All of these functions are spatially dependent, and their values vary from cell to cell in the model according to local nutrient concentrations (including CO2), incident solar radiation, salinity, and temperature.

For the lab-scale parameterization of the algae growth model, algae were grown in well-mixed lab conditions and the effects of predation, settling, pH, and CO2 limitation can be neglected. In addition, for the initial validation study, the larger scale systems are assumed to obey the same conditions defined at the lab scale. It is acknowledged that this may not hold true and future studies will address these components of the model. The basal metabolism rate varies with temperature according to:

$$ {B}_{\mathrm{M}}(T)={B}_{\mathrm{M}}\left({T}_0\right) \exp \left[{K}_{{\mathrm{T}}_B}\left(T-{T}_0\right)\right] $$
(3)

where T 0 is 20 ºC and B M(T 0) is set to 0.01 day−1, and \( {K}_{{\mathrm{T}}_B} \) is the effect of temperature on the metabolism and is set to 0.069 ºC−1 (Cerco and Cole 1994). This results in the basal metabolic rate increasing to 0.03 day−1 at 36 ºC. These are general values for algae due to a lack of published data available for specific strains. While this parameter is uncertain, the fitted growth rate will largely account for error in the basal metabolism rate, δB M. The algae growth model is implemented in the commercial computational fluid dynamics code ANSYS FLUENT (Fluent 2012) to allow for fluid flow and heat transfer calculations in a wide variety of systems.

Two types of domains are used for the current study. First is a simplified single-cell rectangular domain with dimensions representative of the experiment, which assumes the culture is well-mixed and conditions such as light intensity and temperature are uniform within the culture. However, the light intensity changes as the culture density increases (which the model accounts for), while the temperature remains constant. We determine at which scale and conditions it is no longer appropriate to use the simplified domain and expand the complexity of the domain to account for the spatial variations in the light and temperature conditions. The second domain is a 2D rectangular representation of the raceway pond. Both domains are shown in Fig. 1.

Fig. 1
figure 1

Two solver domains used in study: (a) simplified single-cell rectangular domain and (b) meshed 2D rectangular representation of raceway pond

Full size image

Model parameterization

Model parameterization occurs in two steps. First, limitation functions (described below) are fit individually to the normalized measured growth rate versus the growth variable (light intensity, temperature, and salinity) using CLS. Second, the maximum ideal productivity is fit to the growth data (described in the “Results and Discussion” section). To assess the agreement, the R 2 value is calculated according to:

$$ {R}^2=1-\frac{{\displaystyle \sum {\left({C}_{\mathrm{data}}-{C}_{\mathrm{prediction}}\right)}^2}}{{\displaystyle \sum {\left({C}_{\mathrm{data}}-{\overline{C}}_{\mathrm{data}}\right)}^2}} $$
(4)

where C data is the concentration value of the data point, C prediction is the concentration predicted by the model at the same time, and \( {\overline{C}}_{\mathrm{data}} \) is the average concentration for all the data points.

Nutrients

Growth limitation due to nutrient availability is based on the Monod equation (Monod 1949):

$$ f\left(\nu \right)=\frac{\nu }{K_X^h+\nu } $$
(5)

where ν is the nutrient concentration and K h X is the half-saturation constant. For example, the nutrient function for green algae can be nutrient limited by dissolved ammonium, nitrate, phosphate, or CO2, yielding:

$$ f\left(\nu \right)= \min \left(\frac{{\mathrm{NH}}_4+{\mathrm{NO}}_3}{K_N^h+{\mathrm{NH}}_4+{\mathrm{NO}}_3},\frac{{\mathrm{PO}}_4}{K_P^h+{\mathrm{PO}}_4},\frac{{\mathrm{CO}}_2}{K_C^h+{\mathrm{CO}}_2}\right) $$
(6)

Here, NH4 is the ammonium concentration, NO3 is the nitrate concentration, PO4 is the dissolved phosphate concentration, CO2 is the dissolved carbon dioxide concentration, and K h N , K h P , and K h C are the corresponding half-saturation constants.

Half-saturation constants are typically defined for the low concentrations of nutrients common in environmental systems and are on the order of 0.01 g m−3. The half-saturation constants used in this model are 0.01 g m−3 (Cerco and Cole 1994), 0.002 g m−3 (Cerco and Cole 1994), and 0.028 g m−3 (Hecky et al. 1993) for nitrogen, phosphorous, and CO2, respectively. For algal growth systems (raceways), nutrients are often added in excess and the nutrient limiting function is close to unity. However, CO2 is often difficult to maintain at sufficient concentrations particularly during high-growth periods, in large reactors, and at high algae concentrations. Also, when algae are nutrient deprived (e.g., to trigger lipid production (Hu et al. 2008)), the value of the half-saturation constant will play a more important role in algae growth.

To properly model the effect of nutrients, we must ensure appropriate amounts of nutrients are removed from the simulation with increased algae concentration. Algae atomic composition ratio was measured at the end of the greenhouse experiment on day 7 yielding a C/N/P ratio of 358:38:1. For reference, the Redfield ratio for marine plankton in open oceans is 106:16:1 (Redfield 1934). Significant variability of elemental composition exists across strains and even within strains due to environmental stressors and adaptations. Nutrients recycle in the system as algae metabolize the inorganic forms of nitrate and phosphate into their dissolved organic forms. These dissolved organic nitrates and phosphates are mineralized back into their inorganic forms at rates of 0.015 and 0.1 day−1 (Cerco and Cole 1995). All of these water quality variables are tracked in the model.

Light

The growth of algae is a strong function of irradiance, which is a function of average daylight, light extinction, light intensity at the water surface, optimal light intensity, and depth of the algae below the water surface. Algae grow as the light intensity increases to some saturation (optimum) intensity (I s), beyond which growth rates decline due to photo inhibition. The function for non-optimal illumination is derived from Steele’s equation (DiToro et al. 1971; DiToro and O'Connor 1975):

$$ g(I)=\frac{I(z)}{I_{\mathrm{s}}}{e}^{1-\frac{I(z)}{I_{\mathrm{s}}}} $$
(7)

where I(z) is the instantaneous light intensity at depth z and I s is the optimal light intensity. If the growth medium is not well-mixed, then the rate of change of light intensity I(z) changes with depth (or model layer) due to non-uniform growth of algae. If, on the other hand, the system is well-mixed, then the biomass concentration will be homogeneous (constant light extinction). For such a system (i.e., the single-layer model studied in this work), the growth limitation is:

$$ g(I)=\frac{e}{K_{\mathrm{e}}d}\left({e}^{-{\alpha}_1}-{e}^{-{\alpha}_0}\right) $$
(8)

where d is the water-layer depth, K e is the light extinction coefficient, α 0 is the light intensity ratio at the top of the water surface:

$$ {\alpha}_0=\frac{I_0}{I_{\mathrm{s}}} $$
(9)

and α 1, the ratio at the bottom (of the layer), is:

$$ {\alpha}_1=\frac{I_0}{I_{\mathrm{s}}}{e}^{-{K}_{\mathrm{e}}d} $$
(10)

Note that recursive calculations are necessary for multilayer models.

The light extinction coefficient, K e, in a single-layer model and within a particular layer in a multilayer hydrodynamics model is considered to be a constant and formulated as

$$ {K}_{\mathrm{e}}={k}_{\mathrm{b}}+{k}_{\mathrm{c}}B $$
(11)

where k b is the constant background light extinction coefficient due to water and other suspended particulates and k c is the constant light extinction due to suspended carbon (or biomass) concentration in the layer. A standard value of 0.1 m−1 is used for k b (Cerco and Cole 1995).

The absorptivity curve that yields the light extinction coefficient, k c, was generated for N. salina grown in the laboratory. Because the majority of light is absorbed by the chlorophyll and the light absorbed by chlorophyll contributes greatest to the growth, the light extinction coefficient was calculated for the wavelength of peak chlorophyll absorption. At 678 nm, the light extinction value was calculated to be 0.3501 m2 g−1 C. The concentration-dependent absorptivity is calculated from measured values in terms of cell count (4.19 × 10−9 mL cell−1 cm−1), the measured cell mass of 2.7 pg cell−1, which is similar to reported values for Nannochloropsis (Briassoulis et al. 2010), and the estimated fraction of carbon in biomass as 0.45 g C g−1 B.

The optimal light intensity was fit to the lab-scale growth rate data to determine I s = 20 W m−2. Although the growth rate continued to increase slightly at higher light levels, the health of the algae appeared to deteriorate in the higher light conditions as the algae pigment changed from green to yellow.

Temperature

Algal growth rate increases with temperature up to an optimal and decreases at temperatures beyond the optimal (Cossins and Bowler 1987). Temperature effects are defined by an exponential function of water temperature, the optimal temperature for growth, and the temperature effect coefficients below and above the optimal temperatures:

$$ h(T)=\left\{\begin{array}{c}\hfill \exp \left[-{K}_1^T{\left(T-{T}_1\right)}^2\right]\kern1.32em \mathrm{for}\kern0.24em T\le {T}_1\hfill \\ {}\hfill 1\kern5.28em \mathrm{for}\kern0.24em {T}_1<T\le {T}_2\hfill \\ {}\hfill \exp \left[-{K}_2^T{\left({T}_2-T\right)}^2\right]\kern0.5em \mathrm{for}\kern0.24em T>{T}_2\hfill \end{array}\right. $$
(12)

where T is the local temperature from the hydrodynamic model, T 1 is the lower optimal growth temperature, T 2 is the upper optimal growth temperature, K T1 is the temperature effect below the optimal growth temperature, and K T2 is the temperature effect above the optimal growth temperature.

The fitted lower and upper optimal growth temperatures are 21.5 and 23.5 °C, respectively. These values are lower than the 26–28 °C values reported by others for this strain, but are consistent with other measurements made on our lab’s version of the strain (James et al. 2013; Huesemann et al. 2013; Boussiba et al. 1987). The fitted temperature effects below and above optimal are 0.015 and 0.01 °C−2, respectively. The resulting R 2 for the temperature parameter fitting was 0.8.

Salinity

Marine algae growth rates have an optimum salinity above and below which the growth rate decreases (Brock 1975; Auken and McNulty 1973; García et al. 2007; Fabregas et al. 1984; Batterton and Baalen 1971). The salinity of the media is limited to a range between zero for a completely non-saline solution to its maximum solubility in water. The effect of salinity on algae growth has yet to be formulated into a general equation that can be applied to a variety of halotolerant/halophilic algae species. Given the similarity in curve shape to temperature, we propose an exponential function for salinity:

$$ i(S)=\left\{\begin{array}{cc}\hfill \exp \left[-{k}_{s_1}{\left(S-{S}_{\mathrm{opt}}\right)}^2\right]\hfill & \hfill \mathrm{for}\;S\le {S}_{\mathrm{opt}}\hfill \\ {}\hfill \exp \left[-{k}_{s_2}{\left(S-{S}_{\mathrm{opt}}\right)}^2\right]\hfill & \hfill \mathrm{for}\;S>{S}_{\mathrm{opt}}\hfill \end{array}\right. $$
(13)

where S is the salinity, S opt is the optimal salinity, \( {k}_{s_1} \) is the salinity effect below the optimal salinity, and \( {k}_{s_2} \) is the salinity effect above the optimal salinity.

The fitted optimal NaCl concentration is 20 ppt or 0.35 M and the fitted salinity effect above optimal is 9 × 10−4 ppt−2, salinities below the optimal value were not studied so the sub-optimal-effect parameter is assumed equal to the super-optimal. The resulting R 2 for the salinity parameter fitting was 0.9. The optimal salinity measured is less than that previously measured for a similar strain, but given the long period that our strain was grown in f/2 and the other differences between strains, this is not unexpected (Boussiba et al. 1987).

To determine the parameters for the growth model described above, lab-scale experiments were conducted and the parameters were fit to the data. In the following section, we describe how we verified the parameter fitting by simulating the lab-scale experiments and ensuring that we predict the growth appropriately. Subsequently, we validated the model scale-up by comparing it to both the modeled and the experimental results of larger scale systems.

Results and discussion

Lab scale

The developed empirical fits were supplied to the model and compared with the lab-scale measurements and ensure that the model is appropriately parameterized. The model was set up in the simplified well-mixed domain with dimensions of 15 × 2.2 × 2.2 cm3 for the representative rectangular culture volume of the test tubes used in the experiments (equivalent volume and depth). The modeled test tube is exposed to light from one side at the specified intensities. The initial nutrient concentrations for the f/2 medium were 2.3 mM NO3 (32.2 g m−3) and 0.067 mM PO4 (2.075 g m−3). The initial CO2 concentration was 0.9 g m−3 (Burkhardt et al. 1999). The absorption of CO2 into the media from the bubbling of air is assumed to be sufficient to sustain this amount of CO2 (2.31 μg s−1). The initial algae concentrations were set to the initial measured concentrations.

The resulting parameters for the ideal growth conductions for N. salina are a NaCl concentration of S opt = 0.35 M NaCl, a light intensity of I s = 20 W m−2, and temperatures between T 1 = 21.5 and T 2 = 23.5 °C. The theoretical maximum growth rate at ideal conditions, P M, from Eq. (2) was used to fit the model to the measurements and was determined to be 2.5 day−1. Using this value, the model generally replicates the data well. The resulting R 2 value is 0.79. Figure 2 shows the algae concentrations from measurements and simulations over time at temperatures of 18, 22, 26, and 30 °C, respectively, for various light intensities and NaCl concentrations.

Fig. 2
figure 2

Plot of the predicted (curves) and measured (symbols) algae concentration over time comparison at 18, 22, 26, and 30 °C for various representative light intensity and salinity conditions at the lab scale

Full size image

The maximum measured daily average growth rate in the lab-scale study was 0.55 day−1, which when divided by 2/3 for the fraction of the day with light gives \( \overline{P-{B}_{\mathrm{M}}}=0.825\kern0.5em {\mathrm{day}}^{-1} \) the maximum average daily growth rate observed, which includes reductions due to non-ideal conditions and basal metabolism. The expected trends were observed; growth rates decreased at temperatures and salinities above and below the optimal values. Growth rates also diminished at light intensities below the optimal intensity and leveled out at higher intensities. Although pigment change was observed at the highest light intensity (green to yellow), no decrease in growth rate was observed. The maximum instantaneous growth rate found in the simulation was P − δB M = 1.3 day−1, which includes reductions due to non-ideal conditions and uncertainty in basal metabolism, δB M.

Greenhouse tanks

To validate the model and show its potential to predict larger scale systems, it must be compared with a larger scale measurement that is completely independent of the growth rate function parameterization. As a first step in validation of the model and its scalability, the parameter values obtained from the laboratory measurements are applied to the greenhouse setup. Two tanks are simulated as fully mixed 1.67 × 1.5 m2 rectangular tanks with a 0.211-m depth consisting of approximately 0.53 m3 of medium. The light and water temperature measured in the tank cultures over the course of the 7-day experiment are shown in Fig. 3. The CO2 absorbed into the medium from the bubbling is calculated using the same method as James et al. (2013).

Fig. 3
figure 3

Plot of the measured temperature for the 5 % CO2 (solid) and ambient CO2 (dashed) and light intensity (dash-dot) experienced by the greenhouse tanks over the course of the measurement

Full size image

The results from the measurements and the model are plotted in Fig. 4. The model reasonably predicts the algae concentration for each tank operating with different CO2 sources. The resulting R 2 values were 0.91 for the tank bubbled at 85 L h−1 CO2 and 0.83 for the tank bubbled with air only.

Fig. 4
figure 4

Plot of the measured (symbols) and modeled (curves) algae concentrations over time for the greenhouse tanks at 5 % (solid/triangle) and ambient (dash-dot/square) CO2 bubbling concentrations

Full size image

The three most significant parameters limiting algal growth are light, temperature, and CO2 concentration. The limitation factors for each of these are plotted in Fig. 5. For this case, the ideal light and temperature are well aligned due to diurnal fluctuations. However, the CO2 concentration becomes limiting during high-growth periods under ideal light and temperature conditions, both of which limited growth even during high-CO2 concentration bubbling. The maximum simulated instantaneous growth rate for the conditions of the experiment was P − δB M = 1.2 day−1.

Fig. 5
figure 5

Plot of the limitation factors over time for the greenhouse ponds for light (dotted), temperature (dash-dot), and CO2 at 5 % (solid) and ambient (dashed) bubbling concentrations

Full size image

Open-channel raceway

Given that the model with the simplified domain reasonably simulated the greenhouse tanks, it was extended to an open-channel raceway system. The optimal parameter values from the laboratory experiment (I s, S opt, T 1, and T 2) were again applied to the experimental open-channel raceway. The raceway was simulated as well-mixed with simplified domain 24.3 × 2.44 m2 rectangular pond with a 0.20-m depth and 11.9 m3 of medium. Sufficient CO2 is assumed because the growth in the pond is greatly limited by the temperature, pH remained relatively constant, and CO2 is introduced to the culture through an air stone sparger and paddle wheel mixing.

The model greatly under predicts the algae growth for this case. The resulting R 2 value for this case is only 0.63, which suggests that at least one of the model assumptions was not valid. The question is: to what degree are differences in algae strains, scale up, and the fully mixed assumption the source of disagreement? The two largest contributors to limiting algal growth for this case are light and water temperature with measured data shown in Fig. 6. The limitation factors for each of these are plotted in Fig. 7. For this case, the ideal light and temperature are not well aligned. When the light is sufficient, the temperature of the pond is above its optimal value. When the light is limiting, the temperature reduces to more optimal values. This causes most of the growth to occur in the morning and evening periods, while at mid-day and at night the growth is limited and zero, respectively.

Fig. 6
figure 6

Plot of the measured temperature (dashed) and light intensity (solid) experienced by the open-channel raceway over the course of the measurement

Full size image
Fig. 7
figure 7

Plot of the limitation factors for light (dash-dot), temperature (dashed), and their combined limitation (solid) over time for the open-channel raceway

Full size image

Recent research has shown that the mixing in these large raceway ponds is much less than in the laboratory test tubes or the jet mixed greenhouse tanks (Mendoza et al. 2013; Singh et al. 2012; Bernard et al. 2013). Mendoza et al. (2013) found mixing times ranging between 1.4 and 6 h (nearly half of the daylight). Singh et al. (2012) found that the vertical mixing rates were only 0.5 % of the longitudinal mixing times. Bernard et al. (2013) showed that except for at the paddle wheel, very little vertical mixing occurs. The algae concentrations were much higher in the raceway than in either the lab or the greenhouse ponds. The resulting self-shading becomes more important, while the reduced mixing causes a non-uniform algae concentration. This nonlinear effect cannot be appropriately accounted for by a simple well-mixed model. The light intensity and environmental effects, however, were much higher for the raceway measurement than either the lab or greenhouse, which may result in large temperature variations with depth. Given the high concentration of algae and high variability of light and temperature with depth, the algae concentration will also vary with depth and the fully mixed assumption is not appropriate for this system.

To relax the fully mixed assumption, the temperature variation with depth is calculated. This requires heat transfer calculations within the pond and between the pond and its surroundings including the effects produced by convection with the air, evaporation, conduction through the bottom of the raceway, and radiation to the atmosphere and from the sun.

The temperature is calculated by performing an energy balance at the surface of the pond. Given the small penetration depth of infrared light in water compared to the depth of the pond (majority of IR radiation is absorbed in the first 1-2 cm (Hale and Querry 1973; Kou et al. 1993)), the heat flux from radiation can simply be applied to the surface. Two types of radiation must be accounted for, the shortwave radiation, which is essentially the measured solar radiation obtained from a weather station, and the longwave radiation, which is typically not detected by the sensors and must be calculated. The heat flux due to longwave radiation, q″ lw, is given by:

$$ q^{\prime }{\prime}_{\mathrm{lw}}={\varepsilon}_{\mathrm{s}}\sigma \left({T}_{\mathrm{s}\mathrm{ky}}^4-{T}_{\mathrm{s}}^4\right) $$
(14)

where σ is the Stefan Boltzmann constant, ε s is the emissivity of water, T s is the temperature of the water surface, and T sky is the temperature of the sky, which can be estimated from experimental data or empirical relationships (Martin and Berdahl 1984).

Heat flux due to convection, q″ conv, between the pond surface and the surrounding air is given by:

$$ q^{\prime }{\prime}_{\mathrm{conv}}=\overline{h}\left({T}_{\infty }-{T}_{\mathrm{s}}\right) $$
(15)

where \( \overline{h} \) is the average convective heat transfer coefficient, and T ∞ is the temperature of the surrounding air. The average convective heat transfer coefficient depends on the system geometry and the turbulent nature of the air flow (Incropera 2007). For laminar flow, it is given by:

$$ \overline{h}=\frac{k_{\mathrm{a}}}{L}\left(0.644{\mathrm{Re}}_L^{1/2}{ \Pr}^{1/3}\right) $$
(16)

where k a is the thermal conductivity of the air, L is the length of the pond surface, Re is the Reynolds number, and Pr is the Prandtl number. For turbulent flow, it is given by:

$$ \overline{h}=\frac{k_a}{L}\left(0.037{\mathrm{Re}}_L^{4/5}-871\right){ \Pr}^{1/3} $$
(17)

Heat flux due to evaporation, q″ evap, depends on the latent heat of vaporization, h fg , and the amount of water being evaporated and is given by:

$$ q^{\prime }{\prime}_{\mathrm{evap}}={h}_{fg}{h}_{\mathrm{m}}\left({c}_{\mathrm{sat}}-{c}_{\infty}\right) $$
(18)

where h m is the mass transfer coefficient, c sat is the saturation value for the water vapor concentration, and c ∞ is the value of the water vapor concentration in the surrounding air. The mass transfer coefficient is related to the convective heat transfer coefficient by the heat and mass transfer analogy:

$$ \frac{h}{h_{\mathrm{m}}}=\rho {C}_p{\mathrm{Le}}^{1-n} $$
(19)

where ρ is the air density, C p is the air specific heat, Le is the Lewis number, and n is a constant approximated as 1/3 (Incropera 2007).

Finally, the conductive heat flux, q″ cond, occurs between the ground and pond and is given by:

$$ q^{\prime }{\prime}_{\mathrm{cond}}=\frac{k_g}{L_g}\left({T}_{\mathrm{bot}}-{T}_g\right) $$
(20)

where T bot is the temperature of the bottom of the pond, T g is the temperature of ground, L g is the distance into the ground the measurement is made, and k g is the thermal conductivity of the ground, which can be determined based on experimental data and will depend on soil type and moisture content. These heat fluxes are then applied to the model as boundary conditions on the appropriate surfaces to determine the spatiotemporal variation of temperature within the pond.

Weather data for Mesa, Arizona, was acquired from the Arizona Meteorological Network and included air and ground temperatures, solar radiation, relative humidity, and wind speed. Figure 8 is a comparison between the predicted and measured temperature during cultivation 10 cm from the water surface. The model reasonably matches the measured temperature values. On day 7, flocculation was observed on the surface of the pond, which affected the pond temperature and caused a deviation between the measured and predicted temperatures.

Fig. 8
figure 8

Plot of the measured (dashed) and modeled (solid) temperatures 10 cm below the water surface

Full size image

The temperature calculation allows us to estimate the temperature as a function of depth with the assumption of non-ideal pond mixing. Figure 9 shows the predicted temperature variation with depth at different representative times of the day. At mid-day, for instance, the solar radiation and air temperature are relatively high in an outdoor pond and the radiation and convection occur at the surface; consequently, the surface temperature of the water rises much faster than the deeper water of the raceway. Likewise, in the evening, heat escapes from the surface causing the temperature of the water near the surface to decrease more rapidly. The temperature variation on the surface closely resembles that measured by (Reichardt et al. 2013) at a similar raceway with a spectroradiometer that also gives an in situ measurement of biomass and pigment optical activity. Consequently, because the light intensity is attenuated with depth, the interplay between the light and temperature over the course of the day is important for estimating algae growth.

Fig. 9
figure 9

Plot of the modeled temperatures versus depth at representative times during the day: mid-day (solid), mid-night (dashed), evening/dusk (dash-dot), and morning/dawn (dotted)

Full size image

Accounting for variations in light and temperature with depth yields a much better agreement between the model and the measurements. Figure 10 compares modeled and measured values. The resulting R 2 value is 0.97.

Fig. 10
figure 10

Plot of the measured (circle) and predicted (solid curve) algae concentrations over time for the open-channel raceway accounting for variation of light and temperature with depth

Full size image

Conclusions

Multifactorial measurements of N. salina were conducted to populate the empiricisms for an algae growth kinetics model. The effect of salinity on growth was added to the base CE-QUAL model to simulate marine algal species. The laboratory-parameterized model for N. salina was scaled up to simulate two larger, outdoor experimental studies. The model accurately predicted the growth trends in greenhouse tanks using a simplified well-mixed domain and an open-channel raceway using a more complex domain accounting for spatial variations in temperature and light intensity. The model (using parameters derived from the lab-scale experiment) was used to determine which environmental factors are most limiting to growth (light and temperature). This model could also be used to study the scale-up effect through comparisons of the lab-scale kinetics and a larger scale system including the effects of predation, depth-decay of light (light extinction), and optimized nutrient and CO2 delivery. The model could be expanded to study growth in production-scale photobioreactors and open-channel raceways, thus eliminating the need for expensive large-scale experiments. As more multifactorial data are accumulated for a variety of algal strains, the model could be used to select appropriate algal species for various geographic and climatic locations.