1 Introduction

The progress of quantum optics has offered a great chance to generate a different kinds of light theoretically and experimentally.

The non classical property has attracted much attention of theorists and experimentalists from various areas in different fields of quantum information processing, quantum key distribution, quantum teleportation and quantum computation [1,2,3,4]. This property which manifested in different measurements such as sub-poissonian statistical [5], the role of squeezing [6], photon anti-bunching [7] and non classicality depth [8] for a quantum state is one of the condition that state should satisfy to get used in quantum information processing.

On the other hand, a Gaussian state is considered as the typical robustness state, that had played an important role in various tasks of quantum information processing, quantum teleportation, dense coding and quantum cloning [9]. As matter of fact the most interesting experiment of quantum information are done using a Gaussian light [10]. Mathematically, the state is Gaussian, if its distribution function in phase space is in Gaussian form. Unfortunately, the Gaussian states are critical to noise channel, therefore, non Gaussian state is called for long distances communications protocols, e.g. entanglement distillation [11] and entanglement swapping [12] which require a non Gaussian operations. Furthermore quantum teleportation and cloning of quantum states could be improved using non Gaussian states, which is the second condition that a state should satisfy after it satisfies the non classical property. The non Gaussian state could be generated from a Gaussian state using photon subtraction like NOON state [13, 14], superposition of Fock states [15, 16], photon tensor network states [17,18,19]. To quantify this property, a various measurements have been proposed, Hilbert Shmidt distance [20] entropic measures [21].

The aim of this work is to investigate the non classical and non Gaussian properties of photons added then subtracted PAS and subtracted then added PSA to multiheaded cat state N-HCS. With intention to distill the better one for the implementation in quantum information processing, and to compare it with photon added then subtracted coherent state PASCS [22], multi-headed cat state itself and coherent state [23, 24].

In the second section, we discuss the multi-headed cat state, we define the density operator of PASN-HCS and PSAN-HCS and their normalization constant. The third section is concerned to investigate both the non classical and non Gaussian properties of the two states respectively using Mandel’s Q parameter, Wigner function, non Gaussian measurement and fidelity. Then we plot our results for different cases of (N;k; l and α). We give an experimental scheme of photon addition and subtraction then we close this manuscript by a concluding remarks.

2 Multi-Headed Cat State

The superposition of Glauber coherent states [24] has been extensively investigated during the last decades. In particular, their non classical property has been the subject of various works [22, 25]. The entangled coherent states are expected to play an important role in different fields of quantum information processing [25]. In addition, coherent states, as a useful resource can be easily generated with the available laser technology and encoding quantum information in continuous variables states. This constitutes an alternative way to overcome the difficult encountered with single photon sources in implementing several quantum tasks, especially in quantum cryptography.

The superposition of coherent states SCS with two different phases and three different phases were discussed in various works [26, 27], the last one was considered to produce superposition of three photons [28].

Recently, superposition with up of four coherent states was implemented in a cavity quantum electrodynamics system using the coupling between a wave guide cavity resonator and superconducting transmon qubits [29]. A superposition of coherent state with four different phases was proposed to protect the logical qubit against relaxation [30].

The Glauber coherent state associated with a single radiation mode are labeled by complex variable ɀ as

(1)

where |n〉 denote the standard Fock states. The state |ɀ〉 satisfies a|ɀ〉 = ɀ |ɀ〉 where a is the annihilation operator associated with the harmonic oscillator \( a\mid n\operatorname{}\left\rangle =\sqrt{n}\mid n-1\right\rangle \).

In this work, we shall mainly focus on the N-headed cat state N ≥ 1 defined as

$$ \mid {C}_N\left(\alpha \right)\left\rangle =\frac{1}{\sqrt{{\mathcal{M}}_N\left(\alpha \right)}}\sum \limits_{n=0}^{N-1}\mid \alpha {e}^{i2\pi \frac{n}{N}}\right\rangle $$
(1)

where α ∈ ℂ and the normalization factor is defined by

$$ {\mathcal{M}}_N\left(\alpha \right)=\sum \limits_{n,m=0}^{N-1}{e}^{-{\left|\alpha \right|}^2\left(1-{e}^{i\frac{2\pi }{N}\left(n-m\right)}\right)} $$
(2)

The states |CN(α)〉 are eigenstates of the harmonic oscillator annihilation operator

$$ {a}^N\mid {C}_N\left(\alpha \right)\left\rangle ={\alpha}^N\mid {C}_N\left(\alpha \right)\right\rangle $$
(3)

To generate the k photons added multi-headed cat states, we apply the creation operator (a+)k. This leads to the state (a+)k |CN(α)〉 and to generate l photons subtracted multi-headed cat states, we apply the annihilation operator (a)l. This leads to the state al|CN(α)〉 Thus, the photon added then subtracted N-headed cat states are defined by

$$ \mid k,l,{C}_N\left(\upalpha \right)\left\rangle ={\left({\mathrm{N}}_{asN}^{k,l}\right)}^{-\frac{1}{2}}{a}^l{a}^{+k}\mid {C}_N\left(\upalpha \right)\right\rangle $$
(4)

and the photon subtracted then added N-headed cat state are defined by

$$ \mid l,k,{C}_N\left(\upalpha \right)\left\rangle ={\left({\mathrm{N}}_{\mathrm{saN}}^{l,k}\right)}^{-\frac{1}{2}}{a}^{+k}{a}^l\mid {C}_N\left(\upalpha \right)\right\rangle $$
(5)

The creation and annihilation operators satisfies [a, a+] = I. The normalization factors \( {\mathrm{N}}_{asN}^{k,l} \) and \( {\mathrm{N}}_{saN}^{I,k} \) are defined by

$$ {\mathrm{N}}_{asN}^{k,l}\left(\alpha \right)=\frac{e^{-{\left|\alpha \right|}^2}}{{\mathcal{M}}_N\left(\alpha \right)}\sum \limits_{j=0}^l\frac{{\left(l!\right)}^2\left(k+l-j\right)!}{{\left(-1\right)}^jj!{\left(\left(l-j\right)!\right)}^2}\sum \limits_{n,m=0}^{N-1}{L}_{k+l-j}\left(-{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast}\right){e}^{{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast }.} $$
(6)
$$ {\mathrm{N}}_{\mathrm{saN}}^{l,k}\left(\alpha \right)=\frac{e^{-{\left|\alpha \right|}^2}}{{\mathcal{M}}_N\left(\alpha \right)}\sum \limits_{n,m=0}^{N-1}\sum \limits_{j=0}^{+\infty }{\left|\alpha \right|}^{2\left(j+l\right)}{\left({\gamma}_n{\gamma}_m^{\ast}\right)}^{\left(j+l\right)}\frac{\left(k+j\right)!}{{\left(j!\right)}^2} $$
(7)

where \( {\gamma}_n={e}^{i\frac{2\pi }{N}n},{\gamma}_m\ast ={e}^{-i\frac{2\pi m}{N}} \) and Ln(x) is the Laguerre polynomial of n order. For N = 1, one gets the normalization constant \( {\mathrm{N}}_{as1}^{k,l} \) (α) of PASCS given in [22]. We notice also that for (k,l) = (0,0) and N = 1, recovers the Glauber coherent state [24].

3 Non Classical and Non Gaussian Properties

The non classical and non Gaussian properties of PASN-HCS or PSAN-HCS can be investigated by many methods, There are several tools such us: Photon Number Distribution PND [31], Q function [32], P function [33], Mandel parameter [34], Wigner function [35, 36]. We compute Mandel parameter and Wigner function for N-HCS, PASN-HCS and PSAN-HCS. We compare their quantum properties with unknown states, coherent state and PASCS [22], to decide the better one to implement in quantum information processing.

3.1 Mandel Parameter

The Mandel parameter [34] measures the deviation of photon number statistics from the poissonian distribution. In particular, when (Q = 0) the field obeys a poissonian photon statistics, for (Q > 0) the field obeys a super-poissonian photon statistics, and for (Q < 0) the field obeys a sub-poissonian photon statistics. The negativity of Q refers to nonclassicality of the state.

The negativity of Q is only sufficient condition, but not necessarily to distinguish a non classical state from a classical one [22]. The Mandel parameter is defined by

$$ Q=\frac{\left\langle {a}^{+2}{a}^2\right\rangle }{\left\langle {a}^{+}a\right\rangle }-\left\langle {a}^{+}a\right\rangle $$
(8)

3.1.1 Photons Added Then Subtracted Multi-Headed Cat State

In PASN-HCS, the mean values of the operators 〈a+a〉 and a+2a2 are defined by

$$ {\displaystyle \begin{array}{c}\left\langle {a}^{+}a\right\rangle =\frac{e^{-{\left|\alpha \right|}^2}}{{\left({\mathrm{N}}_{asN}^{k,l}\right)}^{-1}}\\ {}\times \sum \limits_{j=0}^{l+1}\frac{{\left(\left(l+1\right)!\right)}^2\left(\mathrm{k}+l+1-j\right)}{{\left(-1\right)}^jj!{\left(\left(l+1-j\right)!\right)}^2}\sum \limits_{n,m=0}^{N-1}{L}_{k+l+1-j}\left(-{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast}\right){e}^{{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast }}\end{array}} $$
(9)

and

$$ {\displaystyle \begin{array}{c}\left\langle {a}^{+2}{a}^2\right\rangle =\frac{e^{-{\left|\alpha \right|}^2}}{\left({\mathrm{N}}_{asN}^{k,l}\right){-}^1}\\ {}\times \sum \limits_{j=0}^{l+2}\frac{{\left(\left(l+2\right)!\right)}^2\left(k+l+2-j\right)}{{\left(-1\right)}^jj!{\left(\left(l+2-j\right)!\right)}^2}\sum \limits_{n,m=0}^{N-1}{L}_{k+l+2-j}\left(-{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast}\right){e}^{{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast }}\end{array}} $$
(10)

In the Fig. 1, we analyzed the behavior of Mandel parameter for different values of k (addition), l (subtraction) and N (number of superposition).

Fig. 1
figure 1

(a) Mandel parameter of N-HCS ((k, l) = (0,0)), for different values of N. (b) Mandel parameter of PASN-HCS for N = 3 and different values of k (k = l), (c) Mandel parameter of PASN-HCS for N = 3 and different values of k and l for (k  ≠ l)

Full size image

Three situations are depicted in Fig. 1. The Fig. 1-a shows a nonclassicality of N-HCS for N > 1, N = 1 is the coherent state associated curve. The nonclassicality aspects manifest when N increases but on strait interval of α. Figure 1-b (k = l) shows that the nonclassicality depth becomes important and the domain of α where Q is positive started fading when the couple (k = l) reaches to their tops values, Fig. 1-c (k ≠ l) the nonclassicality manifests in all situations, but it’s important when k > l. We can conclude from Fig. 1 that adding then subtracting operation has a great effect on increasing the nonclassicality feature of the state.

3.1.2 Photons Subtracted Then Added Multi-Headed Cat State

In this case the mean values of the operators 〈a+a〉 and 〈a+2a2〉 are defined by

$$ \left\langle {a}^{+}a\right\rangle =\frac{\sum \limits_{n,m=0}^{N-1}\sum \limits_{j=0}^{+\infty }{\left|\alpha \right|}^{2j}{\left({\gamma}_n{\gamma}_m^{\ast}\right)}^{\left(j+l\right)}\frac{\left(\mathrm{k}+1+\mathrm{j}\right)!-\left(\mathrm{k}+\mathrm{j}\right)!}{{\left(\mathrm{j}!\right)}^2}}{\sum \limits_{n,m=0}^{N-1}\sum \limits_{j=0}^{+\infty }{\left|\alpha \right|}^{2j}{\left({\gamma}_n{\gamma}_m^{\ast}\right)}^{\left(j+l\right)}\frac{\left(\left(k+j\right)!\right)}{{\left(j!\right)}^2}} $$

and

$$ \left\langle {a}^{+2}{a}^2\right\rangle =\frac{\sum \limits_{n,m=0}^{N-1}\sum \limits_{j=0}^{+\infty }{\left|\alpha \right|}^{2j}{\left({\gamma}_n{\gamma}_m^{\ast}\right)}^{.\left(j+l\right)\frac{\left(\left(k+2+j\right)!-4\left(k+j\right)!+2\left(k+j\right)!\right)}{{\left(j!\right)}^2}}}{\sum \limits_{n,m=0}^{N-1}\sum \limits_{j=0}^{+\infty }{\left|\alpha \right|}^{2j}{\left({\gamma}_n{\gamma}_m^{\ast}\right)}^{\left(j+l\right)}\frac{\left(\left(k+j\right)!\right)}{{\left(j!\right)}^2}} $$

Two situations are depicted in Fig. 2. Figure 2-a shows a strong non classical property of PSAN-HCS for all values of (k, l) ≥ (1,1), the nonclassicality depth increases when the couple (k = l) increases. Furthermore, it’s more interesting compared to Fig. 1-b, there is no positives values of Q even for the feeble values of α. Likely in Fig. 2-b, the nonclassicality manifest in all situations, and it’s interesting compared to Fig. 1-c, it preserves high nonclassicality depth longer than PASN-HCS k ≠ l. We can remark that subtracting then adding operation has an interesting effect compared to adding then subtracting operation on increasing and performing the non classical property.

Fig. 2
figure 2

(a) Mandel parameter of PSAN-HCS for N = 3 and different values of k (k = l), (b) Mandel parameter of PSAN-HCS for N = 3 and different values of (k ≠ l)

Full size image

3.2 Wigner Function

To confirm the results discussed above, we employ the Wigner function to study the non classical property of photon added-subtracted multi headed cat state. It is well known that the negativity of Winger function is a strong indication of the nonclassicality for a given state [36]. However, it must noticed that the total positivity is not always a synonym of classicality. For instance, the Wigner function of a squeezed vacuum state is totally positive but in the literature it’s a non classical state [6]. In the coherent state representation |ɀ〉, the Wigner function is defined by [37, 38].

$$ W\left(\beta, {\beta}^{\ast },z\right)={e}^{2{\left|\beta \right|}^2}{\int}_{-\infty}^{+\infty}\frac{d^2z}{\pi^2}\left\langle -z|\rho |z\right\rangle {e}^{-2\left({\beta}^{\ast }z-\beta {z}^{\ast}\right)} $$
(11)

where ρ is the density operator. TheWigner function of associated states is measured with taken into account the IWOP technique measurement [39].

– For photon added then subtracted multi-coherent state

$$ {\displaystyle \begin{array}{c}{W}_N^{k,l}\left(\beta, \alpha \right)=\frac{e^{-2{\left|\beta \right|}^2-{\left|\alpha \right|}^2}}{{\mathrm{N}}_{asN}^{k,l}{\mathcal{M}}_N}\sum \limits_{n,m=0}^{N-1}\sum \limits_{h=0}^k\frac{{\left(-1\right)}^h{\left(k!\right)}^2}{h!{\left(\left(k-h\right)!\right)}^2}{H}_{k-\mathrm{h},l}\left(-i\left(2{\beta}^{\ast }-{\alpha}^{\ast }{\gamma}_m^{\ast}\right),- i\alpha {\gamma}_n\right)\\ {}\times {H}_{l,k-h}\left(i{\alpha}^{\ast }{\gamma}_m^{\ast },i\left(2\beta -\alpha {\gamma}_n\right)\right){e}^{-{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast }+2\beta {\alpha}^{\ast }{\gamma}_m^{\ast }+2{\beta}^{\ast}\alpha {\gamma}_n}\end{array}} $$
(12)

  • For photon subtracted then added multi-coherent state

$$ {\displaystyle \begin{array}{c}{W}_N^{l,k}\left(\beta, \alpha \right)=\frac{e^{-2{\left|\beta \right|}^2-{\left|\alpha \right|}^2}}{{\mathrm{N}}_{saN}^{k,l}{\mathcal{M}}_N}\sum \limits_{n,m=0}^{N-1}\sum \limits_{h=0}^k\frac{{\left(-1\right)}^h{\left(k!\right)}^2}{h!{\left(\left(k-h\right)!\right)}^2}{H}_{k-h,l}\left(\left(2{\beta}^{\ast }-{\alpha}^{\ast }{\gamma}_m^{\ast}\right),\alpha {\gamma}_n\right)\\ {}\times {H}_{l,k-h}\left({\alpha}^{\ast }{\gamma}_m^{\ast },\left(2\beta -\alpha {\gamma}_n\right)\right){e}^{-{\left|\alpha \right|}^2{\gamma}_n{\gamma}_m^{\ast }+2\beta {\alpha}^{\ast }{\gamma}_m^{\ast }+2{\beta}^{\ast}\alpha {\gamma}_n}\end{array}} $$
(13)

where Hn,m is the bivariate Hermite polynomial [40].

In Fig. 3 we give the contour plots representation of PASN-HCS and PSAN-HCS’s Wigner function for different cases of (N, k, l, α). With intention to explore the effect of each parameter. βi and βr stand for real and imaging parts of the complex variable β(β = βr + iβi).

Fig. 3
figure 3

Contours plots of photon added-subtracted N-HCS’s Wigner function for different situation of parameters (N,k, l and a), (a) N = 3 with (k = 0, l = 0) and a = 1 (b) N = 3 with k = l = 1 and a = 5 (c) N = 3 in case of k = l with k = l = 2 and a = 1 for PASN-HCS (d) N = 3 in case of k = l with k = l = 2 and a = 1 for PSAN-HCS (e) N = 3 in case of k ≠ l with (k = 2, l = 1) and a = 1 for PASN-HCS (f) N = 3 in case of k ≠ l with (k = 2, l = 1) and a = 1 for PSAN-HCS for various values of N

Full size image

Figure 3 resume a various aspects of photon added-subtracted multi-coherent state, by manipulating the parameters characterizing the state (N, k, l, α) in the Wigner function and the order of adding subtracting operators. The effect of increasing the number of superposition N is depicted in Fig. 3-a which represent three parts negatives for N = 3 indicating a non classical aspect of the state, with taken into account that null photon is added or subtracted k = l = 0 and α = 1. As long as the number of superposition N increases we find exactly N parts negative with the same negativity deep (N = 4 - four parts negative ...). The non classicality aspect is preserved even for a high values of α Fig. 3-b. The non classical property increases when the couple (k, l) numbers take a value. For k = l ≠ 0 and k ≠ l ≠ 0 in Fig. 3-e-f respectively, the non classicality deep becomes important compared to the first contour plot Fig. 3-a where k = l = 0 confirming the Mandel Q parameter result in section 3.1. Furthermore, the order of adding and subtracting operations has a magnificent influence on the non classical behavior of the result state. The non classicality deep of photon subtracted then added multi-coherent state Fig. 3-d-f is interesting compared to the opposite scenario PAS-NHCS Fig. 3-c-e with respecting the same conditions of all other parameters in the both scenarios.

For summarizing, in all cases discussed formerly within Mandel parameter and Wigner function, the non classical property manifests for all situations, except for (k = l = 0, N = 1). Furthermore, the non classical property is important with photons subtracted then added multi-headed cat states compared to photons added then subtracted multi-headed cat states. Besides the effect of k, l, and N parameters had a great influence in improving the non classical property for the two cases, challenging by that coherent state and PASCS [22].

The role of Wigner distribution is not limited only on measuring the non classical property. But it gives us also an idea about the non Gaussian property through the forms that the contours plots take. The non-Gaussian character manifests in all figures except for the coherent state representation [24] which has a Gaussian form. This property it can be verified by measuring the non-Gaussianity function S[ρ] and the fidelity F. This is discussed in the next sections.

3.3 Non-Gaussianity measures

We define the non-Gaussianity S[ρ] of state ρ [41, 42] as a quantity based on distance between ρ and reference Gaussian state τ which depends itself on ρ. It’s given by

$$ S\left[\rho \right]=\frac{1}{2}+\frac{Tr\left[{\tau}^2\right]-2 Tr\left[\rho \tau \right]}{2 Tr\left[{\rho}^2\right]} $$
(14)

and four our case, τ is the density operator of the typical Gaussian state |α〉 (coherent state) S[τ] = 0 and ρ is the density operator of PASN-HCS or PSAN-HCS.

Figure 4-a show that PASN-HCS has non Gaussian property more than the famous non Gaussian cat state (red curve), they show also that adding then subtracting operation increases the non Gaussian property especially when k > l.

Fig. 4
figure 4

(a) Plot of non-Gaussianity S[ρas] of ρas density operator of PASN-HCS. (b) Plot of non-Gaussianity S[ρsa] of ρsa density operator of PSAN-HCS

Full size image

Figure 4-b show a strong behavior of PSAN-HCS compared to PASN-HCS. The non Gaussian property takes a high value from the first values of α for all (k ≠ 0, l ≠ 0).

3.4 Fidelity

The fidelity measures the similarity degree between two given states if the properties of such a state are known, it is called the reference state, and we denote it |ϕ〉 and the state whose properties are unknown we denote it |ψ〉. The expression of fidelity as a function of |ϕ〉 and |ψ〉 is given by

$$ F={\left|\left\langle \psi |\phi \right\rangle \right|}^2 $$

where |ϕ〉 and |ψ〉 are two dependent states. For our case, we seek the similarity degree of the non Gaussian and non classical properties, so the reference state must satisfies both the Gaussian and classical properties. The coherent state are the typical Gaussian and classical states known in the literature [43]. Thus to discuss the similarity degree of the states PASN-HCS and PSAN-HCS, we shall compute their overlap with coherent state |α〉

$$ F=\mid \Big\langle {\psi}_N\left(\alpha \right){\left|\alpha \Big\rangle \right|}^2 $$

The effect of adding and subtracting in N-HCS is examined by computing the overlap between the (PASN-HCS, PSAN-HCS) and N-HCS.

$$ F=\mid \Big\langle {\psi}_N(a){\left|{C}_N(a)\Big\rangle \right|}^2 $$

Figure 5 discusses on one hand the similarity degree between coherent state and multi-headed cat state concerning the Gaussian and classical properties. Which shows that multi-headed cat state has non-Gaussian and non-classical properties and which is totally different with the coherent state, confirming by this the results of Mandel’s parameter and the Wigner function. On the other hand, it represents the degree of similarity between multi-headed cat state and photon added-subtracted multi-headed cat state which show the effect of addition and subtraction operation on increasing the non Gaussian and non-classical properties.

Fig. 5
figure 5

(a) Plot of the similarity degree between PAS3-HCS and a coherent state and 3-HCS in case of (k = l). (b) Plot of the similarity degree between PSA3-HCS and a coherent state and 3-HCS in case of (k = l)

Full size image

3.5 Experimental Scheme of Photon Addition and Subtraction

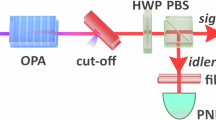
The main devices for the implementation of the photon addition and subtraction are the parametric-down conversion PDC and a high transmission beam splitter HT-BS. They share a very similar quantum description despite of tools differences. To realize photon addition Fig. 6-a we combine the mode \( \hat{a} \) with second mode \( \hat{b} \) prepared in its vacuum state using a weak non linear optical down conversion process PDC; which is a crystal produces pair of daughter photons from a single pump. Because the energy and momentum conversion laws have to be obeyed in the process. If a photon is detected in the output \( \hat{b} \) mode then the output \( \hat{a} \) mode conditioned on this detection will be the photon added state. To realize photon subtraction we proceed in the same way but utilize a high transmission beam splitter HT-BS as described in Fig. 6-b. If a photon is detected in the output \( \hat{b} \) mode then the output \( \hat{a} \) conditioned on this detection will be the photon subtracted state. For the mathematical description of the two processes see [44]. We can realize at least in principle multiple photon subtracted or added by combining a number of single photon subtraction or addition [45, 46], and to eliminate the devices noise while implementing photon addition and photon subtraction, there is a protocol of noise reduction [47] or filtering the light state using an appropriate device integrated in the hall manipulation of photon addition and subtraction [48].

Fig. 6
figure 6

Experimental scheme of (a): photon addition using parametric down conversion PDC and (b): photon subtraction using a high transmission beam splitter HT-BM

Full size image

4 Conclusions and Discussion

We have shown the non classicality of multi-headed cat state for all values of N > 1, then we analyzed the effect of adding / subtracting photons on the behavior of N-HCS in two different ways, add first then subtract and subtract first then add.

We exhibit using Mandel parameter and Wigner function, that the nonclassicality is more interesting with PSAN-HCS than PASN-HCS in different situations of parameters N, k, l, α by absence of positive values on Mandel parameter representation and an important negativity depth presented in the Wigner function representations. Results showing a strong properties compared to coherent state and to PASCS [22]. The non Gaussian property also discussed by mean of non Gaussian measurement, the non Gaussianity manifests essentially with PSAN-HCS than PASN-HCS, by presenting a strong non Gaussian character from the feeble values of α in contrary to PASN-HCS, and it’s become important when the couple (k, l) increases. Fidelity complete the analyzes of both properties by displaying a strong properties of PASN-HCS and PSAN-HCS compared to N-HCS and coherent state.

From all analyzes below, PSAN-HCS is the robust candidate to implement in quantum information processing, due to their solid properties.