Experimental preparation of multiphoton-added coherent states of light

Abstract

Conditional addition of photons represents a crucial tool for optical quantum state engineering and it forms a fundamental building block of advanced quantum photonic devices. Here we report on experimental implementation of the conditional addition of several photons. We demonstrate the addition of one, two, and three photons to input coherent states with various amplitudes. The resulting highly nonclassical photon-added states are completely characterized with time-domain homodyne tomography, and the nonclassicality of the prepared states is witnessed by the negativity of their Wigner functions. We experimentally demonstrate that the conditional addition of photons realizes approximate noiseless quantum amplification of coherent states with sufficiently large amplitude. We also investigate certification of the stellar rank of the generated multiphoton-added coherent states, which quantifies the non-Gaussian resources required for their preparation. Our results pave the way towards the experimental realization of complex optical quantum operations based on combination of multiple photon additions and subtractions.

Introduction

Preparation and controlled manipulation of non-classical states of light lies at the heart of quantum optics and represents a key tool for the rapidly developing optical quantum technologies. In optical quantum state engineering, the experimentally accessible operations include Gaussian transformations^1,2 such as squeezing, interference at beam splitters, or coherent displacements, and single-photon detection. The photon number measurement brings in the required effective nonlinear interaction and is the key enabling tool for conditional preparation of highly non-classical quantum states of light^3,4, and for engineering transformations of optical quantum states beyond the realm of Gaussian operations.

The most fundamental elementary quantum operations on optical modes are arguably the addition or subtraction of a single photon described by the bosonic creation and annihilation operators ${\hat{a}}^{\dagger }$ and $\hat{a}$, respectively. Conditional photon addition^5,6,7,8 and subtraction^9,10,11,12 are powerful tools in quantum photonics and they are utilized in a wide range of schemes and experiments. Possible applications include continuous-variable entanglement distillation^{13,14,15,16,17}, implementation of noiseless quantum amplifiers^{18,19,20,21,22}, enhancement of squeezing^23,24, generation of Schrödinger cat-like states^{10,11,12,25,26,27,28,29,30,31,32,33,34}, Gottesman-Kitaev-Preskill (GKP) states^35,36 or arbitrary single-mode quantum states^37,38,39, preparation of hybrid entangled states of light^40,41, and emulation of strong Kerr nonlinearity at the few-photon level^18,42. On the more fundamental side, coherent combinations of sequences of single-photon addition and subtraction enabled experimental test of the fundamental quantum commutation relation $[\hat{a},{\hat{a}}^{\dagger }]=\hat{1}$⁴³, and the quantum-to-classical transition was studied by adding single photons to coherent states with progressively increasing amplitude⁵.

For advanced applications and flexible quantum state engineering, simultaneous subtraction or addition of several photons is indispensable. While subtraction of up to ten photons has been demonstrated experimentally^44,45, the experimental photon additions were limited to one photon^5,7,8. In this paper, we report on the conditional addition of up to three photons to coherent states of various amplitudes. Photons are generated in an optical parametric amplifier and coherently added to the input state directly in the nonlinear crystal. Preparation of n-photon-added coherent state in a signal mode of the amplifier is heralded by the detection of n photons in the auxiliary idler mode. Prepared states are detected using a custom-built time-domain homodyne detector facilitating stable measurements on a time scale of hours.

We comprehensively characterize the generated quantum states by quantum state tomography. We achieve high fidelity of the generated states and observe their highly nonclassical features such as the negativity of the Wigner function. Following recent theoretical proposal²², we experimentally demonstrate that multiple photon addition enables approximate noiseless amplification of coherent states with large enough amplitude. Finally, we also analyze the certification of the stellar rank^46,47,48 of the prepared states. The stellar rank quantifies the non-Gaussian resources required for the preparation of the state. For ideal n-photon-added coherent states, the stellar rank is equal to the number of added photons. Our results significantly broaden the range of experimentally available elementary non-Gaussian quantum operations and pave the way towards complex engineering of quantum states and operations via combinations of multiple photon additions and subtractions.

Results

Generation of multiphoton-added coherent states

Photon-added coherent states (PACS) are obtained by repeated action of creation operator ${\hat{a}}^{\dagger }$ on a coherent state $\left\vert \alpha \right\rangle$⁴⁹,

$$\left\vert \alpha ,n\right\rangle ={{\mathcal{N}}}_{n}(\alpha ){\hat{a}}^{\dagger n}\left\vert \alpha \right\rangle .$$

(1)

Here ${{\mathcal{N}}}_{n}(\alpha )={[\langle \alpha | {\hat{a}}^{n}{\hat{a}}^{\dagger n}| \alpha \rangle ]}^{-1/2}$ is a normalization factor and n denotes the number of photons added to the coherent state. The n-photon-added coherent state $\left\vert \alpha ,n\right\rangle$ can be expressed as a coherently displaced superposition of the first n + 1 Fock states⁴⁹,

$$\left\vert \alpha ,n\right\rangle ={{\mathcal{N}}}_{n}(\alpha )\hat{D}(\alpha )\left[\mathop{\sum }\limits_{m=0}^{n}\frac{n!{({\alpha }^{* })}^{n-m}}{\sqrt{m!}(n-m)!}\left\vert m\right\rangle \right],$$

(2)

where $\hat{D}(\alpha )=\exp (\alpha {\hat{a}}^{\dagger }-{\alpha }^{* }\hat{a})$ denotes the displacement operator. Therefore, up to coherent displacement in the phase space, the generation of PACS $\left\vert \alpha ,n\right\rangle$ amounts to the preparation of specific coherent superpositions of the first n + 1 Fock states.

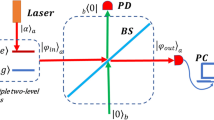
To experimentally generate the n-photon-added coherent states we utilize an optical parametric amplifier (OPA) in a pulsed single-pass regime^50,51, see Fig. 1. The input signal mode (S) is seeded with a coherent state $\left\vert \alpha \right\rangle$ while the idler mode (I) is initially in a vacuum state. The nonlinear interaction in OPA generates correlated photon pairs in signal and idler modes. Detection of n photons in output idler mode by a photon-number-resolving detector based on spatial multiplexing (see Methods) then heralds the addition of n photons into the signal mode. Note that the implemented addition of photons is probabilistic but fully heralded and does not require postselection. The generated multiphoton-added coherent states in the signal mode at the crystal output are freely propagating and are fully available and accessible for further processing and interactions. In our experiment, the generated states in signal mode are measured by a home-built balanced homodyne detector (BHD) with a 12 dB signal-to-noise ratio and 100 MHz bandwidth. More details on the experimental setup are provided in the Supplementary Information.

Fig. 1: Schematic of the preparation of n-photon-added coherent states.

A coherent state $\left\vert \alpha \right\rangle$ is seeded into the signal mode of an optical parametric amplifier (OPA). Once the residual pump field is filtered out, the signal and idler modes are separated by the polarizing beam splitter (PBS). Detection of n photons at the photon number resolving detector (PNRD) in the idler mode projects the signal mode to the desired n-photon-added coherent state.

Experimental results

In our experiment, we generate the single-photon-added coherent states,

$${\hat{a}}^{\dagger }\left\vert \alpha \right\rangle =\hat{D}(\alpha )\left(\left\vert 1\right\rangle +{\alpha }^{* }\left\vert 0\right\rangle \right),$$

(3)

two-photon-added coherent states,

$${\hat{a}}^{\dagger 2}\left\vert \alpha \right\rangle =\hat{D}(\alpha )\left(\sqrt{2}\left\vert 2\right\rangle +2{\alpha }^{* }\left\vert 1\right\rangle +{\alpha }^{* 2}\left\vert 0\right\rangle \right),$$

(4)

and also three-photon-added coherent states

$${\hat{a}}^{\dagger 3}\left\vert \alpha \right\rangle =\hat{D}(\alpha )\left(\sqrt{6}\left\vert 3\right\rangle +3\sqrt{2}{\alpha }^{* }\left\vert 2\right\rangle +3{\alpha }^{* 2}\left\vert 1\right\rangle +{\alpha }^{* 3}\left\vert 0\right\rangle \right).$$

(5)

We comprehensively characterize the generated states by homodyne tomography. We utilize the maximum likelihood algorithm^52,53 to reconstruct the density matrix of a state from the sampled homodyne data. We estimate that the homodyne detection is affected by total losses of 43% (see Methods). These losses are compensated for in the reconstruction and included in the description of the effective POVM that describes the homodyne detection.

The reconstructed density matrices $\hat{\rho }$ are compared with the ideal states (1) and their fidelity $F=\langle \alpha ,n| \hat{\rho }| \alpha ,n\rangle$ is computed. We achieve good quality of state preparation with many of the fidelities exceeding 90%. We also calculate the purity of the reconstructed states, ${\mathcal{P}}={\rm{Tr}}[{\hat{\rho }}^{2}]$, and the heralding probability P_H, which is determined as the ratio of the number of heralding events N_H and the number of all emitted laser pulses N_L within the measurement time t. We summarize the parameters of the generated states in Table 1. The amplitudes α in the second column of Table 1 were determined from tomographic reconstructions of the input coherent states based on collected homodyne data.

Table 1 Fidelity F and purity ${\mathcal{P}}$ of the experimentally generated n-photon-added coherent states with input amplitude α are listed together with the corresponding experimental probability P_H of generation of each state

In Fig. 2 we plot Wigner functions of several experimentally generated n-photon-added coherent states. We can see that the generated states are highly non-classical. The experimental Wigner functions are negative in some regions of the phase space and exhibit interference patterns whose complexity increases with the number of added photons. All the generated n-photon-added coherent states also exhibit sub-Poissonian photon number distribution, as witnessed by Fano factors smaller than 1 (see Supplementary Information).

Fig. 2: Wigner functions of the experimentally generated n-photon-added coherent states.

Shown are the Wigner functions of single-photon-added coherent states with initial seed amplitudes 0.43 (a) and 0.98 (b), Wigner functions of two-photon-added coherent states with seed amplitudes 0.34 (c) and 0.71 (d), and Wigner functions of three-photon-added coherent states with seed amplitudes 0.32 (e) and 0.94 (f).

Besides the Wigner functions, it is also instructive to look at the reconstructed density matrices in the Fock basis. As an example, we plot in Fig. 3 density matrices of three experimentally generated PACS. For reference and comparison, we plot in this figure also the corresponding reconstructed input coherent states. As expected, the addition of n photons largely suppresses the population of the lowest Fock states up to $\left\vert n-1\right\rangle$. The remaining population of these states is caused by experimental imperfections. In order to better visualize the structure of the generated states, we apply to each reconstructed density matrix of PACS an inverse coherent displacement $\hat{D}(-{\alpha }_{j})$, where α_j denotes the amplitude of the corresponding seed coherent state. The resulting states become localized in the Fock space and have the expected form of a superposition of the first n + 1 Fock states (2), and only very small fraction of the states lies outside this subspace. The generated states exhibit similar complexity as states prepared by conditional measurement on one part of two-mode entangled state, which also enables engineering of various superpositions of Fock states^54,55,56,57. The advantage of our present approach is that the heralded conditional quantum operation ${\hat{a}}^{\dagger n}$ can be applied to any input state, which represents an important enabling step towards engineering of complex non-Gaussian optical quantum operations¹⁸.

Fig. 3: Examples of reconstructed density matrices in Fock basis.

Density matrices of the initial coherent states are plotted in the first column. Density matrices of the experimentally generated n-photon-added coherent states are displayed in the second column. Finally, the last column shows the density matrices of the n-photon-added coherent states coherently displaced by $\hat{D}(-\alpha )$, which in theory should result in a finite superposition of Fock states up to $\left\vert n\right\rangle$. The results are shown for single-photon-added coherent state with α = 1.43 (a–c), two-photon-added coherent state with α = 0.71 (d–f), and three-photon-added coherent state with α = 0.94 (g–i). Real parts of the reconstructed density matrices are plotted. The imaginary parts of the matrix elements ρ_jk are mostly negligible and in all cases smaller than 0.075. The insets contain plots of photon number distributions of the reconstructed states.

The high quality of our source of correlated photon pairs enables fast collection of sufficient data for complete tomography of the generated n-photon-added coherent states. Still, the heralding probability rapidly decreases with the increasing number of added photons. A single-photon addition has a typical heralding probability of 10⁻⁴ per pulse. By contrast, the typical heralding probability of two-photon addition decreases to 10⁻⁶ per pulse, and for three-photon addition it is further reduced below 10⁻⁹ per pulse. With the laser repetition rate of 76 MHz, the collection of several thousands of quadrature samples requires only a few seconds for the single-PACS state. This increases to minutes for two-PACS and to several hours for the three-PACS. The main factor affecting the heralding probability scaling is the probability of pair generation in the nonlinear crystal. Nevertheless, limited single-photon detection efficiency η and the design of our photon number resolving detector also contribute to reduced P_H. Just by using highly efficient superconducting single-photon detectors and a PNRD with a large enough number of channels, we could increase the heralding probability of three-PACS by an order of magnitude.

Noiseless amplification of light via photon addition

As theoretically shown in ref. ²², conditional photon addition can result in approximate noiseless amplification of the input coherent state (see Methods). This noiseless quantum amplifier works well for larger coherent state amplitudes, while it gives poor results for small ∣α∣ because it transforms a vacuum state onto Fock state $\left\vert n\right\rangle$. Amplification gain of the noiseless amplifier based on conditional addition of n photons can be defined as the ratio of complex amplitudes of the input and output states,

$${g}_{n}(\alpha )=\frac{\langle \alpha ,n| \hat{a}| \alpha ,n\rangle }{\alpha }.$$

(6)

For n = 1 and n = 2 we explicitly obtain^22,58

$${g}_{1}(\alpha )=\frac{2+| \alpha {| }^{2}}{1+| \alpha {| }^{2}},\qquad {g}_{2}(\alpha )=\frac{6+6| \alpha {| }^{2}+| \alpha {| }^{4}}{2+4| \alpha {| }^{2}+| \alpha {| }^{4}}.$$

(7)

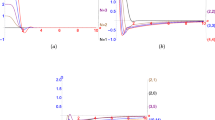
The gain is larger than 1, which is a signature of amplification. We plot the theoretical gains in Fig. 4a, b together with the experimentally determined gains for several different values of ∣α∣. The gain is a decreasing function of ∣α∣ and it approaches g = 1 for large ∣α∣. The experimental gains are not exactly real and exhibit small imaginary parts, caused by fluctuations and experimental imperfections. This means that the complex amplitude of the n-photon-added coherent state is not perfectly aligned with the amplitude of the input coherent state. In Fig. 4a, b we conservatively plot real parts of the complex gains, which for the observed small imaginary parts of the gains is almost indistinguishable from plotting the absolute values of the gains.

Fig. 4: Characterization of noiseless amplification of coherent states by n-photon addition.

a, b The theoretical amplification gains g₁(α) and g₂(α) are plotted as lines and dots mark the experimental data. c, d Experimentally determined variances of amplitude quadratures V_x (purple squares) and phase quadratures V_p (blue triangles) of the amplified states are plotted together with the theoretical dependencies (purple dot-dashed lines and blue dashed lines). As a benchmark, the red solid lines in (c, d) indicate quadrature variance achievable by deterministic amplifier with the theoretical gains g₁(α) and g₂(α), respectively. The red dots show variances for deterministic amplification with the experimentally observed gains. Vacuum variance is set to 1 and indicated by the black dashed line. The error bars represent one standard deviation. For most of the data, the error bars are smaller than the symbol size. Data are plotted for n = 1 (a, c) and n = 2 (b, d).

As visible from the plots of Wigner functions in Fig. 2, the photon-added coherent states are not fully symmetric and the variances of phase and amplitude quadratures differ. Without loss of generality, we can choose α to be real in which case the amplitude and phase quadratures are defined as $\hat{x}=a+{a}^{\dagger }$ and $\hat{p}=i({a}^{\dagger }-a)$, respectively. The quadrature variances can be expressed analytically for any n⁴⁹, but the expressions are rather lengthy and are provided in the Supplementary Information. Here we give explicit expressions for the single-photon-added and two-photon-added coherent states. For n = 1 we have

$${V}_{x}=\frac{3+| \alpha {| }^{4}}{{\left(1+| \alpha {| }^{2}\right)}^{2}},\qquad {V}_{p}=\frac{3+| \alpha {| }^{2}}{1+| \alpha {| }^{2}},$$

(8)

while for n = 2 we obtain

$${V}_{x}=\frac{20+8| \alpha {| }^{2}+12| \alpha {| }^{4}+4| \alpha {| }^{6}+| \alpha {| }^{8}}{{\left(2+4| \alpha {| }^{2}+| \alpha {| }^{4}\right)}^{2}},\qquad {V}_{p}=\frac{10+8| \alpha {| }^{2}+| \alpha {| }^{4}}{2+4| \alpha {| }^{2}+| \alpha {| }^{4}}.$$

(9)

The photon-added coherent states are non-Gaussian states, and therefore they are not minimum uncertainty states, and V_xV_p > 1. Nevertheless, the variances of both the amplitude and phase quadratures are smaller than the variances of the output of a deterministic linear phase insensitive amplifier with gain g. In this latter case

$${V}_{x}={V}_{p}=2{g}^{2}-1.$$

(10)

In Fig. 4c, d we plot the theoretical dependence of quadrature variances on ∣α∣ together with the experimentally observed values. The quadrature variances of the experimentally generated states are indeed well below the limit of a deterministic amplifier. This clearly demonstrates that the noise added by our probabilistic amplifier is much smaller than the noise that would be added by an ordinary linear quantum limited amplifier with the same amplification gain. This is one of the key properties and advantages of noiseless quantum amplifiers.

The phase quadrature variances V_p are monotonically decreasing functions of ∣α∣. The amplitude variances V_x also initially decrease but become increasing functions of ∣α∣ for large ∣α∣. Both V_x and V_p are maximized at ∣α∣ = 0 when the generated state is the Fock state $\left\vert n\right\rangle$. By contrast, we have V_x = V_p = 1 in the limit ∣α∣ → ∞. Interestingly, the amplitude quadrature V_x is reduced below the level of vacuum fluctuations, V_x < 1, for sufficiently large ∣α∣. Therefore, the n-photon-added coherent states can exhibit quadrature squeezing. This squeezing is not a consequence of interaction in a medium with high enough quadratic nonlinearity, but is a result of engineering specific superpositions of Fock states which exhibit this effect. We do observe this quadrature squeezing experimentally for specific states, see Fig. 4.

The closeness of the photon-added coherent state to some coherent state $\left\vert \beta \right\rangle$ can be quantified by fidelity ${F}_{c}(\beta )={\left\vert \langle \beta | \alpha ,n\rangle \right\vert }^{2}$. This fidelity is maximized for

$${\beta }_{{\rm{opt}}}=\frac{\alpha }{2}\left(1+\sqrt{1+\frac{4n}{| \alpha {| }^{2}}}\right).$$

(11)

Observe that ∣β_opt∣ > ∣α∣ yet also ∣β_opt∣ < g_n(α)∣α∣. As illustrated in Fig. 5, the maximal fidelity F(β_opt) is a monotonically increasing function of ∣α∣ and asymptotically approaches unity. For comparison, we plot in Fig. 5 also the theoretical and experimentally determined fidelity of the n-photon-added coherent state with coherent state with amplitude g_n(α)α. The graphs in Fig. 5 quantitatively illustrate how the similarity of the n-photon-added coherent state with an ordinary coherent state increases with increasing ∣α∣. For small ∣α∣ the state $\left\vert \alpha ,n\right\rangle$ is very different from a coherent state hence the fidelity F_c is small. In this region, the fidelity with coherent state $\vert {\beta }_{\mathrm{opt}}\rangle$ is significantly larger than the fidelity with the coherent state $\vert g(\alpha )\alpha\rangle$. Consider in particular the point α = 0, where the generated n-photon added state is the n-photon Fock state $\left\vert n\right\rangle$. For n > 0 fidelity of this state with vacuum vanishes, while the fidelity with a coherent state with optimal amplitude β_opt is nonzero. Specifically, we have $\mathop{\lim }\nolimits_{| \alpha | \to 0}{\beta }_{{\rm{opt}}}=\sqrt{n}$. It can be concluded from the fidelity plots in Fig. 5 that the noiseless amplification of coherent states based solely on addition of one or two photons works well for ∣α∣ ≳ 1 where the fidelities become large enough and the differences between the amplitudes β_opt and g_n(α)α practically vanish.

Fig. 5: Fidelities of n-photon-added coherent states with exact coherent states.

Red solid lines represent the theoretical dependence of fidelity with the coherent state with amplitude β_opt given by Eq. (11). Blue dashed lines depict theoretical fidelities with the coherent states with amplitude g_n(α)α, where g_n(α) is the amplification gain (7). Red circles and blue squares are the corresponding experimental fidelities determined from the reconstructed density matrices of the generated states. Data are plotted for n = 1 (a) and n = 2 (b).

Stellar rank of PACS

The conditional photon addition generates highly non-classical and quantum non-Gaussian states. Intuitively, one expects that the nonclassicality of the state increases with the number of added photons. This concept can be made rigorous by introducing the so-called stellar rank of quantum states⁴⁷. A pure single-mode quantum state $\left\vert \psi \right\rangle$ is said to have a stellar rank m if it can be transformed by some Gaussian unitary operation ${\hat{U}}_{G}$ to a superposition of the m + 1 lowest Fock states from $\left\vert 0\right\rangle$ up to $\left\vert m\right\rangle$,

$${\hat{U}}_{G}\left\vert \psi \right\rangle =\mathop{\sum }\limits_{n=0}^{m}{c}_{n}\left\vert n\right\rangle ,$$

(12)

with nonzero amplitude c_m. Equivalently, such states can also be called genuinely m-photon quantum non-Gaussian states⁴⁶. In the experimental practice, we deal with mixed states and it is therefore important to extend the definition of stellar rank to mixed states^47,48. We say that a state $\hat{\rho }$ has a stellar rank at least m if it cannot be expressed as a mixture of pure states with stellar rank m − 1. The n-photon-added coherent state has stellar rank n, which immediately follows from Eq. (2).

We can use fidelity $F=\langle {\psi }_{m}| \hat{\rho }| {\psi }_{m}\rangle$ of a quantum state $\hat{\rho }$ with some non-Gaussian state $\left\vert {\psi }_{m}\right\rangle$ with stellar rank m to certify the stellar rank of $\hat{\rho }$^47,48,59. For each stellar rank k ≤ m it is possible to establish a threshold fidelity F_th,k such that the state $\hat{\rho }$ has at least stellar rank k if

$$F \,>\, {F}_{{\rm{th}},k}$$

(13)

holds. Let us now specifically consider the fidelity with the n-photon-added coherent state, which can be used to certify stellar rank up to n. The corresponding fidelity thresholds for certification of various stellar ranks k = 1, 2, 3 are plotted in Fig. 6. Since coherent displacement is a Gaussian operation, we can equivalently consider fidelities with the finite Fock state superpositions in Eqs. (3), (4), and (5). The maximum fidelity of a coherent superposition of vacuum and single-photon state $\vert \psi \rangle ={c}_{0}\vert 0\rangle +{c}_{1}\vert 1\rangle$ with a Gaussian state was calculated numerically in ref. ⁴⁸. We have derived analytical formulas for the optimal Gaussian state that maximizes the fidelity, see Supplementary Information. The resulting fidelity threshold is plotted in Fig. 6a. The fidelity thresholds for two-photon and three-photon-added coherent states are plotted in Fig. 6b, c and were obtained numerically following the procedure described in refs. ^48,59.

Fig. 6: Fidelity thresholds F_th for certification of stellar ranks one (blue solid lines), two (red dashed lines) and three (green dot-dashed line) by fidelity with n-photon-added coherent state.

The thresholds are plotted for n = 1 (a), n = 2 (b) and n = 3 (c). Black dots indicate the experimentally obtained fidelities, as listed in Table 1. The insets show the reconstructed photon number distributions P_m of the experimentally generated single-photon, two-photon, and three-photon Fock states. Fidelity of the generated Fock state $\left\vert n\right\rangle$ is equal to P_n.

Figure 6 illustrates that the certification of stellar rank via fidelity becomes progressively more difficult with the increasing amplitude of the coherent state ∣α∣. This can be seen as quantification of the quantum-to-classical transition that is observed for photon-added coherent states when ∣α∣ increases⁵. For large ∣α∣ the vacuum term in the Fock-state superpositions (3), (4), and (5) becomes dominant while for α = 0 we get the Fock state $\left\vert n\right\rangle$. From the experimentally determined fidelities listed in Table 1 and plotted in Fig. 6 as black dots we can certify stellar rank one for five states and stellar rank two for only one state. We note that the fidelities are not necessarily the best stellar rank witnesses and one can attempt to construct more general witnesses⁵⁹. For instance, stellar rank one of the experimentally generated n-photon-added coherent states is witnessed by the negativity of their Wigner functions, c.f. Fig. 2.

Note also that achieving the observed fidelities of n-photon-added coherent states with a state of lesser stellar rank than n would generally require squeezing in addition to coherent displacements and photon addition. Although squeezing is considered to be experimentally feasible Gaussian operation, implementation of a pure unitary squeezing operation on a propagating ultra-short pulsed beam of light may be challenging. One could then modify the definition of the stellar rank and instead of all Gaussian operations ${\hat{U}}_{G}$ consider only passive single-mode Gaussian operations in Eq. (12), i.e. coherent displacements and phase shifts. This would result in criteria with lower threshold. Investigation of such modified criteria is beyond the scope of the present paper and will be the subject of future work.

Figure 6 suggests that certification of high stellar rank may be easiest for α = 0, when Fock state $\left\vert n\right\rangle$ is generated under ideal conditions. We plot in the insets of Fig. 6 the photon number distributions of the experimentally generated Fock states $\left\vert 1\right\rangle$, $\left\vert 2\right\rangle$ and $\left\vert 3\right\rangle$, respectively. Indeed, the fidelities of Fock states $\left\vert 1\right\rangle$ and $\left\vert 2\right\rangle$ are large enough to certify the stellar rank one and two, respectively. On the other hand, the data for Fock state $\left\vert 3\right\rangle$ are deteriorated due to low generation rate and long acquisition time, so than only stellar rank one can be certified for this state. Especially for Fock states, the certification of their stellar rank from homodyne detection appears to be more difficult than certification based on photon counting measurements⁴⁶. Certification of stellar rank of Fock states based on photon counting measurement can be achieve by observation of absence (or great suppression) of the n + 1-fold coincidences with respect to the n-fold coincidences. On the other hand, homodyne detection probes the photon number statistics only indirectly, and the state must be reconstructed by quantum tomography, which results in nonzero (albeit small) tail in the reconstructed photon number distribution. Nevertheless, the coherent homodyne detection is absolutely crucial in our experiment, because it allows full characterization of the generated states, including their coherences, off-diagonal density matrix elements in Fock basis, and complete Wigner functions.

Discussion

In summary, we have successfully experimentally implemented conditional addition of up to three photons to coherent states of light. The input coherent state is injected into the signal mode of an optical parametric amplifier and successful addition of n photons is heralded by detection of n photons in the output idler mode of the amplifier. We have completely characterized the generated state by a home-built time-domain homodyne detector with stable long-term operation over the time of 4 hours. The experimentally generated n-photon-added coherent states exhibit high fidelities, negative Wigner functions with complex interference patterns in phase space, and sub-Poissonian photon number statistics. Our analysis of the stellar rank of the generated photon-added coherent states confirms that our experimental setup provides an advanced non-Gaussian quantum resource. As an application, we have experimentally demonstrated approximate noiseless quantum amplification of coherent states by conditional photon addition, which works well for coherent states with not too small amplitude. The demonstrated results significantly broaden the range of experimentally available elementary non-Gaussian quantum operations and pave the way towards the experimental realization of complex optical quantum operations based on combination of multiple photon additions and subtractions.

In particular, by realizing coherent combinations of various sequences of additions and subtractions of N photons, we can implement arbitrary operations diagonal in Fock basis which can be expressed as polynomials of N-th order in the photon number operator $\hat{n}$¹⁸. This would extend the already experimentally demonstrated coherent superpositions of single-photon additions and subtractions $\hat{a}{\hat{a}}^{\dagger }$ and ${\hat{a}}^{\dagger }\hat{a}$^42,43 to higher N. A possible implementation is illustrated in Fig. 7. The photons can be subtracted both before and after the photon addition^18,42,43. The two beams that may contain the subtracted photons are spatially recombined at polarizing beam splitter PBS and projected onto a specific pure N-photon polarization state. This projection, together with the heralded addition of N photons, creates the coherent superposition of various sequences ${\hat{V}}_{j}={\hat{a}}^{N-j}{\hat{a}}^{\dagger N}{\hat{a}}^{j}$, with 0 ≤ j ≤ N. Each term ${\hat{V}}_{j}$ is a polynomial of N-th order in photon number operator. By projecting onto various N-photon polarization states we can generate arbitrary linear combinations of the N + 1 independent polynomials ${\hat{V}}_{j}$. Additional details are provided in the Supplementary Information, including an example of implementation of the single-mode nonlinear sign gate relevant in the context of quantum computing with linear optics.

Fig. 7: Schematic of implementation of coherent superpositions of various sequences of additions and subtractions of N photons^18,42,43.

Detection of N photons at the photon number resolving detector D₁ heralds the addition of N photons. Photons can be subtracted both before and after the addition using two unbalanced beam splitters BS₁ and BS₂. Detector D₂ projects the two polarization modes onto a specific pure N-photon polarization state which erases the which-way information and creates coherent superposition of various sequences of ${\hat{a}}^{N-j}{\hat{a}}^{\dagger N}{\hat{a}}^{j}$.

The achievable success probability of multiphoton addition can be significantly increased by addressing the limitations of our present setup. First, the limited detector efficiency of the utilized avalanche photodiodes and the design of our photon number resolving detector contribute to reduced success probability. Second, we have observed a low damage threshold of our PPKTP nonlinear crystals used in the OPA which strongly limited the gain of the OPA and forced us to operate it with a relatively weak pump beam focusing resulting in lower brightness of the source. By using more robust nonlinear crystals, highly efficient superconducting single-photon detectors, and increasing the number of detection channels of the multiplexed PNRD, the success probabilities can be increased by several orders of magnitude thereby paving way to experimental addition of even higher number of photons. Already with the present setup the experimental combination of conditional addition of two photons and conditional subtraction of two photons appears to be feasible and will be the subject of future work.

Methods

PNRD based on spatial multiplexing

Our PNRD is based on spatial multiplexing and consists of a combination of two tunable optical beam splitters formed by a half-wave plate and polarizing beam splitter, and three single-photon avalanche diodes serving as single-photon detectors (SPD) that can distinguish the presence or absence of photons. The addition of n photons is heralded by n-fold coincidence click of the detectors. We use a specific beam division configuration for each n. For single-photon addition, we send the whole idler beam to SPD₁. If we want to herald a two-photon addition, we evenly split the idler mode to SPD₁ and SPD₂. Finally, to herald the three-photon addition we evenly split the idler mode among all three detectors. Electronic outputs from SPDs are processed in a custom programmable coincidence unit. The coincidence unit allows to set coincidence window in the range of 0.5–5 ns, while a tunable time delay for each input channel is used for synchronization.

In the spatially multiplexed PNRD, multiple photons can sometimes impinge on the same SPD, which reduces the success probability of multiphoton detection. With our PNRD design, we can detect the incoming single photon with probability η, two photons with probability η²/2 and three photons with probability 2η³/9, where η is the detection efficiency of the SPD. The heralding can be also affected by false triggers arising from higher pair events, when at least n + 1 photons are present in the idler beam but only n-fold coincidence detection is observed. However, since the probability of pair generation in the crystal is less than 0.01 these higher photon contributions are negligible.

In our experiment, we change the configuration of the heralding photon-number resolving measurement in dependence on the targeted number of added photons n. However, this is done for technical reasons only. Specifically, the utilized coincidence logic did not allow us to evaluate more than one coincidence pattern. With a more sophisticated coincidence unit it would be possible to use a single fixed conditioning measurement scheme with several channels and several single-photon detectors, and process the signal from the detectors to count the number of detected idler photons at each run of the experiment. The heralding signal would then provide the information how many photons were added to the input state. In typical applications of photon addition one usually aims to perform some specific quantum operation which involves a well defined fixed number of photon additions. Therefore, the need to reconfigure the conditioning device depending on the number of targeted photon additions is not a significant limitation.

Estimation of the effective efficiency of homodyne detection

We estimate that the homodyne detection is affected by total losses of 43%. This includes losses due to the filtering optical fiber inserted in the path of the output signal beam (T₁ = 0.80), losses in other optical components after the crystal output (T₂ = 0.89), limited visibility of interference with the local oscillator (V = 0.96, T₃ = 0.92), quantum efficiency of the photodiodes in homodyne detector (T₄ = 0.92) and effective losses caused by finite SNR of the homodyne detector (T₅ = 0.944). The losses can be estimated as 1 − T, where $T=\mathop{\prod }\nolimits_{j = 1}^{5}{T}_{j}$ is the overall effective transmittance. Our calibration of the homodyne detector efficiency and the resulting estimation of the coherent-state amplitudes α can be cross-checked by measurements of the relative heralding probabilities of preparation of the n-photon-added coherent states. These measurements, which do not involve data from homodyne detector, confirm the consistency of our estimation of α (see Supplementary Information).

The optical fiber inserted in the path of the output signal beam is not strictly necessary, although there is some convenience in having the fiber in the setup. The alignment of the signal with the homodyne local oscillator is simplified because the signal and the local oscillator are outcoupled by the same type of outcoupler, ensuring good mode matching and thus visibility of the homodyne detection. Also, fiber-based distribution of the signal is space efficient. If we do not include the losses imposed by the fiber into the total detection efficiency budget, we still obtain losses of 29%, given by $1-\mathop{\prod }\nolimits_{j = 2}^{5}{T}_{j}$. For comparison, we have performed reconstruction of the generated quantum states without compensating for the losses imposed by the fiber. The fidelities and purities of the reconstructed states remain high and are typically reduced only by a few percent with respect to the full loss compensation. For details, see Table S1 in the Supplementary Information.

Noiseless amplification via photon addition

Deterministic noiseless amplification of coherent states is forbidden by the laws of quantum mechanics. An ideal probabilistic noiseless quantum amplifier is described by the operator ${g}^{\hat{n}}$, with $\hat{n}={\hat{a}}^{\dagger }\hat{a}$ and g > 1, and we have⁶⁰

$${g}^{\hat{n}}\vert \alpha \rangle ={e}^{({g}^{2}-1)| \alpha {| }^{2}/2}\vert g\alpha \rangle .$$

(14)

The operator ${g}^{\hat{n}}$ is unbounded and therefore unphysical. Experimental implementations of the noiseless quantum amplifiers^{20,21,61,62,63,64} therefore approximate the unphysical operation (14). Noiseless amplification requires modulation of amplitudes of Fock states such that the amplitudes of higher Fock states are enhanced with respect to the amplitudes of the low Fock states. A canonical example is the noiseless quantum amplifier based on the combination of conditional photon addition and subtraction, which applies the operation $\hat{a}{\hat{a}}^{\dagger }=\hat{n}+1$ to the input state^18,19,21. Alternative implementations based on quantum scissors enhance the amplitude of the single-photon state with respect to the amplitude of the vacuum state, while removing the rest of the state^61,62. One may then wonder how the noiseless amplification based solely on photon addition fits into this picture.

To get some insight, recall that coherent state is the eigenstate of the annihilation operator, $\hat{a}\left\vert \alpha \right\rangle =\alpha \left\vert \alpha \right\rangle$. Therefore, the state ${\hat{a}}^{\dagger n}\left\vert \alpha \right\rangle$ is identical to the state ${\hat{a}}^{\dagger n}{\hat{a}}^{n}\left\vert \alpha \right\rangle$, up to a normalization factor. Thus, for input coherent states, the addition of n photons is equivalent to the application of a quantum filter diagonal in Fock basis, as far as the generated state is concerned. The difference is only in the success probability of the applied conditional operation. In particular, for n = 1 we get the Fock diagonal filter $\hat{n}$, while for n = 2 we get $\hat{n}(\hat{n}-1)$. For not too small complex amplitudes α, these Fock-amplitude modulations reasonably well approximate the noiseless amplification (14).

In the experiment, we reconstruct both the photon-added coherent state and the corresponding input coherent state and determine the effective noiseless amplification gain as the ratio of their complex amplitudes. We emphasize that the determination of the gain is not affected by the efficiency η_H of the homodyne detector, because this factor cancels out when we calculate the ratio of two complex amplitudes,

$${g}_{\exp }=\frac{{\alpha }_{{\rm{out}}}}{\alpha }=\frac{{\eta }_{H}{\alpha }_{{\rm{out}}}}{{\eta }_{H}\alpha }.$$

(15)