1 Introduction

In regular daily existence, there are numerous circumstances when it is important to hide the actual contents of secret information transmitted over an insecure line of communication. Many traditional cryptosystems were utilized to perform these tasks in order to encrypt the confidential information. However, in a near future all these classical cryptosystems merely computational secure. The existing classical cryptographic algorithms fundamentally rely on limited computationally development of computer power and mathematical structures. Traditional cryptography experiences key distribution issue, how to convey the key safely between two sets of clients. For quite a long time, it was trusted that the main plausibility to take care of the key dissemination issue was to send some physical medium. With the advancement of technologies, this criterion is obviously unconventional. Moreover, it is even impossible to validate the authentication, integrity and non-repudiation of the transmitted digital contents. Public key cryptography addressed this issue in a quite decent way, yet these algorithms are moderate and cannot be utilized to scramble a lot of information at the same time. Asymmetric key cryptography endures in light of the fact that despite the fact that restricted capacities have not been yet switched with innovative and mathematical advances it is conceivable. The development of quantum cryptography can truly debilitate their security. Previously, there has been a decent arrangement of another cryptographic strategy whose security depends on the principal laws of quantum information science and quantum cryptography. The principle accomplishment is that it can tackle the issue of key distribution. From the reasonable perspective, it is fascinating that quantum cryptography may properly be acknowledged by methods for quantum optics and the optical fiber fills in as a transmission channel [9, 10]. To encode data for instance polarization (disparity, division) or different phases can be utilized. The fundamental principle of quantum mechanism is that the light waves are comprised of a huge number of discrete quanta called photons which are mass less and have energy, momentum and angular momentum called spinning. The spinning of photon conveys the polarization. These photons are unified much like atoms, it simply that they are units of lights [8] .

Photon polarization describes how light photons can have polarized in specific directions. Photon filter with the correct polarization can only detect a polarized photon. The one way characteristics of photons along with the Heisenberg uncertainty principle make quantum cryptography an attractive option to ensure the privacy and defeating eavesdroppers [2]. Some particles, like electrons, neutrinos and quarks have half integer internal angular momentum also called spin . We develop a spinor representation in this paper for spin 1/2 to give a new direction to cryptography via spinning operators of quantum mechanics [1], [3]− [7]. We have shown here, not only the keys but the message can also be encrypted via this technique. The important aspect of our suggested algorithm is phase information, because phase is used to encrypt and decrypt the keys and message. To achieve maximum security, we use different phases for key and message. To decrypt the message, first we have to decrypt the keys by using phase information and then by using keys with phase information of message to decrypt the message.

The rest of the paper is organized as follow. We have added basic definition of finite state machine in Section 2. The derivation of rotation operator is given in Section 3. The proposed quantum spinning and rotations based algorithm illustrate with example and sensitivity analysis are given in Section 4. Finally, conclusion is given in Section 5.

2 Finite State Machine

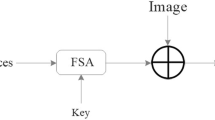
Finite state automation (FSA) or finite state machines (FSM) are models of behaviors for a system or a complex object, with a limited number of defined modes or conditions, where mode transitions change in circumstances [7].

A DFA (deterministic finite automation) is quintuple M = (X, \(\sum ,~q_{0},\wp ,\digamma ),~\)where

X :

is state of finite sets,

\(\sum \) :

is input symbols of finite set,

q 0 :

is start state indicated by an arrow \(\rightarrow ,\)

℘ :

is transition function \(\wp :X\times \sum \rightarrow X,\) i.e.,, ℘(q0,a) = qi ∈ X,

\(\digamma \subset X\) :

is a finite set of final set of final states.

The input symbols can be letters or digits. We say that a string M is accepted by DFA (Deterministic Finite Automaton-self operating machine), if the set of languages accepted by a DFA ‘X’ is denoted by L(X). In DFA, there is only one transition out of each state on the same input symbol. NDFA (Nondeterministic Finite Automaton) can also be considered here as a mathematical model. In NDFA, we considered here a Moore machine and we use NDFA in our algorithm. In Moore machine, the output depends on the transitions (Fig. 1).

Fig. 1
figure 1

Finite state machine algorithm

Full size image

3 Derivation of Rotation Operators

The laws of physics not depend on what axis we choose for our coordinate system (rotational symmetry). If we make an infinitesimal rotation (through and angle dϕ) about ther −axis, we get the transformed coordinates [5],

$$\begin{array}{@{}rcl@{}} p^{^{\prime }}&=&p-d\phi q, \\ q^{^{\prime }}&=&q+d\phi p. \end{array} $$
(1)

Apply Taylor series on (1) to expand the function.

$$\begin{array}{@{}rcl@{}} f(p^{\prime},q^{\prime})&=& f(p,q)-\frac{\partial f}{\partial p} d\phi q + \frac{\partial f}{\partial q} d \phi p=\left( 1+\frac{\iota}{\text{h}{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}d\phi S_{r}\right)~f(p,q), \\ R_{r}(d\phi)&=&\left( 1+\frac{\iota}{\text{h}{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}d\phi S_{r}\right), \end{array} $$

where his internal angular momentum. A finite rotation can be made by applying the operator for an infinitesimal rotation over and over. Let 𝜃r = ndϕ, then

$$ R_{r}(\theta )=\underset{n\rightarrow \infty }{\lim }\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}\frac{\theta }{n}S_{r}\right)^{n}=e^{i\theta \frac{S_{r}}{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}}. $$
(2)

If we make an infinitesimal rotation about the q −axis, we get the transformed coordinates

$$\begin{array}{@{}rcl@{}} p^{^{\prime }}&=&p-d\phi r \\ r^{^{\prime }}&=&r+d\phi p \end{array} $$
(3)

Apply Taylor series on (3) to expand the function given below

$$\begin{array}{@{}rcl@{}} f(p^{^{\prime }},r^{^{\prime }})&=&f(p,r)-\frac{\partial f}{\partial p}d\phi r+\frac{\partial f}{\partial r}d\phi p=\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}d\phi S_{q}\right)~f(p,r), \\ R_{q}(d\phi )&=&\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}d\phi S_{q}\right). \end{array} $$

A finite rotation can be made by applying the operator for an infinitesimal rotation over and over. Let 𝜃q = ndϕ, then

$$ R_{q}(\theta )=\underset{n\rightarrow \infty }{\lim }\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}\frac{\theta }{n}S_{q}\right)^{n}=e^{i\theta \frac{S_{q}}{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}}. $$
(4)

If we make an infinitesimal rotation about the p −axis, we get the transformed coordinates

$$\begin{array}{@{}rcl@{}} q^{^{\prime }}&=&q-d\phi r, \\ r^{^{\prime }}&=&r+d\phi q. \end{array} $$
(5)

Apply Taylor series on (5) to expand the function.

$$\begin{array}{@{}rcl@{}} f(q^{^{\prime }},r^{^{\prime }})&=&f(q,r)-\frac{\partial f}{\partial q}d\phi r+\frac{\partial f}{\partial r}d\phi q=\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}d\phi S_{p}\right)~f(q,r), \\ R_{p}(d\phi )&=&\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}d\phi S_{p}\right). \end{array} $$

A finite rotation can be made by applying the operator for an infinitesimal rotation over and over. Let 𝜃p = ndϕ, then

$$ R_{p}(\theta )=\underset{n\rightarrow \infty }{\lim }\left( 1+\frac{\iota }{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}\frac{\theta }{n}S_{p}\right)^{n}=e^{i\theta \frac{S_{p}}{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}}. $$
(6)

3.1 Derive Spin \(\frac {1}{2}~\)Operators

We use eigenstates of Sr as the basis states [6]

$$\begin{array}{@{}rcl@{}} X_{+}&=&\left( \begin{array}{c} 1 \\ 0\end{array}\right) ,\\ X_{-}&=&\left( \begin{array}{c} 0 \\ 1\end{array}\right) ,\\ S_{r}~X_{\pm }&=&\pm \frac{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}{2}X_{\pm }, \\S_{r}&=&\frac{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}{2} \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) . \end{array} $$

It must be diagonal, since the basis states are eigenvectors of the matrix. Now to perform the raising and lowering operators [6], we have

$$\begin{array}{@{}rcl@{}} S_{+}X_{-}&=&\overset{S_{+}X_{+}= 0,}{\sqrt{s(s + 1)-m(m + 1)}}\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}X_{+}=\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}X_{+}, \\ S_{+}&=&\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}} \left( \begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right) , \\ S_{-}X_{-}&=&0,\\ S_{-}X_{+}&=&\sqrt{s(s + 1)-m(m-1)}\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}X_{-}=\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}X_{-}, \\ S_{-}&=&\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}} \left( \begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right). \end{array} $$

Now we can calculate Sp and Sq.

$$ S_{p}=\frac{1}{2}(S_{+}+S_{\_})=\frac{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}{2} \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) , $$
(7)
$$ S_{q}=\frac{1}{2\iota }(S_{+}-S_{\_})=\frac{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}{2\iota } \left( \begin{array}{cc} 0 & -\iota \\ \iota & 0 \end{array}\right) . $$
(8)

The Pauli spin matrices are defined as [4],

$$ S_{i}=\frac{\text{h{\hskip-.2em}\llap{\protect \rule[1.1ex]{.325em}{.1ex}}{\hskip.2em}}}{2}\sigma_{i}. $$
(9)

Compare (7)-(8) and (9) with (10) to get σ(Pauli matrices).

$$\begin{array}{@{}rcl@{}} \sigma_{p}&=& \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) , \\ \sigma_{q}&=& \left( \begin{array}{cc} 0 & -\iota \\ \iota & 0 \end{array}\right) , \\ \sigma_{r}&=& \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) . \end{array} $$
(10)

These are traceless Hermitian matrices, and HCode \(\sigma _{p}^{2}=\sigma _{q}^{2}=\sigma _{r}^{2}=I\) (identity) [1]. Now put (10) in (2), (4) and (6) to get rotation operators with respect to σ.

$$\begin{array}{@{}rcl@{}} R_{p}(\theta )&=&e^{i\frac{\theta }{2}\sigma_{p}}, \\ R_{q}(\theta )&=&e^{i\frac{\theta }{2}\sigma_{q}}, \\ R_{r}(\theta )&=&e^{i\frac{\theta }{2}\sigma_{r}}, \end{array} $$
(11)
$$ e^{i\frac{\theta}{2}\sigma_{j}}=\sum\limits_{n = 0}^{\infty}\frac{\left( i\frac{\theta}{2}\right)^{n}}{n!}{\sigma_{j}^{n}}. $$
(12)

Now deriving the rotation operators of (11) with the help of (12) [6].

$$ R_{p}(\theta )=e^{i\frac{\theta }{2}\sigma_{p}}=\left( \begin{array}{cccc} \sum\limits_{n = 0,2,4,...}^{\infty} & \frac{\left( i\frac{\theta}{2}\right)^{n}}{n!} & \sum\limits_{n = 1,3,5,...}^{\infty} & \frac{\left( i\frac{\theta }{2}\right)^{n}}{n!} \\ \sum\limits_{n = 1,3,5,...}^{\infty} & \frac{\left( i\frac{\theta}{2}\right)^{n}}{n!} & \sum\limits_{n = 0,2,4,...}^{\infty} & \frac{\left( i\frac{\theta }{2}\right)^{n}}{n!} \end{array}\right) =\left( \begin{array}{cc} \cos \frac{\theta }{2} & \iota \sin \frac{\theta }{2} \\ \iota \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right) , $$
(13)
$$ R_{q}(\theta )=e^{i\frac{\theta }{2}\sigma_{q}}=\left( \begin{array}{ccccc} \sum\limits_{n = 0,2,4,...}^{\infty} & \frac{\left( i\frac{\theta}{2}\right)^{n}}{n!} & -\iota & \sum\limits_{n = 1,3,5,...}^{\infty} & \frac{\left( i\frac{\theta }{2}\right)^{n}}{n!} \\ \iota & \sum\limits_{n = 1,3,5,...}^{\infty} & \frac{\left( i\frac{\theta}{2}\right)^{n}}{n!} & \sum\limits_{n = 0,2,4,...}^{\infty} & \frac{\left( i\frac{\theta }{2}\right)^{n}}{n!} \end{array}\right) =\left( \begin{array}{cc} \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right) , $$
(14)
$$ R_{r}(\theta )=e^{i\frac{\theta }{2}\sigma_{r}}=\left( \begin{array}{cc} \sum\limits_{n = 0}^{\infty} \frac{\left( i\frac{\theta }{2}\right)^{n}}{n!} & 0 \\ 0 & \sum\limits_{n = 0}^{\infty} \frac{\left( -i\frac{\theta }{2}\right)^{n}}{n!} \end{array}\right) =\left( \begin{array}{cc} e^{i\frac{\theta }{2}} & 0 \\ 0 & e^{-i\frac{\theta }{2}} \end{array}\right) . $$
(15)

4 Proposed Algorithm

We have derived the rotation operators around p,q and r axis. By using the results, we encrypt the key and message by following algorithm. We ignore the imaginary numbers and used real axis for calculations.

$$\begin{array}{@{}rcl@{}} a&=&\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right) =I, \\ b&=&\left( \begin{array}{cc} \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right) =R_{p}(\theta ), \\ c&=&\left( \begin{array}{cc} \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right) =R_{q}(\theta ), \\ d&=&\left( \begin{array}{cc} e^{\frac{\theta }{2}} & 0 \\ 0 & e^{-\frac{\theta }{2}} \end{array}\right) =R_{r}(\theta). \end{array} $$
(16)

Let entangle 2 × 2 matrices of (16) to form the set A of 4 × 4 entangle matrices. The elements of the set A are:

$$\begin{array}{@{}rcl@{}} A_{1}&=& \left[\begin{array}{cc} a & b \\ c & d \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2}\\ 0 & 1 & \sin \frac{\theta }{2} & \cos \frac{\theta }{2}\\ \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & e^{\frac{\theta }{2}} & 0 \\ -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 & e^{-\frac{\theta }{2}} \end{array}\right]\\ A_{2}&=& \left[\begin{array}{cc} a & b \\ d & c \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & 1 & \sin \frac{\theta }{2} & \cos \frac{\theta }{2}\\ e^{\frac{\theta }{2}} & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & e^{-\frac{\theta }{2}} & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right],\\ A_{3}&=& \left[\begin{array}{cc} a & d \\ b & c \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & e^{\frac{\theta }{2}} & 0 \\ 0 & 1 & 0 & e^{-\frac{\theta }{2}}\\ \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right],\\ A_{4}&=& \left[\begin{array}{cc} a & d \\ c & b \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & e^{\frac{\theta }{2}} & 0 \\ 0 & 1 & 0 & e^{-\frac{\theta }{2}}\\ \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right],\\ A_{5}&=& \left[\begin{array}{cc} a & c \\ d & b \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & 1 & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2}\\ e^{\frac{\theta }{2}} & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & e^{-\frac{\theta }{2}} & \sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right]\\ A_{6}&=& \left[\begin{array}{cc} a & c \\ b & d \end{array}\right] =\left[\begin{array}{cccc} 1 & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & 1 & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2}\\ \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & e^{\frac{\theta }{2}} & 0 \\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 & e^{-\frac{\theta }{2}} \end{array}\right],\\ A_{7}&=& \left[\begin{array}{cc} b & a \\ c & d \end{array}\right] =\left[\begin{array}{cccc} \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & 1 & 0 \\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 & 1\\ \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & e^{\frac{\theta }{2}} & 0 \\ -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 & e^{-\frac{\theta }{2}} \end{array}\right],\\ A_{8}&=& \left[\begin{array}{cc} b & a \\ d & c \end{array}\right] =\left[\begin{array}{cccc} \cos \frac{\theta }{2} & \sin \frac{\theta }{2} & 1 & 0\\ \sin \frac{\theta }{2} & \cos \frac{\theta }{2} & 0 & 1\\ e^{\frac{\theta }{2}} & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & e^{-\frac{\theta }{2}} & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right],\\ &&\qquad \qquad \qquad \qquad \vdots\\ A_{24}&=& \left[\begin{array}{cc} d & b \\ a & c \end{array}\right] =\left[\begin{array}{cccc} e^{\frac{\theta }{2}} & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2}\\ 0 & e^{-\frac{\theta }{2}} & \sin \frac{\theta }{2} & \cos \frac{\theta }{2}\\ 1 & 0 & \cos \frac{\theta }{2} & \sin \frac{\theta }{2} \\ 0 & 1 & -\sin \frac{\theta }{2} & \cos \frac{\theta }{2} \end{array}\right]. \end{array} $$

4.1 Encryption

  1. 1.

    Define the phase for defined rotation matrices (known to sender and receiver only),

  2. 2.

    Convert the message into numeric vector of order 4 × n, say M,

  3. 3.

    Define finite state machine,

  4. 4.

    Decide a key for secret communication,

  5. 5.

    Convert they key into binary,

  6. 6.

    Start with left most bit for encryption of message with rotation matrices and add one by one the key bits towards right and convert to decimal at each step and mod the key to 24. Round of encryption depends on key length,

  7. 7.

    Convert the numeric matrix into alphabets at each step to get different ciphers,

  8. 8.

    Finally, cipher alphabets received by using the full length of the key, say Mc.

4.2 Decryption

  1. 1.

    Enter the phase where the message was encrypted,

  2. 2.

    Convert alphabetical cipher message into numeric matrix of order 4 × n, say Mc,

  3. 3.

    Enter the key for which the message encrypted and convert it into binary,

  4. 4.

    Now start with full length key under mod 24 and operate the cipher with inverse rotation matrices and then subtract 1 by 1 bit from right side under mod 24 to operate with rotation matrices,

  5. 5.

    The final numeric vector obtained by performing the inverse rotation matrix of left most bit with previous cipher,

  6. 6.

    Convert the numeric matrix into alphabetical vector to get original message.

4.3 Example

Let us consider a message ‘INCOMPREHENSIBLE’ to be encrypted and decrypted at phase 𝜃 = 320∘ with key 59.

$$M=INCOMPREHENSIBLE= \left[\begin{array}{cccc} 8 & 13 & 2 & 14 \\ 12 & 15 & 17 & 4 \\ 7 & 4 & 13 & 18 \\ 8 & 1 & 11 & 4 \end{array} \right] . $$

4.3.1 Finite State Machine

The mathematical expression of finite state machine which will be used in our proposed algorithm is given below

$$q_{k + 1}=q_{k}~\times ~\left[R_{(\sec \text{ret~code in~decimal~form mod 24})}\right]^{output~q_{k + 1}~state}. $$

4.3.2 Encryption

The following components are basic requirement for the encryption of plain text ‘INCOMPREHENSIBLE’ (see Table 1).

Table 1 Basic components for encryption of proposed algorithm
Full size table

We are now utilizing the fundamental components which are selected in Table 1, by transforming the plaintext into a ciphertext. A comprehensive procedure of our proposed encryption algorithm is given in Table 2.

Table 2 Encryption process of proposed algorithm
Full size table

4.3.3 Decryption

The decryption is an inverse process of encryption to transform the ciphertext into a plaintext. The fundamental steps in decryption of information in proposed algorithm are same but apply in a reverse way (see Tables 3 and 4).

Table 3 Basic components for decryption of proposed algorithm
Full size table
Table 4 Decryption process of proposed algorithm
Full size table

4.4 Sensitivity Analysis

We have applied, our designed algorithm on different texts in which some texts shown in Table 5. By changing the phase, key or both lead to change the cipher. The beauty and versatility of designed algorithm is to change any term (either key or phase) lead to change the cipher and it is not possible to retrieve the plaintext exactly. The reverse process of this scheme by knowing the key is not possible because phase 𝜃 has infinite points.

Table 5 Sensitivity analysis of proposed algorithm
Full size table

5 Conclusion

The efficiency of designed algorithm test on texts, by changing the phase only 0.010 lead to change the cipher. Both parties can do secure data transmission with limited key space in very short time and can encrypt/ decrypt data character by character in defined range of phases. The above results of plain texts have different ciphers clarified that by changing either key or phase to get different results. We can create million of ciphers by changing phases of one original plain text. In this paper, the algorithm refers symmetric cryptography. The described algorithm refers to half spinning, so the points in between − 720∘to720∘ are infinite and possible combinations of rotation matrices are 24!. It is not possible for any machine to store infinite points in each of 24! matrices. All of these rotation matrices become the identity matrix for rotations through 720∘ and are minus the identity for rotations through 360∘. The purpose of using FSM is to enhance the security.