1 Introduction

With the rapid development of information processing technology and the popularity of the internet, the traditional voting method will be gradually replaced by electronic voting schemes. The traditional voting method requires voters to vote at the designated place, and the votes are artificially counted. This voting process is not only inefficient, but also easily influenced by human factors and causes many mistakes and irregularities. Therefore, the design of an electronic voting scheme has been a hot research topic in the area of information security. As a result, a plenty of protocols as electronic voting [1] have been proposed and successfully applied in the last decade, which meet confidentiality, authentication, and data security. The key technologies used in electronic voting schemes are quantum proxy blind and group signatures [2,3,4,5].

Blind signature is a special kind of digital signature [6,7,8,9,10] that allows the signer to generate a signature without knowing the content of the message. To ensure schemes unconditional security, quantum blind signature was introduced by combining classical cryptography and quantum theory. Recently, the application of quantum signature in electronic voting also attracted some attention. In 2006, Hillery et al. [11] proposed some voting patterns, which contains traveling ballot scheme and distributed ballot scheme. In 2007, Vaccaro et al. [12] defined the standard of quantum voting protocol. Hereafter, many efforts have been made on it and lots of quantum voting protocols [13,14,15] are presented in recent years. In 2016, Tian et al. [16] proposed a voting protocol based on the controlled quantum operation teleportation. Recently, Cao et al. [17] proposed an electronic voting scheme achieved by using quantum proxy signature.

In this paper, we put forward a distributed electronic voting scheme based on quantum group blind signature. This is the first time to apply quantum group blind signature in the distributed electronic voting scheme, which could really protect the message owner’s privacy and anonymity. Quantum key distribution and one-time pad are adopted in our scheme in order to guarantee unconditional security [18,19,20,21]. Moreover, our scheme is very scalable in terms of both signers and users. Furthermore, compared with the related schemes [16, 17], our scheme adds an important property of authentication, which makes our voting scheme more secure and efficient. Our scheme only need Bell-state measurement, it can be implemented easily with the current experimental conditions.

2 Preliminary Theory

Group signature allows a member to sign a message on behalf of the group and no one knows who signs it except group administrator (manager). Blind signature, the message owner could get the authentic signature for his own message, but not reveal the specific content of the message. In real life, voters from different parts of the country may be able to find local authorities to seal the votes. But in the final count of votes, according to the official seal on the ballot, it is easy to determine the location of the owner of the message and other information. In this case, even if the blind signature is used, the anonymity of the message owner can not be protected. Therefore, for the above mentioned distributed electronic voting scheme, we adopt a quantum group blind signature scheme which satisfies both group signature and blind signature properties.

Different from classical signature scheme, our quantum group blind signature scheme is based on the theory below. The four Bell states of 2-qubit are

$$ |\phi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|00\rangle\pm|11\rangle),|\psi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|01\rangle\pm|10\rangle). $$
(1)

Suppose that Alice and Bob share a Bell state

$$ |\phi^{+}\rangle_{AB}=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{AB}=\frac{1}{\sqrt{2}}(|++\rangle+|--\rangle)_{AB}, $$
(2)

where

$$|+\rangle=\frac{|0\rangle+|1\rangle}{\sqrt{2}},|-\rangle=\frac{|0\rangle-|1\rangle}{\sqrt{2}}. $$

Due to the entanglement characteristic of EPR pairs, after Alice having measured particle A, particle B will collapse to the same state as particle A. Thus, if Alice and Bob choose the same base \(B_{z}= \{|0\rangle ,|1\rangle \}\) or \(B_{x}= \{|+\rangle ,|-\rangle \}\) to measure their particles respectively, they will get the similar results. For example, if both Alice and Bob choose base \(B_{z}\) and Alice gets \(|0\rangle \), then Bob’s measuring result must be \(|0\rangle \). However, after Alice’s measurement, if Bob chooses a different base from Alice, Bob will get a random result.

2.1 A Model of Distributed Electronic Voting Scheme

In a distributed election scheme, each voter belongs to a particular organization, and each organization has an administrator. All the organization’s administrator formed a group, and the group has a supervisor who is responsible for supervising each administrator. In order to make the election safer and more reliable, the following security properties need to satisfy.

  1. (1)

    Each voter’s ballot must be signed by the administrator of his organization to make the ballot legal.

  2. (2)

    All signed ballots shall be examined by the tallyman. It is necessary to ensure that the tallyman does not know which administrator signed the ballot. Even if he does not know who the signer is, he can easily verify the validity of the vote.

  3. (3)

    No one can trace any vote. That is to say, whether the administrators or the supervisor of the whole group can not know the any content of the vote.

  4. (4)

    After all the votes have been verified, the verifier needs to publish the legal votes. This is not only to announce the results of the election, but also to make the voters convince that their votes are valid. Therefore, at the time of the public vote, all voters are able to check whether their votes have been modified or discarded in order to ensure that there is no fraud.

  5. (5)

    If there was a dispute, the supervisor of the administrator has the right to public the dispute signature and see which administrator in the group has signed the ballot.

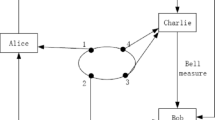
The structure of the distributed electronic voting scheme is shown in Fig. 1.

Fig. 1
figure 1

The structure of the distributed electronic voting scheme

Full size image

2.2 Controlled Quantum Teleportation

Our quantum group blind signature is based on controlled quantum teleportation. In this section, we will introduce the controlled teleportation using four-particle cluster state [22] as quantum channel. It is given by

$$ |\xi \rangle_{1234}= \frac{1}{2}(|0000\rangle+|0101\rangle+|1010\rangle-|1111\rangle)_{1234}. $$
(3)

The sender Alice owns particles 1, the controllers Charlie owns particles (2,3) and the particle 4 belongs to the receiver Bob.

Suppose that the quantum state of particle M carrying message in Alice is

$$ |\psi\rangle_{M}=\frac{1}{\sqrt{2}}(|0\rangle+b|1\rangle)_{M}, $$
(4)

in which \(b\)= 1 and \(b\)=− 1 is corresponding to \(M(i)\)= 1 and \(M(i)\)= 0, respectively.

The combined state \(|{\Psi }\rangle _{M1234}\) of the whole system composed of particles M and (1,2,3,4) is given by

$$ |{\Psi}\rangle_{M1234}=|\psi\rangle_{M}\otimes|\xi \rangle_{1234} =\frac{1}{\sqrt{2}}(|0\rangle+b|1\rangle)_{M}\otimes|\xi \rangle_{1234}. $$
(5)

The details of the controlled teleportation are as follows.

  1. 1)

    Alice performs a Bell-state measurement on particles \(\textit {M}\) and 1. The measurement can collapse the state of particles (2,3,4) into one of the following states

    $$ \begin{array}{ll} \left<\phi^{\pm}_{M1}|{\Psi}\right>_{M1234} =& \frac{1}{2}(|000\rangle+|101\rangle\pm b|010\rangle\mp b|111\rangle)_{234}, \\ \left<\psi^{\pm}_{M1}|{\Psi}\right>_{M1234} =& \frac{1}{2}(|010\rangle-|111\rangle\pm b|000\rangle\pm b|101\rangle)_{234}. \end{array} $$
    (6)
  2. 2)

    If Charlie agrees Alice and Bob to perform their teleportation, Charlie performs a Bell-state measurement on his particles (2,3). Suppose that Alice’s measurement result is \(|\phi ^{+}\rangle _{M1}\), the measurement will collapse the state of particle 4 into one of the following states

    $$ \begin{array}{ll} \left<\phi^{\pm}_{23}|\phi^{+}_{M1}|{\Psi}\right>_{M1234} =& \frac{1}{\sqrt{2}}(|0\rangle\mp b|1\rangle)_{4}, \\ \left<\psi^{\pm}_{23}|\phi^{+}_{M1}|{\Psi}\right>_{M1234} =& \frac{1}{\sqrt{2}}(b|0\rangle\pm |1\rangle)_{4}. \end{array} $$
    (7)
  3. 3)

    According to Alice’s, Charlie’s measurement results, Bob operates one of four unitary operations (I,σz,σx,iσy) on particle 4 to reconstruct the unknown quantum state \(|\psi \rangle _{M}\). For example, assume Alice’s measurement result is \(|\phi ^{+}\rangle _{M1}\) and Charlie’s measurement result is \(|\phi ^{-}\rangle _{23}\), respectively, Bob’s operation on particle 4 is \(I\). For other cases, the relationship between Alice’s, Charlie’s measurement results and Bob’s operation is listed in Table 1.

    Table 1 The relationship between Alice’s, Charlie’s measurement results and Bob’s operation
    Full size table

3 The Distributed Electronic Voting Scheme

Our distributed electronic voting scheme based on quantum group blind signature involves the following four participants:

  1. (1)

    Alice: One of the eligible voters and the owner of the vote messages, she belongs to an organization managed by Charlie.

  2. (2)

    Bob: A trustworthy tallyman who will not conspire with either party. He will verify the messages and signatures and publish legal ballots.

  3. (3)

    Charlie: The administrator of Alice’s organization. He will sign the Alice’s ballot.

  4. (4)

    David: A supervisor. In our scheme, David is trustworthy, he will not attempt to forge the signature of any administrator in the group. He will supervise the behavior of administrators of all organizations.

Our distributed electronic voting scheme works in the following processes.

3.1 Initial Phase

Step1 :

The voter Alice holds a n-bit vote message (including the vote contents etc.) to be signed and transfers it to a quantum state message in the basis \(\{|0\rangle ,|1\rangle \}\):

$$ m^{j}=\{m^{j}(1),m^{j}(2),\cdots,m^{j}(i),\cdots,m^{j}(n)\}(m^{j}(i)\in\{|0\rangle,|1\rangle\}). $$
(8)
Step2 :

Quantum Key Distribution. Charlie shares secret key \(K_{AC}\) with Alice. The supervisor David shares secret key \(K_{BD}\) with the tallyman Bob. Charlie applied to David to register as an administrator of an organization. After registration, David shares secret key \(K_{CD}\) with Charlie. All secret keys are distributed through QKD protocols, which have been proved to be unconditionally secure [18,19,20,21]. If a new user wants to join an organization, he needs to apply for a key from the organization’s administrator.

Step3 :

Serial Number Distribution. Bob generates a set of serial number and transfers it to a quantum state message in the basis \(\{|0\rangle ,|1\rangle \}\), which is used to identify each signature process. The serial number is recorded as \(SN=\{SN^{1},SN^{2},\cdots ,SN^{j},\cdots ,SN^{n}\}(SN^{j}\in \{|0\rangle ,|1\rangle \})\). Bob encrypts serial number \(SN\) with the key \(K_{BD}\) to get the message \(E_{K_{BD}}\{SN\}\) and sends it to David. After David received the message \(E_{K_{BD}}\{SN\}\) from Bob, he decrypts it with the key \(K_{BD}\) to get the message \(SN\). Subsequently, David distributes the serial number randomly to each member of the group. For instance, David sends the message \(E_{K_{CD}}\{SN^{j}\}\) to Charlie. Charlie decrypts it with the key \(K_{CD}\) to get the message \(SN^{j}\). Then David recorded the serial number \(SN^{j}\) and the corresponding signer Charlie. So David puts the serial number and the corresponding signer in his own database.

Step4 :

Vote \(ID\) Distribution. The administrator Charlie checks whether Alice’s identify is eligible and whether her vote is the first one. If not, Charlie will refuse to award ticket. Otherwise, if Alice satisfies the vote conditions, her administrator Charlie will randomly give Alice a unique vote \(ID^{j}\).

Step5 :

Quantum Channel Setup. Charlie generates \(n\) EPR pairs such that

$$ |\psi_{i}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{A_{i}C_{i}}, i = 1,2,\cdots,n. $$
(9)

In every EPR pair, Charlie sends particle \(A_{i}\) to the voter Alice while leaving \(C_{i}\) to himself. Bob generates \(n\) four-qubit cluster states as shown in (3), he gives particle 1 to Charlie, particles (2,3) to the supervisor David and he holds particle 4.

3.2 Voting Phase

Step1 :

Alice selects \(k\) decoy factors from {|0〉,|1〉,|+〉,|−〉} and inters them randomly into the message \(m^{j}\). Then, the vote message \(m^{j}\) has been blinded into \(M^{j}\). Alice writes down the message of \(k\) decoy factors and the position they insert. Then Alice tells Bob the states of decoy factors in \(M^{j}\) and the position of the decoy factors. Bob and Alice adopt the decoy factors checking technique to ensure the transmit secure.

Step2 :

Alice encrypts \(M^{j}\), \(ID^{j}\) with the key \(K_{AC}\) to get the secret message \(O_{AC}\), which is denoted as

$$ O_{AC}=E_{K_{AC}}\{M^{j},ID^{j}\}. $$
(10)

We adopt one-time pad [23] as the encryption algorithm to guarantee the unconditional security. Then Alice sends the secret message \(O_{AC}\) to her administrator Charlie through the QSDC protocols [24,25,26,27,28].

3.3 Signing Phase

Step1 :

After Charlie received the secret message \(O_{AC}\), he decrypts it with the key \(K_{AC}\) to get the message \(M^{j}\), \(ID_{*}^{j}\).

Step2 :

When Charlie received a notice of Alice’s request for signature, if \(ID_{*}^{j}=ID^{j}\), Charlie performs a Bell-state measurement on particles (Ci,1) and records the measurement results as \(\gamma _{_{C}}=({\gamma (i)_{_{C_{i}1}},i = 1,2,\cdots ,n})(\gamma (i)_{_{C_{i}1}}\in {|\phi ^{\pm }\rangle ,|\psi ^{\pm }\rangle })\). Then Charlie sends the secret message \(O_{CD}=E_{K_{CD}}\{M^{j},ID^{j},\gamma _{_{C}},\\SN^{j}\}\) to David.

Step3 :

After David received the secret message \(O_{CD}\) from Charlie, he decrypts it with the key \(K_{CD}\) to get the message \(M^{j}, ID^{j}, \gamma _{_{C}}, SN_{*}^{j}\). If \(SN_{*}^{j}=SN^{j}\), he will help Alice and Bob complete the controlled quantum teleportation. Then David performs a Bell-state measurement on particles (2,3) and records the measurement results as \(\gamma _{_{D}}=({\gamma (i)_{_{23}},i = 1,2,\cdots ,n})(\gamma (i)_{_{23}}\in {|\phi ^{\pm }\rangle ,|\psi ^{\pm }\rangle })\).

Step4 :

David encrypts \((M^{j},SN^{j},\gamma _{_{C}},\gamma _{_{D}},ID^{j})\) with the key \(K_{BD}\) to get the message \(O_{BD}=E_{K_{BD}}\{M^{j},SN^{j},\gamma _{_{C}},\gamma _{_{D}},ID^{j}\}\) and sends \(O_{BD}\) to Bob.

3.4 Verifying Phase

Step1 :

After Bob received the message \(O_{BD}\), he decrypts it with the key \(K_{BD}\) to get the message \(M^{j},SN^{j},\gamma _{_{C}},\gamma _{_{D}},ID^{j}\).

Step2 :

According to \(\gamma _{_{C}}\) and \(\gamma _{_{D}}\), Bob measures particle 4 on appropriate base to successfully reconstruct the original unknown quantum state information. The measuring results could be wrote as \(d\). If \(d=M^{j}\), the signature is valid. Otherwise, Bob will reject it.

Step3 :

Then Bob unblinds \(M^{j}\), based on the message he has obtained, Bob measures these decoy factors according to the information from Alice. Then Bob can get the message \(m^{j}\). Bob confirms the signature \(S_{j}=(m^{j},\gamma _{_{C}},\gamma _{_{D}})\).

3.5 Authenticating Message Phase

Step1 :

If the validity of the signature \(S_{j}\) is verified, Bob publishes the message \(M^{j}\), \(ID^{j}\) and the serial number \(SN^{j}\) together on the bulletin board. The records on the bulletin board are shown in Table 2.

Table 2 The records on the bulletin board
Full size table
Step2 :

Alice searches the bulletin board for \(ID^{j}\) and its corresponding message \(M^{*}\). If \(M^{*}=M^{j}\) and \(ID^{j}\) also exists on the bulletin board, so Alice was convinced that her message was accepted without question. And Charlie can query \(SN^{j}\) to determine whether his signature is valid.

3.6 Confirming Election Results Phase

If there is no dispute, the election process is effective. In our scheme, Bob is credible, so the results he announces must be believable. Therefore, if there was a dispute, the dispute signature \(S_{j}\) and its corresponding serial number \(SN^{j}\) are sent to David. Since David records the signer for each serial number, he can find the signer of the dispute signature in his own record.

4 Security Analysis and Discussion

4.1 Group Property

Only registered legal group members can represent the group to sign the message. In order to be able to sign Alice’s message \(m^{j}\), Charlie should share the key \(K_{AC}\) with Alice. According to \(\gamma _{_{C}}\) and \(\gamma _{_{D}}\), the verifier Bob can check the validity of the signature \(S_{j}\). But Bob does not know which group member David will send to the serial number \(SN^{j}\), so he does not know the specific signer. However, in order to prevent disputes, the group supervisor David has recorded the serial number and the corresponding signer. When there were a dispute, the group supervisor David can detect the source of the signature based on a signature’s serial number \(SN\).

4.2 Messages Blindness

In our scheme, the vote message \(m^{j}\) has been translated into \(M^{j}\) by Alice. If Charlie attempts to obtain the message \(m^{j}\), the only way is to know the states of decoy factors in \(M^{j}\) and the position of the decoy factors. However, Charlie can not know any information about decoy factors. If Charlie randomly guesses decoy factors, then he can determine it with the probability at most \(\frac {1}{2^{n}}\), which will approximate zero if \(n\) is large enough. As a result, Charlie can not learn the message \(m^{j}\). Bob is reliable, so he will not reveal the message he received. Hence, our scheme can guarantee the message \(m^{j}\) blindness.

4.3 Verifiability

The verifier Bob can verify the validity of the signature in the verifying phase. For the message \((M^{j},SN^{j},\gamma _{_{C}},\gamma _{_{D}},ID^{j})\), according to \(\gamma _{_{C}}\) and \(\gamma _{_{D}}\), Bob measures particle 4 on appropriate base. The measuring results could be wrote as \(d\). If \(d=M^{j}\), the signature \(S_{j}\) is valid.

4.4 Non-repeatability

Each legal voter can vote just once, and any voter can not repeat voting. In our scheme, the legal voter’s voting ID is randomly distributed by their administrator Charlie, so voters can not arbitrarily forge a legal voting ID. Then repeat voting will easy to be found.

4.5 Impossibility of Disavowal

On the one hand, if the legal signature is signed by Charlie, he will not be able to deny it. For the message \((M^{j},SN^{j},\gamma _{_{C}},\gamma _{_{D}},ID^{j})\), with the help of the serial number \(SN^{j}\), the supervisor David can track the signer Charlie. So Charlie could not deny that he had signed it. On the other hand, Bob can not deny that he indeed have received the signature. It is obvious that Bob knows the secret key \(K_{BD}\) and can obtain the signature by Step1 in 3.4. Moreover, the process of the verifying indicates he has received it. Therefore, Bob could not deny that he had received it.

4.6 Impossibility of Forgery

David is a supervisor. He is responsible for overseeing the group of administrators of all organizations. In this paper, David is a trustworthy supervisor and Bob is a trustworthy tallyman, so they will not conspire with either party and will not attempt to forge the signature of any administrator in the group. All secret keys are distributed via QKD protocols, which have been proved unconditionally secure. Therefore, the attacker can not get any information about the secret key by eavesdropping.

Suppose that an attacker or eavesdropper Eve forge Charlie’s signature \(\gamma _{_{C}}\) for \(m^{j}\). However, he not be able to know the secret key \(K_{CD}\) shared between Charlie and David, so he can not send message encrypted by \(K_{CD}\), in other words, it is impossible for Eve to forge Charlie’s signature. Assume that Eve guesses \(K_{CD}\) randomly, then he can produce the valid signature with the probability at most \(\frac {1}{2^{n}}\), which vanishes zero if \(n\) is large enough. Therefore, Eve can not forge Charlie’s signature. If an attacker Eve attempts to eavesdrop the quantum state from the quantum channel to get the information, the interference caused by his eavesdropping will cause legitimate users to find his eavesdropping behavior.

4.7 Authentication

In our scheme, the verifier Bob publishes all the messages and all the vote \(ID\) together on the bulletin board. Since the vote \(ID^{j}\) of the message \(m^{j}\) is unique and distributed by Charlie, Alice can query the vote \(ID^{j}\) on the bulletin board. If \(ID^{j}\) is present on the bulletin board and its corresponding message is consistent with \(M^{j}\), Alice can be sure that her message has been accepted without question.

4.8 Message Owner’s Anonymity

According to Step4 in 3.1, the legal voter’s voting ID is randomly distributed by her administrator Charlie. So the voter’s identity is not known except her administrator Charlie. Therefore, our scheme protects the anonymity of the message owner.

4.9 Unconditional Security

Our scheme ensures security from the following three aspects. First, the protocol BB84 is adopted for quantum key distribution; Second, we adopt one-time pad to encrypt; Third, our protocol is based on the secure quantum channel, which has instantaneous transmission not restricted by distance, time or obstacles, all of these are proved to be unconditional security.

4.10 Advantages of Our Scheme

  1. (1)

    Our scheme is the first time to apply quantum group blind signature in the distributed electronic voting scheme.

  2. (2)

    Our scheme is very scalable in terms of both signers and users. If a new user wants to join an organization, he needs to apply for a key from the organization’s administrator.

  3. (3)

    Our scheme adds an important property of authentication.

  4. (4)

    Our scheme combines the advantages of group signature and blind signature and the principle of quantum mechanics provides a good solution for electronic voting scheme.

  5. (5)

    Compared with other schemes, our scheme is based on four-particle cluster state with less resource and as the key techniques of our scheme only rely on the Bell-state measurement, which can make the scheme reliable and practical.

5 Conclusion

Combining election scheme in real life, we propose a choreographed distributed electronic voting scheme in this paper. It is based on quantum group blind signature. Quantum one-time pad and quantum key distribution are adopted in our scheme in order to guarantee unconditional security. Compared with the related scheme [29], Our scheme is based on four-qubit cluster state with less resource, which can make the scheme reliable and practical. Compared with [17], our scheme only perform twice measurement rather than four times. Additionally, compared with previous works [11,12,13, 15,16,17], our distributed electronic voting scheme could really protect the message owner’s privacy and anonymity. Furthermore, when there was a dispute, the group supervisor David can detect the source of the signature based on the signature’s serial number \(SN\). Therefore, our scheme achieves a higher security and it is feasible to implement with current technologies and experimental conditions.