1 Introduction

The traditional voting method requires voters to vote at the designated place, and the votes are artificially counted. This voting process is not only inefficient, but also easily influenced by human factors and causes many mistakes and irregularities. With the rapid development of information processing technology and the popularity of the Internet, the traditional voting method will be gradually replaced by electronic voting schemes. In the past twenty years, we have done a lot of researches on the electronic voting schemes, and put forward many classical voting protocols [1, 2]. The key technologies used in electronic voting schemes are quantum proxy blind and group signatures [3]. The classical group signature and blind signature schemes are mostly based on the computational complexity problems, and these schemes can not be guaranteed the unconditional security. Fortunately, quantum cryptography is concerned in that it can make up for these deficiencies. The security of quantum cryptography is based on the physical properties of the quantum states and not the computational complexity, such as some quantum key distribution protocols, BB84 protocol and B92 protocol are strictly proved to be unconditionally secure [4].

Many research results of blind and group quantum signature schemes based on quantum cryptography are proposed [5–15]. Barnum et al. [5] pointed out a no-go theorem for the application of the quantum signature in 2002. Although Barnum et al.’s conclusion created a serious obstacles for quantum signature schemes, the study of the quantum signature schemes have not stopped. In 2002, Zeng and Keitel [6] first proposed an arbitrated quantum signature (AQS) protocol, which is called the ZK protocol. This work gave an elementary model to overcome Barnum et al.’s no-go theorem for quantum signature schemes. Afterwards, Li et al. found that the arbitrator is unnecessary to entangle with the other two participants in the AQS scheme presented in ref. [10], and thus the three-particle entangled GHZ states used in the scheme can be replaced with two-particle entangled Bell states. Wen et al. [8, 9] proposed some multi-signature schemes.

Quantum entanglement states can be used as quantum resources to carry out a lot of computational and information process tasks. In this paper we propose a new electronic voting scheme based on Bell States by using quantum proxy signature. In our scheme, voter Alice, vote management center Bob, teller Charlie and scrutineer Diana respectively holds a particle of quantum channels. They only perform single particle measurements to realize the electronic voting scheme. It reduces the technical difficulty and increases the safety and operation efficiency. We use quantum key distribution and one-time pad to guarantee the unconditional security and signature anonymity. It is shown to be unconditionally secure, i.e., may not be forged or modified in any way by the receiver or attacker. In addition, it may neither be disavowed by the signatory, nor be deniable by the receiver. The new scheme adjusts the quantum voting model, and introduces the scrutineer Diana to prevent cheating. This adjustment abandons the complex quantum fingerprinting function [16], and makes the voting protocol more secure and efficient, and easy to be operated.

2 Preliminary theory

Particles (1,2) and (3,4) are in the following Bell states, respectively

$$ |\phi^{+}\rangle_{12}=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{12},|\phi^{+}\rangle_{34}=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{34}. $$
(1)

The combined state |Ψ〉1234 of the whole system composed of particles (1,2,3,4) is given by

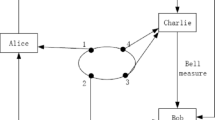
$$ |{\Psi}\rangle_{1234}=|\phi^{+}\rangle_{12}\otimes |\phi^{+}\rangle_{34}=\frac{1}{2}(|0000\rangle+|0011\rangle+|1100\rangle+|1111\rangle)_{1234}. $$
(2)

Alice owns particle 1, Bob holds particle 2, particle 3 is belong to Charlie and Diana has particle 4.

If Alice, Bob, Charlie and Diana all use base B z to measure their particles, there is quantum coherence among these measurement results. The measurement result of anyone can be inferred from the measurement results of others.

The measurement base B z is {|0〉,|1〉}. The measurement base B x is {| + x〉,|−x〉}, where

$$ |+x\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle),|-x\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle). $$
(3)

Based on B x , the state |Ψ〉1234 can be expressed as

$$\begin{array}{@{}rcl@{}} |{\Psi}\rangle_{1234}&=&\frac{1}{2}(|+x\rangle|+x\rangle+|-x\rangle|-x\rangle)_{12}\otimes(|+x\rangle|+x\rangle+|-x\rangle|-x\rangle)_{34} \\ &=&\frac{1}{2}(|+x\rangle|+x\rangle|+x\rangle|+x\rangle+|+x\rangle|+x\rangle|-x\rangle|-x\rangle\\&&+|-x\rangle|-x\rangle|+x\rangle|+x\rangle+|-x\rangle|-x\rangle|-x\rangle|-x\rangle)_{1234}. \end{array} $$
(4)

3 The Proposed Electronic Voting Scheme

It is similar to the classical voting method, the proposed electronic voting scheme by using quantum proxy signature includes the following several parties:

  1. (1)

    The voter Alice is a elector and the owner of the vote messages.

  2. (2)

    Vote management center Bob will check the qualifications of voters, distributes ballots and is also a signer.

  3. (3)

    Charlie is a teller.

  4. (4)

    Diana is scrutineer. He supervises the behavior of Charlie. Charlie and Diana will verify the messages and signatures.

3.1 System Initialization

3.1.1 Setting Up Quantum Channels and Detecting the Security of Quantum Channels

Step 1:

Preparing quantum channels

The vote management center Bob prepares Q(Q>N) |Ψ〉1234 states and can be written as

$$ \{|{\Psi}(1)\rangle_{1234},|{\Psi}(2)\rangle_{1234},\cdots,|{\Psi}(i)\rangle_{1234},\cdots,|{\Psi}(Q)\rangle_{1234}\}, $$
(5)

where

$$ |{\Psi}(i)\rangle_{1234}=\frac{1}{2}(|0000\rangle+|0011\rangle+|1100\rangle+|1111\rangle)_{1234}(i=1,2,\cdots,Q). $$
(6)
Step 2:

Distributing particles

In the ith sequence quantum entangled particles, Bob leaves particle 2 for himself, then distributes particles 1,3,4 to Alice, Charlie and Diana respectively.

Step 3:

Detecting the safety of quantum channels

The quantum channels must be detected to be secure in order to prevent intercepting and resenting attacks or insider attacks. First, Bob randomly selects Q−N entangled particles from his particle sequences, and randomly uses B z basis or B X basis to measure them. Bob announces the sequence numbers of measured particles and the measurement results through the classical channel. The remaining three peoples then sequentially measure the corresponding numbers particles based on B z or B X according to Bob’s measurement results. Alice, Bob, Chalie and Diana compare their measurement results publicly. If these results are relevance, there are no intercepting and resenting attacks or insider attacks. The rest N groups of particles are shared by four peoples and the secure quantum channels are established.

3.1.2 Distributing Quantum Key Bits

Bob shares N-bit quantum key bits K B C with Charlie and N-bit quantum key bits K B D with Diana respectively. Charlie shares N-bit quantum key bits K C D with Diana. The quantum key distribution protocols use the well-known B B84 quantum key distribution protocol [17–19].

3.2 Registration Phase

The voter Alice firstly sends her identification information to the vote management center. Then the awarded teller Bob checks whether Alice’s identity is eligible and whether this vote is the first one. If not, he will refuse to award tickets. Conversely, if Alice satisfies the vote conditions, the vote management center will randomly present Alice a unique vote ID and this means that the voter registration is successful.

3.3 Vote Stage

3.3.1 ᅟ

Alice converts the vote message (including her own vote ID, the vote contents etc.) M into a N-bit binary sequence. That is

$$ M=\{m(1),m(2),\cdots,m(i),\cdots,m(N)\}(i=1,2,\cdots,N). $$
(7)

According to m(i), Alice measures particle 1 based on | + x〉 or |−x〉, respectively. The measurement rule is as follows

$$ m(i)=0\rightarrow|+x\rangle, m(i)=1\rightarrow|-x\rangle. $$
(8)

The vote message M is blind to M ′. Alice does not announce her measurement results. The voter Alice has completed the voting operation. The workers Bob, Charlie and Diana, respectively belong to the vote management center, the counting center and the scrutineers center, must do as the following steps to receive and calculate Alice’s quantum vote.

3.3.2 ᅟ

Charlie arbitrarily chooses the measuring base of | + x〉 or |−x〉 to measure particle 3. He encodes his measurement outcomes into the classical bits c(i) using the following rule

$$ |+x\rangle\rightarrow c(i)=0,|-x\rangle\rightarrow c(i)=1. $$
(9)

All measurement results of particle 3 can be expressed as

$$ C=\{c(1),c(2),\cdots,c(i),\cdots,c(N)\}(i=1,2,\cdots,N). $$
(10)

Then Charlie encrypts C with the shared key bits K B C with Bob and K C D with Diana to get the secret messages \(E_{K_{BC}}(C)\) and \(E_{K_{CD}}(C)\). Charlie sends \(E_{K_{BC}}(C)\) and \(E_{K_{CD}}\) to Bob and Diana respectively.

3.3.3 ᅟ

Bob randomly selects the measuring basis | + x〉 or |−x〉 to measure particle 2. The encoding rule of measurement results is:

$$ |+x\rangle\rightarrow b(i)=0,|-x\rangle\rightarrow b(i)=1. $$
(11)

All measurement results of particle 2 can be expressed as

$$ B=\{b(1),b(2),\cdots,b(i),\cdots,b(N)\}(i=1,2,\cdots,N). $$
(12)

Bob uses encryption key bits K B C that shared with Charlie to encrypt B, and gets the signature of blind message M ′

$$ sig(M^{\prime})=E_{K_{BC}}(B) $$
(13)

Bob sends s i g(M ′) to Charlie. Bob use encryption key K B D that shared with Diana to encrypt B, and gets \(E_{K_{BD}}(B)\). He sends \(E_{K_{BD}}(B)\) to Diana. As this, Alice’s vote is successfully received.

3.4 Supervising and Counting Ballots Stage

3.4.1 Scrutinizing Billing and Counting Ballots

Step 1:

After Diana has received the messages \(E_{K_{BD}}(B)\) and \(E_{K_{CD}}(C)\), she decrypts them with her keys K B D and K C D to get the messages B and C.

Step 2:

According to the messages of b(i) and c(i), Diana measures particle 4 based on {| + x〉,|−x〉}. The measurement results will be encoded into binary classic information by the following rule

$$ |+x\rangle\rightarrow d(i)=0,|-x\rangle\rightarrow d(i)=1. $$
(14)

We will obtain the message

$$ D=\{d(1),d(2),\cdots,d(i),\cdots,d(N)\}(i=1,2,\cdots,N). $$
(15)
Step 3:

Diana encrypts D with the shared key bits K C D whit Charlie to get \(E_{K_{CD}}(D)\). Diana sends \(E_{K_{CD}}(D)\) to Charlie.

Step 4:

Charlie decrypts \(E_{K_{CD}}(D)\) using the shared decryption key bits K C D to get D. After he has received \(sig(M^{\prime })=E_{K_{BC}}(B)\), he can decrypt it to get Bob’s measurement results B. According to the messages B, C and D, Charlie can deduce Alice’s secret information M to open Alice’s vote.

Step 5:

Under the supervision of the scrutineer Diana, the teller Charlie gets every voter’s ballot. He begins to statistics these ballots. When Alice’s, Bob’s, Charlie’s and Diana’s measurement results are satisfied the quantum correlation in (4), the blind signature can be verified, and the ballot is valid. Otherwise, it indicates the presence of cheating.

Step 6:

Every voter’s ballot number and election contents are posted on bulletin boards for the voters to confirm information later.

3.4.2 Confirming Stage

In order to make election more transparent, open and fair, our scheme designs voters confirming stage and the details are as follows: The teller lists every voter’s sequence number and vote contents. If voters do not find their own sequence number or find that the vote contents are tampered, the cheating phenomenon can be found.

3.4.3 Announcing Election Results

Within the prescribed deadline, if there is no dispute, they can announce to the public that the election is effective and announce the election results.

4 Security Analysis and Discussion

4.1 Classical Security

The proposed quantum voting protocol satisfies the following safety requirements.

4.1.1 Anonymity

All election voters are required to protect the voter’s privacy and perform a secret vote. The measures must be adopted so that anyone can not associate the vote contents with the voters.

In our scheme, the owner of voting messages M Alice measures a particle of quantum channels. After she delivers the messages to the teller and scrutineer, she quits the vote. During the process, Alice does not leave any personal characteristic information, so it is difficult for others to find out the affiliation between M and blind signature s i g(M ′). The three management parties are unable to find the intrinsic link between the ballot information and Alice, therefore Alice can not be tracked.

4.1.2 Legality and Signature Blindness

The scheme shows the strong blind signature features. The aim of signature is to ensure the legitimacy of the vote. The blindness of signature is to protect the voters’ privacy. In this scheme, Bob behalf of the central administration proposes a signature on the legitimate vote, and he does not know Alice’s voting information. After Alice measures her own particles according to the information, she does not public the measurement results, so Bob’s signature is blind.

4.1.3 Fairness

The electoral process can not be affected and induced, especially the intermediate results of vote can not be leaked, otherwise the voting tend will be influenced. Charlie must rely on Diana’s measurement results to open and statistics ballots. Diana’s presence balances Charlie’s right to protect the vote fairness.

4.1.4 Verifiability and Completeness

Because the protocol designs scrutineer and verification processes, all legitimate ballots are correctly statisticsed and certificated. If the correct of ballots is in doubt, anyone can verify it. If the ballots are tampered or missed, it is very easy to be found by scrutineer or voter.

4.1.5 Un-repeatability

In this scheme, only legitimate voters can register and obtain ballot from management center, and anyone could not repeatedly vote.

4.2 Anti-Deceptive

Ballot management center Bob is trusted, and the results passed to teller Charlie is also reliable. We can assume that the scrutineer Diana is the trusted third party authorized by management ballot center. The results that Diana passed to teller Charlie is reliable. More importantly, Bob or Charlie, they can only get the state information of one particle among four particles, so their measurements are blind and unable to influence the outcome of the vote. The teller Charlie is supervised by Diana and the voting contents are public to the voters for confirmation, so it is impossible to forge the vote results.

4.3 Unconditional Security

As a quantum electoral protocol, it must also have unconditional security. Based on quantum key distribution, encryption algorithms and transmission channels, this scheme is unconditional security.

5 Conclusions

Combining election protocol in real life, this paper designs a quantum vote scheme. In order to achieve unconditional security that the classic electronic polling schemes can not obtain, we use quantum entangled states—Bell states as quantum channels.The security of our scheme is guaranteed by the quantum one-time pad and quantum key distribution. Hence, it is unconditionally secure. Using Bell states and BB84 QKD protocol, the scheme can be easily realized. It reduces the technical difficulty, and increases the safety and operation efficiency.