1 Introduction

With the rapid development of e-business, the third-party e-payment, as one of the basic links of e-business development, has become the way that people are familiar with and accepted. The key to building an efficient and secure electronic cash payment system is to design a favorable cryptogram protocol.

Since Chaum [1] proposed the concept of electronic cash, kinds of e-cash schemes [2,3,4,5,6,7,8] based on signature techniques, have been presented. The current e-cash systems depend mainly on classical signature schemes, whose securities are based on complex mathematic problems, such as factorization problem, discrete logarithm problem. However, these problems will be solved easily as the quantum computer is growing quickly. Fortunately, in the quantum information processing and computation, quantum cryptography can provide unconditionally secure communication based on the laws of physics, especially with the no-cloning theorem [9].

Inspired by the properties, some scholars have proposed a few e-payment schemes based on quantum signatures [10,11,12,13,14]. In 2010, an e-payment protocol based on group signature was proposed to solve the conditional security problem by Wen et al. [10]. The disadvantage of this protocol is that the system was only applied within the same banks. Then, they presented also a new inter-bank protocol based on quantum proxy blind signature which could not only protect user’s anonymity but also implement among different banks in 2013 [11]. But Cai et al. [12] indicated that the scheme is insure because purchase information could be tampered by the dishonest merchant. In 2014, an online banking system based on quantum cryptography communication is proposed by Zhou et al. [13]. They used two sets of GHZ states to ensure safety in this paper. In 2016, Yang et al. [14] presented a third-party e-payment protocol based on quantum group blind in which message of signer could be protected.

To the best of our knowledge, previous schemes use entanglement states to finish transaction. To simplify the operation, a trusted third-party e-payment protocol which adopts quantum blind signature without entanglement is proposed. Compared with classical e-payment protocols, our scheme can provide unconditional security which is a outstanding characteristic of quantum cryptography. Meanwhile, in the process of payment, the payment message has been blinded by owner of information, which can keep other people from obtaining it except verifier. To achieve it, quantum key distribution (QKD) protocol [15,16,17] and quantum Z gate are adopted in our scheme. Furthermore, the proposed scheme not only can resist the attacks by inserting decoy photons but also be applied in different banks. In addition, this scheme can be realized easily since we only use single-particle states. Therefore, it will have a good application value in current condition.

The rest of this paper is organized as follows. In Section 2, we introduce the basic theories of quantum Z gate. In Section 3, we present the detail content of third-party e-payment protocol. In Section 4, we give an example to describe this scheme. The security is analyzed in Section 5. Finally, we draw conclusions.

2 Basic Theory

In this section, we introduce basic theory that will be used in the later section.

2.1 Quantum Z Gate

Quantum Z gate is expressed as

$$ Z=|0\rangle\langle0|-|1\rangle\langle1|. $$
(1)

It is used to transform for single quantum bit({| + X〉,|− X〉} and {| + Y 〉,|− Y 〉} refer to two different bases), such as

$$\begin{array}{@{}rcl@{}} Z|+X\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)=|-X\rangle,\\ Z|-X\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)=|+X\rangle,\\ Z|+Y\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle-i|1\rangle)=|-Y\rangle,\\ Z|-Y\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle+i|1\rangle)=|+Y\rangle.\\ (|+X\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle), |-X\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle),\\ |+Y\rangle &=& \frac{1}{\sqrt{2}}(|0\rangle+i|1\rangle), |-Y\rangle=\frac{1}{\sqrt{2}}(|0\rangle-i|1\rangle)) \end{array} $$

Its matrix representation is

$$ Z= \left[\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right]. $$
(2)

2.2 Quantum Key Generation and Distribution

Alice shares a secret key KAB1 with Bob1 and the trusted third-party Trent shares secret keys KTA with Alice, KTB1 with Bob1, KTC with Charlie. These secret keys’ length is n and they are distributed via quantum key distribution (QKD) protocol [15,16,17] to ensure security. Then, Trent operates KTA, KTB1 and KTC by adding mod 2 and obtains key K.

$$K=K_{TA}\oplus K_{TB1}\oplus K_{TC}. $$

3 Trusted Third-Party E-Payment Protocol

Our e-payment system involves five roles as follows.

  1. (1)

    Alice: payor;

  2. (2)

    Bob1: Alice’s agent bank;

  3. (3)

    Charlie: payee;

  4. (4)

    Bob2: Charlie’s agent bank;

  5. (5)

    Trent: the trusted third-party e-payment platform.

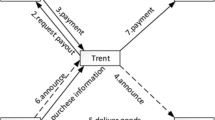
When Alice wants to give payment to Charlie, she will ask Trent to distribute secret keys. Then, she starts to carry through payment. Firstly, after receiving Alice’s message, Trent will inform Bob1 to transmit money to himself. At the same time, Bob1 can deduct the corresponding quantity from Alice’s account. Secondly, Charlie will verify the validity of message and send message to Trent. Finally, if all participants have no dispute, Trent will transmit these money to Bob2.

The brief procedure of our payment has been illustrated in Fig. 1.

Fig. 1
figure 1

The model of third-party e-payment

Full size image

3.1 Initial Phase

  • Step1: Alice divides her payment information into two parts: m1, involving the amount that Alice should pay; m2 = {m2(1),m2(2),⋯ ,m2(i),⋯ ,m2(n)}(m2(i) ∈{00,01,10,11}), meaning compact which is shared between Alice and Charlie before payment. If the length of compact is a odd number, they appoint to add a number 0 at the end of it.

    Alice produces quantum sequence M = {M(1),⋯ ,M(i),⋯ ,M(n)} according to message m2 as follows.

    $$ M(i)= \left\{\begin{array}{l} |+X\rangle,\quad if\quad m2(i)= 00\\ |-X\rangle,\quad if\quad m2(i)= 01\\ |+Y\rangle,\quad if\quad m2(i)= 10\\ |-Y\rangle,\quad if\quad m2(i)= 11 \end{array}\right., 1\leq i\leq n. $$
    (3)

    Nobody knows this encoded rule expect Alice and Charlie.

  • Step2: Alice performs unitary operations on her quantum sequence M according to her secret key KTA as follows. If KTA(i) is equal to 0, Alice does nothing on M(i). If KTA(i) is equal to 1, Alice performs Z gate operation on M(i).

    $$ M1(i)= \left\{\begin{array}{l} IM(i),\quad if \quad K_{TA}(i)= 0\\ ZM(i),\quad if \quad K_{TA}(i)= 1 \end{array}\right. , 1\leq i\leq n. $$
    (4)

    Then she obtains a new quantum sequence M1.

  • Step3: In order to prevent truncation or middle attack, Alice selects t decoy photons from {|0〉,|1〉,| + X〉,|− X〉} and inserts them randomly into M1 to obtain a new quantum sequence M1′. Then Alice sends M1′ and \(E_{K_{AB1}}\{m1\}\) which is encrypted by using the one-time pad with the key KAB1 to Trent. Meanwhile, she writes down message of t decoy photons. Afterward, Alice informs Trent of the information including positions of selected qubits and corresponding particle states. With the information from Alice, Trent could determine error rate. If the error rate is more than the threshold value, he will cancel this payment, or else, he will proceed to the next step.

3.2 Payment Phase

  • Step1: Trent removes these decoy photons according to information published by Alice and obtains the initial quantum sequence M1. Then, Trent encrypts \(E_{K_{AB1}}\{m1\}\) with key KTB1 and gains \(E_{K_{TB1}}\{E_{K_{AB1}}\{m1\}\}\). He also chooses t decoy photons from {|0〉,|1〉,| + X〉,|− X〉} to get M1″ the same as Alice. After that, he sends \(E_{K_{TB1}}\{E_{K_{AB1}}\{m1\}\}\) and M1″ to Bob1.

  • Step2: After Bob1 has received Trent’s signature requirement, Trent and he adopt the decoy photon checking technique to guarantee the security of transmission. If there is a eavesdropper, they will give up this transmission. Or else, Bob1 will go on and obtain M1. Meanwhile, he will decrypt \(E_{K_{AB1}}\{m1\}\) and perform unitary operation on M1 depending on his key KTB1 if he agrees Alice to trade in the third-party platform. Based on (4), if KTB1(i) is equal to 0, Bob1 does nothing on M1(i). If KTB1(i) is equal to 1, Bob1 performs quantum Z gate operation on M1(i) and gains quantum signature M2.

    Then Bobl creates a unique number N = {N1,N2,⋯ ,Nn} whose length is n. According to N, he inserts \(\left [\frac {n}{2}\right ]\) additional particles into M2.

    1. 1)

      The rule that he generates them as follows (A(i) denotes the i th additional particle).

      $$ A(i) \left\{\begin{array}{l} |0\rangle,\quad if \quad N_{2i-1}N_{2i}= 00\\ |1\rangle,\quad if \quad N_{2i-1}N_{2i}= 01\\ |+X\rangle,\quad if \quad N_{2i-1}N_{2i}= 10\\ |-X\rangle,\quad if \quad N_{2i-1}N_{2i}= 11 \end{array}\right. \quad, 1\leq i\leq \left[\frac{n}{2}\right]. $$
      (5)
    2. 2)

      The positions where these additional particles should insert are determined by the following way.

    If \(N_{2i-1}= 0\left (i = 1,2\cdots ,\left [\frac {n}{2}\right ]\right )\), the i th additional particle is inserted in front of \(M2(2i)\left (i = 1,2\cdots ,\left [\frac {n}{2}\right ]\right )\). Otherwise, the additional particle is behind \(M2(2i)\left (i = 1,2\cdots ,\left [\frac {n}{2}\right ]\right )\). After that, he sends \(E_{K_{TB1}}\{m1\}\), \(E_{K_{TB1}}\{N\}\) and M2′ to Trent.

  • Step3: After Trent has received Bob1’s message, he decrypts \(E_{K_{TB1}}\{N\}\) and measures these additional particles according to N. Then, he verifies whether the measurement results are consistent with the generation rules and determines whether there exists eavesdropping. If there exists eavesdropping, Trent will inform other participants abort the scheme. Otherwise, he discards these additional particles and obtains M3. At the same time, Trent also inserts t decoy photons into M3 to detect eavesdropping and get M3′. After that, he sends M3′ and KTC{m1} to Charlie.

  • Step4: Similarly, after receiving Trent’s message M3′ and KTC{m1}, Charlie carries out some operations and obtains M4 and m1. Then, based on compact m2 which is shared with Alice, he measures quantum sequence M4 on appropriate bases according to the rule by the step1 in Section 3.1. The measurement results could be wrote as m2′. If m2′ = m2, the signature is valid, otherwise, Charlie will reject it.

  • Step5: If there is no dispute, Charlie will inform Trent to send message to Bob2, meanwhile Bob2 could receive the proper amount from Trent.

4 An Example: the Trusted Third-Party Payment Scheme

For the sake of clearness, we will give an example to describe our scheme. Assumed the channel is safe and the compact which is shared between Alice and Charlie is wrote as m2 = 01100011 (8 qubit), and the shared keys are wrote as KTA = 0110, KTB1 = 1100, KTC = 0001 and K = KTA ⊕ KTB1 ⊕ KTC = 1011. For simplify, we skip the quantum key distribution process and the transmission process of the payment account m1. The main process is showed as follows.

  • Step1: Following the rule of step 1 and step 2 of Section 3.1, firstly, Alice needs to prepare a four-qubit quantum sequence M = {|− X〉,| + Y 〉,| + X〉,|− Y 〉} according to content of compact m2 = 01100011. Then, she uses her key KTA = 0110 and performs Z gate operations on M to get M1 = {|− X〉,|− Y 〉,|− X〉,|− Y 〉}. (If KTA(i) = 0, she does nothing on M(i), else, she performs Z gate operations.)

  • Step2: After Bobl has received Alice’s message M1, he performs Z gate operation on M1 and obtains M2 = {| + X〉,| + Y 〉,|− X〉,|− Y 〉} according to his key KTB1 = 1100. The operation process also follows the rule of step 2 of Section 3.1.

  • Step3: When receiving Bob1’s message M2, Trent carries out some operations and gains M3 = {|− X〉,| + Y 〉,| + X〉,| + Y 〉} according to his key K = 1011, as Bob1 does.

  • Step4: Similarly, Charlie can also gain M4 = {|− X〉,| + Y 〉,| + X〉,|− Y 〉}. Then, he measures his quantum sequence M4 on appropriate bases according to compact m2. If m2(i) = 00 or m2(i) = 01, he selects base \(\{|+X\rangle =\frac {1}{\sqrt {2}}(|0\rangle +|1\rangle ),|-X\rangle =\frac {1}{\sqrt {2}}(|0\rangle -|1\rangle )\}\). Else, he selects base \(\{|+Y\rangle =\frac {1}{\sqrt {2}}(|0\rangle +i|1\rangle ),|-Y\rangle =\frac {1}{\sqrt {2}}(|0\rangle -i|1\rangle )\}\) if m2(i) = 10 or m2(i) = 11. Then, he can rebuilt the content of compact m2′ = 01100011.

The result is showed in Table 1.

Table 1 The result of the third-party e-payment
Full size table

5 Scheme Properties and Security Analysis

5.1 Blind Property

In our scheme, Bob1 is blind from the content of compact. Because he neither has encoded rule (3) which is shared between Alice and Charlie nor selects appropriate bases {| + Y 〉,|− Y 〉} or {| + X〉,|− X〉} to measure quantum sequence. Assumed Bob1 attempts to gain the information m2, he will choose {00,01,10,11} randomly. Then he can get it with the probability (1/4)n which is negligible if n is large enough. As a result, the agency bank Bob1 can not get content of compact in the process of transaction.

5.2 Unforgeability

The third-party e-payment platform is trusty in our scheme. Those who want to forge would be detected. Obviously, Bob1’s signature on compact is generated by the key KTB1. Meanwhile, M2′ is composed of M2 and some additional particles which are generated according to N. Supposed that internal participant Alice is dishonest and wants to counterfeit the signatory of Bob1 to own his benefit, the only way to finish it is obtaining Bob1’s secret key KTB1, however, it is impossible. In addition, they can’t forge the signature even if Alice collaborates with Charlie. Because all secret keys are distributed via quantum key distribution (QKD) protocol [15,16,17] which has proved unconditional security.

What’s more, if the external attacker Eve tries to forge Bob1’s signature, on the one hand, he needs to elude additional particles’ checking, on the other hand, he should know secret key KTB1 and M, otherwise, Trent will expose his forgery by step 3 in Section 3.2. Therefore, the forgery of Bob1’s signature is impossible for everyone.

5.3 Undeniability

During the phase of signature verifying, Charlie can use his key KTC and initial compact m2 to rebuild a new compact m2′ if Alice and Bob1 faithfully implements the trade procedure and no eavesdropper exists. If the content of compact is valid, he will accept it and inform Trent to finish payment. Once Charlie attempts to disavow the receipt of signature, Trent can expose him. Similarly, Bob1 can not disavow his signature either.

5.4 Unconditional Security

Firstly, we employ BB84 protocol [15] which is proved to be unconditional security to distribute keys. Secondly, the payment amount is encrypted by one-time pad algorithm [18]. Finally, we adopt the decoy photon checking technique and insert some additional particles to achieve the transmissive security. Therefore our scheme is unconditional security.

6 Conclusion

With a detailed security analysis, we show that the proposed scheme meets all the characteristics of quantum blind signature [19,20,21,22,23,24]. Furthermore, the proposed scheme can resist internal and external attack by taking advantage of the special encoded rules and quantum key distribution protocol (QKD) [15,16,17]. In addition, as described in [10,11,12,13,14, 25], most of the previous signatures’ operations are complex. However, in our scheme, all participants only need to employ single-particle quantum Z gate operations in the process of payment, which make the scheme more practical and convenient than them.