1 Introduction

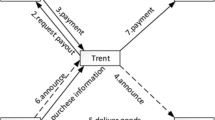
Nowadays, E-commerce is in a period of rapid development and choosing an appropriate model of payment is very important for E-commerce transaction. Since Chaum [1] proposed the concept of E-cash, many researchers have dedicated to study E-cash system and proposed a number of E-cash payment schemes [2–6]. Compared with other payment methods, E-cash has the properties of anonymity and off-line transferability and is becoming an ideal method of payment. The current E-payment system is mainly based on blind signature and group signature to achieve.

Digital signature is one of the most important components of modern cryptography, which serves as a basic module to design cryptography protocols [7]. Blind signature is a special kind of digital signature [8–12] in which the message anonymity could be guaranteed. In blind signature schemes, the message owner could always get the authentic signature of his own message even though the signer knows nothing about the content that he signed, quantum blind signature is supposed to provide unconditionally secure. Quantum blind signature has many applications like electronic voting systems and electronic payment systems, so it attracts widespread attention [13–15]. In 2010, Wen and Nie proposed an E-payment system based on quantum blind and group signature, employing two third trusted party instead of one to enhance the systems robustness [16]. In succession, Wen et al proposed an inter-bank E-payment protocol based on quantum proxy blind signature (named WCF protocol hereafter) [17]. However, Cai et al. [18] showed that the dishonst merchant can succeed to change the purchase information of the customer in this protocol.

In this paper, we propose an E-payment protocol based on quantum multi-proxy blind signature. In our system, quantum key distribution and one-time pad are adopted in order to guarantee unconditional security. Compared with previous E-payment systems and quantum signature schemes, we have made the following contributions. To the best of our knowledge, we are the first to apply quantum multi-proxy blind signature. The property of quantum multi-proxy blind signature could protect the anonymity of E-payment systems, while the quantum protocol could guarantee unconditional security. Moreover, different from existing quantum signature schemes, our protocol only need Bell-measurement, it can be implemented easily with the current experimental conditions.

2 Preliminary Theory

2.1 Multi-Proxy Blind Signature

Proxy signature allows a designated person, called proxy signer, to sign on behalf of an original signer. Proxy signatures are widely used in the fields of grid computing, mobile agent, mobile communications, e-commerce etc. [19, 20]. As for blind signature, the message owner could get the authentic signature for his own message, but not reveal the specific content of the message. In some cases, such as an inter-bank trading system, both the property of proxy signature and that of blind signature were required for application and security concern, so multi-proxy blind signature was proposed.

Different from classical blind signature scheme, our multi-proxy blind scheme is based on the theory below. The four Bell states of 2-qubit are

$$ |\phi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|00\rangle\pm|11\rangle),|\psi^{\pm}\rangle=\frac{1}{\sqrt{2}}(|01\rangle \pm|10\rangle). $$
(1)

Suppose that Alice and Bob share a Bell state

$$ |\phi^{+}\rangle_{AB}=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{AB}=\frac{1}{\sqrt{2}}(|++\rangle+|--\rangle)_{AB}, $$
(2)

where

$$|+\rangle=\frac{|0\rangle+|1\rangle}{\sqrt{2}},|-\rangle=\frac{|0\rangle-|1\rangle}{\sqrt{2}}. $$

Due to the entanglement characteristic of EPR pairs, after Alice has measured particle A, particle B will collapse to the same state as particle A. Thus, if Alice and Bob choose the same base B z = {|0〉,|1〉} or B x = {|+〉,|−〉} to measure their particles respectively, they will get the similar results. For example, if both Alice and Bob choose base B z and Alice gets |0〉, then Bob’s measuring result must be |0〉 too. However, after Alice’s measurement, if Bob chooses a different base from Alice, Bob will get a random result.

2.2 Controlled Quantum Teleportation

The quantum multi-proxy blind signature is based on controlled teleportation. In this section, we will introduce the controlled teleportation using four-particle cluster state as quantum channel. It is given by

$$ |\xi \rangle_{1234}= \frac{1}{2}(|0000\rangle+|0011\rangle+|1100\rangle-|1111\rangle)_{1234}. $$
(3)

The sender Alice owns particles 4, the controller Charlie owns particles (2, 3) and the particle 1 belongs to the receiver Bob.

Suppose that the quantum state of particle M carrying message in Alice is

$$ |\psi\rangle_{M}=(\alpha|0\rangle+\beta|1\rangle)_{M}, $$
(4)

where the coefficients α and β are unknown and satisfy |α|2+|β|2=1.

The state |Ψ〉 M1234 of whole system composed of particles M and (1, 2, 3, 4) is given by

$$ |{\Psi}\rangle_{M1234}=|\psi\rangle_{M}\otimes|\xi \rangle_{1234} =(\alpha|0\rangle+\beta|1\rangle)_{M}\otimes|\xi \rangle_{1234}. $$
(5)

The details of the controlled teleportation are as follows.

  1. 1)

    Alice performs a Bell-state measurement on particles M and 4. The measurement can collapse the state of particles (1, 2, 3) into one of the following states

    $$\begin{array}{@{}rcl@{}} \left<\phi^{\pm}_{M4}|{\Psi}\right>_{M1234} &=& \frac{1}{2\sqrt{2}}(\alpha|000\rangle+\alpha|110\rangle\pm \beta|001\rangle\mp \beta|111\rangle)_{123}, \\ \left<\psi^{\pm}_{M4}|{\Psi}\right>_{M1234} &=& \frac{1}{2\sqrt{2}}(\alpha|001\rangle-\alpha|110\rangle\pm \beta|000\rangle\pm \beta|110\rangle)_{123}. \end{array} $$
    (6)

    Alice sends her measurement outcomes to Charlie and Bob.

  2. 2)

    If Charlie agrees Alice and Bob to perform their teleportation, Charlie performs a Bell-state measurement on his particles (2, 3). Suppose that Alice’s measurement result is |ϕ +〉 M4, The measurement will collapse the state of particle 1 into one of the following states

    $$\begin{array}{@{}rcl@{}} \left<\phi^{\pm}_{23}|\phi^{+}_{M4}|{\Psi}\right>_{M1234} =& \frac{1}{4}(\alpha|0\rangle\mp \beta|1\rangle)_{1}, \\ \left<\psi^{\pm}_{23}|\phi^{+}_{M4}|{\Psi}\right>_{M1234} =& \frac{1}{4}(\beta|0\rangle\pm \alpha|1\rangle)_{1}. \end{array} $$
    (7)
  3. 3)

    According to Alice’s and Charlie’s measurement outcomes, Bob operates one of four unitary operations (I, σ z ,σ x ,i σ y ) on particle 1 to reconstruct the unknown quantum state |ψ〉 M . For example, assume Alice’s measurement result is |ϕ +〉 M4 and Charlie’s measurement result is |ϕ +〉23, respectively, Bob’s operation on particle 1 is σ z . For other cases, the relationship between Alice’s, Charlie’s measurement outcomes and Bob’s operation is listed in Table 1.

    Table 1 The relationship between Alice’s, Charlie’s measurement outcomes and Bob’s operation
    Full size table

3 Quantum E-payment Protocol

To clarify our quantum E-payment protocol, three characters are defined as follows:

  1. (1)

    Alice is defined as the customer who blinds the payment messages into the blinded messages, and sends the blinded messages to the businessman.

  2. (2)

    U j (j = 1, 2, ⋯ ,t) is defined as the representative of the bank Charlie, who signs the blinded messages to make a blind signature.

  3. (3)

    Bob is defined as the businessman, who receives and verifies the payment messages and the signature.

3.1 Initial Phase

Step1

The customer Alice holds a n-bit purchase message string (information bits) to be signed:

$$ m=\{m(1),m(2),\cdots,m(n)\}=\{m(i),i=1,2,\cdots,n\}. $$
(8)

Step2

Alice, U j and Charlie share secret keys K A B , \(K_{BU_{j}}\) and K B C with Bob, respectively. All these keys are distributed via QKD protocols, which have been proved unconditionally secure [21–23].

Step3

U j generates n EPR pairs such that

$$ |\psi_{i}\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)_{A_{i}B_{i}}. $$
(9)

where A i and B i denote the ith two entangled particles. In every EPR pair, U j sends particle A i to the customer Alice while leaving B i to himself. Bob generates tn entangled four particle cluster states as showed in (3), he gives particle 4 to U j , particles (2, 3) to the bank Charlie and he holds particle 1.

3.2 Blind the Purchase Message Phase

Step1

Alice measures her particle sequence according to message m, If m(i) = 0, she measures A i on the base B z = {|0〉, |1〉}. If m(i) = 1, she chooses the base B x = {|+〉,|−〉}. Alice records the measuring results as m ′={m ′(1),m ′(2),⋯ ,m ′(i)⋯ ,m ′(n)}(m ′(i) ∈ {|0〉, |1〉, |+〉, |−〉}). The four states |0〉, |1〉, |+〉, |−〉 could be encoded into two classical bits as following

$$ |0\rangle\rightarrow00, |1\rangle\rightarrow01, |+\rangle\rightarrow10, |-\rangle\rightarrow11. $$
(10)

Thus, the message m (n-bit) has been blinded into m ″(2n-bit).

Step2

Alice encrypts m ″ with the key K A B to get the secret message M, which is denoted as

$$ M=E_{K_{AB}}\{m^{\prime\prime}(1),m^{\prime\prime}(2),\cdots, m^{\prime\prime}(i)\cdots,m^{\prime\prime}(n)\}. $$
(11)

We adopt one-time pad as the encryption algorithm to guarantee the unconditional security. Alice sends the secret message M to the businessman Bob through the classical channel.

3.3 Authorizing and Signing Phase

Step1

To distinguish each proxy signers, Alice creates a unique serial number, which is denoted as SN and transfers it to a quantum state sequence |S N〉 in the basis {|0〉,|1〉}. Then she sends |S N j 〉 to U j .

Step2

After U j received |S N j 〉, he performs a Bell-state measurement on particles B i and 4. He combines the resulting records with his serial number as \(\beta _{U_{j}}=({\alpha (i)_{B_{i}4},i=1,2,\cdots ,n},|SN_{j}\rangle )(\alpha (i)_{B_{i}4}\in {|\phi ^{+}\rangle , |\phi ^{-}\rangle ,|\psi ^{+}\rangle ,|\psi ^{-}\rangle })\), where \(\beta _{U_{j}}\) is \(U_{j}^{\prime }s\) individual signature of message. U j sends \(S_{U_{j}}=E_{K_{BU_{j}}}\{\beta _{U_{j}}\}\) to Bob, and \(\beta _{U_{j}}\) to Charlie as his request.

Step3

If the bank Charlie agrees U j to sign the message on behalf of himself, he will help U j and the businessman Bob to complete the controlled teleportation. Charlie performs a Bell-state measurement on his particles (2, 3) and combines the records with |S N j 〉 as β C j = (β(i)23,i = 1,2,⋯ ,n, |S N j 〉)(β(i)23∈|ϕ +〉,|ϕ −〉,|ψ +〉,|ψ −〉). Then Charlie sends \(S_{Cj}=E_{K_{BC}}\{\beta _{Cj}\}\) to Bob.

3.4 Verifying Phase

Step1

Bob receives the secret message M from Alice, then he decrypts it with the key K A B to get the blind message m ″.

Step2

Bob decrypts messages \(S_{U_{j}}\) and S C j with keys \(K_{BU_{j}}\) and K B C to get the signature \(\beta _{U_{j}}\) and the message β C j , respectively. According to \(\beta _{U_{j}}\) and β C j , Bob performs a corresponding unitary operation on particle 1 to successfully reconstruct the unknown state on particle 1. The relationship between \(U_{j}^{\prime }s\), Charlie’s measurement results and Bob’s operation is listed in Table 1. (We replace Alice’s measurement results which is listed in Table 1 with \(U_{j}^{\prime }s\)).

Step3

Based on the real message the businessman Bob has obtained, Bob measures particle 1 on appropriate base according to the rule by the step1 in 3.2. The measuring results could be encoded into two classical bits according to (10). The results are wrote as c(j). If c(j) = m ″, the proxy signature is valid, otherwise, Bob will reject it.

Step4

Bob collects \(\{S_{U_{j}},j=1,2,\cdots ,t\}\) and gets the messages {c(j), j = 1, 2, ⋯ ,t}, if c(j) = c(j+1) = m ″(j = 1,2,⋯ ,t−1), he will confirm the signature and generate the final signature \( S=\{S_{U_{1}},S_{U_{2}},\cdots ,S_{U_{t}}\} \), else terminates the process.

4 Security Analysis and Discussion

Inspired by some articles [24–26], we have carried out the security analysis and discussion from the following aspects.

4.1 Message’s Blindness

In our scheme, the payment message m has been translated by Alice into m ′, where every m ′(i) ∈ {|0〉, |1〉, |+〉, |−〉}. If U j attempts to obtain the message m ′, the only way is to perform measurements. However, U j can not know Alice choose which base to measure her particle A i , so U j can not learn the message m ′, thus, he also can not deduce the original message m from it. Therefore, each proxy signatory knows nothing about the message that he has signed. That is, our scheme has the property of blindness.

4.2 Impossibility of Denial

In our scheme, we show that the bank Charlie can not disavow his delegation and U j can not deny his signature. According to Step 2 in 3.4, businessman Bob decrypts messages S C j and \(S_{U_{j}}\) with key K B C and key \(K_{BU_{j}}\) can get Charlie’s authorization, \(U_{j}^{\prime }s\) proxy request and his serial number S N j , respectively. All keys are distributed via QKD protocols, which have been proved unconditionally secure and all messages are sent through the secure quantum channel. Hence, Charlie can not deny his delegation and U j can not deny his signature.

4.3 Impossibility of Forgery

Firstly, we show that it is impossible for the dishonest insider attackers to forge U j ’s signature. Suppose that the businessman Bob is not honest, and attempts to forge customer’s message or U j ’s signature. Since Bob knows the shared secret keys between customer Alice and himself, he would not be able to forge the message, blind message or signatures. If this disagreement happens, Alice will find Bob’s behaviors. U j and Charlie are able to measure their particles respectively to uncover Bob’s trick. Similarly, Alice and U i (i ≠ j) can not forge U j ’s signature. In a word, the dishonest insider attackers can not forge signature.

Secondly, we discuss the forgery made by the outsider attacker Eve. As analyzed above, it is impossible for Eve to forge U j ’s signature under the condition that he has no knowledge of the secret key \(K_{BU_{j}}\). Therefore, if Eve aims to forge U j ’s signature successfully, the only way is to get the information about \(K_{BU_{j}}\). However, it is impossible, because the secret key is generated by the QKD protocol which has been proved unconditionally secure. Hence, Eve can not forge U j ’s signature.

4.4 Unconditional Security

Our scheme ensures security from the following three aspects. First, the protocol BB84 is adopted for quantum key distribution; Second, we employ one-time pad to encrypt; Third, our protocol is based on the secure quantum channel, which has instantaneous transmission not restricted by distance, time or obstacles, all of these are proved to be unconditional secure.

5 Conclusion

Combined with the actual demand for E-payment, in this paper, we proposed an E-payment protocol based on quantum multi-proxy blind signature. Compared with previous works, our protocol can realize the customer blind the payment messages into the blinded messages, which can protect the payment messages. Furthermore, our protocol is based on four-particle cluster state with less resource and as the key techniques of our protocol only rely on the Bell-measurement, which can make the protocol reliable and practical.

Additionally, in our scheme the Bell state |ϕ +〉 A B can be replaced by the other three Bell states, the E-payment protocol can be finished and proved secure.(We will not repeat the details of the protocol).