1 Introduction

Quantum correlations, as a fundamental character of a multipartite quantum system and an essential resource for quantum information processing [1], was initially studied in the entanglement-versus-separability scenario [2–4]. Even though entanglement has attracted much attention to many authors, it is not a unique characteristic of a quantum system, and it has no any advantage for some quantum information tasks. In some cases [5–7], although there is no entanglement, certain quantum information processing tasks can still be done efficiently by using quantum discord [8–10], which is believed more workable than the entanglement. The quantum discord (QD), first introduced by Ollivier and Zurek [8] and by Henderson and Vedral [9], is a measure of quantum correlations, which extends beyond entanglement, and a quantum-versus-classical paradigm for correlations [11–13].

Since the calculation of quantum discord involves a difficult optimization procedure, generally it is not easy to obtain analytical results except for a few typical examples of two-qubit states [14–22]. Huang has proved that computing quantum discord is NP-complete: the running time of any algorithm for computing quantum discord is believed to grow exponentially with the dimensions of the Hilbert space. Therefore, computing quantum discord even with a moderate size is impossible in practice [23]. Recently, some authors have to restrict their researches to two-qubit X states, which are frequently encountered in condensed matter systems, quantum dynamics, etc. [20, 22, 24–27] with an interest in the dynamics of quantum discord [28]. Ali et al. first studied the quantum discord for two-qubit X states and derived an explicit expression for X states [14, 15], but Lu immediately found a counterexample to his results [29]. After that, Chen pointed out that Ali’s algorithm is only valid for a class of X states. However, for some family of X states, Ali’s algorithm is not correct because of the inequivalence between the minimization over positive operator-valued measures and that over von Neumann measurements [30]. Indeed, Ali’s algorithm is not correct even if we only consider von Neumann measurements. The main reason for this error is that Ali did not find all extrema. Soon after, Rau and his co-authors [14, 15] extended the procedure of calculating discord of two-qubit X-states used in Ref.[14] to so-called extended X-states with N qubits. They also gave a formula to calculate the geometric measure of quantum discord for qubit-qudit systems [31]. In this aspect, Huang also found a counterexample to the analytical formula derived in [25], and proposed an analytical formula with a very small worst-case error [32].

Considering the difficulty in calculating the quantum discord, Dakić et al. [33] introduced a geometric measure of quantum discord Footnote 1 and obtained an analytic formula for two-qubit states. Very soon, Luo and Fu generalized GD to an arbitrary bipartite system and derived an explicit tight lower bound on it [34]. Rana et al. and Hassan et al. also obtained a rigorous lower bound to GD [35, 36] independently. Girolami et al. got another expression of GD for qubit-qubit states [37, 38]. Tufarelli et al. proposed an algorithm to calculate GD for any 2×d systems, which is valid for d→∞ case [39].

Because the original definitions of both QD and GD consider a set of local measurements only on one subsystem, it is not symmetric for two subsystems in the two partite case, Rulli et al. suggested a symmetric extension of QD named global quantum discord(GQD) [40], which has been extended to q-global quantum discord [41]. Some analytical expressions of GQD for some special quantum states have also been found [42]. On the other hand, inspired by Rulli’s work, Xu generalized the geometric quantum discord to multipartite states and proposed a geometric global quantum discord (GGQD) [43], which is alternatively known as symmetric or two-side geometric measure of quantum discord for two-qubit system [44, 45]. Almost at the same time, Hassan and Joag proposed total quantum correlations (TQC) and presented an algorithm to calculate TQC for a N-partitle quantum state [46]. It is worth pointing out that GD has attracted considerable attention to many authors, but there existed some argument on the geometric measure of quantum discord [47]. Piani argued that the geometric measure of quantum discord is not a good measure for the quantum correlations. Tafarelli et al. analyzed GD and indicated that it has two fatal weaknesses, i.e., both of them are related to the Hilbert-Schmidt norm or distance. They further defined a Hilbert space metric based on the Hilbert-Schmidt norm and proposed the so-called rescaled geometric discord (RGD) [48]. A detailed discussion about this issue is out of the scope of this paper. Nevertheless, we will compare the GGQD, GD and RGD of the same states. Compared with QD and GD, obviously, the study of GQD and GGQD as well as TQC is not yet enough. Hence, in this paper we first prove that GGQD and TQC are identical and then restrict ourselves to the study of GGQD. We attempt to derive an explicit analytical expression of GGQD for two-qubit X states.

This paper is organized as follows. In the next section, we give a brief review of GD, GGQD and TQC as well as RGD. We will prove that GGQD and TQC are identical. We derive the analytical formulas of GGQD and GD of two-qubit X states in Section 3. Some particular examples are given in Section 4. A related discussion is presented in Section 5 and we give concluding remarks in the last section.

2 Brief Review of Geometric Measure of Quantum Discord and Geometric Global Quantum Discord

We start with a brief review of QD, GD, GGQD and TQC as well as RGD. The QD of a bipartite state ρ on a system H a⊗H b with marginals ρ a and ρ b can be expressed as

$$ Q(\rho)=\underset{{\Pi}^{a}}{\min}\left\{I(\rho)-I({\Pi}^{a}(\rho))\right\}. $$
(1)

Here the minimum is over von Neumann measurements \({\Pi }^{a} = \{{{\Pi }^{a}_{k}}\}\) on subsystem a, and

$$ {\Pi}^{a}(\rho)=\sum\limits_{k}\left( {{\Pi}^{a}_{k}}\otimes I^{b})\rho ({{\Pi}^{a}_{k}}\otimes I^{b}\right) $$
(2)

is the resulting state after the measurement. I(ρ)=S(ρ a)+S(ρ b)−S(ρ) is the quantum mutual information, S(ρ)=−trρlnρ is the von Neumann entropy, and I b is the identity operator on H b. The GD for a state ρ is defined as [33]:

$$ D(\rho)=\underset{\chi}{\min}\|\rho-\chi\|^{2}, $$
(3)

where the minimum is over the set of zero-discord states (i.e., Q(χ)=0) and ∥ρ−χ∥2:=tr(ρ−χ)2 is the square of Hilbert-Schmidt norm of Hermitian operators. The GD of any two-qubit state is evaluated as

$$ D(\rho)=\frac{1}{4} \left( \|\textbf{x}\|^{2}+\|\textbf{T}\|^{2}-k_{max}\right), $$
(4)

where x:=(x 1, x 2, x 3)t is a column vector, \(\|\textbf {x}\|^{2} := {\sum }_{i} {x_{i}^{2}}\), x i = tr(ρ(σ i ⊗I b)), T:=(t i j ) is a matrix and t i j = tr(ρ(σ i ⊗σ j )), k m a x is the largest eigenvalue of matrix x x t+T T t.

Since Dakić et al. proposed the GD, many authors extended Dakić’s results to the general bipartite states. Luo and Fu evaluated the GD for an arbitrary state ρ and obtained an explicit formula

$$ D(\rho)=\text{tr}(\textbf{C}\textbf{C}^{t})- \underset{A}{\max}~\text{tr}(\textbf{A} \textbf{C} \textbf{C}^{t} \textbf{A}^{t}), $$
(5)

where C = (c i j ) is a m 2×n 2 matrix, given by the expansion \(\rho =\sum c_{ij} X_{i}\otimes Y_{j}\) in terms of orthonormal operators X i ∈L(H a), Y j ∈L(H b) and A = (a k i ) is an m×m 2 matrix given by a k i = tr|k〉〈k|X i = 〈k|X i |k〉 for any orthonormal basis |k〉 of H a. They also gave a tight lower bound for GD of arbitrary bipartite states [34]. Recently, a different tight lower bound for GD of arbitrary bipartite states was given by Rana et al. [35], and Hassan et al. [36] independently. Other explicit expressions of GD for two-qubit system and 2⊗d systems are also found [37–39].

On the other hand, in order to overcome the weaknesses of the GD, Tafarelli et al defined the distance of two density matrices ρ 1 and ρ 2 as

$$ d_{T}(\rho_{1},\rho_{2})=\left \|\frac{\rho_{1}}{\|\rho_{1}\|}-\frac{\rho_{2}}{\|\rho_{2}\|}\right \|, $$
(6)

where ∥⋅∥ stands for the Hibert-Schmidt norm as usual. Then, they proposed the rescaled geometric discord D T (ρ) for a state ρ as [48]

$$ D_{T}(\rho)=\beta_{A}~ \underset{{\Pi}^{A}}{\min}~d_{T}(\rho,{\Pi}^{A}[\rho])^{2}, $$
(7)

where β A is a normalization constant and depends on the dimension of H A . If the convention α A = d A /(d A −1) with d A = dim{H A } was adopted ,

$$ \beta_{A}= \frac{\sqrt{d_{A}}}{2 \left( \sqrt{d_{A}}-1\right)}. $$
(8)

Finally, they derived the RGD as

$$ D_{T}(\rho)=\beta_{A}\left[ 2-2\sqrt{1-\frac{D_{G}(\rho)}{\alpha_{A} \text{Tr} \{\rho^{2}\}}}\right], $$
(9)

where D G (ρ) is the GD defined as (3).

The QD and GD have been revealed as useful measurements, but they are originally not symmetric for its all subsystems. As an extension of QD, Rulli proposed a global quantum discord (GQD) for an arbitrary multipartite state \(\rho _{A_{1}{\cdots } A_{N}}\) as [40]:

$$ D(\rho_{A_{1}{\cdots} A_{N}})= \underset{\{{\Pi}_{k}\}}{\min}[S(\rho_{A_{1}{\cdots} A_{N}}\| {\Phi}(\rho_{A_{1}\cdots A_{N}}))-\sum\limits_{j=1}^{N}S(\rho_{A_{j}}\|{\Phi}_{j}(\rho_{A_{j}}))], $$
(10)

where \({\Phi }_{j}(\rho _{A_{j}})={\sum }_{j^{\prime }}{\Pi }_{A_{j}}^{j^{\prime }}\rho _{A_{j}}{\Pi }_{A_{j}}^{j^{\prime }}\) and \({\Phi }(\rho _{A_{1}{\cdots } A_{N}}) ={\sum }_{k}{\Pi }_{k}\rho _{A_{1}{\cdots } A_{N}}{\Pi }_{k}\), with \({\Pi }_{k}={\Pi }_{A_{1}}^{j_{1}} \otimes {\cdots } \otimes {\Pi }_{A_{N}}^{j_{N}}\) and k denoting the index string (j 1⋯j N ).

To calculate \(D(\rho _{A_{1}{\cdots } A_{N}})\) conveniently, Xu has given an equivalent expression of (10)[42]

$$ D(\rho_{A_{1}{\cdots} A_{N}})=\sum\limits^{N}_{k=1}S(\rho_{A_{k}})-S(\rho_{A_{1}A_{2}{\cdots} A_{N}}) -\underset{\Pi}{\max}\left [\sum\limits_{k=1}^{N} S({\Pi}_{A_{k}}(\rho_{A_{k}}))-S({\Pi}(\rho_{A_{1}{\cdots} A_{N}}))\right ], $$
(11)

where \({\Pi }={\Pi }_{A_{1}A_{2}{\cdots } A_{N}}\) is any locally projective measurement performed on A 1 A 2⋯A n .

The definition of GGQD for state \(\rho _{A_{1}A_{2} {\cdots } A_{N}}\) is

$$ D^{G}(\rho_{A_{1}A_{2} {\dots} A_{N}}) = \underset{\sigma_{A_{1}A_{2}{\cdots} A_{N}}}{\min} \{ \text{tr}[\rho_{A_{1}A_{2} {\cdots} A_{N}}-\sigma_{A_{1}A_{2}{\cdots} A_{N}}]^{2}~~~ :D(\sigma_{A_{1}A_{2}\cdots A_{N}})=0\}, $$
(12)

where \(D(\sigma _{A_{1}A_{2}{\cdots } A_{N}})\) is defined by (10). To simplify the calculation of (12), Xu derived two equivalent formulas of GGQD. The first one is:

$$\begin{array}{@{}rcl@{}} D^{G}(\rho_{A_{1}A_{2} {\dots} A_{N}})& =&\underset{\Pi}{\min}\left\{\text{tr}\left[\rho_{A_{1}A_{2} \cdots A_{n}}-{\Pi}(\rho_{A_{1}A_{2} {\cdots} A_{N}})\right]^{2}\right\}\\&=& \text{tr}\left[\rho_{A_{1}A_{2} \cdots A_{N}}\right]^{2}-\underset{\Pi}{\max}\left\{ \text{tr}\left[{\Pi}(\rho_{A_{1}A_{2} {\cdots} A_{N}})\right]^{2}\right\}, \end{array} $$
(13)

where π is the same as the one in (11).

The second formula of GGQD can be expressed as

$$ D^{G}(\rho_{_{A_{1}A_{2} {\dots} A_{N}}})=\sum\limits_{\alpha_{1},\alpha_{2},{\cdots} \alpha_{N}}\left( C_{\alpha_{1}\alpha_{2}{\cdots} \alpha_{N}}\right)^{2} -\underset{\Pi}{\max}\sum\limits_{i_{1}i_{2}{\cdots} i_{N}}\left( \sum\limits_{\alpha_{1},\alpha_{2},{\cdots} \alpha_{N}}A_{\alpha_{1}i_{1}}A_{\alpha_{2}i_{2}}{\cdots} A_{\alpha_{N} i_{N}}C_{\alpha_{1}\alpha_{2}{\cdots} \alpha_{N}}\right)^{2}\!\!, $$
(14)

where \(C_{\alpha _{1}\alpha _{2}{\cdots } \alpha _{N}}\) and \(A_{\alpha _{k}i_{k}}\) are determined by

$$ \rho_{_{A_{1}A_{2} {\cdots} A_{N}}}=\sum\limits_{\alpha_{1}\alpha_{2}{\cdots} \alpha_{N}}C_{\alpha_{1}\alpha_{2}\cdots \alpha_{N}}X_{\alpha_{1}}\otimes X_{\alpha_{2}}\otimes {\cdots} \otimes X_{\alpha_{N}}, $$
(15)
$$ A_{\alpha_{k}i_{k}}=\langle i_{k}|X_{\alpha_{k}}|i_{k}\rangle $$
(16)

and \(\{X_{\alpha _{k}}\}_{\alpha _{k}=1}^{{n_{k}^{2}}}\) are orthonormal bases of L(H k ), which were constituted by all Hermitian operators on H k ; \(\{|i_{k}\rangle \}_{i_{k}=1}^{{n_{k}^{2}}}\) are orthonormal bases of H k . For any two-qubit state ρ A B , (14-16) are reduced to:

$$ D^{G}(\rho_{AB})=\sum\limits_{\alpha\beta}\left( C_{\alpha\beta}\right)^{2}-\underset{A B}{\max}\sum\limits_{i,j}\left( \sum\limits_{\alpha \beta}A_{i\alpha} B_{j\beta}C_{\alpha\beta}\right)^{2}, $$
(17)
$$ C_{\alpha\beta}=\text{tr}\left( \rho_{AB} X_{\alpha} Y_{\beta}\right), $$
(18)
$$ A_{i\alpha}=\langle i|X_{\alpha}|i\rangle,~~B_{j\beta}=\langle j|Y_{\beta}|j\rangle,~~~i, j=1,2; ~~\alpha,\beta=0,1,2,3. $$
(19)

Here, for consistency with other literatures, such as [34, 36], we have exchanged the indexes of A and B in (19), which do not affect the following results. On the other hand, In (18) and (19), \(X_{0}=\mathbf {I}^{A}/\sqrt {2},~~X_{i}={\sigma _{i}^{A}}/\sqrt {2}, i=1,2,3;~ Y_{0}=\mathbf {I}^{B}/\sqrt {2},~~Y_{j}={\sigma _{j}^{B}}/\sqrt {2},j=1,2,3\), where I A and \({\sigma _{i}^{A}}\) are 2×2 unitary matrix and Pauli matrix for qubit A, I B and \({\sigma _{j}^{B}}\) are the same for qubit B, respectively. We can further express (17) in the matrix form,

$$ D^{G}(\rho_{AB})=\text{tr}(C C^{t})-\underset{A B}{\max}~\text{tr}(ACB^{t}BC^{t}A^{t}), $$
(20)

where X t denote the transpose of matrix X, A = {A i α }, B = {B j β } and C = {C α β }. Equation (20) is obviously the generalization of (5) in [34] to the case of GGQD.

Now, we turn our attention to TQC. Hassan and Joang introduced total quantum correlations in a state ρ 12⋯N [46]. They assumed that the non-selective von Neumann projective measurements \(\widetilde {\Pi }^{(1)}, \widetilde {\Pi }^{(2)},\cdots , \widetilde {\Pi }^{(N)}\) are acted on N parts 12⋯N of the system successively. The corresponding post-measurement states are expressed as

$$\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N}), \widetilde{\Pi}^{(2)}(\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N})),\cdots,\widetilde{\Pi}^{(N)}({\cdots} (\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N}){\cdots} )).$$

The GDs of these successive measurement states are given by

$$D_{1}(\rho_{12{\cdots} N}),D_{2}(\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N})),\cdots, D_{N}(\widetilde{\Pi}^{(N-1)}({\cdots} (\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N})){\cdots} )).$$

Then, the geometric measure of total quantum correlations of a N-partite quantum state ρ 12⋯N is defined as

$$ Q(\rho_{12{\cdots} N})= D_{1}(\rho_{12{\cdots} N})+D_{2}(\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N}))+{\cdots} + D_{N}(\widetilde{\Pi}^{(N-1)}({\cdots} (\widetilde{\Pi}^{(1)}(\rho_{12{\cdots} N})){\cdots} )). $$
(21)

In the following, we shall see that the definitions of GGQD and TQC are different in form, but they are identical to each other. To this end, we recall that 1) (13) is also obviously valid for GD with π=πk, k = 1,2,⋯ , N, which only performed on kth part of the system; 2) the projector \(\widetilde {\Pi }^{(1)}\) is defined as the von Neumann measurement minimizing the quantity ∥ρ−π(1)(ρ)∥2 [46], which implies that

$$ \text{tr}[\widetilde{\Pi}^{(1)}(\rho)]^{2}=\underset{{\Pi}^{(1)}}{\max}\left\{ \text{tr}\left[{\Pi}^{(1)}(\rho)\right]^{2}\right\}. $$
(22)

Keeping these in mind, we can rewrite (21) for N = 2 as

$$\begin{array}{@{}rcl@{}} Q(\rho) &=& D_{1}(\rho)+D_{2}(\widetilde{\Pi}^{(1)}(\rho)) = \text{tr}[\rho]^{2}-\underset{{\Pi}^{(1)}}{\max}\left\{ \text{tr}\left[{\Pi}^{(1)}(\rho)\right]^{2}\right\}+ \text{tr}\left[\widetilde{\Pi}^{(1)}(\rho)\right]^{2}-\underset{{\Pi}^{(2)}}{\max}\left\{ \text{tr}[{\Pi}^{(2)}(\widetilde{\Pi}^{(1)}(\rho))]^{2}\right\}\\ &=&\text{tr}[\rho]^{2}-\underset{{\Pi}^{(2)}}{\max}\left\{\text{tr}\left[{\Pi}^{(2)}(\widetilde{\Pi}^{(1)}(\rho))\right]^{2}\right\} =\text{tr}[\rho]^{2}-\underset{\Pi}{\max}\left\{\text{tr}\left[{\Pi}(\rho)\right]^{2}\right\}=D^{G}(\rho). \end{array} $$
(23)

There are two key points to be emphasized. First, the terms \(\underset {{\Pi }^{(1)}}{\max }\{ \text {tr}[{\Pi }^{(1)}(\rho )]^{2}\}\) and \(\text {tr}[\widetilde {\Pi }^{(1)}(\rho )]^{2}\) after the second equal sign naturally canceled out each other because of (22). Second, since \(\widetilde {\Pi }^{(1)}\) has been determined by (22), therefore, we can write \(\underset {{\Pi }^{(2)}}{\max }\{\text {tr}[{\Pi }^{(2)}(\widetilde {\Pi }^{(1)}(\rho ))]^{2}\}\) as \(\underset {\Pi }{\max }\{\text {tr}[{\Pi }(\rho )]^{2}\) with \({\Pi }={\Pi }^{(2)}\widetilde {\Pi }^{(1)}\). The proof of Q(ρ)=D G(ρ) for N≥3 cases is similar and straightforward. The identity of GGQD with TQC is not surprising, because both of them use the original definition of the geometric measure of quantum discord to every individual of the system. This can be further manifested by observing that (64) for TQC in Ref.[46] and the (14) for GGQD are the same. Due to this identity, therefore, hereafter we use the name ’geometric global quantum discord (GGQD)’, which also stands for ’total quantum correlations (TQC)’. In the next section, we are going to use (20) to calculate the GGQD of X state.

3 GGQD of Two-qubit X State

The two-qubit X state usually arises as the two-particle reduced density matrix in many physical systems. In the computational basis |00〉,|01〉,|10〉,|11〉 , the visual appearance of its density matrix resembles the letter X, so it is commonly known as X state in literatures. The density matrix of a two-qubit X state

$$ \rho_{AB}=\left( \begin{array}{cccc} \varrho_{00} & 0 & 0 & \varrho_{03} \\ 0 & \varrho_{11} & \varrho_{12} & 0 \\ 0 & \varrho_{12}^{*} & \varrho_{22} & 0 \\ \varrho_{03}^{*} & 0 & 0 & \varrho_{33}\\ \end{array} \right) $$
(24)

has nonzero elements only on the diagonal and the antidiagonal, where ϱ 00, ϱ 11, ϱ 22, ϱ 33≥0 satisfy ϱ 00+ϱ 11+ϱ 22+ϱ 33 = 1. The antidiagonal elements ϱ 03, ϱ 12 are generally complex numbers, but can be made real and nonnegative by the local unitary transformation \(e^{-i \theta _{1} \sigma _{z}}\otimes e^{-i \theta _{2} \sigma _{z}}\) with 𝜃 1 = −(argϱ 03+ argϱ 12)/4, 𝜃 2 = −(argϱ 03− argϱ 12)/4, where σ is the Pauli matrix. Hereafter we assume ϱ 03, ϱ 12≥0. Recall that the matrix C in (20) can be written as [34, 35]

$$ C=(C_{ij})=\frac{1}{2} \left( \begin{array}{cc} 1 & \textbf{y}^{t} \\ \textbf{x} & \textbf{T} \\ \end{array} \right), $$
(25)

Matrix A and B in (20) can be expressed as [34]

$$ A=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & \textbf{a} \\ 1 & -\textbf{a} \\ \end{array} \right), $$
(26)
$$ B=\frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & \textbf{b} \\ 1 & -\textbf{b} \\ \end{array} \right), $$
(27)

where \(\textbf {a}=\{a_{1},a_{2},a_{3}\}=\sqrt {2}(A_{11},A_{12},A_{13})\), \(\textbf {b}=\{b_{1},b_{2},b_{3}\}=\sqrt {2}(B_{11},B_{12},B_{13})\) and ∥a∥=∥b∥=1. Using (25–27), we can easily get the first term in (20)

$$ \text{tr}(CC^{t}) = \frac{1}{4}\left( 1+\|\textbf{x}\|^{2}+\|\textbf{y}\|^{2}+\|\textbf{T}\|^{2}\right) $$
(28)

and the second term

$$ \text{tr}(ACB^{t}BC^{t}A^{t}) =\frac{1}{4}\left[1 +\textbf{y}^{t}\textbf{b}^{t}\textbf{b}\textbf{y}+\textbf{a}(\textbf{x}\textbf{x}^{t}+\textbf{T}\textbf{b}^{t} \textbf{b}\textbf{T}^{t})\textbf{a}^{t}\right]. $$
(29)

The maximization over matrixes A and B in (20) can be done by two steps. First, we maximize a(x x t+T b t b T t)a t on matrix A. The maximum of this term is the largest eigenvalue λ m a x−A of matrix x x t+T b t b T t. According to the Lemma 1 of Ref. [45], which states that for any two vectors |a〉 and |b〉 (not necessarily normalized) in \(\mathbb {R}^{3}\), the largest eigenvalue of the matrix |a〉〈a|+|b〉〈b| is \(\lambda =[a^{2}+b^{2}+\sqrt {(a^{2}-b^{2})^{2}+4 \langle a|b\rangle ^{2}}]/2\) with a 2 = 〈a|a〉 and b 2 = 〈b|b〉, we get

$$ \lambda_{max-A}= \frac{1}{2}[\|\textbf{x}\|^{2}+\| \textbf{T}\textbf{b}^{t}\|^{2}+\sqrt{(\|\textbf{x}\|^{2}-\|\textbf{T}\textbf{b}^{t}\|^{2})^{2}+4 (\textbf{x}^{t} (\textbf{T}\textbf{b}^{t}))^{2}}]. $$
(30)

Substituting (28 – 30) into (20), we obtain the GGQD of any two-qubit systems

$$\begin{array}{@{}rcl@{}} D^{G}(\rho_{AB}) &=& \frac{1}{4}\left\{\|\textbf{x}\|^{2}+\|\textbf{y}\|^{2}+\|\textbf{T}\|^{2} -\frac{1}{2} \underset{ \textbf{b}}{\max}\left[\|\textbf{x}\|^{2}+\| \textbf{T}\textbf{b}^{t}\|^{2}\right.\right.\\ &+&\left.\left.\sqrt{(\|\textbf{x}\|^{2}-\|\textbf{T}\textbf{b}^{t}\|^{2})^{2}+4 (\textbf{x}^{t} (\textbf{T}\textbf{b}^{t}))^{2}}+2 \|\textbf{by}\|^{2}\right]\right\}. \end{array} $$
(31)

The second step to maximize tr(A C B t B C t A t) in (20) is reduced to maximize \(\|\textbf {x}\|^{2}+\| \textbf {T}\textbf {b}^{t}\|^{2}+\sqrt {(\|\textbf {x}\|^{2}-\|\textbf {\textbf {T}}\textbf {b}^{t}\|^{2})^{2}+4 (\textbf {x}^{t} (\textbf {\textbf {T}}\textbf {b}^{t}))^{2}}+2 \|\textbf {by}\|^{2}\) in above equation on b = {b 1, b 2, b 3} . For X state (24),

$$\begin{array}{@{}rcl@{}} \textbf{x}^{t} &=& \{x_{1},x_{2}, x_{3}\}=\{0, 0, \varrho_{00} +\varrho_{11} -\varrho_{22} -\varrho_{33}\}, \end{array} $$
(32)
$$\begin{array}{@{}rcl@{}} \textbf{y}^{t} & =& \{y_{1},y_{2},y_{3}\} =\{0, 0, \varrho_{00} -\varrho_{11} +\varrho_{22} -\varrho_{33}\}, \end{array} $$
(33)
$$ \textbf{T} = \left( \begin{array}{ccc} T_{11} & 0 & 0 \\ 0 & T_{22}& 0 \\ 0 & 0 & T_{33} \\ \end{array} \right) = \left( \begin{array}{ccc} 2(\varrho_{12}+\varrho_{03}) & 0 & 0 \\ 0 & 2(\varrho_{12}-\varrho_{03})& 0 \\ 0 & 0 & \varrho_{00} -\varrho_{11} -\varrho_{22}+\varrho_{33} \\ \end{array} \right), $$
(34)
$$ \begin{array}{lll} &\|\textbf{x}\|^{2} + \|\textbf{T}\textbf{b}^{t}\|^{2}+2\|\textbf{by}\|^{2}+\sqrt{(\|\textbf{x}\|^{2}-\| \textbf{T}\textbf{b}^{t}\|^{2})^{2}+4 (\textbf{x}^{t} (\textbf{T}\textbf{b}^{t}))^{2}}\\ &={x_{3}^{2}}+V+ 2 {b_{3}^{2}}{y_{3}^{2}} +\sqrt{\left( {x_{3}^{2}}-V\right)^{2}+4(V-W){x_{3}^{2}}},\\ \end{array} $$
(35)

where

$$\begin{array}{@{}rcl@{}} W &=& {b_{1}^{2}} T_{11}^{2} + {b_{2}^{2}} T_{22}^{2},~~~~~V= {b_{3}^{2}} T_{33}^{2}+ W. \end{array} $$
(36)

To complete the maximization in (35), let

$$b_{1}=\sin\theta \cos\phi,~b_{2}=\sin\theta \sin\phi, ~b_{3}= \cos \theta.$$

The half of (35) becomes

$$\begin{array}{@{}rcl@{}} f(\theta,\phi) &=& \frac{1}{2} \left[x_{3}^{2}+2 {y_{3}^{2}} \cos^{2}\theta +\gamma (\theta,\phi)\right. \left. +\sqrt{(\gamma (\theta ,\phi) -{x_{3}^{2}})^{2}+4 T_{33}^{2} {x_{3}^{2}} \cos^{2}\theta)}\right], \\ \gamma(\theta,\phi)&=& T_{33}^{2}\cos^{2}\theta+\mu(\phi)\sin^{2}\theta, \\ \mu(\phi)&=&T_{11}^{2}\cos^{2}\phi + T_{22}^{2}\sin^{2}\phi. \end{array} $$
(37)

We find

$$ \begin{array}{ll} \left\{\frac{\partial f(\theta,\phi)}{\partial \theta},\frac{\partial f(\theta,\phi)}{\partial \phi}\right\}|_{\theta=0}=0, & f(0,\phi)= {x_{3}^{2}} + {y_{3}^{2}}+T_{33}^{2},\\ \left\{\frac{\partial f(\theta,\phi)}{\partial \theta},\frac{\partial f(\theta,\phi)}{\partial \phi}\right\}|_{\theta=\frac{\pi}{2},\phi=0\bigvee\pi}=0, & f(\frac{\pi}{2},0\bigvee \pi)=\left\{ \begin{array}{cc} T_{11}^{2}, & \mathrm{for~~} T_{11}^{2}\geq {x_{3}^{2}};\\ {x_{3}^{2}} & \mathrm{for~~}T_{11}^{2} < {x_{3}^{2}}, \end{array} \right. \\ \left\{\frac{\partial f(\theta,\phi)}{\partial \theta},\frac{\partial f(\theta,\phi)}{\partial \phi}\right\}|_{\theta=\frac{\pi}{2},\phi=\frac{\pi}{2}\bigvee \frac{3\pi}{2}}=0, & f(\frac{\pi}{2},\frac{\pi}{2}\bigvee \frac{3\pi}{2})= \left\{ \begin{array}{cc} T_{22}^{2}, & \mathrm{for~~}T_{22}^{2}\geq {x_{3}^{2}};\\ {x_{3}^{2}} & \mathrm{for~~}T_{22}^{2} < {x_{3}^{2}}. \end{array} \right. \end{array} $$
(38)

Obviously, \({x_{3}^{2}} + {y_{3}^{2}}+T_{33}^{2}\geq {x_{3}^{2}}\) and \(T_{11}^{2}\geq T_{22}^{2}\), therefore, \(\max [f(\theta ,\phi )]=\max [{x_{3}^{2}} + {y_{3}^{2}}+T_{33}^{2},T_{11}^{2}]\). Substituting expressions of x 3, y 3, T 11 and T 33 into this expression, we obtain the maximum value of f(𝜃, ϕ),

$$\max[f(\theta,\phi)]=\max\left[\varrho_{00}^{2} + \varrho_{11}^{2} + \varrho_{22}^{2} + \varrho_{33}^{2} - 1/4, (\varrho_{12} +\varrho_{03})^{2}\right]$$

and the GGQD of X states

$$ D^{G}(\rho_{X})\,=\,\varrho_{00}^{2} + \varrho_{11}^{2} + \varrho_{22}^{2} + \varrho_{33}^{2} - \frac{1}{4}+2\left( \varrho_{12}^{2}+\varrho_{03}^{2}\right) -\max\!\left[\varrho_{00}^{2} \!+ \varrho_{11}^{2} \!+ \varrho_{22}^{2} + \varrho_{33}^{2} - \frac{1}{4}, (\varrho_{12} \!+\varrho_{03})^{2}\right]. $$
(39)

For comparing GGQD with GD for some X states in the next section, we also calculated the GD of X state according to Ref.[34] and got the following formula:

$$\begin{array}{@{}rcl@{}} D(\rho_{X})&=& \frac{1}{2}\left( \varrho_{00}^{2} + \varrho_{11}^{2} + \varrho_{22}^{2} + \varrho_{33}^{2}\right) - \varrho_{00} \varrho_{22} - \varrho_{11}\varrho_{33} +2\left( \varrho_{12}^{2}+\varrho_{03}^{2}\right) \\ &-&\max\left[\frac{1}{2}\left( \varrho_{00}^{2} + \varrho_{11}^{2} + \varrho_{22}^{2} + \varrho_{33}^{2}\right) - \varrho_{00} \varrho_{22} - \varrho_{11}\varrho_{33}, \left( \varrho_{12} +\varrho_{03}\right)^{2}\right]. \end{array} $$
(40)

This formula can also be derived by (23) of Ref.[31]. In simplifying (39,40) the condition ϱ 00+ϱ 11+ϱ 22+ϱ 33 = 1 has been used repeatedly. It is easy to obtain the corresponding expression of D T by substituting (40) into (9).

4 Illustrative Examples

In this section, we give some concrete examples to illustrate how to use these formulas obtained above.

(1) The first example is to consider the initial state ρ = a|ϕ +〉〈ϕ +|+(1−a)|1 A ,1 B 〉〈1 A ,1 B |(0<a≤1), where \(|\phi ^{+}\rangle =(|0_{A},0_{B}\rangle +|1_{A},1_{B}\rangle )/\sqrt {2}\) is a maximally entangled state [14]. The density matrix of this state is given by

$$ \rho_{X}=\left( \begin{array}{cccc} \frac{a}{2} & 0 & 0 & \frac{a}{2} \\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \frac{a}{2} & 0 & 0 & 1 - \frac{a}{2} \\ \end{array} \right). $$
(41)

The corresponding GGQD, GD and D T are

$$ D^{G}(\rho_{X})=D(\rho_{X})=\frac{a^{2}}{2}. $$
(42)
$$ D_{T}(\rho_{X})=\frac{2+\sqrt{2}}{2} \left( 2-\sqrt{\frac{3 a^{2}-4 a+4}{a^{2}-a+1}}\right ). $$
(43)

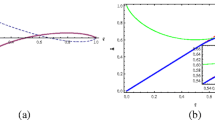
We plot D G(ρ X ), D(ρ X ) and D T (ρ X ) in Fig.1, which shows that D G(ρ X ) and D(ρ X ) are completely coincident, but D T (ρ X ) is unequal to D G(ρ X ) and D(ρ X ) in this state.

Fig. 1
figure 1

(Color online) Graphs of D G(ρ X )(black line), D(ρ X )(red dashed line) and D T (ρ X ) (blue dotted line) as functions of the parameter a for the class of states in (41).

Full size image

(2) We take a class of states defined as ρ = a|ψ +〉〈ψ +|+(1−a)|1 A ,1 B 〉〈1 A ,1 B |(0≤a≤1),where \(|\psi ^{+}\rangle =(|0_{A},1_{B}\rangle +|1_{A},0_{B}\rangle )/\sqrt {2}\) is a maximally entangled state [14]. The density matrix of this state is:

$$ \rho_{X}=\left( \begin{array}{cccc} 0 & 0 & 0 & 0\\ 0 & \frac{a}{2} & \frac{a}{2} & 0\\ 0 & \frac{a}{2} & \frac{a}{2} & 0\\ 0 & 0 & 0 & 1 - a\\ \end{array} \right). $$
(44)

The corresponding GGQD and GD are

$$ D^{G}(\rho_{X}) = \left\{\begin{array}{ll} \frac{a^{2}}{2}, & 0 \leq a \leq \frac{3}{5} \\ \frac{1}{4} (3 - 8 a + 7 a^{2}), & \frac{3}{5} < a \leq 1.\\ \end{array}\right. $$
(45)
$$ D(\rho_{X})=\left\{\begin{array}{ll} \frac{a^{2}}{2}, & 0 \leq a \leq \frac{1}{2} \\ \frac{1}{2} (1 - 3 a + 3 a^{2}), & \frac{1}{2} < a \leq 1.\\ \end{array}\right. $$
(46)

We plot D G(ρ X ), D(ρ X ) and D T (ρ X ) for the state (44) in Fig.2. We see that D G(ρ X )=D(ρ X ), for \(0\leq a \leq \frac {1}{2}\) and D G(ρ X )≥D(ρ X ), for \( \frac {1}{2} < a \leq 1\). Finally D G(ρ X )=D(ρ X ) when a = 1. The D G(ρ X ), D(ρ X ) and D T (ρ X ) have the similar trend, but D T (ρ X ) does not always greater or less than D G(ρ X ), D(ρ X ).

Fig. 2
figure 2

(Color online) Graphs of D G(ρ X )(black line), D(ρ X )(red dashed line) and D T (ρ X )(blue dotted line) as functions of the parameter a for the class of states in (44).

Full size image

(3) We take a class of states defined as \(\rho =\frac {1}{3}\{(1-a)|0_{A},0_{B}\rangle \langle 0_{A},0_{B}|+2 |\psi ^{+}\rangle \langle \psi ^{+}|+a|1_{A},1_{B}\rangle \langle 1_{A},1_{B}|\} (0\leq a\leq 1)\), where |ψ +〉 is the same as that in example (2) [14]. The density matrix of this state is:

$$ \rho_{X} =\left( \begin{array}{cccc} \frac{1-a}{3} & 0 & 0 & 0\\ 0 & \frac{1}{3} & \frac{1}{3} & 0\\ 0 & \frac{1}{3} & \frac{1}{3} & 0\\ 0 & 0 & 0 & \frac{a}{3}\\ \end{array} \right). $$
(47)

The corresponding GGQD and GD are

$$ D^{G}(\rho_{AB}) = \frac{2}{9} \left( a-\frac{1}{2}\right)^{2}+\frac{5}{36}, $$
(48)
$$ D(\rho_{AB}) = \frac{1}{9} \left( a-\frac{1}{2}\right)^{2}+\frac{5}{36}. $$
(49)

We plot D G(ρ X ), D(ρ X ) and D T (ρ X ) for the state (47) in Fig.3. We see that D G(ρ X ) and D(ρ X ) have the same minimum values \(\frac {5}{36}\approx 0.14\) at \(a=\frac {1}{2}\), but D T has the minimum value \(\frac {1}{2}(2+\sqrt {2})(2-\frac {\sqrt {31}}{3})\approx 0.25\) at the same point. The three curves are symmetric about \(a=\frac {1}{2}\).

Fig. 3
figure 3

(Color online) Graphs of D G(ρ X )(black line), D(ρ X )(red dashed line) and D T (ρ X )(dotted blue line) as functions of the parameter a for the class of states in (47)

Full size image

(4) Two atoms in the Tavis-Cumming model [49]. We consider two atoms (A and B), each of which interacts resonantly with a single quantized cavity field (system C) in a Fock state. This system is described by the two-atom Tavis-Cummings (TC) Hamiltonian: \(H =\hbar g[(\sigma _{A} + \sigma _{B})a_{C}^{\dag } + (\sigma _{A}^{\dag } + \sigma _{B}^{\dag })a_{C}]\), where σ j and \(\sigma _{j}^{\dag }\) denote the Pauli ladder operators for the jth atom, a(a ‡) stands for the annihilation (creation) operator of photons in cavity C, and g is the coupling constant. We consider that the system is initially in the state \(|\psi (0)\rangle = (\alpha |0_{_{A}} 0_{_{B}}\rangle + \beta |1_{_{A}} 1_{_{B}}\rangle )|n_{_{C}}\rangle \). Because the total number of excitations is conserved by TC Hamiltonian, the cavity mode will develop within a five-dimensional Hilbert space spanned by \(\{|(n-2)_{_{C}}\rangle ,|(n-1)_{_{C}}\rangle ,|n_{_{C}}\rangle ,|(n + 1)_{_{C}}\rangle ,|(n + 2)_{_{C}}\rangle \}\) for n≥2. When n = 0,1 the dimension is 3 and 4, respectively. On the other hand, since the atomic system evolves within the subspace \(\{|0_{_{A}}0_{_{B}}\rangle ,|+\rangle ,|1_{_{A}}1_{_{B}}\rangle \}\) with \(|+\rangle = (|1_{_{A}}0_{_{B}}\rangle + |0_{_{A}}1_{_{B}}\rangle )/\sqrt {2}\) independently of n, for our purpose, we only consider n = 0 case. By solving the Schrödinger equation, we obtain the state of the system at time t,

$$ |\psi(t)\rangle = c_{1}(t)|0_{_{A}} 0_{_{B}}\rangle|2_{_{C}}\rangle + c_{2}(t )|+\rangle| 1_{_{C}}\rangle +c_{3}(t )|1_{_{A}}1_{_{B}}\rangle|0_{_{C}}\rangle + c_{4}(t)|0_{_{A}}0_{_{B}}\rangle|0_{_{C}}\rangle $$
(50)

with the following probability amplitudes

$$\begin{array}{@{}rcl@{}} c_{1}(t)&=&-\frac{\sqrt{2}}{3} \beta \left[1 - \cos(\sqrt{6} g t)\right], \\ c_{2}(t)&=&-\frac{i \beta}{\sqrt{3}}\sin(\sqrt{6} g t), \\ c_{3}(t)&=&\beta\left\{1 + \frac{1}{3} [\cos(\sqrt{6} g t)-1]\right\},\\ c_{4}(t)&=& \alpha. \end{array} $$
(51)

Now, we take trace of the density operator ρ = |ψ(t)〉〈ψ(t)| over cavity C resulting in the reduced density matrix of the qubit-qubit system

$$ \rho_{AB}=\left( \begin{array}{cccc} |c_{1}|^{2} +|c_{4}|^{2} & 0 & 0 & |c_{3} c_{4}|\\ 0 & \frac{|c_{2}|^{2}}{2} & \frac{|c_{2}|^{2}}{2} & 0\\ 0 & \frac{|c_{2}|^{2}}{2} & \frac{|c_{2}|^{2}}{2} & 0\\ |c_{3} c_{4}| & 0 & 0 & |c_{3}|^{2}\\ \end{array} \right). $$
(52)
Fig. 4
figure 4

(Color online) The evolution of D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) as functions of the dimensionless time \(\tau =\sqrt {6}gt/(2 \pi )\) for the initial state \(|\psi (0)\rangle = (\alpha |0_{_{A}} 0_{_{B}}\rangle + \beta |1_{_{A}} 1_{_{B}}\rangle )|n_{_{C}}\rangle \) with \(\alpha =\beta = 1/\sqrt {2}\). The black solid line corresponds to D G(ρ A B ), the red dashed line to D(ρ A B ) and the blue dotted line to D T (ρ A B )

Full size image

Using (39) and (40), we obtain

$$\begin{array}{@{}rcl@{}} D^{G}(\rho_{AB})&=&\left( |c_{1}|^{2} +|c_{4}|^{2}\right)^{2} + |c_{2}|^{4} + |c_{3}|^{4} + 2 |c_{3}c_{4}|^{2} -\frac{1}{4} \\ &-&\max\left[\frac{1}{2}|c_{2}|^{4} + |c_{3}|^{4} + \left( |c_{1}|^{2} + |c_{4}|^{2}\right)^{2} -\frac{1}{4}, \left( \frac{1}{2}|c_{2}|^{2} + |c_{3} c_{4}|\right)^{2}\right], \end{array} $$
(53)
$$\begin{array}{@{}rcl@{}} D(\rho_{AB}) &=& \frac{1}{2} \left( |c_{1}|^{4} + 4 |c_{2}|^{4} + |c_{3}|^{4} + |c_{4}|^{4} - |c_{2}|^{2}\right) + \left( |c_{1}|^{2} + 2 |c_{3}|^{2}\right) |c_{4}|^{2} \\ &-& \max\left [\frac{1}{2} \left( \frac{1}{2}|c_{2}|^{4} - 1 - |c_{2}|^{2}\right) + (1 - |c_{2}|^{2})|c_{3}|^{2} , \left( \frac{1}{2}|c_{2}|^{2} + |c_{3} c_{4}|\right)^{2}\right ]. \end{array} $$
(54)

In this case, D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) as functions of dimensionless time \(\tau =\sqrt {6}gt/(6\pi )\) are plotted in Fig.4, which shows that three curves change periodically with a period T τ = 1. In addition, they simultaneously arrive to their maximums and minimums. Furthermore, the practical calculation shows the results for n≥1 are the same as those in Fig.4, which enhances that the evolution of two atomic system is independent of n, as pointed out earlier.

(5) As a final example, let us consider two atoms A and B in a common reservoir C [49]. We suppose that the initial state of this system was \(|{\Psi }(0)\rangle =(|g_{A}g_{B}\rangle + |e_{A}e_{B}\rangle )|\bar {0}\rangle _{C},\) where \(|\bar {0}\rangle = {\prod }_{k} |0\rangle _{k}\) is the reservoir vacuum state. The overall state of the system at time t can be written as

$$ |{\Psi}(t)\rangle = \alpha |g_{A}g_{B}\rangle |\bar{0}_{C}\rangle+c_{1}(t)|e_{A}e_{B}\rangle |\bar{0}_{C}\rangle + c_{2}(t)|+\rangle_{AB}|\bar{1}_{C}\rangle+c_{3}(t)|g_{A}g_{B}\rangle |\bar{2}_{C}\rangle, $$
(55)

where \(|+\rangle _{AB}=(|e_{A}g_{B}\rangle +|g_{A}e_{B}\rangle )/\sqrt {2}\) and \(|\bar {k}\rangle \) denotes the collective states of the reservoir in k excitations. The probability amplitudes for this case are

$$\begin{array}{@{}rcl@{}} c_{1}(t) &=& \beta e^{-\gamma t},~~~c_{2}(t)=\beta \sqrt{2 \gamma t} e^{-\gamma t}, \\ c_{3}(t) &=& \sqrt{1-\alpha^{2}-{c_{1}^{2}}(t)-{c_{2}^{2}}(t)}. \end{array} $$
(56)

Tracing out the reservoir, we obtain the density matrix of atomic subsystem

$$ \rho_{AB}=\left( \begin{array}{llll} \alpha^{2}+{c_{3}^{2}} & 0 & 0 & \alpha c_{1} \\ 0 & \frac{{c_{2}^{2}}}{2} & \frac{{c_{2}^{2}}}{2} & 0\\ 0 & \frac{{c_{2}^{2}}}{2} & \frac{{c_{2}^{2}}}{2} & 0\\ \alpha c_{1} & 0 & 0 & {c_{1}^{2}} \end{array} \right), $$
(57)

which is just an X state. The corresponding GGQD and GD are

$$ D^{G}(\rho_{AB}) = 3/4 - 2\left[{c_{1}^{2}} \left( {c_{2}^{2}} + {c_{3}^{2}}\right) + {c_{2}^{2}} \left( {c_{3}^{2}} + \alpha^{2}\right)\right] -\max\left[ {c_{1}^{4}} + {c_{2}^{4}}/2 + \left( \alpha^{2}+{c_{3}^{2}}\right)^{2}-1/4, \left( {c_{2}^{2}}/2 + \alpha c_{1}\right)^{2}\right], $$
(58)
$$ D(\rho_{AB}) = \frac{1}{4}\left[2 + 7 {c_{2}^{4}} - 6 {c_{2}^{2}} - 4 {c_{1}^{2}} \left( {c_{3}^{2}} - \alpha^{2}\right)\right] - \max\left\{\frac{1}{2} \left[1 - 3 {c_{2}^{2}} \left( 1 - {c_{2}^{2}}\right)- 2 {c_{1}^{2}} \left( {c_{3}^{2}} + \alpha^{2}\right) - {c_{2}^{4}}/ 2\right],\left( {c_{2}^{2}}/2 +\alpha c_{1}\right)^{2}\right\}. $$
(59)

In deducing above two equations, \({c_{1}^{2}}+{c_{2}^{2}}+{c_{3}^{2}}+\alpha ^{2}=1\) has been used. We plot D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) as functions of the dimensionless time γ t in Fig.5. D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) have the similar behavior with γ t: they have two relative maximums as well as one relative minimum, respectively. Their corresponding relative maximums and relative minimums are close to each other. In addition, D G(ρ A B ) and D(ρ A B ) have the same initial values 2α 2(1−α 2), which is greater than the initial values of D T (ρ A B ). Finally, when t→∞, D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) simultaneously approach zero.

Fig. 5
figure 5

(Color online) The evolution of D G(ρ A B ), D(ρ A B ) and D T (ρ A B ) as functions of the dimensionless time γ t for the initial state \(|\psi (0)\rangle = (\alpha |0_{_{A}} 0_ {_{B}}\rangle + \beta |1_{_{A}} 1_{_{B}}\rangle )|\bar {0}_{_{C}}\rangle \) with α = 0.1 and \(\beta =\sqrt {1-\alpha ^{2}}\). The black solid line corresponds to D G(ρ A B ), the red dashed line to D(ρ A B ) and the blue dotted line to D T (ρ A B )

Full size image

5 Discussion

We have derived analytical formulas of GGQD and GD for two-qubit X states. Here we give some useful remarks. First, it should be pointed out that (20, 31), from which (39) was derived, are applicable not only to two-qubit X states, but also to any two-qubit states. Second, because of tr(A C B t B C t A t)=tr(B C t A t A C B t), we can alternatively first optimize system B, then system A. This is equivalent to exchange subsystems A and B, and transpose matrix C. Of course, the two procedures give the same results. Third, more importantly, we find that GGQD are always greater than or equal to GD in five examples given in Section 4. In fact, this is true for any X state. We give a proof below.

First, using tr(ρ X )=ϱ 00+ϱ 11+ϱ 22+ϱ 33 = 1 we easily obtain

$$\begin{array}{@{}rcl@{}} &&\left( \varrho_{00}^{2}+\varrho_{11}^{2}+\varrho_{22}^{2}+\varrho_{33}^{2} - 1/4\right) -\left[\left( \varrho_{00}^{2}+\varrho_{11}^{2}+\varrho_{22}^{2}+\varrho_{33}^{2}\right)/2- \varrho_{00} \varrho_{22} - \varrho_{11} \varrho_{33}\right] \\ &=&[2 (\varrho_{00} + \varrho_{22})-1]^{2}/4 =[2 (\varrho_{11} + \varrho_{33})-1]^{2}/4\geq 0, \end{array} $$
(60)

which means \(\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2} - 1/4\geq (\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2})/2- \varrho _{00} \varrho _{22} - \varrho _{11} \varrho _{33}\). Therefore, there are only three cases need to be considered.

  • (1) \((\varrho _{12}+\varrho _{03})^{2}\geq \varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2} - 1/4\geq \left (\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2}\right )/2- \varrho _{00} \varrho _{22} - \varrho _{11} \varrho _{33} \):

    $$\begin{array}{@{}rcl@{}} D^{G}(\rho_{AB})&=& \varrho_{00}^{2}+\varrho_{11}^{2}+\varrho_{22}^{2}+\varrho_{33}^{2} -\frac{1}{4}+ (\varrho_{12}-\varrho_{03})^{2}, \end{array} $$
    (61)
    $$\begin{array}{@{}rcl@{}} D(\rho_{AB})&=& \frac{1}{2} \left[(\varrho_{00} - \varrho_{22})^{2} + (\varrho_{11} - \varrho_{33})^{2}\right]+(\varrho_{12}-\varrho_{03})^{2}, \end{array} $$
    (62)
    $$ D^{G}(\rho_{AB})-D(\rho_{AB})=\frac{1}{4} [ 2(\varrho_{00} + \varrho_{22})-1]^{2} =\frac{1}{4} [ 2(\varrho_{11} + \varrho_{33})-1]^{2}\geq 0. $$
    (63)

  • (2) \(\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2} - 1/4 \geq (\varrho _{12}+\varrho _{03})^{2}\geq \left (\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2}\right )/2- \varrho _{00} \varrho _{22} - \varrho _{11} \varrho _{33} \):

    $$\begin{array}{@{}rcl@{}} D^{G}(\rho_{AB}) &=& 2 \left( \varrho_{12}^{2}+\varrho_{03}^{2}\right), \end{array} $$
    (64)
    $$\begin{array}{@{}rcl@{}} D(\rho_{AB}) &=&\frac{1}{2} \left[(\varrho_{00} -\varrho_{22})^{2} + (\varrho_{11}-\varrho_{33})^{2}\right] + (\varrho_{12}-\varrho_{03})^{2}, \end{array} $$
    (65)
    $$\begin{array}{@{}rcl@{}} &&D^{G}(\rho_{AB})-D(\rho_{AB}) =(\varrho_{12}+\varrho_{03})^{2} -\frac{1}{2} \left[(\varrho_{00} -\varrho_{22})^{2} + (\varrho_{11}-\varrho_{33})^{2}\right]\geq\\ & & \frac{1}{2}(\varrho_{00}^{2}\,+\,\varrho_{11}^{2}\,+\,\varrho_{22}^{2}\,+\,\varrho_{33}^{2})\! -\! \varrho_{00} \varrho_{22} \,-\, \varrho_{11} \varrho_{33} \!-\frac{1}{2} \!\left[\!(\varrho_{00} \,-\,\varrho_{22})^{2} \,+\, (\varrho_{11}\!-\varrho_{33})^{2}\right]\!=0. \end{array} $$
    (66)

  • (3) \( (\varrho _{12}+\varrho _{03})^{2} \leq (\varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2})/2- \varrho _{00} \varrho _{22} - \varrho _{11} \varrho _{33}\leq \varrho _{00}^{2}+\varrho _{11}^{2}+\varrho _{22}^{2}+\varrho _{33}^{2} - 1/4 \):

    $$ D^{G}(\rho_{AB})=D(\rho_{AB})=2 (\varrho_{12}^{2} + \varrho_{03}^{2}). $$
    (67)

We conclude that D G(ρ A B )≥D(ρ A B ) for any X state from (60, 63, 66, 67). However, our examples show that D T is not always greater than D G(ρ A B ) or D(ρ A B ).

6 Summary

In summary, we have first proven GGQD and TQC are the same and then obtained analytical formulas of GGQD and GD for two-qubit X states. We have also compared GGQD, TQC and RGD by five concrete examples. We have further found that GD is the tight lower bound of GGQD, which means that GD is a good approximation for GGQD at least for X states. There are still some interesting opening problems to be studied in this aspect, such as, are there any analytical expressions of GGQD for qubit-qudit system? Can GD be a tight lower bound of GGQD for any bipartite system? We shall report our research results on these issues later.