1 Introduction

Quantum communication is one of the important components of quantum information. The basic idea is that classical or quantum information can be transmitted through a quantum channel. Quantum communication exhibits better security and higher capability which can’t be replaced by the classic communication because quantum mechanics takes on some unique natures, for examples, quantum coherence, quantum non-cloning, etc. Therefore, quantum communication has many potential applications in the military, secure communication, signal transmission and other fields [1–6].

In all quantum communication schemes reported previously, the quantum secure direct communication (QSDC) is an ideal scheme and has attracted comprehensive attention quickly. Its advantages are the quantum key does not need to appoint in advance and the quantum entanglement is used to achieve secure bidirectional communication. Since Beige et al. proposed QSDC ideas [7], Boström et al., Deng et al. have designed a ping-pong protocol and a two-step protocol, respectively [8, 9]. The safety is discussed and a specific operation scheme for quantum direct communication processes is proposed. After that, Cao et al. extended information carrier of the schemes from the Bell state of two-body to w state of three-body [10]. Deng et al. discussed further QSDC security [11]. Recently, Lin et al. designed the QSDC scheme based on χ-type entangled states [12] and Yu et al. investigated the QSDC scheme based on non-orthogonal state [13]. These fruitful works establish a solid foundation for the theoretical and application research of QSDC.

So far, the investigations about QSDC schemes are mainly two-body or three-body entangled system, which has exposed limitations in the direct communication. Not only less information is transferred in a single communication and all particles are intercepted easily by attacker owing to the constitution with limited number particles, but also the difficulty of physical realization is increased because of the influence of physical implementation in which communication scheme is confined on two-body or three-body particles. In recent years, Barreior et al. researched photonic superdense coding by using pairs of photons entangled in their spin and orbital angular momentum, and achieved a dense-coding experiment with a large channel capacity [14]. Subsequently, a experimental demonstration of a hyper-entangled Schröinger cat state have also been reproted [15]. These achievements make it valuable to discuss a high-dimensional quantum communication process. In view of the above reasons, the QSDC scheme based on multi-body entangled system to complete the direct communication is proposed in this paper. Firstly, we give the mathematical description of the QSDC scheme and analyze the process of direct communication based on multi-body entangled system. At the same time, we design a general method of information coding. The communication model based on four-body systems is taken as an example to validate the effectiveness of the scheme proposed in our work. The results show that the scheme is of universal and convenient because the specific communication scheme can be designed expediently according to the required number of particles in practical physics system.

This paper is organized as follows. In Section 2 the general design method of QSDC based on multi-body particle system and the corresponding mathematical description are given. In Section 3 the QSDC communication process based on 2m entangled system is investigated, and QSDC scheme using four-body entangled system to complete the direct communication is taken as an example. Finally we conclude our results in Section 4.

2 The Basic Processes of QSDC and the Mathematical Description

2.1 The Basic Processes of QSDC

The QDCS scheme based on two-body two-level system has been investigated repeatedly since the concept of quantum direct communication has been proposed. Here, we give a universal process of realizing quantum direct communication scheme base on the existing ones.

Assume that S is a complete set of orthogonal basis vectors in n dimensional Hilbert space. U = U A ⊗ U B is conversion operator set and the operator in U can change every state in S to another, i.e.

$$ S=\{\left|\psi_{1}\right\rangle, \left|\psi_{2}\right\rangle, \cdot \cdot \cdot,\left|\psi_{n}\right\rangle\}, \langle\psi_{i}|\psi_{j}\rangle=\delta_{ij} $$
(1)
$$ U_{A} =\left\{{U_{A}^{1}} ,{U_{A}^{2}} ,\cdot \cdot \cdot ,{U_{A}^{n}} \right\}, U_{B} =\left\{{U_{B}^{1}} ,{U_{B}^{2}} ,\cdot \cdot \cdot ,{U_{B}^{n}} \right\}, \quad U^{i}U^{i\dag }=I $$
(2)

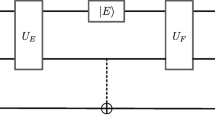
The basic process of quantum direct communication can be formed by the following steps:

  1. a.

    Alice and Bob, who want to communicate, engage a same arbitrary state |Ψ k 〉 chosen from the set S before communication, take it as the initial state and share a EPR-pair which on this state. At the same time, they encode for each operation in U A and U B .

  2. b.

    In communication, Alice and Bob do the local operations for their particles respectively using the operation corresponding with their information transferred.

  3. c.

    Alice sends all the particles owned by herself to Bob. Then Bob measures all the particles in the basis S and announces the measurement results.

This moment, Alice and Bob have known respectively the information as follows: the selected initial state, the measurement results of final state and the operations done by themselves. Therefore, they can figure out operations in the opposite side based on the decode formula and seize information each other. It should be noted that the scheme would return to the common QSDC scheme based on two-body system if taking S = {|ϕ +〉, |ϕ −〉, |φ +〉, |φ +〉 and U A = U B = {σ 0, σ x , i σ y , σ z }.

2.2 The Mathematical Description of QSDC Scheme

A simple representation method will be given for two-body quantum state [16–18].

Suppose vector

$$ \mathbf{e}=(\left|0\right\rangle ,\left|1\right\rangle ,\cdot \cdot \cdot ,\left|n\right\rangle ) $$
(3)
$$ \textbf{\~{e}}^{\mathbf{T}}=(\left\langle0 \right|,\left\langle 1 \right|,\cdot\cdot \cdot ,\left\langle n \right|)^{\textbf{T}} $$
(4)

And for a given two-body state |ψ k 〉 A B , it can be expressed as

$$ \left|\psi_{k}\right\rangle_{AB}=\mathbf{e}T_{k}\textbf{\~{e}}^{\mathbf{T}} $$
(5)

here, T k is a coefficient matrix which is used to represent the quantum state |ψ k 〉 A B .

Then, two particles are operated by \({U_{A}^{i}} \) and \({U_{B}^{j}} ,_{\mathrm {}}\) respectively.

$$ {U_{A}^{i}} \otimes {U_{B}^{j}} \left|\psi_{k} \right\rangle_{AB} $$
(6)

also be written as

$$ {U_{A}^{i}} T_{k} U_{B}^{jT} $$
(7)

Thus, the quantum direct communication process described above can be thought of as the mathematical process as follow:

$$\begin{array}{@{}rcl@{}} &&\forall \left| {\Psi}_{k}\right\rangle_{AB} \in S,\\ &&\forall {U_{A}^{i}} \otimes {U_{B}^{j}} \in U_{A} \otimes U_{B} ,\\ &&\exists \left|{\Psi}_{m}\right\rangle_{AB} \in S,\\ &&\left| {\Psi}_{m}\right\rangle_{AB}=U^{i}_{A} \otimes U^{j}_{B}|{\Psi}_{k}\rangle_{AB} \end{array} $$
(8)

According to the forms of (5)–(7), (8) can be expressed as

$$ T_{m} ={U_{A}^{i}} T_{k} U_{B}^{jT} $$
(9)

so, the decode formula based on (9) can be derived as

$$ {U_{A}^{i}} =T_{m} \left(U_{B}^{jT} \right)^{-1}(T_{k} )^{-1} $$
(10)
$$ U_{B}^{jT} =(T_{k} )^{-1}\left({U_{A}^{i}} \right)^{-1}T_{m} $$
(11)

3 The QSDC Based on Multi-Body Particles

It is unnecessary to consider the dimension of the set S in the quantum direct communication process above-mentioned, so the scheme can be extended to any numbers of particles so long as an apposite set of complete orthogonal basis vectors S and a set of conversion operators U which corresponds with S are found. The key of designing a QSDC scheme was reduced to find a complete orthogonal basis set S and the corresponding set of conversion operators U. In this section, a QSDC scheme based on a four-body two-level system is proposed, and on this basis, the general design method of a QSDC scheme based on multi-body particles is discussed.

Assume that four-body particles with the following state are used to communicate directly:

$$ \left|\psi_{0}\right\rangle_{1234}=\frac{1}{2}[|00\rangle_{13}|00\rangle_{24}+|01\rangle_{13}|01\rangle_{24}+ |10\rangle_{13}|10\rangle_{24}+|11\rangle_{13}|11\rangle_{24}] $$
(12)

If let |00〉 → |0〉, |01〉 → |1〉, |10〉 → |2〉 and |11〉 → |3〉, The state describing four-body can be rewritten as a “two-body like” state, i.e.

$$ \left|\psi_{0}\right\rangle=\frac{1}{2}[|0\rangle|0\rangle+|1\rangle|1\rangle+|2\rangle|2\rangle+|3\rangle|3\rangle] $$
(13)

Therefore, a set of complete orthogonal vectors basis S can be written as:

$$ {\begin{array}{l} S= \\ \left\{\left|\psi_{0}\right\rangle\! =\!\frac{1}{2}[\left|0\right\rangle \left|0\right\rangle \,+\,\left| 1\right\rangle \left|1\right\rangle\! +\!\left|2\right\rangle \left|2\right\rangle \,+\,\left|3\right\rangle \left|3\right\rangle ],\left| \psi_{1}\right\rangle=\frac{1}{2}[\left|0\right\rangle \left|0\right\rangle + \left|1\right\rangle\left|1\right\rangle -\left|2\right\rangle \left|2\right\rangle -\left|3\right\rangle \left|3\right\rangle ], \right.\\ \left|\psi_{2}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|0\right\rangle - \left|1\right\rangle \left|1\right\rangle - \left|2\right\rangle \left|2\right\rangle \,+\, \left|3\right\rangle \left|3\right\rangle ], \left|\psi_{3}\right\rangle=\frac{1}{2}[\left|0\right\rangle \left|0\right\rangle - \left|1\right\rangle \left|1\right\rangle +\left|2\right\rangle \left|2\right\rangle - \left|3\right\rangle \left|3\right\rangle ], \\ \left|\psi_{4}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|3\right\rangle+ \left|1\right\rangle \left|2\right\rangle + \left|2\right\rangle \left|1\right\rangle + \left|3\right\rangle \left|0\right\rangle ], \left|\psi_{5}\right\rangle\,=\,\frac{1}{2}[\left|0\right\rangle \left|3\right\rangle + \left|1\right\rangle \left|2\right\rangle -\left|2\right\rangle \left|1\right\rangle - \left|3\right\rangle \left|0\right\rangle ], \\ \left|\psi_{6}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|3\right\rangle - \left|1\right\rangle \left|2\right\rangle - \left|2\right\rangle \left|1\right\rangle + \left|3\right\rangle \left|0\right\rangle ], \left|\psi_{7}\right\rangle\,=\,\frac{1}{2}[\left|0\right\rangle \left|3\right\rangle - \left|1\right\rangle \left|2\right\rangle +\left|2\right\rangle \left|1\right\rangle - \left|3\right\rangle \left|0\right\rangle ], \\ \left|\psi_{8}\right\rangle\! =\!\frac{1}{2}[\left|0\right\rangle \left|1\right\rangle + \left|1\right\rangle \left|0\right\rangle + \left|2\right\rangle \left|3\right\rangle + \left|3\right\rangle \left|2\right\rangle ], \left|\psi_{9}\right\rangle\,=\,\frac{1}{2}[\left|0\right\rangle \left|1\right\rangle + \left|1\right\rangle \left|0\right\rangle -\left|2\right\rangle \left|3\right\rangle - \left|3\right\rangle \left|2\right\rangle ], \\ \left|\psi_{10}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|1\right\rangle \,-\, \left|1\right\rangle \left|0\right\rangle\! -\! \left|2\right\rangle \left|3\right\rangle \,+\, \left|3\right\rangle \left|2\right\rangle ], \left|\psi_{11}\right\rangle=\frac{1}{2}[\left|0\right\rangle \left|1\right\rangle - \left|1\right\rangle \left|0\right\rangle +\left|2\right\rangle \left|3\right\rangle - \left|3\right\rangle \left|2\right\rangle ], \\ \left|\psi_{12}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|2\right\rangle \,+\, \left|1\right\rangle \left|3\right\rangle \,+\, \left|2\right\rangle \left|0\right\rangle \,+\, \left|3\right\rangle \left|1\right\rangle ], \left|\psi_{13}\right\rangle=\frac{1}{2}[\left|0\right\rangle \left|2\right\rangle + \left|1\right\rangle \left|3\right\rangle -\left|2\right\rangle \left|0\right\rangle - \left|3\right\rangle \left|1\right\rangle ], \\ \left.\left|\psi_{14}\right\rangle \,=\,\frac{1}{2}[\left|0\right\rangle \left|2\right\rangle \,-\, \left|1\right\rangle \left|3\right\rangle \,-\, \left|2\right\rangle \left|0\right\rangle \,+\, \left|3\right\rangle \left|1\right\rangle ], \left|\psi_{15}\right\rangle\,=\,\frac{1}{2}[\left|0\right\rangle \left|2\right\rangle \,-\, \left|1\right\rangle \left|3\right\rangle \,+\,\left|2\right\rangle \left|0\right\rangle - \left|3\right\rangle \left|1\right\rangle ],\right\} \\ \end{array}} $$
(14)

It is known from above discussion that once an apposite U corresponding S can be found, the design of the scheme can be completed. Here, a convenient method of finding the set U is given.

All the states in S can be predigested firstly into the format given in Section 2.2 and a coefficient matrix set T will be obtained. Afterward, the matrix in T is transformed to the unitary matrix T′ ∈ S.

$$ \begin{array}{c} S= \\ \left\{\left({{\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} }}\right. \right),\left({{\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ \end{array} }} \right) \\ ,\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right) \\ ,\left({{\begin{array}{*{20}c} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 0 \hfill & 0 \hfill & {-1} \hfill & 0 \hfill \\ \end{array} }} \right) \\ ,\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 1 \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left({{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ {-1} \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 1 \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right),\left(\left. {{\begin{array}{*{20}c} 0 \hfill & 0 \hfill & 1 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {-1} \hfill \\ 1 \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {-1} \hfill & 0 \hfill & 0 \hfill \\ \end{array} }} \right)\right\} \\ \end{array} $$
(15)

The operation set U can be expressed after rewriting the T′:

$$ \begin{array}{l} U=\{\sigma_{0} \otimes \sigma_{0} ,\sigma_{z} \otimes \sigma_{0} ,\sigma_{z} \otimes \sigma_{z} ,\sigma_{0} \otimes \sigma_{z} ,\sigma _{x} \otimes \sigma_{x} ,i\sigma_{y} \otimes \sigma_{x} ,i\sigma_{y} \otimes i\sigma_{y} ,\sigma_{x} \otimes i\sigma_{y} , \\ \sigma_{0} \otimes \sigma_{x} ,\sigma_{z} \otimes \sigma_{x} ,\sigma _{z} \otimes i\sigma_{y} ,\sigma_{0} \otimes i\sigma_{y} ,\sigma_{x} \otimes \sigma_{0} ,i\sigma_{y} \otimes \sigma_{0} ,i\sigma_{y} \otimes \sigma_{z} ,\sigma_{x} \otimes \sigma_{z} \} \\ \end{array} $$
(16)

where σ i ⊗ σ j means that σ i is used to act on the first particle and σ j to act on the second particle.

The QSDC can be performed while Alice and Bob encode and operate by using the operators in (16), respectively.

At this point, a QSDC scheme based on 2m-body 2-level particles (m∈N) can be summarized as following:

  1. a.

    Alice and Bob, who want to communicate, rewrite the 2m-body state as a “two-body like” state and find the set S of complete orthogonal vectors.

  2. b.

    Alice and Bob get the coefficient matrix T corresponding with each state in S and transform them to the unitary matrix. In the process, the operation operator set U can be found and the information can be encoded into each conversion operator.

  3. c.

    Alice and Bob prepare the particles held by themselves on the engaged initial state and each person holds m particles.

  4. d.

    In communication, Alice and Bob do the local operations for their particles respectively using the operation corresponding with their information transferred.

  5. e.

    Alice sends all the particles she owned to Bob. Then, Bob measures all the particles in the basis S and announces.

  6. f.

    Based on the measurement results and added operation, Alice and Bob can figure out respective information by the decoding formula (10) and (11).

4 Conclusion

The process of the direct communication using multi-body entangled system is presented in this paper and its mathematical description is given on the basis of the existing QSDC scheme of two-body system. A four-body system is taken further as an example to research the QSDC scheme based on multi-body particles and the general design method of QSDC scheme based on 2m-body system is concluded. This work provides the theoretical basis for realizing QSDC scheme and the communication scheme required can be designed conveniently according to the number of particles in practical physical system because the method proposed in our work exhibits universality.