1 Introduction

Quantum entanglement [1] has been recognized as a powerful tool for quantum information processing [2]. For example, it plays an important role in superdense coding [3] and quantum teleportation [4], and is necessary for the exponential speedup of quantum algorithms compared to classical algorithms [5, 6]. The entanglement can be produced either by direct interactions or indirect interactions through a third party between two quantum systems. In real situations, an entangled composite quantum system can never be isolated and will inevitably interact with its environment, which usually causes unwanted disentanglement, and brings obstacles to the practical implement of quantum information processing. In order to maintain quantum entanglement for a longer time for many applications of interest, much attention has been paid to understand of the decoherence mechanism [7–13] and find suitable candidates for quantum computation and quantum information [14–16].

Due to the long decoherence and relaxation time, the spin system becomes one of the most promising candidates for quantum computation. Recently, the decoherent behavior of a single spin or disentanglement behavior of several spins interacting with a spin bath has attracted much attention [17–25]. The interaction between central spins and a bath of environmental spins often leads to strong non-Markovian behavior, which is characterized by pronounced memory effects, finite revival times and non-exponential behavior of damping and decoherence. The dynamics of central spins systems in a spin bath has been analyzed without making the Markovian approximation, but using a perturbative expansion method [22], a mean-field approximation [23], a novel operator technique [24], and numerical simulation [25].

However, in all of the previous works, the central spin was in the spin bath with different coupling types, and the non-Markovian effect would be induced by the spin-bath strong coupling. What will happen to the central spins if they are in a composite spin environment? Are there any new characteristics of non-Markovian evolutions to better understand non-Markovianity [26–30]? To answer these questions, we consider a new model, which is an extension of the above models, to study the non-Markovian effect on the dynamics of entanglement in this paper. In our model, two coupled central spins interact with a spin star environment, and each bath spins is further coupled to a local boson reservoir. And the interaction between the central spins, and the interaction between the central spin and the spin environment are all of the Heisenberg XY type and can all be taken into account simultaneously. The dynamics of the model could be distinguished between the Markovian and non-Markovian regime by using the spectral width of the boson reservoir [31]. The model is exactly solvable because of the symmetry of the structure under consideration. Meanwhile, the model is a simple open quantum model that is relevant for the physics of nitrogen-vacancy centers in diamonds [14] and molecular nanomagnets [15, 16]. Our model is similar to model discussed in Ref. [32], which found that non-Markovian effect would be buried by the forgetful mechanism induced not only by the spin-bath coupling, but also by parameters such as the mismatch between the energy of the central spin and of the spin environment.

The paper is organized as follows. In Sect. 2, the model Hamiltonian is introduced and the time evolution of reduced density matrix for central spins is calculated. From the reduced density matrix, the entanglement measure of concurrence of the coupled spin system is calculated in Sect. 3. Conclusions are given in Sect. 4.

2 The Model and Its Solution

The model consists of a spin-star system and boson reservoirs. We consider two central spin-qubits (labelled a and b) have Heisenberg XY interaction between each other and at the same time they interact with N outer bath spins. The interactions between bath spins are also of XY type, and each bath spins is further coupled to a local boson reservoir. The total Hamiltonian of the spin-star system is

$$ \hat{H}{=}\hat{H}_0{+}\hat{H}_S{+}\hat{H}_{SB}. $$
(1)

Here, H 0 is the free energy of the whole system, H s is the hamiltonian describing the interaction between all spins, and H SB is the interaction between outer spin and its own boson bath. They can be written as

$$\begin{aligned} \hat{H}_0 =&\sum_{i=a,b}{ \mu_i \hat{\sigma}^{z}_{i}}+ \sum _{j=1}^N{\mu_j \hat{\sigma}^{z}_{j}}+\sum_{j=1}^N{ \sum_k{\omega_{k,j} \hat{b}_{k,j}^\dagger \hat{b}_{k,j}}} \end{aligned}$$
(2a)
$$\begin{aligned} \hat{H}_S =& J\bigl(\sigma_a^+{\sigma_b^-}+ \sigma_a^-{\sigma_b^+}\bigr) + J'\sum_{ij}\sum _{(j\neq i~\mathrm{or}~a, b)}\bigl(\sigma_i^+{\sigma_j^-}+ \sigma_i^-{\sigma_j^+}\bigr) \end{aligned}$$
(2b)
$$\begin{aligned} \hat{H}_{B} =& \sum^N_{j{=}1}\sum _k \bigl(g_{k,j} \hat{\sigma}^+_j \hat{b}_{k,j} + g^*_{k,j} \hat{\sigma}^-_j \hat{b}^{\dagger}_{k,j}\bigr) \end{aligned}$$
(2c)

where the parameters \(\hat{\sigma}^{s}_{i}\)(i=a,b,1,…,N) are the Pauli matrices for the spin i (s=x,y,z), μ i is the transition frequency between spin states |0〉 j and |1〉 j , which are the eigenstates of \(\sigma_{z}^{i}\). \(\hat{\sigma}^{\pm}_{j}=(\hat{\sigma}^{x}_{j}\pm i\hat{\sigma}^{y}_{j})/2\) are the spin-flip operators of the spin i. J represents the coupling constant between central spins, and J′ represents the coupling constant between central-spin and bath spins. The index k labels the different field modes of the reservoir with frequencies ω k,j , the creation annihilation operators \(\hat{b}_{k,j}^{\dagger}\), \(\hat{b}_{k,j}\), and coupling constants g k,j .

In the interaction picture the state |Ψ(t)〉 of the whole system obeys to the Schrödinger equation

$$ \frac{\partial}{\partial t}\bigl|\varPsi(t)\bigr\rangle = -i\hat{H}_I(t)\bigl| \varPsi(t)\bigr\rangle , $$
(3)

where the hamiltonian in interaction picture is given by

$$\begin{aligned} H_I(t) =& J\bigl(\sigma_a^+{ \sigma_b^-}+\sigma_a^-{\sigma_b^+}\bigr) + J'\sum_{ij}\sum _{(j\neq i~\mathrm{or}~a, b)}\bigl(\sigma_i^+{\sigma_j^-}+ \sigma_i^-{\sigma_j^+}\bigr) \\ &{}+ \sum_{j=1}^N{\sum _k \bigl( g_k \sigma^j_+ b_k e^{i (\mu_j-\omega_{k,j})t} + h.c.\bigr)}. \end{aligned}$$
(4)

here we assume there is no energy mismatch between the central and bath spins for simplicity. It is easy to check that the ‘particle number’ operator \(N=\sum_{i}{\sigma_{i}^{z}}+\sum_{j}({\sigma_{j}^{z}} +(\sum_{k} b_{k}^{\dagger}b_{k})_{j})\) commutes with the total Hamiltonian \(\hat{H}\), and any initial state of the form

$$\begin{aligned} \bigl|\varPsi(0)\bigr\rangle =&\bigl(c_0|00 \rangle^{ab}+\alpha(0)|01\rangle^{ab}+\beta(0)|10 \rangle^{ab}\bigr) \mathbf{|0\rangle}^S\mathbf{|0 \rangle}^B \\ &{}+\sum_{j=1}^N c_j(0) |00 \rangle^{ab}\mathbf{|j\rangle}^S\mathbf{|0 \rangle}^B +\sum_{j=1}^N \sum _k c_{kj}(0)|00\rangle^{ab} \mathbf{|0\rangle}^S\mathbf{|k\rangle}_j^B \end{aligned}$$

evolves after time t into the state

$$\begin{aligned} \bigl|\varPsi(t)\bigr\rangle = &\bigl(c_0|00 \rangle^{ab}+\alpha(t)|01\rangle^{ab}+\beta(t)|10 \rangle^{ab}\bigr) \mathbf{|0\rangle}^S\mathbf{|0 \rangle}^B \\ &{}+\sum_{j=1}^N c_j(t) |00 \rangle^{ab}\mathbf{|j\rangle}^S\mathbf{|0 \rangle}^B +\sum_{j=1}^N \sum _k c_{kj}(t)|00\rangle^{ab} \mathbf{|0\rangle}^S\mathbf{|k\rangle}_j^B, \end{aligned}$$
(5)

where the state \(\mathbf{|0\rangle}^{S}\) denotes the product state \(\bigotimes_{j=1}^{N}|0\rangle^{j}\) and \(\mathbf{|j\rangle}^{S}=\sigma^{+}_{j}\mathbf{|0\rangle}^{S}\) for the sites on the spin bath; \(\mathbf{|0\rangle}^{B}\) is the vacuum state of all the reservoirs, and \(\mathbf{|k\rangle}_{j}^{B} = b_{k,j}^{\dagger}|0\rangle_{j}\) the state with one particle in mode k in the jth reservoir.

The amplitude c 0 is constant in time because of \(H_{I}(t)|00\rangle^{ab} \mathbf{|0\rangle}^{S} \mathbf{|0\rangle}^{B} = 0\). The time development of time dependent amplitudes α(t), β(t), c j (t), and c kj (t) are governed by a system of differential equations which is derived from the Schrödinger equation (3),

$$ \begin{aligned}[c] \frac{d}{dt}\alpha(t)&=-i J \beta(t)-i J' \sum _{j=1}^N c_j(t), \\ \frac{d}{dt}\beta(t)&=-i J \alpha(t)-i J' \sum _{j=1}^N c_j(t), \\ \frac{d}{dt}c_j(t)&=-i J' \bigl[\alpha(t)+ \beta(t)\bigr]-i\sum_k c_{kj}(t) g_{kj} e^{i(\mu_j-\omega_{kj})t}, \\ \frac{d}{dt}c_{kj}(t)&=-i g_{kj}^* c_j(t) e^{-i(\mu_j-\omega_{kj})t}. \end{aligned} $$
(6)

Integrating the fourth differential equation and inserting the solution into the third one, we can get the equation for c j (t),

$$\begin{aligned} \frac{d}{dt}c_j(t)=-i J' \bigl[\alpha(t)+\beta(t) \bigr] - \int_0^t c_j(t_1) f_j(t-t_1)dt_1, \end{aligned}$$
(7)

where we define the kernel

$$ f_j(t-t_1) =\int J(\omega_{kj})e^{-i(\mu_j-\omega_{kj})(t-t_1)}d \omega_{kj}, $$
(8)

is the environmental correlation function with the spectral density defined as J(ω kj )=∑ k |g kj |2 δ(μ j −ω kj ).

In the following of this paper, we assume the initial state of the system is

$$\begin{aligned} \bigl|\varPsi(0)\bigr\rangle = \bigl(c_0|00 \rangle^{ab}+\alpha(0)|01\rangle^{ab}+\beta(0)|10 \rangle^{ab}\bigr) \mathbf{|0\rangle}^S\mathbf{|0 \rangle}^B, \end{aligned}$$
(9)

here all bath spins are in the |0〉 state and all boson reservoirs are in the vacuum state initially, i.e. c j (0)=c kj (0)=0. With this initial condition, the differential equations for the probability amplitude α(t), β(t), and c j (t) can be solved conveniently by passing in the Laplace domain:

$$ \begin{cases} \begin{aligned}[c] s \tilde{\alpha}[s]&=\alpha(0)-iJ\tilde{\beta}[s] -i J' \sum_{j=1}^N \tilde{c_j}[s],\\ s \tilde{\beta}[s]&=\beta(0)-iJ\tilde{\alpha}[s] -i J' \sum_{j=1}^N \tilde{c_j}[s],\\ s \tilde{c_j}[s]&=-i J'\bigl[\tilde{\alpha}[s]+\tilde{\beta}[s]\bigr] - \tilde{c_j}[s]\tilde{f}_j[s]. \end{aligned}\end{cases} $$
(10)

By assuming that all the reservoirs are the same (f j (t)=f(t) ∀j) for simplicity, we can get

$$ \begin{cases}\begin{aligned} \tilde{\alpha}[s]&=\frac{1}{(\tilde{f}[s]+s)(J^2+s^2)+2J'^2N(s-iJ)} \\ &\quad{}\times\bigl\{ \alpha(0)\bigl[J'^2N+s(\tilde{f}[s]+s)\bigr]-\beta(0)\bigl[J'^2N+iJ\bigl(\tilde{f}[s]+s\bigr)\bigr]\bigr\} \\ \tilde{\beta}[s]&=\frac{1}{(\tilde{f}[s]+s)(J^2+s^2)+2J'^2N(s-iJ)} \\ &\quad{}\times\bigl\{ \beta(0)\bigl[J'^2N+s\bigl(\tilde{f}[s]+s\bigr)\bigr]-\alpha(0)\bigl[J'^2N+iJ\bigl(\tilde{f}[s]+s\bigr)\bigr] \bigr\} \end{aligned}\end{cases} $$
(11)

The memory effect registered in the kernel function f(t−t 1) is determined by the spectral density J(ω). We consider the spectral density for each bath has a Lorentzian form

$$ J(\omega ) = \frac{1}{{2\pi }}\frac{{\gamma \lambda ^2 }}{{(\mu - \omega )^2 + \lambda ^2 }}, $$
(12)

where γ is the coupling constant between the bath spin and the reservoir, λ defines the spectral width of the coupling at the resonance point, and in this case one can verify that the correlation function decays exponentially

$$ f(t)=\frac{1}{2}\gamma\lambda \exp\bigl(-\lambda |t|\bigr), $$
(13)

which means that the parameter λ characterizes the spectral width of the reservoir, and it is associated with the reservoir correlation time by the relation τ B =λ −1 and the parameter γ is related to the relaxation time scale τ R by the relation τ R =γ −1. If \(\gamma>\frac{\lambda}{2}\), the memory effect of the reservoir should not be neglected and the decoherence dynamics in this situation is non-Markovian. While \(\gamma<\frac{\lambda}{2}\), the memory effect of the reservoir is negligible and the decoherence dynamics is Markovian.

Finally, one can obtain the analytical form of α(t) and β(t) by substituting the Laplace transforming of exponentially decaying f(t) into Eq. (11) and anti-transforming as

$$\begin{aligned} \alpha(t) =&\frac{1}{2}e^{iJt}\bigl[\alpha(0)- \beta(0)\bigr] +\bigl[\alpha(0)+\beta(0)\bigr] \\ &{}\times\frac{\sum^3_{i=1} (-1)^{i-1}e^{s_i t}(s_j{-}s_k)(2s^2_i+2\lambda s+\gamma+\lambda)}{(s_1-s_2)(s_2-s_3)(s_1-s_3)}, \end{aligned}$$
(14)
$$\begin{aligned} \beta(t) =&\frac{1}{2}e^{iJt}\bigl[\beta(0)- \alpha(0)\bigr] +\bigl[\alpha(0)+\beta(0)\bigr] \\ &{}\times\frac{\sum^3_{i=1} (-1)^{i-1}e^{s_i t}(s_j{-}s_k)(2s^2_i+2\lambda s+\gamma+\lambda)}{(s_1-s_2)(s_2-s_3)(s_1-s_3)}, \end{aligned}$$
(15)

where s i are the roots of equation

$$\begin{aligned} 2s^3+2(\lambda+iJ)s^2+\bigl(4J'^2N+ \lambda\gamma+2iJ\bigr)s +4J'^2N\lambda+iJ\gamma\lambda=0. \end{aligned}$$
(16)

For any N>1, α(t) and β(t) are obtained from the expression valid for N=1 with the re-definition \(J'\rightarrow J'/ \sqrt{N}\) by a simple scaling law [19]. Then, the time-dependent reduced density matrix of the central qubits under the initial condition can be obtained straightforwardly from the exact dynamical map

$$ \rho(t) = \operatorname{Tr}_{S+B} \bigl\{ \bigl|\varPsi(t) \bigr\rangle \bigl\langle \varPsi(t)\bigr| \bigr\} = \left (\begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1-|\alpha(t)|^2-|\beta(t)|^2 & c_0^*\alpha(t) & c_0^*\beta(t) & 0 \\ c_0\alpha^*(t) & |\alpha(t)|^2 & \alpha(t)^*\beta(t) & 0\\ c_0\beta^*(t) & \alpha(t)\beta(t)^* & |\beta(t)|^2 & 0 \\ 0 & 0 & 0 & 0\\ \end{array} \right ), $$
(17)

3 Concurrence and Entanglement Dynamics

We use the concurrence [33, 34] to measure the entanglement between the two central spins. It is defined as

$$\begin{aligned} C_{ab}=\textrm{max}\{\lambda_1-\lambda_2- \lambda_3-\lambda_4,0\}, \end{aligned}$$
(18)

where the quantities λ 1≥λ 2≥λ 3≥λ 4 are the square roots of the eigenvalues of the operator \(R_{ab}=\rho_{s} (\sigma^{y}_{a}\otimes\sigma^{y}_{b} )\rho_{s}^{*} (\sigma^{y}_{a}\otimes\sigma^{y}_{b} )\).

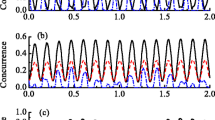
Figures 1 and 2 show several interesting features of entanglement evolution for different values of the coupling constant J between central spins. Clearly in Fig. 1, we see that the entanglement oscillates and decays with time evolution, and the entanglement decays to zero in finite time. The increasing value of J results in the decrease of the decay rate of entanglement. The increasing of J also results in the decrease of the oscillating frequency.

Fig. 1
figure 1

Quantum entanglement versus scaled time J′t for different values of the coupling constant J between central spins, and the central spins are in Bell state with \(\alpha=\beta=\sqrt{2}/2\) initially. Values of the other parameters are λ=1 and γ=1

Full size image
Fig. 2
figure 2

Quantum entanglement versus scaled time J′t for different values of the coupling constant J between central spins, and the central spins are in the product state with α=1, and β=0 initially. Values of the other parameters are λ=1 and γ=1

Full size image

In Fig. 2, there is no initial entanglement between the two spins. It is interesting to notice that the entanglement between the two spins is present and oscillating into a certain value as shown in Fig. 2, even though there is no coupling between the two spins, i.e. J=0. This confirms that the environment which usually makes the decoherence of the system happen can also entangle qubits that are initially prepared in a separable state. The reason to cause what happens is by the fact that the two central spins are coupled to the same environment which then in turn generates some effective interactions between the two spins even if they were originally decoupled.

We can see the time evolution of entanglement for different values of the coupling constant J′ between central spin and bath spins from Fig. 3. For J′=0, the system of the two central spins is closed, and the entanglement dose not evolute with time. While for J′≠0, the entanglement of central spins is affected by the environment and disentanglement occurs. When the coupling strength between central spins and bath spins is weak, we see that the concurrence decreases faster as the coupling strength is increasing. As the coupling strength is further increases, the decay rate and the oscillating frequency of entanglement decrease.

Fig. 3
figure 3

Quantum entanglement versus scaled time Jt for different values of the coupling constant J between central spins, and the central spins are in Bell state with \(\alpha=\beta=\sqrt{2}/2\) initially. Values of the other parameters are λ=1 and γ=1

Full size image

In Fig. 4, we plot the dynamics behavior of the concurrence for different values of the parameter γ. The increasing of γ results in the decrease of the oscillating frequency, and the decoherence dynamics becoming non-Markovian from Markovian. Different from other non-Markovian effects, which influence the entanglement dynamics for lasting longer life and give rise to a revival of entanglement even after complete disentanglement for finite time periods [35], the memory effect of the reservoir in our model causes the increase of the decay rate of entanglement. This interesting phenomenon is triggered by the indirect influence of the non-Markovian reservoir on the central spin.

Fig. 4
figure 4

Quantum entanglement versus scaled time Jt for different values of the coupling constant J between central spins, and the central spins are in Bell state with \(\alpha=\beta=\sqrt{2}/2\) initially. Values of the other parameters are λ=1 and J′=J

Full size image

4 Summary and Discussion

In this paper, we have studied the exact entanglement evolution of two coupled central spins in a model of a quantum spin star configuration, and each bath spin is further coupled to a local boson reservoir. The dynamics of the reduced density matrix of the two coupled central spins is analytically obtained for only one excitation in the whole system. The time evolutions of the concurrence of the two coupled central spins for different initial conditions are evaluated exactly. The results show that the dynamics of the entanglement strongly depends on the initial state of the central system, the coupling between the two central spins, the interaction between the central system and the environment, as well as interactions between the bath spin and the reservoir. We have also found that finite entanglement will be created, no matter how strong the coupling between the two central spins is. The numerical results further shows that the entanglement decreases rapidly in non-Markovian case.

We believe that the presented analysis can be useful for a more complete knowledge about Non-Markovian dynamics and entanglement dynamical properties.