1 Introduction

It is believed that the most part of Universe filled with dark matter and dark energy. Therefore, dark energy and related topics are important subjects to study in theoretical physics and cosmology. An important problem is determining nature of dark Universe. It is found that the dark matter may be consists of neutrinos [1] axions [2] or WIMPs (weak interactive massive particles) [3]. In that case there are several ways to specify the nature of the dark Universe. For example studying time-dependent density help to give information about dark matter [4] and dark energy [5].

After that we need a model to describe dark Universe. In that case there are some phenomenological and theoretical models which based on discovery of the accelerating expansion of the Universe [6, 7]. Some of the famous phenomenological models for dark energy briefly explained below.

The cosmological constant and its generalizations are the simplest way to modeling the dark energy [8]. Another candidates for the dark energy are scalar-field dark energy models. A quintessence field [9] is a scalar field with standard kinetic term, which minimally coupled to gravity. In that case the action may has a wrong sign kinetic term (minus instead of plus), which the scalar field is called phantom or ghost [10]. While there is a quantum instability in the phantom models but this model to be consistent with CMB observations [11]. Combination of the quintessence and the phantom is known as the quintom, which is another model for dark energy [12].

Extension of kinetic term in Lagrangian yields to a more general frame work on field theoretic dark energy, which is called k-essence [13, 14]. A singular limit of k-essence is another model, named Cuscuton [15]. This model has an infinite propagating speed for linear perturbations, however causality is still valid.

The most general form for a scalar field with second order equation of motion is the Galileon field which could behave as dark energy [16]. Another extension of these models is called the ghost condensation, which also solved the quantum instability of phantom dark energy [17]. There are also various studies in holographic dark energy models (see Refs. [18–22]).

However, presence of a scalar field is not only requirement of the transition from a Universe filled with matter to an exponentially expanding Universe. The matter components in cosmology are written in terms of fluids, so most of dark energy models have fluid description. Therefore, Chaplygin gas (CG) used as an exotic type of fluid, which is a model for dark energy [23–25]. This model based on Chaplygin equation of state [26] to describe the lifting force on a wing of an air plane in aerodynamics. The CG was not consistent with observational data of SNIa, BAO, CMB, and so on [27–30]. Therefore, an extension of CG model proposed [31–34], which is called generalized Chaplygin gas (GCG), and indeed proposed unification of dark matter and dark energy. However, observational data ruled out such a proposal. Then, GCG extend to the modified Chaplygin gas (MCG) [35]. There is still more extension such as generalized cosmic Chaplygin gas (GCCG) [36]. In this paper we continue recent study of the next extension which is modified cosmic Chaplygin gas (MCCG) [37–39].

In all cases the time-dependent density calculated approximately for the vanishing cosmological constant, and also under some assumption for simplicity.

Now, in this paper we would like to study MCCG with arbitrary α and non-zero cosmological in presence of space curvature. Also we use methods of non-linear differential equation to obtain more exact solutions.

2 Modified Cosmic Chaplygin Gas Model

One of the recent cosmological models which is based on the use of exotic type of perfect fluid suggests that our Universe filled with the Chaplygin gas with the following equation of state [40, 41],

$$ p=-\frac{B}{\rho}, $$
(1)

where B is a positive constant. The Chaplygin gas is also interesting subject of holography [42], string theory [43], and supersymmetry [44]. It is also possible to study FRW cosmology of a Universe filled with CG [23]. In order to have coincident with observational data the CG equation of state (1) has been developed to the form,

$$ p=-\frac{1}{\rho^{\alpha}} \bigl[C+\bigl(\rho^{1+\alpha}-C \bigr)^{-\omega } \bigr], $$
(2)

where C is a constant. The speciality of this model is stability so the theory is free from unphysical behaviors even when the vacuum fluid satisfies the phantom energy condition. The next extension is also possible which is the MCCG with the following equation of state [37–39],

$$ p=\gamma\rho-\frac{1}{\rho^{\alpha}} \biggl[\frac{B}{1+\omega }-1+\biggl(\rho ^{1+\alpha}-\frac{B}{1+\omega}+1\biggr)^{-\omega} \biggr]. $$
(3)

3 FRW Cosmology

As we know the Friedmann-Robertson-Walker (FRW) Universe is described by the following metric,

$$ ds^2=-dt^2+a(t)^2\biggl( \frac{dr^2}{1-kr^{2}}+r^{2}d\varOmega^{2}\biggr), $$
(4)

where dΩ 2=dθ 2+sin2 θdϕ 2, and a(t) represents the scale factor. The θ and ϕ parameters are the usual azimuthal and polar angles of spherical coordinates, with 0≤θ≤π and 0≤ϕ<2π. The constant k defined space curvature so, k=0,1, and −1 represents flat, closed and open spaces respectively. In that case the Einstein equation is given by,

$$ R_{\mu\nu}-\frac{1}{2}g_{\mu\nu}R=T_{\mu\nu}+g_{\mu\nu} \varLambda, $$
(5)

where we assumed c=1 and 8πG=1. It is assumed that our Universe is filled with the MCCG which plays role of dark energy with equation of state (3). Using the line element (4) and the Einstein equation (5), the energy-momentum tensor corresponding to the fluid is given by the following relation,

$$ T_{\mu\nu}=(\rho+p)u_{\mu}u_{\nu}-pg_{\mu\nu}, $$
(6)

where ρ and p are the dark energy density and pressure respectively. Also u μ is the velocity vector with normalization condition u μ u ν =−1. It is also assumed that the dark energy is conserved with the following conservation equation,

$$ \dot{\rho}+3H(p+\rho)=0. $$
(7)

In the next section we write field equations of MCCG, and then try to solve them for dark energy density.

4 Field Equations

By using the relations of previous section one can obtain the following field equations,

$$\begin{aligned} \begin{aligned} \rho&=3H^{2}+\frac{3k}{a^{2}}-\varLambda, \\ p&=-2\frac{\ddot{a}}{a}-H^{2}-\frac{k}{a^{2}}+\varLambda, \end{aligned} \end{aligned}$$
(8)

where dot denotes derivative with respect to cosmic time t and Hubble expansion parameter defined as \(H=\dot{a}/a\). The energy-momentum conservation law (7) reduced to the following equation,

$$ \dot{\rho}+3(\rho+p)\sqrt{\frac{\rho}{3}-\frac{k}{a^{2}}+ \frac {\varLambda}{3}}=0, $$
(9)

where ∂ ν T μν=0 is used.

Now, we would like to solve (9) to obtain time-dependent energy density. Using the equation of state (3) in the energy-momentum conservation formula (9) gives the following differential equation,

$$ \dot{\rho}+3\sqrt{\frac{\rho}{3}-\frac{k}{a^{2}}+ \frac{\varLambda}{3}} \biggl[(1+\gamma)\rho-\frac{B-\omega-1}{(1+\omega)\rho^{\alpha }}-\frac {(\rho^{1+\alpha}-\frac{B}{1+\omega}+1)^{-\omega}}{\rho^{\alpha }} \biggr]=0. $$
(10)

In order to find time-dependent energy density we need to remove scale factor from (10). In the next section we consider special forms of scale factor.

5 Scale Factor and Observational Data

There are some well-known relation for scale factor as ordinary phase [45, 46],

$$ a(t)=t^{n}, $$
(11)

with n>0. and the quasi-exponential phase,

$$ a(t)=a(0)t^{n}e^{\beta t}, $$
(12)

with β>0. In order to find appropriate value of n in the scale factors (11) and (12) we use the following observational parameters [47]. Declaration parameter is given by the following relation,

$$ q=-\frac{a}{\dot{a}^{2}}\frac{d^{2}a}{dt^{2}}, $$
(13)

and jerk parameter is given by,

$$ j=\frac{a^{2}}{\dot{a}^{3}}\frac{d^{3}a}{dt^{3}}. $$
(14)

Current value of these parameters (q 0 and j 0) appear in the following Taylor expansion around a 0,

$$ \frac{a}{a_{0}}=1+H_{0}t-\frac{1}{2}q_{0}H_{0}^{2}t^{2}+ \frac {1}{6}j_{0}H_{0}^{3}t^{3}+ \cdots. $$
(15)

Following we use results of the Refs. [47–51] to fix our parameters.

According to the SNeIa observational data the current value of the jerk parameter may be j 0=1. This situation obtained by choosing n=2/3. Therefore, we have a=t 2/3 as ordinary phase of our Universe and a=a(0)t 2/3 e βt for the quasi-exponential phase of our Universe.

According to the ΛCDM observational data the current value of the declaration parameter may be q 0=−0.6. On the other hand the scale factors (11) and (12) give the following relation,

$$ q_{0}=-\frac{1-n}{n}, $$
(16)

which suggests n=0.625.

On the other hand, according to the best fitted parameters of the Ref. [47] we know q 0=−0.64 and j 0=1.02, which yield to n∼0.6.

We see that all cases suggest n∼0.6, so we choose this value and try yo obtain dark energy density. Also we can see that the scale factor (12) at β=0 limit yields to scale factor (11), therefore we consider the quasi-exponential phase only.

6 Time-Dependent Energy Density

we find that the scale factor may have the following form coincide with observational data,

$$ a(t)=t^{0.6}e^{\beta t}, $$
(17)

with a(0)=1. Therefore we obtain the following non-linear differential equation,

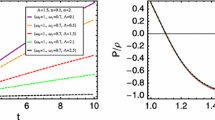
$$ \dot{\rho}+3\sqrt{\frac{\rho+\varLambda}{3}-\frac {k}{t^{1.2}e^{2\beta t}}} \biggl[(1+ \gamma)\rho-\frac{B-\omega-1}{(1+\omega)\rho ^{\alpha }}-\frac{(\rho^{1+\alpha}-\frac{B}{1+\omega}+1)^{-\omega}}{\rho ^{\alpha }} \biggr]=0. $$
(18)

One can solve above equation numerically and draw behavior of density as a function of time (Fig. 1). Figure 1 suggests that the energy density may has a unified form for all Λ=0 and Λ=±1,

$$ \rho=\frac{at^2+bt+c}{dt^2+et+f}, $$
(19)

where a,b,c,d,e and f are constants which will be fixed by using observational data and stability condition. First of all, by using equation of state parameter of total universe, p=Ωρ, (where 0>Ω>−1 show phantom-like universe) we can obtain constraints that c=2 and f=1. These yield to Ω≈−0.95 which is agree with observational data.

Fig. 1
figure 1

Time-dependent energy density. B=3.4, α=0.5, β=1, γ=0.3, ω=−0.05. k=−1 (solid line), k=0 (dashed line)

Full size image

7 Stability

There are several ways to investigate stability of a theory. In this paper we use reality of sound speed,

$$ C_{s}^{2}=\frac{dp}{d\rho}\geq0. $$
(20)

We can choose appropriate constants in the energy density (19) to have stable model. A possible case may be plotted as the Fig. 2. It shows that our model may be stable at the late time.

Fig. 2
figure 2

Squared sound speed as a function of time. a=−5, b=−0.5, d=−0.5 and e=−3.5

Full size image

8 Variable Cosmological Constant

Now we assume that cosmological constant varies with t, ρ, a, or H.

8.1 Λ∝t n

This case with some values of n illustrated in the Fig. 3 which show expected behavior. We can see that increasing n increase dark energy density.

Fig. 3
figure 3

Time-dependent energy density for Λ∝t n. B=3.4, α=0.5, β=1, γ=0.3, ω=−0.05, and k=−1. n=1 (solid line), n=−1 (dashed line), n=−2 (dotted line)

Full size image

8.2 Λ∝ρ n

In that case we can obtain solid line of the Fig. 3, which shows that variation of n is not important in final solution.

8.3 Λ∝a(t)n

Dark energy density corresponding to this case plotted in the Fig. 4 for n=1,−2,−4 which shows similar behavior as previous cases.

Fig. 4
figure 4

Time-dependent energy density for Λ∝a(t)n. B=3.4, α=0.5, β=1, γ=0.3, ω=−0.05, and k=−1. n=1 (solid line), n=−4 (dashed line), n=−2 (dotted line)

Full size image

8.4 Λ∝H n

In this case we have plot of the Fig. 5 which show opposite behavior with previous cases. It means that for cosmological constant proportional to Hubble parameter, the dark energy density decreased by increasing n.

Fig. 5
figure 5

Time-dependent energy density for Λ∝H n. B=3.4, α=0.5, β=1, γ=0.3, ω=−0.05, and k=−1. n=1 (solid line), n=−1 (dashed line), n=2 (dotted line)

Full size image

9 Conclusion

In this paper we constructed modified cosmic Chaplygin gas in presence of the variable cosmological constant and space curvature. First of all we added cosmological constant to the Einstein equation as a constant parameter. Our main goal is calculating time-dependent density which determines distribution of dark energy in the Universe. By using numerical analysis we found special polynomial form for density and fixed constant parameter by using observational data and stability condition. We then found that our model may be stable at the late time.

In the previous section we consider some cases of variable cosmological constant depend on time, density, scale factor, or Hubble parameter. We found that the last case (Λ∝H n) has opposite behavior with another cases. However all cases behave as expected for dark energy density.

In that case it is interesting to consider effect of viscosity on cosmological parameters [34]. Also it is possible to consider various interaction terms similar to the [52–54]. Finally it may be interesting to consider varying MCG [55] and extend our model.