Abstract
The paper is devoted to quantization of extensive games with the use of both the Marinatto-Weber and the Eisert-Wilkens-Lewenstein concept of quantum game. We revise the current conception of quantum ultimatum game and we show why the proposal is unacceptable. To support our approach, we present a new idea of the quantum ultimatum game. Our scheme also makes a point of departure for a general protocol for quantizing extensive games.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the last thirteen years of research into quantum games the theory has been already extended beyond 2×2 games. Since the majority of noncooperative conflict problems are described by games in extensive form, it is interesting to place extensive games in the quantum domain. Although there is still no commonly accepted idea of how to play quantum extensive games, we have proved in [1] that it is possible to use the framework [2] of strategic quantum game to get some insight into quantum extensive games. Namely, we have shown that a Hilbert space  , a unit vector
, a unit vector  , the collection of subsets \(\{\mathcal{U}_{j}\}_{j=1,2,3}\) of SU(2), and appropriately defined functionals E
1 and E
2 express the normal representation of a two stage sequential game. Moreover, it allows us to get results inaccessible in the game played classically. In this paper, the above-mentioned quantum computing description will be used to a two proposal variant of the ultimatum game [3]. It is a game in which two players take part. The first player chooses one of two proposals how to divide a fixed amount of good. Then the second player either accepts or rejects the proposal. In the first case, each player receives the part of goods according to player 1’s proposal. In the second case, the players receive nothing. A game-theoretic analysis shows that player 1 is in a better position. Since player 2’s rational move is to accept each proposal, player 1’s rational move is to choose a proposal of maximal payoff for her. As we will show in this paper, the Eisert-Wilkens-Lewenstein (EWL) approach [4] as well as the Marinatto-Weber (MW) approach [5] can change the scenario of the ultimatum game, significantly improving the strategic position of player 2. Our paper also provides an argument indicating that the previous idea [6] of quantum ultimatum game is not sufficient to describe the game in the quantum domain. We will explain that, in fact, the formerly proposed protocol does not quantize the ultimatum game but some other kind of 2×2 game. The last part of the paper is devoted to drawing a game tree of the quantum ultimatum game, where we provide the procedure how to determine the game tree when the game is played according to the MW approach.
, the collection of subsets \(\{\mathcal{U}_{j}\}_{j=1,2,3}\) of SU(2), and appropriately defined functionals E
1 and E
2 express the normal representation of a two stage sequential game. Moreover, it allows us to get results inaccessible in the game played classically. In this paper, the above-mentioned quantum computing description will be used to a two proposal variant of the ultimatum game [3]. It is a game in which two players take part. The first player chooses one of two proposals how to divide a fixed amount of good. Then the second player either accepts or rejects the proposal. In the first case, each player receives the part of goods according to player 1’s proposal. In the second case, the players receive nothing. A game-theoretic analysis shows that player 1 is in a better position. Since player 2’s rational move is to accept each proposal, player 1’s rational move is to choose a proposal of maximal payoff for her. As we will show in this paper, the Eisert-Wilkens-Lewenstein (EWL) approach [4] as well as the Marinatto-Weber (MW) approach [5] can change the scenario of the ultimatum game, significantly improving the strategic position of player 2. Our paper also provides an argument indicating that the previous idea [6] of quantum ultimatum game is not sufficient to describe the game in the quantum domain. We will explain that, in fact, the formerly proposed protocol does not quantize the ultimatum game but some other kind of 2×2 game. The last part of the paper is devoted to drawing a game tree of the quantum ultimatum game, where we provide the procedure how to determine the game tree when the game is played according to the MW approach.
2 Preliminaries to Game Theory
Definitions in the preliminaries are based on [7]. This section starts with the definition of a finite extensive game.
Definition 1
Let the following components be given.
-
A finite set N={1,2,…,n} of players.
-
A set H of finite sequences that satisfies the following two properties:
-
1.
the empty sequence ∅ is a member of H;
-
2.
if (a k ) k=1,2,…,K ∈H and K>1 then (a k ) k=1,2,…,K−1∈H.
Each member of H is a history and each component of a history is an action taken by a player. A history (a 1,a 2,…,a K )∈H is terminal if there is no a K+1 such that (a 1,a 2,…,a K ,a K+1)∈H. The set of actions available after the nonterminal history h is denoted A(h)={a:(h,a)∈H} and the set of terminal histories is denoted Z.
-
1.
-
The player function P:H∖Z→N∪{c} that points to a player who takes an action after the history h. If P(h)=c then chance (the chance-mover) determines the action taken after the history h.
-
A function f that associates with each history h for which P(h)=c an independent probability distribution f(⋅|h) on A(h).
-
For each player i∈N a partition \(\mathcal{I}_{i}\) of {h∈H∖Z:P(h)=i} with the property that for each \(I_{i} \in \mathcal{I}_{i}\) and for each h, h′ ∈I i an equality A(h)=A(h′):=A(I i ) is fulfilled. Every information set I i of the partition corresponds to the state of player’s knowledge. When the player makes move after certain history h belonging to I i , she knows that the course of events of the game takes the form of one of histories being part of this information set. She does not know, however, if it is the history h or the other history from I i .
-
For each player i∈N a utility function \(u_{i}\colon Z \to \mathbb{R}\) which assigns a number (payoff) to each of the terminal histories.
A six-tuple \((N, H, P, f, \{\mathcal{I}_{i}\}, \{u_{i}\})\) is called a finite extensive game.
Our deliberations focus on games with perfect recall (although Definition 1 defines extensive games with imperfect recall as well)—this means games in which at each stage every player remembers all the information about a course of the game that she knew earlier (see [7] and [8] to learn about formal description of this feature).
The notions: action and strategy mean the same in static games, because the players choose their actions once and simultaneously. In the majority of extensive games a player can make her decision about an action depending on all the actions taken previously by herself and also by all other players. In other words, players can make some plans of actions at their disposal such that these plans point out to a specific action depending on the course of a game. Such a plan is defined as a strategy in an extensive game.
Definition 2
A pure strategy s i of a player i in a game \((N, H, P, f, \{\mathcal{I}_{i}\}, \{u_{i}\})\) is a function that assigns an action in A(I i ) to each information set \(I_{i} \in \mathcal{I}\).
Like in the theory of strategic games, a mixed strategy t i of a player i in an extensive game is a probability distribution over the set of player i’s pure strategies. Therefore, pure strategies are of course special cases of mixed strategies and from this place whenever we shall write strategy without specifying that it is either pure or mixed, this term will cover both cases. Let us define an outcome O(s) of a strategy profile s=(s 1,s 2,…,s n ) in an extensive game without chance moves to be a terminal history that results when each player i∈N follows the plan of s i . More formally, O(s) is the history (a 1,a 2,…,a K )∈Z such that for 0≤k<K we have \(s_{P(a_{1}, a_{2},\ldots, a_{k})}(a_{1}, a_{2},\dots, a_{k}) = a_{k+1}\). If s implies a history that contains chance moves, the outcome O(s) is an appropriate probability distribution over histories generated by s.
Definition 3
Let an extensive game \(\varGamma = (N, H, P, \{\mathcal{I}_{i}\}, \{u_{i}\})\) be given. The normal representation of Γ is a strategic game \(( N, \{S_{i}\}, \{u_{i}'\} )\) in which for each player i∈N:
-
S i is the set of pure strategies of a player i in Γ;
-
\(u_{i}'\colon \prod_{i \in N}S_{i} \to \mathbb{R}\) is defined as \(u_{i}'(s)\mathrel{\mathop{:}}=u_{i}(O(s))\) for every s∈∏ i∈N S i and i∈N.
One of the most important notions in game theory is a notion of an equilibrium introduced by John Nash in [9]. A Nash equilibrium is a profile of strategies where the strategy of each player is optimal if the choice of her opponents is fixed. In other words, in an equilibrium none of the players has any reason to unilaterally deviate from the equilibrium strategy. A precise formulation is as follows:
Definition 4
Let (N,{S i } I∈N ,{u i } i∈N ) be a strategic game. A strategy profile \((t^{*}_{1},\dots,t^{*}_{n})\) is a Nash equilibrium (NE) if for each player i∈N and for all s i ∈S i
A Nash equilibrium in an extensive game with perfect recall is a Nash equilibrium of its normal representation, hence Definition 4 applies to strategic games as well as extensive ones.
3 The Ultimatum Game
The ultimatum game is a problem in which two players face a division of some amount € of money. The first player makes the second one a proposal of how to divide € between them. Then the second player has to decide either accept or reject that proposal. The acceptance means each player receives a part of € according to the first player’s proposal. If the second player rejects the proposal, each player receives nothing. Let us consider the variant of the ultimatum game in which player 1 has two proposals to share €: a fair division u f=(€/2,€/2) and unfair one u u=(δ€,(1−δ)€), where the δ is a fixed factor such that 1/2<δ<1. This problem is an extensive game with perfect information that takes the form
with components defined as follows:
-
H={∅,c 0,c 1,(c 0,d 0),(c 0,d 1),(c 1,e 0),(c 1,e 1)};
-
P(∅)=1, P(c 0)=P(c 1)=2;
-
\(\mathcal{I}_{1} = \{\emptyset\}\), \(\mathcal{I}_{2} = \{\{(c_{0})\},\{(c_{1})\}\}\);
-
u(c 0,d 0)=(€/2,€/2), u(c 1,e 0)=(δ€,(1−δ)€), u(c 0,d 1)=u(c 1,e 1)=(0,0).
The extensive and the normal representation of Γ 1 are shown in Fig. 1 (notation d i e j means the strategy that specifies action d i (e j ) at the first (second) information set of the second player). Equilibrium analysis of the normal representation gives us three pure Nash equilibria: (c 0,d 0 e 1), (c 1,d 0 e 0) and (c 1,d 1 e 0). There are also mixed equilibria: a profile where player 1 chooses c 0 and player 2 chooses d 0 e 0 with probability p≤1/(2δ) and d 0 e 1 with probability 1−p, and a profile where player 1 decides to play c 1 and player 2 chooses any probability distribution over strategies d 0 e 0 and d 1 e 0. However, we can put these ones aside since both mixed equilibria generate the same utility outcomes as the pure ones: (€/2,€/2) and (δ€,(1−δ)€), respectively. The key feature that makes the game Γ 1 so curious is that only equilibrium profile (c 1,d 0 e 0) with the unfair outcome (δ€,(1−δ)€) is a reasonable scenario among all the equilibria of the ultimatum game (many experiments show that people are inclined to choose fair division (€/2,€/2), however we stick to the basic assumption of game theory that players are striving to maximize their payoffs). The strategy combination (c 1,d 0 e 0) is the unique equilibrium that is subgame perfect—the well-known equilibrium refinement formulated by Selten [12]. It is a profile of strategies that induces a Nash equilibrium in every subgame (there are three subgames in Γ 1: the entire game, a game after the action c 0 and a game after the action c 1). The subgame perfection rejects equilibria that are not credible. Let us consider, for example, the profile (c 0,d 0 e 1). Here, the strategy d 0 e 1 of player 2 demands action e 1 when player 1 chooses c 1. However, when c 1 occurs, a rational move of player 2 is e 0. Similar analysis shows that also profile (c 1,d 1 e 0) is not a subgame perfect equilibrium. Note that we can easily determine subgame perfect equilibria in any two stage extensive game with perfect information (or even in a wider class of extensive games) through an analysis of its normal representation. In the game Γ 1 an action taken by player 1 determines a subgame in which only player 2 makes a move. Thus a subgame perfect equilibrium in Γ 1 is a Nash equilibrium with a property that a strategy of player 2 is the best response to every strategy of player 1 (i.e., a strategy that weakly dominates the others). We will take advantage of this fact in the further part of the paper.
4 Criticism of the Previous Approach to Quantum Ultimatum Game
A misrepresentation of the classical ultimatum game is the source of its incorrect quantum representation in [6]. The Author describes the ultimatum problem as a 2×2 game and then applies the MW and EWL schemes to construct the quantum game. However, as we have seen in Fig. 1b, only dimension 2×4 is proper to represent the ultimatum game in normal form. A hypothetical case of the ultimatum game in which player 2 has only two strategies considered by the Author of [6] implies that player 2 is deprived of capability to make her move conditioned on the action of the first player. That is tantamount to an event where the players take their actions at the same time or one of the players chooses her action as the second but she does not have any information about an action taken by her opponent. It does not correspond to a description of the ultimatum game where the second player knows a proposal of her opponent and makes her action depending on the move of the first player. Although the player 2 has only two actions: accept or reject in the two-proposal ultimatum game, in fact she has four pure strategies defined as her plans of an action at each of her information sets. Therefore, a 2×2 strategic game cannot depict the ultimatum game. Consequently, the MW and the EWL approach used for quantization of a 2×2 game cannot produce a quantum version of this game; neither of these quantum realizations contains the classical ultimatum game.
5 The Quantum Ultimatum Game Obtained by Quantization of the Normal Representation of the Classical Game
First, let us remind the protocol for playing quantum games defined in [1]. It is a six-tuple

where the components are defined as follows:
-
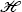 is a complex Hilbert space \((\mathbb{C}^{2} )^{\otimes m}\) with an orthonormal basis \(\mathcal{B}\).
is a complex Hilbert space \((\mathbb{C}^{2} )^{\otimes m}\) with an orthonormal basis \(\mathcal{B}\). -
N is a set of players with the property that |N|≤m.
-
|ψ in〉 is the initial state of a system of m qubits |φ 1〉,|φ 2〉,…,|φ m 〉.
-
ξ:{1,2,…,m}→N is a surjective mapping. A value ξ(j) indicates a player who carries out a unitary operation on a qubit |φ j 〉.
-
For each j∈{1,2,…,m} the set \(\mathcal{U}_{j}\) is a subset consisting of unitary operators from the group SU(2) that are available for a qubit j. A (pure) strategy of a player i is a map τ i that assigns a unitary operation \(U_{j} \in \mathcal{U}_{j}\) to a qubit |φ j 〉 for every j∈ξ −1(i). The final state |ψ fin〉 when the players have performed their strategies on corresponding qubits is defined as
$$ |\psi_{\mathrm{fin}}\rangle := (\tau_{1}, \tau_{2},\dots,\tau_{n})|\psi_{\mathrm{in}}\rangle = \bigotimes_{i\in N}\bigotimes _{j\in \xi^{-1}(i)}U_{j} |\psi_{\mathrm{in}}\rangle. $$(4) -
For each i∈N the map E i is a utility (payoff) functional that specifies a utility for the player i. The functional E i is defined by the formula
$$ E_{i} = \sum_{|b\rangle \in \mathcal{B}}v_i(b) \bigl|\langle b |\psi_{\mathrm{fin}}\rangle\bigr|^2, \quad \mbox{where}\ v_i(b) \in \mathbb{R}. $$(5)
The above scheme is adapted for extensive games with two available actions at each information set so that we could use only qubits for convenience. Any classical game richer in actions can be transferred to quantum domain by using quantum objects of higher dimensionality.
The idea framed in [1] is based on identifying unitary operators performed on a qubit with actions chosen at an information set of classical game. Therefore, three qubits are required to express the ultimatum game in quantum information language. Since the first player has one information set and the second player has two ones, player 1 performs a unitary operation on only one qubit and player 2 operates on the rest. Like in [6] we examine the two approaches: the MW approach and the EWL approach to quantizing Γ 1.
5.1 The MW Approach
Let us consider the following six-tuple

where
-
 is a Hilbert space \((\mathbb{C}^{2} )^{\otimes 3}\) with the computational basis states |x
1,x
2,x
3〉, x
j
=0,1;
is a Hilbert space \((\mathbb{C}^{2} )^{\otimes 3}\) with the computational basis states |x
1,x
2,x
3〉, x
j
=0,1; -
the initial state |ψ in〉 is a general pure state of three qubits
$$ |\psi_{\mathrm{in}}\rangle = \sum_{x \in \{0,1\}^3} \lambda_{x}|x \rangle, \quad \mbox{where}\ \lambda_{x} \in \mathbb{C}\ \mbox{and}\ \sum_{x \in \{0,1\}^3}| \lambda_{x}|^2 = 1; $$(7) -
the map ξ on {1,2,3} given by the formula

-
 and
and  ;
; -
the payoffs functionals E i , i=1,2, are of the form
 (8)
(8) (9)
(9)
By definition of ξ in \(\varGamma^{\mathrm{MW}}_{1}\), player 1 acts on the first qubit and treats the operators \(\sigma^{1}_{0}\) and \(\sigma^{1}_{1}\) as her strategies. Player 2 acts on the second and the third qubit, hence her pure strategies are \(\sigma^{2}_{0} \otimes \sigma^{3}_{0}\), \(\sigma^{2}_{0} \otimes \sigma^{3}_{1}\), \(\sigma^{2}_{1} \otimes \sigma^{3}_{0}\) and \(\sigma^{2}_{1} \otimes \sigma^{3}_{1}\) (the upper index denotes a qubit on which an operation is made).
Let us determine for each profile \((\sigma^{1}_{\kappa_{1}}, (\sigma^{2}_{\kappa_{2}}, \sigma^{3}_{\kappa_{3}} ) )\), where κ 1,κ 2,κ 3∈{0,1}, the corresponding expected utility E i by using formulae (4)–(5) and the specification of (6). We illustrate it by calculating \(E_{i} (\sigma^{1}_{0}, (\sigma^{2}_{1}, \sigma^{3}_{0} ) )\) for i=1,2. The initial state after choosing the profile \((\sigma^{1}_{0}, (\sigma^{2}_{1}, \sigma^{3}_{0} ) )\) by the players takes the form \(|\psi_{\mathrm{fin}}\rangle=\sigma^{1}_{0}\otimes\sigma^{2}_{1}\otimes\sigma^{3}_{0}| \psi_{\mathrm{in}}\rangle\). Thus, we have
where \(\overline{x}_{2}\) is the negation of x 2. Putting the final state (10) into (8) we obtain

Obviously, we have (1−δ)€ instead of δ€ in the expected utility E 2. Therefore, the payoff vector (E 1,E 2) associated with \((\sigma^{1}_{0}, (\sigma^{2}_{1}, \sigma^{3}_{0} ) )\) is u f(|λ 010|2+|λ 011|2)+u u(|λ 100|2+|λ 110|2) where u f=(€/2,€/2) and u u=(δ€,(1−δ)€). Payoff vectors (E 1,E 2) for all possible profiles \((\sigma^{1}_{\kappa_{1}}, (\sigma^{2}_{\kappa_{2}}, \sigma^{3}_{\kappa_{3}} ) )\) are placed in the matrix representation in Fig. 2 (for convenience we convert binary indices (x 1,x 2,x 3)2 of \(\lambda_{x_{1},x_{2}, x_{3}}\) to the decimal numeral system).
Let us examine the game in Fig. 2 to answer to what degree passing to the quantum domain may influence the result of the game. Note first that (6) is indeed the quantum game in the spirit of the MW approach—the normal representation of Γ 1 can be obtained from \(\varGamma^{\mathrm{MW}}_{1}\) by putting |λ 0|2=1 and |λ x |2=0 for x=1,2,…,7, i.e., if we put |ψ in〉=|000〉. More generally: \(\varGamma^{\mathrm{MW}}_{1}\) coincides to a game isomorphic to the normal representation of Γ 1 if we put as |ψ in〉 any state |x 1,x 2,x 3〉 of the basis. Then \(\varGamma^{\mathrm{MW}}_{1}\) is equal to Γ 1 up to the order of players’ strategies.
As we learned in Sect. 3, the game Γ 1 favors player 1. Thus an interesting problem is to look for another form of the initial state (7) that imply fairer solution unavailable in the game Γ 1. Let us study first
Through the substitution |λ 0|2=|λ 1|2=|λ 4|2=|λ 6|2=1/4 (the other squares of the modules equal 0) to entries of the normal representation in Fig. 2 we obtain a game where the only reasonable equilibrium profile is \(\sigma^{1}_{0} \otimes \sigma^{2}_{0} \otimes \sigma^{3}_{0}\) with corresponding expected utility vector (E 1,E 2)=(u f+u u)/2. The other pure equilibria: \(\sigma^{1}_{1} \otimes \sigma^{2}_{0} \otimes \sigma^{3}_{1}\) and \(\sigma^{1}_{1} \otimes \sigma^{2}_{1} \otimes \sigma^{3}_{1}\)—both generating the utility outcome (u f+u u)/4 are obviously worse for both players, thus they won’t be chosen. Moreover, \(\sigma^{1}_{0} \otimes \sigma^{2}_{0} \otimes \sigma^{3}_{0}\) imitate a subgame perfect equilibrium—the strategy of the second player \(\sigma^{2}_{0}\otimes\sigma^{3}_{0}\) is the best response to any strategy of the first player. To sum up, initial state (12) is better for player 2 in comparison with the classical case.
It turns out that the answer to the question: is there a state |ψ in〉 allowing to obtain a fair division of €, is positive as well. Let us consider any state of the form
Once again the profile \(\sigma^{1}_{0} \otimes \sigma^{2}_{0} \otimes \sigma^{3}_{0}\) constitutes a Nash equilibrium and the strategy of the second player \(\sigma^{2}_{0} \otimes \sigma^{3}_{0}\) weakly dominates her other strategies as a result of putting |λ
0|2=1/2δ′ and |λ
1|2=1−1/2δ′ in the game in Fig. 2. Since there are no other profiles with that property, \(\sigma^{1}_{0} \otimes \sigma^{2}_{0} \otimes \sigma^{3}_{0}\) is the most reasonable scenario and it implies  . The essential thing to obtain the fair division result is the state of the third qubit (the second qubit of player 2). It is not possible to achieve δ€ by player 1 and at the same time the payoff €/2 becomes the most attractive for her now.
. The essential thing to obtain the fair division result is the state of the third qubit (the second qubit of player 2). It is not possible to achieve δ€ by player 1 and at the same time the payoff €/2 becomes the most attractive for her now.
The conclusions we can draw from the analysis of the MW approach to the ultimatum game are as follows. First, the game \(\varGamma^{\mathrm{MW}}_{1}\) that begins with |ψ in1〉 discloses a game tree different from the one in Fig. 1a). If there is a protocol for quantizing the extensive game Γ 1 directly without using its normal representation as in our case, then the output game tree must be different from the game tree of Γ 1 in general. It follows form the fact that the game tree in Fig. 1a and four utility outcomes assigned to its terminal histories imply the normal representation specified by only these four payoff outcomes. However, the game \(\varGamma^{\mathrm{MW}}_{1}\), where the initial state takes the form (12) has five different outcomes. Note that this property is not irrelevant bearing in mind the fact that the bimatrix of a strategic game played classically as well as played by the MW protocol have always the same dimension. We will deal with the problem of extensive form in Sect. 6.
The case where the game \(\varGamma^{\mathrm{MW}}_{1}\) begins with the state (13) shows that even a separable initial state can influence significantly a result of Γ 1. It is not a strange property. Any nontrivial superposition of the basis states causes some limitation on players’ influence on their qubits as we have seen in the case (12). In particular, if each qubit of the initial state is in the state \(|+\rangle = (|0\rangle + |1\rangle )/\sqrt{2}\), no player can affect amplitudes of her qubit applying only σ 0 and σ 1 (measurement outcomes 0 and 1 on qubit occur with the same probability regardless of whether one pick σ 0 or σ 1). Then the result of the game is determined only by the initial state |ψ in〉=|+〉|+〉|+〉.
5.2 The EWL Approach
As we have seen, the two-element set of unitary operators used for quantization of a game is too poor in some cases. The two-parameter subset of unitary operations used in the EWL protocol [4] allows players to avoid powerlessness when they act on |+〉, and each player can essentially affect amplitudes of the initial state. Thus, it is interesting to find a result of the ultimatum game played according to the EWL approach. Let the following six-tuple be given:

where
-
 is a Hilbert space \((\mathbb{C}^{2} )^{\otimes 3}\) with the basis \(\{|\psi_{x_{1}, x_{2}, x_{3}}\rangle\colon x_{j} = 0,1\}\) of entangled states defined as follows
is a Hilbert space \((\mathbb{C}^{2} )^{\otimes 3}\) with the basis \(\{|\psi_{x_{1}, x_{2}, x_{3}}\rangle\colon x_{j} = 0,1\}\) of entangled states defined as follows  (15)
(15) -
the mapping ξ is the same as in six-tuple (6);
-
the subset {U(θ,β):θ∈[0,π],β∈[0,π/2]} of the unitary operators, studied, for example, in the paper [10], form an alternative to two-parameter unitary operations used in [4]. They are of the form
$$ U(\theta, \beta) = \left (\begin{array}{c@{\quad }c} \cos(\theta/2) & ie^{i\beta}\sin(\theta/2) \\ ie^{-i\beta}\sin(\theta/2) & \cos(\theta/2) \end{array} \right ); $$(16) -
E i for i=1,2 are the payoff functionals (8) and (9) specified for the basis (15)
 (17)
(17) (18)
(18)
Each strategy U 1 of player 1 is simply U(θ 1,β 1). The strategies of the second player are chosen in a similar method to the one in \(\varGamma^{\mathrm{MW}}_{1}\)—they are tensor products U 2⊗U 3=U(θ 2,β 2)⊗U(θ 3,β 3). The final state |ψ fin〉 corresponding to a profile τ=((θ 1,β 1),(θ 2,β 2,θ 3,β 3)) is as follows:
where
j=1,2,3, x j =0,1, and \(\overline{x}_{j}\) is the negation of x j . Putting (19) together with (20) into formulae (17) and (18) we obtain the expected payoff vector (E 1(τ),E 2(τ)) equal to

Let us first check that \(\varGamma^{\mathrm{EWL}}_{1}\) generalizes the classical ultimatum game Γ 1. Classical pure strategies of the first player are represented by U(0,0) and U(π,0). Similarly, pure strategies of player 2 in Γ 1 are represented by the set {U(θ 2,0)⊗U(θ 3,0):θ 2,θ 3∈{0,π}}. It follows from the fact that the set of profiles
in (14) and the set of profiles
in (2) generate the same payoffs. Equivalents of behavioral strategies of Γ 1 (i.e., independent probability distributions (p,1−p), (q,1−q) and (r,1−r) over the actions (c 0,c 1), (d 0,d 1) and (e 0,e 1), respectively, specified by players at their own information sets) can be found among unitary strategies as well. If we restrict unitary actions to U(θ,0), i.e., to profiles of the form ((θ 1,0),(θ 2,0,θ 3,0)), θ j ∈[0,π], the right-hand side of (21) takes the form
By substituting p for cos2(θ 1/2), q for cos2(θ 2/2), and r for cos2(θ 3/2) we obtain the expected payoffs corresponding to any behavioral strategy profile ((p,1−p),((q,1−q),(r,1−r))) in Γ 1.
Let us examine the impact of the unitary strategies on a result of the EWL approach to Γ 1. In particular, we ask the question which is more probable the unfair division u u or the fair division u f in \(\varGamma^{\mathrm{EWL}}_{1}\). Note, that strategy profile ((θ 1,β 1),(θ 2,β 2,θ 3,β 3))=((π,0),(0,0,0,0)) that corresponds to subgame perfect equilibrium (c 1,d 0 e 0) in Γ 1, is not a Nash equilibrium in \(\varGamma^{\mathrm{EWL}}_{1}\). The second player can gain by choosing, for example, (θ 2,β 2,θ 3,β 3)=(π,π/2,π,0) instead of (0,0,0,0). Then she obtains the fair division payoff. Moreover, for any other strategy of the first player (θ 1,β 1), player 2 can select, for instance, (0,0,0,0) to obtain a payoff being a mixture of u f and u u. This proves that the unfair division u u cannot be an equilibrium result of (14). The fair division u f, in turn, can be achieved through continuum of Nash equilibria. Denote by \(\mathrm{NE}(\varGamma^{\mathrm{EWL}}_{1})\) the set of all Nash equilibria of \(\varGamma^{\mathrm{EWL}}_{1}\). An examination of (21) shows that
as well as
Moreover, all strategy profiles generate the payoff vector u f for any division factor 1/2<δ<1. To prove inclusion (25) let us consider any strategy \((\theta'_{1},\beta'_{1})\) of player 1 given that player 2’s strategy from (25) is fixed. Then for β 2+β 3≤π/4 we have

Since β 2+β 3≤π/4, the maximum value of (27) is achieved if the second element of the sum is 0. It implies that the best response of player 1 is \(\theta'_{1} = \pi\) and \(\beta_{1}'= \pi/2 - \beta_{2}-\beta_{3}\). The second player cannot gain by deviating as well because she cannot obtain more than €/2 in \(\varGamma^{\mathrm{EWL}}_{1}\). Therefore, each profile of set (25) indeed constitutes Nash equilibrium. Inclusion (26) can be proved in similar way. Observe that there are also Nash equilibria different from (25) and (26) that generate the payoff outcome €/2 for both players, for example, a strategy profile ((π,π/4),(π,π/4,π/2,0)).
Intuitively, the huge number of fair solutions to \(\varGamma^{\mathrm{EWL}}_{1}\) being NE together with the lack of equilibrium outcome u u favor the second player in comparison with the classical game Γ 1. However, it does not assure the second player the fair payoff €/2 yet. Since the players choose their strategies simultaneously, they cannot coordinate them. If the first player unilaterally deviates from an equilibrium strategy dictated by (26) and she plays a strategy being a part of (25) then both players receive nothing as we have E 1,2((π,β 1),(0,β 2,π,0))=0 for all β 1,β 2∈[0,π/2]. On the other hand, it turns out that the statement that each of these equilibria is equally likely to occur is not true. Let us investigate which equilibria in Γ 1 are preserved in \(\varGamma^{\mathrm{EWL}}_{1}\) bearing in mind that the unitary strategies U(θ,0) are quantum counterparts to classical moves in Γ 1. As we have seen there is no equilibrium profile in \(\varGamma^{\mathrm{EWL}}_{1}\) that allows the first player to gain δ€. Therefore, in particular, the unfair division equilibrium (c 1,d 0 e 0) of Γ 1 cannot be generated by any unitary operations U(θ,0). However, each fair division equilibrium (pure or mixed) of (2) can be reconstructed in (14). The profile ((0,0),(0,0,π,0)) corresponding to the equilibrium (c 0,d 0 e 1) in Γ 1 is a Nash equilibrium of \(\varGamma^{\mathrm{EWL}}_{1}\) since it is an element of the set (26). Next, the mixed equilibria mentioned in Sect. 3 can be implemented in \(\varGamma^{\mathrm{EWL}}_{1}\) as follows: they are the profiles where the first player chooses U(0,0) and the second player chooses either U(0,0)⊗U(0,0) with probability p∈[0,1/2δ] and U(0,0)⊗U(π,0) with probability 1−p, or in the language of behavioral strategies she just takes an operator from the set \(\{U(0,0) \otimes U(\theta,0)\colon \theta \in [2\arccos (1/\sqrt{2\delta} ), \pi/2 ] \}\). According to the concept of Schelling Point [11] players tend to select a solution that is the most natural as well as the most distinctive among all possible choices. Therefore, if we assume that the players prefer the fair division, they choose a profile that is an equilibrium of both Γ 1 and \(\varGamma^{\mathrm{EWL}}_{1}\) among all fair equilibria of \(\varGamma^{\mathrm{EWL}}_{1}\), i.e., ((0,0),(0,0,π,0)). This pure equilibrium is the most natural and it ought to be chosen as the Schelling Point.
6 Extensive Form of the Quantum Ultimatum Game
In Sect. 5.1 we made observation that an extensive game and its quantum realization differ not only in utilities but also in game trees. Now, we are going to give the answer to the question how a game tree of such quantum realization would look like? Let us reconsider an extensive game given by the game tree in Fig. 1a, where the components H, P and \(\mathcal{I}_{i}\) are derived from Γ 1, and the outcomes O 00, O 01, O 10 and O 11, are assigned to the terminal histories (c 0,d 0),(c 0,d 1),(c 1,e 0) and (c 1,e 1), respectively, instead of particular payoff values. Let us denote this problem as follows:
Then the tuple \(\varGamma^{\mathrm{MW}}_{2}\) associated with Γ 2 is derived from \(\varGamma^{\mathrm{MW}}_{1}\) and only the payoff functionals E i undergo appropriate modifications. Let us write \(\varGamma^{\mathrm{MW}}_{2}\) in the language of density matrices, for convenience. That is

where
-
ρ in is a density matrix of the initial state (7);
-
the outcome operator X is a sum of X 0+X 1 defined by the following operators:
 (30)
(30) (31)
(31)
In this case, the density matrix ρ fin of the final state |ψ fin〉 takes a form

The outcome functionals (5) are then equivalent to the following one:
In order to give extensive form to determine the final state ρ fin in \(\varGamma^{\mathrm{MW}}_{2}\) let us modify the way (32) of calculating the final state ρ fin. To begin with, player 1 acts on the first qubit. Next, player 2 carries out a measurement on that qubit in the computational basis to find out what is a current state of the game. Then she performs an operation on either the second or the third qubit of the post-measurement state depending on whether the measurement outcome 0 or 1 has occurred. The operation of the second player ultimately defines the final state that is inserted to the formula (33). This sequential procedure can be formalized as follows:
Sequential procedure | ||
1. | \(\sigma^{1}_{\kappa_{1}}\rho_{\mathrm{in}}\sigma^{1}_{\kappa_{1}} = \rho_{\kappa_{1}}\) | player 1 performs an operation \(\sigma^{1}_{\kappa_{1}}\) on her qubit of the initial state ρ in |
2. | \(\displaystyle\frac{M_{\iota}\rho_{\kappa_{1}} M_{\iota}}{\mathrm{tr}(M_{\iota} \rho_{\kappa_{1}})} = \rho_{\kappa_{1},\iota}\), \(p_{\kappa_{1},\iota} = \mathrm{tr}(M_{\iota}\rho_{\kappa_{1},\iota})\) | player 2 prepares the measurement {M
0,M
1} defined by |
3. | \(\sum_{\iota} p_{\kappa_{1},\iota}\sigma^{2+\iota}_{\kappa_{2+\iota}} \rho_{\kappa_{1},\iota} \sigma^{2+\iota}_{\kappa_{2+\iota}} = \rho'_{\mathrm{fin}}\) | if a measurement outcome ι occurs, player 2 performs an operaton \(\sigma_{\kappa_{\iota+2}}\) on ι+2 qubit of the post-measurement state |
It turns out that for any strategy profile \((\sigma^{1}_{\kappa_{1}}, (\sigma^{2}_{\kappa_{2}}, \sigma^{3}_{\kappa_{3}} ) )\) the final state ρ fin defined both by the formula (32) and by the sequential procedure determine the same outcome of the game \(\varGamma^{\mathrm{MW}}_{2}\).
Proof
Let density operator ρ in of a state (7) be given. Then the state \(\rho'_{\mathrm{fin}}\) after the third step of the sequential procedure can be expressed as

where the second term of (34) follows from the fact that


Since X κ M ι =δ κι X κ, where δ κι is the Kronecker’s delta, we obtain
Note that operation σ 1 on the second (third) qubit of any state (7) does not influence the measurement of outcomes O 10 and O 11 (O 00 and O 01) because of the form of X 1 (X 0), which means that
Inserting (38) into formula (37) we obtain
The right-hand side of (39) is equal to the expected outcome given by formula (33). Thus, the two ways of determining the final state are outcome-equivalent. □
We claim that performing quantum measurement is a more natural manner to play quantum games than observation of player’s actions taken previously—the way suggested by games played classically. Since a payoff outcome of a quantum game is determined by the measurement outcome of the final state instead of actions taken by players, each stage of the quantum game also ought to be set via a quantum measurement of a current state. Moreover, if we assumed the second player’s move dependence on actions of the first player in Γ 2, then it would imply the same game tree as in Fig. 1a. This way, however, stands in contradiction to the results obtained in Sect. 5.1 that tell us that the game trees must be different. Of course, if the initial state is |000〉〈000| (i.e., when game given by (29) boils down to a game (28)), classical observation of actions at the course of the game and the observation by means of quantum measurement coincide.
Let us study what a game tree corresponding to the game \(\varGamma^{\mathrm{MW}}_{2}\) is yielded by the above-mentioned procedure. According to the first step, the initial history ∅ is followed by two actions of the first player. Next, the measurement on the first qubit is made. The two possible measurement outcomes ι=0,1 can be identified with two actions (following each player 1’s move) of a chance mover that are taken with probability \(p_{\kappa_{1},\iota}\). Finally player 2 acts on ι+2 qubit of the state ρ ι after each history associated with the outcome ι. Therefore, all histories followed by given outcome ι constitutes an information set of player 2. Such description in the form of game tree is illustrated in Fig. 3. The outcomes \(O'_{0.\kappa_{1}{,}\kappa_{2}}\) and \(O'_{1.\kappa_{1}{,}\kappa_{3}}\) are determined by the following equations:
We have proved that the two approaches to calculate the final state (32) and the sequential one given by the sequential procedure are outcome-equivalent. Therefore, it should be expected that extensive forms of Γ 2 and \(\varGamma^{\mathrm{MW}}_{2}\) coincide when the initial state is a basis state. Indeed, given ρ in=|000〉〈000|, the probabilities \(p_{\kappa_{1},\iota}\) are expressed by the formula \(p_{\kappa_{1},\iota} = \delta_{\kappa_{1},\iota}\), where κ 1,ι∈{0,1}. Then, the available outcomes given by (40) are as follows: \(O'_{0.00} = O_{00}\), \(O'_{0.01} = O_{01}\), \(O'_{1.10} = O_{10}\) and \(O'_{1.11} = O_{11}\). By identifying \(\sigma^{1}_{\kappa_{1}} \mathrel{\mathop{:}}= c_{\kappa_{1}}\), \(\sigma^{2}_{\kappa_{2}} \mathrel{\mathop{:}}= d_{\kappa_{2}}\), \(\sigma^{3}_{\kappa_{3}} \mathrel{\mathop{:}}= e_{\kappa_{3}}\) the extensive game in Fig. 3 represents game Γ 2.
7 Conclusion
We have shown that our proposal extends the ultimatum game to the quantum area. Although the proposed scheme is suitable only for the normal representation of the ultimatum game in which some features of corresponding game in extensive form are lost, it yields valuable information about how passing to the quantum domain influences a course of extensive games. The dominant position of player 1, when the ultimatum game is played classically, can be weakened in the case of playing the game via both the MW approach and the EWL approach. Another thing worth noting is that the quantization significantly extends the game tree in comparison with the classical case. Therefore, the normal representation is better to analyze the quantum game than its extensive form.
References
Frąckiewicz, P.: Quantum information approach to normal representation of extensive game. Int. J. Quantum Inf. 10, 1250048 (2012)
Eisert, J., Wilkens, M.: Quantum games. J. Mod. Opt. 47, 2543 (2000)
Güth, W., Schmittberger, R., Schwarze, B.: An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 3, 367 (1982)
Eisert, J., Wilkens, M., Lewenstein, M.: Quantum games and quantum strategies. Phys. Rev. Lett. 83, 3077 (1999)
Marinatto, L., Weber, T.: A quantum approach to static games of complete information. Phys. Lett. A 272, 291 (2000)
Mendes, R.V.: The quantum ultimatum game. Quantum Inf. Process. 4, 1 (2005)
Osborne, M.J., Rubinstein, A.: A Course in Game Theory. MIT Press, Cambridge (1994)
Myerson, R.B.: Game Theory: Analysis of Conflict. Harvard University Press, Cambridge (1991)
Nash, J.F.: Non-cooperative games. Ann. Math. 54, 286 (1951)
Flitney, A.P., Hollenberg, L.C.L.: Nash equilibria in quantum games with generalized two-parameter strategies. Phys. Lett. A 363, 381 (2007)
Schelling, T.C.: The Strategy of Conflict. Harvard University Press, Cambridge (1960)
Selten, R.: Spieltheoretische Behandlung eines Oligopolmodells mit Nachfrageträgheit – Teil I: Bestimmung des dynamischen Preisgleichgewichts. Z. Gesamte Staatswiss. 121, 301 (1965)
Acknowledgements
Work by Piotr Fra̧ckiewicz was supported by the Polish National Science Center under the project number DEC-2011/03/N/ST1/02940. Work by Jan Sładkowski was supported by the Polish National Science Center under the project number DEC-2011/01 /B/ST6/07197.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Fra̧ckiewicz, P., Sładkowski, J. Quantum Information Approach to the Ultimatum Game. Int J Theor Phys 53, 3248–3261 (2014). https://doi.org/10.1007/s10773-013-1633-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10773-013-1633-0


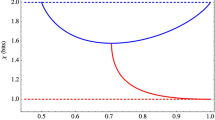
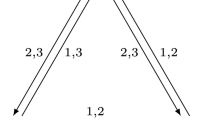


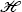 is a complex Hilbert space
is a complex Hilbert space  is a Hilbert space
is a Hilbert space 
 and
and  ;
;


 is a Hilbert space
is a Hilbert space 




 , ι=0,1 on the first qubit of the state
, ι=0,1 on the first qubit of the state 