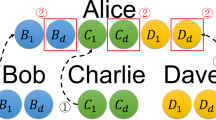Quantum communication has become one of the most promising applications of quantum mechanics in quantum information science today. Quantum secret information sharing (QSIS), which is a quantum mechanical version of classical secret sharing scheme [1, 2], is an useful tool in the cryptographic applications and has attracted a lot of attention [3–11]. The interesting aspect of employing quantum mechanics for secret sharing is that it allows for the unconditionally secure distribution of the information between the participants. The basic idea of secret sharing in the simplest case is that a secret message is shared between two persons, say Bob and Charlie who are not entirely trusted by Alice, in such a way that it can only be absolutely recovered if both of them agree to collaborate. In 1999, Hillery et al. [3] first proposed a QSIS scheme using three-particle and four-particle Greenberger-Horne-Zeilinger (GHZ) entangled states for distributing a private key among some agents and sharing a classical information. Subsequently, Karlsson et al. [4] put forward another QSIS scheme with a two-photon polarization-entangled state. So far a lot of QSIS schemes [6, 7, 10, 12–19] have been proposed in both theoretical and experimental aspects. In all these QSIS schemes [6–19], quantum entanglement plays a important role. In other words, multiparticle entangled states are widely used to implement the QSIS schemes.

Very recently, a particular quantum key distribution (QKD) scheme has been proposed by Kye and Kim [20], in which the basis reconciliation via a classical channel is not necessary as a advantage. In this paper, based on Kye-Kim’s QKD scheme, we propose a MQSIS scheme by using single-qubit with arbitrarily random rotation angle. In this MQSIS scheme, Alice randomly chooses a value of angle θ i and prepares a single-qubit state with the rotation of that angle. The receivers rotate the received qubit states by −θ i and then measure the qubits to read out the states of qubits, i.e., Alice’s secret messages. If all the receivers agree to cooperate, they can successfully share Alice’s secret messages. Otherwise, nobody can get access to Alice’s secret messages with 100% certainty.

Now let us turn to depict our MQSIS scheme. For convenience, let us first describe a three-party QSIS scheme, and then generalize it to the case of N agents. Suppose that Alice is the boss, Bob and Charlie are two employees in an enterprise. Here Alice wants to send a secret message to two distant employees, Bob and Charlie. However, Alice doubts that one of them may be dishonest and she does not know who the dishonest one is, but she knows that if the two employees coexist, the honest one will keep the dishonest one from doing any damage. Bob and Charlie, can obtain Alice’s secret messages only by their mutual cooperation. In this three-party QSIS scheme, Alice, Bob and Charlie agree that they utilize the formula: \(M_{A_{i}}=M_{B_{i}}\oplus M_{C_{i}}\) (i=1,2,3,…,m) to decode Alice’s secret messages, where \(M_{A_{i}}\) represents Alice’s secret message, \(M_{B_{i}}\) represents Bob’s measurement result, \(M_{C_{i}}\) represents Charlie’s measurement result, ⊕ represents an addition mod 2, and \(M_{A_{i}}, M_{B_{i}}, M_{C_{i}}\in\{0,1\}\). This three-party QSIS scheme can be completed with the following procedures below.

Step 1: Suppose that Alice has a secret message sequence \(\{M_{A_{1}}, M_{A_{2}}, \ldots, M_{A_{m}}\}\) (\(M_{A_{i}}\in\{0, 1\}, i=1,2, \ldots, m\)), she prepares two sets of ordered sequences of qubits according to her secret message sequence: [B 1, B 2, …, B m ], [C 1, C 2, …, C m ], where B i ,C i ∈{|0〉,|1〉}, the subscript indicates each qubit’s order in the sequence, and |0〉 and |1〉 represent two orthogonal states of the qubit respectively. We call them B sequence and C sequence, respectively. For instance, if Alice’s secret message is 0, she prepares qubits B i , C i in the states |0〉 B ,|0〉 C or |1〉 B ,|1〉 C ; if Alice’s secret message is 1, she prepares qubits B i , C i in the states |0〉 B ,|1〉 C or |1〉 B ,|0〉 C . Then Alice rotates each qubit in sequence B by a arbitrary angle \(\theta_{B_{i}}\), and a arbitrary angle \(\theta_{C_{i}}\) for each qubit in sequence C. After that, the state of qubit becomes:

$$ \begin{array}{rcl}|0\rangle \longrightarrow {U_y}(\theta)|0\rangle&=&\cos\theta |0\rangle+\sin\theta |1\rangle,\\[6pt]|1\rangle \longrightarrow {U_y}(\theta)|1\rangle&=&{-}\sin\theta |0\rangle+\cos\theta |1\rangle,\end{array}$$
(1)

where U y (θ)=cosθI−isinθσ y is the unitary operator which rotates the arbitrary angle along the y axis and I is the identity operator, σ y is the Pauli-y operator. Then Alice first sends the B sequence to Bob.

Step 2: Bob confirms Alice that he has received the B sequence via classical channel. Then he checks the security of transmission for sequence B with Alice. Usually, in order to check the security of transmission, the common method is to use a public channel to reveal some part of qubits [6, 7]. That verification method has two disadvantages. (1) It usually degrades the efficiency for qubits. (2) It does not guarantee the integrity of the remaining qubits. In order to overcome those problems, we utilize the one-way hash function as Ref. [20] for checking the integrity of the qubits.

Step 3: Alice first announces some of the values of angle \(\theta_{B_{i}}\) that she rotated for each qubit in sequence B and the one-way hash function H via a classical channel.

Step 4: Bob rotates the corresponding angle of each qubit in sequence B by \(-{\theta_{B_{i}}}\) and then measures them under the measuring basis (MB) Z≡{|0〉,|1〉}. Alice and Bob evaluate the hash function values, \(h_{A_{1}}=H(k_{A_{1}})\) and \(h_{B_{1}}=H(k_{B_{1}})\) respectively, where \(k_{A_{1}}\) and \(k_{B_{1}}\) are shared keys in Alice and Bob. If \(h_{A_{1}}=h_{B_{1}}\), they keep the shared keys, and Alice announces the other values of angle \(\theta_{B_{i}}\) that she rotated for each qubit in sequence B. Otherwise, they abolish the keys and start the process again from Step 1. Alice and Bob evaluate the hash function values of the remaining qubits respectively, \(h_{A_{2}}=H(k_{A_{2}})\) and \(h_{B_{2}}=H(k_{B_{2}})\). If \(h_{A_{2}}=h_{B_{2}}\), they keep the shared keys, otherwise, they abolish the keys and start the process again from Step 1.

In Step 4, the difference between h A and h B (\(h_{A}=h_{A_{1}}+h_{A_{2}}\) and \(h_{B}=h_{B_{1}}+h_{B_{2}}\)) shows that Alice and Bob do not share the exactly same keys. This is due to imperfection in the transmission or to Eve (eavesdropper) who intervened between Alice and Bob.

Step 5: After ensuring the security of the transmission for sequence B, Alice sends the sequence C to Charlie and announces the one-way hash function H via a classical channel.

Step 6: Alice and Charlie check the security of transmission for sequence C, similar to that for sequence B. If h A =h C , they keep the shared keys, otherwise, they abolish the keys and start the process again from Step 1.

Step 7: If Bob and Charlie collaborate, they can decode Alice’s secret messages utilizing the formula: \(M_{A_{i}}=M_{B_{i}}\oplus M_{C_{i}}\). Otherwise, neither of them can get Alice’s secret messages with the probability 100%.

So far we have proposed a three-party QSIS scheme based on Kye-Kim’s QKD scheme [20] by using single-qubit with arbitrarily random rotation angle. In Kye-Kim’s scheme, in order to share a key between Alice and Bob, the qubit need being transmitted three times, it is not secure because of too many times of transmission between the sender and the receiver (see [21] in detail). Different from Kye-Kim’s scheme, in the present scheme, in order to share a key between Alice and Bob (or Alice and Charlie), the qubit only need being transmitted once depending on adding classical communication once, which ensures the security of the present scheme against eavesdropping which we will discuss later.

Now let us generalize the three-party QSIS scheme to the case of N agents, Bob, Charlie, Dick, …, and Zack. The basic step of the MQSIS scheme is the same as that in the three-party QSIS scheme.

Step I: Alice prepares N sets of ordered sequences of qubits according to her secret message sequence: [B 1, B 2, …, B m ], [C 1, C 2, …, C m ], …, [Z 1, Z 2, …, Z m ]. Then Alice first sends sequence B to Bob.

Step II: Bob confirms Alice that he has received the B sequence. Alice first announces some of the values of angle \(\theta_{B_{i}}\) that she rotated for each qubit in sequence B and the one-way hash function H. Bob rotates the corresponding angle of each qubit in sequence B by \(-{\theta_{B_{i}}}\) and then measures them under the MB Z. Alice and Bob evaluate the hash function values, \(h_{A_{1}}=H(k_{A_{1}})\) and \(h_{B_{1}}=H(k_{B_{1}})\) respectively. If \(h_{A_{1}}=h_{B_{1}}\), they keep the shared keys, and Alice announces the other values of angle \(\theta_{B_{i}}\) that she rotated for each qubit in sequence B. Otherwise, they abolish the keys and start the process again from Step 1. Alice and Bob evaluate the hash function values of the remaining qubits respectively, \(h_{A_{2}}=H(k_{A_{2}})\) and \(h_{B_{2}}=H(k_{B_{2}})\). If \(h_{A_{2}}=h_{B_{2}}\), they keep the shared keys, otherwise, they abolish the keys and start the process again from Step 1.

Step III: After ensuring the security of the transmission for sequence B, Alice sends sequence C to Charlie.

Step IV: After repeating the step II N times, the Z sequence is received securely by the last agent, say Zach. Then Alice and Zach evaluate the hash function values, h A =H(k A ) and h Z =H(k Z ) respectively. If h A =h Z , they keep the shared keys, otherwise, they abolish the keys and start the process again from Step 1.

Step V: If all the agents collaborate, they can decode Alice’s secret messages utilizing the formula: \(M_{A_{i}}=M_{B_{i}}\oplus M_{C_{i}}\oplus\ldots\oplus M_{Z_{i}}\).

So far we have established a MQSIS scheme based on single-qubit with arbitrarily random rotation angle. In our MQSS scheme, only the single-qubit states are used, the multi-qubit GHZ states in all the existing MQSS schemes [3, 13, 14] are not necessary. Although in [18], they claimed that only the Bell states are required, they must distinguish the multi-qubit GHZ states, which makes the scheme experimentally difficult to realize. It is known that the preparation of multi-qubit entangled states is very complicated and difficult in experiment, so our scheme is easier and simpler than the existing MQSIS schemes [3, 13, 14, 18] to the implementation of MQSIS.

Now we analyze the security of the present scheme. For a perfect quantum channel with single-qubit, it is obvious that Eve can not obtain much information by the measure-resend attack, disturbance attack, intercept-and-resend attack, and entangle-measure attack as all the transmissions of qubits are of random rotation. In this scheme, the random rotation depend on the equator of the Poincaré sphere. The optimum estimation of a qubit in this case gives the fidelity 3/4 [22] where the fidelity is one when the estimation is perfect or zero when the initial state is orthogonal to the estimation.

Let us continue to discuss how the present MQSIS scheme can efficiently resist the measure-resend attack, disturbance attack, intercept-and-resend attack, entangle-measure attack, and PNS attack, respectively.

Measure-resend attack—Eve intercepts the qubits emerging from Alice and measures them under the MB Z, then she resends them to the receiver M. The initial superposition states of qubits will probabilistically collapse into |0〉 states or |1〉 states of qubits after Eve’s measurement. The receiver M rotates the states of qubits by \(-{\theta_{M_{i}}}\) and then measures them, he will probabilistically obtain |0〉 states or |1〉 states of qubits. Hence Eve’s attack will be detected after the receiver M compares the values of hash function with Alice.

Disturbance attack—Eve can intercept the qubits when the qubits are transmitted from Alice to the receiver M and randomly perform one of the four unitary operations I, σ x , iσ y , and σ z (I is the identity operator, and σ x , iσ y , and σ z are the Pauli operators) on each qubit. By doing so, the initial superposition states of qubits will be changed. In this case, after the receiver M rotates the states of qubits by \(-{\theta_{M_{i}}}\) and measures them, he will obtain the wrong results. This behavior will be found after the receiver M compares the values of hash function with Alice.

Intercept-and-resend attack—Suppose that Eve prepares a lot of the single qubits in the state (|0〉, |1〉) or (α|0〉+β|1〉, α|0〉−β|1〉) randomly. When Alice sends qubits to the receiver M, Eve intercepts the qubits and keeps them with him, and sends the qubits that he prepared to the receiver M. The receiver M will take the fake qubits for Alice’s, and rotate the fake qubits by \(-{\theta_{M_{i}}}\) and measure them. This behavior can also be found after the receiver M compares the values of hash function with Alice.

Entangle-measure attack—Eve may steal some information by entangling his auxiliary qubit (prepared, say, in the state |χ〉 E ) with a qubit m (assumed to be in the state |i〉 M ) before the qubit reaches the receiver M: \({|\chi\rangle_{E}}{|i\rangle_{m}}\longrightarrow\alpha{|\chi_{i}\rangle_{E}}{|i\rangle_{m}}+\beta{{|\overline{\chi}_{i}\rangle}_{E}}{|i\oplus1\rangle_{m}}\) where |α|2+|β|2=1 and \(_{E}\langle\chi_{i}|{\overline{\chi}_{i}\rangle}_{E}=0\). Then he resends the qubit m to the receiver M. After the receiver M rotates the states of qubits by \(-{\theta_{M_{i}}}\), the state of qubits E, m become a two-qubit entangled state consist of the basis {|00〉,|01〉,|10〉,|11〉}. The initial state prepared by Alice is completely destroyed. When the receiver M measures the qubit m, he will obtain the correct and wrong result with the probability 1/2 respectively, while Eve can not obtain the correct secret message too. But after the receiver M compares the values of hash function with Alice, they will find the existence of Eve.

In the above discussions, we analyze the security of the present scheme and show that how the present scheme can efficiently against different kinds of attacks only for the perfect quantum channel, i.e., a noise-free quantum channel. In a noise quantum channel, the error correction and the privacy amplification techniques should be used on those qubits for improving the security. The quantum error correction technique is not difficult in principle to be implemented, and a quantum privacy amplification way for the single-qubit was proposed also [23]. Now let us consider the most efficient attack in practice, i.e., PNS attack.

PNS attack—In practice, a reliable single-photon source for MQSIS is not very economical, we can use not-so weak coherent laser pulses as qubits in the present scheme. It is known that if a message is encoded on a coherent-state pulse, the scheme may be insecure under the PNS attack which is a conventional strategy for weak coherent laser pulses. Eve can split out a qubit from each pulse and keep it in the quantum storage. In Kye-Kim’s scheme [20], they give out the maximum amount of information Eve can get from the channel

(2)

Where

(3)

is the probability of there being n photons in the coherent state \(|\sqrt{1-\eta^{2}}\rangle\alpha\), and

(4)

is the maximal mean fidelity of the optimum state estimation from n qubits. The amount of information I E which Eve can get grows as η (η is the amplitude transmittivity of the beam splitter) grows but it eventually converges to I E =0.5 as η 2⟶1. On the other hand, if Eve can split out a qubit from each pulse, then after Alice announces the values of angle \(\theta_{B_{i}}\) to Bob, Eve rotates the corresponding angle of each qubit by \(-{\theta_{B_{i}}}\) and then measures them under the MB Z, Eve can absolutely get the message of the sequence B without being detected. In order to prevent the PNS attack of Eve’s, Alice should also put some PNSs near the single-photon source and split out the qubits from each pulse and keep them in her own quantum storage so that only one complete single-photon quantum signal being sent to the receiver. In this way, Eve cannot split out a qubit from each pulse and get Alice’s messages without being found.

In summary, we proposed a new MQSIS scheme using single-qubit with arbitrarily random rotation angle. Alice rotates each qubit by a arbitrary angle θ i , which is equivalent to the encryption on each qubit with a random key, which makes any other one have no ability for reading out the information on the qubit. Since we do not need to reveal some qubits to check the security of transmission for the qubits by using hash function, its intrinsic efficiency for qubit approaches the maximal value. The measure-resend attack, disturbance attack, intercept-and-resend attack, and entangle-measure attack can be detected via comparing the hash function between Alice and the receivers. The PNS attack can also be prevented by using the PNSs to split out the qubits from each pulse so that only one complete single-photon quantum signal being sent to the receiver. If all the receivers agree to cooperate, they can successfully share Alice’s secret messages. Otherwise, nobody can get access to Alice’s secret messages.