Threshold quantum secret sharing based on single qubit

Abstract

Based on unitary phase shift operation on single qubit in association with Shamir’s (t, n) secret sharing, a (t, n) threshold quantum secret sharing scheme (or (t, n)-QSS) is proposed to share both classical information and quantum states. The scheme uses decoy photons to prevent eavesdropping and employs the secret in Shamir’s scheme as the private value to guarantee the correctness of secret reconstruction. Analyses show it is resistant to typical intercept-and-resend attack, entangle-and-measure attack and participant attacks such as entanglement swapping attack. Moreover, it is easier to realize in physic and more practical in applications when compared with related ones. By the method in our scheme, new (t, n)-QSS schemes can be easily constructed using other classical (t, n) secret sharing.

1 Introduction

It is very popular and critical to keep a secret among a group of users securely and robustly in many applications. Suppose the dealer Alice has a secret message (e.g., a confidential recipe of some food or medicine) which is supposed to be confidential to others except for her agents. If she wants to share the secret with her agents through networks, she may have two methods to attain this goal: (a) duplicating the secret and allocating each agent a copy, but the secret may be disclosed in case any agent is comprised or leak the copy to the outside intentionally or accidentally. Therefore, this method is not secure enough and (b) breaking the secret S into n pieces such that S can be derived from all pieces, e.g., $S = {k_1} + {k_2} + \cdots + {k_n}$, each agent with a piece. However, the secret cannot be recovered as long as an agent is absent, and thus, this method lacks robustness in keeping the secret. To solve the problem of confidentiality and robustness in keeping a secret among users, (t, n) threshold secret sharing scheme (or (t, n)-SS) was first presented by Shamir [1] and Blakely [2], respectively, in 1979. A (t, n)-SS scheme divides a secret into n pieces such that any t or more than t out of n pieces can recover the secret, while less than t pieces cannot. Today, (t, n)-SS has become a fundamental cryptographic primitive and is widely used in many aspects such as threshold signature, threshold encryption, group authentication, group key agreement and secure multiparty computation.

Recently, with the development of quantum information and quantum computation, which leads to unconditionally secure communication [3, 4], quantum secret sharing scheme (QSS) is attracting more and more interest. The first QSS scheme was presented by Hillery et al. [5], which used the entangled Greenberger–Horne–Zeilinger (GHZ) state in 1999. In their scheme, the dealer splits the GHZ triplet and allocates a particle to each of 2 agents; then, both agents randomly measure their respective particle in x or y base and consequently determine the dealer’s measurement result by combining their own ones. Obviously, this allows the dealer to establish a joint secret with both agents. On the basis of [5], Imoto et al. [6] implemented a secret sharing scheme with Bell entangled state and proposed the two state QSS. In the same year, Lo et al. [7] proposed a (t, n) threshold QSS scheme based on quantum error correcting code, but it requires special coding which maps the quantum state into n quantum states to support the scheme construction. Since then, more and more scholars begun to focus on this area and have proposed various QSS schemes based on different physical characteristics. According to the type of shared information, QSS schemes can be divided into Classical Information Sharing [5, 8, 13,14,15, 18,19,20] or Quantum Information (i.e., Quantum States) Sharing [5,6,7, 9, 10, 16, 17]. According to quantum states used in secret sharing, QSS schemes can be divided into entanglement-based QSS [5, 6, 10,11,12, 18,19,20] and non-entangled QSS [7,8,9, 13,14,15,16,17, 21]. According to the number of participants in secret recovering, QSS can be divided into one-to-two [5] (i.e., one dealer with 2 participants), one-to-many [6,7,8,9,10,11,12, 14,15,16,17,18,19,20,21] and many-to-many [13, 22] QSS.

However, most existing schemes are (n, n) structure, which are not authentic threshold secret sharing in nature because they require all n shareholders to participate in secret recovering. Obviously, (t, n) threshold QSS is more flexible and useful in practice for $n \ge t$. In 2005, Tokunaga et al. [8] presented the notion of threshold collaborative unitary transformation or threshold quantum cryptography. It employs Shamir’s (t, n)-SS and avoids the constraint of the quantum no-cloning theorem. Distinct from [7] using quantum error correcting code, this work presents a new way in constructing (t, n) threshold QSS. However, it is still complicated and can only share classical information. There are some other threshold schemes, e.g., Yang et al. [19] employed the orthogonal multipartite entangled states in d-qudit system to construct a QSS scheme which is ramp; Song et al. [20] constructed a d-level threshold QSS based on quantum Fourier transform, but it is complicated to realize.

Therefore, the paper proposes a simple (t, n)-QSS scheme based on Shamir’s (t, n)-SS and unitary operation on quantum state. In the scheme, the dealer divides a private value into n shares and allocates each share to a shareholder using Shamir’s (t, n)-SS, and then, it embeds the private value into initial quantum states. Any t or more than t shareholders can perform phase shift operations related to their respective shares on the quantum state one by one to remove the private value, and finally recover the secret.

Compared with existing schemes, the proposed scheme has the following properties:

• 1. It can be used to share both classical information and quantum states.

• 2. Any t or more than t participants out of n shareholders are allowed to use their private shares repeatedly to recover a secret.

• 3. Simply based on unitary operation on a single qubit, the scheme is easier to realize in physic and more practical in applications when compared with related ones.

• 4. The scheme can also be constructed using other classical (t, n)-SS schemes while keeping the above properties.

The rest of the paper is organized as follows: In Sect. 2, we propose the threshold scheme which can share both classical information and quantum states. Section 3 shows the correctness of the scheme. Section 4 gives a concrete example of the scheme, Sect. 5 presents security analysis, related work and comparisons, a generic method to construct (t, n)-QSS is given in Sect. 6 and Sect. 7 concludes the paper.

2 Proposed (t, n) QSS based on single qubit

2.1 Overview

The proposed (t, n) QSS consists of two protocols: (1) Classical Information Sharing and (2) Quantum States Sharing. Both protocols share the same process, classical private share distribution.

To distribute classical private shares, the dealer divides a private value s into n private shares based on classical Shamir’s (t, n)-SS and allocates each share to a shareholder; when they need to recover the secret, they can exchange their value of shares; after collecting at least t shares, each shareholder can compute the private value by polynomial interpolation, such that any t or more than t shareholders can recover the private value. These shareholders are also called participants when they collaborate to recover the private value. Classical private share distribution prepares private shares, and each participant uses the share to perform unitary phase shift on qubit in both protocols.

In the protocol of Classical Information Sharing, the dealer first prepares a sequence of qubits and embeds the secret by performing a unitary operation related to the private value on each qubit. Each participant then performs in sequence the unitary operation, related to the private share, on the qubit. Finally, the secret is recovered by the last participant when the private value is removed from each qubit by the cooperation of any t or more than t participants.

The protocol of Quantum States Sharing is similar to Classical Information Sharing except that all participants share the initial state of a qubit sequence as the secret.

2.2 Classical private share distribution

Shamir’s (t, n) secret sharing scheme [1] consists of 2 steps: (1) share distribution and (2) secret reconstruction. In share distribution, the dealer chooses a polynomial to generates n shares, each for a shareholder; in secret reconstruction, t out of n shareholders collaborate to recover the secret by pooling their shares together.

In the proposed scheme, classical private share distribution is the same as share distribution in [1]. In detail, the dealer Alice distributes the classical private shares to n shareholders as follows.

• 1. Alice picks a random polynomial f(x) of degree $t-1$ over finite field GF(p):

  $$\begin{aligned} f(x) = {a_0} + {a_1}x + \cdots + {a_{t - 1}}{x^{t - 1}}\bmod p, \end{aligned}$$

  where $s = {a_0} = f(0)$ is the private value and all coefficients ${a_j}, j = 0,1,\ldots ,t - 1$, are in finite field GF(p) for large prime p.

• 2. Alice computes $f({x_j})$ as the share of shareholder $\text {Bob}_j$ for $j = 1,2,\ldots ,n$, where ${x_j}, {x_j} \in GF(p)$ is the public information of $\text {Bob}_j$ with ${x_j} \ne {x_v}$ for $j \ne v$.

• 3. Alice sends each share ${y_j}=f({x_j})$ to corresponding shareholder $\text {Bob}_j$ through quantum secure direct communication presented in [23, 24].

2.3 Classical Information Sharing

To share a bit string as the secret, the dealer first prepares a sequence of quantum states including four different phase values and then embeds a private value into the initial quantum states by phase shift operation to mix the phase values. Based on Shamir’s (t, n)-SS, any t or more than t participants can perform phase shift operations sequentially on each quantum state of the sequence and finally remove the private value. These participants publish the classes of their operations, and the dealer determines the measurement base. After the last participant measures and publishes the result, all participants can share a bit string as the secret according to the dealer’s definition of bits.

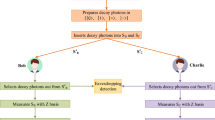
The protocol (see Fig. 1) can be described in detail as follows.

Dealer Alice first randomly prepares a sequence of qubits, $\text {Qs} = \{ \left| {{\varPhi _k}} \right\rangle |k = 1,2,\ldots , m\}$, and each qubit $\left| {{\varPhi _k}} \right\rangle$ has one state in $\left| { \pm \, x} \right\rangle ,\left| { \pm \, y} \right\rangle$ of two mutually unbiased bases x and y with

$$\begin{aligned} \left| { \pm \, x} \right\rangle= & {} \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle \pm \, \left| 1 \right\rangle } \right) \\ \left| { \pm \, y} \right\rangle= & {} \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle \pm \, i\left| 1 \right\rangle } \right) . \end{aligned}$$

In this case, each qubit can be written as

$$\begin{aligned} \left| {{\varPhi _k}} \right\rangle = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i{\varphi _k}}}\left| 1 \right\rangle } \right) ,k = 1,2,\ldots ,m, \end{aligned}$$

where $\left\{ {\varphi _k}|{\varphi _k} \in \left\{ {0,\pi ,{\pi / 2},{{3\pi } /2}} \right\} ,k = 1,2,\ldots ,m\right\}$ is used to carry the secret.

• 1. Embedding private value into quantum state Alice performs the unitary phase operation $U({\psi _0})$ on each qubit, where $U(\psi _0 ) = \left| 0 \right\rangle \left\langle 0 \right| + {e^{i\psi _0 }}\left| 1 \right\rangle \left\langle 1 \right| , \psi _0 = \frac{{\mathrm{{ - 2}}\pi s}}{p}$ and s is the private value. Then each qubit $\left| {{\varPhi _k}} \right\rangle$ in Qs will be in the state

  $$\begin{aligned} \left| {{\varPhi _k}} \right\rangle _0 = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i({\varphi _k} + {\psi _0})}}\left| 1 \right\rangle } \right) ,k = 1,2,\ldots ,m. \end{aligned}$$

• 2. Inserting decoy photons Alice prepares some decoy photons, each with the state in $\left\{ {\left| 0 \right\rangle ,\left| 1 \right\rangle ,\left| { +\, x} \right\rangle ,\left| { -\, x} \right\rangle } \right\}$, randomly inserts them into Qs to obtain an expanded sequence $\text {Qs}'$ and then records the position as well as state of each decoy photon in $\text {Qs}'$. Suppose that t participants $\left\{ {\text {Bob}_1,\text {Bob}_2,\ldots ,\text {Bob}_t} \right\}$ need to reconstruct each initial quantum state $\left| {{\varPhi _k}} \right\rangle$ in Qs to achieve the value of ${\varphi _k}$ for $k = 1,2,\ldots ,m$, and Alice sends the expanded sequence $\text {Qs}'$ to the first participant $\text {Bob}_1$ through quantum communications.

• 3. Checking eavesdropping by decoy photons After $\text {Bob}_1$ receives $\text {Qs}'$, Alice sends the position and state of each decoy photon to $\text {Bob}_1$ through classical communications. Then $\text {Bob}_1$ measures each decoy photon in the corresponding base and analyzes every measurement result according to the published positions and states. If the error rate exceeds the threshold value, $\text {Qs}'$ will be discarded and Alice then starts a new sequence. Otherwise, $\text {Bob}_1$ obtains the sequence Qs and the protocol proceeds with step 4. Note that each participant $\text {Bob}_j$ employs decoy photons to check eavesdropping as $\text {Bob}_1$ does after receiving an expanded sequence from the preceding participant $\text {Bob}_{j - 1}, j = 2,3,\ldots , t.$

• 4. Performing phase shift operation by private share After computing the component ${c_1} = f({x_1})\prod \nolimits _{r = 2}^t {\frac{{{x_r}}}{{{x_r} - {x_1}}}} \bmod p, \text {Bob}_1$ performs the unitary phase operation $U({\psi _1})$, with ${\psi _1} = {\phi _1} + \frac{{2\pi {c_1}}}{p},{\phi _1} \in \left\{ {0,\pi ,{\pi /2},{{3\pi } /2}} \right\} ,$ on each qubit ${\left| {{\varPhi _k}} \right\rangle _0}$ to get ${\left| {{\varPhi _k}} \right\rangle _1} = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i({\varphi _k} + {\psi _0} + {\psi _1})}}\left| 1 \right\rangle } \right)$, and then sends ${\left| {{\varPhi _k}} \right\rangle _1}$ to $\text {Bob}_2$ for $k = 1,2,\ldots , m.$

• 5. Performing respective phase shift operations $\text {Bob}_j,j = 2,3,\ldots ,t,$ repeats the same procedure as $\text {Bob}_1$ does in step 4. That is, $\text {Bob}_j$ first computes the component ${c_j} = f({x_j})\prod \nolimits _{r = 1,r \ne j}^t {\frac{{{x_r}}}{{{x_r} - {x_j}}}} \bmod p$ and then performs unitary phase operation $U({\psi _j})$ on each qubit ${\left| {{\varPhi _k}} \right\rangle _{j - 1}}$ to obtain ${\left| {{\varPhi _k}} \right\rangle _j} = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i({\varphi _k} + {\psi _0} + \sum \nolimits _{v = 1}^j {{\psi _v}} )}}\left| 1 \right\rangle } \right) , k = 1,2,\ldots ,m$, with ${\psi _j} = {\phi _j} + \frac{{2\pi {c_j}}}{p},{\phi _j} \in \left\{ {0,\pi ,{\pi /2},{{3\pi } /2}} \right\}$. At last, he sends ${\left| {{\varPhi _k}} \right\rangle _j}$ to the next participant $\text {Bob}_{j + 1}$. After the last participant $\text {Bob}_t$ performs the unitary phase operation on each qubit ${\left| {{\varPhi _k}} \right\rangle _{t - 1}},k = 1,2,\ldots ,m$, the states of them become

  $$\begin{aligned} {\left| {{\varPhi _k}} \right\rangle _t}&=\frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i\left[ {{\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}} + \frac{{2\pi }}{p}\left( {\sum \nolimits _{j = 1}^t {{c_j} - s} } \right) } \right] }}\left| 1 \right\rangle } \right) \\&=\frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i\left( {{\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}} } \right) }}\left| 1 \right\rangle } \right) ,k = 1,2,\ldots ,m. \end{aligned}$$

• 6. Determining measurement base Each participant divides his operation into 2 classes, X and Y, representing choices ${\phi _j} \in \left\{ {0,\pi } \right\}$ and ${\phi _j} \in \left\{ {{\pi / 2},{{3\pi }/ 2}} \right\}$, respectively. They inform the dealer Alice about their classification of operation for each qubit through classical communications. According to classes of all participants’ phase operations on each qubit, Alice determines the base in which $\text {Bob}_t$ measures the qubit. Specifically, the measurement base is x for $\left| {\cos ({\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}} )} \right| = 1$ and y for $\left| {\sin ({\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}} )} \right| = 1$. After the measurement, $\text {Bob}_t$ publishes each result ${k_t},k = 1,2,\ldots ,m$ through classical communications.

• 7. Recovering the secret After the t participants exchange their choice of ${\phi _j},j = 1,2,\ldots ,t,$ any participant can infer the initial values ${\varphi _k},k = 1,2,\ldots ,m.$ Given the definition ${\varphi _k} = 0 \Rightarrow 00,{\varphi _k} = {\pi /2} \Rightarrow 01,{\varphi _k} = \pi \Rightarrow 10$ and ${\varphi _k} = 3{\pi / 2} \Rightarrow 11$ (i.e., a qubit carries 2 bits), all participants can collectively share a string of 2 m bits as the secret.

Fig. 1

Sequential operations on each qubit in Classical Information Sharing. $({\varphi _k}$-initial phase value of each qubit $\left| {{\varPhi _k}} \right\rangle , k = 0,1,2,\ldots ,m; {\psi _0}$-phase shifted by the dealer Alice on the qubit; ${\psi _j} = ({\phi _j} + 2\pi {c_j}/p)$-phase shifted by $\text {Bob}_j$ on the qubit, $j = 1,2, \ldots , t; {k_t}$-result measured by the last participant $\text {Bob}_t$)

2.4 Quantum States Sharing

This protocol is similar to Classical Information Sharing; the dealer first prepares a sequence of initial quantum states as the secret, and then embeds a private value into the sequence by phase shift operation. After any t or more than t participants complete respective phase shift operations sequentially on each quantum state, the initial quantum states can be recovered. The protocol (see Fig. 2) can be described as follows.

Alice first prepares a sequence of m quantum states $\text {Qs} = \{ \left| {{\varPsi _k}} \right\rangle |\left| {{\varPsi _k}} \right\rangle = {\alpha _k}\left| 0 \right\rangle + {\beta _k}\left| 1 \right\rangle ,{\left| {{\alpha _k}} \right| ^2} + {\left| {{\beta _k}} \right| ^2} = 1,k = 1,2,\ldots ,m\}$, and then, she can share Qs with at least t shareholders by taking the following steps.

• 1. Just like the steps in 2.3, Alice performs the unitary phase operation $U({\psi _0})$ on each quantum state $\left| {{\varPsi _k}} \right\rangle$ in Qs with ${\psi _0} = \frac{{{-\,\mathrm { 2}}\pi s}}{p}$; then, $\left| {{\varPsi _k}} \right\rangle$ becomes ${\left| {{\varPsi _k}} \right\rangle _0} = {\alpha _k}\left| 0 \right\rangle + {\beta _k} \cdot {e^{i{\psi _0}}}\left| 1 \right\rangle ,k = 1,2,\ldots ,m$.

• 2. Suppose that t participants $\left\{ {\text {Bob}_1,\text {Bob}_2,\ldots ,\text {Bob}_t} \right\}$ need to reconstruct the initial state of Qs as the secret. Similarly to the case in Classical Information Sharing, Alice and $\text {Bob}_1$ employ decoy photons to check eavesdropping as in 2.3. Then, $\text {Bob}_1$ performs the unitary phase operation $U({\psi _1})$, with ${\psi _1} = \frac{{2\pi {c_1}}}{p}$ and ${c_1} = f({x_1})\prod \nolimits _{r = 2}^t {\frac{{{x_r}}}{{{x_r} - {x_1}}}} \bmod p,$ on each qubit ${\left| {{\varPsi _k}} \right\rangle _0}$ and obtains the new state ${\left| {{\varPsi _k}} \right\rangle _1} = {\alpha _k}\left| 0 \right\rangle + {\beta _k} \cdot {e^{i({\psi _0} + {\psi _1})}}\left| 1 \right\rangle ,k = 1,2,\ldots ,m$. Subsequently, $\text {Bob}_1$ sends ${\left| {{\varPsi _k}} \right\rangle _1},k = 1,2,\ldots ,m$ to $\text {Bob}_2$.

• 3. Each of the other participants, $\text {Bob}_j,j = 2,3,\ldots ,t,$ repeats the procedure as $\text {Bob}_1$ does in last step. That is, $\text {Bob}_j$ first performs the unitary phase operation $U({\psi _j})$ on each quantum state ${\left| {{\varPsi _k}} \right\rangle _{j - 1}} = {\alpha _k}\left| 0 \right\rangle + {\beta _k} \cdot {e^{i\left( {\psi _0} + \sum \nolimits _{v = 1}^{j - 1} {{\psi _v}} \right) }}\left| 1 \right\rangle$ and obtains the next state ${\left| {{\varPsi _k}} \right\rangle _j} = {\alpha _k}\left| 0 \right\rangle + {\beta _k} \cdot {e^{i\left( {\psi _0} + \sum \nolimits _{v = 1}^j {{\psi _v}} \right) }}\left| 1 \right\rangle$ for $k = 1,2,\ldots ,m$, where ${\psi _j} = \frac{{2\pi {c_j}}}{p}, {c_j} = f({x_j})\prod \nolimits _{r = 1,r \ne j}^t {\frac{{{x_r}}}{{{x_r} - {x_j}}}} \bmod p$ for $j = 2,3,\ldots ,t - 1.$ Then, $\text {Bob}_j$ sends ${\left| {{\varPsi _k}} \right\rangle _j}$ to the next participant $\text {Bob}_{j + 1}$.

• 4. After the last participant $\text {Bob}_t$ completes the unitary phase operation $U({\psi _t})$, each quantum state becomes ${\left| {{\varPsi _k}} \right\rangle _t} = {\alpha _k}\left| 0 \right\rangle + {\beta _k} \cdot {e^{\frac{{2\pi i}}{p}\left( {\sum \nolimits _{j = 1}^t {{c_j} - s} } \right) }}\left| 1 \right\rangle = {\alpha _k}\left| 0 \right\rangle + {\beta _k}\left| 1 \right\rangle , k = 1,2,\ldots ,m$. Consequently, all participants reconstruct the initial quantum state of sequence Qs successfully.

Fig. 2

Sequential operations on each qubit in Quantum States Sharing. $(\left| {{\varPsi _k}} \right\rangle$-each initial qubit, $k = 1,2,\ldots ,m; {\psi _0}$-phase shifted by the dealer Alice on the qubit; ${\psi _j} = 2\pi {c_j}/p$-phase shifted by $\text {Bob}_j$ on the qubit, $j = 1,2,\ldots ,t$)

3 Correctness

We now show the correctness of two proposed protocols based on Lemmas 1 and 2.

Lemma 1

In Shamir’s (t, n)-SS, suppose each participant $\text {Bob}_j$ has the public information ${x_j}$ and the share $f({x_j}), j = 1,2,\ldots ,k,n \ge k \ge \mathrm{{t}}\mathrm{{.}}$ All participants are able to recover the secret $s = f(0)$, if they sum up each component ${c_j} = f({x_j})\prod \nolimits _{r = 1,r \ne j}^k {\frac{{{x_r}}}{{{x_r} - {x_j}}}} \bmod p$. That is, $s = f(0) = \sum \nolimits _{j = 1}^k {{c_j}} \bmod p = \sum \nolimits _{j = 1}^k {f({x_j})\prod \nolimits _{r = 1,r \ne j}^k {\frac{{{x_r}}}{{{x_r} - {x_j}}}} } \bmod p$, where f(x) is the polynomial of degree t-1 over GF(p), p is a prime.

Proof

Lemma 1 can be immediately obtained by Lagrange interpolation formula. $\square$

Lemma 2

The unitary phase operation performed on the qubit $\left| \varphi \right\rangle = \alpha \left| 0 \right\rangle + \beta \left| 1 \right\rangle , {\left| \alpha \right| ^2} + {\left| \beta \right| ^2} = 1$ has the following feature

$$\begin{aligned} U({\psi _1})U({\psi _2})\left| \varphi \right\rangle = \alpha \left| 0 \right\rangle + \beta \cdot {e^{i({\psi _1} + {\psi _2})}}\left| 1 \right\rangle = U({\psi _1} + {\psi _2})\left| \varphi \right\rangle . \end{aligned}$$

• 1. Correctness of Classical Information Sharing The initial state of each qubit in the sequence is $\left| {{\varPhi _k}} \right\rangle = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i{\varphi _k}}}\left| 1 \right\rangle } \right) , {\varphi _k} \in \left\{ {0,\pi ,{\pi / 2},{{3\pi } /2}} \right\} , k = 1,2,\ldots ,m$. After Alice performs the operation $U({\psi _0}),\begin{array}{*{20}{c}}{}\end{array}{\psi _0} = \frac{{\mathrm{{ - 2}}\pi s}}{p}$, the state becomes ${\left| {{\varPhi _k}} \right\rangle _0} = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i({\varphi _k} + {\psi _0})}}\left| 1 \right\rangle } \right) .$ When all participants have completed their respective operations $U({\psi _j}), j = 1,2,\ldots , t$, the state is finally converted into ${\left| {{\varPhi _k}} \right\rangle _t}$. For each qubit ${\left| {{\varPhi _k}} \right\rangle _t}$, we have

  $$\begin{aligned} {\left| {{\varPhi _k}} \right\rangle _t}&= U\left( {\psi _0} + \sum \limits _{j = 1}^t {{\psi _j}} \right) \left| {{\varPhi _k}} \right\rangle = U\left[ {\sum \limits _{j = 1}^t {{\phi _j}} + \frac{{2\pi }}{p}\left( {\sum \limits _{j = 1}^t {{c_j} - s} } \right) } \right] \left| {{\varPhi _k}} \right\rangle \\&= U\left[ {\sum \limits _{j = 1}^t {{\phi _j}} + \frac{{2\pi }}{p}\left( {Np + s - s} \right) } \right] \left| {{\varPhi _k}} \right\rangle = U\left( \sum \limits _{j = 1}^t {{\phi _j}} + 2N\pi \right) \left| {{\varPhi _k}} \right\rangle \\&= \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i\left( {{\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}} } \right) }}\left| 1 \right\rangle } \right) .\begin{array}{*{20}{c}}{}&{}\end{array}(N \in Z) \end{aligned}$$

  Using the measurement base determined by the dealer, $\left( {\varphi _k} + \sum \nolimits _{j = 1}^t {{\phi _j}}\right) \bmod 2\pi$ can be pinpointed by $\text {Bob}_t$. Therefore, the initial state of each qubit $\left| {{\varPhi _k}} \right\rangle$ can be reconstructed and ${\varphi _k}$ can be eventually recovered by $\text {Bob}_t$ with the knowledge of ${\phi _j},j = 1,2,\ldots ,t$.

• 2. Correctness of Quantum States Sharing Each initial state of a qubit in the sequence is $\left| {{\varPsi _k}} \right\rangle = {\alpha _k}\left| 0 \right\rangle + {\beta _k}\left| 1 \right\rangle , k = 1,2,\ldots ,m.$ After all the unitary operations $U({\psi _j}),j = 0,1,\ldots ,t,$ the last participant $\text {Bob}_t$ can reconstruct the initial state $\left| {{\varPsi _k}} \right\rangle , k = 1,2,\ldots ,m,$ due to the following equation

  $$\begin{aligned} U\left( {\psi _0} + \sum \limits _{j = 1}^t {{\psi _j}}\right) \left| {{\varPsi _k}} \right\rangle = U\left[ {\frac{{2\pi }}{p}\left( {\sum \limits _{j = 1}^t {{c_j} - s} } \right) } \right] \left| {{\varPsi _k}} \right\rangle = U(2N\pi )\left| {{\varPsi _k}} \right\rangle = \left| {{\varPsi _k}} \right\rangle , \end{aligned}$$

  $N \in Z.$ Therefore, at least t participants can collaborate to reconstruct the sequence of initial quantum states as the secret.

4 Concrete example of the scheme

To make the proposed scheme clearer, an example of (4, 6) threshold quantum secret sharing, which shares two bits of classical information by a single qubit, is given as follows.

During share distribution, the dealer Alice first chooses a random polynomial f(x) of degree 3 over GF(23): $f(x) = 17 + 5x + 12{x^2} + 6{x^3}\bmod 23$, and thus, the private value is ${a_0} = s = f(0) = 17$ with threshold $t = 4$ and the prime $p = 23$. Then she computes and allocates a share ${y_j}$ to each shareholder $\text {Bob}_j$ with public information ${x_j} = j + 1$ for $j = 1,2,\ldots ,6$. As a result, ${y_1} = f({x_1} = 2) = 123\bmod 23 = 8, {y_2} = f({x_2} = 3) = 302\bmod 23 = 3, {y_3} = f({x_3} = 4) = 15, {y_4} = f({x_4} = 5) = 11, {y_5} = f({x_5} = 6) = 4$ and ${y_6} = f({x_6} = 7) = 7$.

To share 2 bits of classical information by a single qubit in Classical Information Sharing, Alice first prepares a qubit in the state $\left| \varPhi \right\rangle = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + i\left| 1 \right\rangle } \right) ,$ i.e., $\varphi = {\pi /2}$, and performs the unitary phase operation $U({\psi _0})$ on the qubit, ${\psi _0} = \frac{{ - 2\pi s}}{p} = \frac{{ - 34\pi }}{{23}}$. Suppose participants $\text {Bob}_j,j = 1,3,4,6$, need to reconstruct the initial state and share 2 bits of classical information, they compute a component each by Lagrange interpolation as follows:

$$\begin{aligned} {c_1}= & {} f({x_1})\prod \limits _{r = 2}^t {\frac{{{x_r}}}{{{x_r} - {x_1}}}} \bmod p = f(2) \cdot \frac{4}{{4 - 2}} \cdot \frac{5}{{5 - 2}} \cdot \frac{7}{{7 - 2}}\bmod 23 = 22,\\ {c_3}= & {} f({x_3})\prod \limits _{r = 1,r \ne 3}^t {\frac{{{x_r}}}{{{x_r} - {x_3}}}} \bmod p = f(4) \cdot \frac{2}{{2 - 4}} \cdot \frac{5}{{5 - 4}} \cdot \frac{7}{{7 - 4}}\bmod 23 = 9,\\ {c_4}= & {} f({x_4})\prod \limits _{r = 1,r \ne 4}^t {\frac{{{x_r}}}{{{x_r} - {x_4}}}} \bmod p = f(5) \cdot \frac{2}{{2 - 5}} \cdot \frac{4}{{4 - 5}} \cdot \frac{7}{{7 - 5}}\bmod 23 = 3,\\ {c_6}= & {} f({x_6})\prod \limits _{r = 1,r \ne 6}^t {\frac{{{x_r}}}{{{x_r} - {x_6}}}} \bmod p = f(7) \cdot \frac{2}{{2 - 7}} \cdot \frac{4}{{4 - 7}} \cdot \frac{5}{{5 - 7}}\bmod 23 = 6. \end{aligned}$$

Then each participant picks ${\phi _j}$ as ${\phi _1} = {\pi / 2}, {\phi _3} = 0,{\phi _4} = \pi ,{\phi _6} = {{3\pi } / 2}$ and performs the unitary phase operation $U({\psi _j})$ with ${\psi _j} = {\phi _j} + \frac{{2\pi {c_j}}}{p}$ on the qubit in sequence for $j = 1,3,4,6$. After $\text {Bob}_6$ completes the unitary operation, the final state is

$$\begin{aligned} {\left| \varPhi \right\rangle _4}&= U({\psi _0} + {\psi _1} + {\psi _3} + {\psi _4} + {\psi _6})\left| \varPhi \right\rangle \\&= U({\varphi _1} + {\varphi _3} + {\varphi _4} + {\varphi _6} + \frac{{2\pi }}{{23}}(22 + 9 + 3 + 6 - 17))\left| \varPhi \right\rangle \\&= U({\pi / 2} + 0 + \pi + {{3\pi }/2} + 2\pi )\left| \varPhi \right\rangle \\&= U(\pi )\left| \varPhi \right\rangle . \end{aligned}$$

All participants inform the dealer of their operation classifications which are class Y, X, X, Y. Then Alice determines the measurement base is y because of $\left| {\sin \left( \varphi + \sum \nolimits _{j = 1}^t {{\phi _j}} \right) } \right| = 1$. The last participant $\text {Bob}_6$ measures the qubit in y base and publishes the measurement result of ${\left| \varPhi \right\rangle _4} = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle - i\left| 1 \right\rangle } \right)$, i.e., $\left( \varphi + \sum \nolimits _{j = 1}^t {{\phi _j}} \right) \bmod 2\pi = {{3\pi }/ 2}$. After participants $\text {Bob}_j,j = 1,3,4,6$ exchange their ${\phi _j}$, they all know the dealer’s value of $\varphi$ is ${\pi / 2}$ because of $(\varphi + \pi ) \bmod 2\pi = {{3\pi } /2}$. According to the definition $\varphi = 0 \Rightarrow 00,\varphi = {\pi / 2} \Rightarrow 01,\varphi = \pi \Rightarrow 10$ and $\varphi = 3{\pi / 2} \Rightarrow 11$ , all participants share the 2-bit classical information 01 by a qubit.

5 Security analysis, related work and comparison

5.1 Security

In both proposed protocols, the decoy photons are used to check eavesdropping. Consequently, when eavesdropper Eve mounts the intercept-and-resend attack and tries to obtain the transmitted message, he can only intercept the quantum sequence but without the sequence states, and thus fails to resend a perfect copy of the sequence due to Heisenberg uncertainty principle and quantum no-cloning principle. Furthermore, Eve doesn’t know the positions and states of the decoy photons, so the attack will cause an increase in error rate and thus be detected with the probability $1 - {({1 /4})^n}$, where n is the number of the decoy photons. Obviously, the probability converges to 1 for large integer n. Another attack Eve may take is entangle-and-measure attack; however, also due to the decoy photon, he will not get any useful information about the secret.

In Classical Information Sharing, as the participant attack, the first recipient $\text {Bob}_1$ maybe want to infer the secret without the help of other participants. Knowing true positions of quantum states in the expanded sequence, he can directly measure the quantum states. However, Alice has performed unknown unitary phase shift operation $U({\psi _0})$ on these quantum states. If $\text {Bob}_1$ happens to choose the true base in the measurement of each qubit ${\left| \varPhi \right\rangle _0} = \frac{1}{{\sqrt{2} }}\left( {\left| 0 \right\rangle + {e^{i({\varphi _k} + {\psi _0})}}\left| 1 \right\rangle } \right) ,k = 1,2,\ldots ,m,$ he will get $({\varphi _k} + {\psi _0})$, instead of ${\varphi _k}$ itself. Generally speaking, due to ${\psi _0} = \frac{{\mathrm{{ - 2}}\pi s}}{p},s \in GF(p), \text {Bob}_1$ figures out ${\varphi _k}$ with the probability 1 / p without the exact value of ${\psi _0}$. However, ${\varphi _k} \in \{ 0,\pi /2,\pi ,3\pi /2\}$ and $p > 4$ means $\text {Bob}_1$ has the probability of 1 / 4 to obtain the value of each ${\varphi _k}$. That is, $\text {Bob}_1$ gets no additional information about each ${\varphi _k}, k = 1,2,\ldots ,m$.

Another possible participant attack is entanglement swapping [25]. To mount the attack, an malicious participant prepares an EPR pair and sends the second qubit of the pair to the following participant while keeping the protocol’s qubit to himself. Based on collective measurement result, the participant can determine which action he should take to avoid being detected. Although this attack works in [14], it doesn’t work in our scheme. Concretely, suppose that the qth participant ${R_q}$ cheats by entanglement swapping during the protocol, in the first case: Since some participant ${R_j}(j < q)$ has not broadcast the class of his operation, using entanglement swapping without information about measurement base ${R_q}$ gains no information about ${\varphi _k}$; in the second case: After all participants ${R_j}(j < q)$ broadcast the classes of their operations, ${R_q}$ will know ${E_{q - 1}} \equiv \left| {\cos \left( \sum \nolimits _j^{q - 1} {{\phi _j}} \right) } \right|$ although he does not know each ${\phi _j}$, but when he measures the qubit in the base $\left\{ {{{\left| 0 \right\rangle \pm \, {i^{1 - {E_{q - 1}}}}\left| 1 \right\rangle }/ {\sqrt{2} }}} \right\}$, he will face the same problem in the first attack strategy because of the unitary phase operation $U({\psi _0})$ performed by Alice, and thus, he cannot achieve the value of ${\varphi _k}$.

In Quantum States Sharing, the case is similar to that in Classical Information Sharing when any less than t participants mount the participant attack, because these participants fail to reconstruct the phase value ${\psi _0} = \frac{{\mathrm{{ - 2}}\pi s}}{p}$ of the dealer. Therefore, they cannot achieve any information about the quantum states.

5.2 Related work and comparison

The existing (t, n) threshold quantum secret sharing schemes in [8, 15] change the field of Shamir’s (t, n)-SS into ${F_{{2^N}}}$ and use Hadamard transformations in association with simple rotations to encode classical bit string. Compared with our scheme, they are complicated since each participant has to apply different operations to quantum state according to the classical share. Moreover, both schemes only allow to share classical information and thus cannot be used to share quantum information.

Cleve et al.’s scheme [7] uses quantum error correcting to construct the (t, n) threshold scheme, but this method needs a special coding to map the quantum state into n shares, such that any t participants can use linear transformation to recover the initial state. However, preparing a special coding to map states makes the scheme difficult to design and implement. Yang et al. [19] employed orthogonal multipartite entangled states in d-qudit system to construct (t, n) threshold QSS scheme. In addition to being harder to design because of the dependence on entangled state, the scheme is a ramp one in security, which means there exits information leak about the secret in some cases. In comparison, our scheme is perfect, i.e., no information about the secret is leaked if less than t participants try to recover the secret. Moreover, our scheme is easier to design and realize since it merely employs simple phase shift operation on single qubit.

Recently, Song et al. [20] proposed a (t, n) threshold d-level QSS scheme based on several unitary operations such as d-level CNOT, (inverse) quantum Fourier transform and generalized Pauli operator performed on particles. As a (t, n) threshold d-level QSS, it is more universal and practical than our two-level QSS. Nevertheless, our scheme is easier to realize if compared with Song’s scheme, because our scheme only uses phase shift operation on single qubit and a single qubit can be more easily produced as well as operated in physics.

Qin–Zhu–Dai’s scheme [16] is similar to our scheme which also uses phase shift operation and Shamir’s (t, n)-SS , but the scheme is wrong. In the proof, the scheme takes $\sum \nolimits _{i = 1}^t {\frac{{{L_i}f({x_i})}}{N}} = \frac{S}{N}$ for granted. As a matter of fact, $\sum \nolimits _{i = 1}^t {\frac{{{L_i}f({x_i})}}{N}}$ is equivalent to $\frac{{S + kd}}{N},k \in Z$ instead of $\frac{S}{N}$. Consequently, this leads to the scheme cannot recover the initial state correctly. In our scheme, each participant $\text {Bob}_j$ performs the novel phase shift operation $U({\psi _j})$ with ${\psi _j} = {\phi _j} + \frac{{2\pi {c_j}}}{p}$ (in Classical Information Sharing) or ${\psi _j} = \frac{{2\pi {c_j}}}{p}$ (in Quantum States Sharing), ${\phi _j} \in \left\{ {0,\pi ,{\pi /2},{{3\pi } /2}} \right\}$ on each qubit. As a result, each initial state of a qubit can be successfully reconstructed after the dealer and all participants complete their operations.

In summary, our scheme is allowed to share both classical information and quantum states. Moreover, a shareholder can use his single private share repeatedly to share a bit string or a sequence of quantum states. The only dependence on single qubit and phase shift operation makes our scheme easier to realize and more practical to use when compared to schemes using entangled state.

6 Generic method to construct (t, n)-QSS based on single qubit

In the proposed (t, n)-QSS scheme, we acquire the property of (t, n) threshold by classical Shamir’s (t, n)-SS. As a matter of fact, our scheme presents a generic method to realize a (t, n) threshold QSS based on phase shift operation on single qubit. That is, other classical (t, n)-SS schemes such as linear code-based (t, n)-SS [26, 27], geometry-based (t, n)-SS [2] and Chinese remainder theorem-based (t, n)-SS [28, 29] can also be used to construct (t, n)-QSS schemes based on unitary phase operation on qubit, which have the same properties as our scheme.

Note that each secret in the above classical (t, n)-SS schemes, i.e., the private value s in our (t, n)-QSS, can be uniformly expressed as $s = \sum \nolimits _{i = 1}^m {{c_i}} \bmod M = \sum \nolimits _{i = 1}^m {{a_i}} {s_i}\bmod M$, where ${c_i}$ is the participant $\text {Bob}_i's$ component evaluated from the share and some parameter ${a_i}$, m $(m \ge t)$ is the number of participants and M is a modulus. In this case, to share the initial state of a qubit sequence as the secret, the dealer Alice first performs the phase shift operation $U({\psi _0}),{\psi _0} = - 2\pi s/M$ on each qubit; every participant $\text {Bob}_i$ then takes phase shift operation $U({\psi _i}),{\psi _i} = - 2\pi {c_i}/M, i = 1,2,\ldots ,m,$ on the qubit one by one and participant $\text {Bob}_m$ can reconstruct initial state of the qubit. As a result, the secret (i.e., initial state of the qubit sequence) can be finally reconstructed. Similarly, to share classical information as the secret, one can follow the same way in Classical Information Sharing. Consequently, a (t, n)-QSS scheme, capable of sharing both classical information and quantum states, can be constructed easily.

7 Conclusion

The paper proposes a (t, n) threshold quantum secret sharing scheme, and it employs Shamir’s (t, n)-SS in association with phase shift operation on single qubit to embed and reconstruct initial states to share a secret. In the scheme, the dealer first performs the unitary operation on each qubit using the phase values to encode the secret; then, any t or more than t participants perform unitary operation one by one on each qubit using their private shares. As a result, initial quantum states are recovered and the secret is shared among participants. Analyses show that the scheme is resistant to typical intercept-and-resend attack, entangle-and-measure attack and participant attack such as entanglement swapping attack.

In conclusion, the proposed scheme allows any t or more than t participants to repeatedly use their private shares to share a bit string or quantum states as the secret. Compared with related schemes, the scheme is easier to realize and more practical in applications.