An Algorithm Template for Domain-Based Parallel Irregular Algorithms

Abstract

The parallelization of irregular algorithms has not been as widely studied as the one of regular codes. In particular, while there are many proposals of parallel skeletons and libraries very well suited to regular algorithms, this is not the case for irregular ones. This is probably due to the complexity of finding common patterns, behaviors and semantics in these algorithms. This is unfortunate, as the parallelization of irregular algorithms would benefit even more than that of regular codes from the higher degree of abstraction provided by skeletons. This work proposes to exploit the concept of domain defined on some property of the elements to process in order to enable the simple and effective parallelization of irregular applications. Namely, we propose to use such domains both to decompose the computations in parallel tasks and to detect and avoid conflicts between these tasks. A generic C++ library providing a skeleton for multicore systems built on this idea is described and evaluated. Our experimental results show that this library is a very practical tool for the parallelization of irregular algorithms with little programming effort.

1 Introduction

During the past years, extensive research has been carried out on the best ways to express parallelism. This has led to an evolution from low level tools [4] to a variety of new higher level approaches. The large majority of these tools [2, 6, 8, 10–14, 20, 33] are well suited to parallelize regular algorithms, whose computations are relatively easy to distribute among different cores. Opposed to this regular parallelism, there is the amorphous data-parallelism [22], found in many irregular applications, i.e., those characterized by handling pointer-based data structures such as graphs or lists. These applications require a different approach, as it is more complex, and sometimes even impossible to find an a priori distribution of work in them that avoids conflicts among the parallel threads of execution and balances their workload. Tracking these conflicts is also complicated by the lack of regularity and the dynamic changes in the relations among the data items that participate in a computation, synchronization mechanisms being usually required before accessing each element to process.

As a result of this situation, the parallelization of irregular algorithms typically requires much more work from the programmer. One of the best options to hide the complexity of the parallelization of irregular applications is the use of skeletons [9]. Built on parallel design patterns, skeletons provide a clean specification of the flow of execution, parallelism, synchronization and data communications of typical strategies for the parallel resolution of problems. Unfortunately, most skeleton libraries [2, 8, 10, 12, 13, 15, 33] focus on regular problems. Parallel libraries that can support specific kinds of irregular algorithms exist [1, 3], but there are only a few general-purpose developments based on broad abstractions.

This work presents a parallelization strategy for irregular algorithms based on a domain defined in terms of some property of the elements of the data structure. This domain is used both to partition the computation, by assigning the elements of different subdomains to different parallel tasks, and to avoid conflicts between these tasks, by checking whether the accessed elements are owned by the subdomain assigned to the task. Our proposal applies a novel recursive scheduling strategy that avoids locking the partitions generated, instead delaying work that might span partitions until later in the computation. Among other benefits, this approach promotes the locality in the parallel tasks, avoids the usage of locks, and thus the contention and busy waiting situations often related to them, and provides guarantees on the maximal number of abortions due to conflicts between parallel tasks during the execution of an irregular algorithm. An implementation as a C++ library is also described and evaluated.

The rest of this paper is structured as follows. Section 2 introduces the concepts behind our domain-based computing proposal, while in Sect. 3 our library is described. Section 4 describes the algorithms used in its programmability and performance evaluation, performed in Sect. 5. Section 6 deals with related work. Finally, Sect. 7 is devoted to conclusions and future work.

2 Domain-Based Parallel Irregular Algorithms

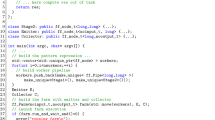
Many irregular algorithms have a workflow based on the processing of a series of elements belonging to an irregular structure, called workitems. The elements to process are stored in a generic worklist, which is updated when new workitems are found. Figure 1 shows the general workflow of these algorithms. Line 1 fills the initial worklist with elements of the irregular structure. Any irregular structure could fit our generic description of the pseudocode and our subsequent discussion. In what follows we will use the term graph, as it is a very generic irregular data structure and many others can be represented as graphs too. Some algorithms start with just one root element, while others have an initial subset of the elements or even the full graph. The loop in Lines 2–6 processes each element of this worklist. Line 3 represents the main body of the algorithm being implemented. If this processing results in new work being needed, as checked in Line 4, it is added to the worklist in Line 5. This is repeated until the worklist is empty.

Fig. 1

Common pseudocode for an algorithm that uses irregular data structures

An important characteristic of these algorithms is whether the workitems must be processed in some specific order. Since non-ordered versions of irregular algorithms present more parallelism and scale better than the ordered versions [17], our subsequent discussion focuses on unordered algorithms. These algorithms can be parallelized by having different threads operating on different elements of the worklist, provided that no conflicts appear during the simultaneous processing of any two workitems.

The workitems found in irregular algorithms usually have properties (in the following, property refers to a data item, such as for example a data member in a class) defined on domains, such as names, coordinates or colors. Therefore a sensible way to partition the work in an irregular algorithm is to choose a property of this kind, and classify the workitems according to it. Specifically, the domain of the property would be divided in subdomains and a parallel task would process the workitems of each subdomain. The property used should fulfill a few characteristics in order to attain good performance. If no intrinsic property of the problem meets them, an additional property satisfying them should be defined in the workitems for the sake of a good parallelization following this scheme.

The first characteristic is that the property domain should be divisible in as many subdomains as hardware threads are available, the subdomains being as balanced as possible in terms of workitems associated. In fact, it would be desirable to generate more subdomains than threads in order to provide load balancing by assigning new subdomain tasks to threads as they finish their previous task. Second, if the processing of a workitem generates new workitems, it is desirable that the generated workitems belong to the same subdomain as their parent. We call this characteristic, which depends also on the nature of the operation to apply on the workitems, affinity of children to parents. If this were not the case, either the rule of ownership of the workitems by tasks depending on the subdomain they belong to would be broken, or intertask communication would be required to reassign these workitems to the task that owns their subdomain. Third and last, there is the proximity characteristic; that is, that the larger the similarity in the values of the chosen property, the shorter the distance between the associated workitems in the graph. Very often the processing of a workitem requires accessing part of its neighborhood in the graph. If some element(s) in this neighborhood belong to other tasks the processing is endangered by potential parallel modifications by other threads. Nevertheless, if all the elements required belong to the subdomain of the workitem that started the processing, everything is owned by the task for that subdomain and the processing can proceed successfully. This way, if the rule of ownership is fulfilled, i.e, all the elements of the graph that belong to a certain subdomain are owned by the same task, subdomains can be used not only to partition work, but also to identify potential conflicts. Furthermore, the process will be efficient if the property chosen to define the work domains implies proximity for the elements that belong to the same subdomain. For this reason, in algorithms where the processing of a workitem requires accessing its neighborhood, the characteristics of the affinity of children to parents and proximity are very desirable.

2.1 A Novel Parallelization Scheme Based on Domains

The data-centric partitioning and work assignment just presented is a basic idea that can be put into practice in very different ways. We propose here a scheme based on the recursive subdivision of a domain defined on the elements of the irregular data structure, so that the workitems of each subdomain are processed in parallel, and the potential conflicts among them are exclusively detected and handled using the concept of membership of the subdomain. Locality of reference in the parallel tasks is naturally provided by the fact that most updates in irregular applications are usually restricted to small regions of the shared heap [22, 25]. Our scheme further reinforces locality if the domain used in the partitioning has the proximity characteristic, so that the elements associated with a subdomain, and thus with a task, are nearby. The processing of the workitems begins in the lowest level of subdivision, where there is the maximum number of subdomains, and thus of parallel tasks. The workitems that cannot be processed within a given subdomain, typically because they require manipulations of items associated with other subdomains, are later reconsidered for processing at higher levels of decomposition using larger subdomains. We now explain in detail our parallelization method, illustrated in Fig. 2. This figure shows a mesh of triangles, which can be stored in a graph where each node is a triangle and the edges connect triangles which are next to each other in the mesh. The big dots represent the possible limits of the subdomains. In this case, the domain chosen is defined on the coordinates of the triangles.

Fig. 2

Structure of the domain-based parallelization of irregular algorithms, exemplified with a mesh of triangles

2.1.1 Recursive Subdivision

An algorithm starts with an initial worklist, containing nodes from the whole graph domain, as shown in the initial step in Fig. 2. Before doing any processing, the domain is recursively subdivided until there are enough subdomains to exploit all the cores available. The domain decomposition algorithm chosen can have a large impact on the performance achieved. The reason is that the size of the different parallel tasks generated, which is critical for the load balancing, and the shape of the subdomains they operate on, which influences the number of potential conflicts during the parallel processing, largely depend on it. Over-decomposition, i.e., generating more subdomains than cores, can be applied in order to enable load balancing by means of work-stealing mechanisms. The domain subdivisions implicitly partition both the graph and the worklist. This logical partitioning can optionally give place to a physical partitioning. That is, the graph and/or the worklist can be partitioned in (mostly) separate data structures so that each one corresponds to the items belonging to a given subdomain and can be manipulated by the associated task with less contention and improved locality. We talk about mostly separate structures because for structures such as the graph, tasks should be able to access portions assigned to other tasks. It is up to the implementation strategy to decide which kind of partitioning to apply to each data structure. In our abstract representation, for simplicity, we show 2 subdivisions to get 4 different subdomains, in Steps 1 and 2. Then, in Step 3, a parallel task per subdomain is launched, whose local worklist contains the elements of the global worklist that fall in its subdomain. During the processing of each workitem two special events can happen: an access to an element outside the local subdomain, and the generation of new workitems to process. We describe the approach proposed for these two situations in turn.

2.1.2 Conflict Detection

In many algorithms, the processing of a workitem requires accessing a given set of edges and nodes around it. This set, called the neighborhood, is often found dynamically during the processing and its extent and shape can vary for different workitems. This way we must deal with the possibility that the neighborhood of a workitem reaches outside the subdomain of the associated task. Accessing an element outside the local subdomain is a risk, since it could be in an inconsistent state or about to be modified by another task. Thus, we propose that whenever a new element in the neighborhood of a workitem is accessed for the first time, its ownership by the local domain is checked. If the element belongs to the domain, the processing proceeds. Otherwise there is a potential conflict and the way to proceed depends on the state of our processing. If the operation is cautious [27], that is, it reads all the elements of its neighborhood before it modifies any of them, all it needs to do when it finds an element owned by another task is to leave, as no state of the problem will have been modified before. Otherwise, the modifications performed would need to be rolled back.

When a task fails to process a workitem because part of its neighborhood falls outside its domain, it puts the workitem in a pending list to be processed later, which is different from the local worklist of workitems to process. The processing of this pending list will be discussed in Sect. 2.1.4.

Notice that the more neighbors a node has, the higher the chances all its neighborhood does not fit in a single subdomain. For this reason nodes with a large number of neighbors will tend to generate more conflicts, and thus lower performance, depending on the domain and decomposition chosen. The programmer could avoid this problem by choosing a domain with a subdivision algorithm that fits this kind of graphs for the specific problem she is dealing with. For example the domain and splitting algorithm could be designed such that nodes with many neighbors always, or at least often, fit in the same subdomain with their neighbors.

2.1.3 Generation of New Workitems

The new workitems generated by a task that belong to the local subdomain are simply added to its local worklist, so that the task will process them later. The new workitems outside the local subdomain can be added to the pending list, so that their processing is delayed to later stages, exactly as with workitems whose neighborhood extends outside the local subdomain. Another option is to push them onto the worklists associated with their domains, so they are processed as soon as possible. The latter option is useful for algorithms that have a small initial worklist with elements from just one subdomain. The processing of the algorithm can start in this subdomain, and the runtime will spawn new tasks for the neighboring subdomains when they are needed.

2.1.4 Domain Merging

When a subdomain task empties its local worklist, it finishes and the processing can proceed to the immediately higher level of domain subdivision, as shown in Step 4 in Fig. 2. The implementation of the change of level of processing can be synchronous or not. In the first case, the implementation waits for all the tasks for the subdomains of a given level to finish before building and launching the tasks for the domains in the immediately upper level. In an asynchronous implementation, whenever the two child subdomains of a parent domain finish their processing, a task associated to that parent domain is built and sent for execution. In either case, both child domains of a given parent subdomain are rejoined, forming that parent domain, and the pending lists generated in the children subdomains are also joined forming the worklist of the task for the parent domain. An efficient implementation should perform the merging, and schedule for execution the task associated with the parent domain, in one of the cores in which the children run in order to maximize locality. When it runs, the task associated with the parent domain tries to process the workitems whose processing failed in the child domains. The task will successfully process those workitems whose neighborhood did not fit in any of the child subdomains, but which fits in the parent domain. Typically the processing of some workitems will fail again because their neighborhood falls also outside this domain. These workitems will populate the pending list of the task. This process takes place one level at a time as the processing returns from the recursive subdivision, until the initial whole domain is reached, and the remaining elements are processed, which is depicted as the final Step 5 in Fig. 2. This way, the tasks for all the joined regions—except the topmost one—are processed in parallel.

2.1.5 Discussion

As we have seen, this scheme avoids the need of locks both on the elements of the graph and on the subdomains and implied partitions generated, thus avoiding the busy waiting and contention problems usually associated with them. Also, its strategy to deal with conflicts provides an upper bound for the number of attempts to process workitems whose neighborhood extends outside the partition assigned to their tasks. Those workitems are considered at most once per level of subdivision of the original domain, rather than being repetitively reexamined until their processing succeeds. Both characteristics are very desirable, particularly as the number of cores, and therefore parallel tasks and potential conflicts, increases. This strategy, though, has the drawback of eventually serializing the processing of the last elements. But because of the rejoining process, which tries to parallelize as much as possible the processing of the workitems whose processing failed in the bottom level subdomains, the vast majority of the work is performed in parallel. In fact, as we will see in Sect. 5, in our tests only a very small percentage of the workitems present conflicts that prevent their parallel processing. This also confirms that optimistic parallelization approaches such as ours are very suitable for irregular applications [23, 24].

3 The Library

We have developed a C++ library that supports our domain-based strategy to parallelize irregular applications in shared-memory systems. Programmers are free to use just the library components, derive from them or implement their own from scratch, as long as they meet the interface requirements. Our library includes template classes for graphs, domains, and worklists of elements with the usual semantics. Its most characteristic component is the algorithm template that implements the parallelization approach just described, which is

where the name of each parameter indicates the kind of object it expects. This function is in charge of the domain splitting process, task creation and management, splitting and merging the worklists, getting elements from them to run the operation, and adding to the pending worklists workitems whose neighborhood extends outside the current domain. This skeleton physically partitions the worklists, so that each parallel task has its own separate worklist, which is of the type provided by the user in the invocation of the skeleton. Thanks to the physical partitioning, the worklists need not support simultaneous accesses from parallel tasks. However, the fact that these containers are extensively read and modified during the parallel execution makes their design important for performance. The partition of the graph made by our skeleton is only logical, that is, it is virtually provided by the existence of multiple subdomains, there being a single unified graph object accessed by all the tasks. This implies that our library graphs can be safely read and updated in parallel, as long as no two accesses affect the same element simultaneously—unless they are all reads.

First, the domain, whose class must support the interface shown in Fig. 3, is recursively split, creating several leaf domains. The subdivision process stops when either a domain is not divisible or $\mathtt{parallel\_domain\_proc}$ decides there are enough tasks for the hardware resources available. This is the same approach followed by popular libraries such as [30], which we have used as underlying tool to generate and manage the parallel tasks. Our current implementation partitions the domain until there are at least two subdomains per hardware thread. The aim of the over-decomposition is to balance the load among the threads, as they take charge of new tasks as they finish the previous one. The initial workload is distributed among these subdomains, assigning each workitem to a subdomain depending on the value of its data. Then a task is scheduled for each subdomain, which will process the worklist elements belonging to that subdomain and which will have the control on the portion of the graph that belongs to that domain.

Fig. 3

Required interface for a $\mathtt{Domain}$ class

The $\mathtt{Operation}$ to perform on the workitems is provided by the user as a functor, a function pointer or a C++11 lambda function with the form $\mathtt{void~op(Workitem*}\mathtt{e,~Worklist \& ~wl,~Domain \& ~s)}$. These parameters, which will be provided by our algorithm template in each invocation, are the current workitem to process, the local worklist and the current subdomain. The local worklist is supplied to receive the new workitems created by the operation. When accessing the neighbors of a workitem, the operation is responsible for checking whether they belong to the local subdomain $\mathtt{s}$. When this is not the case, the operation must throw an exception of a class provided by our library. This exception, which is captured by our algorithm template, tells the library to store the current workitem in the pending list, so it can be processed when the subdomains are joined. The domain classes provided by our library offer a method that automatically throws this exception when the element checked does not belong to them.

The boolean template parameter $\mathtt{redirect}$ controls the behavior of the algorithm template with respect to the workitems whose processing fails because their neighborhood extends outside the local subdomain. When $\mathtt{redirect}$ is $\mathtt{false}$—which is its default—they are simply pushed in the task pending list. When it is $\mathtt{true}$, the behavior depends on the state of the task associated with the workitem subdomain at the bottom level of subdivision. If this task or a parent of it is already running, the workitem is also stored in the pending list of the task that generated it. Otherwise, it is stored in the local worklist of the task that owns its subdomain, which is then scheduled for execution. To facilitate the redirection of workitems, this configuration of the algorithm template does not schedule for execution tasks whose worklists are empty. Notice that redirect is a performance hint, as all the workitems will be correctly processed no matter which is its value. Redirection mostly benefits algorithms in which the initial workitems belong to a few bottom level subdomains, and where the processing gradually evolves to affect more subdomains.

The skeleton builds the worklist of the tasks associated with non-bottom subdomains by merging the pending lists of their respective children. This way, these tasks try to process the elements that could not be processed in their children. This process happens repetitively until the root of the tree of domains—i.e., the initial domain provided by the user—is reached.

4 Tested Algorithms

The four benchmarks used in the evaluation are now described in turn.

Boruvka’s algorithm computes the minimal spanning tree through successive applications of edge-contraction on the input graph. In edge-contraction, an edge is chosen from the graph and a new node is formed with the union of the connectivity of the incident nodes of the chosen edge, as shown in Fig. 4. In the case that there are duplicate edges, only the one with smallest weight is carried through in the union. Boruvka’s algorithm proceeds in an unordered fashion. Each node performs edge contraction with its nearest neighbor. This is in contrast with Kruskal’s algorithm where, conceptually, edge-contractions are performed in increasing weight order.

Fig. 4

Example of an edge contraction of the Boruvka algorithm

The pseudocode for the algorithm is shown in Fig. 5. First, it reads the graph in Line 1, and fills the worklist with all the nodes of the graph. The nodes of the initial MST are the same as those of the graph, and they are connected in the loop in Lines 4–9. For each node, the minimum weighted edge to its neighbors is selected in Line 5. Then, in line 6, this edge is contracted: it is removed from the graph, added to the MST in Line 7, and one node represents now the current node and its neighbor. This new node is added to the worklist in Line 8.

Fig. 5

Pseudocode of the Boruvka minimum spanning tree algorithm

The parallelism available in this algorithm decreases over time. At first, all the nodes whose neighborhoods do not overlap can be processed in parallel, but as the algorithm proceeds the graph gets smaller, so there are fewer nodes to be processed.

Another benchmark is Delaunay mesh refinement [7]. A 2D Delaunay mesh is a triangulation of a set of points that fulfills the condition that for any triangle, its circumcircle does not contain any other point from the mesh. A mesh refinement has the additional constraint of not having any angle with less than 30 degrees. This algorithm takes as input a Delaunay mesh that may contain triangles not meeting the constraint, which are called bad triangles. It produces as output a refined mesh by iteratively re-triangulating the affected positions of the mesh. Figure 6 shows an example of a refined mesh.

Fig. 6

Retriangulation of cavities around bad triangles

The pseudocode for the algorithm is shown in Fig. 7, and it works as follows. Line 1 reads a mesh definition and stores it as a $\mathtt{Mesh}$ object. From this object, we can get the bad triangles as shown in Line 2, and save them as an initial worklist in $\mathtt{wl}$. The loop between Lines 3 and 9 is the core of the algorithm. Line 4 builds a $\mathtt{Cavity}$, which represents the set of triangles around the bad one that are going to be retriangulated. In Line 5 this cavity is expanded so that it covers all the affected neighbors. Then the cavity is retriangulated in Line 6, and the old cavity is substituted with the new triangulation in Line 7. This new triangulation can in turn have created new bad triangles, which are collected in Line 8 and added to the worklist for further processing.

Fig. 7

Pseudocode of the Delaunay mesh refinement algorithm

The triangles whose neighborhood does not overlap can be processed in parallel, because there will be no conflicts when modifying them. When the algorithm starts, chances are that most bad triangles can be processed in parallel.

Our third benchmark, graph component labeling, involves identifying which nodes in a graph belong to the same connected cluster. We have used the CPU algorithm presented in [18], whose pseudocode is shown in Fig. 8. The algorithm initializes the colors of all vertices to distinct values in Lines 6–9. For simplicity we use as initial color the index or relative position of the node in the container of nodes of the graph. It then iterates over the vertex set $V$ and starts the labeling procedure for all vertices that have not been labelled yet, in Lines 11–15. The labeling procedure iterates over the edge set of each vertex, comparing in Line 21 its color value with that of its neighbors. If it finds that the color value of a neighbor is greater, it sets it to the color of the current vertex and recursively calls the labeling procedure on that neighbor in Lines 23 and 24. If the neighbor has a lower color value, Lines 29 sets the color of the current vertex to that of the neighbor and Line 30 starts iterating over the list of edges of the node from the beginning again. As a result of this processing all the nodes in the same connected cluster end up labelled with the smallest label found in the cluster.

Fig. 8

Pseudocode of the graph labelling algorithm

Our last benchmark computes the spanning tree of an unweighted graph. It starts with a random root node, and it checks its neighbors and adds to the tree those not already added. The processing continues from each one of these nodes, until the full set of nodes has been checked and added to the graph. This algorithm is somewhat different from the ones previously explained, because it starts with just one node in the worklist, while the others have an initial worklist with a set of nodes distributed over all the domain of the graph. The pseudocode is shown in Fig. 9.

Fig. 9

Pseudocode of the spanning tree algorithm

The aforementioned steps are performed as follows: Line 1 reads the graph, and Lines 2 and 3 create an empty tree and a worklist with a random node respectively. The loop in Lines 5–10 adds to the MST the neighbors of the current node that are not already in it, and then inserts such neighbors in the worklist for further processing.

The parallelism in this algorithm works inverse to Boruvka. As it starts with a single node, the initial stages of the algorithm are done sequentially. As more nodes are processed, eventually nodes outside the initial domain are checked, allowing new parallel tasks to start participating in the processing.

5 Evaluation

All the algorithms required little work to be parallelized using our library. The main loops have been substituted with an invocation to the $\mathtt{parallel}\mathtt{\_domain\_proc}$ algorithm template, and the only extra lines are for initializing the $\mathtt{Domain}$ and checking whether a node belongs to a subdomain. This is shown in Fig. 10. This code computes the weight of the minimum spanning tree using Boruvka, and stores it in $\mathtt{contracted}$. This is an atomic integer, because all the tasks are accumulating in it the weight of the tree as they compute it. We used the C++11 lambda function notation to represent functions used as argument for algorithm templates, in Lines 5 and 10. The lambda functions used begin with the notation $\mathtt{\left[ \& \right] }$ to indicate that all the variables not in the list of arguments have been captured by reference, i.e., they can be modified inside the function. Line 5 is a for loop that initializes the worklist and stores it in $\mathtt{wl}$. Then, Line 9 creates the domain, in this case with a two-dimensional plane that encompasses the full graph. Finally, the skeleton is run in Line 10. In Line 16, the helper method of the $\mathtt{Domain2D}$ class $\mathtt{check\_node\_and\_neighbors}$ checks whether node $\mathtt{lightest}$ and all its neighbors fall within domain $\mathtt{d}$. If not, it throws an out-of-domain exception.

Fig. 10

Boruvka algorithm implemented with our library

The impact of the use of a different approach on the ease of programming is not easy to measure. In this section two quantitative metrics are used for this purpose: the SLOC (source lines of code excluding comments and empty lines) and the cyclomatic number [26], which is defined as $V=P+1$, where $P$ is the number of decision points or predicates in a program. The smaller the $V$, the less complex the program is.

We measured the whole source code for each algorithm and version. The relative changes of these metrics are shown in Fig. 11 as the percentual difference between the parallel and the sequential version. It can be seen that despite the irregularity of the algorithm, only small changes are required in order to go from a sequential to a parallel version, and the growth of any complexity measure is at most 3 % in the parallel version. In fact, in the case of the cyclomatic number, it is often lower for the parallel version than for the sequential one. This is because there are conditionals that are hidden by the library, such us the check for nonexistent workitems. This way, the simplicity of the parallelization of irregular algorithms using our library is outstanding.

Fig. 11

Relative percentages of the SLOCs and the cyclomatic number of the parallelized version with respect to the sequential one

The speed-ups achieved, calculated with respect to the serial version, are shown in Fig. 12. The system used has 12 AMD Opteron cores at 2.2 GHz and 64 GB. The Intel icpc v12 with $\mathtt{-fast}$ optimization level was used. The inputs of the algorithms were:

• Boruvka A graph defining a street map with $6\times 10^6$ nodes and $15\times 10^6$ edges, taken from the DIMACS shortest path competition [34]. In this graph, the nodes are labeled with the latitude and longitude of the cities, so we can use a two-dimensional domain.

• Delaunay Mesh Refinement A mesh triangulated with Delaunay’s triangulation algorithm with $10^5$ triangles, taken from the Galois project input massive.2 [24]. With this mesh, a graph is built where each node correspond to one triangle. We use the coordinates of the first vertex of the triangle as the label of the node, to use it with a two-dimensional domain.

• Graph labeling Disjoint graph with $3\times 10^6$ nodes and $8\times 10^6$ edges distributed on at least $10^4$ disconnected clusters, similar to those in [18]. In this graph, each node has a unique and consecutive ID in a one-dimensional domain.

• Spanning tree A regular grid with height 3000 and width 3000 grid points, where each node except the boundary nodes has 4 neighbors. The grid structure allows us to assign $x$ and $y$ coordinates to each node, therefore making it suitable for a two-dimensional domain.

  Fig. 12

  

  Speedups with respect to optimized serial versions

The parallel times were measured using the default behavior of generating two bottom-level subdomains per core used. Since the number of subdomains generated by our skeleton is a power of two, 32 subdomains were generated for the runs on 12 cores.

The minimal slowdown in Fig. 12 for a single processor shows that the overheads of the skeleton are very small. This was expected because the irregular access patterns characteristic of these algorithms, coupled with the small number of computations in most of these benchmarks, turn memory bandwidth and latency into the main factor limiting their performance.

The speedups achieved are very dependent on the processing performed by each algorithm. Namely, labeling and spanning, which do not modify the graph structure, are the benchmarks that scale better. Recall that labeling only modifies data (the color of each node), while spanning inspects the graph from some starting point just adding a single edge to the output graph whenever a new node is found. Delaunay refinement operates on a neighborhood of the graph removing and adding several nodes and edges, but it also performs several computations. Finally Boruvka is intensive on graph modifications, as it involves minimal computations, and it removes and adds an enormous number of nodes and, particularly, edges. This way the latter two algorithms suffer from more contention due to synchronizations required for the simultaneous deletions and additions of their parallel tasks on the shared graph. An additional problem is that parallelization worsens the performance limitations of these algorithms due to the memory bandwidth because of the increasing number of cores simultaneously accessing the memory. For these reasons, the speedups achieved are typical for such applications [23, 32].

Speedups are also very dependent on the degree of domain over-decomposition used. Figure 13 shows the relative speedup achieved using 8 cores with several levels of over-decomposition with respect to the execution without over-decomposition, that is, the one that generates a single bottom-level subdomain per core. In the figure, $n$ levels of over-decomposition imply $2^n$ subdomains per core. This way the results shown in Fig. 12 correspond to the first bar, with one level of over-decomposition. We can see that just by not over-decomposing the input domain, Delaunay refinement gets a very important performance boost, while spanning successfully exploits large levels of over-decomposition.

Fig. 13

Relative speedup with respect to no over-decomposition in runs with 8 cores. 100 is the baseline, that is, achieving 100 % of the speedup (i.e. the same speedup) obtained without overdecomposition

Figure 14 shows the percentage of elements that fall outside the domain, and therefore have to be deferred to upper levels of domain subdivision, also for runs with 8 cores. It is interesting to see that even when we are not using a small number of cores, and thus of subdivisions of the domain, the number of workitems aborted never exceeds $3\,\%$ in the worst case. These values help us explain the results in Fig. 13. Labeling has no conflicts because in its case the role of the domain is only to partition the tasks; when two tasks operate simultaneously on an area, the one with the smallest color will naturally prevail. So over-decomposition does not play any role with respect to conflicts in this algorithm; it only helps its load balancing. As for Delaunay refinement, even when only $3\,\%$ of its workitems result in conflicts, this ratio is proportionally much higher than for the other algorithms, and their individual cost is also larger. This way, although decreasing over-decomposition might reduce load balancing opportunities, this is completely offset by the important reduction in the number of conflicts. Spanning is the second algorithm in terms of conflicts, but two facts decrease their importance for this code. First, this algorithm begins with a single workitem from which the processing of neighboring domains are later spawned. This way if there is no over-decomposition some threads begin to work when the processing reaches their domains, and stop when their domain is completely processed. This leads to a very poor usage of the threads. Over-decomposing allows threads that finish with a given subdomain to begin working on new domains reached by the processing. The second fact is that delayed workitems because of conflicts often find that they require no additional processing when they are reconsidered in an upper level of subdivision because they were already connected to the spanning tree by their owner task at the bottom level. Finally, Boruvka has relatively few conflicts and their processing cost is neither negligible nor as large as in Delaunay refinement. Thus, a small degree of over-decomposition is the best in terms of balancing the amount of work among the threads, potentially more so for an increasing number of subdomains, and the number of conflicts, which also increase with the number of subdomains.

Fig. 14

Percentage of out-of-domain elements running with 8 cores and 16 bottom-level subdomains

6 Related Work

Since our strategy relies on partitioning the initial work to perform in chunks that can be mostly processed in parallel, our approach is related to the divide and conquer skeleton implemented in several libraries [8, 10, 15, 30]. Nevertheless, all the previous works of this kind we are aware of are oriented to regular problems. As a result those skeletons assume that the tasks generated are perfectly parallel, providing no mechanisms to detect conflicts or to deal with them once found. Neither do they support the dynamic generation of new items to be processed by the user provided tasks. This way, they are not well suited to deal with the irregular problems we are considering.

One of the approaches to deal with amorphous data parallel algorithms is Hardware or Software Transactional Memory  (HTM/STM) [19]. HTM limits, sometimes heavily, the maximum transaction size because of the hardware resources it relies on. The Blue Gene/Q was the first system to incorporate it, and although it is present in some Top500 supercomputers, its adoption is not widely spread. Several implementations exist for STM [16, 31], but their performance is often not satisfactory [5]. With STM, the operations on an irregular data structure are done inside transactions, so when a conflict is detected, such as overlapping neighborhoods for two nodes, it can be rolled back.

Another hardware option is Thread Level Speculation (TLS) [29], which from a sequential code creates several parallel threads, and enforces the fulfillment of the semantics of the source code using hardware support. But, just as the solutions based on transactional memory, it cannot take advantage of the knowledge about the data structure as ours does.

The Galois system [24] is a framework for this kind of algorithm that relies on user annotations that describe the properties of the operations. Its interface can be simplified though, if only cautious and unordered algorithms are considered. Galois has been enhanced with abstract domains [23], defined as a set of abstract processors optionally related to some topology, in contrast to our concept of set of values for a property of the items to process. Also, these domains are only an abstraction to distribute work, as opposed to our approach, where domains are the fundamental abstraction to distribute work, schedule tasks and detect conflicts, thus eliminating the need of locks and busy waits found in [23]. Neither do we need over-decomposition to provide enough parallelism, which allows for higher performance in algorithms with costly conflicts, as Delaunay refinement shows in Fig. 13. Finally, lock-based management leads conflicting operations in [23] to be repeatedly killed and retried until they get the locks of all the abstract processors they need. Nevertheless, the computations that extend outside the current domain in our system are just delayed to be retried with a larger subdomain. This way the number of attempts of a conflicting task is at most the number of levels of subdivision of the original domain. With the cautions that the input and implementation languages are not the same and that they stop at 4 cores, our library and Galois yield similar speedups for Delaunay in a comparable system [23].

Chorus [25] defines an approach for the parallelization of irregular applications based on object assemblies, which are dynamically defined local regions of shared data structures equipped with a short-lived, speculative thread of control. Chorus follows a bottom-up strategy that starts with individual elements, merging and splitting assemblies as needed. These assemblies have no relation to property domains and their evolution, i.e., when and with whom to merge or split, must be programmatically specified by the user. We use a top-down process based on an abstract property, and only a way to subdivide its domain and to check the ownership are needed. Also, the evolution of the domains is automated by our library and it is oblivious to the algorithm code. Moreover, Chorus is implemented as a language, while we propose a regular library in a widely used language, which eases the learning curve and enhances code reusability. Also, opposite to Chorus’ strategy, ours does not require locks, which favors scalability, and there are no idle processes, so the need for over-decomposition is reduced. Finally, and in part due to these differences, our approach performs noticeably better on the two applications tested in [25].

Partitioning has also been applied to an irregular application in [32]. Their partitioned code is manually written and it is specifically developed and tuned for the single application they study, Delaunay mesh generation. Additionally, their implementation uses transactional memory for synchronizations.

7 Conclusions

Amorphous data parallelism, found in algorithms that work on irregular data structures is much harder to exploit than the parallelism in regular codes. There are also few studies that try to bring structure and common concepts that ease the parallelization of these algorithms. In this paper we explore the concept of domain on the data to process as a way to partition work and avoid synchronization problems. In particular, our proposal relies on (1) domain subdivision as a way to partition work among tasks, on (2) domain membership, as a mechanism to avoid synchronization problems between tasks, and on (3) domain merging to join worksets of items whose processing failed within a given subdomain, in order to attempt their processing in the context of a larger domain.

An implementation of our approach based on a skeleton operation and a few classes with minimal interface requirements is also presented. An evaluation using several benchmarks indicates that our algorithm template allows to parallelize irregular problems with little programmer effort, providing speed-ups similar to those typically seen for these applications in the bibliography.

As for future work, we plan to enable providing more hints to the library to improve load balancing and performance. Relatedly, the usage of domains that rely on well-known graph partitioners [21, 28] for their splitting process is a promising approach to explore the generation of balanced tasks, particularly when the user lacks information on the structure of the input. Also, methods to backup data to be modified so that they can be restored later automatically by the library if the computation fails can be added in order to support non-cautious operations. Finally, making a version of the library suited to distributed memory systems would allow to process very large inputs. The library is available upon request.