The Characteristic Curves of Water

Abstract

In 1960, E. H. Brown defined a set of characteristic curves (also known as ideal curves) of pure fluids, along which some thermodynamic properties match those of an ideal gas. These curves are used for testing the extrapolation behaviour of equations of state. This work is revisited, and an elegant representation of the first-order characteristic curves as level curves of a master function is proposed. It is shown that Brown’s postulate—that these curves are unique and dome-shaped in a double-logarithmic p, T representation—may fail for fluids exhibiting a density anomaly. A careful study of the Amagat curve (Joule inversion curve) generated from the IAPWS-95 reference equation of state for water reveals the existence of an additional branch.

1 Introduction

In 2002, Wagner and Pruß published a reference equation of state which became known as the IAPWS-95 (International Association for the Properties of Water and Steam) equation [1]. This equation is a complicated multi-parameter function which is able to describe all experimental data for the thermodynamic properties of water up to 1000 MPa and 1273 K within their uncertainties. Later a simplified version of this equation became a part of the GERG (Groupe Européen de Recherches Gazières) equation of state for mixtures [2]. As water is used as a working fluid in most of the world’s thermal power plants, plays a major role in geology and meteorology, and is an important solvent or reactant in chemical industry, the importance of the IAPWS-95 equation cannot be underrated.¹

One of the many tests that the IAPWS-95 had to pass was the calculation of Brown’s characteristic curves (a.k.a. ideal curves). These are curves in the pressure–temperature plane along which one property of a real gas has the same value as that of an ideal gas. Brown defined a number of such curves [5] and proposed some rules about their shapes and arrangements. These rules were in part based on thermodynamic laws and physical insight, but to some extent also on experience.

Of course—in comparison to the present situation—Brown was working with a rather limited set of experimental data in 1960. But his rules were found to be good for nonpolar fluids, and therefore, the calculation of Brown’s characteristic curves is recommended for all new equations of state [6, 7].

This immediately leads to the questions whether Brown’s rules are applicable to a strongly polar and hydrogen-bonding fluid like water and—in particular—whether the IAPWS-95 reference equation of state obeys Brown’s rules.

2 Theory

2.1 The Characteristic Curves

The compression factor Z of an ideal gas is 1 for all temperatures T and molar volumes $V_\mathrm{m}$,

$$\begin{aligned} Z \equiv \frac{p V_\mathrm{m}}{R T} = 1. \end{aligned}$$

(1)

Moreover, for an ideal gas, the configurational internal energy U is zero for all volumes and temperatures. Therefore, all derivatives of Z or U with respect to temperature or pressure are zero, too.

For a real gas, Z usually deviates from 1, and the derivatives of Z usually have nonzero values. In his work “On the thermodynamic properties of fluids”, however, Brown [5] points out that, for each thermodynamic property, there are special states where it has the same value as in an ideal gas. For pure fluids, such states can be represented by curves in the p, T plane. Brown studied derivatives of the compression factor and defined a hierarchy of such curves, which are nowadays called Brown’s ideal curves or characteristic curves. In this work, the so-called first-order curves are of particular interest, i.e., curves along which a first-order derivative of Z vanishes.² There are three such curves:

• 1. The Amagat curve, also called Joule inversion curve. Its mathematical condition is any one of the following:

  $$\begin{aligned} \left( \frac{\partial Z}{\partial T} \right) _{V} = 0,\quad \left( \frac{\partial Z}{\partial p} \right) _{V} = 0,\quad \pi _T \equiv \left( \frac{\partial U}{\partial V} \right) _{T} = 0,\quad \left( \frac{\partial p}{\partial T} \right) _{V} = \frac{p}{T}. \end{aligned}$$

  (2)

  $\pi _T$, the so-called internal pressure, is usually negative, i.e., an isothermal compression lowers the internal energy. At very high pressures or temperatures, however, the molecules are driven into the repulsive branches of their interaction potentials, and then a compression increases the internal energy. At the Joule inversion point, the configurational internal energy is independent of density. The Amagat curve starts at high temperatures and zero pressure at the temperature $T_\mathrm{A}$ for which the second virial coefficient $B_2$ has its maximum, hence

  $$\begin{aligned} B_2^\prime (T_\mathrm{A}) = 0, \end{aligned}$$

  (3)

  where the prime indicates a differentiation with respect to temperature. The terminal slope at this endpoint is³

  $$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}T}\Big \vert _{T \rightarrow T_\mathrm{A}} = \frac{B_2^\prime (T_\mathrm{A}) R T_\mathrm{A}}{B_3(T_\mathrm{A})}. \end{aligned}$$

  (4)

  From there it passes through a pressure maximum to lower temperatures, until it ends (in a p, T projection) on the vapour pressure curve. For most substances, however, this endpoint is not accessible because crystallization sets in before the endpoint can be attained. The maximum of the Amagat curve lies at very high pressures, typically 50–100 times the critical pressure. For water, the maximum is expected around 2.6 GPa. This is a rather high value, beyond the scope of present technical applications, but within range of experiments, and certainly of geological interest.

• 2. The Boyle curve, which is defined by one of

  $$\begin{aligned} \left( \frac{\partial Z}{\partial V} \right) _{T} = 0,\quad \left( \frac{\partial Z}{\partial p} \right) _{T} = 0,\quad \left( \frac{\partial p}{\partial V} \right) _{T} = -\frac{p}{V}. \end{aligned}$$

  (5)

  This curve originates on the temperatures axis at the Boyle temperature $T_\mathrm{B}$, i.e., at the temperature for which

  $$\begin{aligned} B_2(T_\mathrm{B}) = 0. \end{aligned}$$

  (6)

  Its terminal slope is$^3$

  $$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}T}\Big \vert _{T \rightarrow T_\mathrm{B}} = \frac{B_2^\prime (T_\mathrm{B}) R T_\mathrm{B}}{2 B_3(T_\mathrm{B})}. \end{aligned}$$

  (7)

  From there the curve passes through a pressure maximum and ends on the vapour pressure curve⁴ near to the critical point.

• 3. The Charles curve, also known as Joule–Thomson inversion curve. It is defined by any one of

  $$\begin{aligned} \left( \frac{\partial Z}{\partial T} \right) _{p} = 0 ,\ \left( \frac{\partial Z}{\partial V} \right) _{p} = 0 ,\ \left( \frac{\partial H}{\partial p} \right) _{T} = 0 ,\ \left( \frac{\partial V}{\partial T} \right) _{p} = \frac{V}{T} ,\ \left( \frac{\partial T}{\partial p} \right) _{H} = 0 . \end{aligned}$$

  (8)

  The Charles curve starts on the temperature axis at the temperature at which the slope of the second virial coefficient matches that of the secant,

  $$\begin{aligned} B_2^\prime (T_\mathrm{C}) = \frac{B_2(T_\mathrm{C})}{T_\mathrm{C}}; \end{aligned}$$

  (9)

  the terminal slope is$^3$

  $$\begin{aligned} \frac{\mathrm{d}p}{\mathrm{d}T} \Big \vert _{T \rightarrow T_\mathrm{C}} = - \frac{B_2^{\prime \prime }(T_\mathrm{C}) R T_\mathrm{C}}{B_3^\prime (T_\mathrm{C}) - \frac{2}{T_\mathrm{C}} B_3(T_\mathrm{C})}. \end{aligned}$$

  (10)

  Like the Amagat and Boyle curves, it runs through a pressure maximum to lower temperatures and ends on the vapour pressure curve. The Charles curve marks the transition from cooling to heating upon isenthalpic throttling [8].

For completeness’ sake we mention the Zeno curve, the zeroth-order characteristic curve, which is the locus of the states obeying $Z = 1$. It originates at high temperatures at the same point as the Boyle curve. From there it runs to lower temperatures above the Boyle curve and intersects the Charles and the Amagat curves.

In his article, Brown formulates some postulates about the behaviour of the first-order characteristic curves:

Fig. 1

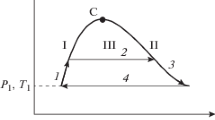
Overview of Brown’s first-order characteristic curves for the IAPWS-95 equation of state.

: Amagat curve,

: Boyle curve,

: Charles curve, grey: vapour pressure curve, $\circ$: critical point,

: melting pressure curves, $\triangle$: triple points. The equation of state is not valid for metastable states beyond the melting pressure curves

• There is exactly one Amagat, Boyle, and Charles curve.

• The Amagat, Boyle, and Charles curves must not cross, but surround each other (Boyle inside Charles inside Amagat), as can be seen in Fig. 1, which shows these curves for the IAPWS-95 equation of state for water.

• In a double-logarithmic diagram, the Amagat, Boyle, and Charles curves have negative curvatures everywhere (i.e., they are dome-shaped, with a single maximum and no inflection points), and their slopes tend to infinity for low pressures.

2.2 Response Functions

Of considerable practical interest are various thermodynamic response functions, which describe how a property changes when some other property is varied. Basic second-order thermodynamic response functions are the isochoric and isobaric heat capacities, which for a pure system are defined by

$$\begin{aligned} C_V \equiv \left( \frac{\partial U}{\partial T} \right) _{V} = T \left( \frac{\partial S}{\partial T} \right) _{V} \quad \text {and} \quad C_p \equiv \left( \frac{\partial H}{\partial T} \right) _{p} = T \left( \frac{\partial S}{\partial T} \right) _{p}, \end{aligned}$$

(11)

the isobaric thermal expansivity,

$$\begin{aligned} \alpha _p \equiv \frac{1}{V} \left( \frac{\partial V}{\partial T} \right) _{p}, \end{aligned}$$

(12)

and the isothermal compressibility,

$$\begin{aligned} \kappa _T \equiv -\frac{1}{V}\left( \frac{\partial V}{\partial p} \right) _{T}. \end{aligned}$$

(13)

For the study of Brown’s characteristic curves, it is advantageous to define dimensionless response functions (n: amount of substance):

$$\begin{aligned} c_V \equiv \frac{C_V}{n R}, \quad c_p \equiv \frac{C_p}{n R}, \quad c_T \equiv T \alpha _p. \end{aligned}$$

(14)

Because of the well-known thermodynamic relation

$$\begin{aligned} C_p = C_V + \frac{V T \alpha _p^2}{\kappa _T}, \end{aligned}$$

the isothermal compressibility can be expressed by

$$\begin{aligned} \kappa _T = \frac{Z}{p c_\kappa } \quad \text {with} \quad c_\kappa \equiv \frac{c_p - c_V}{c_T^2} \ge 0, \end{aligned}$$

(15)

where $c_\kappa$ denotes another dimensionless response function. The inequality in Eq. 15 follows from thermodynamic stability.

2.3 Derivatives of the Compression Factor

To compute the derivatives of Z appearing in the definitions of the Amagat, Boyle, and Charles curves, Eqs. 2–8, we define some dimensionless logarithmic slopes, namely the dimensionless isochoric slope

$$\begin{aligned} q_\mathrm{A}\equiv \left( \frac{\partial \ln p}{\partial \ln T} \right) _{V} = \frac{T}{p} \left( \frac{\partial p}{\partial T} \right) _{V} = \frac{c_\kappa c_T}{Z}, \end{aligned}$$

(16)

the dimensionless bulk modulus

$$\begin{aligned} q_\mathrm{B}\equiv \left( \frac{\partial \ln p}{\partial \ln V} \right) _{T} = -\frac{V}{p} \left( \frac{\partial p}{\partial V} \right) _{T} = \frac{c_\kappa }{Z}, \end{aligned}$$

(17)

and the dimensionless thermal susceptibility

$$\begin{aligned} q_\mathrm{C} \equiv \left( \frac{\partial \ln V}{\partial \ln T} \right) _{p} = \frac{T}{V} \left( \frac{\partial V}{\partial T} \right) _{p} = c_T = \frac{q_\mathrm{A}}{q_\mathrm{B}}. \end{aligned}$$

(18)

Then the Z derivatives become

$$\begin{aligned} \mathcal {A}_1:\; +T \left( \frac{\partial Z}{\partial T} \right) _{V}= & {} c_\kappa c_T - Z = Z (q_\mathrm{A}- 1),\nonumber \\ \mathcal {A}_2:\; -p \left( \frac{\partial Z}{\partial p} \right) _{V}= & {} Z\left( \frac{Z}{c_\kappa c_T} - 1 \right) = Z \frac{1 - q_\mathrm{A}}{q_\mathrm{B}},\nonumber \\ \mathcal {B}_1:\; -p \left( \frac{\partial Z}{\partial p} \right) _{T}= & {} Z\left( \frac{Z}{c_\kappa } - 1 \right) = Z \frac{1 - q_\mathrm{B}}{q_\mathrm{B}},\nonumber \\ \mathcal {B}_2:\; +V \left( \frac{\partial Z}{\partial V} \right) _{T}= & {} Z - c_\kappa = Z (1 - q_\mathrm{B}),\nonumber \\ \mathcal {C}_1:\; +T \left( \frac{\partial Z}{\partial T} \right) _{p}= & {} Z (c_T - 1) = Z \frac{q_\mathrm{B}- q_\mathrm{A}}{q_\mathrm{B}} = Z(1 - q_\mathrm{C}),\\\mathcal {C}_2:\; +V \left( \frac{\partial Z}{\partial V} \right) _{p}= & {} Z\left( 1 - \frac{1}{c_T} \right) = Z \frac{q_\mathrm{A}- q_\mathrm{B}}{q_\mathrm{A}} = Z\left( 1 - \frac{1}{q_\mathrm{C}} \right) . \end{aligned}$$

(19)

Details of the derivations are given in Appendix 1.

In the following, we consider the compression factor as a function Z(p, T) of temperature and pressure, continuous except along the coexistence curve, where one gets different limits $Z^\mathrm{l}$ and $Z^\mathrm{g}$ when one approaches it from the liquid or the vapour side, respectively.

The limiting behaviour of thermodynamic quantities as temperature or pressure tends to zero or infinity is known from statistical mechanics and summarized in Table 1:

• At low densities the behaviour of a fluid is described by the virial equation of state,

  $$\begin{aligned} Z(\rho ,T) = 1 + B_2(T) \rho + O\big ( \rho ^2 \big ), \end{aligned}$$

  (20)

  where $\rho = V_\mathrm{m}^{-1}$ denotes the molar density. $B_2(T)$, the second virial coefficient, can be computed from the intermolecular pair potential. In particular, for realistic pair potentials, i.e., potential functions not having a rigid core, the limit $\lim _{T \rightarrow \infty } B_2(T) = 0$ is approached from above. Substitution of Eq. 20 into Eqs. 16–18 immediately yields the low-density limits of the $q_X$:

  $$\begin{aligned} \lim _{\rho \rightarrow 0} q_\mathrm{A}= & {} 1 + \frac{\mathrm{d}(T B_2)}{\mathrm{d}T} \rho ,\nonumber \\ \lim _{\rho \rightarrow 0} q_\mathrm{B}= & {} 1 + B_2 \rho ,\nonumber \\ \lim _{\rho \rightarrow 0} q_\mathrm{C}= & {} 1 + T \frac{\mathrm{d}B_2}{\mathrm{d}T} \rho . \end{aligned}$$

  (21)

  As a consequence, Z, $q_\mathrm{A}$, $q_\mathrm{B}$, and $q_\mathrm{C}$ all approach 1 for $\rho \rightarrow 0$.

• The high-density behaviour of matter is governed by formulas derived from the so-called quantum-statistical model, an extension of the Thomas–Fermi theory.⁵ This model [9] was used to derive the entries for $p \rightarrow \infty$ as well as $T \rightarrow 0$ in Table 1. The low-pressure, high-density behaviour is derived from the Vinet equation [10], which has been reported to work very well for solids [9].

Table 1 Limiting values of the compression factor and related quantities

Figure 2 represents, in nonlinearly transformed $q_\mathrm{A},q_\mathrm{B}$ coordinates, the IAWPS-95 reference equation of 1995 for water [1]. That the 270 K isotherm is curved to the left is a consequence of the density anomaly of water.

Fig. 2

Isolines of pressure and temperature in the $q_\mathrm{A}, q_\mathrm{B}$ plane, computed for the IAPWS-95 equation of state [1].

: isobars 1–100 MPa,

: isotherms 270–600 K isotherms,

: connodes, red: boundary of the vapour–liquid 2-phase region, blue: Amagat (A), Boyle (B), and Charles (C) curves. The nonlinearly transformed coordinates $f(q_X) = q_X/(10 + \vert q_X \vert ), X = A, B$ were chosen to make details discernible (Color figure online)

2.4 First-Order Characteristic Curves

A comparison of the definitions of Brown’s first-order characteristic curves, Eqs. 2–8, with Eqs. 16–18 immediately shows that these curves can be characterized by

$$\begin{aligned} q_\mathrm{A}= & {} 1 \quad \text {Amagat curve},\\q_\mathrm{B}= & {} 1 \quad \text {Boyle curve},\\q_\mathrm{A}= & {} q_\mathrm{B}\quad \text {Charles curve}. \end{aligned}$$

(22)

Therefore, these three characteristic curves are level curves of the thermodynamic variable

$$\begin{aligned} q_\mathrm{R} \equiv \frac{1 - q_\mathrm{B}}{q_\mathrm{A}+ 2 q_\mathrm{B}- 1} = {\left\{ \begin{array}{ll} -2 &{} \text {in the Thomas--Fermi limit},\\ -\frac{1}{2} &{} \text {along the Amagat curve},\\ -\frac{1}{3} &{} \text {along the Charles curve},\\ \pm 0 &{} \text {along the Boyle curve}. \end{array}\right. } \end{aligned}$$

(23)

The value $q_\mathrm{R} = -2$ comes from the Thomas–Fermi theory, which gives $q_\mathrm{A}\rightarrow 0$ and $q_\mathrm{B} \rightarrow \frac{5}{3}$ in the high-density limit; this limit is not attainable. The level curves $q_\mathrm{R} = \mathrm{const}$ therefore interpolate continuously between the characteristic curves, which explains their onion ring-like arrangement.

Fig. 3

$q_\mathrm{R}$ as a function of pressure and temperature for water (IAPWS-95 equation of state). The level curves for $q_\mathrm{R} = -\frac{1}{2}$, $-\frac{1}{3}$, and 0 define the Amagat curve, Charles curve, and Boyle curve, respectively. The frayed portion at the left side of the graph corresponds to the vapour–liquid two-phase region, where the equation of state is undefined

A double-logarithmic plot of $q_\mathrm{R}$ for water, based on the IAPWS reference equation of state, as a function of p and T is given in Fig. 3, exhibiting the typical shape of the characteristic curves. (The bottom left part is in the metastable domain, where the IAWPS-95 equation is not reliable.).

For water, the minimal value of $q_\mathrm{R}$ attained (for p = 2000 MPa, the maximal value of the pressure tried here, which exceeds the range of validity of the equation of state) was found to be approximately −0.5982; the maximal value attained (for $p = 0$ and T slightly below the critical temperature) is about 1.0333; the value at the critical point is about 0.23694 .

Since—except at critical points—$q_\mathrm{A}$ and $q_\mathrm{B}$ depend continuously on T and p, the existence of all three characteristic curves follows from the inequalities⁶

$$\begin{aligned} q_\mathrm{A}<&1 <q_\mathrm{B}\quad \text {if } p \text { is large or } T \text { is small},\nonumber \\ q_\mathrm{A}>&1 >q_\mathrm{B}\quad \text {close to the critical point}, \end{aligned}$$

or equivalently

$$\begin{aligned} c_T<&\frac{Z}{c_\kappa } <1 \quad \text {if } p \text { is large or } T \text { is small},\\c_T>&\frac{Z}{c_\kappa } >1 \quad \text {close to the critical point}. \end{aligned}$$

(24)

By the discussion in Section 2.3, this is satisfied for real fluids; cf. Table 1.

The characteristic curves are nonintersecting⁷ because their $q_\mathrm{R}$ values differ, and have a characteristic shape. Because of Eq. 24, it is easy to see that at the critical temperature all three curves must lie above the critical point and surround it. These properties are probably shared by all level curves $q_\mathrm{R} = \mathrm{const} \ge 0$.

It is suggested in [7] that, in a double-logarithmic plot, the characteristic curves should have a unique maximum and no inflection points. The only argument for this (given in the appendix of [6]) seems to be based on the corresponding-states principle and hence has little force.

Under Brown’s assumptions,

$$\begin{aligned} c_T >0 \end{aligned}$$

(25)

must hold in a fluid phase, for then—and only then—the criteria $\mathcal {A}_1$ and $\mathcal {A}_2$ as well as $\mathcal {C}_1$ and $\mathcal {C}_2$ in Eq. 19 are equivalent.

2.5 The Amagat Curve of Water at Low Temperatures

$c_T \le 0$, however, might cause a second Amagat and a second Charles curve, for a change of sign of $c_T$ causes a change of sign of $\mathcal {A}_2$ and $\mathcal {C}_2$, as will be discussed in a moment.

Moreover, a negative $c_T$ has implications for the behaviour of pressure isotherms. Indeed, two isotherms, with temperatures $T_1$ and $T_2$ cross if there is a density $\rho$ such that $p(\rho , T_1) = p(\rho , T_2)$. Because of the mean value theorem, this implies the existence of an intermediate temperature T for which

$$\begin{aligned} \frac{\mathrm{d}p(\rho , T)}{\mathrm{d}T} = \left( \frac{\partial p}{\partial T} \right) _{V_\mathrm{m}} = \frac{R c_T c_\kappa }{V_\mathrm{m}} \end{aligned}$$

vanishes. Since $\kappa _T \ge 0$ by Eq. 15, crossing isotherms appear in regions where $c_T$ and hence the thermal expansivity $\alpha _p = c_T / T$ change their sign. Because of Inequality (25), this would be impossible in a fluid phase under Brown’s assumptions. The experimentally observed density anomaly of water, however, results in a negative thermal expansivity for $T<$ 3.983 $^\circ$C at atmospheric pressure. As a result, the Amagat line of water, which enters the metastable⁸ region at low temperatures and a pressure of about 1100 MPa, becomes stable again at about 390 MPa and then remains stable down to zero pressure, as shown in Fig. 4.

Fig. 4

Amagat curves of water.

: IAPWS-95 equation of state,

: equation of state of Holten et al.,

: melting pressure curve, $\triangle$: triple point; grey area: region of negative $\alpha _p$, grey curve: poles of $\alpha _p$,

: inflection points of $U_\mathrm{m}(V_\mathrm{m})$ (the latter three calculated for the IAPWS-95 equation). It should be noted that the IAPWS-95 equation is not valid in the metastable region beyond the melting pressure curves. (a) Overview: double-logarithmic representation. (b) Detail: low-temperature range. (c) Detail: high-temperature range

A closer study of the low-temperature, high-pressure region reveals two peculiarities: Close to the endpoint, the Amagat curve has a negative slope in p, T coordinates. In the double-logarithmic representation, this curve must therefore have an inflection point. This is at variance with Brown’s postulates.

The other peculiarity is the existence of a second Amagat curve (Fig. 4), which is metastable with respect to crystallization. One might be tempted to write it off as an artifact of the IAPWS-95 equation, but the matter is more complicated:

Fig. 5

Schematic representation of an expansion from very high pressure towards the critical region.

: Amagat condition ($q_\mathrm{A}= 1$),

: Boyle condition ($q_\mathrm{B}= 1$),

: Charles condition ($q_\mathrm{A}= q_\mathrm{B}$), $\circ$: critical point, $\bullet$: Thomas–Fermi limit ($T \rightarrow 0$, $p \rightarrow \infty$. The high-temperature endpoints of the characteristic curves are in the vicinity of the intersection point ($q_\mathrm{A}= q_\mathrm{B}= 1$), the low-temperature endpoints at high $q_\mathrm{A}$ or $q_\mathrm{B}$ values. 1-2-3-4: expansion path of a normal fluid, 1’: possible starting point of a fluid exhibiting a density anomaly

To explain this phenomenon we consider Fig. 5: In this diagram, the Amagat, Boyle, and Charles conditions correspond to a vertical, horizontal, and diagonal line, respectively. The crossing point of these lines is a hypothetical state of infinite temperature and low pressure. The high-temperature endpoints of the characteristic curves lie in its vicinity; the low-temperature endpoints lie “outward”, at high $q_\mathrm{A}$ or $q_\mathrm{B}$ values. The indicated path 1$\rightarrow 2\rightarrow 3\rightarrow 4$ represents an isothermal expansion starting at a very high pressure. This path necessary crosses the Amagat, Charles, and Boyle lines—in this sequence and exactly once, as postulated by Brown.

For a fluid exhibiting a density anomaly, however, the initial state may lie at $q_\mathrm{A}<0$ (state 1’ in the diagram). From here, an alternative expansion path is possible that intersects the Charles and then the Amagat line, and thus gives rise to a second Charles and Amagat curve in a p, T diagram, respectively.

As a check, we looked at the equation of state of Holten et al. [11], which describes the low-temperature and supercooled regions, particularly the solid–liquid equilibria of water. This equation predicts a second Amagat curve, too. But here the arrangement of the curve branches is different. A comparison of the Amagat curves obtained for the IAPWS-95 equation and that of Holten et al. suggests that, in a continuous deformation connecting the two thermodynamic descriptions, a bifurcation occurs between these two equations at which the Amagat curves exchange branches.

It is conceivable, of course, that both the IAPWS-95 equation and that of Holten et al. suffer from artifacts But if this is the case, they do so because there is sensitive spot in the p, T plane, and there may be a physical explanation for this sensitivity. This is corroborated by the observation that the portion of the IAPWS-95 Amagat curve running from the high-temperature endpoint to the temperature minimum at about 258.2 K and 255 MPa is a locus of minima of $U_\mathrm{m}(V_\mathrm{m})$, whereas the portion from there to the endpoint at about 277 K is a locus of maxima. Evidently, there is a curve of inflection points of $U_\mathrm{m}(V_\mathrm{m})$ lying between the two Amagat curve branches.

The shaded regions in Fig. 4a and b indicate the region of the density anomaly ($\alpha _p <0$). Where its border is close to an Amagat curve, this curve is a locus of maxima. Thus, the secondary Amagat curve that the IAPWS-95 equation predicts is also a locus of maxima. Below 660 MPa, the border is a locus of points for which $\alpha _p = 0$ holds; above that pressure, the border is a locus of poles. The transition point appears to be the origin of the secondary Amagat curve.

This shows that the behaviour of the Amagat curve(s) at low temperatures is linked to the sign of $\alpha _p$. Evidently, Brown’s postulates do not fully apply to fluids exhibiting a density anomaly.

2.6 The Amagat Curve of Water at High Temperatures

At the high-temperature endpoint, the Amagat curve obtained with the IAPWS-95 equation exhibits a positive slope, again in contradiction to Brown’s postulates. The positive slope implies that the third virial coefficient of water increases with temperature (cf.2). For nonpolar fluids, $B_3$ is usually negative at low temperatures, passes through a (positive) maximum below the critical temperature, and then declines towards zero. For polar fluids the maximum is less pronounced [12]; for water, the maximum is very shallow, as can be seen in Fig. 6. Unfortunately, the experimental datasets for water do not agree very well, reliable experimental data are scarce beyond 800 K, and none appear to exist beyond 1200 K. But even so, experiments and theoretical calculations based on polarizable interaction potentials all agree that the maximum occurs in the range of 550 K to 900 K [13–15]. Beyond this maximum, the slope of $B_3$ is negative, and hence the terminal slope of the Amagat curve must be negative, too. Therefore, the positive terminal slope derived from the IAPWS-95 equation is probably an artifact.

Fig. 6

The third virial coefficient $B_3$ of water as a function of reciprocal temperature. $\circ$: computed from the GCPM water interaction potential [13],

: spline interpolation through these points with the restriction that $B_3$ and $B_3^\prime$ must vanish for $T \rightarrow \infty$, $\square$: computed from the potential of Góra et al. [15]; filled symbols: experimental data: $\blacktriangledown$: Vukalovich et al. [17], $\blacktriangle$: Kell et al. [18], and $\bullet$: Abdulagatov et al. [19]

In fact, a close inspection of the third virial coefficient function obtained from the IAPWS-95 equation in Fig. 6 shows that there is a shallow minimum around 1400 K and a maximum above 7000 K; the function declines to zero monotonously beyond that maximum. It must be pointed out, however, that this unphysical behaviour of the IAPWS-95 equation is of little importance, for this equation is claimed to be valid up to 1273 K only. Moreover, at 5000 K, water would undergo decomposition to a significant extent. But as in practical applications equations of state are often used beyond their limits of validity, it is important to know about this problem of the IAPWS-95 equation.

3 Conclusion

In this work, a novel formulation of Brown’s first-order characteristic curves is proposed, in which these curves are obtained as level functions of a master function $q_\mathrm{R} = \mathrm{const}$. As already observed by Brown, the Amagat curve surrounds the Charles curve in a double-logarithmic p, T diagram, and the Charles curve surrounds the Boyle curve.

Brown postulated that these curves are unique and dome-shaped, with a single pressure maximum and no inflection points. We show here, and we verify it at the example of water, that for fluids exhibiting a density anomaly the Amagat and Charles curves may have more than one branch. For such fluids it is possible to have a vanishing thermal expansivity, $\alpha _p = 0$, as well as $p(\rho )$ isotherm crossing.

For water, the initial slope of the Amagat curve (i.e., the slope at low pressures and at low temperatures) is negative, which is in conflict with Brown’s postulates. The terminal slope at high temperatures is positive, again in conflict with Brown’s postulates, but there it can be shown that, most likely, the IAPWS-95 equation of state is at fault and cannot be extrapolated⁹ to 5000 K.

We conclude that Brown’s analysis of the characteristic curves, particularly of the Amagat curve, is qualitatively correct for fluids having $\alpha _p >0$ for all stable thermodynamic states. Caution is advised when the characteristic curves are computed for fluids exhibiting a density anomaly.

Appendices

Appendix 1: Thermodynamic Derivatives

All derivatives are computed at constant amount of substance n.

isochoric tension coefficient:

$$\begin{aligned} \beta _V \equiv \left( \frac{\partial p}{\partial T} \right) _{V} = -\left( \frac{\partial p}{\partial V} \right) _{T} \left( \frac{\partial V}{\partial T} \right) _{P} = \frac{\alpha _p}{\kappa _T}. \end{aligned}$$

(26)

derivatives appearing in Eq. 19:

$$\begin{aligned} \left( \frac{\partial Z}{\partial T} \right) _{V}= & {} \frac{V}{n R T} \left( \frac{\partial p}{\partial T} \right) _{V} - \frac{p V}{n R T^2} = \frac{Z \alpha _p}{p \kappa _T} - \frac{Z}{T} = \frac{c_\kappa c_T - Z}{T},\nonumber \\ \left( \frac{\partial Z}{\partial p} \right) _{V}= & {} -\frac{p V}{n R T^2} \left( \frac{\partial T}{\partial p} \right) _{V} + \frac{V}{n R T} = \frac{Z}{p} \left( 1 - \frac{p \kappa _T}{T \alpha _p} \right) = \frac{Z}{p} \left( 1 - \frac{Z}{c_\kappa c_T} \right) ,\nonumber \\ \left( \frac{\partial Z}{\partial p} \right) _{T}= & {} \frac{p}{n R T} \left( \frac{\partial V}{\partial p} \right) _{T} + \frac{V}{n R T} = \frac{Z}{p} (1 - p \kappa _T) = \frac{Z}{p} \left( 1 - \frac{Z}{c_\kappa } \right) ,\nonumber \\ \left( \frac{\partial Z}{\partial V} \right) _{T}= & {} \frac{V}{n R T} \left( \frac{\partial p}{\partial V} \right) _{T} + \frac{p}{n R T} = \frac{p - \kappa _T^{-1}}{n R T} = \frac{Z - c_\kappa }{V},\nonumber \\ \left( \frac{\partial Z}{\partial T} \right) _{p}= & {} \frac{p}{n R T} \left( \frac{\partial V}{\partial T} \right) _{p} - \frac{p V}{n R T^2} = Z \alpha _p - \frac{Z}{T} = \frac{Z}{T} (c_T - 1),\nonumber \\ \left( \frac{\partial Z}{\partial V} \right) _{p}= & {} -\frac{p V}{n R T^2} \left( \frac{\partial T}{\partial V} \right) _{p} + \frac{p}{n R T} = \frac{Z}{V} \left( 1 - \frac{1}{T \alpha _p} \right) = \frac{Z}{V} \left( 1 - \frac{1}{c_T} \right) .\nonumber \\ \end{aligned}$$

(27)

Appendix 2: The Terminal Slopes of the Characteristic Curves at High Temperatures

Schaber presents expressions for the terminal slopes of Brown’s characteristic curves in his thesis [16], but does not give the proofs. For the readers’ convenience, these proofs are offered here.

For small pressures and large molar volumes the fluid can be described with a 3-term virial equation (cf. Eq. 20),

$$\begin{aligned} Z = 1 + \frac{B_2(T)}{V_\mathrm{m}} + \frac{B_3(T)}{V_\mathrm{m}^2}. \end{aligned}$$

(28)

The molar volume as a function of pressure is then, neglecting higher-order terms,

$$\begin{aligned} V_\mathrm{m}\approx \frac{R T}{p} + B_2(T) + \frac{p B_3(T)}{R T}. \end{aligned}$$

(29)

1.1 (a) The Terminal Slope of the Amagat Curve

Applying the first one of the Amagat criteria in Eq. 2 to the virial equation yields

$$\begin{aligned} \left( \frac{\partial Z}{\partial T} \right) _{V_\mathrm{m}} = \frac{B_2^\prime (T)}{V_\mathrm{m}} + \frac{B_3^\prime (T)}{V_\mathrm{m}^2} = 0 \end{aligned}$$

or

$$\begin{aligned} B_2^\prime (T) + \frac{B_3^\prime (T)}{V_\mathrm{m}} = 0. \end{aligned}$$

(30)

In the limit $p \rightarrow 0$, $V_\mathrm{m}\rightarrow \infty$ the second term can be neglected, and therefore $B_2^\prime (T) = 0$ is the criterion for the endpoint of the Amagat curve, which corresponds to a maximum of the second virial coefficient.

Let $T_\mathrm{A}$ denote the temperature of this endpoint, and $\Delta T = T - T_\mathrm{A}$ and $\Delta p = p$ the temperature and pressure deviations, respectively, from this point. Then, in the vicinity of $T_\mathrm{A}$, $B_2^\prime (T)$ can be approximated by

$$\begin{aligned} B_2^\prime (T) \approx B_2^{\prime \prime }(T_\mathrm{A}) \Delta T , \end{aligned}$$

where $B_2^{\prime \prime }(T_\mathrm{A})$ denotes the curvature of the second virial coefficient function at the Amagat endpoint. Substituting this into Eq. 30 and switching from molar volume to pressure yields

$$\begin{aligned} B_2^{\prime \prime }(T_\mathrm{A}) \Delta T + \frac{B_3^\prime (T)}{\frac{R T}{\Delta p} + B_2 + \ldots } = 0 \end{aligned}$$

and, after some rearrangements,

$$\begin{aligned} \frac{\Delta p}{\Delta T} = - \frac{B_2^{\prime \prime }(T_\mathrm{A})}{B_3^\prime (T)} \left( R T + \Delta p B_2(T) + \ldots \right) . \end{aligned}$$

In the limit $\Delta p \rightarrow 0, T \rightarrow T_\mathrm{A}$ this reduces to

$$\begin{aligned} \lim _{T \rightarrow T_\mathrm{A}} \frac{\mathrm{d}p}{\mathrm{d}T} \Big \vert _{q_\mathrm{R} = -\frac{1}{2}} = -\frac{B_2^{\prime \prime }(T_\mathrm{A}) R T_\mathrm{A}}{B_3^\prime (T_\mathrm{A})}. \end{aligned}$$

(31)

1.2 (b) The Terminal Slope of the Boyle Curve

Applying the criterion Eq. 5 to the virial equation gives

$$\begin{aligned} \left( \frac{\partial Z}{\partial V_\mathrm{m}} \right) _{T} = - \frac{B_2(T)}{V_\mathrm{m}^2} - \frac{2 B_3(T)}{V_\mathrm{m}^3} = 0 \end{aligned}$$

and hence

$$\begin{aligned} B_2(T) + \frac{2 B_3(T) p}{R T + B_2(T) p + \ldots } = 0. \end{aligned}$$

(32)

In the limit $p \rightarrow 0$, this reduces to $B_2 = 0$: At the endpoint of the Boyle curve, at the Boyle temperature $T_\mathrm{B}$, the second virial coefficient vanishes.

Again using deviation variables, we can write the previous equation as

$$\begin{aligned} B_2^\prime (T_\mathrm{B}) \Delta T + \frac{2 B_3(T) \Delta p}{R T + \Delta p B_2(T) + \ldots } = 0. \end{aligned}$$

or

$$\begin{aligned} \frac{\Delta p}{\Delta T} = -\frac{B_2^\prime (T_\mathrm{B})}{2 B_3(T)} \left( R T + \Delta p B_2(T) + \ldots \right) . \end{aligned}$$

In the limit $\Delta p \rightarrow 0, T \rightarrow T_\mathrm{B}$ this reduces to

$$\begin{aligned} \lim _{T \rightarrow T_\mathrm{B}} \frac{\mathrm{d}p}{\mathrm{d}T} \Big \vert _{q_\mathrm{R} = 0} = -\frac{B_2^\prime (T_\mathrm{B}) R T_\mathrm{B}}{2 B_3(T_\mathrm{B})}. \end{aligned}$$

(33)

1.3 (c) The Terminal Slope of the Charles Curve

For the derivation of this property, it is advantageous to start from the pressure-based virial equation of state,

$$\begin{aligned} Z = 1 + \bar{B}_2(T) p + \bar{B}_3(T) + p^2. \end{aligned}$$

(34)

The pressure-based virial coefficients are related to the volume-based ones by

$$\begin{aligned} \bar{B}_2(T) = \frac{B_2(T)}{R T} \quad \text {and} \quad \bar{B}_3(T) = \frac{B_3(T) - B_2^2(T)}{(R T)^2}. \end{aligned}$$

(35)

Applying the appropriate criterion in Eq. 8 gives

$$\begin{aligned} \left( \frac{\partial Z}{\partial T} \right) _{p} = \frac{p}{R T}\left( B_2^\prime (T) - \frac{B(T)}{T} \right) + \left( \frac{p}{R T} \right) ^2 \left( B_3^\prime (T) - \frac{2 B_3(T)}{T} - 2 B_2(T) B_2^\prime (T) + \frac{2 B_2^2(T)}{T} \right) = 0. \end{aligned}$$

or

$$\begin{aligned} B_2^\prime (T) - \frac{B_2(T)}{T} + \frac{p}{R T} \left( B_3^\prime (T) - \frac{2 B_3(T)}{T} - 2 B_2(T) B_2^\prime (T) + \frac{2 B_2^2(T)}{T} \right) = 0. \end{aligned}$$

(36)

The endpoint, at $p \rightarrow 0$, is evidently characterized by $B_2^\prime (T) - B_2(T)/T = 0$.

In order to obtain the terminal slope, we expand this criterion around the endpoint temperature $T_\mathrm{C}$,

$$\begin{aligned} B_2^\prime (T) - \frac{B_2(T)}{T} \approx \left( B_2^{\prime \prime }(T_\mathrm{C}) - \frac{B_2^\prime (T_\mathrm{C})}{T_\mathrm{C}} + \frac{B_2(T_\mathrm{C})}{T_\mathrm{C}^2} \right) \Delta T = B_2^{\prime \prime }(T_\mathrm{C}) \Delta T. \end{aligned}$$

Then Eq. 36 becomes

$$\begin{aligned} B_2^{\prime \prime }(T_\mathrm{C}) \Delta T = -\frac{\Delta p}{R T} \left( B_3^\prime (T) -\frac{2 B_3(T)}{T} - 2 B_2(T) \left[ B_2(T)^\prime - \frac{B_2(T)}{T}\right] \right) = 0. \end{aligned}$$

In the limit $\Delta p \rightarrow 0, T \rightarrow T_\mathrm{C}$, where the term in brackets vanishes, this yields the terminal slope,

$$\begin{aligned} \lim _{T \rightarrow T_\mathrm{C}} \frac{\mathrm{d}p}{\mathrm{d}T} \Big \vert _{q_\mathrm{R} = -\frac{1}{3}} = -\frac{B_2^{\prime \prime }(T_\mathrm{C}) R T_\mathrm{C}}{B_3^\prime (T_\mathrm{C}) - \frac{2}{T_\mathrm{C}} B_3(T_\mathrm{C})} . \end{aligned}$$

(37)