1 Introduction

The thermophysical properties of water are commonly known (if we pass the anomalies of water or the supercooled water region). For example, the density of pure water at \(20\,^{\circ }\hbox {C}\) at standard atmospheric pressure is known with a relative uncertainty of 1 ppm or less [1]. The surface tension of water is an exception. The surface tension is a fundamental physical parameter. Many issues and open problems are connected with measurement of the surface tension. Common inaccuracy comes from failure to control air–liquid–solid contact conditions or account for liquid meniscus geometry and buoyancy corrections. Just look at the controversy presented in [2–4]. For surface-tension measurements, the reference values for water at \(20\,^{\circ }\hbox {C}\) or \(25\,^{\circ }\hbox {C}\) are important. The surface-tension values at the temperatures mentioned above are used as reference values for calibrations and for relative measurements of surface tension [5–7]. We have decided to process the values of the surface tension at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\) statistically, in order to get the most likely value.

2 Experimental Values of the Surface Tension of Pure Water

There are selected air–water interfacial tension values of experimental measurements at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\) in Tables 1 and 2.

Table 1 Experimental values of the surface tension of pure water at \(20\,^{\circ }\hbox {C}\)
Full size table
Table 2 Experimental values of the surface tension of pure water at \(25\,^{\circ }\hbox {C}\)
Full size table

Uncertainties in Tables 1 and 2 are divided into four categories in the last columns of the tables. Symbol A represents the standard deviation, B means the mean absolute error, C denotes the estimated accuracy of measurements, and D is used in the cases where a comparison with data of known reliability or our own estimate of accuracy of the measurement was made.

Some of the Sentis data [8] were used in The International Critical Tables published in 1928 [46]. A linear fit [8] was used to calculate surface-tension values at reference temperatures. The uncertainty of the measurements can be estimated to be about \(0.1\,\hbox {mN}{\cdot }\hbox {m}^{-1}\). Harkins and Brown [9] critically evaluated the surface-tension data in the literature and indicated that almost all of the data are 3 % or more too low. In their experiments, several different samples of water and several different capillaries were used. The uncertainty of the measurements can be estimated to have been about \(0.07 \hbox { mN}{\cdot }\hbox {m}^{-1}\) [48]. Harkins later argued [13, 20] that most of the data obtained before 1916 are in error.

Sugden stated that “tap water and distilled water were found to give identical and consistent values” [10], this makes the data questionable (see [32]). The estimated total error of the Sugden measurement is \(0.22 \hbox { mN}{\cdot } \hbox {m}^{-1}\); we increased the estimated error to \(0.5 \hbox { mN}{\cdot } \hbox {m}^{-1}\). The Cockett and Ferguson values were calculated from a correlation in [12]. The uncertainty of the Cockett and Ferguson data was calculated as a standard deviation of the experimental data from the correlation, for temperatures between \(17\,^{\circ }\hbox {C}\) and \(31\,^{\circ }\hbox {C}\). The results of Moser [11] were used for the compilation of the international tables of the surface tension of water and the IAPWS equation [47]. There was a systematic error in the Voljak data [14], and the uncertainty is estimated to be up to 1 % [48]. We estimated the uncertainty at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\) to be \(0.5 \hbox { mN}{\cdot } \hbox {m}^{-1}\).

For the experimental Hacker data, we used a linear approximation from 15.5 \(^{\circ }\hbox {C}\) to \(27.5 \, ^{\circ }\hbox {C}\), and then we calculated the surface-tension values at \(20\, ^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\). The Teitelbaum et al.’s data [16] were used in a discussion about possible inflections in the plots of surface tension versus temperature [19, 41]. Many of the relevant experimental details are missing in the paper [16], and we have estimated the uncertainty of the measurements to have been about \(0.4\,\hbox {mN}{\cdot }\hbox {m}^{-1}\). Fox and Chrisman [17] measured the surface tension by the differential capillary-rise method and by the ring method at \(20\,^{\circ }\hbox {C}\). Their data for the ring method were recalculated by Huh and Mason [24]. We have used the same uncertainty for the Huh and Mason data as for the Fox and Chrisman data. Padday and Russell [18] used the Wilhelmy-plate method with two modifications: plate equilibrium and detachment methods. Both results of the measurements are presented in Table 1.

Drummond et al. [44] do not give any error for their measurements [32]; we have estimated the uncertainty of the measurement to have been about 0.1 \(\hbox { mN}{\cdot } \hbox {m}^{-1}\). The same estimation we have made for the Drost–Hansen measurement. The experimental data of Gittens [19] were recalculated to get values at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\). For the capillary-rise method at \(20\,^{\circ }\hbox {C}\), we used the value of the derivative based on the IAPWS 2014 formulation [47] and recalculated the experimental value at 19.98 \(^{\circ }\hbox {C}\) to the value at \(20\,^{\circ }\hbox {C}\). The other values of Gittens in Tables 1 and 2 were calculated based on a linear extrapolation of measured values. Bonnet and Pike [20] measured values of the surface tension at 20 \(^{\circ }\hbox {C}\), 30 \(^{\circ }\hbox {C}\), and 40 \(^{\circ }\hbox {C}\). The error in the linear approximation [20] is quite big, and we did not use it to calculate the value at \(25\,^{\circ }\hbox {C}\). The Vargaftik et al. experimental data [21] in the temperature interval from 0.4 \(^{\circ }\hbox {C}\) to 53.4 \(^{\circ }\hbox {C}\) were approximated by a quadratic function, and then the data at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\) were calculated.

For Padday et al. [22], we selected nine values for rods c, d, e, presented in the paper as more precise, and we used the least-squares method to create a linear approximation of the measured values. Based on the approximation we calculated the values at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\). For Patterson and Ross we calculated the mean average from four values [27]. For the Kayser data [25], we calculated the values from the presented correlation in the paper. Kayser measured the surface tension of water in contact with its saturated vapor. The differences between the surface tension in the presence or absence of air are of the order of the experimental errors, perhaps \(\pm \, 0.1 \hbox { mN}{\cdot } \hbox {m}^{-1}\) [2].

Zhang et al. [35] used methods of sphere tensiometry. We have calculated an average of two presented values, with a standard deviation of \(0.11 \hbox { mN}{\cdot } \hbox {m}^{-1}\). Because the relevant analysis of the estimated accuracy of the measurements is missing for Khattab et al.’s data [36] at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\), we have estimated the uncertainty to be \(0.5 \hbox { mN}{\cdot } \hbox {m}^{-1}\).

For the Padday value, we used the derivative calculated from the IAPWS approximation [47] (see also Eq. 2), and we recalculated the value of the surface tension at 25.75 \(^{\circ }\hbox {C}\) to the value at \(25\,^{\circ }\hbox {C}\). The same procedure was applied to the measured value of Slowinski and Masterson [40] at 27 \(^{\circ }\hbox {C}\), and to the Holcomb and Zollweg data [33], where the temperatures were measured in K. We recalculated the values from the temperatures of 293 K and 298 K to \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\). Kawanishi et al. [42] measured the surface tension at 25.2 \(^{\circ }\hbox {C}\); we recalculated the measured value to \(25\,^{\circ }\hbox {C}\).

We excluded some known experimental data from our overview. Richards and Carver [50] used the capillary-rise method essentially calibrated by reference to the Harkins data. Floriano and Angell [5] calibrated actual diameters of used capillaries by measurements of the rise of distilled water at \(25\,^{\circ }\hbox {C}\), with a given value of the surface tension at the temperature. Cini et al. [6] used the normalized value of \(72.785 \hbox { mN}{\cdot } \hbox {m}^{-1}\) for the surface tension at \(20\,^{\circ }\hbox {C}\). Warren [51] measured relative values based on the surface tension at 15 \(^{\circ }\hbox {C}\). Ramsay and Shields [52] underestimated the values of the surface tension [48] in their measurements. Hrubý et al. [7] used the reference surface tension at \(20\,^{\circ }\hbox {C}\), obtained from an IAPWS correlation [47], to evaluate the capillary diameters.

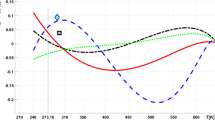
We illustrated the selected data from Tables 1 and 2 graphically in Figs. 1 and 2.

Fig. 1
figure 1

Experimental values at \(20\,^{\circ }\hbox {C}\). Solid line shows the final average, and dashed lines show the calculated uncertainties. Kayser’s data were identified as outliers

Full size image
Fig. 2
figure 2

Experimental values at \(25\,^{\circ }\hbox {C}\). Solid line shows the final average, and dashed lines show the calculated uncertainties. Kayser’s data and Smith and Sorg’s data were identified as outliers

Full size image

We calculated the weighted average from the experimental values for each temperature, where the weight of the measurement is equal to the reciprocal value of the uncertainty. The same weights were used for calculation of the standard deviations. We marked the data of Kayser [25] and Smith and Sorg [37] as outliers (see Figs. 1, 2), and we removed the data from the calculation of the surface tension at reference temperatures. The procedure used for determination of outliers is the following conditions:

  1. (a)

    We calculated weighted averages from all measured data in Tables 1 and 2, together with a weighted standard deviation.

  2. (b)

    We got \(\sigma _{20 \,^{\circ }\mathrm{C}} =\left( {72.84\pm 0.15} \right) \hbox { mN}{\cdot } \hbox {m}^{-1}\) and \(\sigma _{25\,^{\circ }\mathrm{C}} =\left( {72.04\pm 0.18} \right) \, \hbox {mN}{\cdot } \hbox {m}^{-1}\).

  3. (c)

    We decided to identify some of the measured values of the surface tension as outliers, if they are more than two standard deviations away from the average.

Uncertainties in Tables 1 and 2 are based on the estimates made by the investigator in reporting his measurement.

In Table 3, values of the surface tension without outliers are presented, together with the standard deviation. Other literature values of the surface tension of water at the reference temperatures are presented in Table 3.

Table 3 Tabulated values of the surface tension—ICT [46], Harkins [13], IAPWS [47], Jasper [49], Pallas and Harrison [32], and this paper
Full size table

3 Independence of the International Temperature Scales

For the surface tension, very old measurements are still used. Our experimental dataset started in 1916. The first international temperature scale (ITS) was adopted in 1913. Now the ITS-90 temperature scale is valid [53]. The differences in temperatures between different international temperature scales are not significant for the surface-tension measurements. In order to estimate errors caused by the use of different international temperature scales, we can use the following famous modification of the Van der Waals equation:

$$\begin{aligned} \sigma =B\tau ^{\mu }(1+b\tau ), \end{aligned}$$
(1)

where

$$\begin{aligned} B=235.8\;\hbox {mN}{\cdot } \hbox {m}^{-1},\, \tau =1-\frac{T}{T_\mathrm{C}},\, \mu =1.256,\, b=-0.625,\, T_\mathrm{C} =- 647.096\hbox { K} \end{aligned}$$

Equation 1 is a recommended formulation of IAPWS for the surface tension of water [47]. This equation is valid between the triple point (0.01 \(^{\circ }\hbox {C}\)) and the reference temperature \(T_{\mathrm{C}}\). The equation also provides reasonably accurate values when extrapolated into the supercooled region, to temperatures as low as \(-25\,^{\circ }\hbox {C}\) [7, 47].

We get the formula for the derivative of the surface tension:

$$\begin{aligned} \frac{\hbox {d}\sigma }{\hbox {d}T}=-\frac{B}{T_\mathrm{C}}\tau ^{\mu -1}\left[ {\;\mu +b\left( {\mu +1} \right) {\cdot } \tau \;} \right] . \end{aligned}$$
(2)

To estimate a deviation caused by differences in temperatures in different temperatures scales, we get

$$\begin{aligned} \Delta \sigma \;=\;\frac{\hbox {d}\sigma }{\hbox {d}T}\Delta T. \end{aligned}$$
(3)

In this formula \(\Delta \sigma \) is an estimated deviation if we use an old temperature scale, \(\frac{\hbox {d}\sigma }{\hbox {d}T}\) is calculated in Eq. 2, and \(\Delta T\) is the difference of the measured temperatures that are expressed on different temperature scales.

We get very small differences for \(\Delta \sigma \). For ITS-90 and IPTS-48, the difference \(\Delta T\) at \(20\,^{\circ }\hbox {C}\) is \(- 0.012\,^{\circ }\hbox {C}\) [54], and an estimation of error of \(\Delta \sigma \) is 0.0017 \(\hbox { mN}{\cdot } \hbox {m}^{-1}\). For the difference of \(\Delta \sigma \) at \(25\,^{\circ }\hbox {C},\, \Delta T\) at \(25\,^{\circ }\hbox {C}\) is \(-0.014 ^{\circ }\hbox {C}\), and the estimation of error of \(\Delta \sigma \) is then 0.0022 \(\hbox {mN}{\cdot } \hbox {m}^{-1}\). The differences are negligible.

4 Conclusions

There are many experiments on the surface tension of water, using different methods and with different results. The reference values of the surface tension of water at \(20\,^{\circ }\hbox {C}\) and \(25\,^{\circ }\hbox {C}\) are often used for different purposes, most often for calibration of measurement devices or calculation of correlations to the measurements. We have carefully selected the existing experimental data for these temperatures, and we have calculated the average of these values. We have obtained the surface tension of 72.83 \(\hbox { mN}{\cdot } \hbox {m}^{-1}\), with a standard deviation of 0.12 \(\hbox { mN}{\cdot } \hbox {m}^{-1}\) at \(20\,^{\circ }\hbox {C}\), and \(72.01 \hbox { mN} {\cdot } \hbox { m}^{-1}\), with a standard deviation of \(0.10 \hbox { mN}{\cdot } \hbox {m}^{-1}\) at \(25\,^{\circ }\hbox {C}\).