1 Introduction

The surface tension of water is a property that is important for chemical and biological research or for the exploration of atmospheric phenomena. The surface tension between a vapor and liquid phase is important for modeling precipitation forming in clouds, aircraft icing, and condensation shocks in supersonic flow. Water is frequently used for the calibration of measuring instruments. If we need to know the surface tension of aqueous systems (e.g., surface tension of seawater), we need to know the surface tension of pure water. The surface tension of water plays an important role in many natural, environmental, and technological processes.

Water has a high surface tension (72.8 mN·m−1 at 293.15 K [1]) compared to that of most other liquids. However, the surface tension of water has another peculiarity. We do not know its exact value. While water density can be measured with an accuracy of 1 ppm since the 1990s (between 273.15 K and 313.15 K [2]), the dispersion of surface tension measurements is much greater. There are many different measurements of the surface tension of water, where the authors declare their high-precision measurements, yet the measured values differ from each other even by ten times the declared measurement uncertainties. What is the surface tension of water when different measurements differ from each other?

The International Association for the Properties of Water and Steam (IAPWS) approved the table and equation for surface water tension in 1976 [3], and since then, this version has been in force, with only minor modifications. During this long period of time, there have been significant changes. For example, transitioning to the new temperature scale ITS-90 changed the critical temperature value of water, which is the parameter used in the IAPWS temperature dependence equation for surface tension. Significant new measurements have been made, such as for supercooled water. There are reasons for a major revision of the equation for the temperature dependence of surface tension.

2 Previous Equations of Surface Tension

Together with the measurement of the surface tension of water, it has been shown that surface tension is highly dependent on the temperature. Consequently, equations were created that mathematically described the dependence of the surface tension on the temperature. The breakthrough measurement was Voljak’s measurement [4], in which the surface tension of water was measured from 273.15 K to 643 K. This measurement allowed to create an equation for the surface tension valid from triple to critical point.

Selected equations of surface tension for water are summarized in Table 1.

Table 1 Selected equations for the temperature dependence of the surface tension of water valid from the triple point up until the critical point
Full size table

First, purely empirical equations, given either by polynomial or as rational fracture functions, have been developed (Eqs. 1 and 2 in Table 1). The degree of the polynomials used is relatively high, and the equations are not currently in use.

The following equations Eqs. 3–10 in Table 1 are based on the corresponding state-based principle, which leads to correlations describing the temperature dependence of surface tension in a universal form for different fluids.

The history of these types of equations starts in 1894, when van der Waals [7] proposed the following relationship for the temperature dependence of surface tension, which is actually the basis of all modern equations for surface tension:

$$\sigma \sim {\left({T}_{\mathrm{c}}-T\right)}^\frac{3}{2},$$
(11)

where \(\sigma\) is the surface tension, \({T}_{\mathrm{c}}\) is the critical temperature, and \(T\) is the temperature (in K). When defining the dimensionless variable \(\tau =1- \frac{T}{{T}_{\mathrm{c}}}\), the asymptotic form of the temperature dependence of the surface tension of the water (when the temperature approaches the critical one) can be written as.

$$\sigma = {\sigma }_{0} {\tau }^{\mu }.$$
(12)

We designate the coefficient \(\mu\) as a critical exponent. Thus, we can say that for van der Waals-type fluids, the value μ = 1.5.

Widom and Fisk [12, 13] state that near the critical point.

$$\sigma \sim {\tau }^{\mu },$$
(13)

where the exponent \(\mu\) belongs to the so-called critical exponents.

Widom and Fisk estimated (from the known values of the other critical exponents) that \(\mu\) lies in the interval (1.22, 1.33).

For water, the asymptotic form Eq. 12 is insufficient. To describe experimental data at the widest temperature range, additional parts must be added. Straub et al. [7] tested a very elegant form of the equation for surface tension. The approximation Eq. 4 was only slightly better than the approximation Eq. 3; this is why the authors prefer the equation in the form Eq. 3.

The Eighth International Conference on the Properties of Water and Steam adopted a resolution to compile international tables of the surface tension of water. Three drafts of tables were considered, i.e., tables submitted by the Japanese delegation, tables presented by the USSR delegation, and tables put forward by the delegates of West Germany. Because the recommended values of surface tension of water in the datasets differed, the arithmetic means of the values were used. The table was adopted by the International Association for the Properties of Steam (IAPS), and it was promulgated in an official release in 1976 [14, 15].

The IAPS adopted Eq. 3 to describe the recommended values of \(\sigma\), where \(B\) = 235.8 mN·m−1, \(b\) = − 0.625, and \(\mu\)= 1.256. This equation used \({T}_{\mathrm{C}}\) = 647.15 K. This equation is still valid, although the temperature of the critical point slightly changed by the new temperature scale ITS-90 to \({T}_{\mathrm{C}}\) = 647.096 K. Because new measurements of the surface tension of water in supercooled water have appeared, another modification was adopted in 2014, namely, “The region of validity is the entire vapor–liquid saturation curve, from the triple point to the critical point. It also provides reasonable results when extrapolated to metastable (supercooled) conditions, down to at least − 25 °C” [3]. The triple point of pure water is at 273.16 K and 611.22 Pa, the critical point is at 647.096 K and 22.064 MPa.

Somayajulu calculated the values of the three needed parameters for 64 fluids, including water. Somayajulu’s results [8] indicate that the three-constant Eq. 7 fits the data much better than the two-constant Eq. 6. Equations 6 and 7 describe the temperature dependence of the surface tension of water from the triple point to the critical point.

Mulero et al. (see Eq. 8) used surface tension data of 82 fluids [9] and tested the model.

$$\sigma = {\sum }_{i=0}^{k-1}{\sigma }_{i} {\tau }^{{n}_{i}}.$$
(14)

For water, 797 data points were used. The temperature range of the data was from 233.22 K to 646.15 K, the temperature of the critical point is 647.096 K (ITS-90).

Pátek et al. (Eq. 9) revised a large set of experimental data (1620 data points) and developed a new correlation in a similar form to IAPWS, namely,

$$\sigma =233.58 {\tau }^{1.2527}\left(1-0.615946\tau \right).$$
(15)

The last mentioned Eq. 10 in Table 1 is the Weibull-type equation [11]. Yi et al. used the model for 117 liquids. However, the Weibull model does not give good results for water over a wide temperature range [11].

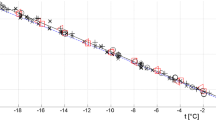
Somayajulu used the table data of Vargaftik et al. [14] to determine constants in Eqs. 6 and 7. The region of validity is the entire vapor–liquid saturation curve, from the triple point to the critical point. We extrapolated the equations into the supercooled water region to 240 K (see Fig. 1). Because the source of the data is based on the IAPWS release, the Somayajulu equations give results similar to those of the IAPWS equation.

Fig. 1
figure 1

Comparison of selected correlations of Table 1 with standard release IAPWS (Eq. 5). Red solid line—Pátek et al. (Eq. 9), blue dash line—Mulero et al. (Eq. 8), black dash-dot line—Somayajulu (Eq. 6), green dot line—Somayajulu (Eq. 7). Blue diamond—reference value at 20 °C ((72.83 ± 0.12)  mN·m−1 [1]), Black square—reference value at 25 °C ((72.01 ± 0.10)  mN·m−1[1]) (Color figure online)

Full size image

Mulero et al. (Eq. 8) and Pátek et al. (Eq. 9) used new experimental data. Vargafik et al. [14, 15] recalculated their experimental data. The recalculated data (to higher surface tension values) were used to construct the IAPWS equation. Therefore, Eq. 8 shows large deviations above 423 K. The equation also shows higher surface tension values than the IAPWS equation at 293.15 K and 298.15 K. The next benefit of Eq. 8 is that its form is used to describe another 80 liquids, only the constants of the equations are changed.

It is also interesting that the Eq. 8 declares a range of validity from 233.22 K to 646.15 K. So far, the lowest temperature reached for measuring the temperature dependence of the surface tension of water is 240.88 K [16]. So not all the data used in [9] were experimental. Mulero published their paper in 2012, so it does not include the most recent experimental data, especially in supercooled water [16,17,18,19,20,21].

Similarly, the Pátek et al. Equation 9 gives slightly lower values above 373.15 K than the IAPWS equation. This occurs possibly because Pátek et al. used the uncorrected data of Voljak [4]. The data were later recalculated by the author [14, 15], and some of them were not included in the fit of the IAPWS equation.

There is another interesting finding regarding the differences between the Pátek et al. and IAPWS equations. Pátek et al. used the new experimental data in the supercooled region [17], and it seems that the Pátek et al. equation shows higher values of surface tension of water in the area. We will discuss the phenomena later.

The IAPWS launched a debate several years ago on the revision of the IAPWS equation Eq. 5 for the following reasons.

  • The IAPWS standard has been approved since 1975. Negotiations and fine tuning took place prior to approval, which means that the data before 1974 were used to fit the equation. Since then, a number of significant measurements have taken place. For example, very precise measurements at reference values of 20 and 25 °C [22,23,24,25] were made. Since 2014, new measurements have been performed in supercooled water [16,17,18,19,20,21, 26, 27]. It is important to mention the recent measurement [10] in the temperature range from 272.6 K to 343.5 K.

  • The new temperature scale was introduced in 1990. Not only the temperatures of the measured data points but also the critical temperatures have changed. The value is used for calculation of dimensionless variable \(\tau\), which is used in the up-to-date correlations.

  • Because the table of the values of surface tension of water was a compromise (the values in the table were calculated as average from three drafts of tables), the IAPWS standard for the surface tension provides relatively large uncertainties at temperatures close to room temperature [17]. This is unpleasant in the situation when we want to use the values for calibration (see, e.g., [17, 18]).

3 Pátek’s Equation

Equation 9 solves the issues associated with the IAPWS equation. Pátek et al. [10] collected 211 original papers measuring the surface tension of water. A measurement of the surface tension of water was made by the authors themselves, who measured surface tension in the interval from 272 K to 344 K. The authors used the same form of the equation as IAPWS.

The collected experimental data are of different quality. Therefore, Pátek et al. [10] mention criteria for the basic quality of data included in further processing. The authors of the experimental data must declare the measurement accuracy in their articles, state the purity of the sample, and the variance of the polynomial-fit data must be less than the declared uncertainties. The authors must give a clear description of the measurement method, and data must be original, nonsmoothed.

The authors [10] then state that it is not possible to meet these criteria for the surface tension of water because approximately 50% of the authors do not provide any quantitative estimate of the accuracy of the measurement. Therefore, they chose the method of gradual data exclusion in the iterative process described in Pátek et al. [10].

That is why authors based the development of the recommended values for the surface tension primarily on a mutual intercomparison of the available experimental data [10]. According to the authors, the drop weight (drop volume) and the du Noüy ring methods require great empirical corrections and are only less accurate reproductions of the results of other methods. The data were excluded from further analysis. The authors also excluded three datasets: data points by Ramsay and Shields [28] and Sutherland [29] due to extreme average deviations and data points by Gittens [30] “with a large number of data points” [30].

We see (Fig. 1) that in the area of subcooling water, the surface tension values according to the Pátek et al. equation are slightly higher than what would correspond to the extrapolation of the IAPWS correlation. Nevertheless, important new measurements [17,18,19] are calibrated by reference values from the IAPWS table [3]. We can compare different sources of the reference values of surface tension of water at 20 °C in Table 2. We can see that the IAPWS value of the surface tension of water at 20 °C is the lowest. If Pátek et al. use the measurements based on the IAPWS values, it is clear that the values of the Pátek et al. equation are close to the IAPWS values. Nevertheless, Eq. 15 leads to slightly higher values in the subcooled area compared to IAPWS.

Table 2 Reference values of the surface tension of water at 20 °C
Full size table

Another problem lies in the relatively large inaccuracy of the reference values of the IAPWS table (see reasons for revision of the IAPWS equation). Another sources, e.g., Pallas and Harrison [24] and Kalová and Mareš [1] declare narrower uncertainties, and if we recalculate the relative measurements [16,17,18,19,20,21] with these reference values, we also obtain narrower uncertainties for experimental values of measured surface tension [18].

We can obtain other information from Fig. 1. We have discussed above that Eq. 15 gives lower values for temperatures of approximately 400 K. There are not too many experiments for temperatures above 400 K (in contrast to temperatures in the range from 288 K to 330 K). The crucial measurements are the measurements of Vargaftik et al. [4, 6, 14, 15, 34, 35] in the range of temperatures. Pátek et al. [10] incorporated the data of Voljak [4, 14, 15], and Vargaftik et al. [34] into their procedure as those that cannot be excluded. However, later, a correction was introduced to Volyak’s data for the contact angle, and for IAPWS tables, only the corrected data in the interval from 373 K to 523 K were used [14]. Pátek et al. used uncorrected data from Volyak, which is why their equation gives lower values than IAPWS in this temperature region.

It is necessary to mention a problem with relative measurements. Many of the measurements use some reference value that is used for calibration of the experimental device. For example, very often, the surface tension of water at a reference temperature is used for calculation of the capillary diameter in the capillary rise method. We can mention recent measurements in supercooled water [16,17,18,19,20,21] or a paper by Floriano and Angell [36]. Pátek et al. have used many relative measurements, and some of them were included in the primary data on the surface tension for water (Hrubý et al. [17], Vinš et al. [18], Butler et al. [37, 38], Voronkov [39]; Maham and Mather [40]). The measurements that contain only one measurement value should be excluded, and this value was used for calibration (e.g., [36,37,38,39,40]). The relative measurements that contain more data [17, 18] must be recalculated according to the independently evaluated surface tension at reference temperatures. If we use the reference values from the IAPWS table, we must not be surprised that the experimental data reproduce the IAPWS values, at least in the vicinity of the reference temperature.

The abovementioned problems with IAPWS and Pátek’s equations have led us to a decision to create a new equation for the temperature dependence of the surface tension of water based on the following principles:

  • We have to be careful in using “relative measurements”. Many of the measurements use some reference value that is used for calibration of the experimental device. We suggest using independent reference values that are obtained directly from measurements at reference temperatures [1].

  • It is useful to use the experience of the authors of the IAPWS formulation and their critical evaluation of experimental data (known before 1976)—see [35, 41].

  • Within the discussion in the IAPWS, it was suggested to use the fixed exponent, because \(\mu\) belongs to critical exponents. The exponents are universal. They can be measured by experiments or calculated from theory. The calculation is quite complex, and during calculations, it is necessary to use some approximation methods. According to Hasenbuch [42], \(\mu = 1.26004\)(20), and we can fix the coefficient to the value \(\mu = 1.26\). This value is very close to the value of the exponent used in the IAPWS equation.

  • We have tested different forms of correlation for the temperature dependence of the surface tension of water [43], and we have decided to use Wegner’s form of the description of the thermophysical properties near the critical point, namely, \(\sigma ={\sigma }_{0} {\tau }^{\mu }\left(1+{\sigma }_{1}{\tau }^{\Delta }+{\sigma }_{2}{\tau }^{2\Delta }+{\sigma }_{3}{\tau }^{3\Delta }\dots \dots \right)\). According to theory, \(\Delta \approx 0.5.\)

4 How to Create a New Equation

Based on the previous remarks, we want to create a new equation for the surface tension of water in the form

$$\sigma ={\sigma }_{0} {\tau }^{1.26}\left(1+{\sigma }_{1}{\tau }^{0.5}+{\sigma }_{2}\tau \right).$$
(16)

In the equation \(\tau =1- \frac{T}{{T}_{\mathrm{c}}}\) where Tc = 647.096 K

We need to fit three coefficients \({\sigma }_{0}\), \({\sigma }_{1}\), and \({\sigma }_{2}\). We have developed the new equation in several steps.

  1. Step 1:

    Source List of Experimental Data We evaluated the data used in the paper of Pátek et al. [10]. We added new datasets to the sources of data. Some of them were newer data [16, 20, 21, 44], while others were older, and they complemented the list of data sources.

    A list of all data can be found in the Supplementary materials.

  2. Step 2:

    Secondary Selection The source list is then subjected to a primary evaluation, and its criteria or the reasons for data exclusion in this step can be found in the Supplementary materials. The detailed reasons for excluding some data are provided in a brief note in the source list line. The last field indicates whether the data source has been included in further processing (YES).

  3. Step 3:

    Data Editing Selected data are eventually corrected, for example, according to the Vargaftik manual from 1979 [14]. Some reasons are given above. In detail, for the recalculation of relative data, correction for contact angle for higher temperatures, partial exclusion of some data from the primary selection—see detailed description in the Supplementary materials.

    Finally, we recalculated the temperatures in the experiments to the temperatures given by ITS-90.

  4. Step 4:

    Determination of Weights Intuitively, some weights should be used. The problem is to determine which weights. An estimate of the measurement accuracy is offered. Before 1950, the accuracy of the measurement was not considerably mentioned; rather, it was an exceptional matter, when, for example, the accuracy of the temperature measurement was stated. In other works, for example, the standard deviation or an estimate of the measurement accuracy is given, or the accuracy is estimated by comparison with usually one randomly selected piece of literature data. Therefore, because tensiometers measure the force very accurately, the accuracy of measurement is estimated to be 0.001 mN·m−1. The opposite extreme is the work of Hrubý et al. [17]. The relative uncertainty are up to 0.54%, i.e., approximately 0.4 mN·m−1. The capillary method usually gives an uncertainty of 0.1 mN·m−1. Some authors state a measurement accuracy of 0.01 mN·m−1, but the values then significantly differ from the data of other authors. Therefore, we decided that the estimation of measurement uncertainty is a qualitative indicator that in some situations can be used to decide whether to include measurements in the selection or not but cannot serve as a qualitative indicator according to which the weights of individual measurements would be calculated.

    Another question is how to take into account the number of measured values when creating the equation. Pátek et al. [10] did not use weights, nor were weights likely to be used in the development of IAPWS R1-76 (2014). However, the amount of data should be taken into account. Some measurements contain a large amount of data. On the other hand, we have very good measurements at one or two temperatures, such as Pallas and Pethica [23] or Pallas and Harrison [24], which, if we do not use weights, strongly suppress their importance.

    If we took the weight of a single 1/N measurement, where N is the number of data points in a given set of measurements, we would significantly favor data at approximately 20 and 25 °C (where measurements with one or a few experimental points predominate) and disadvantage measurements from 373 K to 643 K or below 273.15 K (where measurements at multiple points significantly predominate). Therefore, we chose the weight 1/√N, which we see as a reasonable compromise, which slightly corrects the effect of measurements with a large number of experimental points.

    To somehow take into account that older measurements do not include an analysis of measurement accuracy, that they often do not state the accuracy of temperature measurements, and that sometimes there are no accurate data on water purity, we multiply the weights obtained according to the abovementioned instructions by either 0.5 (for pre-1950 measurements) or by 1 (for measurements in 1950 and later).

  5. Step 5:

    Provisional Equation Over Primary Corrected Data From the primary data (possibly slightly corrected) and using the weights determined above, mathematical regression is used to create a provisional equation. We have.

    $$\sigma =248.72194 {\tau }^{1.26}\left(1-0.14613145{\tau }^{0.5}-0.48611793\tau \right).$$
    (17)

    This is the auxiliary equation for the secondary round of data evaluation—see below.

  6. Step 6:

    Graphical Comparison of Data with Eq. 17 The graphical comparison of the primary experimental data with Eq. 17 is provided in the Supplementary materials. Using this comparison, e.g., outliers can be excluded (see Supplementary material).

  7. Step 7:

    Calculation of Regression Coefficients Now, we calculate the regression coefficients again. We obtain the equation.

    $$\sigma =246.27375663537{\tau }^{1.26}\left(1-0.1185233731376{\tau }^{0.5}-0.5119887378159\tau \right).$$
    (18)

    We solved the mathematical equation in MATLAB (Statistic Toolbox) using the nlinfit procedure. The method of least squares was used and the sum of the squares of the absolute deviations of the surface tension was minimized. The standard uncertainties of individual coefficients are 0.94, 0.011, and 0.010. The uncertainties of individual coefficients are disproportionately worse than those in the equation of Pátek et al. [10]. This occurs because the tabular, already smoothed values of Pátek’s equation fit, while our calculation of Eq. 18 takes place over selected experimental data.

  8. Step 8:

    Rounding of Coefficients We round the coefficients to 5 significant digits. Thus, the definitive form of the equation is:

    $$\sigma =246.27 {\tau }^{1.26}\left(1-0.11852{\tau }^{0.5}-0.51199\tau \right).$$
    (19)

    The error due to rounding is shown in Fig. 2.

    Fig. 2
    figure 2

    Rounding error. σround is given by Eq. 19 with rounded coefficients calculated according to Eq. 18, where the coefficients are not rounded

    Full size image

    The maximum effect of rounding is 0.0004 mN°m−1, which in our opinion is reasonable given the accuracy of determining the surface tension of water.

  9. Step 9:

    Determination of Uncertainty Intervals For IAPWS, the uncertainties are given in the table [3]. The estimated uncertainty is 0.38 mN·m−1 at 273.15 K and gradually decreases to 0.1 mN·m−1 at 643 K. Pátek et al. [10] stated that the maximum uncertainty of tabular data is 0.1 mN·m−1.

    The uncertainty of Eq. 19 is calculated as follows:

    We will divide the experimental data according to the temperature of the intervals (for temperatures above 373 K due to the number of experimental data, we will divide it into thirty-degree intervals, and below 373 K, into ten-degree intervals). For each interval, the standard deviation from the obtained equation is calculated according to the formula.

    $${u}_{T}\left(\sigma \right)= \sqrt{{\sum }_{1}^{n}{w}_{i}{\left({\sigma }_{i}-{\sigma }_{i, \mathrm{fit}}\right)}^{2}},$$
    (20)

    where n is the number of experimental points in the given temperature interval, \({\sigma }_{i}\) is the surface tension measured at a given temperature in a given interval, \({\sigma }_{i,\mathrm{fit}}\) is the surface tension calculated from Eq. 19 for the same temperature, and w(i) is the normalized weight. As mentioned above, we chose the weight 1/√n.

    The deviations of the measured values from the approximation equation and the estimated standard deviations calculated after the temperature intervals according to Eq. 20 are shown in Fig. 3.

    Fig. 3
    figure 3

    Deviations of experimental data from Eq. 19 and representation of the uncertainty interval. Blue curve is the uncertainty of the IAPWS table values, and red curve is the estimate of the uncertainty of the new equation Eq. 19 (Color figure online)

    Full size image

    Uncertainties are also shown in Table 3.

    Table 3 Possible uncertainties of Eq. 19
    Full size table

5 Properties of the New Equation

In Fig. 1, we compared Pátek's equation [10] with the IAPWS equation. Now we can add a new equation; the result is shown in Fig. 4. We see that the new equation better takes into account the reference values at 20 °C and 25 °C, which is logical. As we have already stated with Pátek's equation, it is clear that measurements in the subcooled region cannot be solved simply by extrapolating the IAPWS equation to negative temperatures. The new equation is more in line with IAPWS values above 373 K, which may result from the use of wetting angle corrections by Vargaftik et al. [14], i.e., the authors of decisive measurements in this area, which were also applied to the IAPWS equation. The greater deviation from the IAPWS equation in the critical area results, among other things, from the use of another exponent. We also do not know how the tables of the German and Japanese delegations turned out in this area.

Fig. 4
figure 4

Comparison of Pátek’s equation [10] and the new Eq. 19 with the IAPWS equation. The course of the deviation of the new equation from IAPWS is marked in blue, the deviation of Pátek’s equation is in red, the black diamond shows the reference value at 20 °C according to Kalová and Mareš [1], and the blue circle shows the reference value at 25 °C [1] (Color figure online)

Full size image

6 Conclusions

We presented reasons why the IAPWS correlation for the surface tension of water needs to be revised. We reviewed existing forms of correlations and selected a form with a fixed first and second exponent—Wegner’s form. The exponents are calculated in the theory of the critical point. We explored a large quantity of existing experimental points and eliminated the experimental values that did not meet our requirements.

The new equation also includes the latest measurements of water surface tension. When creating the equation, we also used some relative measurements that need some reference values, e.g., to measure the capillary diameter. To do this, we used reference values at 20 °C and 25 °C, which were calculated only with absolute measurements and that did not have a direct link to the IAPWS equation.