1 Introduction

Most analyses of economic behavior and the consequences of changes of health policy investigate the effect of a treatment or policy on an outcome of interest for a population of interestFootnote 1 using observational data. This is either because of the absence of experimentation or because of the reliance on “natural” experiments or quasi experimental designs. However, assignment to treatment or to a policy is typically not random but is instead based on several confounding factors that may also affect outcomes. When all of these confounding factors are observed as variables in the data, the estimation problem can be characterized as “unconfoundedness” or “exogeneity” or “selection on observables” (Rosenbaum and Rubin 1983; Heckman and Robb 1985). A large literature exists on methods that can be used to control for such confounding, including regression methods, propensity score (PS) methods, combinations of both (doubly robust) estimators, and non-parametric matching methods.Footnote 2 Imbens and Wooldridge (2009) provide a comprehensive review of these methods. Although the asymptotic theories behind most of these methods are well established in the literature, their finite sample performance is only beginning to emerge. In particular, finite sample properties of these estimators remain unknown for outcomes with a data generating process typified by the non-linearities commonly found in health care costs or expenditures. In essence, such non-linearities imply that the treatment effects under such data generating processes are heterogeneous in the population. Many other outcomes in economics carry similar features: earnings (Dehajia and Wahba 1999), income (Jalan and Ravallion 2003), and a variety of marketing outcomes, such as sales (Rubin and Waterman 2006). Our discussion will extend readily to these outcomes as well.

The growing literature that studies the finite sample properties of alternative estimators for treatment effect under exogeneity has focused on linear (in X’s) specifications of the outcomes model. Frölich (2000) compares one-to-one pair matching with local polynomial estimators in simulations where outcomes are dependent on only one covariate and finds local linear estimators are better. Abadie and Imbens (2006) show that both estimators have biases that do not disappear in large samples, under the standard N1/2 normalization, when the number of covariates increases. They propose a nonparametric bias-adjustment that renders matching estimators N1/2-consistent. Zhao (2004) compares PS matching methods with covariate matching estimators and finds no clear winner, although he infers that “when the sample size is too small, PS matching does not perform well compared with other matching estimators”. Zhao (2008) studies sensitivity of PS methods to their specifications though Monte Carlo experiments and finds that, under exogeneity, treatment effect on the treated are not sensitive to the specifications. Millimet and Tchernis (2009) find that over-specifying the PS estimator does not impart much of a penalty in terms of inconsistency and inefficiency.

When non-linearities exist, the performances of covariate matching and PS estimators will depend on balancing the entire distribution of X’s across treatment arms and not just balancing mean of the X’s, which is sufficient under linear data generating processes. As Frölich (2004) discovers, when comparing finite sample properties of matching and weighting estimators in estimating the average treatment effect (ATE) on outcomes with varying degrees of non-linearities, the weighting estimator is the “worst of all” (in terms of mean square error) and “it is far worse than pair matching.” However, Busso et al. (2009) points out that Frölich’s results may be driven in part by the fact that Frölich (1) uses true PSs versus estimated PSs [the use of the latter being more efficient (Hirano et al. 2003)], (2) does not normalize the weights, and (3) studies outcomes with very small variances, even when varying degrees of non-linearities are present. Busso et al. (2009) relaxes these assumptions and finds that a suitable version of the weighting estimator “performs at least as well as and usually better that all PS matching estimators considered in Frölich (2004)”.

The use of PS based estimators demands added scrutiny in the presence of nonlinearities in outcomes, just as linear regression models continue to undergo scrutiny under such data generating processes. The central role of the PS lies in its balancing property, such that the potential outcomes under each treatment become independent of treatment assignment conditional on the propensity score (e(X)). Consequently, PSs can help reduce the dimensionality of the matching problem that plagues regression estimators (Lu and Rosenbaum 2004). Furthermore, it may also imply that for outcome data generated via non-linear processes, the asymptotic approximations for the mean treatment parameter generated in finite samples are more accurate with the scalar PS than for multidimensional X (Imbens 2004). Such an implication, however, requires further consideration. The balancing property of PSs suggests that the conditional joint distribution of the observed covariates X given e(X) is the same for treated (D = 1) and control (D = 0) subjects (i.e., X ∐ D | e(X)) (Rosenbaum and Rubin 1983; Zhao 2004). However, the nonparametric convergence rates for the marginal distribution of X across the two treatment groups conditional on e(X) will be faster than the nonparametric convergence rates for the joint distribution of X. Additionally, the rate of convergence for the equality of the conditional higher order moments of X may be slower than for the equality in the conditional means of X. If the outcome generating process is purely linear in X and parameters, then convergence in mean X’s is sufficient to enjoy the dimension reduction advantages of PSs, even in finite samples.Footnote 3 In contrast, for non-linear data generating processes it is often necessary to obtain convergence in the higher order moments and also in the entire joint distribution of X in order to achieve the balancing property adequately. If PS estimators can achieve such a balance in finite samples, then only can they lead to accurate approximation for the mean treatment effect parameters (Rubin 1997).

Moreover, the convergence rate for the joint distribution of X across treatment groups usually slows down with the increased dimensionality of X. Ironically, this implies that the dimensionality of X should also affect the performance of PS estimators in finite samples, when outcomes are generated via non-linear processes.Footnote 4

The primary goal of this paper is to study the proposition that there is no single estimator that is appropriate for all data generating processes typical of health care costs data. However, due to the enormous variety of possible processes, it is next to impossible to test this proposition directly. Instead, we employ a set of simulation designs that can prove this proposition by contradiction. That is, if our simulation results contradict the alternative to this proposition (that there exists one such estimator that applies to all data generating processes), then they provide evidence of proof for the proposition.

We proceed by briefly reviewing three classes of estimators relevant for modeling health care costs: regression estimators, PS-based estimatorsFootnote 5 (Rosenbaum and Rubin 1983), and doubly robust (DR) estimators (a combination of the previous two methods) (Robins et al. 1995; Scharfstein et al. 1999; Bang and Robins 2005) (Sect. 3). We then provide Monte-Carlo evidence on finite sample performance of these estimators in modeling such outcomes and estimating mean treatment effect parameters, such as the ATE (Sect. 4). And finally, we highlight the role of misspecification and also over-specification of the PS estimator and its impact on treatment effect estimation (Sect. 4). To illustrate the corresponding results, we apply the alternative estimators to an empirical example of the costs of breast cancer treatments in Sect. 5. Section 6 concludes with the discussion of our findings.

To our knowledge, this is the first head-to-head comparison of regression estimators, PS estimators, and doubly-robust estimators for estimating treatment effects on outcomes such as health care costs. We begin in the next section describing the potential outcomes framework, standard in the treatment effect literature, in order to highlight the selection biases that make the application of these estimators necessary.

2 The potential outcomes framework

The concept of the potential outcomes framework dates back to Neyman (1923) and has been used by others in economics (Roy 1951; Quandt 1972) and statistics (Rubin 1974; Holland 1986). Each individual (we suppress individual level subscript for clarity) can conceptually have two potential outcomes,Footnote 6 Y T and Y S , corresponding to whether the individual receives treatment or not. In order to compare the estimators we discuss below, we write the data generating process for the potential outcomes by:

$$ \begin{aligned} Y_{T} & = \mu_{T} (X) + U_{T} \\ Y_{S} & = \mu_{S} (X) + U_{S} \end{aligned} $$
(1)

where μ(.) represents a general form of non-linear data generating mechanisms as a function of the observed covariates X = (X 0, X 1,…, X k ) that includes a vector of ones (X 0). U T and U S are random errors, with E(U j ) = 0, j = T, S.

The average treatment effect (ΔATE) parameter for the population is the difference in potential outcome if all patients are treated rather than not treated:

$$ {\Updelta_{\rm ATE}} = E_{X} \left\{{E\left( {Y_{T} - Y_{S} |X} \right)} \right\} = E_{X} \{ \mu_{T} (X) - \mu_{S} (X)\} $$
(2)

Similarly, the Effect on the Treated (ΔTT) parameter is the mean difference in potential outcome if only those patients who actually receive treatment had not received the treatment. Denote D to be an indicator = 1 if T is received and = 0 if S is received. Therefore, ΔTT is given by:

$$\Updelta_{\rm TT} = E_{X|D = 1} \left\{ {E\left( {{{Y}}_{{{T}}} |D = {{1}},{{X}}} \right) - E\left( {{{Y}}_{{{S}}} |D = {{1}}, {{X}}} \right)} \right\}= E_{X|D = 1} \left\{ {E\left( {{{Y}}_{{{T}}} |D = {{1}},{{X}}} \right) - E\left( {{{Y}}_{{{S}}} |D = {{0}}, {{X}}} \right)} \right\}$$
(3)

where the second equality follows from the “unconfoundedness” or the “selection on observables” assumption. This implies that all of the selection into receiving treatment is entirely driven by the observed covariates, and that the receipt of treatment is independent of the potential outcomes with and without treatment, if the observed covariate levels are held constant. Formally, this assumption is written as Y T , Y S ∐ D | X, where ∐ denotes statistical independence.

Note that, in contrast to linear data generating processes for (1), the treatment effect for each individual depends on the levels of one’s own X’s but not on U’s. This implies that the treatment effects are essentially heterogeneous in the population. Therefore, the ATE and the effect of the treated require averaging over the population distribution of X, as in E X (.). In most situations, each individual is only observed in state T or state S, but never both at any point in time. Therefore, the observed outcome (Y) becomes (Fisher 1935; Cox 1958; Quandt 1972, 1988; Rubin 1978):

$$ Y = DY_{T} + ({1-D})Y_{S}.$$
(4)

Consequently, the difference in the sample averages of the outcome variable between the treated and untreated groups may fail to provide a consistent estimate for either ΔATE or ΔTT because

$$E(Y|D = 1) - E(Y|D = 0) = E(Y_{T} |D = 1) - E(Y_{S} |D = 0) = E_{X|D = 1} (\mu_{T} (X)) - E_{X|D = 0} (\mu_{S} (X)) \ne \Updelta_{\rm ATE} ; \ne \Updelta_{\rm TT}$$
(5)

The last inequalities follow because the distribution of the observed covariates may not be independent of the treatment group, i.e., E(X|D) ≠ E(X). Thus, bias is generated because the levels of observed factors (X) influencing outcomes are different for treated and untreated groups and is called the overt selection bias (Rosenbaum 1998).

The primary method of addressing overt biases in observational studies is to adjust for observed information that affects outcomes and selection into treatment. These adjustment methods can be referred to as the methods of matching because they try to match or balance the levels of observed covariates between the treated and the untreated groups (Rosenbaum 1998). However, only a subset of these estimators is officially denoted as “matching estimators” in the economics literature (Imbens 2004).

Regression methods attempt to estimate conditional regression functions μ T (x) and μ S (x). Once these are estimated consistently, estimators for mean treatment effects are readily generated by comparing \( E_{X} \left\{ {\hat{\mu }_{T} (X)} \right\} \) and \( E_{X} \left\{ {\hat{\mu }_{S} (X)} \right\} \) computed based on varying distributions of X. However, one particular concern that plagues estimation of conditional regression functions is the dimensionality of X. This is especially true in non-linear data generating processes, where the nonparametric convergence rate for the mean function over the empirical distribution of X’s can be very slow, and therefore, in finite samples, can often produce a poor approximation for the mean treatment effect parameter of interest (Imbens 2004).

Propensity score methods have been proposed and used as alternatives for estimating these effects. The PS is defined as e(X) = Pr(D = 1 | X), where Y T , Y S ∐ D | e(X) following the proof provided by Rosenbaum and Rubin (1983). Consequently, conditional on this scalar PS, all of the selection bias generated by differences in observed covariate values between the treated and untreated groups can be removed. Alternatively, if one matches an untreated subject with a treated subject sharing the same PS, then averaging over similarly matched cohorts of subjects will remove all overt selection bias, and the difference in the outcomes between these two groups will reflect the effect of treatment for that group. Thus, finding matches across the specific distributions of PSs and then averaging differences in outcomes between the matched treated and untreated subjects provides the estimators for the mean treatment effect parameters. There are a variety of ways through which the balancing property of PSs are used in practice, including weighting by the reciprocal of PSs, blocking on PSs, regression on PSs, and matching on PSs.

In the next section, we describe some of the commonly used estimators of ATE (the primary parameter of interest for this paper) that are commonly employed to model health care costs, presumably generated under non-linear processes.

3 Alternative estimators

3.1 Regression estimators

There is a large literature since the 1960s that addresses skewness in outcome data (e.g., cost or other) and appropriate non-linear covariate adjustment methods (Box and Cox 1964; Duan et al. 1983; McCullagh and Nelder 1989; Mullahy 1998; Blough et al. 1999; Manning and Mullahy 2001). For health care costs and expenditures, denoted by Y hereon, it is typical to find a small number of patients with expenditures much larger than the median patient, which leads to large skewness and kurtosis on the right hand side of the cost distribution. The inapplicability of a linear model for this distribution, both in terms of bias and efficiency, has been consistently demonstrated. Econometricians have historically relied on logarithmic or other Box–Cox transformations of Y, followed by regression of the transformed Y on X using ordinary least squares (OLS) regression, to overcome the skewness, with some hope that such a transformation will also reduce problems of heteroscedasticity and kurtosis (Box and Cox 1964). The main drawback of transforming Y is that the analysis does not result in a model for μ(x) in the original scale, a scale that in most applications is the scale of interest. In order to draw inferences about the mean μ(x) or any functional thereof in the natural scale of Y, one has to implement a retransformation from the scale of estimation to the scale of interest. This involves the distribution of the error terms in the scale of estimation (Duan 1983; Duan et al. 1983; Manning 1998). The retransformation is complicated in the presence of heteroscedasticity on the scale of estimation (Manning 1998; Mullahy 1998).

To avoid such problems of retransformation, biostatisticians and some economists have focused on the use of generalized linear models (GLM) with quasi-likelihood estimation (Wedderburn 1974). In a GLM approach, a link function relates μ(x) to a linear specification x T β of covariates. The retransformation problem is eliminated by transforming μ(x) instead of Y. Moreover, GLMs allow for heteroscedasticity (in the raw-scale) through a variance structure relating \( {\text{Var}}(Y|X = x) \) to the mean, correct specification, which results in efficient estimators and may correspond to an underlying distribution of the outcome measure (Crowder 1987). For example, following the work of Blough et al. (1999), the most common GLM used for modeling heath care expenditures is the Gamma-Log link model, where the mean function μ(x) is related to the linear predictor η, with a log link and a gamma variance structure (with its constant coefficient of variation property) assumed for modeling heteroscedasticity,

$$({\text{Method C1}})\quad \log (\mu(X))=\eta\;{\text{and}}\;\text{Var}(Y|X) = \phi \cdot (\mu(X))^{2} $$
(6)

Estimation is carried out with a Fisher scoring algorithm without full reliance on the gamma distribution. The use of such GLM models is increasingly becoming popular in modeling health care costs data (Bao 2002; Killian et al. 2002; Bullano et al. 2005; Ershler et al. 2005; Hallinen et al. 2006).

However, there is often no theoretical guidance as to what should be the appropriate link function or variance function for the data at hand. One approach to this problem is to employ a series of diagnostic tests for candidate link and variance function models, e.g., the Pregibon Link test (Pregibon 1980) or the modified Hosmer–Lemeshow test (Hosmer and Lemeshow 1995). These tests are diagnostic for misspecification, but they do not provide any guidance on how to fix those problems. Some tests, such as the modified Park test (Manning and Mullahy 2001), can be employed conditional on the appropriate specification of the link function but may be imprecise and contingent on certain strong assumptions.

Basu and Rathouz (2005) propose a semi-parametric method to estimate the mean model μ(x) and the variance structure for Y given X, concentrating on the case where Y is a positive random variable. Following the work of McCullagh and Nelder (1989) and Blough et al. (1998), they use a mean function μ(x) related to the linear predictor, x T β, with a Box–Cox link,Footnote 7

$$({\text{Method C2}})\quad\eta=\left\{\begin{array}{ll}(\mu^{\lambda}-1)/\lambda,&{\text{if}}\;\lambda \ne 0 \\ \log(\mu), &{\text{if}}\;\lambda= 0.\end{array} \right.$$
(7)

where the link parameter is estimated directly from the data (Wooldridge 1992). Additionally, similar to the link function, a family \( h(\mu_{i} ;\theta_{1} ,\theta_{2} ) = \theta_{1} \mu_{i}^{{\theta_{2} }} \)of variance functions indexed by (θ 1, θ 2) is used, where the variance parameters are also directly estimated from the data. All parameters in the model, given by the parameter vector γ = (β T, λ, θ 1, θ 2)T, are estimated simultaneously using an additional set of estimating equations following a Fisher scoring algorithm yielding estimator \( \hat{\gamma }. \) Hence, it is named the Extended Estimating Equations (EEE) estimator. The predicted mean in this model is obtained by

$$ \hat{\mu }(x) = (x^{T} \hat{\beta } \cdot \hat{\lambda } +1)^1/\hat{\lambda}. $$

The flexible estimation method they propose has three primary advantages: (1) it helps to identify an appropriate link function and jointly suggests an underlying model for the error distribution for a specific application, (2) the proposed method itself is a robust estimator when no specific distribution for the outcome measure can be identified, i.e., their approach is semi-parametric in that, while they employ parametric models for the mean and variance of(Y|X), they do not employ further distributional assumptions or full likelihood estimation methods, and (3) their method makes it easy to decouple the scale of estimation for the mean model, determined by the link function, from the scale of interest for the scientifically relevant effects, as found in some the health economics literature. That is, regardless of what link function is estimated from the data, treatment effects, such as the ATE, on any scale, can be obtained.

At the extreme, one could use a fully non-parametric estimator. The advantage of such an estimator is that it can more accurately approximate the conditional regression functions if there is substantially more complex form of non-linearity present.Footnote 8 However, its disadvantage lies mainly in finite samples where a few influential observations may lead the estimator to over-fitting (Seifert and Gasser 1996). More importantly, the advantages of non-parametric curve fitting diminish with the dimensionality of X’s. Consequently, the role of PS becomes important as described below.

3.2 Propensity score based estimators

The first part of a PS estimator is the estimation of PS. The propensity score e(X) is estimated from a model for the likelihood of treatment, such as a logistic regression model, \( \log [e(X)/\{ 1 - e(X)\} ] = X\theta, \) and then uses various methods that effectively match treated and untreated subjects based on the estimated propensity score \( \hat{e}(X) \) or on \( X\hat{\theta }. \)

There are several methods by which estimated PS can be used to achieve a balance of observed covariates, including blocking, conditioning, weighting, or matching.

3.2.1 Stratifying by quintiles of PS

This is one of the most commonly used methods in health services research (Austin 2008). Here, the empirical distribution of the estimated PS across the entire sample (including treated and untreated subjects) is divided into quintiles. Indicator variables for the first four quintiles are then used as covariates, along with the treatment indicator and the interactions between them, in an OLS regression (Rosenbaum and Rubin 1983; Rubin 1997; Little and Rubin 2000),

$$({\text{Method\;P1}})\quad Y = \eta^{\prime} + \varepsilon \;{\text{and}}\;\eta^{\prime} = \alpha_{0} + \alpha_{1} \cdot D + \sum\limits_{j=1}^{4} {\left({\alpha_{2j} \cdot I_{{Q_{j}}}+\alpha_{3j} \cdot D \cdot I_{{Q_{j} }}} \right)} $$
(8)

where \( I_{{Q_{j} }} \) is the indicator for the jth quintile.

3.2.2 Inverse weighting with PS

In this method, the difference in weighted average of the outcomes between treatment and untreated group gives a consistent estimate of the ATE, where the weights are proportional to the inverse of the estimated PSs (Rosenbaum 1998; Hirano et al. 2003). Hirano et al. claim that this approach would also give an efficient estimate of ATE under all data generating processes, although they provide empirical evidence of this claim only in the context of linear models. We follow their proposed method and estimate the ATE as

$$({\text{Method\;P2}})\quad \hat{\Updelta}=\left({\sum\limits_{i =1}^{N} {\frac{{D_{i} }}{{\hat{e}(X_{i} )}}} } \right)^{ - 1} \cdot\sum\limits_{i = 1}^{N} {\frac{{D_{i} \cdot Y_{i}}}{{\hat{e}(X_{i} )}}} - \left( {\sum\limits_{i = 1}^{N} {\frac{{1- D_{i} }}{{1 - \hat{e}(X_{i} )}}} } \right)^{ - 1} \cdot\sum\limits_{i = 1}^{N} {\frac{{(1 - D_{i} ) \cdot Y_{i} }}{{1 -\hat{e}(X_{i} )}}} $$
(9)

Note that this estimator is similar to the Horvitz–Thompson estimator (1952). Also, note that unlike Frölich (2004), we have used the normalized version of the reweighted estimator that is used by Hirano et al. (2003) and Busso et al. (2009).

3.2.3 Matching with PS

There is a large literature on matching PSs to control for bias due to observable variables (Imbens 2004). Matching estimators are also non-parametric in nature, but unlike the weighting estimators shown above, matching estimators are less sensitive to parametric specification of PS (Zhao 2004). Because the number of available matching estimators is quite large, we select two of the most commonly used matching estimators in practice:

  • (Method P3) Kernel-based (using the Epanechnikov kernel) matching estimator, and

  • (Method P4) Local-linear regression based matching estimator that uses a tricube kernel.The basic idea of matching based on PSs involves (Zhao 2004):

    $$ \delta (e_{k} ,e_{l} ) < \varepsilon \Rightarrow\delta^{\prime}({\text{prob}}(X_{i} |e_{k} ),{\text{prob}}(X_{i}|e_{l} )) < \varepsilon^{\prime},$$
    (10)

    where δ and δ′ are distance metrics in the mathematical sense. According to this theory, if exact matching is impossible (which is often so in most finite sample cases) and matching is on some neighbourhood (ε) of e, then the distribution of X is still approximately the same for the treated sample and the untreated sample within the neighbourhood. In non-linear outcome generation settings, this approximation must extend to the entire joint distribution of X’s, a concern that drives our simulations below.

Either the kernel-based or local-linear regression based matching estimator follows the general expression:

$$\hat{\Updelta}=\sum\limits_{i=1}^{N}{\left({\hat{Y}_{1i}-\hat{Y}_{0i}}\right)},\;{\text{where}}\;\hat{Y}_{ki} = I(D_{i} = k) \cdot Y_{i} + I(D_{i} = 1 -k) \cdot \sum\limits_{{j \in P_{1 - k}}}{W(i,j;\varepsilon)\cdot Y_{j}},\quad k = 0, 1.$$
(11)

Here, P 1−k represent the set of individuals for whom D = 1 − k, and W(i, j) represent the weights that a specific kernel or the local linear regression computes based on bandwidth ε. Therefore, \( \hat{Y}_{1i} \) is just observed Y i if subject i had received treatment and is a weighted average of Y j among all treatment recipients if subject i had not received treatment. We use a bandwidth of 0.06 for the kernel-based matching estimator and a central band of N*0.25 for the local-linear regression-based matching estimator. The bandwidth controls the amount by which the data are smoothed. Large values of bandwidth will lead to large amounts of smoothing, resulting in low variance but high bias. Small values of bandwidth will lead to less smoothing, resulting in high variance but low bias. This trade-off is a well known dilemma in applied nonparametric econometrics. Since our primary focus in this paper is bias, we have kept the bandwidths low. In practice, however, much effort needs to be made in selecting bandwidth, including cross-validation exercises. We defer this work to the future.

3.3 Estimators based on combinations of regression and propensity scores

Using simulations, Rubin (1973) found that if the model used for model-based covariate adjustment is correct, then model-based adjustments may be more efficient than PS matching. However, if the regression model is substantially incorrect, model-based adjustments may not only fail to remove overt biases, they may even increase bias, whereas PS matching methods are fairly consistent in reducing overt biases. Similarly, methods based on weighing the data with estimated PSs may be inconsistent if the model used to estimate the PSs is misspecified. Rubin concludes that the combined use of PS matching along with model-based covariate adjustment is the superior strategy to implement in practice, being both robust and efficient. Unfortunately, this approach is almost never followed. Moreover, almost all studies that explore the performance of PS methods combined with covariate adjustment use traditional linear models and sometimes employ the assumption of a normal error as well (Rubin and Thomas 1992, 1996; Lunceford and Davidian 2004).

Recently, DR estimators, which rely on the combination of propensity matching and covariate adjustments (Robins et al. 1995; Scharfstein et al. 1999; Bang and Robins 2005), have been developed. These estimators are consistent for μ(x) whenever at least one of the two models (covariate adjustment or PS) is correct. This class of estimators is referred to as DR because it can protect against misspecification of either the covariate adjustment model or the PS model.

However, newer work (Kang and Schafer 2007) on comparing alternative strategies of addressing missing data reveals that although DR methods perform better than simple inverse-probability weighting, they are sensitive to misspecification of the propensity model when some estimated propensities are small. In addition, none of the DR methods the authors employ improve upon the performance of simple regression-based prediction of the missing values. To date, these methods have not been tried on costs data. We implement the Scharfstein et al. (1999) and the Bang and Robins (2005) versions of DR estimator, as they are represented as sequential regression estimators and form natural analogs to the regression estimators mentioned above. The basic formulation of this DR estimator is as follows:

$$\mu(X)=g(\eta^{\prime\prime})\;{\text{where}}\;\eta^{\prime\prime}= {\beta_{0}} + \beta_{1} \cdot D + X^{T} \beta_{X}+\gamma_{1}\cdot D \cdot \hat{e}(X)^{ - 1} + \gamma_{2} \cdot (1 - D) \cdot(1 - \hat{e}(X))^{ - 1} \;{\text{and}}\;\text{Var}(Y|X) = h(X) $$
(12)

Compared to the covariate adjustment model in Model C1–C2, the linear predictor in Eq. 12 contains two additional covariates that are the inverses of a subject’s estimated PS. Following this generic formulation, we study two different DR estimators mirroring the covariate adjustment methods in Model C1–C2:

  • (Method R1) log-GLM-DR—DR estimator with GLM Gamma model with log link—Here the model is same as in (6) but now η = η″.

  • (Method R2) EEE-DR—DR estimator with EEE regression—Here the model is same as in (7) but now η = η″.

Note that the alternative methods presented here are neither an exhaustive set of available methods nor do they represent newer methods that are emerging (e.g., local-linear ridge regressions). Our choice of these estimators was primarily driven by their popularity within health services research and the medical literature.

For any method, an estimate for the incremental effect of a binary treatment variable D is obtained using the method of recycled predictions (Oaxaca 1973; Manning et al. 1987). In this method, \( \hat{\mu }(x_{i} ,e(x_{i} )) \) is predicted using estimated model parameters from covariate adjustment or PS/DR methods. We average the predictions \( \hat{\mu }(x_{i} ,d_{i} = 1,\hat{e}(x_{i} )) \) across all individuals i (i = 1, 2,…,N). Here, x i and d i are the values of X and D for the ith observation. Note that we have set d i  = 1 for all i. We then assign the value of 0 to D for all individuals as if they are not treated and average the predictions \( \hat{\mu }(x_{i} ,d_{i} = 0,\hat{e}(x_{i} )) \) across these individuals. Here the hat (^) on \( \hat{\mu} \) indicates that the regression parameters have been estimated. The difference in the mean (\( \hat{\mu } \)) between the two scenarios gives us the estimated ATE, \( \hat{\Updelta } \):

$$ \hat{\Updelta }\, = N_{{}}^{ - 1} \sum\limits_{i = 1}^{{N_{{}} }} {\{ \hat{\mu }(x_{i} ,d_{i} = 1,\hat{e}(x_{i} ))} - \hat{\mu }(x_{i} ,d_{i} = 0,\hat{e}(x_{i} ))\} $$
(13)

4 Monte-Carlo evidence

In this section, we develop a Monte Carlo simulation study in two parts. The first part establishes whether balancing on estimated PS achieves convergence beyond the mean X’s in a moderate sample size of 5,000, a sample size typical of most health and other economic applications.

The second part generates outcomes under four different non-linear data generating processes using the same design points to study how covariate adjustment versus PS methods perform in approximating the true Δ. In reality, it is impossible to simulate the vast range of plausible data generating processes here. Since our primary goal is to illustrate that alternative PS methods, very much like alternative regression methods, may perform poorly under certain non-linear data generating processes, we focus on only four data generating processes. Under these four processes, one or more of the covariate adjustment methods represents a misspecified estimator. Similarly, for the PS matching methods P1–P4, the estimator specified to estimate the PS could either be misspecified or correctly specified. Additionally, for the doubly robust methods R1–R2, both, none, or either of the covariate adjustment method or the propensity estimator could be misspecified.Footnote 9 We use a relatively modest dimension of three covariates to illustrate our points. The empirical example in Sect. 6 illustrates the effect of a larger dimension of X.

4.1 First set of simulations

4.1.1 Design

We design a simulation to study whether conditioning on estimated PS not only results in equality of the mean of the covariates across the two treatment groups but also achieves equality on the higher order moments and the joint distribution of these covariates across treatment groups. We simulate the joint distribution of three covariates X = {X 1, X 2, X 3}, where X 1 is a binary covariate. We generated 1,000 replicate samples of 5,000 each for the vector \( X^{\ast} = \{ X_{1}^{\ast} ,X_{2} ,X_{3} \} \) following

  • \( X_{1}^{\ast} \sim Uniform(0,1),X_{1} = (X_{1}^{\ast} > 0.5);\)

  • \( X_{2} \sim 0.62*X_{1}^{\ast} + 2*Uniform(0,1);\) and

  • \( X_{3} \sim 0.42*X_{1}^{\ast} + 2*Uniform(0,1). \)

The correlations between them are given by \( \rho_{{1^{\ast} 2}} = 0.25,\rho_{{1^{\ast} 3}} = 0.18,\rho_{23} = 0.06, \) where \( Corr(X_{j} ,X_{{j^{\prime}}} ) = \rho_{{jj^{\prime}}} . \) These correlations are in line with the typical correlations observed between covariates in a cost regression.Footnote 10 Using these covariates, we then define treatment choice (D = 0.1) using a logit index model where D ~ Bernoulli(p), and

$$ {\text{logit}}(p) = \left( {0 + \ln (1.5) \cdot X_{1} + \ln (0.5) \cdot X_{2} + \ln (0.5) \cdot X_{3} + \ln (1.5) \cdot \left[ {X_{1} \cdot X_{2} } \right] + \ln (2.0) \cdot \left[ {X_{2}^{2} } \right] + \ln (1.75) \cdot \left[ {X_{3}^{2} } \right]} \right) $$
(14)

The coefficients in (14) are fixed arbitrarily so that approximately 70% of the population receives treatment.Footnote 11

We estimate the PS, e(X), in each replicate sample based on a logistic regression of D using the same specification as in (14) so that the PS estimator is not misspecified. We estimate the mean of X and standard deviation of X for each treatment group when they share the same PSs rounded to two decimal places. Similarly, we estimate the correlation between any two X’s for each treatment group when they share the same PSs rounded to one decimal place. Results are averaged over 1,000 replicate samples.

4.1.2 Results from the first set of simulations

Figure 1a reports the densities of estimated PS by treatment group and shows that the densities exist over the same regions for both treatment groups. Figure 1b–d report connected plots of the means, standard deviations, and correlations among the X’s by treatment status conditional on the estimated PS. Conditional on the estimated PS, we find that the X’s have almost identical means in both treatment groups. However, they do not have identical standard deviation or correlations, with the biggest discrepancies arising at the upper end of the estimated PSs. This implies that in many practical instances, PSs may fail to remove imbalances in the joint distribution of covariates across treatment groups. To what extent this limitation would affect estimation of treatment effects would depend on the degree of non-linearity in the data-generating model for a particular study population.

Fig. 1
figure 1

Initial simulation results (averaged over 1,000 replicates): a Distribution of PSs by treatment groups; b mean X’s by treatment status over estimated PS; c Std. deviation of X’s by treatment status over estimated PS; d correlation between X’s by treatment status over estimated PS

Full size image

Our initial simulation exercise motivates our interest in a more formal study of these issues and the next set of simulations.

4.2 Second set of simulations

4.2.1 Design

We use the same design points for the data on covariates and treatment receipt described above. We do not use the exact specification that generated the treatment choice data for estimating the PSs because in an actual analysis the analyst would never know the true functional form of the model that generates choices. Instead, using logistic regression, we estimate a saturated model that includes all second-order polynomials of X and the one-way interactions among them and that closely approximates a non-parametric estimator. Although this is an over-specified model given our data, it should not produce systematic biases in the prediction of PSs. We also estimate an unsaturated model, where only the main effects of X are use. This, therefore, represents a misspecified PS estimator. Therefore, in all, we study 14 estimators corresponding to methods C1–C2 and two versions of P1–P4 and R1–R2 based on varying the model estimating the PSs between the unsaturated and the saturated models.

All of the four outcome data-generating processes (DGP) we consider belong to the gamma distribution (shape = 2.0), which corresponds to a skewed bell-shaped distribution. The population mean for each DGP is scaled to be 1. Higher order moments for each DGP reflect typical characteristics of expenditure data that we see in practice. We highlight some of these similarities in Table 1. The DGPs also differ in their degrees of non-linearity between their mean and X’s through different link functions and non-linear functional forms. The degrees of non-linearity are the main factors determining the performance of the alternative estimators. They are designed to generate a priori hypotheses for estimator performance as described below. The four mean functions are given as:

  1. D1

    \(E(Y|D,X) = (100 + 800 \cdot D + 250 \cdot X_{1} + 250 \cdot X_{2} + 50 \cdot X_{3} )^{2.5} \)

  2. D2

    \(E(Y|D,X) = \left( {2.5 + 0.2 \cdot D - 2 \cdot p(X)} \right)^{ - 4} \)

  3. D3

    \(E(Y|D,X) = \exp (0.05 +0.25\,\cdot\,\exp(X_1/2)+0.1 \,\cdot\,\left(1+(X_1 \cdot X_3)/25\right)^{3}- 0.05\,\cdot\, D \,\cdot\,({X_{1} + X_{3} +2})^{2} - 0.2 \,\cdot\, D\,\cdot\,X_{2}/(11+\exp(X_3)))\)

  4. D4

    \(E(Y|D,X) = \left( {0.4 + 0.266 \cdot D - 0.4 \cdot p(X) + 25 \cdot D \cdot p(X)} \right)^{ - 1}. \)

Here, p(X) is given as the expit(.) of the linear predictor in (14). Y is scaled to have a mean of 1. The coefficients are chosen so that the absolute standardized ATE, where absolute ATE is divided by the standard deviation of Y, is 1 under each DGP.

Table 1 Characteristics of data generating processes used for simulations
Full size table

A priori, we expect the EEE (Method C3) to be a consistent estimator under DGP D1 and potentially unbiased even in finite samples. Consequently, we expect all PS-based estimators and also DR estimators to be consistent under DGP1, although the EEE method should be the most efficient compared to the alternatives under this DGP. For DGPs 2, 3, or 4, however, it is not clear a priori whether any of the regression estimators will be consistent. Even though PS-based methods, which do not depend on identifying appropriate functional forms for a DGPs, should be consistent, it is not clear if they will carry biases in finite samples, as the treatment effects vary over higher-order moments and covariances of X’s. A priori, one might expect a DR estimator using a flexible regression, such as the EEE, to exhibit less bias under misspecification than the other estimators. For estimation of treatment effects, we truncate an estimate of PS greater than 0.95 to 0.95. Overall, the varying degrees of non-linearity of the mean function with respect to X sets up to establish the proof by contradiction that no one estimator may be appropriate under all DGPs.

In order to study these issues, we generate 1,000 replicate samples of 5,000 each under each data generating process (DGP hereon). For each replicate data set j (j = 1,2,…,1,000) and under each of 14 different estimators (k = 1,2,…,14), we estimate the average treatment effect (ATE, hereon) \( \hat{\Updelta }_{jk} \) computed using (13), and the root mean square error \( \left( {RMSE_{jk} } \right) \, = \,\sqrt {n^{ - 1} \cdot \sum\nolimits_{i} {\left( {y_{ijk} - \hat{\mu }_{ijk} (x)} \right)^{2} } }. \) We report the percent mean bias (and 95% CI) in estimating Δ under each method that is given by \( (E_{j} (\hat{\Updelta }_{jk} ) - \Updelta_{True} ) \cdot 100/\Updelta_{True}. \) (A normal theory 95% CI calculated using the standard deviation of \( \hat{\Updelta }_{jk} \) across j.) We also report the relative root mean square error for each method (except for the matching estimators) relative to the inverse-propensity weighting method (Method P3) where the PSs are estimated using the saturated model: \( \left( {RRMSE_{k} } \right) = E_{j} \left( {\left( {RMSE_{jk} } \right)/E_{j} \left( {RMSE_{jk*} } \right)} \right), \) where k* represents Method P3 under saturated PS specification.

4.2.2 Results from the second set of simulations

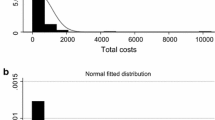
Table 1 reports the descriptive statistics for our DGPs and associated ATE. Figure 2 illustrates the density of outcome Y from each DGP, where Y is scaled to have mean 1 in each case. All DGPs show substantial skewness and kurtosis on the right hand side of the distribution, typical of most costs datasets.

Fig. 2
figure 2

Probability densities of Y under each data generating process, where Y was scaled so that E(Y) = 1 in each case

Full size image
4.2.2.1 Results for DGP1 (Table 2)

Regression methods: As expected, we find that the EEE method (C2) is unbiased while the log-GLM (C1) method is not.

Table 2 Simulation results for DGP 1 and DGP 2
Full size table

Saturated model for PS: All of the PS-based methods produce unbiased estimates of ATE; however, they appear to be inefficient compared to C2. The EEE-DR (R2) produces unbiased estimates of ATE but has approximately 1.3 times higher standard errors for ATE compared to C2. The log-GLM-DR (R1) produces unbiased estimates, upholding its DR feature, although it is even more inefficient than EEE-DR.

Unsaturated model for PS: Misspecification of propensity model does not affect any of the PS-based methods under this DGP and all the approaches produce unbiased estimates of ATE. The log-GLM-DR (R1) produces biased results as it becomes “doubly misspecified” under this data-generating mechanism.

EEE (C2) clearly outperforms other estimators for DGP D1.

4.2.2.2 Results for DGP2 (Table 2)

Regression methods: Log-GLM (C1) is biased. EEE (C2) produces a 14% bias that is not significant.

Saturated model for PS: PS-method P2 (inverse probability weighting (IPW)) produces unbiased estimates of ATE; however, estimates from P1, P3, and P4 are biased. The DR methods have difficulty converging under this DGP.

Unsaturated model for PS: Even P2 produces biased estimates of ATE.

The IPW (P2) estimator with PS estimated from a saturated model appears to be the best choice for DGP D2.

4.2.2.3 Results for DGP3 (Table 3)

Regression methods: Both C1 and C2 regression estimators produce biased estimates of ATE.

Table 3 Simulation results for DGP 3 and DGP 4
Full size table

Saturated model for PS: All PS methods, P1–P4, and also the doubly-robust methods, R1 and R2, produce unbiased estimates of ATE, with P1 or P3 being the most efficient.

Unsaturated model for PS: P1–P4 estimators still produce unbiased estimates, but the DR estimators do not. In DR estimators, the biases from the regression models and the misspecified PS estimator seem to reinforce each other.

Under this DGP, either the PS stratification estimator (P1) or the kernel-based matching estimator (P4) produces the best results when the PS estimates came from the saturated model.

4.2.2.4 Results for DGP4 (Table 3)

Regression methods: Both regression estimators, log-GLM (C1) and EEE (C2), produce biased estimates of ATE.

Saturated model for PS: P1, P3, and P4 estimators are also biased in estimating ATE; however, the inverse-probability weighted estimator, P2, is unbiased. The GLM-DR (R1) produces biased results, indicating that properly specified PS estimates may fail to uphold the DR property when combined with an overly biased regression estimator. In contrast, the EE-DR model produces unbiased results and also is more efficient compared to P2 (41% reduction in RMSE).

Saturated model for PS: All PS-based estimators and the DR estimator produce biased results.

The EE-DR model using estimated PS from a saturated model is the most desirable estimator under this DGP.

4.3 Summary of simulation results

Our simulations reveal several key features about the use of PSs to estimate treatment effects in data generated via non-linear DGPs. It is well known that traditional regression methods may misspecify the link function (such as log-link GLM) and may not always capture the underlying data generating mechanism. To overcome these limitations, the EEE regression method provides quite a bit of flexibility by estimating a link parameter for a power family of link functions from the data and thus can guide the functional form best suited for the data at hand. However, even the EEE is not the answer for all non-linear data generating mechanisms (as we see in the case of DGPs D2–D4). Propensity scores provide an alternative approach to overcome some of the limitations of functional form inherent in regression methods, although these approaches are also sensitive to specification of the PS estimator. More importantly, we find that even when PSs are generated from a correctly specified model, PS-based methods may produce biased estimates of ATE under alternate DGPs. As our simulations show, a different estimator came out to be the best under each of the four DGPs.

Below is a summary of the main results from our simulations:

  1. 1.

    Stratifying by quintiles of estimated PS or matching on them using the kernel-based matching estimator or local-linear regression can be a more efficient alternative to the IPW estimator for a variety of non-linear DGPs. However, like the EEE method, they are not guaranteed to provide unbiased estimates under all types of non-linear DGPs. The local linear regression matching estimator is found to be more robust compared to stratification.

  2. 2.

    The IPW estimator is the most robust PS-based method. It is most likely to be unbiased as long as there is no misspecification in the estimation of the PSs.

  3. 3.

    If an unbiased regression estimator exists, it will usually be more efficient than the IPW estimator.

  4. 4.

    Doubly robust estimators are sensitive to both misspecifications of the PS estimators and also to the regression methods. Misspecification in one of them is often compensated by correctly specifying the other method, but this double robustness comes at an expense of efficiency. Efficiency of DR estimators lie somewhere in between the regression methods and the IPW estimator. Generally, EEE-DR performs better than the GLM-DR with a log link since EEE provides additional flexibility in modeling the data.

We now illustrate the application of these estimators in estimating the ATE between two treatment options amongst breast cancer patients.

5 Empirical example

Breast cancer is the second leading cause of cancer death in women in the United States. With advances of screening and early detection, most cases of breast cancer are diagnosed in the early stages, when chances of survival are excellent (Rias et al. 2000). However, the costs associated with treatment of patients with breast cancer are substantial. Local therapies for early-stage breast cancer include breast-conserving surgery with radiation (BCSRT) and mastectomy. Large clinical trials that studied the efficacy of these treatments found that BCSRT and mastectomy are equivalent in terms of long-term survival (National Institutes of Health Consensus Conference (1991)). These results have increased the relevance of comparing costs across alternative treatments for early-stage breast cancer.

Several cost studies have compared surgical treatments for early-stage breast cancer. These studies indicate that BCSRT may be more expensive than mastectomy, but evidence is not conclusive (Norum et al. 1997; Desch et al. 1999; Given et al. 2001; Barlow et al. 2001; Warren et al. 2002). Most have used OLS regression to model costs; however, Given et al. (2001) used log-OLS regression, although without dealing with issues of retransformation. Polsky et al. (2003) evaluated breast cancer treatments using PSs but found the 5-year incremental cost estimate between BCSRT and mastectomy ($14,054, 95% CI, $9,791–$18,317) to be similar to that estimated via OLS regression ($13,775, 95% CI, $9,853–$17,697).

5.1 Data

Our data consisted of a 5% random sample from the Center for Medicare and Medicaid Services national claims database of all Medicare beneficiaries. The data were collected as part of the Outcomes and Preferences in Older Women Nationwide Survey (OPTIONS) project (Hadley et al. 1992), and were used by other researchers (Hadley et al. 2003; Polsky et al. 2003). The dataset was constructed by the OPTIONS team in four steps: (1) Medicare claims for persons with a breast cancer diagnosis or relevant surgery procedure codes for calendar years 1992–1994 were obtained. (2) Additional exclusions were applied to make BCSRT and mastectomy (MST) be considered equivalent from the clinical point of view for all women in the sample (Hadley et al. 2003; Polsky et al. 2003). Cases for which breast cancer was not the primary diagnosis were deleted. (3) Surgeons identified in the dataset were surveyed to verify study eligibility of the patients. (4) Additional exclusions were applied to exclude patients who were in a Medicare health maintenance organization in the month of the survey because their cost data were not available in the claims file. Finally, patients who had breast-conservation surgery but did not receive radiation were excluded. The data, although over 10 years old at this point, provide a unique opportunity to analyze a large national sample of Medicare beneficiaries with a confirmed diagnosis of early-stage breast cancer. Moreover, we chose this dataset for comparability to other results based on this dataset published in the literature (Hadley et al. 1992, 2003; Polsky et al. 2003).

We use all 5-year Medicare payments from inpatient, outpatient, and physician Part-B claims to estimate direct medical costs, including costs related to breast cancer treatment and all other medical costs covered by Medicare; and calculate total costs using an annual 3% discount rate. The final sample consisted of 2,517 patients, of whom 1,813 patients had mastectomies and the remaining had BCSRT. The distribution of patient characteristics by treatment type is published elsewhere (Polsky et al. 2003). The covariates that we adjust for are variables that are both measurable and theoretically predictive of costs, including age at the time of surgery, cancer stage, Charlson co-morbidity index, and race. Because claims do not contain socioeconomic data, we use percentage college graduates, median household income, and percentage below poverty level by 5-digit zip-code. Additionally, we adjust for county-level data on health system characteristics, such as number of hospital admissions, number of nursing homes, and an indicator for urban area. We assume that there are no unobserved confounders.

Our primary goal of the analysis is to estimate the ATE of BCSRT over MST on total costs (we do not address issues of unobserved confounders here). For the sake of completeness, we apply all the estimators that we evaluated in our simulations. In order to estimate PSs, we start with a saturated logistic regression model that includes all quadratic terms and two-way interactions besides the main-effects. We then follow a stepwise approach with backward selection to arrive at a model that shows reasonably good fit to the treatment choices.

5.2 Results

The final logistic regression estimator for estimating PSs passes all the goodness of fit tests conducted based on raw-scale residuals (Pearson correlation test, ρ = 0.002, P value = 0.94; Pregibon’s Link test, z = −0.20, P value = 0.85; and modified Hosmer–Lemeshow test, F = 0.93, P value = 0.51). Figure 3a shows the distribution of estimated PSs to select BCSRT for the two treatment categories.

Fig. 3
figure 3

a Distribution of estimated PSs by treatment groups; b imbalances in mean and standard deviation of Charlson Index score (ChSc) and the correlation between CHSc and median household income between treatment groups at specific values (ranges in the case of correlation) of estimated PSs

Full size image

We also look at the overall levels of balance in the covariate means. We run a seemingly unrelated regression where each covariate is regressed on the BCSRT indicator and the estimated PS. We find that the P value on the coefficient of the BCSRT indicator is close to 0.98 for every covariate, which indicates excellent overall balance in the covariate means across treatment groups once adjusted for PSs. The joint test of the coefficients across all covariates is also highly insignificant (P value = 0.99). However, a closer look at the distribution of covariates across estimated PS reveals greater discrepancies. Figure 3b shows the level of match attained between treatment groups after conditioning on the estimated PSs for three statistics: (1) the mean and standard deviation of one of the covariates, (2) the Charlson’s score, and (3) the correlation between Charlson’s score and median household income. We find substantial discrepancies in all three statistics even in regions where the estimated PSs have substantial probability density mass.

As with any regression model, any conclusion about the lack of bias for its parameters comes from the goodness of fit of the model to the data. Figure 4 illustrates the goodness of fit for log-GLM and EEE methods and the corresponding DR methods, log-GLM-DR and EEE-DR, in terms of raw-scale residuals over their corresponding deciles of linear predictors. Both the log-link GLM method and its DR alternative show curvature in the raw-scale residuals over the deciles of their linear predictors. Both of these estimators fail the more parsimonious Pregibon’s Link test (GLM: z = −6.01, P value < 0.001; GLM-DR: z = −3.01, P value = 0.003). On the other hand, the EEE method and its doubly-robust counterpart show no systematic biases and pass all goodness of fit tests. In fact the EEE appears to be more efficient in its predictions compared to EEE-DR.

Fig. 4
figure 4

Analysis on cost of breast cancer treatments. Profile of residuals over the deciles of linear predictors for log-GLM and EEE methods and the corresponding DR methods log-GLM-DR and EEE-DR

Full size image

These features translate to the ATEs shown in Table 4. The log-link GLM regression estimator produces ATEs that are significantly different from the EEE estimate at the 5% level, representing a bias (compared to the EEE estimate) of about 24%. All the PS-based estimators also produce big discrepancies compared to the EEE estimator (with bias ranging from 10 to 14%), but each is quite inefficient for its estimate to be significantly different from the EEE estimate. For example, the log-link GLM-DR model, which we know to be a biased estimator based on goodness of fit criteria illustrated in Fig. 4, also produces a bias of about 14%, without being statistically different from the EEE estimator, due to its inefficiency.

Table 4 Estimated ATE of BCSRT versus MST in breast cancer patients
Full size table

As expected from our simulation results, we find that the PS weighting is robust but also inefficient (due to discrepancies in higher order moments of covariates after propensity matching, as illustrated in Fig. 3b). This inefficiency comes with an unstable point estimate, because the empirical example is just one realization of the data. Thus, goodness-of-fit tests can help practitioners evaluate and trade-off potential biases with efficiency. For this data, the EEE appears to be the best estimator both based on its efficiency and also on the evidence of lack of bias based on the goodness-of-fit tests.

6 Discussion

We compare the performance of various regression, PS-based, and DR estimators in estimating ATEs on outcomes generated via non-linear data generating processes that simulate processes common for health care costs. Our simulations suggest that conditioning on estimated PS creates balance across treatment groups in the means but not necessarily in the higher order moments nor in the joint distribution of X’s. This finding does not go away when an over-specified model is used to estimate the PS. As a result, we believe that PS estimators for treatment effects on health care costs are inefficient at best, but biased at worst.

Our second set of simulations demonstrate certain non-linear generating mechanisms where the PS estimators produce biased estimates of treatment effects. Interestingly, when a PS estimand is not misspecified, inverse-probability weighting using PSs is the only unbiased estimator under all data generating mechanisms studied and outperforms matching estimators. This is in line with Busso et al.’s work (2009). However, PS-based estimators are often extremely inefficient when compared to an unbiased regression estimator. All PS-based estimators are prone to bias when PSs estimator is misspecified, which is in contrast to Zhao’s findings (2008). Thus, care, should be taken before naively applying any one estimator to estimate ATEs.

An important caveat to this work is that all our simulations assumed good overlap between the treatment groups, and none of the simulations considered unobserved variables.

Based on our findings, we also conjecture that, like regression methods, PS methods may suffer from the curse of dimensionality when the outcomes data are potentially generated via non-linear data generating processes. This is primarily because matching on propensity must not only ensure matching of covariate means across treatment groups but also the entire joint distribution of the covariates across treatment groups. This second criteria is seldom achieved in a finite sample and gives rise to bias and inefficiency when using PS-based estimators on outcomes that are presumably generated via non-linear processes. Further work in this area can provide useful guidance for researchers.

We hope that our results and discussions will convey to researchers the potential pitfalls of relying on any one estimator exclusively, especially for non-linear outcomes such as health care costs.