1 Introduction

For United States military forces operating in a combat environment, there are two options for transporting a casualty to the nearest medical facility. The first option is to conduct a casualty evacuation (CASEVAC), which consists of transporting the casualty from the point of injury to the nearest appropriate medical facility without dedicated personnel to provide medical care en route. The second option is to conduct a medical evacuation (MEDEVAC), which requires a 9-line MEDEVAC request submission and includes dedicated medical personnel to treat the casualty during transit. MEDEVAC provides timely and efficient medical treatment and transportation for casualties on the battlefield en route to the nearest required medical facility, greatly increasing the probability of a patient’s survivability [8]. The MEDEVAC mission commonly refers to the use of dedicated rotary wing aircraft (i.e., ambulatory helicopters) equipped with medical personnel and equipment [9].

Introduced during the American Civil War, the CASEVAC and MEDEVAC systems continually improved during the next seven major American conflicts, from the Spanish-American War in 1898 to the recent operations in Afghanistan and Iraq. With over a century of development and technological advancement, the current MEDEVAC system is quite successful in preserving the lives of many wounded soldiers [26]. However, challenges remain.

Extensive research has been conducted over the past four decades concerning emergency response systems [21]. These studies analyze several different aspects of the emergency response system: ambulance originating location, repositioning of ambulances post-response, and ambulance dispatch policy. Typical performance measures include response time threshold and patient survival probability. Much of the research since the late 1960’s focuses on the civilian emergency response system; very few studies examine the military’s MEDEVACFootnote 1 system.

We consider a military emergency response system operating in a combat environment. We examine the problem of optimally dispatching ambulatory helicopters to prioritized casualty events in order to maximize steady-state system utility. Our dispatch policy is based on the location of idle MEDEVAC units, the location of the casualty event, and the overall priority class of the casualty event. We define the individual casualty priority levels according to the field medical service technician student manual definitions [11]. They are as follows: urgent means the casualty must be evacuated as soon as possible or within two hours due to possible loss of life, limb, or eyesight; priority means the casualty must be evacuated within four hours and the condition can worsen to urgent; and routine means the casualty must be evacuated within 24 hours.

We formulate an infinite-horizon, undiscounted, average reward Markov decision process (MDP) model to determine how to optimally dispatch MEDEVAC helicopters to casualty events on the battlefield in order to maximize the steady-state expected system utility. A computational example is applied to a MEDEVAC system forward deployed in Afghanistan in support of combat operations. We apply a Hawkes process using Monte Carlo methods to generate data concerning casualties in our scenario of interest and use these results to parameterize our MDP model. Examination of the resulting optimal policies reveals the effect an armed escort requirement has on the performance of these policies. Moreover, we compare the optimal policies to myopic policies (i.e., simply dispatching the closest unit to each casualty) and intra-zone policies (i.e., MEDEVACs serving only their own zones due to airspace restrictions). We assume that the medical treatment facility (MTF) locations are fixed, and that all MEDEVAC helicopters have the same capacities and can be configured to meet the mission requirements specified by the 9-line MEDEVAC request.

Our research extends and applies much of the work of Bandara et al. [1], McLay and Mayorga [36], and McLay and Mayorga [35]. A brief review of each is warranted.

Bandara et al. [1] examine the optimal dispatch policy within the emergency medical service (EMS) system while focusing on the urgency level of an emergency call. They develop an MDP model to identify how to optimally dispatch ambulances to patients. In order to properly consider the optimal policies for decision-making at each discrete time epoch, they use the uniformization method to convert the continuous-time MDP that they initially develop into an equivalent discrete-time MDP. This basic MDP model serves as the basis for the analysis in McLay and Mayorga [36] and McLay and Mayorga [35], as well as in our paper. Bandara et al. [1] mention several studies in which the EMS system greatly improves the patients’ survival probability if their priority level is taken into consideration when deciding which vehicle to dispatch. As such, they employ an optimality criterion based on patient survivability. Their study reveals that the optimal policy is to send the closest unit to the most urgent call and the next idle unit to the less urgent call, regardless of the call order. While this result may seem intuitive, this dispatch policy quickly becomes complex. For example, it may be optimal to dispatch a vehicle that is farther if the closer vehicle is more likely to receive a higher priority call. This policy essentially rations the closer vehicle in anticipation of a more urgent request. For problems with several more service zones and ambulances, the policy might not be as intuitive, although EMS systems stand to benefit greatly from the employment of an optimal policy versus a myopic policy.

McLay and Mayorga [36] examine the optimal dispatch policy within the EMS system while considering patient classification errors. McLay and Mayorga [36] differs from Bandara et al. [1] in that they consider patient classification errors and employ an optimality criterion based on response time threshold (RTT) rather than patient survivability. They focus on the patients’ urgency level with an overall objective of maximizing the average long-run utility of the EMS system, rewarding the expected coverage of high-risk patients. The RTT that they use within their utility calculations, however, is different than the RTT used in our calculations because they define the response time as the time it takes from when the ambulance is dispatched to when it arrives at the injury location.

McLay and Mayorga [35] examine the optimal dispatch policy within a general server-to-customer service system (i.e., an EMS system) while considering the issue of balancing equity and efficiency. They extend the modeling framework employed in McLay and Mayorga [36] by considering a constrained variant of the MDP developed in McLay and Mayorga [36]. They formulate a linear programming model to solve their constrained problem, using an objective of dispatching ambulances to patients to maximize average total reward subject to minimum standards of equity. They report results while considering four different notions of equity.

There are several differences between our paper and the three aforementioned research endeavors. The unique military aspect of our problem requires a more procedural development of the MDP model parameters. Indeed, the lack of unclassified historical, extensible data presents difficulties for those interested in examining military EMS systems. We cannot simply analyze a set of computer-aided dispatch (CAD) data and obtain the necessary parameters for an MDP. When seeking to inform decisions regarding the dispatching of MEDEVAC assets (e.g., in anticipation of a major combat operation), it is necessary to have notions of the anticipated sizes, locations, and dispositions for friendly and adversary forces. (Within a military context, ‘disposition’ denotes whether a unit is passively defending an area, actively patrolling it, or conducting some other deliberate operation.) As such, calls for service (i.e., 9-line MEDEVAC requests after casualty events have occurred) occur due to the interaction of these opposing forces in hostile actions. Such actions are very fluid, both with respect to location and intensity. Even within a counterinsurgency environment such as Afghanistan today, where the sizes, locations, and dispositions of friendly forces are relatively stable, the locations and dispositions of adversary forces are dynamic and challenging to predict. We develop a simulation of the MEDEVAC process that implicitly considers such information in order to generate the data needed to parameterize the MDP model. The selection of the casualty cluster centers used when simulating the MEDEVAC process embeds the information concerning the interaction of friendly and adversary forces. Further differences distinguish our work from prior efforts. We treat the batch arrival of casualties, which none of the previous papers consider. Due to the military context of our problem, we also use a different definition for RTT when defining our reward function. Lastly, we explicitly model the restriction that a given MEDEVAC can only serve a subset of zones because it is not realistic within a military operational environment to assume that every MEDEVAC can serve all zones.

This paper is organized as follows. Section 2 presents further background on MEDEVAC activities and provides a further review of pertinent literature. Section 3 provides a description of the problem for which we develop our model. Section 4 describes the MDP model we use to determine an optimal MEDEVAC dispatch policy. Section 5 describes an application of the MDP model to the analysis of an example based on current day combat operations in Afghanistan. Section 6 provides conclusions and directions for future research.

2 Background

Over the past four decades, many studies have focused on optimizing emergency response systems for both civilian and military applications. Past research examines the originating locations of the emergency units, the dispatch policies that stipulate which unit responds to each service call, and the repositioning of emergency units to specific locations to improve system response times. In the last decade, the United States Army has implemented the results of that research during combat operations in Iraq and Afghanistan.

Recent combat operations in Afghanistan heavily rely upon the MEDEVAC mission due to the rugged terrain and austere environment. Between 2007 and 2008, over 2060 MEDEVAC missions were flown to evacuate more than 3200 casualties, of which 30 % were classified as urgent [23]. The stated MEDEVAC goal, as directed by the Secretary of Defense, is to transport an urgent casualty to an appropriate medical facility within 60 minutes [17] from the receipt of the 9-line MEDEVAC request. In 2007, 12 % of MEDEVAC mission service times were outside the two-hour maximum timeline for an urgent patient. North Atlantic Treaty Organization (NATO) forces reduced that figure to 7 % by 2008 simply by operationally improving command and control and increasing the number of MEDEVAC aircraft. As a result, despite a higher operational tempo and increased violence during those years, the rate of soldiers killed in action (KIA) decreased even while the rate of soldiers wounded in action (WIA) increased [23]. This result indicates an improvement in the MEDEVAC system.

Although recent improvements have been made in the MEDEVAC system, different aspects of the system still require investigation. The Army’s MEDEVAC policies and procedures must continue to adapt to changes in enemy tactics. This fact is critically important when reviewing recent MEDEVAC policies and procedures because, unlike enemies that adhere to the Geneva Convention, the insurgents in Afghanistan consider medical vehicles to be legitimate (i.e., lawful) targets. Garrett [17] points out that, despite the clearly identifiable red cross marking, MEDEVAC aircraft operating in Afghanistan sustain small arms fire hits at the same ratio as other rotary-wing aircraft. As a result, many areas in Afghanistan require MEDEVAC aircraft to be accompanied by an armed escort. This is an essential factor that cannot be ignored.

This requirement has the adverse effect of potentially increasing the effective MEDEVAC response time due to engine warm-up and weapon systems inspections for armed escort aircraft, among other factors [23]. Although Garrett [17] states that from January 2010 to April 2012, only 31 % of MEDEVAC missions required an armed escort, and only 4 % of those missions were delayed as a result of the armed escort units, extra time spent waiting for armed escort availability causes an increase in average MEDEVAC response time, no matter how infrequently it is needed.

The decision-making process in the emergency response system is complex, whether it is a civilian EMS system or a military MEDEVAC system during combat operations. Multiple factors are involved in each step of the process, to include district location, the number of servers (i.e., MEDEVAC units) per district, dispatch policy, server location, repositioning the server location, or whether to focus on response time or patient survivability as the objective. Various methods are used to examine the EMS systems. These methods include, but are not limited to, discrete optimization, stochastic modeling, queuing, and simulation modeling [33].

Research from the late 1960’s and 1970’s focuses primarily on the civilian EMS system. These studies examine aspects such as the optimal placement of emergency vehicles, including both original placement and relocation, to provide the fastest response time. Few studies focus on optimizing the dispatch policy in order to improve the performance of the EMS system; even fewer seek to improve the performance of the MEDEVAC system. Examining the dispatch policy of emergency response vehicles requires a dynamic and stochastic approach. Moreover, many EMS systems’ dispatch policies do not take the priority level of the casualty event into consideration. This results in the nearest emergency response team fulfilling the requirement without regard to the void created in the system by that unit’s temporary absence. This is known as a myopic policy, and such policies have been shown to be inadequate by many researchers [1, 32, 33].

In addition to the three works highlighted in Section 1 that most significantly inform our research, Mayorga et al. [33] consider dispatching and districting policies to examine the performance of an EMS system. Their research improves the performance of the EMS system wherein performance is defined as the probability of patient survivability, which is inversely proportional to response times. Before they examine the dispatch policies, however, they examine the number of districts and district locations by developing a construction heuristic. Their research provides more depth than previous studies by analyzing the dispatch policies for inter-district and intra-district situations. An intra-district situation occurs when a response vehicle within its own district services the call, whereas an inter-district situation occurs when all response vehicles within a district area are busy and the call must be serviced by a response vehicle from a different district. For the inter-district policy, either a myopic policy (i.e., the closest vehicle responds) or a heuristic policy (e.g., as developed in Bandara et al. [1]) is used. While the myopic policy is the most widely used policy in the EMS system, the heuristic policy considers the priority of the call as well as the workload of each crew. For such an implementation, a utilization factor is included to consider the workload of each crew. For the intra-district policy, two policies are considered. The first policy assumes that a sister emergency service (fire department or police department) will respond. The military equivalent of this during combat operations is to have the casualty’s unit conduct first aid and transport him/her to the nearest MTF using its own vehicles, a quick reaction force (QRF), or a non-medical helicopter (i.e., CASEVAC). The second policy uses the heuristic policy that Bandara et al. [1] developed and allows a response vehicle from another district to cross boundary lines.

Fulton et al. [16] and Bastian [3] examine stochastic optimization for the allocation of MEDEVAC units in steady-state combat operations. Fulton et al. [16] present a stochastic optimization model that relocates deployable hospitals, reallocates hospital beds, and determines where emergency response vehicles (both air and ground MEDEVAC assets) should be located prior to a 9-line MEDEVAC request. Their objective is to minimize the amount of time it takes for the MEDEVAC unit to respond and transport the casualty or casualties to the appropriate MTF. Fulton et al. [16] describe a model that focuses on patient severity rather than the proximity to the patient in order to make the dispatch decision. Their patient severity for simulated casualties is determined from the historical data collection of patients’ injury severity scores (ISS) from Operation Iraqi Freedom (OIF). They make many of the same assumptions we make in this paper: since the missions are being conducted during stability operations, we assume the number of helicopters, ground ambulances, and crew members to be fixed. Their idea of using ISS patient survival probabilities in the model is loosely based on the research by Silva and Serra [39] regarding the importance of recognizing the priority levels of patients. The work by Bastian [3] describes a multi-criteria modeling approach that optimizes the emplacement of MEDEVAC assets. Specifically, his work maximizes casualty demand coverage and minimizes MEDEVAC spare capacity and site attack vulnerability, whereas our research provides an optimal dispatch policy in order to maximize the average long-run system utility.

Schmid [38] uses approximate dynamic programming (ADP) to determine optimal policies that minimize response times. Using real data from the EMS system in Vienna, Austria, Schmid [38] suggests that a dispatch policy that deviates from the ordinary dispatch policies can yield a nearly 13 % decrease in expected system response time. Service calls used in the model from this data were generated using a spatial Poisson process, which is the type of process that we use and which we describe at the end of Section 3. Although Schmid examines ambulance relocation and considers a civilian EMS system and we do not, more similarities than differences exist between our respective research endeavors. For example, the graphical representation that Schmid [38] offers in his problem description section is used as a basis for our MEDEVAC mission timeline, as shown later in Fig. 1.

Fig. 1
figure 1

MEDEVAC Mission Timeline

Full size image

Many more research studies relate, at least topically, to our problem and provide important insight into what has already been studied. For example, Berman [4] focuses on repositioning ambulances for follow-on service calls to minimize expected long-term travel times within the system. In his research, the dispatcher uses a myopic policy and considers repositioning only idle ambulances in order to compensate for areas not covered by busy ambulances. Maxwell et al. [32] use ADP to make decisions on where to redeploy ambulances within the EMS system in order to maximize the number of calls reached within a delay threshold. Erkut et al. [13] incorporate a survival function into existing covering models in order to generate new ambulance location models. More useful in our research, while considering our motivating problem in Afghanistan, Chanta et al. [5] focus on ambulance coverage for rural areas. Since many missions in Afghanistan are conducted in an austere, rural environment, the trade-off between efficiency (i.e., coverage) and equity between rural and urban zones examined in their research is relevant. However, their particular research focuses on developing a covering location model specific to ground ambulatory care. Despite their differences, however, all of these papers provide possible methodologies on how to examine problems concerning the emergency response system and offer contributions to the development of our research.

3 Problem description

MEDEVAC requests are submitted with very little, if any, lead time. This means that there is no time to prepare for them, and a quick response is necessary in order to achieve mission success. To complicate matters, many situations with a high threat level may require a team of armed helicopters to escort the MEDEVAC aircraft to the casualty site, creating the potential for further delays in the response time. Consequently, the MEDEVAC system must be extremely flexible and seek to minimize any decision-making delays in order to optimize performance. Developing an optimal policy for such decision-making assists in making this possible. We make the following assumptions when developing our model.

Casualty events arrive according to a Poisson process with rate λ. A single casualty event can have many casualties. Our data suggests four as a reasonable upper bound. Although more than four casualties can occur on a battlefield, placing this constraint on our model allows only one MEDEVAC asset (i.e., helicopter) to be dispatched for each casualty event.

We consider three types of MEDEVAC 9-line requests: urgent, priority, and routine. The same three priorities are used to classify casualties. All priority classes can be serviced by any MEDEVAC asset; that is, we assume all necessary additional equipment is present on every MEDEVAC helicopter. The classification of the casualty event is defined as the highest classification level present at the casualty event (i.e., the most severe casualty).

Response and service times are independent of the casualty event classification. Although a routine casualty event allows a response time of 24 hours in combat situations, we assume that all 9-line MEDEVAC requests are serviced immediately, regardless of the priority classification, if a MEDEVAC unit is available.

There is zero-length queue for casualties; if a 9-line MEDEVAC request cannot be serviced immediately, we assume the casualties are treated on-site and transported to an MTF via CASEVAC. Aerial CASEVAC are common missions in combat according to other-than-MEDEVAC helicopter pilots and Operation Enduring Freedom (OEF) veterans [15].

Inter-zone policies, wherein a MEDEVAC asset from another casualty zone can be dispatched to service the 9-line request, are allowed unless otherwise stated. This allows out-of-zone MEDEVAC assets to assist with 9-line MEDEVAC requests if needed. It also creates the need for the decision maker to determine which MEDEVAC unit to dispatch to each casualty event. However, the nature of our motivating problem is such that only the in-zone MEDEVAC and out-of-zone MEDEVACs located in adjacent zones are allowed to service a given 9-line request.

When examining intra-zone only policies, we restrict MEDEVACs to operating only in their own zones. Military situations, such as execution of a specific, short-duration combat operation, may arise that force strict adherence to such policies to reduce fratricide and collision risks. Moreover, when allied countries are working together in a combat environment, perhaps for the first time and with limitations on their interoperability, intra-zone only policies that force MEDEVACs to only serve their own command’s zones may be prescribed due to communication, chain of command, or political realities.

We assume casualties are evacuated to the nearest MTF and that all MTFs in the area of operations have the same capabilities. Also, if a casualty occurs within close proximity (e.g., less than a 10-minute drive) to an MTF, the military unit on the ground conducts a CASEVAC in lieu of requesting MEDEVAC support. This is often the case in combat since transporting a casualty that is near an MTF will take less time than dispatching a MEDEVAC unit.

After a MEDEVAC asset completes its mission, it must return to its staging location in order to refuel and restock medical supplies before being available for dispatch again.

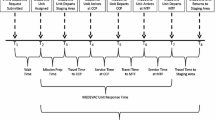
The MEDEVAC dispatching process for a situation requiring an armed escort closely follows a process similar to one outlined by [38] and is described in the timeline depicted graphically in Fig. 1.

Once the 9-line MEDEVAC request is received by an approving authority and the priority level of the request is determined, the appropriate idle MEDEVAC asset is notified and dispatched to the casualty site.

As depicted in Fig. 1, the time that the 9-line MEDEVAC request is received is denoted by t 9, the time at which the MEDEVAC unit is assigned to the mission is denoted by M 9, and the time at which the MEDEVAC unit departs is denoted by M d . The amount of time required between the receipt of the 9-line MEDEVAC request, t 9, and the MEDEVAC departure, M d , is the total dispatching time, D. This time encompasses the process of determining which MEDEVAC unit to dispatch, whether an armed escort is required or not, which armed escort unit to dispatch, if required; notifying the units; and finally preparing the personnel and helicopter for the mission. \({M^{c}_{a}}\) the MEDEVAC units arrive at the casualty site after traveling for T c minutes and begin treating and loading the casualty at time \({w^{c}_{9}}\) after waiting E minutes for the armed escort, if required, to arrive before the MEDEVAC helicopter approaches the casualty event location. Initial treatment and loading ends when the MEDEVAC helicopter departs the casualty site en route to the appropriate MTF and is denoted as \({e^{c}_{9}}\). The amount of time spent at the casualty site is L c. After traveling to the appropriate medical facility for T m minutes, the casualty is unloaded from time \({w^{m}_{9}}\) to time \({e^{m}_{9}}\), after which the casualty treatment continues inside the medical facility. The total unload time is denoted by U m. Once the casualty is unloaded at the medical facility, the MEDEVAC unit travels for T s minutes to its respective staging area. The MEDEVAC unit returns to its staging at time \({w^{s}_{9}}\) completing its mission, and becomes available for dispatch once again.

Note that travel times from the staging area to the casualty site, T c, from the casualty site to an appropriate medical facility, T m, and from the medical facility back to the staging area, T s, are expected to vary based on the conditions of the battlefield (e.g., weather conditions, enemy positions, altitude, the amount of equipment being transported). The respective load and unload times, L c and U m, of the casualties also vary.

EMS systems typically refer to response time as the amount of time required to reach the patient after receiving an emergency call. According to McLay and Mayorga [34], the rapid response to cardiac arrest situations is a primary focus in the EMS system. This is because the EMS system is often evaluated on how it responds to emergency cardiac arrest calls since there is effective treatment for cardiac arrests, and they are time-sensitive. Also, if the EMS system can respond quickly enough to a cardiac arrest call, they are more likely to be successful with similar life-or-death situations. Therefore, it is quite intuitive that the response time for a civilian EMS system is typically defined as the time between the receipt of the emergency call and the time the first emergency response vehicle arrives at the injury site [1].

However, the performance of the MEDEVAC system cannot be evaluated by the same measures as the EMS system since several additional factors are involved when medically evacuating a casualty from a battlefield. Not only can the load times, travel times, and unload times be much greater and vary much more, the primary cause of death on the battlefield is blood loss, not cardiac arrest. Very recent improvements have been made in this area by equipping MEDEVAC units with in-flight blood transfusion capabilities, but not enough data has been generated to alter the MEDEVAC system’s evaluation measure at the time of this research [31]. Garrett [17] reports that 85% of soldiers killed in action (KIA) were a direct result of blood loss. Thus, we consider it to be far more critical to stabilize and transport the casualty to the nearest MTF and into surgery than to simply reach him/her quickly. Thus, we define the response time for MEDEVAC j responding to a casualty event in zone i, denoted as R i j , to be the sum of the dispatch time, D, travel time to the casualty site, T c, potential armed escort delay, E, the load time at the casualty site, L c, travel time to the appropriate MTF, T m, and the unload time at the MTF, U m:

$$ R_{\textit{ij}} = D + T^{c} + E + L^{c} + T^{m} + U^{m}. $$
(1)

Service time, denoted as V i j , is simply the sum of the response time, R i j , and the travel time back to the staging area, T s:

$$ V_{\textit{ij}} = R_{\textit{ij}} + T^{s}. $$
(2)

4 Model formulation

In this section we present an MDP model formulation for determining an optimal MEDEVAC dispatch policy. The objective of this MDP model is to determine which MEDEVAC asset to dispatch in response to a given 9-line MEDEVAC request in order to maximize the long-run average utility over an undiscounted, infinite horizon. We assume 9-line MEDEVAC requests corresponding to casualty events arrive according to a Poisson process with rate λ.

We require the following input sets and parameters for our model.

\(Z\;=\;\left \{1,\;2,\ldots ,z\right \}\) is the set of casualty zones from which 9-line MEDEVAC requests originate, where \(z<\infty \).

\(M\;=\;\left \{1,\;2,\ldots ,m\right \}\) is the set of MEDEVAC assets that service 9-line MEDEVAC requests, where \(m\;<\;\infty \).

\(B_{j}\;\subseteq \;Z\) is the set of casualty zones to which MEDEVAC asset j ∈ M can respond.

λ is the 9-line MEDEVAC request (i.e., casualty event, a group of one or more casualties) arrival rate to the entire system.

ϕ i is the proportion of 9-line MEDEVAC requests from casualty zone i ∈ Z such that \({\sum }_{i\;\in \; Z}\phi _{i}\;=\;1.\)

p k is the proportion of 9-line MEDEVAC requests (i.e., casualty event, a group of one or more casualties) having priority k ∈ {1, 2, 3}, where k = 1, k = 2, and k = 3 correspond to urgent, priority, and routine casualty event classification levels, respectively, and where \({\sum }_{k\;=\;1}^{3} p_{k}\;=\;1\). A casualty event is classified according to the most severely injured casualty present in the group of casualties.

\(\psi _{\textit {ij}}^{k}\;<\;\infty \) is the utility gained by MEDEVAC j ∈ M servicing a casualty event with priority k ∈ {1, 2, 3} in zone i ∈ Z (conditioned implicitly by an associated RTT).

μ i j is the service rate of MEDEVAC j∈M when servicing a casualty event in zone i ∈ Z.

Our model enables the specification of zones to which a MEDEVAC station can – and implicitly cannot – provide service. We assume that the analysis is executed using a viable set of MEDEVAC locations. That is, the tessellation of the region and the definition of B j are such that no station is deemed too far from a casualty event location.

Of note, a military medical planner should select a λ appropriate for the operational conditions being examined. A particular λ can be interpreted as a parameter-value representative of a particular season and time of day (e.g., winter during daylight hours). A military medical planner should utilize λ to investigate peak activity for anticipated conditions when planning for medical support for a large-scale combat operation in an area of operations.

We note that assuming exponentially distributed service times may not be realistic. However, such an assumption is common in the literature. Computational experiments by Jarvis [29] suggest the behavior of the system we are modeling is relatively insensitive to the shape of the service time distribution. Gross and Harris [22] also provide a well-known insensitivity result. McLay and Mayorga [36] conduct a simulation analysis to compare the cases of using exponentially distributed service times versus more realistic service times. They find that the assumption of exponential service times does not dramatically impact the optimal policies. This suggests that optimal policies found using our MDP model provide relevant insights despite the simplifying assumption of exponentially distributed service times.

The MDP model components are as follows.

States:

Let \(S\;=\;S_{1}\;\times \;S_{2}\;\times \;\cdots \;\times \;S_{m}\;\subset \;{\mathbb R}^{m}\) denote the state space of the MEDEVAC system, where \(S_{j}\;=\;B_{j} \cup \left \{0\right \}\) is the state space of MEDEVAC j ∈ M. A zero indicates an idle MEDEVAC. Let s ∈ S denote the state of the MEDEVAC system, where s is the m-tuple s = (s 1,s 2, …, s m ) and where s j denotes the state of MEDEVAC j. As an example, consider a four zone system with four MEDEVAC assets, where each asset is located in a separate zone. When MEDEVAC 2 is busy and all other MEDEVAC assets are idle, we would have:

$$s\;=\;(0,\;i,\;0,\;0), \text{where} \textit{i}\;\in\;\textit{B}_{2}.$$

Actions:

The decision at hand is to determine which MEDEVAC unit to dispatch upon receipt of a 9-line MEDEVAC request from zone i. Let A s (i) denote the set of MEDEVACs available for dispatch when the system is in state s and a 9-line MEDEVAC request is received from zone i:

$$A_{s}(i)=\left\{\textit{j}\in \textit{M}: \textit{i}\in \textit{B}_{j} \text{and}s_{j} = 0\right\}. $$

Both intra- and inter-zone MEDEVAC responses are allowed. The differences between these two broad policy assumptions are captured by the manner in which B j is defined. When intra-zone only policies are enforced, a MEDEVAC may only serve 9-line MEDEVAC requests from its own zone. This is captured by stipulating a B j with only one element: the zone in which the MEDEVAC is stationed. When inter-zone policies are allowed, a MEDEVAC asset may service 9-line requests from zones other than its own originating zone. This is captured by stipulating a B j with more than one element. In some problem instances it may be possible for a MEDEVAC asset to serve all zones, so that B j = Z. However, due to our motivating problem of interest, in which it is not desirable for a MEDEVAC to cross multiple airspace control zones, we assume that MEDEVAC units may serve only adjacent zones. By design, a MEDEVAC asset may not respond to 9-line requests more than one zone away from its staging location. For example, consider a region that is subdivided by North-South boundaries into four zones, numbered 1-4 from West to East, and has one MEDEVAC asset based in each zone. In the event that Zone 2 has a casualty event and submits a 9-line request, only MEDEVAC assets from Zones 1, 2, or 3 are allowed to respond. Moreover, if the MEDEVAC unit in Zone 3 is busy when a 9-line request is submitted for a casualty event in Zone 3, only MEDEVAC units in Zones 2 or 4 can respond, resulting in A s (3) = {2, 4} when s = (0, 0, y, 0), y ≠ 0. Such constraints on the action space can be enforced as required by the context of the particular problem instance. Lastly, note that the current locations of busy MEDEVAC units do not impact the set of available actions.

Rewards:

An immediate expected utility \(\psi _{\textit {ij}}^{k}\) is obtained when MEDEVAC unit j ∈ M responds to a casualty event of priority class k ∈ {1, 2, 3} that occurs in zone i ∈ Z. The utility gained depends on the location, and priority class of the casualty event as well as the originating location of the servicing MEDEVAC.

The casualty event classification is based on the most severe classification of the individual casualties within it. Therefore, to properly classify the casualty event we proceed by developing details of a single casualty event, to include the classification of individual casualties. Note that the MDP model only uses the casualty event classification, which is derived from the individual classifications.

A single casualty event results in α casualties, where α is a discrete random variable with support {1, 2, …, N α }. We assume N α is less than or equal to the servicing capacity of one MEDEVAC helicopter. That is, the number of casualties at any one casualty event will not exceed the number of patients a single MEDEVAC can serve in a single service call. This assumption is reasonable; consider that the number of patients per MEDEVAC request over the first six years of military operations in Afghanistan did not exceed four personnel and the capacity of a single UH-60Q MEDEVAC helicopter is six litter-borne patients [19]. Each individual casualty is labeled as urgent, priority, or routine, and corresponds to a priority index level of h = 1, 2, 3, respectively. Let q = (q 1, q 2, q 3) denote the probabilities of an individual casualty belonging to a particular priority class, where q h is the probability an individual casualty belongs to priority class h. Let c = (c 1, c 2, c 3) denote the set of individual casualties present at a single casualty event, where c h is the number of individual casualties belonging to priority class h. It follows that c is a multinomial random variable with a probability mass function f(c|α;q). We obtain the proportion of 9-line MEDEVAC requests, p k , having priority k ∈ {1, 2, 3} as

$$\begin{array}{@{}rcl@{}} p_{k} = \left\{\begin{array}{ll} {\mathbb{P}}\{c_{1} > 0\} & \text{if } k = 1,\\ {\mathbb{P}}\{c_{1}=0, c_{2} > 0\}& \text{if } k = 2,\\ {\mathbb{P}}\{c_{1} = 0, c_{2} = 0\}& \text{if } k = 3. \end{array}\right. \end{array} $$

The utility r h is gained by servicing a priority h casualty, where we assume r 1 > r 2 > r 3 ≥0. Since we are most interested in servicing casualty events with life-threatening (i.e., urgent) injuries, we adopt a reward structure that incentivizes the servicing of such casualties and diminishes the importance of servicing a casualty event with no life-threatening injuries (i.e., routine). The system gains an expected utility of u(c) for servicing a single casualty event c, where

$$u(\mathbf{c}) = \sum\limits_{h=1}^{3} r_{h}c_{h}f(c_{h}|\alpha,\mathbf{q}). $$

Since we are able to classify a casualty event according to the most severe injury sustained at the casualty event prior to the determination of which MEDEVAC to send, we are able to denote an expected utility

$$u_{k}(\mathbf{c}) = \sum\limits_{h=k}^{3} r_{h}c_{h}f(c_{h}|\alpha,\mathbf{q}), $$

where k is the priority class of the casualty event.

There is a requirement that R i j , the response time of MEDEVAC j servicing a casualty event in zone i, must not exceed the RTT in order for the system to be rewarded. This requirement is captured when expressing the expected utility gained by MEDEVAC j servicing a single priority k casualty event c in zone i as:

$$\psi_{\textit{ij}}^{k}(\mathbf{c}) = u_{k}(\mathbf{c})I_{\left\{R_{\textit{ij}}\leq \textit{RTT}\right\}}, $$

where \(I_{\left \{R_{\textit {ij}}\leq \textit {RTT}\right \}}\) is an indicator variable which equals 1 when R i j ≤ R T T and 0 otherwise.

The utility \(\psi _{\textit {ij}}^{k}(\mathbf {c})\) is naturally contingent on the physical location of the casualty event within its zone and the distances between the MEDEVAC locations and MTFs. When considering a particular instance of our MEDEVAC dispatching problem, we obtain an average utility \(\psi _{\textit {ij}}^{k}\) and an expected service rate μ i j for each zone, MEDEVAC, and priority combination for use in the MDP. These parameters are obtained by simulating the casualty event arrival process and all possible subsequent MEDEVAC system responses for a large number of casualty events and computing the mean utilities and service times. Of particular importance in our simulation procedure is the placement of casualty event cluster locations. Further discussion of the simulation process is provided in Section 5.

Transitions:

State transitions are Markovian with two possible event types governing the transition. The first event type is the completion of service by one of the busy MEDEVAC assets. The second event type is the arrival of a 9-line MEDEVAC request which must be responded to by a MEDEVAC unit if one is available without violating stipulated intra- or inter-zone policies.

Optimality Equations:

Puterman [37] argues that the application of uniformization is desirable when analyzing continuous-time MDPs. Uniformization allows us to state an equivalent discrete-time MDP problem formulation. We proceed by determining the maximum rate of transition:

$$\nu = \lambda + \sum\limits_{\textit{j}\in \textit{M}} \beta_{j}, $$

where

$$\beta_{j} = \max\limits_{i\in Z} \mu_{\textit{ij}},\;j\in M. $$
$$\begin{array}{@{}rcl@{}} J_{n+1}(s) &=& \frac{1}{\nu} \left[\sum\limits_{\textit{j}\in \textit{M}}I_{\{s_{j}=i|i>0\}}\mu_{\textit{ij}}J_{n}(s_{1},s_{2},...,s_{j-1},0,s_{j+1},...,s_{m})\right.\\ &+& \sum\limits_{i\in Z}\sum\limits_{k=1}^{3}\lambda_{i} p_{k} \max_{j\in A_{s}(i)}\kern-1.5pt \left\{\kern-1.5ptI_{\{s_{j}=0\}}J_{n}(s_{1},s_{2},...,s_{j-1},i,s_{j+1},...,s_{m})\kern-1.5pt+\kern-1.5pt(\nu)(\psi_{\textit{ij}}^{k})\kern-1.5pt \right\}\\ &+&\left.(\nu\kern-1.5pt-\kern-1.5pt\lambda\kern-1.5pt-\kern-1.5pt\sum\limits_{\textit{j}\in \textit{M}} I_{\{s_{j}=i|i>0\}}\mu_{\textit{ij}})J_{n}(s)\right], \text{for} n = 0,1,...,N-1. \end{array} $$
(3)

We use relative value iteration with 𝜖 = 0.0001 to find an 𝜖-optimal policy, where the iterations can be interpreted as periods in a corresponding finite-horizon MDP. Let J n (s) denote the value of being in state s during iteration n. We initialize our value function so that J 0(s) = 0 for all s ∈ S. We follow the basic form of McLay and Mayorga [36] in defining our optimality equations. For the N-period case, the optimality equations are expressed as indicated in Eq. (3), where \(I_{\{s_{j}\;=\;i|i>0\}}\) is an indicator variable that denotes MEDEVAC j is busy in zone i, and \(I_{\{s_{j}\;=\;0\}}\) is an indicator variable that denotes MEDEVAC j is idle.

The first term in Eq. (3) describes busy MEDEVAC units becoming idle, the second term describes new 9-line MEDEVAC requests arriving to the system, and the third term describes the system remaining in the same state (i.e., with no new 9-line MEDEVAC requests or any MEDEVAC units becoming idle). To establish the existence of solutions to the optimality equations, consider the following observations. Puterman [37] suggests an MDP classification scheme based on the chain structure of the set of Markov chains induced by all stationary policies. In our MDP all chains are ergodic since a MEDEVAC must be dispatched to a casualty event if all other MEDEVACs capable of serving that casualty event are busy. We can therefore classify this MDP model as unichain. We observe that, since the model is unichain, S and A s are finite and rewards are bounded (i.e., \(\psi _{\textit {ij}}^{k}<\infty \)), for all s∈S and a ∈ A s , then there exists a stationary average reward optimal policy [37].

5 Computational example

In this section, we apply the MDP model to an example set in Afghanistan during steady state combat operations.

5.1 Estimating model parameters

We present an example in which MEDEVAC units are dispatched during steady state combat operations in support of OEF. The southern region of Afghanistan is the area of operation (AO) and is divided into four separate zones: Nimroz province (Zone 1), Helmand province (Zone 2), Kandahar province (Zone 3), and Zabul province (Zone 4). We use four MEDEVAC helicopters, with one based in each of the four separate zones. The MEDEVAC assets transport casualties to one of two MTFs, located in either Zone 2 or 3; Zones 1 and 4 do not have MTFs. The placement of medical assets represents a general realism based on past enemy activity in southern Afghanistan and the authors’ combat experience. Based on historical data, as well as the authors’ experience in Afghanistan, the casualty rates in Zones 2 and 3 are much higher than in Zones 1 and 4.

According to iCasualties.org [27], Helmand (Zone 2) and Kandahar (Zone 3) have been the two most casualty producing provinces in Afghanistan during OEF with 944 and 544 personnel killed in action (KIA), respectively. In contrast, there were six KIAs in Nimroz (Zone 1) and 118 KIAs in Zabul (Zone 4) during the same period. Although these numbers do not account for the numerous other casualties (e.g., military personnel wounded in action (WIA), civilian casualties), they provide an approximation of the threat present in each zone. We use this information to parameterize ϕ i , the proportion of casualties from Zone i. Simple calculations yield the casualty proportions per zone to be ϕ=(0.004,0.585,0.338,0.073).

These casualty proportions are consistent with the greater number of people, Afghan citizens as well as enemy and friendly combatants, who are present in both Helmand and Kandahar. According to the Afghan government, Zones 1-4 have populations of approximately 156,000 people, 880,000 people, 1.15 million people, and 289,000 people, respectively [20]. Moreover, according to United States Army policy [10] as well as the first author’s experience in Afghanistan, it is reasonable to expect that one brigade combat team (BCT) would be assigned Zones 1 and 2 as its area of operations (AO) and that the BCT would most likely assign the majority of its combat power to Zone 2 while assigning one task force (TF), which is a reinforced battalion, to Zone 1. Likewise, one BCT would be assigned Zones 3 and 4 as its AO while assigning the majority of its combat power in Zone 3 and one TF to Zone 4. The relative number of citizens and combatants in each zone suggests that more casualty events are expected to occur in Zones 2 and 3. Therefore, the MEDEVAC units located in Helmand and Kandahar provinces (i.e., Zones 2 and 3, respectively) have co-located MTFs.

Actual data for casualty, MEDEVAC unit, and MTF locations are restricted. Military medical planners anticipate future operations when estimating casualty event arrivals. Therefore, in order to compute utilities, we first generate the response and service times described in Section 3. To avoid using specific data from Afghanistan in order to maintain operational security while OEF stability operations are ongoing, we develop a procedure that leverages military medical planning techniques and the operational combat experience of the authors to model where future casualties may be sustained. Data from past experiences obviously informs this process, but future operations are important as well; data will certainly change with each unique conflict.

In the absence of data, we develop a Monte Carlo simulation and implement a spatial Hawkes process to combine the benefits of identifying arrival times for casualty events based on a self-exciting, conditional intensity [24, 25] with the spatial identification of demand locations via a Poisson cluster process (e.g., see Daley and Vere-Jones [7]). Employment of the Hawkes process to simulate the temporal aspects of criminal and terrorist activities is well documented (e.g., see Egesdal et al. [12] and White et al. [40], respectively), and has recently been shown to well represent casualty incidents within a country fighting an insurgency (see Lewis et al. [30]). To address the spatial distribution of events, casualty cluster centers are selected based on their close proximity to main supply routes (MSR) and rivers where population groupings are present, since these demographic and geographical features indicate common sites of attack during missions supporting OEF. Moreover, the distribution of casualty event locations from a given cluster center is generated on a uniform distribution, both with respect to its latitude and longitude from the cluster center.

Figure 2 depicts the four zones in southern Afghanistan that we use to generate our data, as well as the MEDEVAC and MTF locations. Recall that Zones 1 and 4 do not have MTFs whereas MEDEVACs 2 and 3 are co-located with MTFs 2 and 3, respectively. The casualty cluster centers in each zone are represented by black dots.

Fig. 2
figure 2

MEDEVAC and MTF locations with Casualty Cluster Centers

Full size image

Figure 3 illustrates several casualty events throughout southern Afghanistan within a given time period.

Fig. 3
figure 3

Casualty Events throughout southern Afghanistan

Full size image

The data generated for the variables in Eq.(1) vary with each mission and therefore are represented as random variables. The details of each variable used to calculate the response time, R i j , are described in the following five paragraphs.

According to subject matter experts and US Army MEDEVAC pilots, the flight speed, which accounts for the travel times, T c and T m, are each distributed uniformly over an interval of 120 and 150 knots with a resulting mean of 135 knots [14, 15]. Bastian [2] uses a slightly larger range with a flight speed that is also uniformly distributed between 120 and 193 knots, but we choose to use the narrower range for parameters provided by the pilots.

The dispatch time, D, is exponentially distributed. Bastian [2] uses a mean of 20 minutes based on a 2008 MEDEVAC after action review and a standard deviation of five minutes based on his personal experience. Garrett [17] suggests that only 4 % of MEDEVAC missions exceed the 15-minute launch criteria established by the Commander of the United States Central Command (USCENTCOM). We utilize a mean of 15 minutes rather than 20 minutes.

The delay caused by an armed escort, E, is exponentially distributed with a mean of 10 minutes. According to Garrett [17] there is a 31 % chance of a MEDEVAC mission requiring an armed escort, which we denote as 𝜃 1, and of those escorted missions, approximately 4 % are delayed due to issues with the escort aircraft, denoted by 𝜃 2. These parameters are factored into the computation for the expected response times and, therefore, the utilities.

The armed escort delay is an important feature of our problem and requires further discussion. The 31 % chance reflects the aggregrate proportion of casualty events for which a 9-line MEDEVAC request noted enemies present, thereby requiring an armed escort, as reported by an internal USCENTCOM document [17]. If the information is available, it would be better to define 𝜃 1 and 𝜃 2 with respect to call location. Moreover, these parameters should be influenced by the intensity of conflict in the modeled operational environment. We model the delay times as independent of the level of the traffic in the MEDEVAC system because the delays are caused by having to wait for armed escorts (e.g., AH-64 Apache attack helicopters) to arrive at the casualty event location. Armed escorts are controlled by a different dispatching authority than the one controlling MEDEVAC assets; they are not an integral part of the MEDEVAC system, but they support it. Moreover, we assume a large number of armed escorts are available for MEDEVAC support based on the historical deployments of attack helicopter units to Afghanistan [18, 28], and we therefore model them as exogenous entities. While command and control issues might delay diversion of an armed escort from its assigned mission to MEDEVAC support, we note that delays are also induced by the combination of slower gunship flight speed as well as weapons-check requirements upon start-up. These three root causes are independent of the level of traffic in the MEDEVAC system. However, if the number of armed escorts available for MEDEVAC support in the operational area is relatively small, then our assumption of independence may no longer be valid.

The casualty load time, L c, is exponentially distributed with a mean of 10 minutes. Bastian [2] uses a triangular distribution with a mean of 10 minutes, a minimum of five minutes, and a maximum of 15 minutes. While we agree with the 10 minute mean time, the first author’s personal experiences in Iraq and Afghanistan suggest that there is too high of a likelihood for extreme variance when dealing with issues on the ground at the casualty site. Therefore, we propound that an exponential distribution is more appropriate

The casualty unload time, U m, is exponentially distributed with a mean of five minutes because it typically requires much less time to unload the casualty at the MTF than it does to load the casualty at the initial injury site. Bastian [2] uses a normal distribution with a mean of five minutes. Again, we agree with the five-minute mean time but believe that there is a potential for greater variance in this case. The mean response times we calculate are provided in Table 1.

Table 1 Expected Response Time (minutes)
Full size table

Once the mean response times are calculated, we compute the mean service times using Eq. (2). The distribution for the flight speed mentioned above is used for this travel time as well. The mean service times we calculate are provided in Table 2.

Table 2 Expected Service Time (minutes)
Full size table

In this particular computational example, recall that MEDEVAC units are allowed both intra- and inter-zone responses but are restricted from responding to casualties more than one zone away from their staging location. Since our model in this example applies to a MEDEVAC system with four zones and four MEDEVAC units, we have the following state space, S = (w, x, y, z), where \(w\;=\;\left \{0,\;1,\;2\right \}\), \(x\;=\;\left \{0,\;1,\;2,\;3\right \}\), \(y\;=\;\left \{0,\;2,\;3,\;4\right \}\), and \(z\;=\;\left \{0,\;3,\;4\right \}\). The state space reflects the fact that a MEDEVAC unit cannot respond to casualty events more than one zone away from its staging location.

We compute the expected utilities of each MEDEVAC mission for casualty event classifications of urgent, priority, and routine. The rewards associated with our model for the MEDEVAC system are defined by the utility assigned to the selected decision. Recall that the utility r h is gained by servicing a priority h casualty where r 1 > r 2 > r 3. We let r = (10, 1, 0) represent the utility gained by servicing a priority h casualty dependent upon the response time and RTT. We examine policies for scenarios having RTTs of both 60 minutes, the US standard directed by the Secretary of Defense, and 90 minutes, the NATO standard according to Cordell et al. [6], when computing the utilities of each MEDEVAC mission. Recall that if the MEDEVAC unit’s response time is within the RTT, the mission gains a utility based on the number and classification of the casualties evacuated from the casualty event site. If the response time is greater than the RTT, the mission gains a utility of zero.

Recall that the sum of the utilities for each casualty within the casualty event yields the total utility for servicing the 9-line MEDEVAC request. Fulton et al. [16] report that the probability of a casualty being classified as urgent, priority, or routine is 11 %, 12 %, and 77 %, respectively, resulting in q = (0.11, 0.12, 0.77). Therefore, since r = (10, 1, 0), each MEDEVAC mission that results in a response time less than the RTT will gain utilities of 10, 1 and 0 for each urgent, priority, and routine casualty, respectively. For example, if a MEDEVAC responds to a casualty event within the RTT with a casualty load of one urgent, two priority, and one routine, the system earns a utility of 12. Note that a casualty classified as routine is not awarded utility because it is not life-threatening and we are only concerned with lives saved as a function of response time. Tables 3 and 4 summarize the computed utilities, \(\psi _{\textit {ij}}^{k}\), of these computations with both a 60 minute RTT and a 90 minute RTT, respectively, where \(\psi _{\textit {ij}}^{k}\) is the utility gained by MEDEVAC j servicing a casualty event with priority k in Zone i.

Table 3 Utility (60 minute RTT)
Full size table

We require the overall 9-line MEDEVAC request arrival rate to the entire system. Fulton et al. [16] report that during OIF, an expected 173 casualties were transported by aerial MEDEVAC within a given month. Although we are using OEF as our computational example, we utilize the data provided by Fulton et al. [16] in lieu of data specific for OEF since such data is either classified or unavailable. Furthermore, the data from OIF serves our purposes since both OIF and OEF involve stability operations within a counter-insurgency environment where coalition forces combat similar enemy tactics (e.g., improvised explosive devices and small arms attacks). Fulton et al. [16] also report that, among the total casualty events within a given month in OIF, 57.4 % consisted of one casualty, 36 % consisted of two casualties, 5 % consisted of three casualties, and 1.6 % consisted of four casualties. Therefore, α is a discrete random variable with support {1, 2, 3, 4} and attendant probabilities (0.574, 0.36, 0.05, 0.016). The resulting casualty event rate requiring MEDEVAC support is an average of 134 missions per month, giving us an overall casualty event arrival rate of λ = 1/327 events per minute to the entire system. This λ can be interpreted as a parameter-value representative of the spring season, during daylight hours.

Recall that the probability of a casualty being classified as urgent, priority, or routine is 11 %, 12 %, and 77 %, respectively, giving us q = (0.11, 0.12, 0.77). We can then compute p k , the proportion of 9-line MEDEVAC requests having priority k to be p 1 = 0.1587, p 2 = 0.1574, and p 3 = 0.6839.

5.2 Results and optimal policies

Using the utility values in Tables 3 and 4, we obtain the optimal policy for each state by applying (3). The relative value iteration algorithm was implemented in MATLAB, using a Toshiba Satellite A505 computer with an Intel Core processor and 4 GB RAM. Convergence was reached after 29 iterations and < 1 second. Of the possible state combinations described in the previous subsection, there are three state combinations for which the optimal policies change when the RTT is increased from 60 to 90 minutes. These state combinations are (0, 0, 0, 0), (w, x, 0, 0), and (0, 0, y, z).

Table 4 Utility (90 minute RTT)
Full size table

All other states result in identical policies whether the system RTT=60 or 90. Contrary to what McLay and Mayorga [36] found in their problems of interest, we find that the best MEDEVAC to dispatch to a casualty event does not depend on the locations to which the busy MEDEVACs have been dispatched. Note that this is an observed result and that location-dependent policies are a possibility. In Tables 5, 6, 7 and 8, an asterisk (*) is placed next to MEDEVAC units that do not follow a myopic policy. Changes in the optimal policy caused by one or more parameter changes are highlighted with italicized text within the appropriate table. It is expected that a myopic policy will apply to all urgent casualty events since those priority levels correspond to life threatening casualties and therefore yield the highest utilities.

Table 5 Optimal Policy for State (0,0,0,0), RTT = 60 minutes
Full size table
Table 6 Optimal Policy for State (0,0,0,0), RTT = 90 minutes
Full size table
Table 7 Optimal Policy for State (w>0,x>0,0,0), RTT = 60 minutes
Full size table
Table 8 Optimal Policy for State (w>0,x>0,0,0), RTT = 90 minutes
Full size table

Recall that the arrival rate of 9-line MEDEVAC requests is extremely low for Zones 1 and 4, 0.004 and 0.073, respectively, and much higher for Zones 2 and 3, 0.585 and 0.338, respectively. As expected, when RTT=60 and all MEDEVAC units are idle, the dispatch policy is myopic for all urgent and priority casualty events, as shown in Table 5. In the event of a routine casualty event, however, MEDEVAC 1 is dispatched for any casualty events in Zone 2 in order to reserve MEDEVAC 2 for any higher level casualty events; likewise, MEDEVAC 4 is dispatched for any casualty events in Zone 3 in order to reserve MEDEVAC 3 for any higher level casualty events.

Recall that only one optimal policy changes when RTT=90 rather than 60. Unlike the policy for this state when the RTT=60, as shown in Table 5, MEDEVAC 3 is responsible for Zone 3 rather than MEDEVAC 4. This is because MEDEVAC 4 is afforded more time when the RTT=90, allowing it to respond to Zone 3 if MEDEVAC 3 is busy when a casualty event arrives for Zone 3. This makes it unnecessary to reserve MEDEVAC 3 for future, higher level casualty events.

When the RTT=60 and MEDEVACs 1 and 2 are both busy, a myopic policy applies for urgent and priority casualty events, as shown in Table 7. Although dispatching MEDEVAC 3 to Zone 3 in this situation will potentially allow a casualty event arrival in Zone 2 to encounter a lapse in MEDEVAC coverage, MEDEVAC 4 may be unable to respond in time due to the further distance between Zones 3 and 4. Therefore, despite the potential of missed coverage, it is better to respond as quickly as possible with the closest MEDEVAC asset given an urgent or priority casualty event. With the arrival of a routine casualty event when MEDEVACs 1 and 2 are busy, MEDEVAC 3 is reserved for Zone 2 arrivals only while MEDEVAC 4 will be dispatched to Zones 3 and 4. Since this level of casualty event is not life-threatening, it is better to reserve MEDEVAC 3 for Zone 2 alone, given the higher ratio of 9-line MEDEVAC requests for Zone 2. Since MEDEVACs 1 and 2 are both busy and MEDEVACs 3 and 4 are unable to respond to a casualty event in Zone 1, any casualty event that occurs in Zone 1 will not be supported with MEDEVAC assets.

When RTT=90 and MEDEVACs 1 and 2 are busy, as shown in Table 8, a myopic dispatch policy applies to urgent casualty events as it does when RTT=60. However, with an extra 30 minutes allowed for response time, MEDEVAC 4 has ample time to respond to priority or routine casualty events in Zone 3, allowing MEDEVAC 3 to provide MEDEVAC coverage for Zone 2 only. This reduces the potential for a casualty in Zone 2 to be without MEDEVAC coverage, which is more important given the high ratio of 9-line MEDEVAC request arrivals for Zone 2. Since MEDEVACs 1 and 2 are both busy and MEDEVACs 3 and 4 are unable to respond to a casualty event in Zone 1, any casualty event that occurs in Zone 1 will not be supported with MEDEVAC assets.

Due to the relatively symmetric nature of our representative problem, we observed parallel results when increasing RTT from 60 to 90 minutes for State (0,0,y,z). The symmetry is evident in each zone having one MEDEVAC asset, the two outer zones (i.e., Zones 1 and 4) having the fewest casualties and no co-located MTFs, and the two inner zones (i.e., Zones 2 and 3) having the most casualties and having MTFs co-located with the MEDEVAC assets. Similar to the results for State (w,x,0,0) for MTT=60, analysis showed the optimal dispatch policy for State (0,0,y,z) to be myopic for urgent and priority casualty events: MEDEVAC 1 supports Zone 1, MEDEVAC 2 supports Zones 2 and 3, and no MEDEVAC asset support Zone 4 because it is not adjacent to a zone with an available MEDEVAC asset. The dispatch policy for routine casualties deviates from a myopic policy in that MEDEVAC 1 supports requests from Zone 2, allowing MEDEVAC 2 to be reserved for future, higher-level casualty events in either Zones 2 or 3. As is the case for State (w,x,0,0), the optimal policy for State (0,0,y,z) when RTT=90 changes for priority-level casualties compared to when RTT=60, in that the MEDEVAC asset based in the outer zone (i.e., Zone 1) now supports the adjacent, inner zone (i.e., Zone 2), allowing its MEDEVAC asset with a co-located MTF (i.e., in Zone 2) to be reserved for higher priority casualties in the two center zones (i.e., Zones 2 and 3) as well as routine casualties in its adjacent, inner zone (i.e., Zone 3).

Figure 4 portrays both the long-run expected utility for each zone for the three different policies are implemented on the left graph, and the probability that a MEDEVAC unit will be busy under each policy on the right graph.

Fig. 4
figure 4

Zone Utilities and Busy Probabilities, RTT = 60

Full size image

The expected utilities for Zones 1 and 4 are nearly equal for each policy considered, whereas the expected utilities for Zones 2 and 3 differ slightly among policies. For Zones 2 and 3, an optimal policy slightly outperforms a myopic policy, whereas both outperform an intra-zone policy. Overall, an optimal policy attains a total utility of 1.57 while a myopic policy attains a total utility of 1.568. An intra-zone policy under performs both of these policies, however, with an expected total policy of 1.49. While the differences seem to be negligible when first considered, the accumulation of greater utility over an extended duration of operations corresponds to lives saved.

Greater differences are revealed when the probabilities of each MEDEVAC being busy are examined. Under an optimal policy, MEDEVACs 1 and 4 are busy with probabilities of 0.0579 and 0.0556, respectively, compared to a myopic policy having respective probabilities of 0.0063 and 0.0144, or with an intra-zone policy with probabilities of 0.0006 and 0.0142, respectively. This outcome occurs because MEDEVACs 2 and 3 are effectively rationed under an optimal policy in order to reserve their capabilities for future, higher priority level casualty events. (Recall that Zones 2 and 3 have a higher ratio of casualty event arrivals and therefore require MEDEVAC services more often.) Under a myopic policy, MEDEVAC 2 is dispatched far more often than MEDEVAC 1, resulting in busy probabilities of 0.0676 and 0.0063, respectively, causing a greater likelihood of a lapse in coverage for a casualty event in Zone 2 when RTT=60. Consequently, MEDEVAC 1 is under-utilized when a myopic policy is implemented. Proportionally, the same outcome exists for Zones 3 and 4, where MEDEVAC 4 is under-utilized under a myopic policy compared to an optimal policy. An intra-zone policy simply reflects the proportion of casualty events in each zone; this policy will most likely prove to be inefficient under circumstances of higher threat as well.

When the NATO RTT standard of 90 minutes is applied for the same scenario, as shown in Fig. 5, we observe similar results for the zone utilities but some notable differences with the busy probabilities of MEDEVAC units.

Fig. 5
figure 5

Zone Utilities and Busy Probabilities, RTT = 90

Full size image

The expected utilities for each zone are nearly identical, proportionally, when compared to the scenario with a RTT=60; as expected, the utilities for each of these zones increases slightly due to higher utilities when the MEDEVAC units have 30 additional minutes to respond to a casualty event. The total zone utility under an optimal policy increases to 1.7964 when the RTT=90, and it increases to 1.7960 and 1.7024 under myopic and intra-zone policies, respectively.

Under an optimal policy, the probabilities of each MEDEVAC unit being busy differ greatly when RTT=90 rather than 60 minutes. Although the expected MEDEVAC utilizations remain proportionally similar when an optimal policy is applied, the busy probabilities differ significantly. Therefore we focus on the optimal policy in this case. Illustrated in Figures 4 and 5, the probability that MEDEVACs 3 and 4 are busy when the RTT=90 differs greatly compared to when RTT=60. The busy probability of MEDEVAC 3 increases from 0.0138 to 0.0372, whereas the busy probability of MEDEVAC 4 decreases from 0.0556 to 0.0177 with an additional 30 minutes of allowed response time. This indicates that MEDEVAC 4 is utilized much less when the RTT is 90 minutes, whereas MEDEVAC 3 is utilized much more. This is because the optimal policies change for states (0,0,0,0) and (w,x,0,0) when the RTT = 90. Since MEDEVAC 3 is dispatched to Zone 3 for routine casualty events rather than MEDEVAC 4 and routine casualty events account for 77 % of the MEDEVAC missions, the decrease in usage of MEDEVAC 4 and increase in usage of MEDEVAC 3 well aligns with intuition.

5.3 Sensitivity Analysis

Analysis of the results indicates that, when applying an optimal policy to a MEDEVAC system, the MEDEVAC asset that is dispatched in response to a 9-line MEDEVAC request is highly dependent upon the proportion of casualty events per zone. From studying our computational example, a system that has a relatively low proportion of casualty events in Zones 1 and 4, MEDEVACs 1 and 4 are used as often as possible to respond to casualty events not only in their respective zones but also to casualty events in Zones 2 and 3, respectively, enabling MEDEVACs 2 and 3 to be reserved for only the higher level casualty events. This reduces the likelihood of a MEDEVAC unit being busy servicing a routine casualty event when an urgent or priority casualty MEDEVAC request occurs in its own zone.

Another parameter that is sensitive when applying an optimal policy is the casualty event arrival rate, λ. When this parameter is changed to a relatively high rate (e.g., λ=1/30, mid-summer season, daylight hours.), the optimal policy changed in six of the 10 possible states within our computational example. In contrast, the armed escort delay is not as sensitive as expected. While an increased delay yields lower zone utilities, it only changes the optimal policy for two of the 10 states in our computational example.

Analyzing the results of our model reveals that the myopic policy follows the same dispatch pattern with each parameter alteration. While this policy method produces different zone utilities and probabilities of each MEDEVAC asset being busy, these changes only reflect the increased or decreased ratio of casualty events per zone, regardless of their urgency. MEDEVACs 2 and 3 are consistently busy while MEDEVACs 1 and 4 are under-utilized; this is because a myopic policy does not consider rationing MEDEVAC units whose zones are expected to receive urgent or priority casualty event arrivals more often than other zones. An intra-zone policy simply dispatches MEDEVAC units when a casualty event occurs in their respective zones, giving no consideration to the parameters within our model. With this policy, no decision is required when determining which MEDEVAC unit to dispatch, and many casualty events are likely not serviced when this policy is applied, resulting in a total zone utility that is lower than what the other two policies yield.

6 Conclusions

The nature of the MEDEVAC mission is one of great import, and little time is afforded to the decision maker between when a 9-line MEDEVAC request is received and when a MEDEVAC asset should be dispatched. An instinctive reaction is to dispatch the nearest MEDEVAC unit in order to respond to the casualty event as soon as possible, which is known as a myopic policy. However, this reaction will result in more preventable deaths over extended operations if a MEDEVAC unit is dispatched to a low priority casualty event and is busy when a subsequent, higher priority casualty event occurs in that MEDEVAC asset’s zone. Rapid blood loss on the battlefield is the leading cause of death according to current statistics, and providing rapid medical support is essential to preserving the lives of our soldiers. Losing a soldier to a gunshot wound or injuries sustained from an improvised explosive device because the nearest MEDEVAC unit is busy servicing a routine casualty event such as a broken leg is unacceptable. Our model proves to be useful by providing a decision policy that dispatches the most appropriate MEDEVAC unit to casualty events while potentially rationing a closer MEDEVAC unit for future casualty events that may be more time sensitive, a decision that may seem counterintuitive to a decision maker who does not consider second-order effects. To complicate the decision-making process, situations with a high threat level require armed helicopters to escort the MEDEVAC unit to the casualty site, creating a potential delay in the response time. We use a computational example based on the current operational environment in Afghanistan to apply an MDP model using a relative value iteration dynamic programming algorithm to develop an optimal policy for dispatching MEDEVAC units that will save soldiers’ lives.

Since we know the location and priority level of each casualty event with the receipt of a 9-line MEDEVAC request, we determine which MEDEVAC unit to dispatch in order to maximize the steady-state system utility. The utility gained from servicing a specific request depends on the number of casualties, the priority class of the casualty event, and the locations of both the servicing MEDEVAC unit and casualty site. The location of the casualty site informs the dispatch options, and the priority level informs which MEDEVAC asset to dispatch.

Results reveal that a myopic policy is not always the best method to use for dispatching MEDEVAC units under differing threat conditions while conducting combat operations under a variety of different parameters. Although a myopic policy performs better than an intra-zone policy, an optimal policy yields higher utilities than either of these options. Results indicate that an optimal policy increases steady-state utility by 0.01 utility when compared to a myopic policy and 0.09 when compared to an intra-zone policy. Although this does not seem like a large difference, over a long enough time period even 0.01 in utility can mean the difference of one urgent classified request or ten priority classified events being serviced, which can save lives. Moreover, the optimal policy better balances MEDEVAC asset utilization rates across zones. The maximum deviation between zones for the probability of a MEDEVAC asset being busy is 0.0441 under the optimal policy when RTT=60, compared to 0.0613 and 0.0650 for the myopic and intra-zone policies, respectively. When RTT increases from 60 to 90, the workload balance improves under the optimal policy to a maximum deviation of 0.0402, whereas it does not change for the myopic and intra-zone policies.

The results presented here should interest those within the medical planning community seeking information regarding the allocation and management of aeromedical assets. While our procedure is demonstrated in a military context, the procedure may be of interest to a broader audience that includes those planning emergency response policies for large-scale disasters. Military medical planners must often consider the spatial and temporal aspects of the demand for MEDEVAC services prior to actual combat when examining location and dispatching decisions. A similar process may be appropriate for federal or state agencies planning for the servicing of routine emergency calls immediately after a large-scale disaster. Indeed, as seen after Hurricane Katrina, some EMS assets may face threats at the casualty evacuation site and require police escort to service some calls.

While our model is useful, it also has several limitations, as a number of aspects have yet to be examined. For example, we do not allow MEDEVAC assets to respond to casualty events until they return to their original staging location; realistically, a MEDEVAC asset can divert to service such missions if it has the necessary fuel and equipment. This will certainly reduce the response time for many casualty events when a 9-line MEDEVAC request is received shortly after a nearby MEDEVAC unit has unloaded its casualties. Also, future research could examine the probabilities for the system to be in each state in order to determine how often a lapse in coverage occurs.

We also do not consider that a response time under 60 or 90 minutes could yield a greater utility for urgent casualty events given that a proportion of urgent casualties will not survive under the US or NATO standard RTTs, but they may survive if the mission was completed in less time. Moreover, we do not allow MEDEVAC units to be placed in a queue; if this was possible, MEDEVAC units could be dispatched to casualty event sites from nearby MTFs immediately after unloading casualties from the prior mission. Other than receiving no utility, our model does not capture the negative effect of casualty events not serviced by MEDEVAC assets, thereby using non-standard CASEVAC either by ground or air; a queuing system may provide an otherwise unsupported casualty with crucial medical aid in a more timely manner.

One possibility for future research involves basing the priority level of the casualty event on the zone from which the event originates. For example, the proportion of urgent casualty events may be much greater in Zone 2 than in Zone 1, and those probabilities could be incorporated within the model. Resource emplacement could encompass this aspect of the MEDEVAC system. Our model does not consider resource emplacement such as forward positioning MEDEVAC assets in areas historically likely to receive 9-line MEDEVAC requests, specifically urgent requests. By changing a MEDEVAC unit’s staging location based on current data, the response time could be reduced by enough of a margin to save additional lives.

Lastly, our model does not incorporate the recent MEDEVAC capability of providing blood transfusions en route to the MTF. Recall that our response time, the time required to transport a casualty from receipt of the 9-line MEDEVAC request to an appropriate MTF, is based on the fact that blood loss is the primary cause of death in a combat environment. If this new capability is incorporated into our model, the response time parameters will change. Similarly, further examination could consider survival probabilities for MEDEVAC units providing different medical capabilities; for example, MEDEVAC assets typically have flight medics on board, but on occasion will have a physician’s assistant or surgeon. These additional assets would likely increase the casualty survival rate. While our model is thorough in many aspects, there is room for improvement and all of these limitations should be examined in future research.