A decomposition approach for the combined master surgical schedule and surgical case assignment problems

Abstract

This research aims at supporting hospital management in making prompt Operating Room (OR) planning decisions, when either unpredicted events occur or alternative scenarios or configurations need to be rapidly evaluated. We design and test a planning tool enabling managers to efficiently analyse several alternatives to the current OR planning and scheduling. To this aim, we propose a decomposition approach. More specifically, we first focus on determining the Master Surgical Schedule (MSS) on a weekly basis, by assigning the different surgical disciplines to the available sessions. Next, we allocate surgeries to each session, focusing on elective patients only. Patients are selected from the waiting lists according to several parameters, including surgery duration, waiting time and priority class of the operations. We performed computational experiments to compare the performance of our decomposition approach with an (exact) integrated approach. The case study selected for our simulations is based on the characteristics of the operating theatre (OT) of a medium-size public Italian hospital. Scalability of the method is tested for different OT sizes. A pilot example is also proposed to highlight the usefulness of our approach for decision support. The proposed decomposition approach finds satisfactory solutions with significant savings in computation time.

1 Introduction

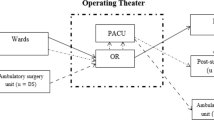
The operating theater (OT), consisting of several operating rooms (ORs), is one of the most critical resources in a hospital because it has a strong impact on the quality of health service and represents one of the main sources of costs (surgical teams, equipment etc.). Given the patient waiting list and various information on OT characteristics and status, OT planning problems consist in deciding the schedule of surgeries in a given time horizon, with the aim of optimizing several performance measures such as operating room utilization, throughput, surgeons’ overtime, lateness etc.

Surgical cases are carried out in OR sessions. An OR session is an uninterrupted time block (typically, half day or a full day). In the management policy usually referred to as block scheduling [6], each OR session is devoted to a specific surgical discipline. This organizational solution is often preferred, since having the same type of surgeries performed in a given room during a given time span typically simplifies the physical handling of equipment and/or materials. A more flexible solution is the open scheduling policy [4], in which no pre-specified session-to-discipline assignment exists, and therefore two cases corresponding to different disciplines can be scheduled in the same OR session. This paper focuses on the block scheduling scenario. Thus, surgical planning in operating theaters can be seen as involving three distinct decision steps [19]:

• (i)   deciding the surgical discipline that will be performed in each OR session (e.g., the OR session “Tuesday morning–Room 2” is assigned to otolaryngology etc.);

• (ii)   selecting elective surgeries to be performed in each OR session;

• (iii)   sequencing surgeries within each OR session.

Problem (i) is often referred to as the Master Surgical Scheduling Problem (MSSP), and returns the Master Surgical Schedule (MSS) [3]. Problem (ii) determines the Surgical Case Assignment (SCA), and is therefore denoted as Surgical Case Assignment Problem (SCAP). Problem (iii) outputs the detailed calendar of elective surgeries for each session.

Literature on all three above decision levels is wide and growing, and it has thoroughly been reviewed by several researchers (e.g., [3, 9, 11, 20, 23]). The three above decision problems have been addressed by a multiplicity of approaches. Research focused on either all three levels concurrently [19], two of them [7, 15, 22], or even single problems [5, 21, 24]. Some approaches have been designed to fit specific issues that may or may not be present in various real-life settings. For instance, Roland et al. [17] propose a model that incorporates requirements related to personnel availability and preferences, Augusto et al. [2] take into account bed occupancy in the wards, Guinet and Chaabane [10] include various hospitalization and overtime cost figures. Denton et al. [5] deal with uncertain durations of surgeries while Holte and Mannino [12] account for uncertainties in patient demand; i.e., the numbers and types of surgeries that will need to be scheduled.

In this paper we focus on efficiently solving MSSP and SCAP, i.e., the first two steps of the decision hierarchy. Our assumptions are similar to those in the papers by Testi et al. [20], Tanfani and Testi [18] and Agnetis et al. [1], who propose an ILP model for MSSP and SCAP, on the basis of the current state of the waiting list. Their approach consists in concurrently defining the MSS and the list of surgical cases to be performed during each OR session of the planning horizon.

Hospital management often faces situations requiring to change the OR plan. This might be due to many reasons, at different decision levels. At the operational level, unpredicted events such as no-shows or emergencies can make the current plan inefficient or even infeasible. At the tactical level, OT management may want to evaluate potential changes in planning policies, assessing the impact of alternative scenarios on efficiency and quality of service. The main contribution of this paper is to meet these management needs through an efficient decomposition approach that addresses MSSP and SCAP separately. This approach is compared with the solution of an integrated ILP model which concurrently solves the two problems [1]. Our ILP model is slightly different from the one in [18], since it reflects the objective of certain hospital managers [1]. In [18] the objective function considers the costs of performing the surgery on a certain day and the costs of not performing it at all. Instead, we assign a score to each surgical case in the waiting list, which accounts for two issues, namely the time spent since the decision date and the priority of the surgery, as in [1]. The objective is to determine MSS and SCA in order to maximize the score of the cases selected for the next time horizon. Finding the optimal solution to the integrated MSSP + SCAP may be time-consuming and may require significant computational resources. This may not be always compatible with time requirements, whenever unpredicted events occur and a new surgical plan has to be produced. Also, scenario analysis can benefit from a decomposition approach, for a rapid—though reliable—assessment of the impact of alternative OT management policies. We will show that the proposed decomposition approach produces very good solutions in a limited computation time. This becomes even more important when considering medium-to-large operating theatres, since computation time of integrated models may grow very fast.

The plan of the paper is as follows. In Section 2 the considered model is described in detail. In Section 3 the mathematical formulations and the algorithms are formally introduced. Computational experiments are illustrated and discussed in Section 4. Finally, in Section 5 some conclusions are drawn.

2 Problem description

This study focuses on the problem of allocating elective surgeries to operating rooms over a given time horizon (e.g., one week) covering the problems denoted as MSSP and SCAP.

All elective surgeries are grouped into surgical disciplines (e.g., orthopedics, day surgery). The main input to the overall planning problem is the waiting list of each discipline, containing all the case surgeries that currently need to be performed. For each case surgery, the following information is specified in the waiting list:

• Surgery code—identifies the specific type of surgery.

• Processing time—expected duration of the surgery (including setup times due to cleaning and OR preparation for the next surgery). We assume all these times to be deterministic; i.e., they are not affected by uncertainty.

• Decision time—date when the surgery entered the waiting list (i.e., the general practitioner recommended the surgical treatment).

• Waiting time—days currently elapsed since the decision time.

• Priority class—surgeries are classified in three priority classes A, B or C (A being the most urgent), according to the national regulations on waiting lists management [13].

• Due date—nominal time by which the surgery should be performed. It is set on the basis of the decision time and the priority class.

Cases are carried out in full-day OR sessions each assigned to a single surgical discipline and the total processing time of the surgeries allocated to each session must not exceed the session duration minus a given slack. The slack is used to absorb possible delays and to reduce the chances of surgeons overtime.

In general, a MSS may be subject to various types of restrictions, which must be accounted for when planning:

• discipline-to-OR restrictions. Certain disciplines can only be performed in a restricted set of ORs, due to size and/or equipment constraints.

• Limits on discipline parallelism. Typically, no more than k OR sessions of a certain discipline can take place at the same time, e.g., because only k surgical teams for that discipline are available.

• OR sessions-per-discipline restrictions. Lower and upper limits to the number of OR sessions assigned to each discipline throughout one week can be specified; e.g., because of workload balancing or other management rules.

• OR reservation. The hospital management may reserve one or more OR sessions to certain disciplines every day.

Notice that the resulting model is flexible enough to account for several characteristics of the OT, thus being applicable to different hospitals.

The objectives of the overall problem are twofold:

• Resource perspective—OR sessions capacity and actual demand should be matched as much as possible, since both under- and over-utilization of an operating room are wasteful;

• Patient perspective—In organizational terms, the quality of service may be expressed by the due date performance of the service, which in turn is related to having cases done within the respective due dates as much as possible. Alternatively, other proxies of the perceived quality of service can be accounted for, e.g. including the satisfaction of preferences about the surgeon and/or the day of the week.

In general, these two objectives may be partially conflicting, since tightly filling OR sessions may ignore surgeries’ due dates, and scheduling surgeries based on their due date only may lead to inefficient utilization of ORs. Hence, we define an objective function that accounts for both these aspects. Namely, we define the score of each surgery as the product of the surgery processing time and a coefficient which depends on how close is the surgery to its due date. Other patient preference dimensions (like those mentioned before) could be easily accounted for in the proposed formulation through a proper definition of the score parameter. Nevertheless, in this paper, we keep the score related to the surgery due date, following [1]. The problem is to decide the MSS and the SCA so that the total score of selected cases is maximized.

3 Formulations and decomposition approach

In what follows, we first present notation and a mathematical programming formulation (Section 3.1), and thereafter we present the decomposition approach proposed to solve MSSP + SCAP (Section 3.2).

3.1 Notation and formulation

In what follows, we denote by S the set of surgical disciplines (indexed by s), and by $I_{s}$ the set of surgeries (indexed by i) in the waiting list of the surgical discipline s. The expected duration of the i-th surgery of discipline s is $P_{is}$. Let $N_{OT}$ be the total number of sessions available for planning in one week in the operating theater and J the set of operating rooms, indexed by r. All sessions have length $O^{max}$ (time). Weekdays are indexed by $w\in \{1, \ldots , 5\}$, from Monday $(w = 1)$ to Friday $(w = 5)$ and we denote by $S_{s}^{min}$ and $S_{s}^{max}$ the minimum and, respectively, maximum number of OR sessions to be allocated to the surgical discipline s in one week. The maximum number of parallel sessions that can be assigned to discipline s is denoted by $PS_{s}$, while $\mathit {NA}_{s}$ is the set of operating rooms not available for discipline s.

For the i-th surgery of discipline s, we define a score as $K_{is}=P_{is}(W-R_{is})$, where W is the maximum allowed waiting time for low-priority surgeries, and $R_{is}$ are the days to due date (this number is negative for late surgeries). The notation adopted throughout the paper is summarized in Table 1.

Table 1 Problem notation

The overall objective is to select a set of surgeries to be performed that maximizes the overall score. Such a product form for the score, frequently adopted in the literature [1, 18], suitably expresses the balance between scheduling long surgeries and accounting for late surgeries. Notice that using the maximum allowed waiting time for low-priority surgeries W guarantees that urgent surgeries have greater impact on the objective function and thus the model has more incentives to select them. Moreover, since in general long surgeries are more difficult to schedule than short surgeries, assigning them higher scores (through including $P_{is}$ in the product form of $K_{is}$) helps ensure they are considered for the schedule.

We next introduce a mathematical programming model of the above problem. In the model, $x_{isrw} = 1$ if the i-th surgery of surgical discipline s is assigned to OR r for the day w, and $y_{srw} = 1$ if the surgical discipline s is assigned to OR r on day w.

$$ \max \;\; \sum\limits_{s} \sum\limits_{i} \sum\limits_{r} \sum\limits_{w} K_{is} \cdot x_{isrw} $$

(1)

$$ \sum\limits_{r} \sum_{w} x_{isrw} \leq 1 \;\;\;\; \forall i, s $$

(2)

$$ \sum\limits_{i} P_{is} \cdot x_{isrw} \leq O^{max} \cdot y_{srw} \quad \forall s,r,w $$

(3)

$$ \sum\limits_{s} y_{srw} \leq 1 \quad \forall r,w$$

(4)

$$ \sum\limits_{w} \sum\limits_{r} y_{srw} \geq S_{s}^{min} \quad \forall s $$

(5)

$$ \sum\limits_{w} \sum\limits_{r} y_{srw} \leq S_{s}^{max} \quad \forall s$$

(6)

$$ \sum\limits_{r} y_{srw} \leq PS_{s} \quad \forall w,s $$

(7)

$$ \sum\limits_{w} \sum\limits_{r \in \mathit{NA}_{s}} y_{srw} = 0 \quad \forall s $$

(8)

$$ x_{isrw} \in \{0,1\} \quad \forall i,s,r,w$$

(9)

$$ y_{srw} \in \{0,1\} \quad \forall s,r,w $$

(10)

Constraint (2) states that each surgery can be performed at most once. Constraint (3) establishes an upper limit to the duration of the surgical cases assigned to the same session. Constraints (4) guarantee that there are no two surgical disciplines assigned to the same OR at the same time. Constraints (5–6) bound the number of weekly OR sessions assigned to each discipline. Constraints (7) limit the number of parallel sessions assigned to the same surgical discipline. Discipline-to-OR restrictions are taken into account by constraint (8).

3.2 Decomposition approach

The mathematical program (1–10) is NP-hard, since even with a single discipline and when constraints (1–8) are not binding, the problem reduces to the well-known NP-hard multiprocessor scheduling problem [8]. Hence, the mathematical model introduced in the previous section may in general require large computation times, even to find suboptimal solutions. In off-line planning this may not be an issue for the OT management, but many situations demand for reduced computation times, e.g., to analyse alternative OR plans. Therefore, in order to quickly reach good solutions for MSSP + SCAP, we propose an efficient decomposition approach. The idea is to address MSSP and SCAP sequentially by first producing an MSS and next, given the MSS as input, determining the SCA.

3.2.1 Solving the MSSP

The algorithm that produces the MSS works as follows:

• (i)   given the waiting list of each surgical discipline as input, for each discipline a number of candidate sets is quickly generated. Each candidate set consists of a set of surgeries such that the sum of their processing times does not exceed $O^{max}$.

• (ii)   a complete surgical case assignment is temporarily produced by filling available sessions during the week with candidate sets.

• (iii)   surgical cases are discarded, and only the MSS is retained.

In step (i), in order to generate the candidate sets, we consider the problem of filling a number of bins (corresponding to candidate sets) of given capacity (the OR session length) with items (the surgical cases), each having a given size (the expected processing time of the surgical case) and a given value (the score associated to the surgery). We consider $S^{max}_{s}$ bins of capacity $O^{max}$. Next, for each surgical case we compute the ratio of $K_{is}$ over processing time $P_{is}$, and we order all the surgical cases of discipline s by non-increasing values of such ratios. Hence, we sequentially fill the bins according to the first-fit rule, i.e., assigning the current item to the first bin that fits. In this way, we generate $S^{max}_{s}$ candidate sets. For the f -th candidate set of discipline s, call it $c_{sf}$, we compute the values $v_{sf}$ as the sum of the scores $K_{is}$ of the surgeries in $c_{sf}$.

In step (ii), we select a subset of the candidate sets generated, to produce a feasible plan. This problem can be formulated as a min-cost flow problem (Fig. 1) on a suitable network $\mathcal {N}(V,A)$, in which the flow in the network represents the assignment of candidate sets to OR sessions. We next describe the structure of the network in detail.

Fig. 1

Example of the min-cost flow formulation

The network $\mathcal {N}(V,A)$ has one source node Q and one sink node R that respectively generate and absorb $N_{OT}$ units of flow. The remaining nodes do not produce or absorb flow, and are divided into six different layers, namely: discipline nodes s ($s=1,\dots ,|S|$), candidate nodes $c_{sf}$ ($s=1,\dots ,|S|$, $f=1,\dots ,S^{max}_{s}$), in-day nodes $(s,w)$ ($s=1,\dots ,|S|$, $w=1,\dots ,5$), out-day nodes $(s',w')$ ($s'=1,\dots ,|S|$, $w'=1,\dots ,5$), room-day nodes $(r,w)$ ($r=1,\dots ,|J|$, $w=1,\dots ,5$) and room nodes r ($r=1,\dots ,|J|$). An arc from node i to node j will be denoted by $[i,j]$.

From the source node Q, there are $|S|$ outgoing arcs $[Q,s]$, one for each discipline node. These arcs have a lower bound on the flow equal to $S^{min}_{s}$. There is no upper capacity nor cost for these arcs. The lower bound on the flow of these arcs guarantees that at least $S^{min}_{s}$ sessions are assigned to discipline s.

From each discipline node s, there are $S^{max}_{s}$ outgoing arcs to candidate nodes $c_{sf}$, each corresponding to a candidate set generated for discipline s. All these arcs have no cost and they all have capacity 1, which guarantees that each candidate set is assigned at most once.

From each candidate node $c_{sf}$ there are 5 outgoing arcs (one for each weekday), connecting $c_{sf}$ to all in-day nodes $(s,w)$, $w=1,\dots ,5$. These arcs have no upper capacity, however the flow on arcs $[c_{sf},(s,w)]$ cannot be greater than 1, since at most one unit of flow enters each candidate node $c_{sf}$. On each of these 5 arcs, the cost associated to the flow is $-v_{sf}$, meaning that $v_{sf}$ is actually gained if candidate session $c_{sf}$ is selected.

Next, there is an arc from each in-day node $(s,w)$ to the respective out-day node $(s',w')$ with $s'=s$ and $w'=w$. The upper capacity of these arcs guarantees that no more than $PS_{s}$ parallel sessions are assigned to discipline s in one day.

Each out-day node $(s',w')$ has one outgoing arc to each corresponding room-day node $(r,w)$ (i.e., such that $w=w'$ and discipline s can be performed in room r). No costs or capacities are associated to these arcs.

From each room-day node $(r,w)$ there is an arc $[(r,w),r]$ to a room node r. Hence, each room node r has 5 ingoing arcs. These arcs have no cost and capacity 1, thus enforcing that at most one discipline is assigned to each room on each day.

Finally, there is one outgoing arc from each room node r to the sink node R with no associated cost or capacity.

The objective function of the min-cost flow model corresponds to maximizing the sum of the values $v_{sf}$ of selected candidate sets, i.e., assigning to the MSS the most profitable candidate sets.

We next show that the solution to the min-cost flow problem generates a surgical case assignment that satisfies the constraints of model (1–10). Compliance with constraints (2) and (3) is ensured by the generation procedure of step $(i)$, which assigns each surgery at most once and produces candidate sets of total duration not exceeding $O^{max}$. Constraints (4) are enforced by the capacities of arcs $[(r,w),r]$ from room-day nodes to room nodes. The capacities of arcs $[Q,s]$ from the source to discipline nodes take care of the constraint (5) on the minimum number of sessions. The constraint (6) on the maximum number of sessions is enforced by the fact that we only generate $S_{s}^{max}$ candidate sets for each discipline s in the procedure of step $(i)$. The constraint (7) on the maximum number of parallel sessions for a discipline s is enforced by the capacity of arcs $[(s,w),(s',w')]$ from in-day to out-day nodes. Finally, discipline-to-OR constraints (8) are taken into account by not generating forbidden arcs between out-day nodes and room-day nodes.

In Fig. 1 an example of an instance with two disciplines and two ORs is shown. For the sake of clarity, arc capacities are not shown when they are not binding. The only nonzero cost arcs are those connecting candidate nodes to in-day nodes. Note that all arcs outgoing a node $c_{sf}$ have the same negative cost $-v_{sf}$. Observe that in this example, discipline 2 cannot be performed in OR 1, hence the arcs from out-day nodes $(s',w')$ to room-day nodes $(r,w)$ are missing for $s'=2$, $r=1$ and $w=w'$.

Finally, in step (iii), once the min-cost flow problem is solved, the MSS structure is defined by the nonzero flows in the arcs connecting out-day and room-day nodes, i.e., arcs $[(s',w'),(r,w)]$ with $w=w'$.

3.2.2 Solving the SCAP

It can be observed that solving the SCAP corresponds to solving s independent multiple-knapsack problems [16], one for each surgical discipline s, where surgeries correspond to items and sessions to knapsacks. Each multiple-knapsack problem corresponds to the following model for a given discipline s:

$$\max \quad \sum\limits_{h} \sum\limits_{i} K_{is} \cdot x_{ish} $$

(11)

$$\sum\limits_{h} x_{ish} \leq 1 \quad \forall i $$

(12)

$$\sum\limits_{i} P_{is} \cdot x_{ish} \leq O^{max} \quad \forall h$$

(13)

$$x_{ish} \in \{0,1\} \quad \forall i,h$$

(14)

The decision variables are $x_{ish}=1$ if the i-th surgery of discipline s is assigned to the h-th OR session of discipline s; otherwise $x_{ish} = 0$.

4 Case study and computational results

In this section we discuss the computational experiments set up for evaluating the proposed decomposition approach against an integrated mathematical model. More specifically, in Section 4.1 we introduce the benchmark instances based on a realistic setting applied to a medium-size Italian hospital. In Section 4.2 we discuss the numerical results obtained for our case study, while Section 4.3 proposes a number of scenarios to better illustrate how our approach can effectively support the OT manager.

4.1 Experimental design and setting

In our computational experiments, we generated 6 different sets of benchmark instances. This is done by considering 3 different OT sizes (5, 10 and 15 ORs) and, for each OT size, 2 different waiting lists by considering 200 or 300 surgical cases for each OR. More in detail, we refer to these sets as $(|J|$,$\beta )$, where $|J|$ is the OT size and $\beta$ the multiplier used to obtain the waiting lists (i.e., (5,200) refers to instances with 5 ORs and having $1000=5\cdot 200$ surgical cases in the waiting lists). For each set $(|J|,\beta )$ we generate 10 realizations of each waiting list. The benchmark waiting lists are derived from the waiting lists $I_{s}$ of the six surgical disciplines of a medium-size Italian hospital [1] through nonparametric bootstrapping [14]. This consists in sampling—with replacement—$\sum n_{s}$ surgeries from the set $\bigcup I_{s}$. Therefore, the size of the waiting list of each discipline is variable even though the total number of surgical cases is $|J|\cdot \beta$. The maximum allowed waiting time for less urgent surgeries is $W = 90$ days.

The following description of the setting adopted in our case study is based on the OT characteristics of San Giuseppe Hospital in Empoli, Italy. The operating rooms are all identically equipped, even though two of them (say, $r = 4, 5$) are bigger than the others. The OT composed of 5 ORs reproduces a setting based on the real hospital OT, actually consisting of 6 ORs. However, the OT manager is interested in testing the performance of this configuration, assuming that one OR is reserved to surgical activities that go beyond the planning under study. Then, to generate the benchmark sets with 10 and 15 operating rooms starting from the original hospital OT, we replicate each OR two or three times respectively. Focusing on elective surgeries only, the weekly surgery plan spans five days, from Monday to Friday. Each session lasts 11.5 hours. However, to account for possible delays and/or uncertainties affecting surgery duration, we introduce a planned slack time of 60 minutes, similarly to [1] and in agreement with the OT manager of San Giuseppe Hospital. The duration of the session is divided into time units of 15 minutes each, thus resulting in $O^{max}=42$.

Six different disciplines have been considered: gynecology ($s = \textsc {gyn}$), general surgery ($s = \textsc {gs}$), otolaryngology ($s = \textsc {ent}$), urology ($s = \textsc {uro}$), day surgery ($s = \textsc {ds}$) and orthopedic surgery ($s = \textsc {orth}$).

A number of constraints included in our setting reproduce the OT characteristics of San Giuseppe Hospital, detailed in what follows. Some disciplines have a set of non-available ORs. That is, gynecology surgeries should always be performed in OR $r=1(\mathit {NA}_{\textsc {gyn}}=\{2,3,4,5\})$, and orthopedic surgeries have to be performed either in room $r = 4$ or $r = 5$. Thus, $\mathit {NA}_{\textsc {orth}}=\{1,2,3\}$. Nevertheless, these ORs are not exclusively assigned to these disciplines. With $|J|=10$ ($|J|=15$) the number of unavailable rooms is duplicated (triplicated). General surgery and orthopedic surgery allow 2 parallel OR sessions ($PS_{\textsc {gs}} = 2$, $PS_{\textsc {orth}} = 2$), whereas all the other surgical disciplines do not allow parallel sessions. When considering larger instances with 10 rooms, the limit is set to 4 for general surgery and orthopedic surgery and to 2 for all other specialities. Analogously, when $|J|=15$ the limit is set to 6 and 3, respectively. The values of $S_{s}^{min}$ and $S_{s}^{max}$ are given in Table 2.

Table 2 Minimum and maximum number of OR sessions in one week

Since the model (1–10) presents symmetries due to the presence of identical rooms, we add a set of symmetry-breaking constraints (15) having the only purpose of speeding up computations. Given an arbitrary order among the disciplines s and rooms r, these constraints guarantee that rooms are assigned to disciplines in this order. For instance, if discipline s has been assigned to the operating room r, then none of the rooms $1,2,\ldots , r-1$ can be assigned to discipline l in the same day, if $l>s$.

$$ y_{srw}+\sum\limits_{k=1}^{r-1} y_{lkw} \leq 1 \qquad \forall s,l\in\{s+1,\ldots,|S|\},r,w $$

(15)

Notice that in our case study, symmetry-breaking constraints are compatible with constraints (8) on discipline-to-OR restrictions. In general, this may not be true.

Tests have been performed on a 3.2 GHz Intel Core i3 processor with 4 GB of RAM, using OPL Studio 6.1 and the CPLEX 11.2 MILP solver for the mathematical programming models. We note that the software implementation of the proposed model is relatively cheap: in fact, it does not have demanding hardware requirements, and can also be solved through open-source optimization solvers. This would certainly promote the adoption of such a tool by several hospitals. Based on a preliminary experimental campaign, we set the maximum computation time to 60 minutes for each optimization run of the integrated model, whereas the decomposition approach is allowed to run for at most 60 seconds to solve MSSP + SCAP. In fact, our preliminary simulation experiments showed that larger computational time limits did not provide significant improvements in the objective function value.

4.2 Numerical results

We now discuss the performance of the proposed decomposition approach on benchmark instances. The main results are presented in Table 3. Each row of the table reports the average values over ten realizations belonging to the same benchmark set. The first column in the table shows the name of the benchmark set ($|J|$,$\beta$). The next 5 columns report the performance indices of the integrated mathematical model, while in the last 5 columns we report the same performance indices for the decomposition approach. More specifically, Column 2 shows the value of the incumbent; i.e., the value $z_{I}$ of the objective function of the current best solution found by the integrated model at the time when computation was truncated (after 3600 sec.). Column 3 gives the optimality gap for the integrated model, i.e., $(UB-z_{I})/z_{I}$, where UB is the upper bound found by the branch and bound algorithm on the integrated model. Column 4 reports the number of empty time units across the whole week in the incumbent solution. An empty time unit is a 15-minute block not assigned to any surgery. Note that the total number of available time units is 1050, 2100 and 3150 for instances having 5, 10 and 15 operating rooms, respectively. Column 5 indicates the total number of surgeries scheduled in the week in the incumbent solution. Column 6 reports the CPU time required by the integrated model. Column 7 shows the value $z_{D}$ of the objective function of the solution found by the decomposition approach. Column 8 indicates the gap with respect to the upper bound value UB, i.e., $(UB-z_{D})/z_{D}$. Column 9 reports the number of empty time units in the heuristic solution. Column 10 indicates the total number of surgeries scheduled in the week in the heuristic solution. Finally, column 11 indicates the CPU time required to compute the heuristic solution. A few comments are in order.

• No overall big differences emerge between the quality of the solutions provided by the integrated and the proposed decomposition approach. More specifically, in terms of objective function the two algorithms provide comparable solutions, with a slightly better performance of the integrated approach. The achieved value of the objective function displays a linear increase as the number of available ORs increases.

• In both approaches, the optimality gap is very small (less than 0.5 % on average) and almost independent of instance size.

• As for the percentage of empty time units, both the approaches provide an efficient use of the OT. In fact, the empty time units never exceed 1 % of total available time units, even in the largest instances. This shows how both the integrated and the decomposition approaches are able to effectively exploit the available OT capacity. Also the total number of surgeries is comparable between the two approaches, showing a linear increase in $|J|$.

• Although the quality of the solutions provided by the two approaches is similar, relevant differences arise when considering CPU times. In fact, the integrated approach is always truncated after one hour of computation time, whereas the proposed decomposition approach only required few seconds to obtain solutions of comparable quality.

Table 3 Comparison between integrated and decomposition approaches

4.3 Illustrative examples

In this section we illustrate two examples in which the models presented can support the manager in making sound decisions in very limited time.

The setting is the same of the computational experiments reported in Section 4.1. More specifically, we consider the benchmark set (5,300); so, the current waiting list contains 1500 surgical cases, divided into 6 surgical disciplines. These are listed in Table 4. When running the proposed algorithm on these data for a weekly planning horizon, 170 surgeries are scheduled (namely, 34, 50 and 86 cases of classes A, B and C respectively), and the MSS with $N_{OT}=25$ in Table 5 is obtained. We refer to this situation as base scenario.

Table 4 Number of surgeries in the waiting lists

Table 5 MSS adopted in the base scenario

4.3.1 Varying the number of OR sessions

A possible situation the OT manager may be facing concerns the opportunity (or, possibly, the need) of varying the surgical capacity for next week. This can happen for several reasons. For example, surgical activity may be partially reduced or modified, due to unplanned changes in personnel availability. This may suggest reducing the total number of OR sessions. Another possible reason is that the management may want to evaluate the effects of adding OR sessions (e.g., on Saturday) to the MSS; to recover from critical situations or to face an unexpected peak of demand. In both these cases, the manager is interested in assessing the impact that one such variation will have on the number of scheduled surgeries, on due date performance as well as on OR saturation (measured by the total number of empty time units). All these evaluations require running the computations for various different settings. The integrated model is definitely suitable whenever these scenarios can be analyzed well in advance. In practice, however, similar situations arise at short notice; therefore, the OT manager is often asked to evaluate such a context in a short amount of time, providing results within minutes, not hours.

In Table 6, we denote by $\mathcal {S}(\alpha )$ the scenario in which the number of OR sessions is $N_{OT} + \alpha$, for $\alpha =\{-5,-4, \ldots 4,5\}$. $\mathcal {S}(0)$ denotes the base scenario.

• In the face of reduced surgical activity ($\alpha < 0$), the managers may accept a given decrease in surgical production, e.g., 5 %. This goal is achieved as long as the reduction of $N_{OT}$ does not exceed 3. One can observe that the solution obtained for $\alpha =-3$ plans only 31 surgeries of class A vs. 34 in the base scenario. Actually, in this respect the solution obtained for $\alpha =-1$ appears more balanced. From the viewpoint of OR saturation, one observes that in all cases available OR sessions are fully exploited.

• Suppose now that the OT management wants to improve specific performance levels, that have been negatively affected by considerable delays accumulated over previous OR sessions. In particular, according to hospital policies, the OT managers want to schedule 30 more surgeries with respect to the base scenario. This means that to offset this situation within one week, according of the data for $\alpha > 0$, at least $\alpha =4$ additional OR sessions (for an increase of 18.2 % in surgical production) must be planned in the week. If only half recovery is pursued during this week, the increase in surgical production allowed by $\alpha =2$ can be deemed already sufficient.

Table 6 Results obtained by varying the number of OR sessions

Observe that, for each of these scenarios, the total computation time required to solve all cases is less than one minute, and thus compatible with operational and, possibly, real-time decisions. Further, these simulations can be quickly run several times; e.g., to perform what-if analyses during operational meetings, thus quantitatively supporting management intuition and experience.

4.3.2 Varying the bounds on OR sessions of surgical disciplines

Another possible situation that the OT manager may be facing concerns the opportunity to reassign some OR sessions to another surgical discipline, maintaining $N_{OT}=25$, as in the base scenario. This may happen, for instance, when surgeons from uro, ent and gyn individually apply for a leave next (or even current) week. In order to decide on its approval, the manager must quickly evaluate how a decrease in the number of sessions for one of these three disciplines would affect the surgical plan, with respect to the base scenario. This situation can be easy modeled by varying the bounds that limit the number of OR sessions of each discipline.

Running the algorithm based on our decomposition approach, the results presented in Table 7 are obtained. Each row refers to a scenario, denoted by $\mathcal {S}(s)$, in which one OR session is removed for each of the three disciplines, specified by s. The base scenario is denoted by $\mathcal {S}()$. OR saturation is the same for all three cases and hence is not displayed.

Table 7 Results obtained by varying the bounds on OR sessions of surgical disciplines

We observe that, in all three cases, the algorithm reallocates the OR session to gs. This might be due to the fact that gs has the longest waiting list. Note that while removing one session for uro or gyn results in an increased overall number of surgeries and in a decrease of surgeries in class A, removing one ent session allows to maintain 34 surgeries performed in class A as for the base scenario, even if the total number of surgeries decreases.

Note that the option of removing one uro session appears dominated by gyn (which allows performing one more surgery in class B). On the other hand, there is no clear winner between gyn and ent options, since in the gyn scenario 3 more surgeries can be performed, but 5 less of class A. The manager can then evaluate the most convenient between these two tradeoffs.

Also in this case the total computation time required to solve all cases is less than one minute. This appears fully compatible with the short time typically required to the OT manager for making similar decisions.

5 Conclusions and future research

In this paper we proposed a heuristic decomposition approach to determine the master surgical schedule and a surgical case assignment (MSS + SCA).

Mathematical programming models for tackling MSSP + SCAP are able to provide optimal or near-optimal solutions, but their computation times are high. For this reason, we propose a heuristic decomposition approach able to provide near-optimal solutions in very small computation time. The approach is based on a two-phase decomposition in which first MSSP is solved as a minimum cost flow problem, and then SCAP is solved as a multiple-knapsack problem. We tested the decomposition approach on several realistic instances of various OT and waiting list sizes. The results show that the decomposition approach is very effective in practice, reducing the computation time by two orders of magnitude while maintaining solutions close to optimality. Hence, the proposed decomposition scheme can also be embedded in a decision support system, as a tool to perform what-if analysis, or to recompute feasible plans in the face of unpredicted events. Moreover, our investigation points out that this tool effectively supports the OT manager in rapidly evaluating the impact of alternative scenarios on operational decisions.

Future research may address possible refinements and improvements of the models and algorithms presented, such as:

• assessing the impact of model parameters, like the slack time, on system performances;

• extending the model to consider detailed surgeons’ timetables and bed occupancy;

• including uncertainties (e.g., in surgical case durations) in the model;

• evaluating even faster approaches in which SCAP is solved by means of a fast heuristic.