The impact of CON regulation on hospital efficiency

Abstract

In this paper we propose an empirically implementable measure of aggregate-level efficiency along the lines of Debreu’s (1951) coefficient of resource utilization but restricted to the production side. The efficiency measure is based on directional distance functions, which allows the overall measure of efficiency to be decomposed into measures of technical and “structural” efficiency. The latter measure, which captures inefficiencies associated with the organization of production within an industry, is further decomposed into measures of scale and mix efficiency. The measures developed in the paper are illustrated using U.S. hospital data. The illustration sheds light on the efficacy of certificate of need (CON) regulations.

1 Introduction

Health care reform has long been a political issue in the United States. The last federal push for comprehensive reform was during the early years of the Clinton administration. More recent health care reform, such as the implementation of Medicare Part D during the Bush administration, has been more focused. Reforms have been initiated at the state level as well [1–4]. The main impetus for these state level health care reforms is increasing insurance coverage for individuals who are currently uninsured or underinsured. However, following one of the objectives of California’s plan, affordability and cost containment [5], efficient production of health care services within the market (the state in this case) is also an important criteria insuring Pareto optimality in reform. Not only are costs relevant, but so is the state wide availability of services, implying that the proper allocation of resources is one that involves a “fair” distribution of resources throughout the state. While health insurance is the dominant issue in health care reform, it is a premise based on market based approaches. We take a slightly different tact and assess the efficiency of resource utilization within each state via regulation. The direct relationship between regulation, in this case certificate of need (CON) laws, and the state-level aggregation of hospital productivity, but the secondary implication is that for any state based reform to be successful, efficient operation is a necessary condition.

Rising health care costs and the increasing share of GDP accounted for by health care spending have been concerns for some time now; hospital costs are an important part of these issues. Prior to the implementation of the Medicare’s prospective payment system (PPS) in 1983, hospitals were reimbursed on a fee-for-service (FFS) basis.¹ Under the FFS model, hospitals were reimbursed on a cost-plus basis for all expenses incurred; it has been widely argued that FFS had led to a “medical arms race” which resulted in ever escalating costs. In an attempt to mitigate this aspect of increasing costs, the federal government implemented The National Health Planning and Resources Development Act of 1974 [6], establishing Certificate of Need (CON) regulation. The intent of CON regulation was to ensure the availability of health care services while guarding against the costly duplication of services and excess capacity. To assess CON’s general contribution toward improving hospital efficiency by limiting excess capacity and duplication of services that would increase inefficiency ceteris paribus, we apply the Debreu [7] concept of the coefficient of resource utilization (CRU) that can be used to measure the overall efficiency of an economy. (However we restrict our analysis to the production sector.) Ranging from 0 to 1, the CRU gives the smallest proportion of available resources technologically necessary to achieve a given level of “satisfaction or standard of living” for an economic system. This aggregate measure of efficiency captures the loss associated with non-optimal outcomes for an economic system. A CRU of 1 indicates that an economy is efficient—i.e., no dead weight loss exists; the CRU is less than 1 when “inefficiency” arises due to the underemployment of available resources, inefficiency in production, or the “inefficiency of economic organization”—i.e., market imperfections or distortions. Farrell [8] introduced a method for measuring the “productive efficiency of an industry” by examining performance at the “production unit” level. In introducing his ideas, Farrell noted the similarity of his measure of technical efficiency to Debreu’s CRU. These two pioneering works are the foundation of various radial “Debreu-Farrell” measures of efficiency that benchmark performance relative to a “best-practice” frontier. This approach, commonly referred to as the Data Envelopment Analysis (DEA) today, was later formalized by Charnes, Cooper, and Rhodes [9] and Färe, Grosskopf, and Lovell [10, 12].

While Debreu and Farrell both addressed “aggregate” efficiency, most of the efficiency studies that have appeared in the literature assess efficiency at the firm level rather than at an aggregate level. Whereas the use of DEA is appropriate for assessing individual hospital efficiency, DEA cannot be used to aggregate individual hospital efficiency scores into an overall measure of state level hospital efficiency. This is because radial measures like DEA cannot be added together in a meaningful way (since the radial distances may be in different directions). Instead of DEA, we use directional distance functions to measure hospital level efficiency and then aggregate the hospital level efficiency scores into state-level measures of efficiency. ² It is the additivity feature of the directional distance function used in deriving the Debreu CRU measure that distinguishes it from the DEA approach. Specifically, in this paper, we present an approach closer to Debreu’s original CRU in that it measures efficiency at an aggregate level—the sectoral or industry level—and decomposes it into two of Debreu’s three potential sources of inefficiency—productive inefficiency and “inefficiency in economic organization,” which we call “structural inefficiency.”^{3 , 4} We also show that structural inefficiency can be further decomposed into measures of scale and mix inefficiency.

Structural efficiency appeared in the literature with Farrell’s discussion of technical efficiency of an industry (p. 261) and the structural efficiency of an industry (p. 262). As defined by Farrell, “…the technical efficiency of an industry with respect to a given efficient isoquant would be simply a weighted average of the technical efficiencies with respect to the same isoquant of its constituent firms,” while the structural efficiency is defined as “…the extent to which an industry keeps up with the performance of its own best firms.” Over time alternative measures of the industry technical and structural efficiencies have been introduced in the literature [13–15]. From our perspective, we define the aggregate of firms’ technical efficiencies based on the firms’ individual technologies. This aggregate is analogous to a weighted average of efficiency indices as defined in Farrell [8]⁵ or a sum of firms’ efficiency measures (as we will do with the directional distance function). On the other hand, we can define an industry’s technical efficiency measure based on the industry production plan defined as the sum of firm’s endowments of inputs and outputs and computed from an industry technology defined as the sum of firms’ technologies. Then structural efficiency can be used to capture the differences between industry technical efficiency and aggregate firm technical efficiency.

After developing our measures of efficiency, we illustrate the measurement of aggregate efficiency and its decomposition by examining U.S. hospital efficiency at the state level.⁶ Thus we also add to the literature on hospital efficiency which to date has focused on the efficiency of individual hospitals. As stated above, we examine hospital efficiency at the state level shedding light on the structural efficiency effects of certificate of need (CON) programs. Even though state health care reforms currently address the demand side of health care, state-level CON legislation is intended to coordinate new services and construction within the health care sector, i.e., the supply side. Since health care reform cannot succeed without effective cost controls on both the demand and supply side, it is pertinent to examine hospitals, the largest cost component in U.S. health care, in an attempt to restrain the rising costs of health care. We use the measures developed in this paper to test two hypotheses. First, is the technical efficiency of the hospital industry the same in states with and without CON programs? Second, and more germane to the intent of CON programs, is hospital sector structural efficiency equal in states with and without CON programs? Even though we examine CON specifically, it is worth noting that this approach can be applied to other forms of health regulations as well as including contracting and prospective fee schedules.

We measure technical and structural efficiency using methods familiar in from the standard Debreu-Farrell framework—linear programming models (or DEA). However, rather than evaluating performance using the radial measures of efficiency common under the Debreu-Farrell framework, we make use of directional distance functions. Employing directional distance functions allows for the simultaneous decrease of inputs and increase of outputs, holding technology constant. Furthermore, the additivity property of directional distance functions is exploited to derive our aggregate performance measures. To reiterate, it is the additivity property of the directional distance function approach that distinguishes it from the more common DEA approach; additivity is crucial to determine aggregate (state level) performance. Hence the directional distance function approach is used rather than the DEA, which is better suited for individual hospital evaluation.

The remainder of the paper unfolds as follows. In the next section, we present the industry-level analog of Debreu’s CRU and its decomposition into technical and structural inefficiency. Section 3 offers an illustration of our models by assessing hospital efficiency at the state level and testing whether efficiency levels differ across states with and without CON programs. The section begins with brief overviews of CON and the empirical literature on the effect of CON regulation on hospital cost, then moves on to our data, results, and implications. Section 4 summarizes the paper.

2 Modeling efficiency at the aggregate level

The CRU of Debreu [7] provides an aggregate measure of the “dead weight loss” associated with the sub-optimal use of scarce resources due to the underemployment of physical resources, inefficiency in production, and imperfections in economic organization. Debreu pointed out that the latter is a subtle source of inefficiency, but argued that it is the inefficiency for which numerical evaluation is the most necessary. However, he did not offer formal definitions of these three components of efficiency nor did he provide a means to measure them. The models developed in this paper can be seen as an intermediate step between the economy-wide CRU of Debreu [7] and the firm-level measures of efficiency introduced by Farrell [8]. Like the former, we offer a means of measuring efficiency at an aggregate level; like the latter, our measure can be decomposed into a number of constituents, including a measure of “structural efficiency” that captures the inefficiency due to imperfect “economic organization.” More specifically, our aggregate measure of inefficiency can be decomposed into measures of the technical inefficiency of the hospitals in an industry as well as the structural inefficiency associated with the misallocation of resources among hospitals within an industry. The latter inefficiency measure is further split into a mix effect—inefficiency due to sub-optimal mixes of inputs/ outputs—and a scale effect—inefficiency that arises from departures from the most productive scale size (MPSS). Recall that one of the explicit objectives in state based reform, most notably, California, hospital care must be accessible to all citizens; therefore the mix effect and scale effect are integral to assessing efficient allocation of inputs.

2.1 A graphical overview the efficiency measures

Before embarking on a formal presentation of the models, we begin with graphical illustrations of our approach to measuring aggregate efficiency. In Fig. 1, a simple one input (x), one output (y) variable returns to scale (VRS) firm level technology (T) is represented together with the two hospitals representing a group within the industry (which has a total of five observations represented by the kinks on the production frontier). The aggregate, or group, technology is simply the sum of the individual hospitals’ technologies and is defined as 2×T(x,y).⁷ The group production plan (i.e., its inputs and the associated outputs) is also defined as the sums of the inputs and outputs of the individual hospitals, A+B. In Fig. 1 we assume that both hospitals A and B operate on the frontier of the hospital-level technology so that there is no technical inefficiency; this allows us to focus attention on structural inefficiency at this point. Furthermore, note that with the simple one input/one output technology, no mix effects can arise. Therefore Fig. 1 illustrates just the scale component of the structural inefficiency. Both hospitals A and B are scale inefficient relative to the most productive scale size (MPSS) of the firm level technology—A is too small and B is too large relative to the MPSS. In Fig. 1, the hospital-level scale inefficiency is represented by the dashed lines rising above A and B up to the ray from the origin that overlaps with the constant returns to scale (CRS) portions of both the hospital and group technologies.

Fig. 1

An illustration of the scale component of the structural efficiency for hospitals A and B

Since neither technical inefficiency nor mix effects are present in Fig. 1, the total group inefficiency measured at the aggregate DMU (A+B) is comprised of only the scale inefficiency. The scale effect, however, is not simply the sum of individual hospitals’ scale inefficiencies; this is because the aggregated production plan itself, A+B, is also scale inefficient relative to the group-level technology. Structural inefficiency computes the maximum feasible increase in output possible given a reallocation of inputs between A and B. Nevertheless it is still possible that some scale inefficiency could remain even after this reallocation. In Fig. 1, the structural inefficiency is the distance from A+B to the frontier of 2T(X,Y) and the remaining scale inefficiency is the distance from 2T(X,Y) to the CRS frontier defined by the ray from the origin.

In Fig. 2, we add technical inefficiency—i.e., both A and B now operate below the frontier of the firm level technology. This changes neither the definition nor the computation of the structural inefficiency, but now the total group inefficiency is the sum of technical inefficiency (the dashed portion of the line above A + B) and structural inefficiency (the solid portion of the line above A + B), as noted in Fig. 2.

Fig. 2

An illustration of the decomposition of the hospital industry level inefficiency between aggregate technical and structural inefficiencies

Figure 3 illustrates the mix component of the structural inefficiency. Again consider the case of just two hospitals A and B comprising the group which form the aggregated production plan (A+B). Now, however, assume that there are two inputs x ₁ and x ₂ and that A and B use the same technology, represented by the input sets L(y ^A) = L(y ^B), respectively. Following [16], the group input set, L(y ^A + y ^B), is the Minkovski sum of the hospitals’ input sets (i.e., ${\text{L}}\left( {y^A \, + \,y^B } \right)\,\, = \,\,{\text{L}}\left( {y^A } \right)\,\, + \,\,{\text{L}}\left( {y^B } \right)\,\,\, = \,\,\,x^A \,\, + \,\,x^B$). To isolate the mix effect, we assume a constant returns to scale technology so that hospitals A and B are scale efficient and technically efficient (i.e., they both operate on the CRS isoquant). Therefore, no inefficiencies arise at the DMU level. Nevertheless, there is inefficiency at the aggregate level—this “structural” inefficiency stems from the misallocation of inputs across the two hospitals. In a perfectly competitive market with a common production technology, the two hospitals should have the same input mix. By the convexity of the isoquant, different mixes among hospitals lead to an inefficient allocation of inputs within the group; this misallocation across hospitals is captured by the mix effect component of the structural inefficiency. In the spirit of the Debreu [7], this inefficient market allocation is an example of “inefficiency in economic organization.” Note that the proper mix effect is computed under an assumption of constant returns to scale in order to separate it from scale inefficiency.

Fig. 3

An illustration of the mix component of the structural efficiency

Finally, all of the components of inefficiency are brought together in Fig. 4. Hospitals A and B have different levels of production under a variable returns to scale (VRS) firm level technology; both are also technically inefficient. As above, the aggregate technology is computed as the sum of individual firm’s technologies—e.g., the open-circled point on the aggregate isoquant is the sum of the two open-circled points on the individual isoquants. Under the VRS assumption and the presence of technical inefficiency, we have the complete decomposition of the group inefficiency between technical, scale and mix effects. It should be noted that we consider here a group of two hospitals (A and B) but if the group comprises all the hospitals in the industry then the group efficiency equals the industry efficiency and the group technology equals the industry technology.

Fig. 4

An illustration of the decomposition of the industry level inefficiency between aggregate technical, scale and mix inefficiency

Constructing the aggregate technology is not a trivial task because we have to consider all the feasible combinations of individual hospitals within the industry and identify the efficient ones. Therefore, we must use a specific linear program (described in the next section) to generate the aggregate isoquant. As noted above, we employ a directional distance function that uses the same direction for all hospitals; this allows us to exploit the additivity property of directional distance functions so that we can form our aggregate measures. The additive nature of the various efficiency measures in turn allows for the proposed decomposition of the total inefficiency into its components.

2.2 Measuring efficiency and its components using directional distance functions

We now present a formal development of our model. Suppose that the industry under analysis is populated by K hospitals. Let $x^k \in R_{ + }^N$ and $y^k \in R_{ + }^M$denote input and output vectors, respectively, for firm k (k = 1..., K). Let T be a production set satisfying the core Shephard axioms (see [17]); in particular, we consider a convex technology T satisfying free disposability of inputs and outputs. As noted above, we adopt the standard assumption that all hospitals face the same technology, T. Under constant returns to scale (CRS),⁸ the firm level technology can be represented by:

$$ T_{CRS} = \left\{ {\left( {x,y} \right):\sum\limits_{k = 1}^K {y_m^k z^k \ge y_m, m = 1,...,M,\sum\limits_{k = 1}^K {x_n^k z^k \le x_n, n = 1,...,N,z^k \ge 0\forall k} } } \right\}, $$

(1)

where x _i and y _j denote the ith and jth elements of x and y, respectively. Note that the aggregate (sectoral/industry) technology inherits its properties from the firm level technology. Formally, we define the industry-level technology T ^I as the summation (aggregation) of the firm-level technology:

$$ T^I = \sum\limits_{k = 1}^K {T^k } = \sum\limits_{k = 1}^K {T;} $$

(2)

the second equality in (2) follows from the assumption that all hospitals within an industry share a common technology. Li and Ng [18] proved that under CRS the aggregate technology is simply equal to the firm level technology:

$$ T_{CRS}^I = \sum\limits_{k = 1}^K {T_{CRS} = T_{CRS} .} $$

(3)

Under variable returns to scale (VRS), firm level technology is given by:

$$ T_{VRS} = \left\{ {\left( {x,y} \right):\sum\limits_{k = 1}^K {y_m^k z^k \ge y_m, \,\,} \,m = 1,...,M,} \right.\sum\limits_{k = 1}^K {x_n^k z^k } \left. { \le x_n, \,\,n = 1,...,N,\sum\limits_{k = 1}^K {z^k } = 1,\,\,z^k \ge 0\,\,\forall \,k} \right\}\,. $$

(4)

Li and Ng [17] also proved that under VRS the aggregate technology is simply:

$$ T_{VRS}^I = \sum\limits_{k = 1}^k {T_{VRS} } = K \times T_{VRS} . $$

(5)

Note that this is the basis for the representations of aggregate technologies as the sums of the firm level technologies illustrated in Figs. 1 through 4.

Given the definitions of technology above, we now present the directional distance function that is used to determine the efficiency with which technology is utilized. The function $\vec{D}_T :\left( {R_{ + }^M \times R_{ + }^N } \right) \times \left( { - R_{ + }^M } \right) \times R_{ + }^N \xrightarrow[{}]{}R_{ + }$ defined by:

$$ \vec{D}_T \left( {x,y;g_x; g_y } \right) = \mathop {\sup }\limits_{\lambda } \left\{ {\lambda \in \mathbb{R}_{ + } :\left( {x - \lambda \cdot g_x, y\, + \lambda \cdot g_y } \right) \in T} \right\}, $$

(6)

is the directional distance function in the direction (g _x ;g _y ). An analysis of the properties of the directional distance function can be found in Chambers et al. [19]. Note that $\left( {x,y} \right) \in T\, \Leftarrow \Rightarrow \vec{D}_T \left( {x,\,y;\,g_x; \,g_y } \right) \ge 0$. Thus, it is possible to characterize the production set by the directional distance function.

We employ the industry level input/output observations to construct the direction of translation used when computing efficiency with the directional distance function; i.e., $\left( {g_x, g_y } \right) = \left( {\sum\limits_k {x^k, \sum\limits_k {y^k } } } \right)$, where k indexes hospitals in the industry. The efficiency of a particular hospital is defined by $\vec{D}_T \left( {x,\,y;\sum\limits_k {x^k, \sum\limits_k {y^k } } } \right);$ as is the case with DEA, this efficiency measure can be computed by solving a linear program (LP). For example, under the assumption of a variable returns to scale (VRS) technology the linear programming problem to be solved is:

$$ \begin{array}{*{20}c} {} \hfill & {\vec{D}_{{T_{VRS} }} \left( {x,\,y;\sum\limits_k {x^k, \sum\limits_k y^k } } \right) = \mathop {\max }\limits_{{z,\lambda }} \lambda } \hfill \\ {s.t.} \hfill & {\sum\limits_{k = 1}^K {z^k y_m^k } \ge y_m + \lambda \sum\limits_k {y_m^k } \forall m = 1, \cdots, M} \hfill \\ {} \hfill & {\sum\limits_{k = 1}^K {z^k x_n^k } \le x_n - \lambda \sum\limits_k {x_n^k } \forall n = 1, \cdots, N} \hfill \\ {} \hfill & {\sum\limits_{k = 1}^K {z^k = 1} } \hfill \\ \hfill & {z_k \ge 0\forall k = 1,...,K} \hfill \end{array} $$

(7)

The industry technical efficiency is defined by $\vec{D}_{{T^I }} \left( {\sum\limits_k {x^k, \sum\limits_k {y^k; } } \sum\limits_k {x^k, } \sum\limits_k {y^k } } \right).$ This measure can be computed by solving the following industry-level linear programming problem (here under a VRS assumption):

$$ \begin{array}{*{20}c} {} \hfill & {\vec{D}_{{T_{VRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \sum\limits_k {x^k }, \sum\limits_k {y^k } } \right) = \mathop {\max }\limits_{{z,\lambda }} \lambda } \hfill \\ {s.t.} \hfill & {K\sum\limits_k {z_k y_m^k } \, \ge \sum\limits_k {y_m^k } + \lambda \sum\limits_k {y_m^k } \forall m = 1, \cdots, M} \hfill \\ \hfill & {K\sum\limits_k {z_k x_n^k } \le \,\sum\limits_k {x_n^k } - \lambda \sum\limits_k {x_n^k } \forall n = 1, \cdots, N} \hfill \\ \hfill & {\sum\limits_k {z_k } = 1} \hfill \\ \hfill & {z_k \ge 0\forall k = 1,...,K} \hfill \end{array} $$

(8)

Collecting terms, (8) simplifies to:

$$ \begin{array}{*{20}c} {} \hfill & {\vec{D}_{{T_{VRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \sum\limits_k {x^k }, \sum\limits_k {y^k } } \right) = \mathop {\max }\limits_{{z,\lambda }} \lambda } \hfill \\ {s.t.} \hfill & {K\sum\limits_k {z_k y_m^k } \, \ge \left( {1 + \lambda } \right)\sum\limits_k {y_m^k } \forall m = 1, \cdots, M} \hfill \\ \hfill & {K\sum\limits_k {z_k x_n^k } \, \le \,\left( {1 - \lambda } \right)\sum\limits_k {x_n^k } \forall n = 1, \cdots, N} \hfill \\ \hfill & {\sum\limits_k {z_k } \, = 1} \hfill \\ \hfill & {z_k \ge 0\forall k = 1,...,K} \hfill \end{array} $$

(9)

For the industry production plan this reduces to the generalized Debreu-Farrell measure of efficiency introduced by Briec [20].

Finally, we turn to the decomposition of the industry technical efficiency measure into measures of aggregate technical efficiency and structural efficiency. The latter measure can be further decomposed into a scale effect and a mix effect.⁹ As explained above, the industry technical efficiency measure at the industry-level is given by:

$$ Ineff^{Industry} = \vec{D}_{{T_{VRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \sum\limits_k {x^k }, \sum\limits_k {y^k } } \right). $$

(10)

The decomposition of this industry-level inefficiency into its aggregate technical and structural inefficiency components is easily accomplished. The use of directional distance functions provides a straight-forward aggregate of hospitals’ technical efficiency:

$$ Ineff^{Aggregate} \,\,\, = \,\,\,\sum\limits_{{k \in s}} {\vec{D}_{{T_{VRS} }} } \,\left( {x^k, y^k; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)\,. $$

(11)

Structural efficiency can now be calculated as a “residual” measure—i.e., it is the difference between the industry technical efficiency and the aggregate technical efficiency:

$$ \begin{array}{*{20}c} {Ineff^{Structural} \,\,}{\, = \,\,\,Ineff^{Industry} \,\,\, - \,\,\,Ineff^{Aggregate} } \\ { = \,\,\,\vec{D}_{{T_{VRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right) - \,\,\sum\limits_k {\vec{D}_{{T_{VRS} }} } \left( {x^k, y^k; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)\,} \end{array} $$

(12)

Structural inefficiency can be further decomposed into a measure of mix inefficiency given by:

$$ Ineff^{Mix} \,\,\, = \,\vec{D}_{{T_{CRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)\, - \,\sum\limits_k {\vec{D}_{{T_{CRS} }} \left( {x^k, y^k; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)} $$

(13)

and, a measure of the scale inefficiency given by:

$$ \begin{array}{*{20}c} \begin{gathered} Ineff^{Scale} \,\,\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} { = \,\left[ {\,\sum\limits_k {\vec{D}_{{T_{CRS} }} } \left( {x^k, y^k; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right) - \,\sum\limits_k {\vec{D}_{{T_{VRS} }} \left( {x^k, y^k; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)} \,} \right]\,} \\ { - \left[ {\vec{D}_{{T_{CRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right) - \vec{D}_{{T_{VRS}^I }} \left( {\sum\limits_k {x^k }, \sum\limits_k {y^k }; \,\sum\limits_k {x^k }, \sum\limits_k {y^k } } \right)} \right]\,\,} \end{array} $$

(14)

To sum up, the decomposition of the industry level inefficiency is given by:

$$ \begin{array}{*{20}c} {Ineff^{Industry} }{ = \,\,\,Ineff^{{Aggregate~firm}} \,\,\, + \,\,\,Ineff^{Structural} } \\ {\,\, = \,\,\,Ineff^{{Aggregate~firm}} \,\,\, + \,\,\,Ineff^{Mix} + \,\,\,Ineff^{Scale} .} \end{array} $$

(15)

3 An application: the effect of con regulation on aggregate hospital efficiency

CON regulation mandated a government review of all hospital requests for capital expansion, allowing for capital expansion only in cases where the medical need warranted it. The argument in favor of CON was also based on quality of care, since it has been widely believed that quality is a function of volume and that by limiting the access to costly technology, physicians in hospitals with the technology would be ensured the volume to perfect their practice, which in turn would lead to better outcomes. Thus it was argued that with CON, social costs would be further reduced indirectly. First, capital would be appropriately utilized leading to sufficient volume and higher quality of care. Second, the higher quality care would lead to a decrease in excess mortality and/or morbidity. Third, this decrease in excess mortality and/or morbidity reduces the social costs due to the burden of disease and loss of productivity.

According to theory, regulation is often enacted to correct for market failures thereby moving the industry, in this case hospitals, to mimic market like behavior. Since markets cannot be perfectly realized in the hospital care market, regulation, at least on the supply side, appears to be one approach toward cost containment rather than out-right governmental control.

CON was implemented at the state level, but some states repealed their CON regulations (see below) after the federal mandate for CON programs was lifted in 1987. If CON serves its intended purpose, then a priori we would expect states with CON regulation to have higher levels of structural efficiency than states without CON regulation. In our illustration of the methods developed above we seek to answer the following question—how does structural efficiency vary with CON regulation? To address this question, we apply our models to state-level hospital data (i.e., we treat each state as having its own hospital “industry”). We first derive the aggregate (“industry”) hospital production technology for each state (and the District of Columbia) by summing all the hospitals’ technologies operating within a given state. Then we gauge the technical (i.e., productive) efficiency of each hospital by comparing it to the global technology defined as the efficient use of inputs to produce outputs of all hospitals operating in the state.

We follow this strategy for the following reasons. First, the difference between best-practice and absolute frontiers is mitigated as the sample size increases [21]. Second, the “same technology” is one criteria of a market; therefore, the difference between the individual hospital and the states’ respective productivity equals the measure of structural inefficiency which is akin to Debreu’s measure of dead weight loss. In a competitive market each firm faces the same output prices and input costs and has access to the same technology therefore each firm (hospital, in our case) has the incentive to be both technically and allocatively efficient. However, in the hospital market output is often exogenous—in part because it is based on a stochastic demand function and hospitals “stand ready to serve.” This supposition is supported by the fact that in some cases, 55% of all admits come via the emergency room [22].

3.1 Previous literature on con regulation’s effect on hospital cost

The effectiveness of CON in reducing hospital costs and inefficiency has been debated in the literature; here we briefly review some of the empirical findings. Sloan [23] analyzed the effects of CON regulation using state level data covering the period 1963–1978. The dependent variables in eight estimated cost functions were state-level mean values of various average cost measures for private, nonprofit hospitals. Sloan used a series of three dummy variables to indicate the presence and “age” of CON regulations in each state. In seven of the eight cost models, none of the CON dummies were statistically significant, leading Sloan to conclude that CON regulation had no effect on the average costs of hospitals.

Mayo and McFarland [24] developed a model that more directly examined the effect of CON regulation on capital formation. They modeled hospital “plant size” (i.e., number of beds) as a function of the degree to which CON regulation restricted hospital expansion. Their measure of regulation was inversely related to the ratio of expansion applications that were approved by CON authorities. Using data on 120 short-stay hospitals operating in Tennessee over the 5 year period 1980 to 1984, they concluded that CON regulation slowed bed growth and helped to control hospital costs.

Conover and Sloan [25] used various panel data sets, covering the late 1970s to the early 1990s, to examine the effects of CON regulation. They found that mature CON policies were associated with a 2 percent decline in bed supply and a 5 percent long-term decline in per capita acute care spending. In addition, they found that for-profit hospitals and states with CON regulations were positively correlated, suggesting that arguments that CON dissuades the development of competition in hospital markets are unfounded. Counter to their a priori hypothesis that CON laws should lead to higher efficiency, Conover and Sloan also found that when the federal mandate for CON was lifted, there was an increase in the number of hospital beds and expense per admission in states that repealed CON, though these increases were not statistically significant.

ICF-Lewin [26] presented evidence that CON reduced hospital costs, and slowed the diffusion of technology, but this reduction was not considered to contribute a great deal to lower costs. Graham and Cowing [27] corroborated ICF-Lewins’ findings that CON had a statistically significant effect on lowering excess capacity, but concluded that this effectiveness was a function of how long the CON regulation had been in effect.

Bates et al. [28] examined the relationship between market structure and technical efficiency for a sample of hospitals in U.S. metropolitan areas. Under the structure-conduct-performance paradigm, the reduction in competition engendered in CON regulation might be expected to reduce technical efficiency. Bates et al. measured technical efficiency using data envelopment analysis (DEA), then they regressed the efficiency scores on a dummy variable for CON regulation and other elements of market structure (e.g., HMO activity). Based on their regression results, Bates et al. concluded that, on average, CON laws did not reduce efficiency.

Finally, Foreman and Keeler [29] discussed the tie between CON and private industry. Automakers in Michigan insisted that the state maintain CON, offering as evidence a comparison of hospital costs in Michigan (with CON regulation) and Indiana and Ohio (with either no CON or weak CON). The automakers were obviously interested in hospital costs due to the employment based health insurance scheme popular in the U.S.

The existing studies of CON regulation’s effect on costs has produced mixed results—some evidence suggests modest desired effects, other evidence suggests (at best) no effect. In a review of regulation in the hospital industry, Banks et al. [30] concluded that the evidence indicates that CON regulation has not been effective and that this lack of effectiveness led the Reagan Administration to repeal the federal mandate for state CON laws in 1987. To date, 14 states have repealed their CON laws.¹⁰

All of the studies cited above are based on hospital level measures of performance. The intent of CON regulation, however, was to improve performance at the aggregate level; our measures of performance therefore offer an assessment of CON regulation that is more consistent with its intent. Furthermore, hospital markets have evolved since many of the earlier studies were done. For example, Devers et al. [31] argued that while in the past hospitals engaged in non-price competition, in the 1990s price-based competition emerged. By the early 2000s the competition revolved around retail strategies such as development of specialty hospitals [32]. In light of this new medical arms race within hospital markets, and the associated higher costs that such supply changes incur, there has been a re-examination of federal and state policies and regulations designed to control hospital capacity and the over-utilization of hospital resources that is not grounded on need-based evidence. Given the mixed results of earlier studies, the renewed interest in regulating capacity, and the continued concern about health care costs, we add to the literature on the effects of CON regulation by assessing its impact on both technical and structural efficiency by using the models developed in the first part of this paper. With our research we hope to increase the understanding of CON regulation’s effects so that more effective public policies addressing health care costs can be developed.

3.2 The data

To implement the models developed above we use panel data covering 1994 to 2002 culled from the American Hospital Association’s Annual Survey of Hospitals, the most exhaustive data set available for the U.S. hospital industry. Using panel data set, we can assess the effects of changes in CON regulation over time. We can also assess factors that are associated with market failure and resulting efficiency (both productive and structural). At the hospital level, the total sample size is 37,956, which consist of 4,217 hospitals over the 9 year period. For the state level analysis, the sample size is 459—50 states plus the District of Columbia observed over the 9 years 1994–2002.

Hospitals are complex organizations. Capturing the scale and size of their operations by specifying their inputs and outputs is a difficult task.^{11 , 12} The inputs and outputs that we use in our analysis parallel those commonly used in studies of hospital efficiency/productivity. The inputs included in our analysis are the number of staffed beds (as a proxy for capital) and four types of labor. The labor inputs included the numbers of full time equivalent (FTE) registered nurses (RNs), FTE licensed practical nurses (LPNs), FTE other staff (OTHER), as well as the number of FTE medical residents and other trainees. We included medical residents and trainees as outputs since they represent the teaching commitment on the part of the hospital which is a social benefit; furthermore, by using the input–output direction we can differentiate between teaching and non-teaching hospitals in our analysis. We excluded the number of physicians because, as they are not formal employees of private hospitals, they are not available for most of the observations in our sample. While this omission almost certainly affects our results, it is, unfortunately, a limitation of most studies of hospital efficiency.

In addition to medical residents, we include four other outputs in our analysis—the total number of case mix adjusted admissions, the total number surgeries, the total number of emergency room visits, and the total number of outpatient visits. The case mix adjusted admissions were derived by multiplying each hospital’s number of admissions by its case mix index. By adjusted admissions, hospitals treating more seriously ill patients can be differentiated from hospitals treating less severely ill patients. Adjusting by case mix is important in reconciling patient care and resource use since efficient resource use and case mix are highly correlated. Table 1 contains some descriptive statistics of the inputs and outputs used in this paper. The statistics are reported separately for states with and without CON regulations; significance tests of the differences across regulatory regimes are also reported.

Table 1 Descriptive statistics for the hospital-level input and output variables

We are also interested in some state level influences on efficiency. For example, the percentage of the state population living in rural areas is included. This may impact efficiency because hospitals serving rural populations do not have the commensurate population base that is present in urban areas. In addition, the concentration of hospital beds by ownership type is included, since different ownership forms have different objective functions that may alter the productive and structural efficiency measures. Descriptive statistics of these state level variables appear in Table 2.

Table 2 Descriptive statistics for the state-level variables

3.3 Results

We first discuss the inefficiency measures by states with and without CON regulations and by year, which are reported in Table 3. Based on Wilcoxon-Rank tests for differences in medians, we find that CON and NOCON states differ on all types of efficiencies. We find that, on average, industry level efficiency is higher in CON states than in NOCON states. The superior performance of CON states is due to higher aggregate technical and mix efficiencies; NOCON states, however, have higher scale efficiency. Therefore, two opposite effects play out in the assessment of structural inefficiency. On one side, the CON regulation seems to improve the mix allocation among hospitals, but on the other side it also seems to constrain the size of hospitals, which have difficulty achieving most productive scale size. On net, structural efficiency is higher in CON states.

Table 3 Mean inefficiencies for CON and NOCON states (51) by year (9) ( N = 459)

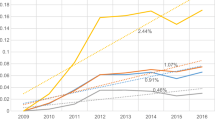
To better appreciate their evolution over time, the mean efficiency scores for CON and NOCON states are presented graphically in Figs. 5, 6, 7.¹³ Figure 5 illustrates the mean aggregate technical inefficiency scores over time by regulatory regime. This graph demonstrates that, in general, the hospitals in states with and without CON regulation have had similar evolutions of technical inefficiency that tends to be constant over time. However a significant gap exists between the two types of states and even if it seems to have decreased periodically over the period it remained relatively large in 2002.

Fig. 5

Evolution of aggregate technical inefficiency for CON and NOCON states

Fig. 6

Evolution of mix inefficiency for CON and NOCON states

Fig. 7

Evolution of scale inefficiency for CON and NOCON states

Figure 6 reveals a different pattern for mix inefficiency. The evolution and the mean of mix inefficiency over time vary for CON and NOCON states. Globally, the mix inefficiency is increasing over 1994–2002. While the average rate of growth seems to be equal between the states, it can differ at different time periods. For example, the gap in mix inefficiency has increased between CON and NOCON states since 2000. Figure 7 reveals the opposite pattern for the scale inefficiency—while CON states are better with respect to aggregate technical and mix efficiency, CON states appear to be less scale efficient than NOCON states. We also note that the scale inefficiency tends to decrease over time for the NOCON states, while it remains constant (though at a higher level) for the CON states.

As discussed above, there may be factors beyond just the presence or absence of CON regulations that affect hospital efficiency. We used ordinary least squares to regress the technical, mix and scale inefficiency scores at the state level on a dummy variable for CON regulation (CON), the percentage of a state’s population living in rural areas (Rural), controls for the effects of different forms of ownership in the form of the percentage of a state’s hospital beds in public (%BdsPub), for-profit (%BdsProf), and federal (%BdsFed) hospitals (the percentage of a state’s beds in not-for-profit hospitals was the omitted group), and time dummy variables (Year) to capture any time effects. As the regressions are based on the aggregated results at the state level, the variables are smooth and continuous without truncated data so there is no need to use a non-linear approach such as truncated regression or Tobit analysis. The regression results appear in Tables 4 and 5 and are discussed below. Note that heteroskedastity was detected, so we report robust standard errors.

Table 4 Determinants of aggregate technical and structural inefficiency (N = 459)

Table 5 Determinants of mix and scale inefficiency (N = 459)

The statistically significant differences in aggregate technical and structural efficiency across CON and NOCON states noted above remains after controlling for other factors in the regression model—CON regulations have a statistically significant, positive effect on aggregate technical and structural efficiency (note that we explain the level of inefficiency and therefore the negative sign associated with a variable implies a positive impact on efficiency). Furthermore, the higher the percentage of the population living in rural areas, the lower are aggregate technical and structural efficiency. This “inefficiency” likely improves the access to hospital services to people in rural areas. Compared to the not-for-profit hospitals (the omitted variable), as the proportion of beds in publicly owned hospitals increases, aggregate technical and structural efficiency decrease—public hospitals are less likely to respond to market forces, so this result seems reasonable. On the contrary, for states where for-profit hospitals have a higher proportion of beds, efficiency is higher vis-à-vis the not-for-profit hospitals. Finally, the coefficients on the time variables for the structural inefficiency scores are all significant, with the exception of 2000, suggesting that structural inefficiency has increased over time while the aggregate technical efficiency has no statistically significant time trend over the sample time period.¹⁴ These finding are consistent with the visual inspection of Figs. 5 and 6.

We now turn to the regression results for mix and scale effects. Like the simple difference of means tests reported in Table 3, the regression results suggest that, controlling for other factors, CON regulation has a statistically significant positive effect on mix efficiency but a negative effect on scale efficiency. A higher percentage of the population living in rural areas again lowers mix and scale efficiency. Interestingly, the effects of ownership concentration for the scale inefficiency model differ from those found when examining aggregate technical, structural, and mix efficiency. Whereas the mix inefficiency increases with increases in the degree of public ownership, the scale inefficiency decreases. The increase in the proportion of beds operated by private, for-profit hospitals is associated with a sizable increase in mix efficiency but a significant decrease in scale efficiency as compared to the private NFP hospitals. We also find a time trend wherein mix inefficiency increases over time for our sample. The findings are just reversed for the scale efficiency. We find statistically significant coefficients only for the years 1996, 2000, and 2002, suggesting no time trend for scale inefficiency over the sample period, a result consistent with the general trend visible in Figs. 6 and 7.

3.4 Discussion

In terms of efficiency, our findings agree with those of [27] who also found a positive time effect of CON regulation’s ability to reduce costs (increase efficiency). We also found that structural efficiency was always higher for states with CON regulations than for states without CON regulation. Our findings also suggest that regulating the hospital industry does have benefits, particularly since hospitals do not necessarily behave in a cost-minimizing/profit-maximizing manner. One goal of hospital regulation is to “force” hospitals to operate in a more cost-conscious fashion. What we have found is that the states with CON regulation accomplished this as demonstrated by a more efficient allocation of resources and outputs than is found in states without CON regulation.

Using ordinary least squares multiple regression techniques to isolate the effect of CON holding other factors thought to impact efficiency constant, we found more evidence with respect to this regulation’s effectiveness in improving relative hospital performance. Our findings suggest that CON regulations did in fact have a positive effect on the aggregate technical and mix efficiencies in states that maintained CON vis-à-vis those that have abandoned CON. The robustness of CON’s positive impact on improved efficiency also provides policy makers with information regarding the benefits of such regulation and that these policy measures should not be abandoned in favor of a market only approach. The duration of the CON regulation also was statistically significant in maintaining higher levels of efficiency in terms of both the aggregate technical efficiency and the structural mix decompositions. In terms of maintaining the correct mix of resources, states that had more beds in for-profit, public and Federal hospitals vis-à-vis not-for-profit hospitals were relatively more efficient, ceteris paribus; but in terms of the scale efficiency of hospitals within a state, this relationship was not maintained. Similar to the structural mix efficiency, the length of time that CON regulations were implemented was positively related to higher levels of aggregate technical efficiency. The policy implications may include these organizations in discussions regarding improved hospital performance across all sectors.

Despite the positive impact CON and the duration of CON had on aggregate technical and structural mix efficiency, we did not find the same to be true in terms of scale efficiency. One reason may be that hospital downsizing may have deterred hospitals from operating at their most productive scale size (MPSS). Another reason may be that changes in other forms of reimbursements, most notably prospective payment systems and managed care have altered the inpatient/outpatient mix. Finally, our finding concurs with [23] earlier result that CON does not have an effect on average costs, implying that if hospitals are not operating at the minimum of average costs, they are not operating at constant returns to scale. Another reason hospitals may not operate at constant returns to scale irrespective of CON regulations is due to the stochastic demand for hospital care, particularly via the emergency room. This finding is borne out that whereas CON regulations did not lead hospitals to have relatively better scale efficiency within the state of operation, NFP ownership of the hospital did have the desired effect, as compared to the other ownership counterpart hospitals. Conversely, the proportion of public hospital beds within a state had a direct positive effect on the aggregate technical, structural, and mix efficiencies suggesting the more direct budgetary control is better in achieving a more efficient use of resources. Future research should more fully examine the scale efficiency issue over time with more detailed data on hospital capital acquisitions.

From our findings we deduce that regulating the hospital sector via CON has merit in increasing efficiency on the production side. Further, regulating the hospital system can be seen as one component in any health care reform which is currently a priority for the U.S; Therefore, as the health policy debate heats up again in the U.S., it will behoove policy and decision makers to regard the benefits of some regulation even if changes on the demand side include some form of national health insurance.

4 Conclusion

Serious health care proposals in the United States are often couched in terms of market based approaches. Whereas many of the current proposals at both the Federal and state level focus on the demand side of the health care market equation, efficient production on the supply side is also required for finding the Pareto optimal allocation of resources. In this paper we presented an approach to modeling efficiency at the industry or sector level—i.e., the supply side of the market. This level of analysis is an intermediate case between Debreu’s [7] economy level coefficient of resource utilization and Farrell’s [8] firm level efficiency measures. Our industry level efficiency measure can be decomposed into measures of aggregate technical efficiency and structural efficiency. The former has a direct analog in the analysis of firm level efficiency; the latter—identified by Debreu as subtle, but important—is introduced in this paper and applies at an aggregate level of analysis as it assesses the efficiency of the allocation of resources and production across the industry.

We illustrated our models by assessing the effect of certificate of need (CON) regulations on hospital efficiency at the state level. In general, we found that the hospital sector in states with active CON regulations performed better in terms of aggregate technical and mix efficiency, irrespective of the stringency or laxness of this oversight. Hence, the presence of any CON has a positive impact measured by improved resource allocation and by definition, lower social costs. This finding permits us to reject the null hypotheses that CON has no effect on either state wide aggregate technical and structural efficiency. We are somewhat surprised that CON had no effect on scale efficiency, since one of the purposes of CON was to eliminate excess capacity which is one reason why hospitals may not operate at CRS. Possible reasons may include the presence of reservation quality [35]—i.e., the maintenance of excess capacity in the case of emergencies which may not be subjected to rigorous CON regulation. We also note that we did not account for the degree of stringency of CON regulations—only the presence of CON regulation—in assessing CON’s effect on efficiency. We did not pursue this line of inquiry because we would have to tradeoff degrees of freedom for more specific information which would disallow any meaningful statistical analysis leading to generalized findings from which some policy application could be devised. What we have found is that generally any CON regulation imposed by states on their hospitals leads to higher levels of efficiency, which is a necessary condition for cost savings. We could also re-apply this approach once more states implement health insurance programs that would account for the changing distribution of demand state-wide and the structural changes in efficiency that hospitals in the state markets will have to adopt to maintain cost containment.