Consensus Modeling with Asymmetric Cost Based on Data-Driven Robust Optimization

Abstract

The robust optimization method has progressively become a research hot spot as a valuable means for dealing with parameter uncertainty in optimization problems. Based on the asymmetric cost consensus model, this paper considers the uncertainties of the experts’ unit adjustment costs under the background of group decision making. At the same time, four uncertain level parameters are introduced. For three types of minimum cost consensus models with direction restrictions, including MCCM-DC,$\varepsilon$-MCCM-DC and threshold-based (TB)-MCCM-DC, the robust cost consensus models corresponding to four types of uncertainty sets (Box set, Ellipsoid set, Polyhedron set and Interval-Polyhedron set) are established. Sensitivity analysis is carried out under different parameter conditions to determine the robustness of the solutions obtained from robust optimization models. The robust optimization models are then compared to the minimum cost models for consensus. The example results show that the Interval-Polyhedron set’s robust models have the smallest total costs and strongest robustness. Decision makers can choose the combination of uncertainty sets and uncertain levels according to their risk preferences to minimize the total cost. Finally, in order to reduce the conservatism of the classical robust optimization method, the pricing information of the new product MACUBE 550 is used to build a data-driven robust optimization model. Ellipsoid uncertainty set is proved to better trade-off the average performance and robust performance through different measurement indicators. Therefore, the uncertainty set can be selected according to the needs of the group.

1 Introduction

Assessment and decision-making will occur in diverse fields, such as politics, economy, management and even daily life. It is also essential to attain a group consensus which is acceptable to most participants. However, due to different social experiences, national culture and educational background of participants, they often have different views and interpretations on the same thing, then they make different decisions. Group decision making (GDM) is to study how to coordinate different decisions to achieve the final group opinions. The main goal of GDM is that all decision-makers (DMs) can reach group consensus.

In the consensus-reaching processes (CRPs), DMs published and modified their opinions according to the moderator’s guidance and finally managed to unify and reach a consensus. CRPs consists of five key elements (Dong et al. 2018a): preference representation, aggregation, consensus measure, feedback mechanism, and selection. Zhang et al. (2017a) summarized the application of CRPs into five categories: CRPs with different preference representation structures (Wu and Chiclana 2014; Dong et al. 2015b; Gong et al. 2018; Wu et al. 2019b; Xu et al. 2019), CRPs considering the behavior or attitude of DMs (Liu et al. 2017; Wu et al. 2019a), CRPs based on consistency and consistency measures (Gong et al. 2017; Xu et al. 2018), CRPs with minimum adjustment or minimum cost (Gong et al. 2015b; Wu et al. 2018), and CRPs in a dynamic environment (Dong et al. 2018b; Xu et al. 2017). Obviously, it will inevitably consume a certain amount of workforce, material, time and money resources in CRPs. Furthermore, the moderator wants to pay as little as possible. Therefore, it is necessary to study how to make rational use of limited resources to reach the optimal decision. For this purpose, Ben-Arieh and Easton (2007) and Ben-Arieh et al. (2008) proposed a consensus model based on minimum cost. The former studied the multi-criterion consensus model with linear cost opinion elasticity, while the latter studied the minimum cost consensus (MCC) with a quadratic cost function. Dong et al. (2010) studied decision-making consensus-based on different aggregation operators in the linguistic environment and proposed a consensus operator. By introducing the aggregation operator into the minimum cost consensus model (MCCM), Zhang et al. (2011) proposed a new MCCM based on an aggregation operator.

Most of the existing research on the consensus problem of minimum cost set the unit adjustment cost of DMs as a certain value. However, the unit adjustment costs determined in many practical GDM problems are challenging to obtain. Such factors may be affected by the regional culture, educational background, and social experience of DMs, resulting in a strong fluctuation of the final consensus cost. This is also a considerable challenge that CRPs needs to overcome at present. Using a mathematical modeling method to deal with the impact of uncertain parameters to achieve the goal of minimizing costs. Based on the interval value theory, Li et al. (2017) put the uncertain unit adjustment cost into an interval, and established an optimization consensus model with uncertain minimum cost, which extended the MCCM to a certain extent. Based on stochastic programming (SP), Zhang et al. (2017b) and Tan et al. (2018) established the MCCM with chance constraint. The former assumed that to reach a consensus, the cost paid by the moderator is lower than the budget at a certain level of confidence. The later took the minimum budget and maximum utility as objective functions and studied the consensus under multiple uncertain information.

However, the interval-valued operation cannot be satisfied in some cases, and the interval subtraction is irreversible. On the other hand, it is difficult to obtain the historical data of uncertain parameters and accurate probability distribution information, which significantly limits the SP method’s application. Meanwhile, in SP, the model’s solution may not be affected by the uncertainty of probability, so that the solution is no longer the optimal solution or even the unfeasible solution. Also, the chance constraint will destroy the model’s convexity to a certain extent, and increase the computational difficulty of the original problem. Inspired by this, we use robust optimization (RO) method to deal with uncertain parameters.

RO method was first proposed by Soyster (1973). It is usually used when the accurate distribution information of uncertain parameters is unknown, and only the boundary values are known. RO solves the effects of uncertain parameters in the model by worst-case analysis and minimax model. Its ultimate goal is to find a solution that satisfies all the constraints, which is feasible in all possible cases and can optimize the objective function’s value in the worst case. RO theory makes the optimal solution of the optimization problem-free from any uncertain factors in the given uncertainty set. The key is to measure the parameters’ uncertainty by constructing an uncertainty set and finding the optimal solution immune to uncertainty. Ben-Tal and Nemirovski (1998, 1999, 2000) proposed the ellipsoidal uncertainty set and established the robust counterpart of the nominal problem, which promoted the development of RO.

With the maturity of RO theory, many researchers began to use different uncertainty sets to solve practical problems in various fields. For example, interval set was applied to emergency medical services (Zhang and Jiang 2014). The ellipsoid set was used to establish emergency medical service network design model (Shishebori and Babadi 2015). Moreover, a polyhedron set was used to solve scheduling problem (Conde 2019). Huang et al. (2019) applied the uncertainty set of the probability distribution to the portfolio problem and established a multi-stage distributionally RO model based on risk aversion. Ji et al. (2020) proposed a fuzzy-robust weighted method to address the uncertainty of the exact weights over each DM’s objectives. However, in GDM, most of the research is focused on robustness (Greco et al. 2012; Nag et al. 2018), while few works of literature use the RO method to solve uncertain problems from the perspective of modeling. For example, Han et al. (2019, 2020) applied uncertainty set (Box set, Ball set, Box-Ball set, and Box-Polyhedron set) and distributionally uncertainty set to the MCCM, which overcame the effects of uncertainties to some extent.

So far, the classical RO methods are mostly based on experience to obtain uncertainty sets, which is highly subjective. The advantages of big data are ignored, and the results are also too conservative. However, the starting point of all uncertainty sets is raw data, a set of observation data of uncertain parameters. These data are then processed to accommodate different assumptions about the shape and size of the uncertainty set and the DM’s preferences. At the same time, tighter uncertainty sets can often lead to better economies. The data-driven RO method (Bertsimas et al. 2018; Chassein et al. 2019) uses historical data to construct uncertainty sets, which improves the rationality and economy of the uncertainty sets of the traditional RO method. However, a few types of research on applying data-driven RO to solve GDM problems.

This paper introduces four uncertainty sets (Box set, Ellipsoid set, Polyhedron set and Interval-Polyhedron set). Base on the three MCCMs with directional constraints proposed by Cheng et al. (2018), we establish four robust optimization consensus models for each directional constraint model based on four uncertainty sets. By placing the DMs’ unit adjustment costs in the uncertainty set, the optimization model’s worst solution can be found. Then the best solution satisfying all cases is obtained in the worst case. Numerical experiments show that:

• 1. The robust model’s uncertain level parameters indicate the degree of risk preference of DMs and measure the conservative degree of constraint conditions. The larger the uncertain level parameter, the larger the minimum cost, the worse the model’s robustness, and the higher the risk aversion degree of the DM. As a result, the Interval-Polyhedron set is the most robust.

• 2. The compromise limit parameter and the cost-free threshold parameter are also closely related to the minimum cost. The compromise limit decreases, the minimum cost increases and goes to infinity. With the increase of the cost-free threshold parameter, the minimum cost decreases and tends to zero.

• 3. The robust model under the Interval-Polyhedron set has the smallest pessimism coefficient and strongest robustness.

Finally, in order to reduce the conservatism of the classical RO method, this paper further introduces the data-driven RO method. The uncertainty set of unit adjustment cost is constructed by using the pricing information of the new product MACUBE 550 of the DEEPCOOL company. By using different indicators to measure the applicability of models of these sets, it is concluded that the Ellipsoid uncertainty set can better trade-off the average performance and robust performance.

The rest of this paper is organized as follows. Section 2 introduces the MCCM and three MCCMs with directional constraints. In Sect. 3, three robust equivalence models with directional constraints are proposed under four uncertainty sets. Section 4 is numerical analysis, and comparisons are made from different perspectives. The data-driven RO method is presented in Sect. 5, and the performance comparison is carried out by taking new product development as an example. Section 6 deals with conclusions and future work.

2 Basic Model of MCC and MCCM with Direction Constraints

The MCC theory has recently been gaining growing attention. Zhang et al. (2013) introduced weighted average operator or ordered a weighted average operator into the maximum expert consensus model, and obtained the equivalent mixed 0–1 linear programming problem. Gong et al. (2014, 2015c) established the MCCM based on the moderator and the maximum return model based on DMs using the primal–dual linear programming theory. In addition, the former studied the MCC problem from the aspect of fuzzy decision making by combining the grey interval preference. The later proposed two minimum cost models for all individuals or one individual. Gong et al. (2015a) established a new consensus model with limited consensus cost and nonlinear utility constraint, which significantly improved the effectiveness of GDM. In the context of distributed linguistic trust, Wu et al. (2018) established a trust model based on social network analysis (SNA) method, and the boundary feedback parameters generated by the minimum adjustment cost optimization model are used to identify inconsistent users. The effect of group attitudes on the consensus-building process was studied in Wu et al. (2019a). The conclusion was obtained that the implementation attitude parameters were proportional to the adjustment cost and consensus level. The deviation of opinion change and the number of DMs who need to change their opinions also affect the cost of consensus. Based on this, a multi-attribute GDM model is established to minimize the deviation of opinion change and minimize the number of DMs who need to change their opinions, so as to reduce the consensus cost (Zhang and Dong 2013; Zhang et al. 2014; Dong et al. 2015a). In recent years, the MCC problem has been applied to problems such as scheme negotiation, urban housing demolition negotiation and road intersection control (Dong et al. 2018b; Gong et al. 2017; Kwok and Lau 2016).

However, most existing studies on MCC theory assume that DMs’ unit adjustment costs on the upward and the downward direction are symmetrical. Cheng et al. (2018) pointed out that in many applications of MCC theories, the assumption that the consensus costs are symmetric in both directions is unreasonable, and they are usually asymmetric. Three consensus models, the minimum cost consensus model with directional constraints (MCCM-DC), the $\varepsilon$-MCCM-DC, and the threshold-based (TB)-MCCM-DC, were proposed to study the MCC problem with directional constraints. It has also been applied to the transboundary pollution control in Taihu Lake Basin, which provides some references for the government to make policy. Research on asymmetric costs have been widely applied in the supply chain (Bolandifar et al. 2017; Mahadevan et al. 2017; Yang et al. 2018).

Next, we introduce the basic model of MCC and the MCCM with direction constraints.

2.1 Basic Model of MCC

Suppose there are m DMs $A=\{a_1,a_2,\ldots ,a_m\}$ in the GDM process. Let $o_i(i=1,2,\ldots ,m)$ represents the original opinion of the ith DM $a_i$, and $o^{c}$ represents the opinion of the moderator (i.e. the ideal opinion). Without loss of generality, assume $0\le o_1\le o_2\le \cdots \le o_m$, that is, the original opinions of DMs are arranged in ascending order. Then the best value of the moderator’s opinion $o^{c}$ should meet $o_1=o_2=\cdots =o_m=o^{c}$. However, in many practical situations, the moderator’s absolute ideal opinion is hard to come by. The moderator must give a relatively ideal opinion, and most DMs are satisfied with it. Such $o^{c}$ is also known as group consensus. Besides, it is not difficult to see that $o_1\le o^{c}\le o_m$ must be true, that is, the value of consensus opinion must be located in the interval between the minimum and maximum values of all DMs’ opinions. Assuming that O is the feasible set of consensus opinion $o^{c}$, then $o^{c}\in O\subset [o_1,o_m]$ (Cheng et al. 2018).

In the process of GDM, every DM hopes that his/her opinion will be fully taken into account, and is more willing to adjust his/her opinion as little as possible. Suppose $d_i(o^{c})=\left| o_i-o^{c}\right|$ represents the deviation between DM $a_i$’s original opinion $o_i$ and consensus opinion $o^{c}$. From the perspective of consensus, the smaller the value of $d_i(o^{c})$, the higher the consensus degree of GDM. Since DMs are generally reluctant to change their opinions for free, the moderator needs to give some compensation to persuade DMs to make changes. Define $c_i$ as the unit adjustment cost of the moderator to persuade the DM $a_i$. Therefore, the smaller the cost $c_id_i(o^{c})$ of persuading the DM $a_i$, the closer the DM’s opinion is to the consensus opinion. Therefore, according to Gong et al. (2015c), the minimum cost consensus model can be expressed as a nonlinear optimization model:

$$\begin{aligned} \begin{aligned} \mathrm{min}&\quad \sum \limits _{i=1}^{m}{{{c}_{i}}\left| {{o}_{i}}-{{o}^{c}} \right| } \\ s.t.&\quad {{o}^{c}}\in O. \\ \end{aligned} \end{aligned}$$

(2.1)

2.2 MCC Model with Direction Constraints

In Sect. 2.1, let $t_i=o_i-o^{c}$, then the cost function of DM $a_i$ is $F_i(t_i)=c_id_i(o^{c})={{c}_{i}}\left| t_i\right|$. At the same time, $F_i(t_i)=F_i(-t_i)$ is established, which indicates that model (2.1) is established under the environment of symmetric cost. In this case, DMs’ unit adjustment costs are equal on the upward and downward. In general, DMs give their opinions according to their interests, and they always want to maximize their interests. It is more difficult for DMs to give up a unit of profit than to accept a unit of profit. Therefore, in many GDM problems, the unit adjustment costs of DMs are asymmetric in both directions. For example, in the problem of new product design, different departments may hold opposite opinions, making the difficulties of adjusting them in two directions are different. Obviously, their unit adjustment costs in two directions are asymmetric. Cheng et al. (2018) proposed the following three minimum cost consensus models with directional constraints.

2.2.1 MCCM-DC

In the MCC problem with direction constraint, the unit adjustment cost of each DM is assumed to be related to the adjustment direction. The DM, whose opinion value is lower than the consensus opinion value, needs to adjust his/her opinion upward. On the contrary, the DM whose opinion value is higher than the consensus opinion value needs to adjust his/her opinion downward. Here, the unit adjustment cost of the DM’s change of opinion in the upward and downward directions are expressed in $c_i^U$ and $c_i^D$, respectively. Thus, MCCM-DC can be obtained as follows:

$$\begin{aligned} \begin{aligned} \mathrm{min}&\quad \sum \limits _{i{:}\,{o}_{i}}<{{o}^{c}}{c_{i}^{U}}({{o}^{c}}-{{o}_{i}})+\sum \limits _{i{:}\,{{o}_{i}}>{{o}^{c}}}{c_{i}^{D}}({{o}_{i}}-{{o}^{c}})\\ s.t.&\quad {{o}^{c}}\in O \\ \end{aligned} \end{aligned}$$

(2.2)

Here, the first part of the objective function represents the cost of persuading the DM whose opinion value is lower than the consensus opinion value. The second part represents the cost of persuading DM, whose opinion value is higher than the consensus opinion value. The constraint is to ensure that the consensus sought is feasible.

Since solving the nonlinear model is very complicated and challenging, positive deviation parameter $\varphi _i^+$ and negative deviation parameter $\varphi _i^-$ are introduced to transform model (2.2) into the following linear programming model:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})} \\ s.t.&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

It is equivalent to

$$\begin{aligned} \begin{aligned} \min&\quad B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}\le B \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(2.3)

Among them, $\varphi _i^+=(o_i-o^{c})^+,\varphi _i^-=(o^{c}-o_i)^+$ represent the positive and negative deviations of DMs’ opinions and consensus opinions respectively. In addition, there is at least one of $\varphi _i^+$ and $\varphi _i^-$ is zero, that is, $\varphi _i^+\cdot \varphi _i^-=0.$ By solving the model (2.3), the minimum cost and consensus opinion of reaching consensus in the GDM problem with direction constraint can be obtained. The value of the positive and negative deviations can be used to calculate the adjusted opinions of DMs.

2.2.2 $\varepsilon$-MCCM-DC

DMs are unlikely to adjust their opinions indefinitely to protect their interests. So they have a scope constraint on the extent of their adjustment, called the compromise limit, which is denoted here by $\varepsilon _i(i=1,2,\ldots ,m)$. Obviously, the larger the $\varepsilon _i$, the higher the adjustment range that the DM can tolerate. Define the deviation between DMs’ opinions and consensus opinions as consensus index of $a_i$, which can be expressed as $CI_i=\left| o_i-o^{c}\right|$. Obviously, when $CI_i\le \varepsilon _i$, the opinion of $a_i$ can be considered as acceptable. This means that all DMs’ opinions are deviated within their tolerance, so the moderator can guide DMs to reach a group consensus through compensation (money, resources, etc.). Similar to Sect. 2.2.1, $c_i^U$ and $c_i^D$ are respectively used to represent the unit adjustment cost of DMs’ change of opinion in the upward and downward directions. Thus, $\varepsilon$-MCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i{:}\,{{o}_{i}}<{{o}^{c}}}{c_{i}^{U}}({{o}^{c}}-{{o}_{i}})+\sum \limits _{i{:}\,{{o}_{i}}>{{o}^{c}}}{c_{i}^{D}}({{o}_{i}}-{{o}^{c}}) \\ s.t.&\quad {{o}^{c}}\in O \\&\quad \left| {{o}_{i}}-{{o}^{c}} \right| \le {{\varepsilon }_{i}},i=1,2,\ldots ,m. \\ \end{aligned} \end{aligned}$$

(2.4)

Introducing positive deviation parameter $\varphi _i^+$ and negative deviation parameter $\varphi _i^-$, let $\varphi _i^+=(o_i-o^{c})^+,\varphi _i^-=(o^{c}-o_i)^+$, and $\varphi _i^+\cdot \varphi _i^-=0$ is satisfied. In addition, when $o_i\ge o^{c}$, $\left| o_i-o^{c}\right| =o_i-o^{c}=\varphi _i^+\le \varepsilon _i$, and $\varphi _i^-=0$. When $o_i\le o^{c}$, $\left| o_i-o^{c}\right| =o^{c}-o_i=\varphi _i^-\le \varepsilon _i$, and $\varphi _i^+=0$. So $0\le \varphi _i^+,\varphi _i^-\le \varepsilon _i$. Therefore, model (2.4) can be converted into the following linear programming model:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})} \\ s.t.&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m.\\ \end{aligned} \end{aligned}$$

It is equivalent to

$$\begin{aligned} \begin{aligned} \min&\quad B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}\le B \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m. \\ \end{aligned} \end{aligned}$$

(2.5)

The opinions of DMs may be unacceptable in many practical situations. This means that the deviations between DMs and consensus are beyond the scope of their commitments. So $o^{c}\in O$ might not be true. At this point, $CI_i\ge \varepsilon _i$, which means that the opinions of DMs are not in the interval $[o_i-\varepsilon _i,o_i+\varepsilon _i]$. The following consensus framework can effectively address the issue of unacceptable opinions.

• 1. Input the DM’s original opinion $o_i(i=1,2,\ldots ,m)$ and compromise limit parameter $\varepsilon _i(i=1,2,\ldots ,m)$. Set the maximum number of iterations $Maxrounds\ge 1$, and set the initial value $t=1$.

• 2. Calculate the acceptable range $[o_i-\varepsilon _i,o_i+\varepsilon _i]$ of DM. The two endpoints are represented by $l_i^t$ and $r_i^t$ respectively. Find the endpoints $l_p^t$ and $r_q^t$ with the most significant difference in the tth round. Then check if there are any other unacceptable comments. If $l_p^t\le r_q^t$, go to step 5. Otherwise, go to the next step.

• 3. By giving some compensation to DMs $a_p$ and $a_q$, the moderator can persuade them to increase their adjustment range constraint parameters.

• 4. If $l_p^t\le r_q^t$ or $t\ge Maxrounds$ is true, go to the next step. Otherwise, let $t=t+1$ and go to step 1.

• 5. Establish the new $\varepsilon$-MCCM-DC and solve the minimum cost and consensus opinion.

Remark

When $\varepsilon _i\rightarrow +\infty$, it may be argued that the decision maker can tolerate unlimited compromise. So in this case, $\varepsilon$-MCCM-DC can be simplified to MCCM-DC.

2.2.3 TB-MCCM-DC

Generally speaking, DMs are more willing to reach a consensus in GDM. Therefore, such scope exists, and when consensus is within this scope, DMs are willing to change their opinions for free. We use $\eta _i(i=1,2,\ldots ,m)$ to represent this range, and call the DMs satisfying this property as threshold-based DMs. So $[o^{c}-\eta _i,o^{c}+\eta _i]$ is the cost-free interval of DM in Sect. 2.2.1, the cost function $F_i(o^{c})$ of $a_i$ can be expressed as:

$$\begin{aligned} \begin{aligned} {{F}_{i}}({{o}^{c}})=\left\{ \begin{array}{ll} c_{i}^{U}({{o}^{c}}-{{\eta }_{i}}-{{o}_{i}}),&{}\quad {{o}_{i}}\in [0,{{o}^{c}}-{{\eta }_{i}}) \\ 0,&{}\quad {{o}_{i}}\in [{{o}^{c}}-{{\eta }_{i}},{{o}^{c}}+{{\eta }_{i}}] \\ c_{i}^{D}({{o}_{i}}-{{\eta }_{i}}-{{o}^{c}}),&{}\quad {{o}_{i}}\in ({{o}^{c}}+{{\eta }_{i}},+\infty ) \\ \end{array} \right. \end{aligned} \end{aligned}$$

(2.6)

Therefore, TB-MCCM-DC can be expressed in the following form:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i{:}\,{{o}_{i}}<{{o}^{c}}-{{\eta }_{i}}}{c_{i}^{U}}({{o}^{c}}-{{\eta }_{i}}-{{o}_{i}})+\sum \limits _{i{:}\,{{o}_{i}}>{{o}^{c}}+{{\eta }_{i}}}{c_{i}^{D}}({{o}_{i}}-{{\eta }_{i}}-{{o}^{c}}) \\ s.t.&\quad ~~{{o}^{c}}\in O. \\ \end{aligned} \end{aligned}$$

(2.7)

Positive deviation parameters $\varphi _i^+,\phi _i^+$ and negative deviation parameters $\varphi _i^-,\phi _i^-$ are introduced. Let $\varphi _i^+=(o_i-o^{c}+\eta _i)^+,\varphi _i^-=(o^{c}-\eta _i-o_i)^+,\phi _i^+=(o_i-\eta _i-o^{c})^+,\phi _i^-=(o^{c}-o_i+\eta _i)^+$, Therefore, model (2.7) can be converted into the following linear programming model:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\phi _{i}^{+})} \\ s.t.&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

It is equivalent to

$$\begin{aligned} \begin{aligned} \min&B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}\le B \\&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(2.8)

Obviously, $\varphi _i^-\in [0,o^{c}-\eta _i],\varphi _i^+\in [o^{c}-\eta _i,o^{c}],\phi _i^-\in [o^{c},o^{c}+\eta _i],\phi _i^+\in [o^{c}+\eta _i,+\infty ]$. And it satisfies $\varphi _i^+\cdot \varphi _i^-=0,\phi _i^+\cdot \phi _i^-=0$.

3 MCCM-DC Based on RO Method

Uncertain parameters often exist in actual GDM problems. For example, DMs’ unit adjustment cost may be affected by factors such as the regional culture, educational background of DMs, resulting in substantial uncertainty of the final consensus cost. However, the MCCMs in the second section are established under the condition that the DMs’ unit adjustment costs are determined and known, ignoring the impact brought by uncertainty. Different from the SP method, this paper adopts the RO method to deal with the uncertainty problem. To some extent, it makes up for the defect that it is not easy to obtain the SP method’s accurate probability distribution of parameters. RO’s key is to measure the uncertainties of parameters by constructing uncertainty sets and finding the optimal solution immune to uncertainty. In this section, we establish a robust counterpart of nominal models (2.3), (2.5) and (2.8) respectively in Box set, Ellipsoid set, Polyhedron set, and Interval-Polyhedron set.

Firstly, considering a general linear programming problem

$$\begin{aligned} \begin{aligned} \underset{x}{\mathop {\min }}\,\left\{ {{c}^{T}}x\left| Ax\ge b \right. \right\} \end{aligned} \end{aligned}$$

(3.1)

where $x\in R^{n\times 1}$ is the decision variable vector, $A\in R^{m\times n}$ is the coefficient matrix with uncertain parameters, and $b\in R^{m\times 1}$ is the vector with uncertain parameters. Then the uncertainty set can be defined as follows:

Definition 1

(Uncertainty set) Uncertain linear optimization problem is a set of linear programming problem ${\mathop {\min }\nolimits _{x}}\,\{c^Tx\left| Ax\ge b\right. \}$${\mathcal {U}}$ with common structure, whose data varies in a given uncertainty set .

$$\begin{aligned} \begin{aligned} \min \left\{ {{c}^{T}}x\left| Ax\ge b,\forall A,b\in {\mathcal {U}} \right. \right\} \end{aligned} \end{aligned}$$

(LO_{\mathcal {U}}})

where A, b are uncertain parameters. When the uncertainty set is assumed to be parameterized, the perturbation vector $\xi$ changes in the form of affine in a given perturbation set ${\mathcal {Z}}$:

$$\begin{aligned} {\mathcal {U}} =\left\{ [a;b]=[{{a}_{0}};{{b}_{0}}]+\sum \limits _{h=1}^{H}{{{\xi }_{h}}[{{a}_{h}};{{b}_{h}}]}{:}\,\xi \in {\mathcal {Z}} \right\} \end{aligned}$$

Definition 2

(Robust feasible solution) For vector $x\in R^{n\times 1}$, it is a robust feasible solution for ($LO_{\mathcal {U}}$) if it satisfies all variations of the uncertainty set constraint.

Definition 3

(Robust goal value) If the candidate solution x satisfies ${\tilde{c}}(x)={\mathop {\sup }\nolimits _{(A,b)\in {\mathcal {U}}}}\,c^Tx$, where ${\tilde{c}}(x)$ is the maximum value of the objective value of ($LO_{\mathcal {U}}$) under the uncertainty set, ${\tilde{c}}(x)$ is called the robust goal value of the RO problem.

Remark

The robust goal value is obtained in the robust worst-case scenario.

Definition 4

(Robust counterpart) The robust counterpart of uncertain optimization problem can be expressed as:

$$\begin{aligned} \underset{x}{\mathop {\min }}\,\left\{ \tilde{c}(x){:}\,\tilde{c}(x)=\underset{(A,b)\in {\mathcal {U}}}{\mathop {\sup }}\,{{c}^{T}}x{:}\,Ax\le b,\forall A,b\in {\mathcal {U}} \right\} \end{aligned}$$

It is the best robust goal value for all robust feasible solutions.

For the ith constraint in (3.1), according to the above definition, let ${\tilde{a}}_{ij}=a_{ij}+\xi _{ij}{\bar{a}}_{ij},{\tilde{b}}_i=b_i+\xi _{i0}{\bar{b}}_i$, where $a_{ij}, b_i$ are the nominal values of uncertain parameters, ${\bar{a}}_{ij}, {\bar{b}}_i$ are perturbation values, and $\xi _{ij}, \xi _{i0}$ represent uncertain factors. In (3.1), the ith constraint can be written as

$$\begin{aligned} \begin{aligned} \sum \limits _{j}{{{a}_{ij}}{{x}_{j}}}+\sum \limits _{j}{{{\xi }_{ij}}{{{\bar{a}}}_{ij}}{{x}_{j}}}\le {{b}_{i}}+{{\xi }_{i0}}{{\bar{b}}_{i}} \end{aligned} \end{aligned}$$

(3.2)

The robust counterpart of (3.1) can be written as follows:

$$\begin{aligned} \begin{aligned} \underset{x}{\mathop {\min }}\,&\quad {{c}^{T}}x \\ s.t.&\quad \sum \limits _{j}{{{a}_{ij}}{{x}_{j}}}+\underset{\xi \in {\mathcal {U}}}{\mathop {\max }}\,\left\{ \sum \limits _{j}{{{\xi }_{ij}}{{{\bar{a}}}_{ij}}{{x}_{j}}-}{{\xi }_{i0}}{{{\bar{b}}}_{i}} \right\} \le {{b}_{i}}. \\ \end{aligned} \end{aligned}$$

(3.3)

Obviously, if x is the robust feasible solution of the model (3.3), all uncertainty set constraints are satisfied. The feasible solution of model (3.3) is the robust feasible solution of model (3.1), and the optimal solution of model (3.3) is the robust optimal solution of model (3.1). Since model (3.3) is a semi-infinite programming problem, it is difficult to solve. Therefore, it is necessary to convert the original problem into a convex optimization problem with polynomial solvability, usually a linear optimization or a quadratic optimization problem. This is also the critical point of RO problem.

In this paper, the unit adjustment costs $c_i^U$ and $c_i^D$ are taken as uncertain parameters. They are placed in uncertainty sets respectively. A robust counterpart corresponding to the MCCM-DC model is established. According to Definition 1, the uncertainty set can be expressed as

$$\begin{aligned} {\mathcal {U}}=\left\{ [{{c}^{U}};{{c}^{D}}]=[c_{0}^{U};c_{0}^{D}]+\sum \limits _{h=1}^{H}{{{\xi }_{h}}[c_{h}^{U};c_{h}^{D}]}{:}\,\xi \in {\mathcal {Z}} \right\}. \end{aligned}$$

3.1 RO-MCCM-DC

According to the form of uncertainty set, the first constraint of the model (2.3) can be written as:

$$\begin{aligned} \begin{aligned} \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}\le B,\forall \left( [{{c}^{U}};{{c}^{D}}]=[c_{0}^{U};c_{0}^{D}]+\sum \limits _{h=1}^{H}{{{\xi }_{h}}[c_{h}^{U};c_{h}^{D}]}{:}\,\xi \in {\mathcal {Z}} \right) . \end{aligned} \end{aligned}$$

(3.4)

Thus, similar to the form of (3.3), the robust equivalent of model (2.3) is

$$\begin{aligned} \begin{aligned} \min&\quad B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})+\underset{\xi \in {\mathcal {U}}}{\mathop {\max }}\,\left\{ \sum \limits _{h=1}^{H}{{{\xi }_{h}}(c_{h}^{U}\varphi _{i}^{-}+c_{h}^{D}\varphi _{i}^{+})} \right\} }\le B \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

Next, we consider RO models in Box set, Ellipsoid set, Polyhedron set and Interval-Polyhedron set, respectively.

3.1.1 Box Set

First, considering that the uncertainty set ${\mathcal {Z}}$ is Box set. The Box set is defined according to the infinite norm $(l_\infty )$. Define ${\mathcal {Z}}^{Box}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le \gamma \}$, where $\gamma$ is an uncertain level parameter. Let $c^U=(c_1^U,c_2^U,\ldots ,c_m^U),c^D=(c_1^D,c_2^D,\ldots ,c_m^D),\varphi ^+=(\varphi _1^+,\varphi _2^+,\ldots ,\varphi _m^+)^T,\varphi ^-=(\varphi _1^-,\varphi _2^-,\ldots ,\varphi _m^-)^T$.

Theorem 1

The RO model of model (2.3) under Box set (BMCCM-DC) can be expressed as:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\gamma {{\left\| u \right\| }_{1}} \\ s.t.&\quad -{{u}_{l}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{l}},h=1,\ldots ,H \\ \text {(BMCCM-DC) }~~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.5)

Proof

According to the form of Box set, (3.4) can be written as $c_0^U\varphi ^-+c_0^D\varphi ^++\sum \nolimits _{h=1}^H\xi _h(c_h^U\varphi ^-+c_h^D\varphi ^+)\le B, \forall (\xi {:}\,\left\| \xi \right\| _\infty \le \gamma )$. Obviously, it is equivalent to ${\mathop {\max }\nolimits _{{{\left\| \xi \right\| }_{\infty }}\le \gamma }}\,\sum \nolimits _{h=1}^H\xi _h(c_h^U\varphi ^-+c_h^D\varphi ^+)\le B-c_0^U\varphi ^--c_0^D\varphi ^+$.

Clearly, the maximum value at the left end of the inequality is $\gamma \sum \nolimits _{h=1}^H(c_h^U\varphi ^-+c_h^D\varphi ^+)$. So the robust counterpart of (3.4) can be obtained. Its linear inequality system can be expressed as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} -{{u}_{h}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{h}},h=1,\ldots ,H, \\ c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\gamma \sum \limits _{l=1}^{L}{{{u}_{h}}}\le B. \\ \end{array} \right. \end{aligned} \end{aligned}$$

(3.6)

Applying (3.6) to model (2.3), (BMCCM-DC) can be established. $\square$

3.1.2 Ellipsoid Set

Considering the uncertainty set ${\mathcal {Z}}$ is Ellipsoid set. The Ellipsoid set is defined in terms of the 2 norm $(l_2)$. Define ${\mathcal {Z}}^{Ellipsoid}=\{\xi \in R^H{:}\,\left\| \xi \right\| _2\le \gamma \}$, where $\varOmega$ is the uncertain level parameter and represents the radius of the ellipsoid set.

Theorem 2

The RO model of model (2.3) under Ellipsoid set (EMCCM-DC) can be expressed as:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varOmega {{\left\| u \right\| }_{2}} \\ s.t.&\quad -{{u}_{h}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{h}},h=1,\ldots ,H \\ \text {(EMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m. \\ \end{aligned} \end{aligned}$$

(3.7)

Proof

According to the form of Ellipsoid set, (3.4) can be written as $c_0^U\varphi ^-+c_0^D\varphi ^++\sum \nolimits _{h=1}^H\xi _h(c_h^U\varphi ^-+c_h^D\varphi ^+)\le B, \forall (\xi {:}\,\left\| \xi \right\| _2\le \varOmega )$. Obviously, it is equivalent to ${\mathop {\max }\nolimits _{{{\left\| \xi \right\| }_2}\le \varOmega }}\,\sum \nolimits _{h=1}^H\xi _h(c_h^U\varphi ^-+c_h^D\varphi ^+)\le B-c_0^U\varphi ^--c_0^D\varphi ^+$. This means $\varOmega \sqrt{\sum \nolimits _{h=1}^H(c_h^U\varphi ^-+c_h^D\varphi ^+)^2}\le B-c_0^U\varphi ^--c_0^D\varphi ^+$. Therefore, the robust counterpart of (3.4) can be obtained: $c_0^U\varphi ^-+c_0^D\varphi ^++\varOmega \sqrt{\sum _{h=1}^H(c_h^U\varphi ^-+c_h^D\varphi ^+)^2}\le B$. Its linear inequality system can be expressed as:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} -{{u}_{h}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{h}},h=1,\ldots ,H, \\ c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varOmega \sqrt{\sum \limits _{h=1}^{H}{{{u}_{h}}^{2}}}\le B. \\ \end{array} \right. \end{aligned} \end{aligned}$$

(3.8)

Applying (3.8) to model (2.3), (EMCCM-DC) can be established. $\square$

3.1.3 Polyhedron Set

Considering the uncertainty set ${\mathcal {Z}}$ is Polyhedron set. The Polyhedron set is defined in terms of the 1 norm $l_1$. Define ${\mathcal {Z}}^{Polyhedron}=\{\xi \in R^H{:}\,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is the uncertain level parameter.

Theorem 3

The RO model of model (2.3) under Polyhedron set (PMCCM-DC) can be expressed as:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varGamma {{\left\| t \right\| }_{\infty }} \\ s.t.&\quad c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{s}_{h}},h=1,\ldots ,H \\ \text {(PMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.9)

Proof

Generally, the dual cone ${\mathcal {Z}}$ can be expressed as ${\mathcal {Z}}=\{\xi \in R^H{:}\,\exists \tau \in R^H{:}\,M\xi +N\tau +m\in K \}$, here K is a nonempty closed convex cone in $R^N$, M, N are given matrices and m is a given vector. Then, ${\mathcal {Z}}^{Polyhedron}=\{\xi \in R^H{:}\,M\xi +m\in K \}$.

Define $M\xi =[\xi _{H\times H};0_{1\times H}],m=[0_{H\times 1};\varGamma ],K =\{(s,t)\in R^H\times R{:}\,\left\| s\right\| _1\le t\}$. Then the maximization problem on the left side of inequality can be expressed as: ${\mathop {\max }\nolimits _{\left\| \xi \right\| _1\le \varGamma }}\,\{\sum _{h=1}^H\xi _h(c_h^U\varphi ^-+c_h^D\varphi ^+){:}\,M\xi +m\in K\}$. Meanwhile, define $g=[s;t]$, where s, t represent dual variables, and s is H-dimensional and t is one-dimensional. According to the properties of dual cone, the dual cone of K is $K^*=\{(s,t)\in R^H\times R{:}\,\left\| s\right\| _\infty \le t\}$. According to the form of Polyhedron set, (3.4) is equivalent to

$$\begin{aligned} \begin{aligned}&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+{{m}^{T}}g\le B, \\&c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}+{{\left( {{M}^{T}}g \right) }_{h}}=0,h=1,\ldots ,H, \\&g\in {{K }^{*}}. \\ \end{aligned} \end{aligned}$$

It can be further written as

$$\begin{aligned} \begin{aligned}&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varGamma t\le B, \\&c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{s}_{h}},h=1,\ldots ,H, \\&{{\left\| s \right\| }_{\infty }}\le t. \\ \end{aligned} \end{aligned}$$

(3.10)

Applying (3.10) to model (2.3), (PMCCM-DC) can be established. $\square$

3.1.4 Interval-Polyhedron Set

Considering the uncertainty set ${\mathcal {Z}}$ is Interval-Polyhedron set. Define ${\mathcal {Z}}^{Int\text{-}Poly}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le 1,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is the uncertain level parameter. Interval-Polyhedron set is a special case of Box-Polyhedron set. Box-Polyhedron set is the intersection of Box set and Polyhedron set, which is defined according to $l_1\bigcap l_\infty$.

Theorem 4

The RO model of model (2.3) under Interval-Polyhedron set (IPMCCM-DC) can be expressed as:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+{{\left\| {{t}_{1}} \right\| }_{1}}+\varGamma {{\left\| {{t}_{2}} \right\| }_{\infty }} \\ s.t.&\quad c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{({{s}_{1}}+{{s}_{2}})}_{h}},h=1,\ldots ,H \\ \text {(IPMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i=1,2,\ldots ,m .\\ \end{aligned} \end{aligned}$$

(3.11)

Proof

Based on the proof of Theorem 3, $\mathcal Z^{Int\text{-}Poly}=\{\xi \in R^H{:}\,M_1\xi +m_1\in K_1,M_2\xi +m_2\in K_2 \}$.

Define $M_1\xi =[\xi _{H\times H};0_{1\times H}],m_1=[0_{H\times 1};1],K_1=\{(s,t)\in R^H\times R{:}\,\left\| s \right\| _\infty \le t \}$. Meanwhile, define $g_1=[s_1;t_1]$, where s, t represent dual variables, and s is H-dimensional, t is one-dimensional. According to the properties of dual cone, the dual cone of $K_1$ is $K_1^*=\{(s,t)\in R^H\times R{:}\,\left\| s\right\| _1\le t\}$. $M_2\xi =[\xi _{H\times H};0_{1\times H}],m_2=[0_{H\times 1};\varGamma ],K_2=\{(s,t)\in R^H\times R{:}\,\left\| s\right\| _1\le t\}$ are defined in the same way. Then the dual cone of $K_2$ is $K_2^*=K_1=\{ \left( s,t \right) \in {{R}^{H}}\times R{:}\,\left\| s\right\| _\infty \le t\}$. According to the form of Interval-Polyhedron set, (3.4) is equivalent to

$$\begin{aligned} \begin{aligned}&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+m_{1}^{T}{{g}_{1}}+m_{2}^{T}{{g}_{2}}\le B, \\&c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}+{{\left( M_{1}^{T}{{g}_{1}} \right) }_{h}}+{{\left( M_{2}^{T}{{g}_{2}} \right) }_{h}}=0,h=1,\ldots ,H, \\&{{g}_{1}}\in K_{1}^{*},{{g}_{2}}\in K _{2}^{*} \\ \end{aligned} \end{aligned}$$

It can be further written as

$$\begin{aligned} \begin{aligned}&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+{{t}_{1}}+\varGamma {{t}_{2}}\le B, \\&c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{({{s}_{1}}+{{s}_{2}})}_{h}},h=1,\ldots ,H, \\&{{\left\| {{s}_{1}} \right\| }_{1}}\le {{t}_{1}}. \\&{{\left\| {{s}_{2}} \right\| }_{\infty }}\le {{t}_{2}}. \\ \end{aligned} \end{aligned}$$

(3.12)

Applying (3.12) to model (2.3), (IPMCCM-DC) can be established. $\square$

3.2 $\varepsilon$-RO-MCCM-DC

In this part, based on $\varepsilon$-MCCM-DC, Box set, Ellipsoid set, Polyhedron set and Interval-Polyhedron set are used to establish the following four robust cost consensus models.

Similarly, similar to the form of (3.3), the robust counterpart of the model (2.5) is

$$\begin{aligned} \begin{aligned} \min&\quad B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})+\underset{\xi \in {\mathcal {U}}}{\mathop {\max }}\,\left\{ \sum \limits _{h=1}^{H}{{{\xi }_{h}}(c_{h}^{U}\varphi _{i}^{-}+c_{h}^{D}\varphi _{i}^{+})} \right\} }\le B \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

Case 1 Considering that the uncertainty set is Box set, without loss of generality, let ${\mathcal {Z}}^{Box}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le \varPhi \}$, where $\varPhi$ is an adjustable uncertain level parameter, so $\varepsilon$-BMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\gamma {{\left\| u \right\| }_{1}} \\ s.t.&\quad -{{u}_{l}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{l}},h=1,\ldots ,H \\ \text {(}\varepsilon \text {-BMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.13)

Case 2 Considering that the uncertainty set is Ellipsoid set, without loss of generality, let ${\mathcal {Z}}^{Ellipsoid}=\{\xi \in R^H{:}\,\left\| \xi \right\| _2\le \varOmega \}$, where $\varOmega$ is an adjustable uncertain level parameter, so $\varepsilon$-EMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varOmega {{\left\| u \right\| }_{2}} \\ s.t.&-{{u}_{h}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}\le {{u}_{h}},h=1,\ldots ,H \\ \text {(}\varepsilon \text {-EMCCM-DC) }~~~~~~&{{o}^{c}}\in O \\&{{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.14)

Case 3 Considering that the uncertainty set is Polyhedron set, without loss of generality, let ${\mathcal {Z}}^{Polyhedron}=\{\xi \in R^H{:}\,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is an adjustable uncertain level parameter, so $\varepsilon$-PMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+\varGamma {{\left\| t \right\| }_{\infty }} \\ s.t.&\quad c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{s}_{h}},h=1,\ldots ,H ~~~~~~~~~~\\ \text {(}\varepsilon \text {-PMCCM-DC) }~~~~~~~~&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.15)

Case 4 Considering that the uncertainty set is Interval-Polyhedron set, without loss of generality, let ${\mathcal {Z}}^{Int\text{-}Poly}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le 1,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is an adjustable uncertain level parameter, so $\varepsilon$-IPMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\varphi }^{+}}+{{\left\| {{t}_{1}} \right\| }_{1}}+\varGamma {{\left\| {{t}_{2}} \right\| }_{\infty }} \\ s.t.&c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\varphi }^{+}}=-{{({{s}_{1}}+{{s}_{2}})}_{h}},h=1,\ldots ,H \\ \text {(}\varepsilon \text {-IPMCCM-DC) }~~~~~~&{{o}^{c}}\in O \\&{{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}} \\&\varphi _{i}^{+},\varphi _{i}^{-}\ge 0 \\&\varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m. \\ \end{aligned} \end{aligned}$$

(3.16)

3.3 TB-RO-MCCM-DC

In this part, based on TB-MCCM-DC, Box set, Ellipsoid set, Polyhedron set and Interval-Polyhedron set are used to establish the following four robust cost consensus models.

Similarly, similar to the form of (3.3), the robust counterpart of the model (2.8) is

$$\begin{aligned} \begin{aligned} \min&\quad B \\ s.t.&\quad \sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})+\underset{\xi \in {\mathcal {U}}}{\mathop {\max }}\,\left\{ \sum \limits _{h=1}^{H}{{{\xi }_{h}}(c_{h}^{U}\varphi _{i}^{-}+c_{h}^{D}\varphi _{i}^{+})} \right\} }\le B \\&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

Case 1 Considering that the uncertainty set is Box set, without loss of generality, let ${\mathcal {Z}}^{Box}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le \varPhi \}$, where $\varPhi$ is an adjustable uncertain level parameter, so TB-BMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\phi }^{+}}+\gamma {{\left\| u \right\| }_{1}} \\ s.t.&\quad -{{u}_{l}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\phi }^{+}}\le {{u}_{l}},h=1,\ldots ,H \\ \text {(TB-BMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.17)

Case 2 Considering that the uncertainty set is Ellipsoid set, without loss of generality, let ${\mathcal {Z}}^{Ellipsoid}=\{\xi \in R^H{:}\,\left\| \xi \right\| _2\le \varOmega \}$, where $\varOmega$ is an adjustable uncertain level parameter, so TB-EMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\phi }^{+}}+\varOmega {{\left\| u \right\| }_{2}} \\ s.t.&\quad -{{u}_{h}}\le c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\phi }^{+}}\le {{u}_{h}},h=1,\ldots ,H \\ \text {(TB-EMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.18)

Case 3 Considering that the uncertainty set is Polyhedron set, without loss of generality, let ${\mathcal {Z}}^{Polyhedron}=\{\xi \in R^H{:}\,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is an adjustable uncertain level parameter, so TB-PMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\phi }^{+}}+\varGamma {{\left\| t \right\| }_{\infty }} \\ s.t.&\quad c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\phi }^{+}}=-{{s}_{h}},h=1,\ldots ,H \\ \text {(TB-PMCCM-DC) }~~~~~~&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \\ \end{aligned} \end{aligned}$$

(3.19)

Case 4 Considering that the uncertainty set is Interval-Polyhedron set, without loss of generality, let ${\mathcal {Z}}^{Int\text{-}Poly}=\{\xi \in R^H{:}\,\left\| \xi \right\| _\infty \le 1,\left\| \xi \right\| _1\le \varGamma \}$, where $\varGamma$ is an adjustable uncertain level parameter, so TB-IPMCCM-DC can be obtained:

$$\begin{aligned} \begin{aligned} \min&\quad c_{0}^{U}{{\varphi }^{-}}+c_{0}^{D}{{\phi }^{+}}+{{\left\| {{t}_{1}} \right\| }_{1}}+\varGamma {{\left\| {{t}_{2}} \right\| }_{\infty }} \\ s.t.&\quad c_{h}^{U}{{\varphi }^{-}}+c_{h}^{D}{{\phi }^{+}}=-{{({{s}_{1}}+{{s}_{2}})}_{h}},h=1,\ldots ,H ~\\ \text {(TB-IPMCCM-DC) }~~~~&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}} \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}} \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m .\\ \end{aligned} \end{aligned}$$

(3.20)

4 Numerical Analysis and Sensitivity Analysis

4.1 Numerical Analysis

Suppose that there are five DMs involved in GDM, and their optimal opinions are $o_1=2, o_2=3.5, o_3=4.5, o_4=6, o_5=9$. In order to reach consensus, their unit cost adjustment on the upward and downward directions are $(c_1^U,c_2^U,c_3^U,c_4^U,c_5^U)=(5,4,2,5,6)$ and $(c_1^D,c_2^D,c_3^D,c_4^D,c_5^D)=(3,2,3,2,3)$, respectively. For experts whose opinion is higher than consensus level, his upward unit adjustment cost’s change does not affect the result of group decision. However, minor changes in downward unit adjustment cost may lead to considerable changes in the results of GDM. On the contrary, for experts whose opinions are below the consensus level, his downward unit adjustment cost will not work. But changes in upward unit adjustment cost are crucial to the results of GDM. Since $[c^U;c^D]=[c_0^U;c_0^D]+\sum _{h=1}^H\xi _h[c_h^U;c_h^D]$, suppose $c_0^U=(c_1^U,c_2^U,c_3^U,c_4^U,c_5^U),c_0^D=(c_1^D,c_2^D,c_3^D,c_4^D,c_5^D)$. Meanwhile, for the upward unit adjustment cost, $c_h^U$ takes the negative deviation of $c_0^U$.

$$\begin{aligned} {{C}^{U}}=\left( \begin{array}{ccccc} -\,0.2 &{}\quad -\,0.2 &{}\quad -\,0.2 &{}\quad -\,0.2 &{}\quad -\,0.2 \\ -\,0.05 &{}\quad -\,0.05 &{}\quad -\,0.05 &{}\quad -\,0.05 &{}\quad -\,0.05 \\ -\,0.03 &{}\quad -\,0.03 &{}\quad -\,0.03 &{}\quad -\,0.03 &{}\quad -\,0.03 \\ -\,0.1 &{}\quad -\,0.1 &{}\quad -\,0.1 &{}\quad -\,0.1 &{}\quad -\,0.1 \\ -\,0.15 &{}\quad -\,0.15 &{}\quad -\,0.15 &{}\quad -\,0.15 &{}\quad -\,0.15 \\ \end{array} \right) \end{aligned}$$

For the downward unit adjustment cost, $c_h^D$ takes the negative deviation of $c_0^D$

$$\begin{aligned} {{C}^{U}}=\left( \begin{array}{ccccc} 0.1 ~&{}\quad 0.1 ~&{}\quad 0.1 ~&{}\quad 0.1 ~&{}\quad 0.1 \\ 0.2 ~&{}\quad 0.2 ~&{}\quad 0.2 ~&{}\quad 0.2 ~&{}\quad 0.2 \\ 0.4 ~&{}\quad 0.4 ~&{}\quad 0.4 ~&{}\quad 0.4 ~&{}\quad 0.4 \\ 0.05 ~&{}\quad 0.05 ~&{}\quad 0.05 ~&{}\quad 0.05 ~&{}\quad 0.05 \\ 0.25 ~&{}\quad 0.25 ~&{}\quad 0.25 ~&{}\quad 0.25 ~&{}\quad 0.25 \\ \end{array} \right) \end{aligned}$$

In addition, it is assumed that the uncertain level parameters in the four sets are 2, i.e., $\varPhi , \varOmega , \varGamma =2$. At the same time, we use the YALMIP toolbox to solve the robust model. YALMIP is characterized by its ability to integrate many external optimization solvers, making general optimization problems very manageable, especially SDP problems. Therefore, the YALMIP toolbox can provide a satisfactory solution to the robust consensus model.

By solving the model (3.5), (3.7), (3.9), (3.11), the minimum costs of the four robust cost models with directional constraints are 41.89, 38.4, 37.59, 36.32, respectively. The positive and negative deviation parameters are $\varphi _{Box}^+=\varphi _{Elli}^+=\varphi _{Poly}^+=\varphi _{Int\text{-}Poly}^+=(\varphi _1^+,\varphi _2^+,\varphi _3^+,\varphi _4^+,\varphi _5^+)=(2.5,1,0,0,0)$ and $\varphi _{Box}^-=\varphi _{Elli}^-=\varphi _{Poly}^-=\varphi _{Int\text{-}Poly}^-=(\varphi _1^-,\varphi _2^-,\varphi _3^-,\varphi _4^-,\varphi _5^-)=(0,0,0,1.5,4.5)$, respectively. The final consensus opinions are $o_{Box}^c=o_{Elli}^c=o_{Poly}^c=o_{Int\text{-}Poly}^c=4.5$.

Let the compromise limit $(\varepsilon _1,\varepsilon _2,\varepsilon _3,\varepsilon _4,\varepsilon _5)=(3,5,3.5,2,4)$ in Sect. 2.2.2, and use the consensus framework to deal with the opinions beyond the compromise limit. Assuming $Maxrounds=3$, when $t=1$, each expert’s acceptable range is calculated, and the left and right endpoints of these ranges are used to identify experts with unacceptable opinions. Obviously, the two most distant experts are $a_1$ and $a_5$. Therefore, the largest left endpoint acceptable to experts is $l_5^1=o_5-\varepsilon _5=6$ and the smallest right endpoint is $r_1^1=o_1+\varepsilon _1=5$. Since $l_5^1=6>5=r_1^1$, experts $a_1$ and $a_5$ need to adjust their opinions, otherwise the group consensus cannot be reached. Let $t=2$, assuming that the adjusted compromise limits of experts $a_1$ and $a_5$ are ${{\tilde{\varepsilon }}}_1=4$ and ${{\tilde{\varepsilon }}}_5=4$, respectively, then $r_1^2=o_1+{{\tilde{\varepsilon }}}_1=6,l_5^2=o_5-{{\tilde{\varepsilon }}}_5=5$. In this case, $l_5^2=5<6=r_1^2$ is established. By solving the models (3.13)–(3.16), the minimum cost of the three robust cost models with directional constraints are 43.7, 40.27, 39.7, 38.6, respectively. The positive and negative deviation parameters are $\varphi _{Box}^+=\varphi _{Elli}^+=\varphi _{Poly}^+=\varphi _{Int\text{-}Poly}^+=(\varphi _1^+,\varphi _2^+,\varphi _3^+,\varphi _4^+,\varphi _5^+)=(3,1.5,0.5,0,0)$ and $\varphi _{Box}^-=\varphi _{Elli}^-=\varphi _{Poly}^-=\varphi _{Int\text{-}Poly}^-=(\varphi _1^-,\varphi _2^-,\varphi _3^-,\varphi _4^-,\varphi _5^-)=(0,0,0,1,4)$, respectively, and the final consensus opinion are $o_{Box}^c=o_{Elli}^c=o_{Poly}^c=o_{Int\text{-}Poly}^c=5$.

Let the tolerance range $(\eta _1,\eta _2,\eta _3,\eta _4,\eta _5)=(2,2,0.5,2,1)$ in Sect. 2.2.3. By solving the model (3.17)–(3.20), the minimum cost of three robust cost models with direction constraints are 18.92, 16.2, 15.2 and 14.6, respectively. The positive and negative deviation parameters are $\varphi _{Box}^+=(\varphi _1^+,\varphi _2^+,\varphi _3^+,\varphi _4^+,\varphi _5^+)=(1.2,0,0.2,0,0)$, $\varphi _{Box}^-=(\varphi _1^-,\varphi _2^-,\varphi _3^-,\varphi _4^-,\varphi _5^-)=(0,0.3, 0,2.8,4.8)$, $\phi _{Box}^+=(\phi _1^+,\phi _2^+,\phi _3^+,\phi _4^+,\phi _5^+)=(5.2,3.7,1.2,1.2,0)$,$\phi _{Box}^-=(\phi _1^-,\phi _2^-, \phi _3^-,\phi _4^-,\phi _5^-)=(0,0,0,0,2.8)$, $\varphi _{Elli}^+=\varphi _{Poly}^+=\varphi _{Int\text{-}Poly}^+=(\varphi _1^+,\varphi _2^+,\varphi _3^+,\varphi _4^+,\varphi _5^+) =(0,0,0,0,0)$, $\varphi _{Elli}^-=\varphi _{Poly}^-=\varphi _{Int\text{-}Poly}^-=(\varphi _1^-,\varphi _2^-,\varphi _3^-,\varphi _4^-,\varphi _5^-)=(0,1.5,1, 4,6)$, $\phi _{Elli}^+=\phi _{Poly}^+=\phi _{Int\text{-}Poly}^+=(\phi _1^+,\phi _2^+,\phi _3^+,\phi _4^+,\phi _5^+)=(4,2.5,0,0,0)$, $\phi _{Elli}^-=\phi _{Poly}^-=\phi _{Int\text{-}Poly}^-=(\phi _1^-,\phi _2^-,\phi _3^-,\phi _4^-,\phi _5^-)=(0,0,0,0,4)$. The final consensus are $o_{Box}^c=5.2, o_{Elli}^c=o_{Poly}^c=o_{Int\text{-}Poly}^c=4$.

By comparing the results of the above three models under different uncertainty sets (Table 1), it can be clearly seen that the minimum cost of the model under the Box set is always the largest, while the minimum cost of the model under the Interval-Polyhedron set is always the smallest. Therefore, IPMCCM-DC, $\varepsilon$-IPMCCM-DC, and TB-IPMCCM-DC have the strongest robustness.

Table 1 The minimum cost of the three models under different uncertainty sets

4.2 Sensitivity Analysis

4.2.1 Effects of Uncertain Level Parameters

When the RO method is used to solve the uncertain problem, the uncertain level parameter reflects the uncertainty set’s perturbation of uncertain elements. Therefore, as an essential parameter, it is worth noting whether the change of uncertain level parameter impacts the minimum cost of reaching consensus. In this part, we compare the minimum cost from the perspective of the model and uncertainty set.

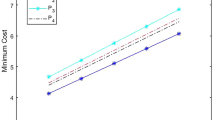
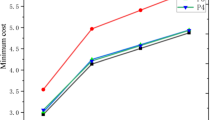
Figure 1 shows the comparison of four uncertainty sets under the same model. The left figure depicts the variation of MCCM-DC’s minimum cost with uncertain level parameter under the four uncertainty sets. The medium figure depicts the change of $\varepsilon$-MCCM-DC, and the figure on the right represents TB-MCCM-DC. As can be seen from Fig. 1, when $\varPhi ,\varOmega ,\varGamma =0$, the three types of models under the four uncertainty sets are converted into nominal models MCCM-DC, $\varepsilon$-MCCM-DC, and TB-MCCM-DC. Their minimum costs are 32, 36, and 12, respectively. When the uncertain level parameter increases, the minimum cost also increases. Obviously, when the uncertainty set is selected as Box set, Ellipsoid set, or Polyhedron set, the model’s minimum cost increases indefinitely. Moreover, the increase of the minimum cost of the model under Box set is the largest, followed by Ellipsoid set and Polyhedron set, and Interval-Polyhedron set is the smallest. This means that their conservatism decreases in turn.

However, in the case of Interval-Polyhedron set, the minimum cost increases with the increase of $\varGamma$ at first, and the change rate decreases simultaneously. When $\varGamma =5$, the minimum costs of IPMCCM-DC, $\varepsilon$-IPMCCM-DC and TB-IPMCCM-DC reach the maximum value and maintain the balance in the subsequent changes. Their maximum values are 37.45, 39.85, and 16, respectively. In fact, the increase of uncertain level parameter is equivalent to the increase of perturbation range of uncertain elements, i.e., unit adjustment cost, which means the increase of uncertainty. Consequently, it will inevitably increase the difficulty of reaching consensus, resulting in an increase in minimum cost. As for the situation of increasing first and then balancing in the Interval-Polyhedron set, the increased interval uncertainty set reduces the model’s conservatism to a certain extent. At the same time, its minimum cost is always the smallest, so it can be considered that the models under the Interval-Polyhedron set are the most robust.

Table 2 shows the comparison of three models under the same uncertainty set. In the single set Box set, Ellipsoid set, and Polyhedron set, MCCM-DC increases the most. From the perspective of model structure, MCCM-DC has weaker constraints and poor anti-interference ability. This proves to some extent that MCCM-DC is a special case of $\varepsilon$-MCCM-DC and TB-MCCM-DC. In addition, under the same set, the changes in different models are similar. For example, under the Interval-Polyhedron set, the three models show the first increasing and then balancing trend. This also explains the similarity of the three models’ change curves in Fig. 1 under different uncertainty sets, where the left side is MCCM-DC, the middle side is $\varepsilon$-MCCM-DC, and the right side is TB-MCCM-DC.

Fig. 1

Comparison of four uncertain sets under the same model

Table 2 Comparison of three models under the same uncertainty set

4.2.2 Effects of Model Parameters

• 1. Effects of $\varepsilon$

Let $\varDelta \varepsilon$ represents the changes of all experts’ compromise limits in the same direction, and calculate the minimum costs and consensus opinions ($o^{c}$) of four robust models of $\varepsilon$-MCCM-DC, respectively. Table 3 shows the effects of the changes of $\varepsilon$ on them, where MC represents the minimum cost.

From Table 3, it is evident that $\varepsilon$ decreases with the decrease of $\varDelta \varepsilon$. The minimum costs of the four robust models increase and tend to infinity. They reach the equilibrium point of 41.89, 38.4, 37.59, and 36.32 at $\varDelta \varepsilon =0.5$. Their consensus at the balance point is 4.5. The consensus opinion decreases with the increase of $\varepsilon$ and reaches the minimum cost balance point. Besides, an interesting finding is that the minimum cost equilibrium points of these four robust models are equal to the optimal values of their corresponding robust minimum cost consensus model with directional constraints. Since the equilibrium point of the minimum cost of $\varepsilon$-IPMCCM-DC is relatively small, it can be considered that $\varepsilon$-IPMCCM-DC has the strongest robustness.

Table 3 Four robust models under different $\varDelta \varepsilon$

According to data analysis in Cheng et al. (2018), the equilibrium points of minimum cost and consensus opinion of $\varepsilon$-MCCM-DC are 32 and 3.5. Figure 2 depicts the minimum cost comparison between $\varepsilon$-MCCM-DC and the four robust models. As show in Fig. 2, the equilibrium point of the minimum cost of $\varepsilon$-IPMCCM-DC is closer to the minimum cost of $\varepsilon$-MCCM-DC, which further verifies the robustness of the robust model under the Interval-Polyhedron set is stronger. In addition, since $\varepsilon$-MCCM-DC reaches equilibrium at $\varDelta \varepsilon =1.5$, it indicates that the variation range of compromise limit parameters in the robust model is small, reducing the effects of uncertainty to some extent.

• 2. Effects of $\eta$

Let $\varDelta \eta$ represents the changes of cost-free thresholds of all experts in the same direction. And then calculates the minimum costs and consensus opinions ($o^{c}$) of four robust models of TB-MCCM-DC, respectively. Table 4 shows the effects of the changes of $\eta$ on them.

Fig. 2

The comparison of $\varepsilon$-MCCM-DC and four robust models

As show in Table 4 and Fig. 3, with the increase of $\varDelta \eta$, the four robust models’ minimum costs decrease and tend to 0. Through comparison with the data in Cheng et al. (2018), it is found that when $\varDelta \eta =-2$, the consensus opinions of the robust model of Polyhedron set and Interval-Polyhedron set reach 3.5, which is the optimal consensus of MCCM-DC. However, their minimum costs are higher than the minimum cost of MCCM-DC, where the optimal value of TB-MCCM-DC is the smallest, which differs from the upper bound of the optimal value of TB-MCCM-DC and is equal to the optimal value of MCCM-DC. In addition, when $\varDelta \eta$ changes, the upper bound of TB-MCCM-DCs consensus opinion reaches the maximum value of expert opinion 9. In the four robust models, the consensus opinions are always at the middle level. This means that experts under the robust model can accept a more comprehensive cost-free threshold, which can significantly reduce the moderator’s cost to reach consensus. As the minimum cost of TB-IPMCCM-DC is always the smallest, the robust model under Interval-Polyhedron set has the most effective robustness.

Table 4 Four robust models under different $\varDelta \eta$

Fig. 3

The comparison of TB-MCCM-DC and four robust models

4.2.3 Comparison Between the Original Model and the Robust Model

In order to detect whether it is meaningful to deal with uncertain factors by using the RO method, this section compares the original model with the corresponding robust model.

Experts usually make decisions based on their personal experience, and their opinions are often subjective. Some experts are risk-averse when making decisions, and their opinions will be relatively conservative (or pessimistic). While other experts consider that the risk and opportunity coexist, they belong to the risk appetite type, so their opinions will be relatively optimistic. Consequently, the consensus opinion of GDM under certain conditions may be too optimistic or too pessimistic; indeed, such a result is not ideal.

Tables 5, 6 and 7 exhibit the comparisons between the three types of models and their corresponding robust models. The optimal solution of the original model is always smaller than that of the robust model. This shows that the original model does not consider the effects of uncertain factors and obtains an overly optimistic decision, thus obtaining a relatively small consensus cost. However, when the final decision is too optimistic, it may not, in the current predicament, as the design problem of new product size, be able to satisfy market demand, or raise processing costs. This will inevitably bring some or even irreparable losses to enterprises. However, in the robust model, considering the data’s uncertainty, although the final total cost increases, the risk of decision-making can be reduced to a certain extent.

Table 5 Comparison of MDDM-DC and its robust model

Table 6 Comparison of $\varepsilon$-MDDM-DC and its robust model

Table 7 Comparison of TB-MDDM-DC and its robust model

In addition, the pessimistic coefficients of the four robust models of MCCM-DC are 0.3091, 0.2000, 0.1747, and 0.1350, respectively. The pessimistic coefficients of the four robust models of $\varepsilon$-MCCM-DC are 0.2139, 0.1194, 0.1028, and 0.0722, respectively. The pessimistic coefficients of the four robust models of TB-MCCM-DC are 0.5767, 0.3500, 0.2667, and 0.2167, respectively. For the pessimistic coefficient $\rho (0<\rho <1)$, $\rho =0$ means that the expert’s decision is too optimistic, and $\rho =1$ means the expert’s decision is too pessimistic. $0<\rho <1$ indicates that the state of the expert’s decision-making is between too optimistic and too pessimistic. The larger the $\rho$, the more pessimistic the experts are. Therefore, the larger the robust model’s pessimistic coefficient is, the more optimistic the consensus reached under the original model is, and the moderator will lose more resources due to the effects of uncertain factors. As the pessimistic coefficients of the three robust models under the Interval-Polyhedron set are relatively small, it means that IPMCCM-DC, $\varepsilon$-IPMCCM-DC, and TB-IPMCCM-DC have the strongest robustness. At this time, the consensus costs are 36.62, 38.6, and 14.6, respectively, and the consensus opinions are 4.5, 5, and 4, respectively.

5 Data-Driven Robust Consensus Models with Asymmetric Costs

Big data usage has received significant attention from researchers with the explosive development of big data and open data. In the third section, we present and use the RO method for a series of robust, asymmetrical-cost consensus models. However, the traditional RO method usually achieves experience based uncertainty sets, making the results too conservative. In contrast, the data-driven RO method uses historical data to construct the uncertainty set. This does not need to know the probability distribution of the uncertain parameters, only needs sufficient historical data. Moreover, with the growing amount of historical data, uncertainty sets can better contain all the possibilities of uncertain parameters, which enhances the rationality and economy of uncertainty sets of the traditional RO method. This section deals more closely with the four uncertainty sets of data-driven solutions, using DEEPCOOL’s price observation data for the new radiator, calculating the various robust solutions and measuring the different companies’ performance to study truly valuable uncertainty sets.

5.1 Uncertainty Set Based on Data-Driven

In the discussion in Sect. 3, we assume that the unit adjustment costs $c_i^U$ and $c_i^D$ in the model (2.3) are uncertain. On the contrary, in this section, we assume that the unit adjustment costs’ observation sets ${{{\mathcal {M}}}_{\text {1}}}$ and ${{{\mathcal {M}}}_{\text {2}}}$ can be obtained, where ${\mathcal {M}}{{}_{1}} =\{c_{i1}^{U},\ldots ,c_{iM}^{U}\},{\mathcal {M}}{{}_{2}} =\{c_{i1}^{D},\ldots ,c_{iM}^{D}\}$ and $c_{ij}^{U},c_{ij}^{D}\in R,j=1,\ldots ,M$. In other words, ${{{\mathcal {M}}}_{\text {1}}}$ and ${{{\mathcal {M}}}_{\text {2}}}$ are the raw data that we can get. Meanwhile, let $c_i^U$ and $c_i^D$ respectively represent the average values of $\{c_{i1}^{U},\ldots ,c_{iM}^{U}\}$ and $\{c_{i1}^{D},\ldots ,c_{iM}^{D}\}$, i.e. ${\hat{c}}_{i}^{U}=\frac{1}{M}\sum _{j\in [M]}{c_{ij}^{U}},{\hat{c}}_{i}^{D}=\frac{1}{M}\sum _{j\in [M]}{c_{ij}^{D}}$, where $[M]=\{1,\ldots ,M\}$. Due to the limited space, we will only show the deformation of $c_{ij}^U$ under different uncertainty sets, and the deformation of $c_{ij}^D$ can be obtained by the same method. Therefore, we need to find a consensus opinion that minimizes the worst-case costs over all the costs in uncertainty set ${\mathcal {Z}}$. This is the robust minimum cost consensus problem:

$$\begin{aligned} \begin{aligned} \min &\left\{ \underset{c_i^U\in {{{\mathcal {Z}}}^{U}},c_i^D\in {{{\mathcal {Z}}}^{D}}}{\mathop {\max }}\,\quad \sum \limits _{i=1}^m{(c_i^U \varphi _i^{-}+c_i^D \varphi _i^{+})}{:}\,\right.\\& \left.\quad {o^{c}}\in O,{o^{c}}+\varphi _i^{+}-\varphi _i^{-}={o_i}\text {,}\varphi _i^{+},\varphi _i^{-}\ge 0,i=1,2,\ldots ,m \right\} \end{aligned} \end{aligned}$$

Next, we introduce several methods for generating ${\mathcal {Z}}$ (Chassein et al. 2019), where each set has a scaling parameter to control its size.

• 1. Interval uncertainty

We set ${\underline{c}}_{i}^{U}={\mathop {\min }\nolimits _{j\in [M]}}\,c_{ij}^{U},\bar{c}_{i}^{U}={\mathop {\max }\nolimits _{j\in [M]}}\,c_{ij}^{U}$, for some $\lambda \ge 0$, there is ${\mathcal {Z}}_{Int}^{U}={\mathop {\times }\nolimits _{i\in [m]}}\,[{\hat{c}}_{i}^{U}+\lambda ({\underline{c}}_{i}^{U}-{\hat{c}}_{i}^{U}),{\hat{c}}_{i}^{U}+\lambda (\bar{c}_{i}^{U}-{\hat{c}}_{i}^{U})]$, where $\times$ is the Cartesian product and $[m]=\{1,\ldots ,m\}$. Notice that ${\mathop {\max }\nolimits _{c_{i}^{U}\in {\mathcal {Z}}_{Int}^{U},c_{i}^{D}\in {\mathcal {Z}}_{Int}^{D}}}\,\sum _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}=\sum _{i\in [m]}{(({\hat{c}}_{i}^{U}+\lambda ({\underline{c}}_{i}^{U}-{\hat{c}}_{i}^{U})})\varphi _{i}^{-}+({\hat{c}}_{i}^{D}+\lambda ({\underline{c}}_{i}^{D}-{\hat{c}}_{i}^{D}))\varphi _{i}^{+})$. Thus, the robust problem obtained is

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{(({\hat{c}}_{i}^{U}+\lambda ({\underline{c}}_{i}^{U}-{\hat{c}}_{i}^{U})})\varphi _{i}^{-}+({\hat{c}}_{i}^{D}+\lambda ({\underline{c}}_{i}^{D}-{\hat{c}}_{i}^{D}))\varphi _{i}^{+}) \\ s.t.&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\ \end{aligned} \end{aligned}$$

• 2. Ellipsoidal uncertainty

Ellipsoid uncertainty set were derived from the observation that the iso-density locus of the multivariate normal distribution is an ellipse. Therefore, it is usually created using the maximum likelihood fit of a normal distribution. According to the theory of mathematical statistics, the best fit of a multivariate normal distribution $N({{\mu }^{U}},{{\varSigma }^{U}})$ of data point $\{c_{i1}^{U},\ldots ,c_{iM}^{U}\}$ is given by ${{\mu }^{U}}={\hat{c}}_{i}^{U},{{\varSigma }^{U}}=\frac{1}{M}\sum _{j\in [M]}{(c_{ij}^{U}-{{\mu }^{U}})}{{(c_{ij}^{U}-{{\mu }^{U}})}^{T}}$. We set an ellipsoid of the form ${\mathcal {Z}}_{Elli}^{U}=\{{{c}^{U}}{:}\,{{(c_{i}^{U}-{\hat{c}}_{i}^{U})}^{T}}{{\varSigma }^{-1}}(c_{i}^{U}-{\hat{c}}_{i}^{U})\le \lambda \}$ with the scaling parameter $\lambda \ge 0$ and it is centered on ${\hat{c}}_{i}^{U}$. Thus, the robust problem obtained is

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+u \\ s.t.&\quad \lambda ({{(\varphi _{i}^{-})}^{T}}\varSigma \varphi _{i}^{-}+{{(\varphi _{i}^{+})}^{T}}\varSigma \varphi _{i}^{+})\le {{u}^{2}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\ \end{aligned} \end{aligned}$$

• 3. Polyhedral uncertainty

A polyhedron defined using linear equations and inequalities is equivalent to a convex hull. We set ${\mathcal {Z}}_{Poly}^{U}={{{\mathcal {M}}}_{1}}$, where the problem is equivalent to using the convex hull of the raw data, i.e. ${\mathcal {Z}}_{Poly}^{U}=conv(\{c_{i1}^{U},\ldots ,c_{iM}^{U}\})$. In order to scale the set, for a given $\lambda \ge 0$, ${\hat{c}}_{i}^{U}+\lambda (c_{ij}^{U}-{\hat{c}}_{i}^{U})$ is used instead of the original point $c_{ij}^U$, and take convex hull of the scaled data points. Thus, the robust problem obtained is

$$\begin{aligned} \begin{aligned} \min&\quad u \\ s.t.&\quad \sum \limits _{i\in [m]}{\sum \limits _{j\in [M]}{(c_{ij}^{U}}\varphi _{i}^{-}+c_{ij}^{D}\varphi _{i}^{+})}\le u,i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\ \end{aligned} \end{aligned}$$

• 4. Interval-Polyhedral uncertainty

This approach is a variant of interval uncertainty. And to reduce the conservatism of this method, it is assumed that only $\lambda \in \{0,\ldots ,m\}$ values can be higher than the midpoint ${\hat{c}}_{i}^{U}$ at the same time. We set ${\mathcal {Z}}_{Int\text{-}Poly}^{U}=\{{{c}^{U}}{:}\,c_{i}^{U}={\hat{c}}_{i}^{U}+(\bar{c}_{i}^{U}-{\hat{c}}_{i}^{U}){{\alpha }_{i}},i\in [m],0\le \alpha \le 1,\sum _{i\in [m]}{{{\alpha }_{i}}}\le \lambda \}$, where the scaling parameter $\lambda$ controls the size of the set ${\mathcal {Z}}_{Int\text{-}Poly}^{U}$. Through the duality of the internal maximization problem, we get the robust problem:

$$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+\lambda u+{{\left\| v \right\| }_{1}} \\ s.t.&\quad (\bar{c}_{i}^{U}-{\hat{c}}_{i}^{U})\varphi _{i}^{-}+(\bar{c}_{i}^{D}-{\hat{c}}_{i}^{D})\varphi _{i}^{+}\le u+{{v}_{i}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\ \end{aligned} \end{aligned}$$

The robust problems of $\varepsilon$-MCCM-DC and TB-MCCM-DC under four uncertainty sets can be obtained in the Appendix.

5.2 Case Study

5.2.1 Case Background and Data Collection

With the increasing complexity of the market environment, organizations are facing increasingly fierce competition. New products are the core for enterprises to form differentiated competition. Enterprises must design and develop new products based on market demand in order to sustain their competitive advantages. Where there is an opportunity, there is a risk. New product pricing is an essential aspect of enterprise pricing. Therefore, whether the pricing of new products is reasonable or not is related to whether the new products can enter and occupy the market smoothly, and is also related to the fate of enterprises. This needs to be considered repeatedly by business leaders. Therefore, there are many decision problems in the pricing process of new products. In this process, experts from various fields will make group decisions on pricing new products and reach a consensus to achieve optimal economic benefits.

DEEPCOOL launched a series of new radiators in 2019. We obtained the pricing information of the MACUBE 550 by querying the official website and consulting the company’s customer service. Enterprises to achieve better economic benefits do not make final decisions randomly but to organize several meetings to decide on the best price possible. New product pricing usually adopts skimming pricing, penetration pricing, and satisfaction pricing. In the seven pricing conferences on MACUBE 550, the sales department and the operation department suggested a low profit and high turnover to open up the product sales and expand the market share at a lower price, giving slightly lower prices according to the penetration pricing method. Production department, marketing department and research and development department through evaluating and quantifying the new radiator’s benefits to consumers (such as the radiator of the ventilation rate, shape, and consumers to the brand relationship, etc.). To determine the upper and lower price’s effectiveness, they usually adopt a satisfactory pricing method to make their own decisions between high and low prices, that is the average price. However, the brand management department tends to make high profits at high prices before competitors enter the market, and quickly recover investment to reduce operational risks before the novelty of products decreases. Therefore, they will use a skimming pricing method to give the price. We will label the experts in these six departments as $e_1,e_2,e_3,e_4,e_5$ and $e_6$, respectively.

Everyone expects their personal views are taken seriously. The chairman, as the moderator, needs to pay some resources (for example, if the price of the product is too high, the difficulty of the sales department’s work will increase with the increase of the price, then the chairman needs to give a certain reward to motivate the enthusiasm of the staff in the sales department) to coordinate the opinions of all parties and reach the optimal opinions. For each expert, if his optimal price is too high, there may be no market for the product at this price, and the enterprise will face unpredictable risks. On the contrary, if his optimal price is too low, the enterprise will need to bear the pressure brought by the massive development cost. It is obvious that the unit adjustment costs of experts in these two directions are asymmetric. This means that the chairman’s resources (time, money, etc.) are asymmetric in both directions. Table 8 shows the pricing data of $e_1,e_2,e_3,e_4,e_5,e_6$ that we observed in the seven meetings, in which $o_i(i=1,\ldots ,6)(unit{:}\, hundred~RMB)$ represents the prices given by the six experts, $c_i^U(i=1,\ldots ,6)(unit{:}\, thousand~RMB)$ and $c_i^D(i=1,\ldots ,6)(unit{:}\, thousand~RMB)$ represent their upward and downward unit adjustment costs, respectively.

Table 8 Pricing data of six department experts

5.2.2 Comparison of Results Under Uniform Scaling Parameters

Obviously, the size of each uncertainty set will be affected by the scaling parameters. Similar to the analysis in Sect. 4, we compare the trends of the four proposed uncertainty sets under the same scaling parameters. Here we set the scaling parameter $\lambda$ from 0 to 6 with a step of 0.2 to observe the change of the minimum cost in a more detailed way. Figure 4 shows the minimum cost change curve with the scaling parameters under the four uncertainty sets. Comparing the results of the traditional RO in Fig. 1, the results of the Polyhedron uncertainty sets here are very close to those of the Interval uncertainty sets, and the results of the Ellipsoid uncertainty sets are better than those of the traditional method. In addition, we still believe that the Interval-Polyhedron set has the strongest robustness due to the upward first and then stable curve trend.

Fig. 4

Comparison of four uncertainty sets under the same model

5.2.3 Evaluation of the Quality of Robust Solutions

In Sect. 5.2.2, we compare the minimum costs of the three models under different uncertainty sets, and conclude that the Interval-Polyhedron set has the strongest robustness. At the same time, it is essential to evaluate the quality of robust solutions. In order to evaluate the performance of robust solutions under all uncertainty sets, the following two performance criteria are used:

• 1. The average objective value for all DMs and all scenarios

  $$\begin{aligned} Average=\frac{1}{m}\sum \limits _{i\in [m]}{\left( \frac{1}{M}\sum \limits _{j\in [M]}{(c_{ij}^{U}\varphi _{i}^{-}+c_{ij}^{D}\varphi _{i}^{+})} \right) } \end{aligned}$$

• 2. The average of the worst-case objective value for each DM

  $$\begin{aligned} Max=\frac{1}{m}\sum \limits _{i\in [m]}{\left( \underset{j\in [M]}{\mathop {\max }}\,(c_{ij}^{U}\varphi _{i}^{-}+c_{ij}^{D}\varphi _{i}^{+}) \right) } \end{aligned}$$

And there are still many other criterion for evaluating quality. Here we also set the scaling parameter $\lambda$ is changed from 0 to 6with a step of 0.2. Meanwhile, we calculate the solution under the average scenario ${\hat{c}}_{i}^{U},{\hat{c}}_{i}^{D}$. Obviously, when the scaling parameter is small enough, this is a special case for all uncertainty sets.

The trade-off between Average and Max objective values is shown in Fig. 5. And the results of 30 scaling parameters belonging to the same uncertainty set of the same model are connected by a line. It can be seen from the Fig. 5 that the solutions calculated using the Interval uncertainty set and the Polyhedron uncertainty set are always very close. Moreover, no matter whether the robustness performance is good or bad, the average performance will remain stable, so they tend to focus on the good average performance. On the other hand, the Ellipsoid uncertainty set shows a broad prospect in these two criteria, and the three models show the trend of increasing (or decreasing) in both average performance and robust performance. For the Interval-Polyhedron uncertainty set, since average performance tends to decrease when robust performance increases to a certain extent, it performs worse for large scaling values and does not exhibit the desired trade-off property. So even though we concluded in the previous section that the Interval-Polyhedron uncertainty set has strong robustness, it does not perform as well as the Ellipsoid uncertainty set in weighing average performance and robust performance. Therefore, we can select different uncertainty sets according to different needs. Note that the proposed data-driven optimization method can also be applied to other GDM problems, such as vehicle platoon coordination, medical diagnostics, and new projects involving multiple stakeholders. The research on these applications will also become our future research direction.

Fig. 5

Performance comparison under Average and Max

6 Conclusion

In this paper, the RO method is used to deal with the uncertainty in the asymmetric cost consensus problem. The uncertain parameters that make changes in the upward and downward unit adjustment costs fluctuate in different uncertainty sets. For the MCCM-DC, $\varepsilon$-MCCM-DC and TB-MCCM-DC models, twelve robust asymmetric cost consensus models are established based on the uncertainty sets. Then, taking the new product design problem as an example, the proposed RO models are solved using the YALMIP toolbox. And the results are interpreted in terms of uncertain level parameters, compromise limit parameters, and cost-free threshold parameters. Three original models are also compared with their respective robust models. The following meaningful conclusions can be drawn through comparative analysis.

• 1. When the value of the uncertain level parameter increases, the perturbation range of the uncertain parameter increases, and the uncertainty of the problem increases, the robustness of the optimization problem is, therefore, worse. Meanwhile, due to the cost of the problem increasing first and then balancing, the composite set Interval-Polyhedron set is more robust than the single uncertainty sets (Box set, Ellipsoid set and Polyhedron set).

• 2. When the compromise limit decreases, the corresponding robust model’s minimum cost increases and tends to infinity. In addition, $\varepsilon$-IPMCCM-DC and TB-IPMCM-DC reached equilibrium before the deterministic models, and their total costs are the smallest, indicating that the Interval-Polyhedron set has the strongest robustness. As the cost-free threshold increases, the minimum cost of the corresponding robust model decreases and tends to zero. The experts under the robust model can accept a larger cost-free threshold.

• 3. In the worst case, the optimal solution obtained by the robust cost consensus model is greater than the optimal solution obtained by the original model. This means the original model does not consider uncertainty, leading to excessively optimistic results. Since the pessimistic coefficients of the three robust models under the Interval-Polyhedron set are relatively small, the Interval-Polyhedron set has the strongest robustness.

Finally, this paper further introduces the data-driven RO method to reduce the conservatism of the traditional RO method. The pricing information of DEEPCOOL’s new product, MACUBE 550, is used to construct the uncertainty set of MCCM. By using different indicators to measure the model applicability of these sets, it is concluded that Ellipsoid uncertainty sets can better trade-off the average performance and the robust performance. In addition, note that the conclusions here are only in the context of the available data. For the MCC problem, the performance of the uncertainty set in other data sets requires further study.

At the same time, this study also has some limitations:

• 1. In many decision-making scenarios, there is usually a social network relationship between DMs (Lu et al. 2020). Therefore, it is necessary to establish a MCCM based on the social network environment.

• 2. In some consensus decision-making issues, the opinions of DMs are also uncertain. Numerous studies have used fuzzy preferences to describe this uncertainty. Therefore, it is also vital to use the RO method to describe the preference information of DMs.

• 3. This paper only considers the result of perturbation of unit adjustment cost in two directions under the same uncertainty set, but the DM’s unit adjustment cost in different directions may be affected by different factors, so it is significant to consider different uncertainty sets in two directions separately. In addition to the application in the development of new products, the proposed robust cost-consensus problem and a data-driven robust cost-consensus problem can also be employed to many other areas of GDM, such as new projects involving multiple stakeholders, sourcing/supplier selection in supply chain management, and vehicle platoon coordination, etc.

Appendix

For $\varepsilon$-MCCM-DC, i.e., model (2.5), its robust minimum cost consensus problem is:

$$\begin{aligned} \begin{aligned}&\min \left\{ \underset{c_{i}^{U}\in {{{\mathcal {Z}}}^{U}},c_{i}^{D}\in {{{\mathcal {Z}}}^{D}}}{\mathop {\max }}\,\sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}{:}\,\right. \\&\left. \qquad {{o}^{c}}\in O,{{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}\text {,}\varphi _{i}^{+},\varphi _{i}^{-}\ge 0,\varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i=1,2,\ldots ,m \right\} . \end{aligned} \end{aligned}$$

Then, its corresponding four uncertainty sets are as follows:

• Interval uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{(({\hat{c}}_{i}^{U}+\lambda ({\underline{c}}_{i}^{U}-{\hat{c}}_{i}^{U})})\varphi _{i}^{-}+({\hat{c}}_{i}^{D}+\lambda ({\underline{c}}_{i}^{D}-{\hat{c}}_{i}^{D}))\varphi _{i}^{+}) \\ s.t.&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i\in [m]. \\ \end{aligned} \end{aligned}$$

• Ellipsoidal uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+u \\ s.t.&\quad \lambda ({{(\varphi _{i}^{-})}^{T}}\varSigma \varphi _{i}^{-}+{{(\varphi _{i}^{+})}^{T}}\varSigma \varphi _{i}^{+})\le {{u}^{2}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i\in [m]. \\ \end{aligned} \end{aligned}$$

• Polyhedral uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad u \\ s.t.&\quad \sum \limits _{i\in [m]}{\sum \limits _{j\in [M]}{(c_{ij}^{U}}\varphi _{i}^{-}+c_{ij}^{D}\varphi _{i}^{+})}\le u,i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i\in [m]. \\ \end{aligned} \end{aligned}$$

• Interval-Polyhedral uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+\lambda u+{{\left\| v \right\| }_{1}} \\ s.t.&\quad (\bar{c}_{i}^{U}-{\hat{c}}_{i}^{U})\varphi _{i}^{-}+(\bar{c}_{i}^{D}-{\hat{c}}_{i}^{D})\varphi _{i}^{+}\le u+{{v}_{i}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad {{o}^{c}}+\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\ge 0,i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-}\le {{\varepsilon }_{i}},i\in [m]. \\ \end{aligned} \end{aligned}$$

For TB-MCCM-DC, i.e., model (2.8), its robust minimum cost consensus problem is:

$$\begin{aligned} \begin{aligned}&\min \left\{ \underset{c_{i}^{U}\in {{{\mathcal {Z}}}^{U}},c_{i}^{D}\in {{{\mathcal {Z}}}^{D}}}{\mathop {\max }}\,\sum \limits _{i=1}^{m}{(c_{i}^{U}\varphi _{i}^{-}+c_{i}^{D}\varphi _{i}^{+})}{:}\, {{o}^{c}}\in O,\varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}},\right. \\&\left. \qquad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}},\varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i=1,2,\ldots ,m \right\} . \end{aligned} \end{aligned}$$

Then, its corresponding four uncertainty sets are as follows:

• Interval uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{(({\hat{c}}_{i}^{U}+\lambda ({\underline{c}}_{i}^{U}-{\hat{c}}_{i}^{U})})\varphi _{i}^{-}+({\hat{c}}_{i}^{D}+\lambda ({\underline{c}}_{i}^{D}-{\hat{c}}_{i}^{D}))\varphi _{i}^{+}) \\ s.t.&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}},i\in [m] \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i\in [m].\\ \end{aligned} \end{aligned}$$

• Ellipsoidal uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+u \\ s.t.&\quad \lambda ({{(\varphi _{i}^{-})}^{T}}\varSigma \varphi _{i}^{-}+{{(\varphi _{i}^{+})}^{T}}\varSigma \varphi _{i}^{+})\le {{u}^{2}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}},i\in [m] \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i\in [m]. \\ \end{aligned} \end{aligned}$$

• Polyhedral uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad u \\ s.t.&\quad \sum \limits _{i\in [m]}{\sum \limits _{j\in [M]}{(c_{ij}^{U}}\varphi _{i}^{-}+c_{ij}^{D}\varphi _{i}^{+})}\le u,i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}},i\in [m] \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i\in [m] .\\ \end{aligned} \end{aligned}$$

• Interval-Polyhedral uncertainty

  $$\begin{aligned} \begin{aligned} \min&\quad \sum \limits _{i\in [m]}{({\hat{c}}_{i}^{U}}\varphi _{i}^{-}+{\hat{c}}_{i}^{D}\varphi _{i}^{+})+\lambda u+{{\left\| v \right\| }_{1}} \\ s.t.&\quad (\bar{c}_{i}^{U}-{\hat{c}}_{i}^{U})\varphi _{i}^{-}+(\bar{c}_{i}^{D}-{\hat{c}}_{i}^{D})\varphi _{i}^{+}\le u+{{v}_{i}},i\in [m] \\&\quad {{o}^{c}}\in O \\&\quad \varphi _{i}^{+}-\varphi _{i}^{-}={{o}_{i}}-{{o}^{c}}+{{\eta }_{i}},i\in [m] \\&\quad \phi _{i}^{+}-\phi _{i}^{-}={{o}_{i}}-{{o}^{c}}-{{\eta }_{i}},i\in [m] \\&\quad \varphi _{i}^{+},\varphi _{i}^{-},\phi _{i}^{+},\phi _{i}^{-}\ge 0,i\in [m] .\\ \end{aligned} \end{aligned}$$