1 Introduction

Group decision-making (GDM) can be viewed as a process where a group of decision makers express their opinions and aim at achieving a collective solution. Consensus reaching process (CRP) is a key issue in GDM by which decision makers are assisted to achieve consensus regarding certain collective solution. Traditionally, “hard” consensus in GDM considers only a lack of consensus state or a state of full or unanimous, which is inconvenient and unnecessary in real life (Kacprzyk et al. 1997, 2010; Kacprzyk and Zadrożny 2010, 2016). Thus, different consensus reaching processes (CRPs) based on a “soft” consensus measure in GDM have been proposed, with some excellent reviews on CRP available in (Herrera-Viedma et al. 2014; Palomares et al. 2014a). In particular, the minimum consensus cost (MCC) and non-cooperative behaviors are becoming hot topics in CRPs.

Generally, preference changing are associated a cost and the resources for consensus building are limited (Ben-Arieh and Easton 2007; Dong et al. 2010, 2015; Dong and Xu 2016; Gong et al. 2017, 2019; Tan et al. 2018). Based on these premises, some CRPs with MCC have been developed (Ben-Arieh and Easton 2007; Ben-Arieh et al. 2008; Cheng et al. 2018; Gong et al. 2015a, b; Zhang et al. 2017, 2019b). Notably, Zhang et al. (2019c) investigated the consensus efficiency of existing CRPs with MCC and provided detailed simulation experiments based on the following comparison criteria: the number of adjusted decision makers; the number of adjusted alternatives; the number of adjusted preference values; the distance between the original and the adjusted preference information; and the number of negotiation rounds required to reach consensus.

In GDM problems, decision makers may behave uncooperatively by expressing dishonest opinions or refusing to change their opinions to favor their own profit. Two mainstream research approaches have been developed in the literature to effectively address non-cooperative behaviors and ensure the quality of the GDM results: (1) managing non-cooperative behaviors in the aggregation process or selection process in the GDM, which focuses on the influence of the non-cooperative behaviors on the aggregation outcome (Dong et al. 2017; Pelta and Yager 2010; Yager 2001, 2002); (2) managing non-cooperative behaviors in the consensus process of the GDM, which mainly analyzes whether a consensus solution can be achieved under the presence of non-cooperative behaviors in the CRP (Dong et al. 2016, 2018b; Palomares et al. 2014b; Quesada et al. 2014).

Although numerous studies have been presented to analyze the MCC and non-cooperative behaviors in CRPs, there still exist two issues that need to be dealt with: the impact of the decision rules and of non-cooperative behaviors on MCC.

  1. (i)

    Impact of decision rules on MCC. In existing CRP studies, decision rules include decision weights and aggregation functions. It is natural that setting decision rules will lead to different consensus outcomes and will have an effect on the consensus cost. For example, in the selection of outstanding research projects, choosing different aggregation functions and decision weights can lead to different consensus outcome and cost. However, the existing research about MCC is to develop some consensus models under the given decision rules and decision weights, and it is still not clear how decision rules influence the minimum cost in reaching consensus in GDM.

  2. (ii)

    Impact of non-cooperative behaviors on MCC. Although non-cooperative behaviors have been extensively studied, the existing research about non-cooperative behaviors focuses on the mangement of non-cooperative behaviors in CRPs, and it is still unclear how non-cooperative behaviors influence on the MCC in CRPs. Therefore, it is necessary to reveal the internal mechanism of the non-cooperative behaviors impact on MCC.

This paper focuses on these two issues and it presents the following research contributions on the impact of decision rules and non-cooperative behaviors on MCC in GDM:

  1. (i)

    From a theoretical point of view, it is proved that the decision rule that minimizes MCC can be modeled with the ordered weighted average (OWA) with decision weigh \( {\text{w}} = \left( {0.5,0, \ldots ,0,0.5} \right)^{\text{T}} \), while the decision rule that maximizes the MCC is modeled with the OWA with decision weight \( {\text{w}} = \left( {1,0, \ldots ,0} \right)^{\text{T}} \) or \( {\text{w}} = \left( {0, \ldots ,0,1} \right)^{\text{T}} \).

  2. (ii)

    From an analytical point of view, Simulation experiments I, II and III are designed to show that the non-cooperative behaviors strongly increase the MCC. The MCC increases with an increase on the number of decision makers. This positive relationship is more obvious when decision makers are less tolerant to inconsistent views or the non-cooperative behaviors in the group are high. We also show non-cooperative behavior is a more determiner factor in influencing the MCC than decision rules. Furthermore, the effect of the consensus within the established target on MCC is also studied in the simulation experiments.

The rest of this paper is organized as follows: Sect. 2 describes the general CRP framework and the minimum-cost consensus model. Section 3 is devoted to the theoretical study to reveal of decision rules impact on MCC. Section 4 provides an analytical study with Simulation experiment I, II and III to further reveals the impact of non-cooperative behaviors and decision rules on MCC. Lastly, Sect. 5 concludes the paper.

2 Background

This section briefly describes the general CRP framework and the minimum-cost consensus model, which will provide the basis of this study.

2.1 The General CRP Framework

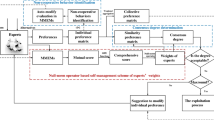
The general CRP framework is depicted in Fig. 1 (Herrera-Viedma et al. 2002; Zhang et al. 2011). Once the individual experts provide their opinions, an aggregation function is carried out to derive the collective opinion. Then, the consensus level among the group of decision makers is measured by looking at the difference between the individual opinions and the collective opinion. If the consensus level is lower than an apriority acceptable consensus threshold value, then a feedback process is carried out to provide support to the decision makers to adjust their individual opinions with the aim of increasing the group consensus. This procedure is repeated for a maximum number of consensus rounds or until the group consensus level reaches the threshold level, whichever comes first.

Fig. 1
figure 1

Framework of the general CRP

Full size image

2.2 Minimum-Cost Consensus Model

In a GDM problem, let \( D = \left\{ {d_{1} ,d_{2} , \ldots ,d_{n} } \right\} \) be the set of decision makers, \( W = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} \) the associated decision makers weights vector, where \( w_{i} \ge 0 \left( {i = 1,2, \ldots ,n} \right) \) and \( \mathop \sum \nolimits_{i = 1}^{n} w_{i} = 1 \); \( A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\} \) be the set of individual opinions, where \( a_{i} \in \left[ {0,1} \right] \) represents the decision maker \( d_{i} \)’s opinion on an alternative.

The minimum-cost consensus model includes three parts:

  1. (1)

    Consensus Measurement Several methods can be used to measure the consensus level in a GDM problem (Fedrizzi 1988; Kacprzyk et al. 1992). The most common is based on the use of a distance based measure, which is the one employed in the minimum-cost consensus model presented in (Chiclana et al. 2013). Let the collective opinion be represented by \( a^{c} \). The consensus level of the decision maker \( d_{i} \) can be measured using the value \( \left| {a_{i} - a^{c} } \right| \) (\( i = 1,2, \ldots ,n) \). Let \( \varepsilon \) be a threshold value (Herrera-Viedma et al. 2002). If

    $$ \left| {a_{i} - a^{c} } \right| \le \varepsilon ,\;{\text{for}}\;{\text{all}}\quad i = 1,2, \ldots ,n, $$
    (1)

    then all decision makers are considered to have reached an acceptable consensus. Otherwise, the decision makers need to adjust their opinions to increase the consensus level.

  2. (2)

    Consensus Cost Let \( \overline{{a_{i} }} \in \bar{A} \) denote the adjusted individual opinion of decision maker \( d_{i} \), and let \( \overline{{a^{c} }} \) be the adjusted collective opinion. Ben-Arieh and Easton (2007) assumed that moving \( d_{i} \)’s opinion 1 unit has associated a cost \( c_{i} \in \left[ 0 \right.,\left. { + \infty } \right) \), and defined the linear consensus cost of moving \( d_{i} \)’s opinion from \( a_{i} \) to \( \overline{{a_{i} }} \) as \( c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| \). Thus, it is natural to minimize the consensus cost, i.e.,

    $$ \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right|. $$
    (2)
  3. (3)

    Aggregation Function In GDM problems, aggregation functions are used to fuse individuals’ opinions to form a collective opinion (Akram et al. 2018, 2019a, b, c; Dong et al. 2010; Ogryczak and Śliwiński 2003; Zhang et al. 2019a). The weighted average (WA) and ordered weighted average (OWA) operators are the most important aggregation functions in GDM problems (Dong et al. 2010; Ogryczak and Śliwiński 2003; Zhang et al. 2011), which are defined by Eqs. (3) and (4), respectively.

$$ F_{WA} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \mathop \sum \limits_{i = 1}^{n} w_{i} a_{i} , $$
(3)
$$ F_{OWA} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right) = \mathop \sum \limits_{i = 1}^{n} w_{i} a_{\left( i \right)} , $$
(4)

where \( a_{\left( i \right)} \) is the \( i \) th largest element of \( A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\} \), and \( W = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} \) is the associated weight vector.

In minimum-cost consensus model, the WA and OWA operators are employed to aggregate individuals’ opinions to obtain the collective decision option \( a^{c} \),i.e.,

$$ a^{c} = F_{W} \left( {a_{1} ,a_{2} , \ldots ,a_{n} } \right). $$
(5)

Formally, Zhang et al. (2011) proposed the following minimum-cost consensus model with aggregation functions:

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ { \overline{{a^{c} }} = F_{W} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right) } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ \end{array} } \right.. $$
(6)

In this study, we denote this model as P1. Solving P1 yields the optimal adjusted opinions. Similarly, the respective minimum-cost consensus models with aggregation functions OWA and WA, denoted models P2 and P3, respectively, are:

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ { \overline{{a^{c} }} = F_{OWA} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right) } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ \end{array} } \right., $$
(7)
$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ { \overline{{a^{c} }} = F_{WA} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right) } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ \end{array} } \right.. $$
(8)

3 Impact of Decision Rules on Minimum Consensus Cost

In a CRP, the aggregation function and its associated decision weight play the role of the decision rules. This section reveals the impact of decision rules on MCC.

3.1 The Decision Rule to Minimize MCC

The solution of the model P4 below will be the optimal adjusted collective opinion that minimizes the MCC.

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ \end{array} } \right.. $$
(9)

Let model P5 be defined by Eq. (10):

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ {\overline{{a^{c} }} = \left( {\mathop {\hbox{min} }\limits_{i} \overline{{a_{i} }} + \mathop {\hbox{max} }\limits_{i} \overline{{a_{i} }} } \right)/2 } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n } \\ \end{array} } \right.. $$
(10)

The following results show that the optimal solution of model P5 is also the optimal solution of model P4.

Theorem 1

Let \( \overline{{a_{i}^{*} }} \left( {i = 1,2, \ldots ,n} \right) \) and \( \overline{{a^{c*} }} \) denote the optimal adjusted individual opinions and adjusted collective opinion obtained by solving model P5. Then, \( \left\{ {\overline{{a_{1}^{*} }} ,\overline{{a_{2}^{*} }} , \ldots ,\overline{{a_{n}^{*} }} ,\overline{{a^{c*} }} } \right\} \) is the optimal solution of model P4.

Proof

Let \( \left\{ {\overline{\overline{{a_{1} }}} ,\overline{\overline{{a_{2} }}} , \ldots ,\overline{\overline{{a_{n} }}} ,\overline{\overline{{a^{c} }}} } \right\} \) be the optimal solution of model P4, and \( \varOmega_{4} \) its feasible set. Similarly, let \( \left\{ {\overline{{a_{1}^{*} }} ,\overline{{a_{2}^{*} }} , \ldots ,\overline{{a_{n}^{*} }} ,\overline{{a^{c*} }} } \right\} \) be the optimal solution of model P5, and \( \varOmega_{5} \) its feasible set.

Based on the condition \( \left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon \) \( \left( {i = 1,2, \ldots ,n} \right) \) of model P4, then we would get

$$ \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| = \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \left[ {\mathop \sum \limits_{{i:a_{i} < \overline{{a^{c} }} - \varepsilon }} c_{i} \left( {\overline{{a^{c} }} - \varepsilon - a_{i} } \right) + \mathop \sum \limits_{{i:a_{i} > \overline{{a^{c} }} + \varepsilon }} c_{i} \left( {a_{i} - \varepsilon - \overline{{a^{c} }} } \right)} \right] $$
(11)

Also because

$$ \begin{aligned} \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| & = \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \left[ {\mathop \sum \limits_{{i:a_{i} < \overline{{a^{c} }} - \varepsilon }} c_{i} \left( {\overline{{a^{c} }} - \varepsilon - a_{i} } \right) + \mathop \sum \limits_{{i:a_{i} > \overline{{a^{c} }} + \varepsilon }} c_{i} \left( {a_{i} - \varepsilon - \overline{{a^{c} }} } \right)} \right] \\ & = \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \left[ {\mathop \sum \limits_{{i:a_{i} < \overline{{a^{c} }} - \varepsilon }} c_{i} \left( {\overline{{a^{c} }} - \varepsilon - a_{i} } \right) + \mathop \sum \limits_{{i:a_{i} > \overline{{a^{c} }} + \varepsilon }} c_{i} \left( {a_{i} - \varepsilon - \overline{{a^{c} }} } \right)} \right] \\ \end{aligned} $$
(12)

Then it will be

$$ \mathop {\hbox{min} }\limits_{{\overline{{a^{c} }} }} \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| = \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right|. $$
(13)

Therefore, model P4 is equivalent to Eq. (14)

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n.} \\ \end{array} } \right. . $$
(14)

Thus, \( \left\{ {\overline{\overline{{a_{1} }}} ,\overline{\overline{{a_{2} }}} , \ldots ,\overline{\overline{{a_{1} }}} ,\overline{\overline{{a^{c} }}} } \right\} \) and \( \varOmega_{4} \) also represent the optimal solution and the feasible set of Eq. (14). Therefore, \( \varOmega_{5} \subseteq \varOmega_{4} \), and we have that:

$$ \begin{aligned} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{\overline{{a_{i} }}} } \right| & = \mathop {\hbox{min} }\limits_{{\left\{ {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} ,\overline{{a^{c} }} } \right\} \in \varOmega_{4} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| \\ & \quad \le \mathop {\hbox{min} }\limits_{{\left\{ {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} ,\overline{{a^{c} }} } \right\} \in \varOmega_{5} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| \\ & = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i}^{*} }} } \right|. \\ \end{aligned} $$
(15)

Moreover, the relationship between \( \overline{\overline{{a^{c} }}} \) and \( \overline{\overline{{a_{i} }}} \) is:

$$ \overline{\overline{{a_{i} }}} = \left\{ {\begin{array}{l} {\overline{\overline{{a^{c} }}} - \varepsilon , i \in \left\{ {i:a_{i} \le \overline{\overline{{a^{c} }}} - \varepsilon } \right\}} \\ {\overline{\overline{{a^{c} }}} + \varepsilon , i \in \left\{ {i:a_{i} \ge \overline{\overline{{a^{c} }}} + \varepsilon } \right\}} \\ {a_{i} ,i \in \left\{ {i:\overline{\overline{{a^{c} }}} - \varepsilon < a_{i} < \overline{\overline{{a^{c} }}} + \varepsilon } \right\}} \\ \end{array} } \right., $$
(16)

which satisfies \( \mathop {\hbox{max} }\limits_{i} \overline{\overline{{a_{i} }}} - \mathop { \hbox{min} }\limits_{{\rm i}} \overline{\overline{{a_{i} }}} \le 2\varepsilon \).

Furthermore, it is \( \left| {\overline{\overline{{a_{i} }}} - \left[ {\left( {\mathop {\hbox{max} }\limits_{i} \overline{\overline{{a_{i} }}} + \mathop { \hbox{min} }\limits_{{\rm i}} \overline{\overline{{a_{i} }}} } \right)/2} \right]} \right| \le \varepsilon \) for all \( i = 1,2, \ldots ,n \). Therefore, \( \left\{ {\overline{\overline{{a_{1} }}} ,\overline{\overline{{a_{2} }}} , \ldots ,\overline{\overline{{a_{n} }}} ,\left[ {\left( {\mathop {\hbox{max} }\limits_{i} \overline{\overline{{a_{i} }}} + \mathop { \hbox{min} }\limits_{{\rm i}} \overline{\overline{{a_{i} }}} } \right)/2} \right]} \right\} \in \Omega_{5} \). Consequently,

$$ \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{\overline{{a_{i} }}} } \right| \ge \mathop {\hbox{min} }\limits_{{\left\{ {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} ,\overline{{a^{c} }} } \right\} \in \varOmega_{5} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i}^{*} }} } \right|. $$
(17)

From Eqs. (15) and (17), it is:

$$ \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{\overline{{a_{i} }}} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i}^{*} }} } \right|. $$
(18)

Thus, \( \left\{ {\overline{{a_{1}^{*} }} ,\overline{{a_{2}^{*} }} , \ldots ,\overline{{a_{n}^{*} }} ,\overline{{a^{c*} }} } \right\} \) is the optimal solution to model P4.

This completes the proof of Theorem 1.

In the following, we further derive the decision rule between the optimal adjusted collective opinion and the optimal individual opinions of model P4. Based on Theorem 1, \( \left\{ {\overline{{a_{1}^{*} }} ,\overline{{a_{2}^{*} }} , \ldots ,\overline{{a_{n}^{*} }} ,\overline{{a^{c*} }} } \right\} \) is the optimal solution of model P4, which still satisfy the functional relationship \( \overline{{a^{c*} }} = \left( {\mathop {\hbox{min} }\limits_{i} \overline{{a_{i}^{*} }} + \mathop {\hbox{max} }\limits_{i} \overline{{a_{i}^{*} }} } \right)/2 \) of model P5, i.e. the decision rule that minimizes the MCC of model P4 is:

$$ \overline{{a^{c} }} = F_{OWA} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right), $$
(19)

with decision weight vector

$$ OWA\_min = \left( {0.5,0, \ldots ,0,0.5} \right)^{T} . $$
(20)

3.2 The Decision Rule to Maximize MCC

Solving the next model P6 will lead to the optimal adjusted collective opinion that maximizes the MCC.

$$ \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{\overline{{a^{c} }} }} \mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ \end{array} } \right.. $$
(21)

First, we provide the following result regarding the optimal solution of model P6

Lemma 1

Let \( \left\{ {o_{1} ,o_{2} , \ldots ,o_{n} ,o^{c} } \right\} \) denote the optimal solution of model P1. Then, it is: \( o^{c} \in \left[ {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right] \).

Proof

Since \( \left\{ {o_{1} ,o_{2} , \ldots ,o_{n} ,o^{c} } \right\} \) is the optimal solution of model P1. Let \( \left\{ {b_{1} ,b_{2} , \ldots ,b_{n} ,b^{c} } \right\} \), \( \left\{ {e_{1} ,e_{2} , \ldots ,e_{n} ,e^{c} } \right\} \), \( \left\{ {f_{1} ,f_{2} , \ldots ,f_{n} ,f^{c} } \right\} \), and \( \left\{ {g_{1} ,g_{2} , \ldots ,g_{n} ,g^{c} } \right\} \) denote feasible solutions of model P1, where \( b^{c} \in \left[ 0 \right.,\left. {\mathop {\hbox{min} }\limits_{i} a_{i} } \right) \), \( e^{c} \in \left( {\mathop {\hbox{max} }\limits_{i} a_{i} } \right.,\left. 1 \right] \), \( f^{c} = \mathop {\hbox{min} }\limits_{i} a_{i} \) and \( g^{c} = \mathop {\hbox{max} }\limits_{i} a_{i} \) and \( \varepsilon \) being a small enough number.

  1. (i)

    For \( b^{c} \in \left[ 0 \right.,\left. {\mathop {\hbox{min} }\limits_{i} a_{i} } \right) \), then

    $$ MCC_{1} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - b_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {a_{i} - b_{i} } \right). $$
    (22)
  2. (ii)

    For \( e^{c} \in \left( {\mathop {\hbox{max} }\limits_{i} a_{i} } \right.,\left. 1 \right] \), then

    $$ MCC_{2} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - e_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - a_{i} } \right). $$
    (23)
  3. (iii)

    For \( f^{c} = \mathop {\hbox{min} }\limits_{i} a_{i} \), then

    $$ MCC_{3} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - f_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {a_{i} - f_{i} } \right). $$
    (24)
  4. (iv)

    For \( g^{c} = \mathop {\hbox{max} }\limits_{i} a_{i} \), then

    $$ MCC_{4} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - g_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {g_{i} - a_{i} } \right). $$
    (25)

Based on Eqs. (22) and (24), it is

$$ MCC_{1} - MCC_{3} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {a_{i} - b_{i} } \right) - \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {a_{i} - f_{i} } \right) = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {f_{i} - b_{i} } \right). $$
(26)

The feasible solutions \( \left\{ {b_{1} ,b_{2} , \ldots ,b_{n} ,b^{c} } \right\} \) and \( \left\{ {f_{1} ,f_{2} , \ldots ,f_{n} ,f^{c} } \right\} \) satisfy the condition \( \left| {b_{1} - b^{c} } \right| \le \varepsilon \) and \( \left| {f_{1} - f^{c} } \right| \le \varepsilon \) \( \left( {i = 1,2, \ldots ,n} \right) \) of model P1, then \( f_{i} \ge f^{c} - \varepsilon \) and \( b_{i} \le b^{c} + \varepsilon \) (for all \( i = 1,2, \ldots ,n) \), hence

$$ MCC_{1} - MCC_{3} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {f_{i} - b_{i} } \right) \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {f^{c} - b^{c} - 2\varepsilon } \right). $$
(27)

When \( \varepsilon \) tends to 0, \( \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {f^{c} - b^{c} - 2\varepsilon } \right) \) tends to \( \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {f^{c} - b^{c} } \right) > 0 \) and therefore it is

$$ MCC_{1} - MCC_{3} > 0. $$
(28)

Thus, \( MCC_{1} > MCC_{3} \).

Based on Eqs. (23) and (25), we have

$$ MCC_{2} - MCC_{4} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - a_{i} } \right) - \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {g_{i} - a_{i} } \right) = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - g_{i} } \right). $$
(29)

The feasible solutions \( \left\{ {e_{1} ,e_{2} , \ldots ,e_{n} ,e^{c} } \right\} \) and \( \left\{ {g_{1} ,g_{2} , \ldots ,g_{n} ,g^{c} } \right\} \) satisfy the condition \( \left| {e_{1} - e^{c} } \right| \le \varepsilon \) and \( \left| {g_{1} - g^{c} } \right| \le \varepsilon \) \( \left( {i = 1,2, \ldots ,n} \right) \) of model P1,then \( e_{i} \ge e^{c} - \varepsilon \) and \( g_{i} \le g^{c} + \varepsilon \) (for all \( i = 1,2, \ldots ,n) \), hence

$$ MCC_{2} - MCC_{4} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - g_{i} } \right) \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - g_{i} - 2\varepsilon } \right). $$
(30)

Taking limits when \( \varepsilon \) tends to 0, we would get that

$$ MCC_{2} - MCC_{4} \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {e_{i} - g_{i} } \right) > 0. $$
(31)

Thus, \( MCC_{2} > MCC_{4} \).

Accordingly, it is clear that \( \left[ 0 \right.,\left. {\mathop {\hbox{min} }\limits_{i} a_{i} } \right) \cup \left( {\mathop {\hbox{max} }\limits_{i} a_{i} } \right.,\left. 1 \right] \) is excluded from the range of the optimal collective opinion \( o^{c} \) of model P1. Therefore, it is concluded that \( o^{c} \in \left[ {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right] \).

This completes the proof of Lemma 1.

Theorem 2

Let \( \left\{ {p_{1} ,p_{2} , \ldots ,p_{n} ,p^{c} } \right\} \) denote the optimal solution of model P 6 . Then, it is:

$$ p^{c} = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{i} p_{i} ,2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} < 0} \\ {\mathop {\hbox{min} }\limits_{i} p_{i} , 2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} > 0} \\ \end{array} } \right.. $$
(32)

Proof

The process of proving Theorem 2 is divided into two steps.

Step 1 Proof \( p^{c} \in \left[ {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right] \).

The aim of solving model P1 is to obtain the optimal solution under the fixed decision rule, while solving model P6 aims at obtaining the optimal adjusted collective opinion that maximizes the MCC, which equals to finding the optimal decision rule that maximizes the MCC based on the Eq. (5).

The MCC obtained with model P1 with this optimal decision rule is the largest of all MCC obtained with model P1 with any decision rule. Obviously, Lemma 1 still applies to model P6 because the optimal solution \( \left\{ {p_{1} ,p_{2} , \ldots ,p_{n} ,p^{c} } \right\} \) of model P6 is also the optimal solution of model P1 with this optimal decision rule. Hence, it is concluded that \( p^{c} \in \left[ {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right] \).

Step 2 Proof \( p^{c} \to \mathop {\hbox{min} }\limits_{i} p_{i} \) or \( \mathop {\hbox{max} }\limits_{i} p_{i} \).

Let \( \left\{ {h_{1} ,h_{2} , \ldots ,h_{n} ,h^{c} } \right\} \), \( \left\{ {f_{1} ,f_{2} , \ldots ,f_{n} ,f^{c} } \right\} \), and \( \left\{ {g_{1} ,g_{2} , \ldots ,g_{n} ,g^{c} } \right\} \) denote feasible solutions of model P6, where \( h^{c} \in \left( {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right) \), \( f^{c} = \mathop {\hbox{min} }\limits_{i} a_{i} \) and \( g^{c} = \mathop {\hbox{max} }\limits_{i} a_{i} \) and \( \varepsilon \) is a small enough number.

  1. (i)

    For \( h^{c} \in \left( {\mathop {\hbox{min} }\limits_{i} a_{i} ,\mathop {\hbox{max} }\limits_{i} a_{i} } \right) \), it is

    $$ MCC_{1} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - h_{i} } \right| = \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {h_{i} - a_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {a_{i} - h_{i} } \right). $$
    (33)
  2. (ii)

    For \( f^{c} = \mathop {\hbox{min} }\limits_{i} a_{i} \), it is

    $$ MCC_{2} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - f_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {a_{i} - f_{i} } \right) = \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {a_{i} - f_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {a_{i} - f_{i} } \right). $$
    (34)
  3. (iii)

    For \( g^{c} = \mathop {\hbox{max} }\limits_{i} a_{i} \), it is

    $$ MCC_{3} = \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - g_{i} } \right| = \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {g_{i} - a_{i} } \right) = \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {g_{i} - a_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {g_{i} - a_{i} } \right) $$
    (35)

Based on Eqs. (33) and (34), it is

$$ \begin{aligned} MCC_{2} - MCC_{1} & = \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {2a_{i} - f_{i} - h_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {h_{i} - f_{i} } \right) \\ & \ge \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {2h_{i} - f_{i} - h_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {h_{i} - f_{i} } \right) \\ & \ge \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {h_{i} - f_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {h_{i} - f_{i} } \right) \\ & \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {h_{i} - f_{i} } \right). \\ \end{aligned} $$
(36)

The feasible solutions \( \left\{ {h_{1} ,h_{2} , \ldots ,h_{n} ,h^{c} } \right\} \) and \( \left\{ {f_{1} ,f_{2} , \ldots ,f_{n} ,f^{c} } \right\} \) satisfy the conditions \( \left| {h_{1} - h^{c} } \right| \le \varepsilon \) and \( \left| {f_{1} - f^{c} } \right| \le \varepsilon \) \( \left( {i = 1,2, \ldots ,n} \right) \) of model P6,then \( h_{i} \ge h^{c} - \varepsilon \) and \( f_{i} \le f^{c} + \varepsilon \) (for all \( i = 1,2, \ldots ,n) \). Taking limits when \( \varepsilon \) tends to 0, we would get that

$$ MCC_{2} - MCC_{1} \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {h^{c} - f^{c} } \right) > 0. $$
(37)

Based on Eqs. (33) and (35), it is

$$ \begin{aligned} MCC_{3} - MCC_{1} & = \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {g_{i} - h_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {g_{i} + h_{i} - 2a_{i} } \right) \\ & \quad \ge \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {g_{i} - h_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {g_{i} + h_{i} - 2h_{i} } \right) \\ & \quad \ge \mathop \sum \limits_{{i:h_{i} \ge a_{i} }} c_{i} \left( {g_{i} - h_{i} } \right) + \mathop \sum \limits_{{i:h_{i} < a_{i} }} c_{i} \left( {g_{i} - h_{i} } \right) \\ & \quad \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {g_{i} - h_{i} } \right). \\ \end{aligned} $$
(38)

The feasible solutions \( \left\{ {h_{1} ,h_{2} , \ldots ,h_{n} ,h^{c} } \right\} \) and \( \left\{ {g_{1} ,g_{2} , \ldots ,g_{n} ,g^{c} } \right\} \) satisfy the conditions \( \left| {h_{1} - h^{c} } \right| \le \varepsilon \) and \( \left| {g_{1} - g^{c} } \right| \le \varepsilon \) \( \left( {i = 1,2, \ldots ,n} \right) \) of model P6,then \( h_{i} \le h^{c} + \varepsilon \) and \( g_{i} \ge g^{c} - \varepsilon \) (for all \( i = 1,2, \ldots ,n) \). Similarly, it would be

$$ MCC_{3} - MCC_{1} \ge \mathop \sum \limits_{i = 1}^{n} c_{i} \left( {g^{c} - h^{c} } \right) > 0. $$
(39)

From Eqs. (37) and (39), it can be concluded that \( MCC_{2} > MCC_{1} \) and \( MCC_{3} > MCC_{1} \) when \( \varepsilon \) is a small enough number, i.e. the closer \( p^{c} \) is to \( \mathop {\hbox{min} }\limits_{i} a_{i} \) or \( \mathop {\hbox{max} }\limits_{i} a_{i} \), the larger the MCC is. Because \( p^{c} \in \left[ {\mathop {\hbox{min} }\limits_{i} p_{i} ,\mathop {\hbox{max} }\limits_{i} p_{i} } \right] \), this conclusion is guaranteed in the limit case, i.e. \( p^{c} = \mathop {\hbox{min} }\limits_{i} p_{i} \) when \( p^{c} \to \mathop {\hbox{min} }\limits_{i} a_{i} \) and \( p^{c} = \mathop {\hbox{max} }\limits_{i} p_{i} \) when \( p^{c} \to \mathop {\hbox{max} }\limits_{i} a_{i} \). Therefore, we have

$$ p^{c} = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{i} p_{i} ,} & {MCC_{3} > MCC_{2} } \\ {\mathop {\hbox{min} }\limits_{i} p_{i} ,} & {MCC_{3} < MCC_{2} } \\ \end{array} } \right. $$
(40)

Taking limits when ε tends to 0, we would get that

$$ p^{c} =\left\{ \begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{i} p_{i} ,} & {2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} < 0} \\ {\mathop {\hbox{min} }\limits_{i} p_{i} ,} & {2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} > 0} \\ \end{array} \right. $$
(41)

This completes the proof of Theorem 2.

Based on the Theorem 2, the decision rule that maximizes the MCC of model P6 is

$$ \overline{{a^{c} }} = F_{OWA} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right), $$
(42)

with the following associated decision weight vector

$$ OWA\_max = \left\{ {\begin{array}{*{20}c} {\left( {1,0, \ldots ,0} \right)^{T} ,} & { 2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} < 0} \\ {\left( {0, \ldots ,0,1} \right)^{T} ,} & { 2\mathop \sum \limits_{i = 1}^{n} c_{i} a_{i} - \left( {\mathop {\hbox{min} }\limits_{i} a_{i} + \mathop {\hbox{max} }\limits_{i} a_{i} } \right)\mathop \sum \limits_{i = 1}^{n} c_{i} > 0} \\ \end{array} } \right.. $$
(43)

4 Simulation Analysis

In this section, we further reveal the impact of non-cooperative behaviors and decision rules on MCC via Simulation experiments I, II and III. In the minimum-cost consensus model, \( c_{i} \) denotes the cost of moving \( d_{i} \)’s opinion 1 unit, and in this study we argue that it can represent the non-cooperative behavior coefficient of decision maker \( d_{i} \) because larger \( c_{i} \) values mean less cooperation to reach consensus. Thus, \( C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\} \) is considered to be the set of non-cooperative behavior coefficients. Meanwhile, we argue that the decision rules consist of the aggregation functions and the associated decision weights.

4.1 Simulation Experiment I: Impact of Non-cooperative Behaviors on MCC

The basic idea of Simulation experiment I is to randomly generate original individual opinions and values of \( c_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \). Particularly, \( c_{i} \) is randomly generated based on the normal distribution \( N\left( {\mu_{c} ,\sigma_{c}^{2} } \right) \) subject to the constraint \( c_{i} > 0 \), where \( \mu_{c} \) and \( \sigma_{c}^{2} \) approximately measure the expectation and variance of \( d_{i} \)’s non-cooperative behavior coefficient, respectively. Thus, we study the impact of non-cooperative behaviors on MCC through \( \mu_{c} \) and \( \sigma_{c}^{2} \). Simulation experiment I can be formally presented as follows.

Simulation experiment I

Input The number of decision makers \( n \), the expectation of \( d_{i} \)’s non-cooperative behavior coefficient \( \mu_{c} \), the variance of \( d_{i} \)’s non-cooperative behavior coefficient \( \sigma_{c}^{2} \), the established threshold value \( \upvarepsilon \) and decision weight \( w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} \).

Output The minimum consensus cost, MCC.

Step 1 Let \( A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\} \) be the original individual opinions set in model P2, where \( a_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \) is randomly selected using the uniform distribution on \( \left[ {0,1} \right] \).

Step 2 Let \( C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\} \) be the set of non-cooperative behavior coefficients in model P2, where \( c_{i} \left( {i = 1,2, \ldots ,n} \right) \) is randomly generated based on \( N\left( {\mu_{c} ,\sigma_{c}^{2} } \right) \) subject to the constraint \( c_{i} > 0 \).

Step 3 Compute the MCC based on model P2.

Without loss of generality, in the simulation we consider two decision rules:

$$ OWA_{1} = \left( {1/n, \ldots ,1/n} \right)^{T} \;{\text{and}}\;OWA_{2} = \left( {0,1/\left( {n - 2} \right), \ldots ,1/\left( {n - 2} \right),0} \right)^{T} . $$

We set different values for \( n \), \( \varepsilon \), \( \mu_{c} \), \( \sigma_{c}^{2} \) and run Simulation experiment I 10,000 times to calculate the average of the MCC values, which is shown in Figs. 2 and 3.

Fig. 2
figure 2

Effects of \( \mu_{c} \) and \( \sigma_{c}^{2} \) on the MCC under different parameters

Full size image
Fig. 3
figure 3

Effects of \( \varepsilon \) and \( n \) on the MCC under different parameters

Full size image

From Figs. 2 and 3, we draw the following observations:

  1. (1)

    Fig. 2 shows that the MCC increases as \( \mu_{c} {\text{and}} \) \( \sigma_{c}^{2} \) increase under different parameters. This implies that the non-cooperative behaviors in the group, defined by \( \mu_{c} \) and \( \sigma_{c}^{2} \), strongly increase the MCC, which translates in an increase in the difficulty when reaching consensus in GDM.

  2. (2)

    Fig. 3 shows that the MCC increases as \( n \) increases under different parameters, being this increment more significant the smaller \( \varepsilon \) values or the larger \( \sigma_{c}^{2} \) values are, respectively. This agrees with the real increase of difficulty in reaching consensus the larger the group experts. Meanwhile, the number of decision makers will have a stronger impact on the consensus reaching in GDM when decision makers are less tolerant to inconsistent views, defined by \( \varepsilon \), or the larger the non-cooperative behaviors in the group are, than otherwise.

4.2 Simulation Experiment II: The Joint Impact of Non-cooperative Behaviors and Decisions Rules on MCC

Let \( C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\} \) be the set of non-cooperative behavior coefficients, defined by unit cost; \( S\left( C \right) = \mathop \sum \nolimits_{i = 1}^{n} c_{i} \) the sum of the non-cooperative behavior coefficients; and \( D\left( C \right) = \left( {\mathop \sum \nolimits_{i = 1}^{n} \left[ {c_{i} - S\left( C \right)/n} \right]^{2} } \right)/n \) the variance of the non-cooperative behavior coefficients. Let \( w_{i} = \overline{{w_{i} }} /\mathop \sum \nolimits_{j = 1}^{n} \overline{{w_{j} }} \) \( \left( {i = 1,2, \ldots ,n} \right) \) and \( \overline{{w_{i} }} \) be randomly generated using normal distribution \( N\left( {0.2,\sigma_{w}^{2} } \right) \) subject to the constraint \( \overline{{w_{i} }} > 0 \). Then, \( \sigma_{w}^{2} \) approximately measures the variance of decision weights.

The basic idea of Simulation experiment II is to randomly generate original individual opinions, and the values of \( w_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \). Then, we investigate the joint impact of non-cooperative behaviors and decisions rules on MCC through \( C \) and \( \sigma_{w}^{2} \). Simulation experiment II can be formally presented as follows.

Simulation experiment II

Input The number of decision makers \( n \), the variance of decision weights \( \sigma_{w}^{2} \), the established threshold value \( \upvarepsilon \) and the non-cooperative behavior coefficients set \( C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\} \).

Output The minimum consensus cost, MCC.

Step 1 Let \( A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\} \) be the original individual opinions set of model P2 (or model P3), where \( a_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \) is randomly selected using the uniform distribution on \( \left[ {0,1} \right] \)..

Step 2 Let \( W = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} \) be decision weight of model P2 (or model P3), where \( w_{i} = \overline{{w_{i} }} /\mathop \sum \nolimits_{j = 1}^{n} \overline{{w_{j} }} \) \( \left( {i = 1,2, \ldots ,n} \right) \), and \( \overline{{w_{i} }} \) is randomly generated using normal distribution \( N\left( {0.2,\sigma_{w}^{2} } \right) \) subject to the constraint \( \overline{{w_{i} }} > 0 \).

Step 3 Compute the MCC based on model P2 (or model P3).

In order to reflect the impact of \( D\left( C \right) \) on MCC, we consider eight non-cooperative behavior coefficients sets:

$$ \begin{aligned} C_{1} & = \left\{ {3,3,3,3,3} \right\},C_{2} = \left\{ {5,4,3,2,1} \right\},C_{3} = \left\{ {1,2,7,3,2} \right\},C_{4} = \left\{ {8,5,2,0,0} \right\} \\ C_{5} & = \left\{ {10,2,1,1,1} \right\},C_{6} = \left\{ {1,2,3,4,5} \right\},C_{7} = \left\{ {7,3,2,1,2} \right\}C_{8} = \left\{ {0,0,8,5,2} \right\}, \\ \end{aligned} $$

with same sum \( S\left( {C_{k} } \right) = 15 \) \( \left( {k = 1,2, \ldots ,8} \right) \) but different variance values:

$$ \begin{aligned} D\left( {C_{1} } \right) & = 0,D\left( {C_{2} } \right) = 2,D\left( {C_{3} } \right) = 4.4,D\left( {C_{4} } \right) = 9.6 \\ D\left( {C_{5} } \right) & = 12.4,D\left( {C_{6} } \right) = 2,D\left( {C_{7} } \right) = 4.4,D\left( {C_{8} } \right) = 9.6. \\ \end{aligned} $$

We set different \( \sigma_{w}^{2} \) values and run Simulation experiment II 10,000 times to calculate the average of the MCC values, which are shown in Figs. 4 and 5.

Fig. 4
figure 4

The differences of models P2 (OWA) and P3 (WA) on MCC with \( n = 5 \) and \( \varepsilon = 0.05 \)

Full size image
Fig. 5
figure 5

The joint impact of \( \sigma_{w}^{2} \) and \( D\left( C \right) \) on MCC

Full size image

From Figs. 4 and 5, we draw the following observations:

  1. (1)

    Fig. 4 shows that the MCC obtained with model P2 is larger than the one obtained with model P3 under different parameters, which means that it is more difficult to reach consensus using OWA than using WA under the same decision weight.

  2. (2)

    In Fig. 5a, S \( \left( {C_{k} } \right) = 15 \left( {k = 1,2,3,4,5} \right) \), \( D\left( {C_{1} } \right) < D\left( {C_{2} } \right) < D\left( {C_{3} } \right) < D\left( {C_{4} } \right) < D\left( {C_{5} } \right) \); and in Fig. 5b, \( S\left( {C_{k} } \right) = 15 \) \( \left( {k = 2,3,4,6,8} \right) \), \( D\left( {C_{2} } \right) = D\left( {C_{6} } \right) < D\left( {C_{3} } \right) = D\left( {C_{7} } \right) < D\left( {C_{4} } \right) = D\left( {C_{8} } \right) \). Figure 5a shows that the MCC, obtained with model P2 and P3, slightly fluctuate around the same fixed value as \( \sigma_{w}^{2} \) increases under the same \( D\left( C \right) \) and \( S\left( C \right) \) values. Figure 5b shows that larger \( D\left( C \right) \) values lead to lower MCC under the same \( S\left( C \right) \) values. This implies that decision rules, defined by decision weights and the aggregation functions, are insensitive to the MCC, while \( C \), defined by \( D\left( C \right) \) and \( S\left( C \right) \), is a main determinant in influencing the MCC.

4.3 Simulation Experiment III: The Impact of the Consensus Within the Established Target on MCC

This section illustrates the relation between MCC and building a consensus opinion \( \overline{{a^{c} }} \) within a desired range  \( \left[ {a,b} \right] \).We firstly consider the following minimum-cost consensus model P7,

$$ \left\{ {\begin{array}{l} {\mathop {\hbox{min} }\limits_{{\overline{{a_{i} }} }} \mathop \sum \limits_{i = 1}^{n} c_{i} \left| {a_{i} - \overline{{a_{i} }} } \right| } \\ { \overline{{a^{c} }} = F_{OWA} \left( {\overline{{a_{1} }} ,\overline{{a_{2} }} , \ldots ,\overline{{a_{n} }} } \right) } \\ {\left| {\overline{{a_{i} }} - \overline{{a^{c} }} } \right| \le \varepsilon ,i = 1,2, \ldots ,n} \\ {a \le \overline{{a^{c} }} \le b } \\ \end{array} } \right., $$
(17)

The basic idea of Simulation experiment III is to randomly generate original individual opinions, and the values of \( c_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \) to investigate the effect of the consensus, within the established target, on MCC through \( \mu_{c} \), \( \sigma_{c}^{2} \), and \( \left[ {a,b} \right] \). Simulation experiment III can be formally presented as follows.

Simulation experiment III

Input The number of decision makers \( n \), the expectation of \( d_{i} \)’s non-cooperative behavior coefficient \( \mu_{c} \), the variance of \( d_{i} \)’s non-cooperative behavior coefficient \( \sigma_{c}^{2} \), the established threshold value \( \upvarepsilon \), decision weight \( w = \left( {w_{1} ,w_{2} , \ldots ,w_{n} } \right)^{T} \) and the established collective solution target range \( \left[ {a,b} \right] \).

Output The minimum consensus cost, MCC.

Step 1 Let \( A = \left\{ {a_{1} ,a_{2} , \ldots ,a_{n} } \right\} \) be the original individual opinions set in model P7, where \( a_{i} \) \( \left( {i = 1,2, \ldots ,n} \right) \) is randomly selected using the uniform distribution on \( \left[ {0,1} \right] \).

Step 2 Let \( C = \left\{ {c_{1} ,c_{2} , \ldots ,c_{n} } \right\} \) be the set of non-cooperative behavior coefficients in model P7, where \( c_{i} \left( {i = 1,2, \ldots ,n} \right) \) is randomly generated using normal distribution \( N\left( {\mu_{c} ,\sigma_{c}^{2} } \right) \) subject to the constraint \( c_{i} > 0 \).

Step 3 Compute the MCC based on model P7.

Without loss of generality, in the simulation we consider two decision rules as follow:

$$ OWA_{1} = \left( {1/n, \ldots ,1/n} \right)^{T} \;{\text{and}}\;OWA_{2} = \left( {0,1/\left( {n - 2} \right), \ldots ,1/\left( {n - 2} \right),0} \right)^{T} . $$

We set different values for \( n \), \( \varepsilon \), \( \mu_{c} \), \( \sigma_{c}^{2} \), \( \left[ {a,b} \right] \) and run Simulation experiment III 10,000 times to calculate the average of the MCC values, which is shown in Figs. 6 and 7.

Fig. 6
figure 6

Effects of \( \left[ {a,b} \right] \) and \( \sigma_{c}^{2} \) on the MCC under different parameters

Full size image
Fig. 7
figure 7

Effects of \( \left[ {a,b} \right] \) and \( \mu_{c} \) on the MCC under different parameters

Full size image

From Figs. 6 and 7, we draw the following observations:

  1. (1)

    Likewise to the observations previously drawn from Figs. 2 and 3, Figs. 6 and 7 also show that the MCC increases as \( \mu_{c} {\text{and}} \) \( \sigma_{c}^{2} \) increase under different parameters.

  2. (2)

    Figs. 6 and 7 show that the MCC increases when the established collective solution target range moves up from \( \left[ {0.5,0.6} \right] \) to \( \left[ {0.9,1} \right] \) through \( \left[ {0.6,0.7} \right] \), \( \left[ {0.7,0.8} \right] \), \( \left[ {0.8,0.9} \right] \) ,which means that it is more difficult to achieve an extreme collective consensus opinion. Meanwhile, this inference is more obvious under larger non-cooperative behaviors in the group, defined by \( \mu_{c} \) and \( \sigma_{c}^{2} \).

5 Conclusion

This paper studied the impact of decision rules and non-cooperative behaviors on MCC in GDM. Theoretically, the decision rule that minimizes or maximizes MCC was derived. Furthermore, the joint impact of non-cooperative behaviors and decision rules on MCC were analyzed via simulation experiments.

In general, a preference adjustment has associated a cost and the consensus reaching resources are limited, which implies that the results obtained in this paper can provide new perspectives to understand how decision rules and non-cooperative behaviors influence the consensus cost.

Meanwhile, social network and opinion dynamics are becoming new tools to model CRP (Dong et al. 2018a; Gong et al. 2020), and we argue that it will be promising to investigate the consensus with minimum cost in social network and opinion dynamics contexts. In particular, it is very necessary to investigate the impact of decision rules and non-cooperative behaviors on MCC in social network and opinion dynamics contexts.