1 Introduction

Black hole thermodynamics is one of great importance subjects in gravitational theory, since it could provide a further insight into the understanding of quantum theories of gravity. Actually, black holes can always behave like an ordinary thermodynamical systems and undergo the phase transition, which is a most remarkable property in black hole thermodynamics and can relate a gravitational system to an accessible experimental system. The pioneering work on black holes phase transition was done by Hawking and Page, who proved that a first order phase transition occurs between a large AdS black hole and a thermal AdS vacuum [1]. Especially, this so-called Hawking-Page phase transition could be explained as the confinement/deconfinement phase transition of gauge field [2], inspired by the AdS/CFT correspondence [3,4,5]. These open a grand window to explore the holographic and quantum understanding of critical phenomena and phase transition in general AdS spacetime. Later, it has been claimed that the first order phase transition of RN-AdS black hole [6, 7] is similar to the liquid/gas phase transition of the van der Waals fluid. After treating the cosmological constant as a thermodynamic pressure and its conjugate quantity as thermodynamic volume [8,9,10,11,12,13], the SBH/LBH phase transition of RN-AdS black hole is established [14], which is precisely analogous to the liquid/gas phase transition of the van der Waals fluid (See also [15, 16] for reviews). More complicated phase structure also emerge in black hole thermodynamics, including the RPT [17, 18] and superfluid phase transition [19].

The RPT is composed of at least two phase transition, which has previously been observed in a nicotine/water mixture [20], granular superconductors, liquid crystals, binary gases, ferroelectrics and gels (see [21] and the references therein). Recently, it revealed that there exist a RPT between the IBH/SBH/LBH in AdS spacetime [17, 18]. This RPT is accompanied by a finite jump in the Gibbs free energy, which referred to a zeroth-order phase transition that has been observed in superfluidity and superconductivity [22]. The study were also generalized to various setups [23,24,25,26,27,28,29,30,31,32]. Furthermore, microscopic origin of the RPTs for AdS black holes has been explored in [33], which is closely related to a quantum statistical systems. These may shed some lights on the microcosmic and quantum understanding of black hole thermodynamics and phase transition.

It is interesting to consider the relationship between RPT and the number of critical points. No matter in classical thermodynamical systems (e.g. van der Waals gas), or in quantum thermodynamical systems (e.g. black hole), the relationship between phase transition and the number of critical points is subtle. It is well known that a first order phase transition always corresponds to a single critical point (e.g. SBH/LBH phase transition of AdS black hole [14]); a second order phase transition always corresponds to infinity critical points (e.g. superfluid phase transition of AdS black hole [19]); while for RPT, there are always two and several critical points. It is worth noting that in all references mentioned above, the RPTs of AdS black holes correspond to two and several physical critical points. However, we get that a thermodynamical systems with a single critical point can possess RPT, other than a first order phase transition. Concretely, we take the Hayward-AdS black hole, i.e. the AdS black hole in the gravity with a nonlinear electrodynamics as an example and we investigate its critical phenomena and phase structure in detail.

The interest for nonlinear electrodynamics has started with the precursor work of Born and Infeld, in order to modify the standard Maxwell theory and eliminate the problem of infinite energy of the electron [34]. Recent, the nonlinear electrodynamics have been proved to be excellent laboratories in order to circumvent some problems that occur in the standard Maxwell theory. Indeed, the nonlinear electrodynamics theory can emerge naturally in the context of low-energy limit of heterotic string theory [35]. Due to the fact that the nonlinear electrodynamics theory is a powerful tool for the construction of regular black hole solutions [36, 37], it becomes more popular and attracts a great attentions (e.g. [38,39,40,41,42,43,44,45,46,47,48,49,50]). Actually, the black hole with a nonlinear electrodynamics presented in this paper, i.e. the Hayward-AdS black hole, can reduce to the famous Hayward black hole, which is just a regular black hole solution. Besides, the thermodynamics properties of the gravity with a nonlinear electrodynamics is also an active research area in the current literature (e.g. [51,52,53,54,55,56,57,58,59,60].) For example, the Born-Infeld AdS black hole has a SBH/LBH phase transition and a RPT between the IBH/SBH/LBH due to the different strength of the nonlinear electrodynamics [17]. These property render more attractive the studies of the gravity with a nonlinear electrodynamics. For the Hayward-AdS black hole case studied in this paper, it also has a complicated phase structure. Especially, an unexpected RPT will be presented for the first time, which only corresponds to a single physical critical point; while usually the RPT should correspond to two physical critical points. The whole phase structure of the Hayward-AdS black hole is also discussed. The number of critical points and the types of phase transition depend on the constant of the nonlinear electromagnetic field, i.e. the strength of the nonlinear electrodynamics. Moreover, we present the way obtaining the critical RPT points \((T_z,P_z)\) and \((T_t,P_t)\), and give their exact values. Especially for the unexpected RPT, \(P_z\) may be negative and physically unacceptable; hence we also derive the physical critical RPT point \((T_0,0)\).

The paper is organized as follows. We will firstly revisit the Hayward-AdS black hole and its extended thermodynamics in next sections. In Sects. 3 and 4, we study the critical behavior and phase transition, respectively. Finally some concluding remarks are given in Sect. 5.

2 The black hole system and its extended thermodynamics

We firstly revisit the Hayward-AdS black hole, which is a general two-parameters family black hole solution in the gravity with a nonlinear electrodynamics [39]

$$\begin{aligned} \mathrm {d}s^{2}&=-f(r)\mathrm {d}t^{2}+\frac{\mathrm {d}r^2}{f(r)} +r^{2}\bigg (\mathrm {d}\theta ^2+\sin ^2\theta \mathrm {d}\phi \bigg ), \end{aligned}$$
(1)
$$\begin{aligned} f(r)&=1-\frac{2M_{eff}}{r}-\frac{2q^3r^{2}}{\alpha (r^{3}+q^{3})}+\frac{r^2}{\ell ^2},\quad \,A={Q_m}\cos \theta \mathrm {d}\phi , \end{aligned}$$
(2)

where \(\Lambda =-\frac{3}{\ell ^2}\) is the cosmological constant the constant \(\alpha >0\) characterizes the strength of the nonlinear electrodynamics field and has the dimension of length squared. q is the parameter related to the magnetic charge of the Hayward-AdS black hole

$$\begin{aligned} Q_m=\frac{q^2}{\sqrt{2\alpha }}. \end{aligned}$$
(3)

The AMD mass of the Hayward-AdS black hole is

$$\begin{aligned} M_{ADM}=M_{eff}+\frac{q^3}{\alpha }, \end{aligned}$$
(4)

which can be read off from the behavior of the metric function at asymptotic infinity

$$\begin{aligned} f(r)=\frac{r^2}{\ell ^2}+1+\frac{2(M_{eff}+q^3/\alpha )}{r}+{\mathcal {O}}(\frac{1}{r^4}). \end{aligned}$$

As in the neutral limit, the solution reduces to the Schwarzschild AdS black hole, one can refer to \(M_{eff}\) as the Schwarzschild mass. Besides, for any non-vanishing \(M_{eff}\), the above black hole solution behaves singular at the origin, which could never be unavoidable. When \(M_{eff}\) is vanishing, the solution reduces to the Hayward black hole [38, 39], which is a famous regular black hole, since its curvature polynomials \(R,R_{\mu \nu }R^{\mu \nu },R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }\) all have a regular limit at the origin. The critical phenomena of the Hayward black hole was study in detail in [39], and a liquid/gas phase transition was found.

Other thermodynamical quantities are also presented in [39]. The black hole temperature, entropy and electric potential are

$$\begin{aligned} T&=\frac{1}{4\pi \,r_+}-\frac{3q^6r_+}{2\pi \alpha (q^3+r_+^3)^2}+\frac{3r_+}{4\pi \ell ^2},\nonumber \\ S&=\pi \,r_+^2,\quad \,\Phi =\frac{3q^4(2r_+^3+q^3)}{\sqrt{2\alpha }(r_+^3+q^3)^2}, \end{aligned}$$
(5)

respectively, where \(r_+\) is the radius of the event horizon. In the following paper, we will discuss thermodynamics in the extended phase space, where the cosmological constant is treated as a thermodynamic variable, i.e.

$$\begin{aligned} P=-\frac{\Lambda }{8\pi }=\frac{3}{8\pi \ell ^2}, \end{aligned}$$
(6)

with the conjugated thermodynamic volume being \(V=\frac{\partial M_{ADM}}{\partial P}|_{(S,Q_m,\alpha )}=\frac{4\pi \,r_+^3}{3}\). Then it is easy to check the first law of thermodynamics

$$\begin{aligned} \mathrm {d} M_{ADM}=T\mathrm {d}S+\Phi \mathrm {d}Q_m+V\mathrm {d}P+\Pi \mathrm {d}\alpha , \end{aligned}$$
(7)

where \(\Pi =\frac{\partial M_{ADM}}{\partial \alpha }|_{(S,Q_m,P)}=\frac{q^6(2r_+^3-q^3)}{4\alpha ^2(r_+^3+q^3)^2}\) conjugates to \(\alpha \). Besides, the Smarr relation becomes

$$\begin{aligned} M_{ADM}=2TS+\Phi \,Q_m-2PV+2\alpha \Pi , \end{aligned}$$
(8)

which is perfectly consistent with the scaling dimensional argument. Finally, in order to observe the global thermodynamic stability, we introduce the Gibbs free energy

$$\begin{aligned} G=M_{ADM}-TS=\frac{r_+}{3}-\frac{1}{3}\pi r_+^2 T +\frac{q^6}{\alpha (q^3+r_+^3)}+\frac{q^6r_+^3}{\alpha (q^3+r_+^3)^2}. \end{aligned}$$
(9)

3 Critical behavior

3.1 Equation of state and critical points

We firstly calculate the critical points of the system. Based on the temperature Eq. (5), we can directly derive the equation of state

$$\begin{aligned} P=\frac{T}{2r_+}-\frac{1}{8\pi r_+^2}+\frac{3q^6}{4\pi \alpha (r_+^3+q^3)^2}. \end{aligned}$$
(10)

Comparing with the van der Waals fluid equation, it is easy to find the specific volume \(v=2r_+\). Therefore we will choose the horizon radius \(r_+\) as the thermodynamical variable in the equation of state for the black hole system hereafter in this paper, instead of the specific volume v.

Always the critical point occurs when P has an inflection point, i.e.

$$\begin{aligned} \frac{\partial P}{\partial r_+}|_{(T=T_c,r_+=r_c)}=\frac{\partial ^2 P}{\partial r_+^2}|_{(T=T_c,r_+=r_c)}=0, \end{aligned}$$
(11)

where the subscript c stands for the quantities at the critical point. We can obtain the critical pressure and temperature

$$\begin{aligned} P_c&=\frac{1}{8\pi r_+^2}+\frac{3q^6(q^3-5r_+^3)}{\alpha \pi (q^3+r_+^3)^3}, \end{aligned}$$
(12)
$$\begin{aligned} T_c&=\frac{1}{2\pi r_+}+\frac{9q^6r_+^4}{\alpha \pi (q^3+r_+^3)^3} \end{aligned}$$
(13)

with the critical horizon radius \(r_c\) which is the root of the equation

$$\begin{aligned} \alpha (q^3+r_+^3)^4+18q^6r_+^5(4q^3-5r_+^3)=0. \end{aligned}$$
(14)

In order to explore the critical points, we would like to introduce some reduced thermodynamical quantities. We first list the length dimensions of the relevant parameters and thermodynamic quantities:

$$\begin{aligned} \ell =[L],\quad \,q=[L],\quad \,\alpha =[L]^2,\quad \,P=[L]^{-2},\quad \,T=[L]^{-1}, \end{aligned}$$
(15)

therefor we can choose the reduced thermodynamical quantities for the critical point and the reduced constant of the electromagnetic field as

$$\begin{aligned} P_c=\frac{p_c}{8\pi r_c^2},\quad \,T_c=\frac{t_c}{2\pi r_c},\quad \,r_c=R q,\quad \,\alpha =\gamma q^2. \end{aligned}$$
(16)

Now we can simplify the critical points as

$$\begin{aligned} p_c&=\frac{60R^2(R^3-R_P^3)(R^3-R_{P1}^3)}{\gamma (R^3+1)^4},\quad \,t_c=\frac{72R^5(R^3-R_T^3)}{\gamma (R^3+1)^4},\quad \,R_{T}=\frac{10^{1/3}}{2}\approx 1.08, \end{aligned}$$
(17)
$$\begin{aligned} R_P&=\frac{(800+300\sqrt{6})^{1/3}}{10}\approx 1.15,\quad \,R_{P1}=\frac{(800-300\sqrt{6})^{1/3}}{10}\approx 0.40, \end{aligned}$$
(18)

where the equation for the critical horizon radius is

$$\begin{aligned} \gamma =\gamma (R)=\frac{18R^5(5R^3-4)}{(R^3+1)^4}. \end{aligned}$$
(19)

For positive pressure p, we find a constraint \(0<R<R_{P1}\) or \(R>R_P\); while positive temperature \(\tau \) leads to

$$\begin{aligned} R>R_{T}. \end{aligned}$$
(20)

To sum up, we find that the physical critical points with positive temperature and pressure require

$$\begin{aligned} R>R_P. \end{aligned}$$
(21)
Fig. 1
figure 1

Curve of \(\gamma -R\), which characterizes different cases for the physical critical points. The (red) dashed line denotes the physical critical points with positive temperature and pressure, while the (black) solid line corresponds to the critical points with positive temperature and negative pressure, and the (black) dotted one corresponds to the critical points with negative temperature and pressure (colour figure online)

Full size image

Since we focus on the physical critical points, we plot the curve of \(\gamma -R\) in Fig. 1. It is easy to observe that there exist some special values of \(\gamma \): \(\gamma _m\) corresponds to the maxima of \(\gamma (R)\); \(\gamma _P\) and \(\gamma _T\) denote the states with vanishing critical pressure and temperature, respectively. Then the discussion about the number of the physical critical points could be divided into the following subcases:

  • When \(\gamma >\gamma _m\), there exists no value of R, namely one can never find a critical horizon radius, hence there is no critical point;

  • When \(\gamma =\gamma _m\), the case corresponds to a double critical horizon radius \(R=R_m\). As \(R_m>R_P>R_T\), the critical pressure and temperature both are positive, there exists a single critical points. Since

    $$\begin{aligned}&\frac{\partial \gamma (R)}{\partial R}=-\frac{360R^4(R^3-R_m^3)(R^3-R_0^3)}{(R^3+1)^5}, \end{aligned}$$
    (22)
    $$\begin{aligned}&R_{m}=\frac{(1700+300\sqrt{21})^{1/3}}{10}\approx 1.45,\quad \,R_{0}=\frac{(1700-300\sqrt{21})^{1/3}}{10}\approx 0.69, \end{aligned}$$
    (23)

    we can get \(\gamma _m=\gamma (R)|_{R=R_m}=\frac{1000}{9(1700+300\sqrt{21})^{1/3}(\sqrt{21}-3)}\approx 4.83\).

  • When \(\gamma _P<\gamma <\gamma _m\), each \(\gamma \) corresponds to two critical horizon radius R with positive pressure and temperature, therefore one can find two physical critical points;

  • When \(\gamma _T<\gamma \le \gamma _P\), there is a single physical critical point, while another corresponds to zero or negative pressure and positive temperature. We can obtain \(\gamma _P=\gamma (R)|_{R=R_P}=\frac{1000}{9(800+300\sqrt{6})^{1/3}(11\sqrt{6}-24)}\approx 3.27\).

  • When \(\gamma \le \gamma _T\), there also exists a single critical horizon radius; while another corresponds to negative pressure and temperature (or zero), thus physically unacceptable. Here we can get \(\gamma _T=\gamma (R)|_{R=R_T}=\frac{40}{81}10^{2/3}\approx 2.29\).

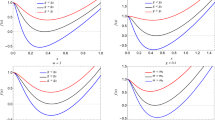
Table 1 The behaviors of critical points for different values of \(\gamma \) (or \(\alpha \)). The values of special \(\gamma \) are \(\gamma _m\approx 4.83,\gamma _P\approx 3.27,\gamma _T\approx 2.29\)
Full size table

We summarize the critical points for different \(\gamma \) in the Table 1. On the other hand, we can calculate the interesting relation \(\frac{P_cv_c}{T_c}\), which is a universal constant for different \(\gamma \) as shown in Fig. 2. The constants are slightly different from the value \(\frac{3}{8}\) of the van der Waals fluid. The curves of \(\frac{P_c v_c}{T_c}-\gamma \) could be divided into two branches: the above branch decreases as \(\gamma \) increases, while \(\gamma \) enlarges the constant \(\frac{P_c v_c}{T_c}\) in the below one. When \(R\rightarrow +\infty \), then \(\gamma \rightarrow 0\), and the constant \(\frac{P_c v_c}{T_c}\) reaches the maxima \(\frac{5}{12}\).

Fig. 2
figure 2

\(\frac{P_c v_c}{T_c}\) vs \(\gamma \). The two-values part of curve denotes the cases with two physical critical points

Full size image

3.2 Critical exponents and coexistence states

Here we would like to explore the critical exponents and coexistence states, which will be useful of the discussion about the complicated phase structure.

For \(\gamma \le \gamma _m\), there always exist critical points, we firstly calculate the critical exponents. We still follow the transformation Eq. (16) and define the following dimensionless thermodynamical variables

$$\begin{aligned} \Theta =\frac{P}{P_c},\quad \,\omega =\frac{T}{T_c}-1,\quad \,\phi =\frac{r}{r_c}-1. \end{aligned}$$
(24)

Then we can obtain the dimensionless equation of state, which has a complicated form and we do not list here. After taking a Taylor expansion, and using the relation Eq. (19), we can derive

$$\begin{aligned} \Theta =1-a \omega (\phi -1)-b\phi ^3+{\mathcal {O}}(\omega \phi ^2,\phi ^4), \end{aligned}$$
(25)

where \(a=\frac{12R^3(R^3-R_T^3)}{5(R^3-R_P^3)(R^3-R_{P1}^3)},b=\frac{2R^3(R^3-R_m^3)(R^3-R_0^3)}{(R^3+1)(R^3-R_P^3)(R^3-R_{P1}^3)}\). It is clear from Eq. (25) that the critical exponents are

$$\begin{aligned} \alpha =0,\quad \,\beta =\frac{1}{2},\quad \,\gamma =1,\quad \,\delta =3, \end{aligned}$$
(26)

which govern the behaviour of the specific heat at constant volume \(C_V\propto |\omega |^{-\alpha }\), the order parameter \(\phi \propto |\omega |^{\beta }\), the susceptibility/compressibility \(\frac{\partial \phi }{\partial \Theta }|_{\omega }\propto |\omega |^{-\gamma }\) and the ordering field \(\Theta \propto |\phi |^{\delta }\) near a critical point, respectively.

Now we using Maxwell’s equal area law to study the coexistence states for the first order phase transition. From Eq. (25), one can obtain the following equation

$$\begin{aligned} 0=\int _{\phi _1}^{\phi _2}\phi \frac{\mathrm {d}\Theta }{\mathrm {d}\phi }\mathrm {d}\phi \Rightarrow \frac{3}{4}b(\phi _1^4-\phi _2^4)+\frac{1}{2}a \omega (\phi _1^2-\phi _2^2)=0, \end{aligned}$$
(27)

where the subscripts 1 and 2 stand for the LBH and SBH phases, respectively. On the other hand, the physical phase equilibrium condition (i.e. the isobar pressure condition) gives

$$\begin{aligned} \Theta |_{\phi _1}=\Theta |_{\phi _2}\Rightarrow a \omega (\phi _1-\phi _2)+b(\phi _1^3-\phi _2^3)=0. \end{aligned}$$
(28)

Equations (27) and (28) together give a unique non-trivial solution (\(\phi _1\ne \phi _2\))

$$\begin{aligned} \phi _{1,2}=\pm \sqrt{-\frac{a}{b}\omega }, \end{aligned}$$
(29)

where

$$\begin{aligned} \frac{a}{b}=\frac{6(R^3-R_T^3)(R^3+1)}{5(R^3-R_m^3)(R^3-R_0^3)}. \end{aligned}$$
(30)

Then when \(a/b<0\), we conclude that the coexistence of smaller and larger black hole phases requires \(\omega >0\); in other words, only when \(T>T_c\) can the two stable black hole phases exist at the same pressure. Conversely, if \(a/b>0\), the phase transition will occur when \(T<T_c\). Noting that the coexistence states depend on the relationship between R and \(R_m,R_T\) (since all R ar bigger that \(R_0\)).

Fig. 3
figure 3

Curves of \(P-r_{+}\) and \(G-P\) for the cases with \(\gamma >\gamma _m\). There exists no critical phenomena and phase transition. In both plots, the temperature of isotherms increase from left to right

Full size image

4 Phase structure

4.1 No phase transition when \(\gamma \ge \gamma _m\)

When \(\gamma >\gamma _m\), there is no critical point. The curves of \(P-r_{+}\) and \(G-P\) are depicted in Fig. 3, where one can not find the \(P-r_+\) oscillatory behavior and the classical “swallow tail”. Therefore, one can never find the critical phenomena and phase transition.

Fig. 4
figure 4

Curves of \(P-r_{+}\) and \(G-P\) for the case with \(\gamma =\gamma _m\). There exists no critical phenomena and phase transition. In left plot, the temperature of isotherms decrease from left to right, while they increase from left to right in the right plot

Full size image

When \(\gamma =\gamma _m\), the situation becomes interesting, as there exists a double critical horizon radius \(R=R_m\). We plot the diagrams of \(P-r_{+}\) and \(G-P\) in Fig. 4, and there exists no \(P-r_+\) oscillatory behavior and the classical “swallow tail” as well. Thus, there is no critical phenomena and phase transition, even this case of the system possess a critical point. One can understand the unexpected phenomena by explore the coexistence states. From Eq. (30), one can find \(\frac{a}{b}\) diverges when \(R=R_m\) (i.e. \(\gamma =\gamma _m\)). As a result, there exists no coexistence state as \(\phi _1=\phi _2\rightarrow \infty \). The double critical point \((p=p_c,t=t_c,R=R_m)\) could not characterize the existence of a first order SBH/LBH phase transition.

4.2 First order SBH/LBH phase transition when \(\gamma \le \gamma _T\)

When \(\gamma \le \gamma _T\), there is a single physical critical point, while another positive critical horizon radius corresponds to negative pressure and negative/zero temperature, thus physically unacceptable. As shown in Fig. 5, one can find the \(P-r_+\) oscillatory behavior and the classical “swallow tail" characterizing the SBH/LBH phase transition when \(T<T_c\), which is denoted as the (red) solid line. This is consistent with the discussion about the coexistence states in the last section. Actually, from Fig. 1, we can obtain that the physical critical horizon radius has the relationship \(R>R_m>R_T>R_0\) when \(\gamma \le \gamma _T\). Considering this relationship and Eq. (30) together, we can find \(\frac{a}{b}>0\), which leads to \(\omega <0\) and indicates the first order phase transition occurring when \(T<T_c\).

Fig. 5
figure 5

Curves of \(P-r_{+}\) and \(G-P\) for the cases with \(\gamma \le \gamma _T\). There are the \(P-r_+\) oscillatory behavior and the classical “swallow tail” characterizing the SBH/LBH phase transition. In both plots, the temperature of isotherms increase from left to right

Full size image

4.3 RPT when \(\gamma _P<\gamma <\gamma _m\)

When \(\gamma _P<\gamma <\gamma _m\), there is two physical critical points which always indicates the existence of a RPT. The behavior of pressure P and Gibbs free energy G are depicted in Fig. 6. For the isotherms with temperature \(T_{c1}<T<T_{c2}\) which is denoted as the (gold) solid line, we can observe two \(P-r_+\) oscillatory behavior and multi-characteristic “swallow tail” behavior characterizing the possible phase transition. We can study the coexistence states to confirm this result. When \(\gamma _P<\gamma <\gamma _m\), we can find the relationship of two physical critical horizon radius from Fig. 1, i.e. \(R_1>R_m>R_2>R_P>R_T>R_0\). Then Eq. (30) leads to \(\frac{a}{b}>0\) near the critical point (\(R_1,T_{c1},P_{c1}\)) implying that the phase transition will occur when \(T<T_{c1}\); while near another critical point (\(R_2,T_{c2},P_{c2}\)), it is \(\frac{a}{b}<0\) and the phase transition will occur when \(T>T_{c2}\); ultimately, a phase transition (at least two “swallow tail”) should occur when \(T_{c2}<T<T_{c1}\).

Fig. 6
figure 6

Curves of \(P-r_{+}\) and \(G-P\) for the cases with \(\gamma _P<\gamma <\gamma _m\). There exists a RPT. In \(P-r_+\) plot, the temperature of isotherms decrease from left to right, while they increase from left to right in \(G-P\) plot

Full size image

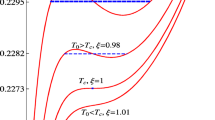
Considering the phase transition when \(T_{c2}<T<T_{c1}\), it is the first order SBH/LBH phase transition occurring for \(T<T_{c1}\) and terminating at \(T=T_{t}\). Especially, there exists a certain range of temperatures \(T\in (T_t,T_z)\), where the global minimum of Gibbs free energy G is discontinuous as shown in the right one of Fig. 6. This results in the so-called “zeroth-order phase transition”, for which two separate branches of IBH and SBH coexist and meanwhile are separated by a finite jump in G. In this range of temperatures, the first order SBH/LBH phase transition and the “zeroth-order phase transition” between the IBH and SBH both appear, which just corresponds to the RPT.

Fig. 7
figure 7

Characteristic behavior of RPT

Full size image

One can denote (\(T_t,P_t\)) and (\(T_z,P_z\)) as the critical RPT points, which are difficult to obtain analytically. Here we present the way to calculate their values, so that one can obtain the exact critical RPT points by the numerical method. The cases for the critical RPT points are depicted in Fig. 7. From the left one in Fig. 7, we see that at the critical RPT point (\(T_z,P_z\)), the two extremal points of \(\frac{\partial P}{\partial r_+}=0\) have the same value of P, i.e. \(P_z\). From the right one in Fig. 7, we find that at the critical RPT point (\(T_t,P_t\)), one extremal point of \(\frac{\partial P}{\partial r_+}=0\) has the same value of P (i.e. \(P_t\)) and G with a SBH (which we denote its thermodynamical quantities as (\(r_c,T_c,P_c\))). After introducing the transformation

$$\begin{aligned} P=\frac{p}{8 \pi q^2},\quad \,T=\frac{\tau }{2 \pi q},\quad \,r_+=R q,\quad \,\alpha =\gamma q^2, \end{aligned}$$
(31)

we can obtain the equations for (\(\tau _z,p_z\)) and (\(\tau _t,p_t\)), namely,

$$\begin{aligned}&\frac{\partial p}{\partial R}|_{(\tau =\tau _z,R=R_a)}=\frac{\partial p}{\partial R}|_{(\tau =\tau _z,R=R_b)}=0,\quad \,p_z=p_a=p_b, \end{aligned}$$
(32)

and

$$\begin{aligned}&\frac{\partial p}{\partial R}|_{(\tau =\tau _t,R=R_a)}=0,\quad \,p_t=p_a=p_c,\quad \,G_t=G_a=G_c. \end{aligned}$$
(33)

respectively. Finding out this point, we can derive the values of the critical RPT points (\(\tau _t,p_t\)) and (\(\tau _z,p_z\)). We present these points for \(\gamma _p<\gamma <\gamma _m\) together with the critical point (\(\tau _{c1,c2},p_{c1,c2}\)) in Table 2.

Table 2 The critical points and the critical RPT points in triple phase diagram when \(\gamma _p<\gamma <\gamma _m\)
Full size table

Finally, this novel RPT can be also clearly illustrated in the \(p-\tau \) diagrams (i.e. \(P-T\) diagrams) as shown in Fig. 8. There exists a SBH/LBH line of coexistence states, which ends in a critical point (\(\tau _{c1},p_{c1}\)) and begins at (\(\tau _t,p_t\)). Meanwhile, there exhibits an IBH/SBH line of coexistence states that terminates at (\(\tau _z,p_z\)) and begins at (\(\tau _t,p_t\)). Especially, a “triple point" between the SBH, IBH and LBH appears in the point (\(\tau _t,p_t\)). We plot the \(p-\tau \) diagrams for different \(\gamma \) in the right one of Fig. 9, it is shown that the values of critical points in \(p-\tau \) diagrams, i.e. (\(\tau _{c1},p_{c1}\)), (\(\tau _t,p_t\)) and (\(\tau _z,p_z\)) increases as \(\gamma \) increases.

Fig. 8
figure 8

\(p-\tau \) diagram for RPT when \(\gamma _P<\gamma <\gamma _m\). The first order SBH/LBH phase transition is depicted by a thick solid line, while the zero oder IBH/SBH phase transition is denoted as the solid line. In the right one, the values of \(\gamma \) for \(p-\tau \) curves increases from the left to right

Full size image

4.4 Unexpected RPT when \(\gamma _T<\gamma \le \gamma _P\)

When \(\gamma _T<\gamma \le \gamma _P\), there exists a single physical critical point, while another positive critical horizon radius corresponds to zero/negative pressure and positive critical temperature, thus physically unobservable. Usually, a single critical point will indicate the first order SBH/LBH phase transition as presented in Sect. 4.2, while two critical points correspond to the RPT as shown in Sect. 4.3. However, when \(\gamma _T<\gamma \le \gamma _P\), it will be interesting to observe an unexpected RPT with a single physical critical point for the first time.

Fig. 9
figure 9

Curves of \(P-r_{+}\) and \(G-P\) for the cases with \(\gamma _T<\gamma \le \gamma _P\). There exists an unexpected RPT. In \(P-r_+\) plot, the temperature of isotherms decrease from left to right, while they increase from left to right in \(G-P\) plot

Full size image

The \(P-r_+\) and \(G-P\) diagrams are depicted in Fig. 9. One can also find two \(P-r_+\) oscillatory behavior and multi-characteristic “swallow tail" behavior for the isotherms with temperature \(0<T<T_{c2}\) (as \(T_{c1}<0\)) denoted as the (gold) solid line. Similarly to the case in last Sect. 4.3, a RPT can occur, which comprises of a first order SBH/LBH phase transition arising in the range of temperatures \(T\in (T_t,T_{c1})\), and a “zero order” IBH/SBH phase transition happening in the range of temperatures \(T\in (T_t,T_z)\). Now we consider the coexistence states to explain this unexpected RPT with a single physical critical point. When \(\gamma _T<\gamma \le \gamma _P\), we can find \(R_1>R_m>R_P>R_2>R_T>R_0\) from Fig. 1. Thus Eq. (30) indicates as well that a phase transition (at least two “swallow tail”) should occur when \(T_{c2}<T<T_{c1}\). Therefore, one can expect that there should exist an unexpected RPT. Since \(T_{c2}\) corresponds to a vanishing or negative pressure \(P_{c2}\), the pressure of the theoretical critical RPT point may be negative. As an effect of the physically unobservable critical point \((T_{c2},P_{c2})\), the range of this RPT temperatures \(T\in (T_t,T_z)\) may be smaller than the theoretical one, comparing with the normal RPT case in last Sect. 4.3.

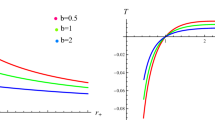
Table 3 The critical points and the theoretical critical RPT points (\(\tau _t,p_t\)) and (\(\tau _z,p_z\)) in triple phase diagram when \(\gamma _T<\gamma \le \gamma _P\). For \(\gamma =\frac{12}{5}\) and \(\frac{5}{2}\), \(p_z\) both become negative and could not be physically observed
Full size table

We follow the same procedure, i.e. Eqs. (31), (32) and (33) to calculate the theoretical critical RPT points (\(\tau _t,p_t\)) and (\(\tau _z,p_z\)) for the cases with \(\gamma _T<\gamma \le \gamma _P\). They are list in Table 3. Even there is a single critical point (\(\tau _{c1},p_{c1}\)), as \(p_{c2}\) are always negative, the critical RPT points (\(\tau _t,p_t\)) and (\(\tau _z,p_z\)) could be physical with positive temperature and pressure, e.g. the cases with \(\gamma =3,\frac{14}{5},\frac{11}{4}\). This novel RPT can be also seen in the \(p-\tau \) diagrams (i.e. \(P-T\) diagrams) as shown in the left one of Fig. 10. However, when \(\gamma \) continues to decrease, the theoretical critical pressure \(p_z\) of the RPT may be negative, e.g. the cases with \(\gamma =\frac{12}{5},\frac{5}{2}\) (See Table 3 and the right one of Fig. 10). We choose \(\gamma =\frac{12}{5}\) as an example shown in Fig. 11. In the left one of Fig. 11, it is easy to find that these is no qualitative change for the first order SBH/LBH phase transition beginning at \((\tau _t,p_t)\) and ending in \((\tau _{c1},p_{c1})\); and the “triple point” (\(\tau _t,p_t\)) between the SBH, IBH and LBH. For the “zero” order IBH/SBH phase transition, it seems to begin at a physically unobservable point \((\tau _z,p_z)\) (i.e. \((0.134922,-0.098192)\)) and ending in \((\tau _{t},p_{t})\). Actually, the physical beginning of the “zero” order IBH/SBH phase transition should be \((\tau _0,0)\), which is denoted in the right one of Fig. 11. \(\tau _0\) could be directly derived by choosing \(p_z=0\) in Eq. (32), namely

$$\begin{aligned}&\frac{\partial p}{\partial R}|_{(\tau =\tau _z,R=R_a)}=\frac{\partial p}{\partial R}|_{(\tau =\tau _z,R=R_b)}=0,\quad \,p_a=p_b=0. \end{aligned}$$
(34)

For \(\gamma =\frac{12}{5}\) and \(\frac{5}{2}\), \(\tau _0\approx 0.179081\) and 0.194280, respectively (See the left one of Fig. 12). For other cases with theoretical critical pressure of RPT \(p_z<0\), \(\tau _0\) of the physical critical RPT for different \(\gamma \) are shown in the right one of Fig. 12.

Fig. 10
figure 10

Theoretical \(p-\tau \) diagram for unexpected RPT when \(\gamma _T<\gamma \le \gamma _P\). In the both plots, the values of \(\gamma \) for \(p-\tau \) curves increases from the left to right

Full size image
Fig. 11
figure 11

Theoretical and physical \(p-\tau \) diagram for unexpected RPT with \(\gamma =\frac{12}{5}\). As \(p_z<0\), the physical beginning of the “zero” order IBH/SBH phase transition should be \((\tau _0,0)\)

Full size image
Fig. 12
figure 12

The left plot is the physical \(p-\tau \) diagram for unexpected RPT with \(\gamma =\frac{12}{5}\) and \(\frac{5}{2}\). If \(p_z<0\), the physical beginning of the “zero” order IBH/SBH phase transition should be \((\tau _0,0)\), where \(\tau _0=0.179081\) and 0.194280 for \(\gamma =\frac{12}{5}\) and \(\frac{5}{2}\), respectively. For other cases with theoretical \(p_z<0\), physical \(\tau _0\) for different \(\gamma \) are shown in the right plot

Full size image

5 Conclusion

In this paper, we present the critical phenomena and phase structure of the Hayward-AdS black hole. The phase structure are very complicated, as there exist not only the liquid/gas like phase transition between LBH and SBH, but also the RPT between the LBH, IBH and SBH. The number of critical points and the types of phase transition depend on the values of \(\gamma \) (i.e. the strength constant \(\alpha \) of the nonlinear electrodynamics), which are summarized in the Table 4. It is interesting to find an unexpected RPT with a single physical critical point for the first time, while usually the RPT should correspond to two physical critical points. Besides, the relation \(\frac{P_cv_c}{T_c}\) is always a universal constant for different \(\gamma \), which are slightly different from the value \(\frac{3}{8}\) of the van der Waals fluid. We also derive the critical exponents and the coexistence states. For the RPT, it comprises of a first order SBH/LBH phase transition beginning at \((T_t,P_t)\) and ending in \((T_{c1},P_{c1})\), and a “zero” order IBH/SBH phase transition beginning at \((T_z,P_z)\) and ending in \((T_{t},P_{t})\). We have presented the way obtaining the critical RPT points \((T_z,P_z)\) and \((T_t,P_t)\), and given their exact values. Especially for the unexpected RPT, if \(P_z\) becomes negative, the physical beginning of the “zero” order IBH/SBH phase transition should be \((T_0,0)\), which is also derived.

Table 4 The behaviors of critical points and phase transition for different values of \(\gamma \) (or \(\alpha \)). The values of special \(\gamma \) are \(\gamma _m\approx 4.83,\gamma _P\approx 3.27,\gamma _T\approx 2.29\)
Full size table

It is interesting to find this unexpected RPT with a single critical point in other AdS black hole background, e.g. the Born-Infeld AdS black hole, Gauss-Bonnet AdS black holes, LoveLock AdS black holes and massive AdS black holes, even the Kerr and other rotating AdS black holes, etc. Besides, it would be of great importance to explore the existence of the RPT with a single critical point beyond the black hole system, namely the quantum multi-body system with interaction, e.g. nicotine/water mixture [20], granular superconductors, liquid crystals, binary gases, ferroelectrics and gels [21], etc. These are all left as the future tasks.