1 Introduction

The motion of test particles under the influence of a gravitational wave (GW), called the Memory Effect [1, 2], has attracted considerable attention as a potential tool to detect gravitational waves. Approximating a gravitational wave by an exact plane wave reveals, in particular, that particles initially at rest will move, after the wave has passed, with constant but non-vanishing relative velocity: this is the Velocity Effect [3,4,5,6,7,8,9,10,11].

In this Letter we point out the central role played by (i) a matrix Sturm–Liouville equation [12]

$$\begin{aligned} \ddot{P}=KP\,, \end{aligned}$$
(1.1)

where K(U) is the profile of the wave, and (ii) by Carroll(type) symmetry [13, 14]. Equation (1.1) (i) determines the isometries; (ii) appears as the key tool for switching from Brinkmann (B) to Baldwin-Jeffery-Rosen (BJR) coordinates and vice versa; (iii) determines the trajectories of particles initially at rest.

In BJR coordinates the symmetries and the trajectories are both conveniently determined in terms of another matrix, H(u) in (2.8) below. In terms of B coordinates, this role is overtaken by the matrix \(Q=PH\) in (3.5), which satisfies again the Sturm–Liouville equation above.

Generic gravitational waves have long been known to have a 5-parameter isometry group [4, 15, 16], recently identified as the subgroup of the Carroll group with rotations omitted [13, 14, 17].Footnote 1

Carroll symmetry has long been considered as a mathematical curiosity irrelevant for physics, for the good reason that a particle with Carroll symmetry can not move [13, 14, 18,19,20]. In this Letter we point out that (broken) Carroll symmetry does play a fundamental rôle, namely in describing particle motion in a gravitational wave background.

2 Killing vectors and isometries

In Brinkmann (B) coordinates \((\mathbf{X},U,V)\) the profile of a plane gravitational wave is given by the symmetric and traceless \(2\times 2\) matrix \(K(U)=K_{ij}(U)\) [15, 16, 21],

$$\begin{aligned} ds^2=\delta _{ij} dX^i dX^j + 2dUdV + K_{ij}(U) X^i X^j dU^2 {\,}, \end{aligned}$$
(2.1a)
$$\begin{aligned} K_{ij}(U){X^i}{X^j}= \frac{1}{2}{{\mathcal {A}_{+}}}(U)\left( \left( X^1\right) ^2-\left( X^2\right) ^2\right) +{\mathcal {A}_{\times }}(U)\,X^1X^2\,, \end{aligned}$$
(2.1b)

where \({\mathcal {A}_{+}}\) and \({\mathcal {A}_{\times }}\) are the \(+\) and \(\times \) polarization-state amplitudes. Previously we studied : (i) linearly polarized waves: \({{\mathcal {A}_{\times }}}=0\) and \({{\mathcal {A}_{+}}}\) is typically a [derivative of a] Gaussian [8, 9, 22] or a Dirac delta [22, 23]; (ii) circularly polarized sandwich wavesFootnote 2 [11]:

$$\begin{aligned} {{\mathcal {A}_{+}}} (U) = C^2\,\frac{\lambda }{\sqrt{\pi }}\,e^{-\lambda ^2U^2} \cos (\omega U){\,}, \quad {{\mathcal {A}_{\times }}} (U) = C^2\,\frac{\lambda }{\sqrt{\pi }}\,e^{-\lambda ^2U^2} \sin (\omega U){\,}; \end{aligned}$$
(2.2)

(iii) circularly polarized waves with periodic profile [11]

$$\begin{aligned} {{\mathcal {A}_{+}}} (U) = C^2 \cos (\omega U){\,}, \qquad {{\mathcal {A}_{\times }}} (U) = C^2\, \sin (\omega U){\,}. \end{aligned}$$
(2.3)

Throughout this Letter, we limit ourselves to sandwich waves with \(C^1\) profile. Impulsive waves with Dirac delta-function profiles have been studied elsewhere [22, 23].

A particularly clear approach to isometries is that of Torre [24] who pointed out that, in Brinkmann coordinates \((\mathbf{X}, U, V)\), the Killing vectors are

$$\begin{aligned} S_i(U){\partial }_i + \dot{S}_i(U) X^i\, {\partial }_V\,, \qquad {\partial }_V, \end{aligned}$$
(2.4)

where the dot means d / dU, and where \(S_i,\, i=1,2 \) is a solution of the vector equation

$$\begin{aligned} \ddot{S}_i(U) = K_{ij}(U) S_j(U)\,. \end{aligned}$$
(2.5)

The simplest example is that of Minkowski space, \(K_{ij}\equiv 0\), when (2.5) is solved by \(S_i=\gamma _i+\beta _iU \) and (2.4) is a combination of translations in the transverse plane and two infinitesimal Galilei boost lifted to (2.1) viewed as a Bargmann space [25, 26],

$$\begin{aligned} Y=(\gamma _i+U\beta _i){\partial }_i + \left( \delta + X^i\beta _i\right) \, {\partial }_V. \end{aligned}$$
(2.6)

The fifth isometry is the “vertical translation” generated by \({\partial }_V\).

Things become more complicated if the profile is non-trivial. In the linearly polarized case \({\mathcal {A}_{\times }}=0\) with a time independent profile \({\mathcal {A}_{+}}=D\ne 0\) a real constant, for example, transverse translations are no longer isometries. In this simple but rather non-physical (non-sandwich) case Eq. (2.5) decouples into two time-independent equations of the oscillator-form, one of them attractive and the other repulsive, depending on the sign of D. The solution of (2.5) is therefore a 4-parameter linear combinations which mixes \(\sinh ( \sqrt{|D|}\,U) \) and \(\cosh ( \sqrt{|D|}\,U)\) in the repulsive, and \(\sin (\sqrt{|D|}\,U)\) and \(\cos (\sqrt{|D|}\,U)\) in the attractive component. But when \(D\ne {\mathrm{const.}}\), the Sturm–Liouville problem (2.5) has no analytic solution in general, and in the polarized case with time dependent profile everything becomes even worse. Various properties of the Killing vector fields and the group they generate were explored in [27].

The problem of solving the Sturm–Liouville equation (2.5) was circumvented by Souriau [4] who suggested using BJR coordinates [28,29,30] instead, in terms of which the metric may be written as

$$\begin{aligned} a_{ij}(u)\,dx^idx^j+2du\,dv, \end{aligned}$$
(2.7)

with \(a(u)=(a_{ij}(u))\) a positive definite \(2\times 2\) matrix, which is an otherwise arbitrary function of “non-relativistic time”, u.Footnote 3 Then natural translations \(\mathbf{x}\rightarrow \mathbf{x}+{\mathbf {c}},\, v\rightarrow v+ w\) are manifest isometries. Moreover, implementing \(\mathbf{b}\in \mathbb {R}^2\) through the \(2\times 2\) matrix valued function

$$\begin{aligned} H(u)=\int _{u_0}^u{\!a^{-1}(w)dw}\,, \end{aligned}$$
(2.8)

as [4, 17],

$$\begin{aligned} \mathbf{x}&\rightarrow \mathbf{x}+ H(u)\,\mathbf{b}, \end{aligned}$$
(2.9a)
$$\begin{aligned} u&\rightarrow u, \end{aligned}$$
(2.9b)
$$\begin{aligned} v&\rightarrow v-\mathbf{b}\cdot \mathbf{x}- {\frac{1}{2}}\mathbf{b}\cdot {}H(u)\,\mathbf{b}, \end{aligned}$$
(2.9c)

yields two further isometries. Souriau’s form (2.9) allows one to determine the group structure with the remarkable result that the above-mentioned generic 5-parameter isometry group [15, 16] we denote here by G may be identified, for any profile, as the subgroup of the Carroll group with rotations omitted [17].

The transformations (2.9) generated by \(\mathbf{b}\) are, in particular, boosts, implemented in an unusual way. In the Minkowski case \(a=\mathrm {Id}\) is the unit matrix so that \( H_{Mink}(u)=(u-{u_0})\,\mathrm {Id}\, \) and the standard extension of the Galilei group [lifted to flat Bargmann space] is recovered.

3 Brinkmann \(\Leftrightarrow \) BJR

The relation between Brinkmann and BJR coordinates is [12]

$$\begin{aligned} {\mathbf{X}}=P(u)\,\mathbf{x}, \quad U=u, \quad V=v-\frac{1}{4}\mathbf{x}\cdot \dot{a}(u)\mathbf{x}\quad \text {with}\quad a(u)=P^{T}\!(u){}P(u)\,, \end{aligned}$$
(3.1)

where the \(2\times 2\) matrix P satisfies

$$\begin{aligned} \ddot{P}=K\,P, \quad P^{T}\dot{P}-\dot{P^{T}}P=0. \end{aligned}$$
(3.2)

The first of these is a matrix Sturm–Liouville equation for P. If this is satisfied, then \(P^{T}\dot{P}-\dot{P^{T}}P=0\) is shown to be a constant of the motion. The second equation is therefore satisfied when it holds at an arbitrary moment.

We emphasise that while the B-coordinates are global, the BJR coordinates are valid only in a finite interval: the mapping (3.1) necessarily becomes singular when

$$\begin{aligned} \det (a)=0\, \quad \text { or equivalently} \quad \det (P)=0. \end{aligned}$$
(3.3)

The mapping (3.1) trades the quadratic “potential” \(K_{ij}(U){X^i}{X^j}\) in (2.1) for a “time”-dependent transverse metric \(a(u)=\big (a_{ij}(u)\big )\) in (2.7) and vice versa.

When expressed in B coordinates, the natural BJR transverse translations \(\mathbf{x}\rightarrow \mathbf{x}+{\mathbf {c}}\) become “time-dependent translations of the Newton–Hooke form” [31, 32]

$$\begin{aligned} \mathbf{X}\rightarrow \mathbf{X}+ P(u)\,{\mathbf {c}}. \end{aligned}$$
(3.4)

Further insight is gained by introducing the \(2\times 2\) matrix

$$\begin{aligned} Q(U)= \big (P{H}\big )(U)=P(U)\int _{{U_0}}^U\big (P^{-1}(P^T)^{-1}\big )(w)dw. \end{aligned}$$
(3.5)

Then combining (2.9) with (3.1) yields, for boosts,

$$\begin{aligned}&\mathbf{X}\rightarrow \mathbf{X}+ Q\, \mathbf{b}, \end{aligned}$$
(3.6a)
$$\begin{aligned}&V \rightarrow V - \mathbf{X}\cdot \dot{Q}\,\mathbf{b}-\frac{1}{2} Q\,\mathbf{b}\cdot \dot{Q}\,\mathbf{b}. \end{aligned}$$
(3.6b)

Equation (3.6) can be tested by inserting the Minkowskian values; reassuringly, the usual Galilean expression is recovered. Moreover, a straightforward calculation using (2.8), (3.1) and (3.2) shows that Q satisfies the same matrix Sturm–Liouville equations (3.2) as P does,

$$\begin{aligned} \ddot{Q}=K\,Q, \quad Q^{T}\dot{Q}-\dot{Q^{T}}Q=0. \end{aligned}$$
(3.7)

Working infinitesimally, only those terms which are linear in \(\mathbf{b}\) contribute, and we recover the rule (2.4) of Torre [24] with \(S_i=P{\mathbf {c}}_i,\, {\mathbf {c}}_1=(1,0)\) and \({\mathbf {c}}_2=(0,1)\) for translations, and \(S_i=Q\mathbf{b}_i\) for boosts, respectively.

4 Trajectories

The G-symmetry implies thatFootnote 4

$$\begin{aligned} {\varvec{p}}\!=\! a(u)\,\dot{\mathbf{x}}, \qquad \mathbf {k}\!=\!\mathbf{x}(u)-H(u)\,{\varvec{p}}, \end{aligned}$$
(4.1)

interpreted as conserved linear and boost-momenta. Reversing these relations, the geodesics may be expressed using the Noetherian quantities above [4, 8, 9],

$$\begin{aligned} \mathbf{x}(u)=H(u)\,{\varvec{p}}+\mathbf {k}, \qquad v(u)=-\frac{1}{2}{\varvec{p}}\cdot H(u)\,{\varvec{p}}+ e\,u+ v_0, \end{aligned}$$
(4.2)

where

$$\begin{aligned} e=\frac{1}{2}g_{\mu \nu }\dot{x}^\mu \dot{x}^\nu \end{aligned}$$
(4.3)

is another constant of the motion, whose sign only depends on the nature (timelike/spacelike or null) of the geodesic. \(v_0\) is a constant of integration. Once the values of the conserved quantities are fixed, the only quantity to be calculated is the matrix-valued function H(u) in (2.8), which thus determines both how the isometries act, (2.9), and also the evolution of causal geodesics, (4.2). H(u) is in turn related to the Sturm–Liouville solution P in (3.2). In flat Minkowski space \(H(u)=u\,\mathrm {Id}\) yields free motion, \( \mathbf{x}(u)=(u-u_0)\,{\varvec{p}}+\mathbf {k},\, v(u)= (u-u_0)(-\frac{1}{2}{\vert {\varvec{p}}\vert }^2 +e)+ v_0. \)

Returning to the general metric (2.7), requiring that our particles be at rest before the gravitational wave arrives implies, by (4.1), \({\varvec{p}}=0\) for all profiles:

$$\begin{aligned} \mathbf{x}=\mathbf{x}_0 \equiv \mathbf {k}={\mathrm{const.}}, \quad v=(u-{u_0})e + v_0. \end{aligned}$$
(4.4)

With tongue-in-cheek, we call it “Carrollian”, since there is no (transverse) motion—the hallmark of “Carrollian” physics [13, 14, 18,19,20].Footnote 5

Remarkably, every geodesic is obtained from a simple one of the form (4.4) by a suitable symmetry transformation [3, 4, 17]. Equation (4.2) says indeed that any geodesic determines and is, conversely, determined by six constants of the motion. Then we note that the isometry group G acts on the constants of the motion \(\Phi =({\varvec{p}},\mathbf {k},e,v_0)\) according to [4, 17]

$$\begin{aligned} ({\varvec{p}},\mathbf {k},e,v_0) \rightarrow ({\varvec{p}}+\mathbf{b},\mathbf {k}+{\mathbf {c}},e, v_0+f-\mathbf{b}\cdot \mathbf {k}). \end{aligned}$$
(4.5)

This action leaves e in (4.3) invariant, however for any fixed value of e we can find an appropriate element of G which brings \(\Phi =({\varvec{p}},\mathbf {k}, e, v_0)\) to \(\Phi _0=({\varvec{p}}=0,\mathbf {k}=0, e, v_0=0)\). Conversely, any given set \(\Phi \) can be reached from \(\Phi _0\) by the action of an isometry. The geodesic with parameters \(\Phi _0\) is (4.4) with \(x_0=0\) and \(v_0=0\), for which the trajectory is simply \( \mathbf{x}(u)=0\,,\; v(u) = (u-{u_0})\,e. \) Conversely, the geodesic with parameters \(\Phi \) is obtained in turn by implementing the \(\Phi _0\rightarrow \Phi \) isometry as in (2.9), as illustrated on Fig. 3 of [17].

One can wonder how all this looks in B coordinates. The answer can be obtained by “exporting” the trajectories from BJR to B using (3.1).Footnote 6 Choosing \(\mathbf{X}_0=\mathbf{x}_0\) in the before zone,

$$\begin{aligned}&\mathbf{X}(U)= P(U)\,\mathbf{X}_0, \end{aligned}$$
(4.6a)
$$\begin{aligned}&V(U) = (U-{U}_0)e+v_0 - \dfrac{1}{4}\frac{d(\mathbf{X}^2)}{dU}(U) \end{aligned}$$
(4.6b)

which, for \(\mathbf{X}_0=0\) and \(v_0=0\), remains “Carrollian” in that \( \mathbf{X}(U)\!=\!0,\, V(U)\!= \!(U-{U_0})\,e. \)

5 Illustration: polarized sandwich waves

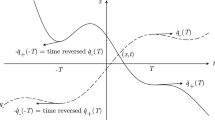
Let us indeed consider a circularly polarised oscillating sandwich wave with Gaussian envelope (2.2) , shown in Fig.1. The simple \({\varvec{p}}=0\) trajectory (4.4) describes the motion of a particle at rest in the before zone. BJR coordinates are valid between caustics, which appear where \(\det \big (P(u_1)\big )=0\); numerically, we found, in the neighborhood of \(u_0=0\), \(u_1= -\,2.80< u < u_2 = 2.74\); Brinkmann coordinates work for all U.

Then (4.6) can be plotted after solving the Sturm–Liouville eqn (3.2) numerically. Figure 2 shows, however, that even such simple trajectories become complicated-looking, with the exception of the one for \(\mathbf{X}_0=0\).

Fig. 1
figure 1

Polarized sandwich wave with Gaussian envelope as given in (2.2). The colors refer to the \({{\mathcal {A}_{+}}}\) and the \({\mathcal {A}_{\times }}\) polarisation components (color figure online)

Full size image
Fig. 2
figure 2

The images under the B \(\Leftrightarrow \) BJR map (4.6) of the simple trajectories (4.4) initially at rest for \(u_0<0\) at \(\mathbf{x}_0^1=\mathbf{X}_0^{(1)}=({1},{0})\) and at \(\mathbf{x}_0^{(2)}=\mathbf{X}_0^{(2)}=({0},{1})\), respectively, are, B coordinates, the two columns of the P matrix. The motion is complicated in the inside-zone but follows straight lines with constant velocity in the after-zone

Full size image

Having calculated (numerically) the matrix P, we can proceed to calculating \(a=P^T\!P\) and then H in (2.8), allowing us to plot finally how boosts are implemented in BJR coordinates in a neighborhood of the origin, \(\mathbf{x}\rightarrow \mathbf{x}+ \delta \mathbf{x},\, \delta \mathbf{x}= H(u)\,\mathbf{b}\), cf. (2.9), shown on Fig. 3. The implementation differs substantially from the Galilean one, \(\delta \mathbf{x}= u\mathbf{b}\).

Fig. 3
figure 3

In BJR coordinates boosts act according to (2.9). The implementation differs substantially from the Galilean one (dashed). We took here \(\mathbf{b}=(1,1)\)

Full size image

6 Conclusion

The Memory Effect boils down to solving the Sturm–Liouville equation (1.1)—a task which can, in general, be done only numerically.

Particles at rest in the before zone have vanishing momenta, implying that in BJR coordinates the trajectory is trivial : all those complicated-looking trajectories obtained before [8, 9, 11, 22] are in fact images of the trivial “Carrollian” ones in (4.4) resp. (4.6b) by a suitable broken-Carroll isometry [3, 4, 17] : all complications are hidden in the Sturm–Liouville equation (1.1). This can be viewed as the gravitational-wave generalization of the observation that any free non-relativistic motion is obtained from static equilibrium by a Galilei transformation. The “no motion” defect of Carrollian dynamics [13, 14, 18,19,20] is thus turned into an advantage.