1 Introduction

1.1 Alternate theories of gravity

A rekindled interest in alternate and higher dimensional theories of gravity has arisen in recent times. The reason for studying these new theories is the fact that conventional Einstein gravity has shortcomings. An example is the fact that the late time expansion of the universe is noted in observations, but isn’t a direct consequence of standard general relativity. One approach to modify general relativity is the introduction of nonlinear forms of the Riemann and Ricci tensor, and the Ricci scalar. The second order equations of motion resulting from linear forms is advantageous in four dimensions; however as shown by Lovelock [1, 2] it is possible to introduce a polynomial form of the Lagrangian which is of quadratic order. This form generates the Einstein–Gauss–Bonnet (EGB) action. Curvature terms which are quadratic in the spacetime appear as corrections to Einstein gravity, and this theory can be considered a consequence of low energy string theory [3, 4]. These higher order curvature terms will have no consequence in four-dimensional gravity unless some surface term is involved. An interesting point to note is that the equations of motion which result from the EGB action are still second order and quasilinear. If the higher order quantities are vanquished or absent, conventional Einstein gravity is regained [5]. Many results are reported in the literature on solutions in EGB gravity. The well known Boulware–Deser solution [6] was an early higher dimensional analogue of the vacuum Schwarszchild solution from general relativity. Bhawal [7] studied the higher dimensional geodesic motion of a Boulware–Deser black hole spacetime and performed comparisons with the higher dimensional Schwarszchild geometry. More recently Davis [8] derived the generalised Israel junction conditions on a membrane and Anabalon et al. [9] found a vacuum solution in EGB gravity with the Kerr-Schild ansatz in five-dimensional space. Recent investigations [10,11,12] have reported new solutions to the EGB field equations for a static spherically symmetric interior of a perfect fluid. The notion of gravitational collapse has also been looked upon. Maeda [13] studied the gravitational contraction of dust in EGB gravity, and efforts have been made to find asymptotically AdS black hole solutions in EGB gravity [14,15,16]. Ghosh et al. [17] studied the gravitational contraction of a spherical cloud of inhomogeneous dust in EGB theory, and Ghosh and Maharaj [18] presented null dust solutions in third order Lovelock gravity for a spherically symmetric string cloud background in arbitrary dimensions. Upon finding black hole solutions, an important task is to study the conserved charges such as the angular momentum; Peng [19] looked at quasi-local conserved charges of dyonic rotating black holes in both EGB gravity and four-dimensional conformal Weyl gravity. Dawood and Ghosh [20] characterised a large family of solutions to Einstein’s equations for a spherically symmetric type II fluid, and showed that the well known black hole solutions are a particular case of this larger family. Ghosh and Dawood [21] further generalised these results to higher dimensions. Ghosh and Dadhich [22] studied the gravitational collapse of a type II fluid in higher dimensions and noted that due to the presence of strange quark matter, as well as the higher dimensions, there was a shrinkage of the initial data space.

These solutions and that of [6] are the EGB generalisations of the vacuum solutions in general relativity. In this paper we will discuss another such generalisation: an EGB Vaidya-like solution.

1.2 The problem

Although the outside geometry as well as the matching conditions have been studied extensively in general relativity with the Vaidya metric [23], we are faced with the following ansatz in the EGB theory: How do we model a five-dimensional realistic, collapsing astrophysical star with a core containing a null fluid and a string fluid which matches to an intermediate radiating Boulware–Deser spacetime enclosed by the Boulware–Deser vacuum exterior? This question is vital for a better understanding of the thermodynamics, dynamics and gravitational collapse in realistic stars, in the context of EGB gravity. The class of spacetimes which forms a natural candidate for models of such interiors are the radiating Boulware–Deser spacetimes. The idea of a radiating Vaidya-like Boulware–Deser spacetime was first brought to light by Kobayashi [24]. The matter fields in these spacetimes will be analagous to those in the four-dimensional generalised Vaidya metrics with type I and type II matter distributions. A general type I matter field (whose energy momentum tensor has three spacelike and one timelike eigenvector), describes null matter, and a type II matter field (whose energy momentum tensor has double null eigenvectors) describes a string fluid and null radiation. A stellar interior with a type II distribution can be matched naturally to an external radiating zone described by a pure radiating Boulware–Deser spacetime, and then finally, this radiation zone can be matched smoothly to the conventional Boulware–Deser vacuum exterior.

1.3 This paper

In the five-dimensional Boulware–Deser spacetime the constant \(\tilde{M}\) can be related to the mass within a hypersurface. We show that it is possible for \(\tilde{M}\) to depend on the spacetime coordinates; the variable \(\tilde{M}\) is consistent with the field equations with a modified energy momentum tensor. Hence, with a type II fluid (consisting of a null fluid and a string source), the standard Boulware–Deser spacetime radiates. In this paper we generate solutions to the radiating interior Boulware–Deser spacetime with null matter and a string fluid for various thermodynamically realistic equations of state. It turns out that it is possible to directly integrate the resulting partial differential equations for linear, quadratic and polytropic equations of state. In recent times Dominguez and Gallo [25] found solutions to the EGB equations which represented dynamic black holes as well as EGB versions of the original Vaidya (dS/AdS) solution, the monopole and the Husain black hole [26]. Our solutions for the linear cases as well as the total solution set are the EGB analogues of those found in [26,27,28] respectively. We also further generalise our results in higher dimensions for pedagogical completeness.

This paper is organised as follows: In the next section, an outline of the theory of EGB gravity is presented as well as the general modified field equations. The Boulware–Deser spacetime is discussed in the following section followed by a detailed description of a radiating Boulware–Deser metric in Sect. 4. Here, the relevant definitions relating to the modified geometry of the spacetime are presented along with the EGB field equations and energy conditions for a physically reasonable model. In Sect. 5 a complete description of how to model an isolated, spherical five-dimensional astrophysical radiating star via the Boulware–Deser geometry is given. In the section following this, solutions to the EGB field equations for the gravitational mass are systematically presented for various realistic equations of state. In Sect. 7 the higher dimensional analogue of the Boulware–Deser metric is discussed and the generalised solutions for equations of state are tabulated.

2 Einstein–Gauss–Bonnet theory

The modified form of the Einstein–Hilbert action in five dimensions is

$$\begin{aligned} S=\frac{1}{16\pi }\int \sqrt{-g}\left[ (R-2\varLambda +\alpha L_{GB})\right] d^5x+S_{matter}, \end{aligned}$$
(1)

which is called the Gauss–Bonnet action where \(\alpha \) is the Einstein–Gauss–Bonnet (EGB) coupling constant, R is the five-dimensional Ricci scalar, \(L_{GB}\) is the Lovelock term and \(\varLambda \) is the cosmological constant. The above action has no direct affect in dimensions of four or less since the Lovelock term does not contribute to the field equations, but is generally nonzero in dimensions higher than four. The cogency of the Lovelock term lies in the fact that the equations of motion are second order and quasilinear despite the fact that the Langrangian is quadratic in the Riemann-curvature tensor, the Ricci tensor and the Ricci scalar.

The EGB field equations may be written as

$$\begin{aligned} \mathcal {G}_{ab}=\kappa T_{ab}, \end{aligned}$$
(2)

where

$$\begin{aligned} \mathcal {G}_{ab}=G_{ab}-\frac{\alpha }{2}H_{ab}. \end{aligned}$$
(3)

In the above, \(G_{ab}\) is the Einstein tensor, \(T_{ab}\) is the energy momentum tensor and \(H_{ab}\) is the Lanczos tensor defined as

$$\begin{aligned} H_{ab}= & {} g_{ab}L_{GB}-4RR_{ab}+8R_{ac}R^c{}_{{}b}\nonumber \\&+8R_{acbd}R^{cd}-4R_{acde}R_{b}{}^{{}cde}, \end{aligned}$$
(4)

where the Lovelock term has the form

$$\begin{aligned} L_{GB}=R^2+R_{abcd}R^{abcd}-4R_{cd}R^{cd}. \end{aligned}$$
(5)

In the limit where \(\alpha \rightarrow 0\), the above Lovelock term (and hence, the Lanczos term) will vanish and conventional Einstein gravity will be regained.

3 The Boulware–Deser spacetime

A static, spherically symmetric, exterior vacuum solution of the modified action (1) was first given by Boulware and Deser [6]. The form of the metric is given by

$$\begin{aligned} ds^2= & {} -f(\textsf {r})dt^2+\frac{1}{f(\textsf {r})}d\textsf {r}^2\nonumber \\&+\,\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(6)

where

$$\begin{aligned} f(\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16\tilde{M}\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$

In the line element (6), \(\tilde{M}\) is the gravitational constant mass of the five-dimensional hypersurface. For our purposes it will be prudent to express (6) in retarded coordinates. Utilising the transformation

$$\begin{aligned} v=t-\int \frac{d\textsf {r}}{f(\textsf {r})}, \end{aligned}$$

the Boulware–Deser metric (6) becomes

$$\begin{aligned} ds^2= & {} -f(\textsf {r})dv^2-2dvd\textsf {r}\nonumber \\&+\,\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(7)

where \((x^a)=(v,\textsf {r},\theta ,\phi ,\psi )\). As \(\tilde{M}\) is a constant mass, all the components of (3) vanish since the Boulware–Deser spacetime is vacuum.

4 An inhomogeneous radiating Boulware–Deser interior

If we consider a radiating inhomogeneous spacetime in EGB gravity then we can obtain a Vaidya-like metric by allowing the mass function to depend on both the retarded null coordinate and the radius of the star

$$\begin{aligned} \tilde{M}\longrightarrow M(v,\textsf {r}). \end{aligned}$$
(8)

Thus we will have

$$\begin{aligned} ds^2= & {} -f(v,\textsf {r})dv^2-2dvd\textsf {r}\nonumber \\&+\,\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(9)

where

$$\begin{aligned} f(v,\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M(v,\textsf {r})\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$
(10)

The nonvanishing components of the Einstein tensor \(G^a{}_{{}b}\) are

$$\begin{aligned} G^0{}_{{}0}= & {} G^1{}_{{}1}=-\frac{3}{2\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}}\nonumber \\&\times \left[ \frac{1}{\alpha \textsf {r}^2}+\frac{8M}{\textsf {r}^4}+\frac{2M_{\textsf {r}}}{\textsf {r}^3}-\textsf {r}^4\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}\right] ,\end{aligned}$$
(11a)
$$\begin{aligned} G^1{}_{{}0}= & {} \frac{3M_{v}}{\textsf {r}^3\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}}, \end{aligned}$$
(11b)
$$\begin{aligned} G^2{}_{{}2}= & {} G^3{}_{{}3}=G^4{}_{{}4}=-\frac{-1}{2\textsf {r}^8\alpha +32\alpha ^2\textsf {r}^4M}\nonumber \\&\times \left[ -3\textsf {r}^8\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}+2M_{\textsf {r}\textsf {r}}\alpha \textsf {r}^6+3\textsf {r}^8+32\alpha ^2\textsf {r}^2M_{\textsf {r}\textsf {r}} -16\alpha ^2\textsf {r}^2M_{\textsf {r}}^2 \right. \nonumber \\&\left. +72\alpha \textsf {r}^4M+128\alpha ^2\textsf {r}M_{\textsf {r}}+128\alpha ^2M^2-48\alpha \textsf {r}^4M\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}\right] , \end{aligned}$$
(11c)

where

The nonvanishing components of (4) become

$$\begin{aligned} H^0{}_{{}0}= & {} H^1{}_{{}1}=-\frac{3}{\alpha ^2\textsf {r}^3(\textsf {r}^4+16\alpha M)}\nonumber \\&\times \left[ \textsf {r}^7\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}+2\alpha \textsf {r}^4M_{\textsf {r}}\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}\right. \nonumber \\&\left. -\textsf {r}^7-2\alpha \textsf {r}^4M_{\textsf {r}}-32\alpha ^2MM_{\textsf {r}}+8\alpha \textsf {r}^3M\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}-16\alpha \textsf {r}^3M\right] ,\qquad \end{aligned}$$
(12a)
$$\begin{aligned} H^1{}_{{}0}= & {} \frac{6M_{v}\left[ \textsf {r}^4\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}-\textsf {r}^4-16\alpha M\right] }{\alpha \textsf {r}^3(\textsf {r}^4+16\alpha M)}, \end{aligned}$$
(12b)
$$\begin{aligned} H^2{}_{{}2}= & {} H^3{}_{{}3}=H^4{}_{{}4}=\frac{\left( 1+\frac{16\alpha M}{\textsf {r}^4}\right) ^{-\frac{1}{2}}}{\alpha ^2\textsf {r}^4(\textsf {r}^4+16\alpha M)}\nonumber \\&\times \left[ 2\alpha \textsf {r}^6M_{\textsf {r}\textsf {r}}\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}+3\textsf {r}^8\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}-2\alpha \textsf {r}^6M_{\textsf {r}\textsf {r}}-3\textsf {r}^8\right. \nonumber \\&+32\alpha ^2\textsf {r}^2MM_{\textsf {r}\textsf {r}}-32\alpha ^2\textsf {r}^2MM_{\textsf {r}\textsf {r}}+16\alpha ^2\textsf {r}^2M^2\nonumber \\&\left. -128\alpha ^2\textsf {r}M_{\textsf {r}}-128\alpha ^2M^2+48\alpha \textsf {r}^4M\sqrt{1+\frac{16\alpha M}{\textsf {r}^4}}-72\alpha \textsf {r}^4M\right] . \end{aligned}$$
(12c)

4.1 The EGB field equations

Using the above expressions (11) and (12), we can calculate the nonzero components of (3). It is remarkable to note that despite the complexity of the nonzero components of the Einstein and Lanczos tensors, their combinations yield rather simple expressions. These are given by

$$\begin{aligned} \mathcal {G}^0{}_{{}0}= & {} \mathcal {G}^1{}_{{}1}=-\frac{3}{r^3}M_{\textsf {r}}, \end{aligned}$$
(13a)
$$\begin{aligned} \mathcal {G}^1{}_{{}0}= & {} \frac{3}{\textsf {r}^3}M_{v}, \end{aligned}$$
(13b)
$$\begin{aligned} \mathcal {G}^2{}_{{}2}= & {} \mathcal {G}^3{}_{{}3}=\mathcal {G}^4{}_{{}4}=-\frac{1}{\textsf {r}^2}M_{\textsf {r}\textsf {r}}. \end{aligned}$$
(13c)

The modified curvature components (13) are generated by an appropriate matter field. Comparing (13) with the field equations (2) gives rise to an energy momentum tensor of the form

$$\begin{aligned} T_{ab}=\mu l_{a}l_{b}+(\tilde{\rho }+P)(l_{a}n_{b}+l_{b}n_{a})+Pg_{ab}, \end{aligned}$$
(14)

where

$$\begin{aligned} l_{a}= & {} \delta _{a}^0,\\ n_{a}= & {} \frac{1}{2}\left[ 1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M\alpha }{\textsf {r}^4}}\right) \right] \delta _{a}^0+\delta _{a}^1,\\ \end{aligned}$$

with \(l_{c}l^c=n_{c}n^c=0\) and \(l_{c}n^c=-1\). The null vector \(l^a\) is a double null eigenvector of the energy momentum tensor (14). Using the form of the energy momentum tensor (14) with (13), we acquire the EGB field equations \(\mathcal {G}^a{}_{{}b}=\kappa T^a{}_{{}b}\) in the form

$$\begin{aligned} \mu= & {} -\frac{3}{\kappa \textsf {r}^3}M_{v},\end{aligned}$$
(15a)
$$\begin{aligned} \tilde{\rho }= & {} \frac{3}{\kappa \textsf {r}^3}M_{\textsf {r}}, \end{aligned}$$
(15b)
$$\begin{aligned} P= & {} -\frac{1}{\kappa \textsf {r}^2}M_{\textsf {r}\textsf {r}}. \end{aligned}$$
(15c)

As \(M_{v}\ne 0\), in general it is clear that the Boulware–Deser class of spacetimes radiates. When \(\tilde{\rho }=P=0\), the above expressions reduce to the single solution obtained for the radiating Boulware–Deser metric when \(M=M(v)\). Furthermore when \(\mu =\tilde{\rho }=P=0\), we regain the vacuum case with constant mass.

The energy conditions for this kind of fluid are

  1. 1.

    The weak and strong energy conditions:

    (16)
  2. 2.

    The dominant energy condition:

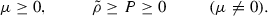    (17)

In the case when \(M=M(v)\) the above energy conditions all reduce to \(\mu \ge 0\), and if \(M=M(\textsf {r})\), then \(\mu =0\) and the matter field becomes a type I fluid.

Finally, we are in the position to state the following theorem:

Theorem 1

Consider the five-dimensional spacetime

$$\begin{aligned} ds^2=-\left[ 1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M\alpha }{\textsf {r}^4}}\right) \right] dv^2-2dvd\textsf {r}\\ +\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$

from a regular epoch, where \(M=M(v,\textsf {r})\) (v is the null retarded time coordinate and \(\textsf {r}\) is the radius) is differentiable in the entire spacetime, and obeys all physically reasonable energy conditions. This spacetime is then consistent with an energy momentum tensor which is a unique combination of the type I and type II matter fields. This geometry represents a solution to the EGB field equations with a superposition of null radiation and a string fluid. In the relevant limit, we regain the radiating case (\(M=M(v)\)) and the Boulware–Deser spacetime (\(M=\tilde{M}=\) const.) when \(\alpha \ne 0\), and Einstein gravity when \(\alpha =0\).

5 The model for an isolated, radiating and dynamic star in five dimensions

Any spherically symmetric five-dimensional astrophysical star is a combination of three distinct concentric zones: the innermost zone is the stellar interior where there are two component matter sources, namely null fluid matter together with radiation. The middle zone is a purely radiative zone while the outermost zone is the vacuum Boulware–Deser exterior (6) that extends approximately to a radius of one light year (for solar mass stars) beyond which galactic dynamics will take over. In this section we briefly outline how to model all three of these zones under a combined framework using a generalised Boulware–Deser class of metric.

5.1 Stellar interior: \(M=M(v,\textsf {r})\)

As described earlier, the best possible candidate for the spacetime of a stellar interior with the mass parameter (8) is

$$\begin{aligned} ds^2= & {} -f(v,\textsf {r})dv^2-2dvd\textsf {r}\nonumber \\&+\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(18)

where

$$\begin{aligned} f(v,\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M(v,\textsf {r})\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$

The mass function M which depends on the coordinates v and \(\textsf {r}\) can be uniquely obtained via the Einstein field equations with the two component matter sources. Let \(M(v,\textsf {r})\) be one such solution for a given combination of fluid and radiation fields. This solution then completely describes the solution of the interior of the star, up to a boundary surface given by \(\textsf {r}=\textsf {r}_b\). Beyond this boundary we enter a pure radiation zone.

5.2 Radiation zone: \(M=M(v)\)

In this zone the matter field is a single component null matter field and the spacetime is well described by the radiating Boulware–Deser metric

$$\begin{aligned} ds^2= & {} -f_{1}(v,\textsf {r})dv^2-2dvd\textsf {r}\nonumber \\&+\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(19)

with

$$\begin{aligned} f_{1}(v,\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16M_{1}(v)\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$

We can naturally relate the Boulware–Deser mass function \(M_1(v)\) in the radiation zone to the generalised Boulware–Deser mass function in the stellar interior in the following way

$$\begin{aligned} M_1(v)=M(v,\textsf {r}_{b}), \end{aligned}$$
(20)

so that M is a function of the retarded coordinate v. This radiation zone continues until some retarded null coordinate value \(v=V_{0}\), beyond which the spacetime is the conventional Boulware–Deser vacuum (as dictated by Birkhoff’s theorem).

5.3 Boulware–Deser exterior: \(M=\tilde{M}\)

This vacuum region is described by the exterior static subset of the completely extended Boulware–Deser manifold, and the metric is given by

$$\begin{aligned} ds^2= & {} -\tilde{f}(\textsf {r})dv^2-2dvd\textsf {r}\nonumber \\&+\textsf {r}^2(d\theta ^2+\sin ^2\theta d\phi ^2+\sin ^2\theta \sin ^2\phi d\psi ^2), \end{aligned}$$
(21)

with

$$\begin{aligned} \tilde{f}(\textsf {r})=1+\frac{\textsf {r}^2}{4\alpha }\left( 1-\sqrt{1+\frac{16\tilde{M}\alpha }{\textsf {r}^4}}\right) . \end{aligned}$$

Here the static mass \(\tilde{M}\) is related to the radiating Boulware–Deser mass \(M_1(v)\) by

$$\begin{aligned} \tilde{M}=M_1(V_{0}), \end{aligned}$$
(22)

which is constant.

5.4 Matching conditions at the boundary surfaces: complete mass function

We note here that the spacetime is divided into three distinct regions for our above mentioned stellar model: the interior region, the radiation zone and the vacuum Boulware–Deser exterior region. The first boundary surface between the inner and the intermediate zone, given by \(\textsf {r}=\textsf {r}_{b}\), is a timelike boundary, whereas the second boundary surface given by \(v=V_0\) is a null boundary. The important point that all the three zones are described by the same class of metric makes the matching conditions between boundaries extremely transparent. To match the first fundamental form all we need is the mass function to be continuous across these boundaries. Hence the complete \(C^2\) mass function for an isolated stellar model can be given in the following form:

$$\begin{aligned} M(v,\textsf {r})={\left\{ \begin{array}{ll} M(v,\textsf {r}) &{} \textsf {r}\le \textsf {r}_b\;, v\le V_{0} \\ M_1(v)\equiv M(v,\textsf {r}_b) &{} \textsf {r}> \textsf {r}_{b}\;, v\le V_{0}\\ \tilde{M}\equiv M_1(V_{0})\equiv M(V_{0},\textsf {r}_{b}) &{} \textsf {r}> \textsf {r}_b\;, v> V_{0} \end{array}\right. } \end{aligned}$$
(23)

We can easily check that this mass function is a solution to the EGB field equations in all three zones mentioned above, and hence it completely describes the spacetime of an isolated collapsing star. To match the second fundamental form, we need the partial derivatives of the mass functions across the boundaries to be continuous. These conditions are given by

$$\begin{aligned} \frac{\partial }{\partial v}M(v,\textsf {r}_{b})= & {} \frac{\partial }{\partial v}M_1(v), \end{aligned}$$
(24a)
$$\begin{aligned} \frac{\partial }{\partial \textsf {r}}M(v,\textsf {r})\bigg |_{\textsf {r}=\textsf {r}_{b}}= & {} 0, \end{aligned}$$
(24b)
$$\begin{aligned} \frac{\partial }{\partial v}M_1(v)\bigg |_{v=V_0}= & {} 0, \end{aligned}$$
(24c)

where \(\textsf {r}=\textsf {r}_{b}\) is the timelike boundary [from equating (7)–(19)] and \(v=V_{0}\) is the null boundary [from equating (19)–(21)]. These boundaries serve as the matching surfaces for the three concentric regions which can be seen in Fig.  1.

Fig. 1
figure 1

Depiction of a five-dimensional spacetime divided into the three distinct regions

Full size image

It is therefore necessary to find physically relevant mass functions, with the structure of (23), to model a dynamical radiating star which is isolated. We achieve this by imposing specific equations of state.

6 Solutions with equations of state

In this section, we will consider various equations of state to solve the system (15).

6.1 Case I(a): \(P=k\tilde{\rho }\)

If we assume a linear equation of state \(P=k\tilde{\rho }\) in the field equations where k is a constant, we then arrive at

$$\begin{aligned} \textsf {r}^2M_{\textsf {r}\textsf {r}}+3k\textsf {r}M_{\textsf {r}}=0, \end{aligned}$$
(25)

which is a second order linear partial differential equation. Since the derivatives occur in one variable, we can integrate it as an ordinary differential equation via reduction of order. There are two solutions. For the case when \(k=\frac{1}{3}\), the solution is given by

$$\begin{aligned} M(v,\textsf {r})=c_{1}(v)\ln (\textsf {r})+c_{2}(v), \end{aligned}$$

where \(c_{1}(v)\) and \(c_{2}(v)\) are functions of integration. For \(k\ne \frac{1}{3}\), the second solution is

$$\begin{aligned} M(v,\textsf {r})=c_{1}(v)\frac{\textsf {r}^{1-3k}}{1-3k}+c_{2}(v). \end{aligned}$$
(26)

6.2 Case I(b): \(P=k\tilde{\rho }+k_{2}\)

Assuming \(P=k\tilde{\rho }+k_{2}\) in the field equations (15) yields

$$\begin{aligned} M_{\textsf {r}\textsf {r}}+\frac{3k}{\textsf {r}}M_{\textsf {r}}+\kappa k_{2}\textsf {r}^2=0, \end{aligned}$$
(27)

which takes the form of a Cauchy–Euler equation. If we let \(y(v,\textsf {r})=M_{\textsf {r}}\) we get the first order linear equation

$$\begin{aligned} y'+\frac{3k}{\textsf {r}}y=-\kappa k_{2}\textsf {r}^2, \end{aligned}$$
(28)

which can be easily integrated to give

$$\begin{aligned} y=-\kappa k_{2}\frac{\textsf {r}^3}{3k+1}+\frac{c_{1}(v)}{\textsf {r}^{3k}}. \end{aligned}$$
(29)

Again, two cases arise. When \(k=\frac{1}{3}\) the first solution for \(M(v,\textsf {r})\) is given by

$$\begin{aligned} M(v,\textsf {r})= c_{1}(v)\ln (\textsf {r})+c_{2}(v)-\frac{\kappa k_{2}\textsf {r}^4}{16}. \end{aligned}$$

The second solution for the mass with \(k\ne \frac{1}{3}\) is given by

$$\begin{aligned} M(v,\textsf {r})=c_{2}(v)+c_{1}(v)\frac{\textsf {r}^{1-3k}}{1-3k}-\frac{\kappa k_{2}}{4(3k+1)}\textsf {r}^4, \end{aligned}$$
(30)

which contains (26) as well as several of the seminal others contained in [25]. It should be noted that this solution also contains the EGB analogues of those found in [26, 27]. These are summarised in Table 1.

Table 1 Solutions contained within the system (30)
Full size table

6.3 Case II(a): \(P=k\tilde{\rho }^2\)

If we assume a quadratic equation of state \(P=k\tilde{\rho }^2\), in the field equations (15), we have

$$\begin{aligned} \textsf {r}^5M_{\textsf {r}\textsf {r}}+\frac{9k}{\kappa }\textsf {r}M_{\textsf {r}}^2=0, \end{aligned}$$
(31)

which is a second order nonlinear equation. A reduction of the order yields the following

$$\begin{aligned} y'+\frac{\eta }{\textsf {r}^4}y^2=0, \end{aligned}$$
(32)

which is a first order nonlinear equation with \(\eta =9k/\kappa \). Integration yields

$$\begin{aligned} y=\frac{-1}{\frac{\eta }{3\textsf {r}^3}+c_{1}(v)}. \end{aligned}$$
(33)

Therefore the mass can be expressed as

$$\begin{aligned} M(v,\textsf {r})=-\int \left( \frac{1}{\frac{\eta }{3\textsf {r}^3}+c_{1}(v)}\right) d\textsf {r}+c_{2}(v). \end{aligned}$$
(34)

The integral on the right hand side of the above expression admits two solutions. When the constant \(c_{1}=0\) the solution is

$$\begin{aligned} M(v,\textsf {r})=-\frac{3}{4\eta }\textsf {r}^4+c_{2}(v). \end{aligned}$$
(35)

When \(c_{1}\ne 0\) the above integral can be evaluated via partial fraction decomposition. The final expression for the mass M is given by

$$\begin{aligned} M(v,\textsf {r})= & {} c_{2}(v)-\frac{\textsf {r}}{3c_{1}(v)}+\left( \frac{\eta }{3c_{1}(v)}\right) ^{1/3}\left( \frac{1}{3\eta }\right) \nonumber \\&\times \left[ \frac{1}{2}\ln \left( \frac{\left( \textsf {r}+\left( \frac{\eta }{3c_{1}(v)}\right) ^{1/3}\right) ^2}{\textsf {r}^2-\left( \frac{\eta }{3c_{1}(v)}\right) ^{1/3}+\left( \frac{\eta }{3c_{1}(v)}\right) ^{2/3}}\right) \right. \nonumber \\&\left. + \sqrt{3}\arctan \left( \frac{2\textsf {r}-\left( \frac{\eta }{3c_{1}(v)}\right) ^{1/3}}{\sqrt{3}\left( \frac{\eta }{3c_{1}(v)}\right) ^{1/3}}\right) \right] . \end{aligned}$$
(36)

As far as we are aware, this solution is not found anywhere in the previous literature.

6.4 Case II(b): \(P=k\tilde{\rho }^2+k_{2}\tilde{\rho }+k_{3}\)

Imposing the equation of state \(P=k\tilde{\rho }^2+k_{2}\tilde{\rho }+k_{3}\) in the field equations (15) yields

$$\begin{aligned} M_{\textsf {r}\textsf {r}}+\frac{9k}{\kappa \textsf {r}^4}M_{\textsf {r}}^2+\frac{3k_{2}}{\textsf {r}}M_{\textsf {r}}+k_{3}\kappa \textsf {r}=0. \end{aligned}$$
(37)

Reducing the order of the above equation yields

$$\begin{aligned} y'+\frac{3k_{2}}{\textsf {r}}y+k_{3}\kappa \textsf {r}=-\frac{\eta }{\textsf {r}^4}y^2, \end{aligned}$$
(38)

with \(\eta =9k/\kappa \), which is a Riccati differential equation. Integration of the above equation gives

$$\begin{aligned} y= & {} -\frac{\textsf {r}^3}{2\eta }\tan \left( \frac{1}{2}\sqrt{\varepsilon }(\ln (\textsf {r})-c_{1}(v))\right) \nonumber \\&\times \left( -\frac{\textsf {r}^3}{2\eta }(\sqrt{\varepsilon }+3+3k_{2})\right) . \end{aligned}$$
(39)

In the above expression, we have the following: \(\varepsilon =4\beta \eta -9k_{2}^2-109-18k_{2}\) and \(\beta =\kappa k_{3}\). Hence, the expression for the mass is given by

$$\begin{aligned} M(v,\textsf {r})=-\int \left[ \frac{\textsf {r}^3}{2\eta }\tan \left( \frac{1}{2}\sqrt{\varepsilon }(\ln (\textsf {r})-c_{1}(v))\right) \right. \nonumber \\ \left. \times \left( \frac{\textsf {r}^3}{2\eta }(\sqrt{\varepsilon }+3+3k_{2})\right) \right] d\textsf {r}+c_{2}(v). \end{aligned}$$
(40)

It should be noted that when \(k_{2}=k_{3}=0\) in the above solution (40), we regain Case II(a), which is to be expected.

6.5 Case III: \(P=k\tilde{\rho }^{\gamma }\)

If we assume the equation of state \(P=k\tilde{\rho }^{\gamma }\), where \(\gamma \) is a constant, we then have

$$\begin{aligned} M_{\textsf {r}\textsf {r}}+k\kappa \left( \frac{3}{\kappa }\right) ^{\gamma }\textsf {r}^{2-3\gamma }M_{\textsf {r}}^{\gamma }=0. \end{aligned}$$
(41)

Reducing the order of the above equation yields

$$\begin{aligned} y'+k\kappa \left( \frac{3}{\kappa }\right) ^{\gamma }\textsf {r}^{2-3\gamma }y^{\gamma }=0, \end{aligned}$$

which is a separable equation. Its general solution is given by

$$\begin{aligned} y=\left[ (\gamma -1)\left( k\kappa \left( \frac{3}{\kappa }\right) ^{\gamma }\frac{\textsf {r}^{3-3\gamma }}{3-3\gamma }+c_{1}(v)\right) \right] ^{\frac{1}{1-\gamma }}. \end{aligned}$$
(42)

Therefore we can express the mass M as

$$\begin{aligned} M(v,\textsf {r})= & {} c_{2}(v)+\int \left[ (\gamma -1)\left( k\kappa \left( \frac{3}{\kappa }\right) ^{\gamma }\right. \right. \nonumber \\&\times \left. \left. \frac{\textsf {r}^{3-3\gamma }}{3-3\gamma }+c_{1}(v)\right) \right] ^{\frac{1}{1-\gamma }}d\textsf {r}. \end{aligned}$$
(43)

It should be noted that in the works of [22, 25, 27], it appears that solutions only for a linear and/or generalised linear equation of state are provided in conventional general relativity in the Vaidya spacetime. Brassel et al. [28] further found solutions for both linear cases as well as quadratic and generalised quadratic equations of state. It should be noted that Husain [26] found a general integral quadrature similar to ours above for the polytropic equation of state in the generalised Vaidya spacetime, however ours differs in the fact that we are dealing with the EGB theory of gravity. In the case of [27], a series solution approach was used to obtain solutions, whereas in our case, a direct integration of the EGB field equations was undertaken. Also we have not assumed separability of the mass functions. This, in a sense, makes our solutions (which are the EGB analogues of those found in [27]) more general.

7 Higher dimensional Boulware–Deser spacetime

Higher dimensional Boulware–Deser spacetimes have been studied in various physical scenarios. Bhawal [7] studied the geodesic motion inside a Boulware–Deser black hole in arbitrary dimensions and Dominguez and Gallo [25] found solutions of radiating black holes for certain equations of state. Ghosh and Dadhich [22] also considered type II black hole solutions and gravitational collapse with a quark equation of state in higher dimensions. Dadhich and Pons [29] found static black hole solutions in both Einstein and EGB gravity in higher dimensions by considering the topology of the product of two spheres \(S^n\times S^n\). This topology comprised of black rings and branes and new solutions were obtained, also, for constant curvature. Gravitational collapse as well as other features may be affected by additional dimensions.

The N-dimensional Boulware–Deser metric is given by

$$\begin{aligned} ds^2=-f(\textsf {r})dv^2-2dvd\textsf {r}+\textsf {r}^2d\varOmega ^2_{n-2}, \end{aligned}$$
(44)

with

$$\begin{aligned} d\varOmega _{N-2}^2=\sum _{i=1}^{N-2}\left[ \prod _{j=1}^{i-1}\sin ^2(\theta ^j)\right] (d\theta ^i)^2, \end{aligned}$$

and where

$$\begin{aligned} f(\textsf {r})=1+\frac{\textsf {r}^2}{2\hat{\alpha }}\left( 1-\sqrt{\frac{8\hat{\alpha }}{N-3}\left( \frac{2M}{\textsf {r}^{N-1}}\right) }\right) . \end{aligned}$$

In the above \(\hat{\alpha }=\alpha (N-3)(N-4)\). If we consider an inhomogeneous radiating metric with

$$\begin{aligned} M\longrightarrow M(v,\textsf {r}), \end{aligned}$$

the nonzero components of (3) are given by

$$\begin{aligned} \mathcal {G}^0{}_{{}0}= & {} \mathcal {G}^1{}_{{}1}=-\frac{(N-2)M_{\textsf {r}}}{\textsf {r}^{(N-2)}} , \end{aligned}$$
(45a)
$$\begin{aligned} \mathcal {G}^1{}_{{}0}= & {} \frac{(N-2)M_{v}}{\textsf {r}^{(N-2)}}, \end{aligned}$$
(45b)
$$\begin{aligned} \mathcal {G}^2{}_{{}2}= & {} \mathcal {G}^3{}_{{}3}=\cdots =\mathcal {G}^{\theta (N-2)}{}_{{}\theta {(N-2)}}=-\frac{M_{\textsf {r}\textsf {r}}}{\textsf {r}^{(N-3)}}. \end{aligned}$$
(45c)

The EGB field equations are thus

$$\begin{aligned} \mu= & {} \frac{(N-2)M_{v}}{\kappa \textsf {r}^{N-2}}, \end{aligned}$$
(46a)
$$\begin{aligned} \tilde{\rho }= & {} \frac{(N-2)M_{\textsf {r}}}{\kappa \textsf {r}^{N-2}}, \end{aligned}$$
(46b)
$$\begin{aligned} P= & {} -\frac{M_{\textsf {r}\textsf {r}}}{\kappa \textsf {r}^{N-3}}. \end{aligned}$$
(46c)

As in the previous section, we find solutions to the EGB field equations and these are presented in Table 2. We do not give the details of the integrations as they are similar to the five-dimensional case. It is also important to note that Theorem 1 can be extended to hold in higher dimensions. We state this as follows:

Theorem 2

Consider an N-dimensional spacetime given by

$$\begin{aligned} ds^2=-f(\textsf {r})dv^2-2dvd\textsf {r}+\textsf {r}^2d\varOmega ^2_{n-2}, \end{aligned}$$

with

Table 2 Equations of state and the higher dimensional gravitational mass
Full size table
$$\begin{aligned} d\varOmega _{N-2}^2=\sum _{i=1}^{N-2}\left[ \prod _{j=1}^{i-1}\sin ^2(\theta ^j)\right] (d\theta ^i)^2, \end{aligned}$$

and

$$\begin{aligned} f(\textsf {r})=1+\frac{\textsf {r}^2}{2\hat{\alpha }}\left( 1-\sqrt{\frac{8\hat{\alpha }}{N-3}\left( \frac{2M}{\textsf {r}^{N-1}}\right) }\right) , \end{aligned}$$

where \(\hat{\alpha }=\alpha (N-3)(N-4)\) and \(M=M(v,\textsf {r})\), which obeys all physically reasonable energy conditions and is differentiable in the entire spacetime. This spacetime is then consistent with an energy momentum tensor which is a unique combination of the type I and type II matter fields, and represents a solution to the EGB field equations with a superposition of null radiation and a string fluid. Again, in the relevant limit, we regain the radiating case (\(M=M(v)\)) and the Boulware–Deser spacetime (\(M=\tilde{M}=\) const.) when \(\alpha \ne 0\), and the Einstein gravity when \(\alpha =0\).

8 Discussion

We have established the principal result that the standard Boulware–Deser spacetime can be made to radiate. In this paper we considered a five-dimensional spherically symmetric radiating star in Einstein–Gauss–Bonnet (EGB) gravity. We noted that any astrophysical star is a combination of three concentric zones: the innermost two-component zone of matter which can be modeled by an inhomogeneous radiating Boulware–Deser metric, the radiation zone in the middle and the outermost zone which is the Boulware–Deser vacuum exterior. A large family of solutions to the EGB field equations were presented for various realistic equations of state. It was shown that solutions were possible via a direct integration of second order differential equations. Many of these solutions cannot be found by the approach used by Wang and Wu [27] in conventional Einstein gravity; they assumed a restrictive series form of the mass function. Other mass functions have been shown to exist in five and higher dimensions which are physically reasonable. It is easy to show the existence of a dynamical star which is radiating, by matching the mass function (23) at the two boundaries. We illustrate this notion with the generalised linear equation of state

$$\begin{aligned} P=k\tilde{\rho }+k_{2}. \end{aligned}$$

At the first interface \(\textsf {r}=\textsf {r}_{b}\), between the two-component region and the null Boulware–Deser zone, the mass function is written as

$$\begin{aligned} M_{1}(v)=c_{2}(v)+c_{1}(v)\frac{\textsf {r}_{b}^{1-3k}}{1-3k}-\frac{\kappa k_{2}}{4(3k+1)}\textsf {r}_{b}^4. \end{aligned}$$
(47)

At the second interface, between this null zone and the vacuum exterior region, the mass function is

$$\begin{aligned} \tilde{M}=c_{2}(V_{0})+c_{1}(V_{0})\frac{\textsf {r}_{b}^{1-3k}}{1-3k}-\frac{\kappa k_{2}}{4(3k+1)}\textsf {r}_{b}^4. \end{aligned}$$
(48)

It is clear that the forms (47) and (48) are always possible due to the freedom permitted by the integration functions \(c_{1}(v)\) and \(c_{2}(v)\). A comparison with earlier results was undertaken and we showed that our solutions generalise earlier results in EGB gravity, including the EGB analogue of Husain’s solution [26]. We then generalised our results to higher dimensions.

An important point to note is the nonlinear nature of gravity, and even more specifically, modified gravity. Despite the fact that the energy momentum tensor can be written as a combination of radiation, matter and modified curvature parts, these quantities intertwine in the metric in such a way as to give physically interesting and reasonable solutions that can be used to model a dynamic star in dimensions five or higher. If the radiation part is absent, for example, then the EGB field equations force the matter that remains to obey an equation of state \(\tilde{\rho }+p_{\textsf {r}}=0\) (\(p_{\textsf {r}}\) is the radial pressure), which is that of an AdS-like space, and is not appropriate for stellar modeling. It is also important to note that if the Gauss-Bonnet connection term tends to zero \((\alpha \rightarrow 0)\), Einstein gravity is regained.

The work presented in this paper can be enhanced by the natural idea of gravitational collapse; whether or not there are special classes of Boulware–Deser mass functions which have an end state of collapse which is regular or singular. This will be a future endeavour.