1 Introduction

Black hole thermodynamics (BHT) is receiving more and more attentions in recent times. The path breaking findings of Hawking and Bekenstein [4, 5, 9] made in 1970s helped us to think that black holes are not truly black but are thermal objects emitting radiations. The main reason for the interest shown in BHT is that it unites quantum theory, gravitation and thermodynamics and it may open a way to quantum formulation of gravity. The normal BHT is evolved by considering the black hole mass as one of the thermodynamic potentials and assuming the area law straightforwardly. We have usual thermodynamic expressions to derive the quantities like temperature, entropy, heat capacity etc. In the thermodynamic studies, heat capacity is quite important because it can tell upon the thermodynamic stability of systems. For example, we could easily find the heat capacity of Schwarzschild black hole where one can see that it is negative and hence we may conclude that Schwarzschild black hole is thermodynamically unstable. In a similar fashion we can extend this stability analysis to other black holes and we could see that certain black holes show both positive and negative heat capacities. The transition is through an infinite discontinuity in the heat capacity. Such a phase transition is called a second order thermodynamic phase transition in BHT.

While closely looking at the normal thermodynamics of black holes, in many cases we could not identify the exact reasons for the abnormalities of energy (mass), temperature and heat capacity shown by the system. During the last few decades many attempts have been made to introduce different geometric concepts into ordinary thermodynamics. Hermann [10] formulated the concept of thermodynamic phase space as a differential manifold with a natural contact structure. In the thermodynamic phase space there exists a special subspace of thermodynamic equilibrium states.

In 1975 Weinhold [26] introduced an alternative geometric method in which a metric is introduced in the space of equilibrium states of thermodynamic systems. There he used the idea of conformal mapping from the Riemannian space to thermodynamic space, in which the new metric could be identified in terms of the thermodynamic potentials. Weinhold metric is given by

$$\begin{aligned} g^{W}_{ij}=\partial _i \partial _j U(S,N^r), \end{aligned}$$
(1)

where \(S\) is the entropy, \(U\) is the internal energy and \(N^r\) denotes other extensive variables of the system. There are systems which Weinhold metric gives correct explanation. In an attempt to formulate the concept of thermodynamic length, in 1979 Ruppeiner [21] introduced another metric which is conformaly equivalent to Weinhold’s metric. The Ruppeiner metric (which is the minus signed Hessian in entropy representation) is given by

$$\begin{aligned} g^{R}_{ij}=-\partial _i \partial _j S(M,N^r). \end{aligned}$$
(2)

The Ruppiner geometry is conformaly related to the Weinhold geometry by [16, 23]

$$\begin{aligned} ds_{R}^{2}=\frac{1}{T} ds^{2}_{W} \end{aligned}$$
(3)

where \(T\) is the temperature of the system under consideration. Since the proposal of Weinhold, a number of investigations have been done to analyze the thermodynamic geometry of various thermodynamic systems. The Weinhold and Ruppeiner geometries have also been used for several black holes to find out the thermodynamic abnormalities [1–3, 6, 8, 11, 12, 14, 15, 17, 22, 24, 25].

Geometrothermodynamics (GTD) [18–20] is the latest attempt in this direction. In order to describe a thermodynamic system with \(n\) degrees of freedom, we consider in GTD, a thermodynamic phase space which is defined mathematically as a Riemannian contact manifold\((\mathcal {T} , \varTheta , G)\), where \(\mathcal {T}\) is a \(2n + 1\) dimensional manifold, \(\varTheta \) defines a contact structure on \(\mathcal {T}\) and \(G\) is a Legendre invariant metric on \(\mathcal {T}\). The pair \(( \mathcal {T}, \varTheta )\) is called a contact manifold [10] only if \(\mathcal {T}\) is differentiable and \(\varTheta \) satisfies the condition \(\varTheta \wedge (d \varTheta )^{n} \ne 0\); which actually preserves the essential Legendre invariance while making the conformal transformations. The space of equilibrium states is an \(n\) dimensional manifold \((\mathcal {E}, g)\), where \(\mathcal {E} \subset \mathcal {T}\) is defined by a smooth mapping \(\phi : \mathcal {E} \rightarrow \mathcal {T}\) such that the pullback \(\phi ^* (\varTheta ) = 0\), and a Riemannian structure \(g\) is induced naturally in \(\mathcal {E}\) by means of \(g = \phi ^{(G)} \). It is then expected in GTD that the physical properties of a thermodynamic system in a state of equilibrium can be described in terms of the geometric properties of the corresponding space of equilibrium states \(\mathcal {E}\). The smooth mapping can be read in terms of coordinates as, \(\phi :(E^{a}) \rightarrow (\varPhi , E^{a} , I^{a} )\) with \(\varPhi \) representing the thermodynamic potential, \(E^{a}\) and \(I^{a}\) representing the extensive and intensive thermodynamic variables respectively if the condition \(\phi ^* (\varTheta ) = 0\) is satisfied, i.e.,

$$\begin{aligned} d\varPhi = \delta _{ab}I^{a}dE^{b}\ , \quad \frac{\partial \varPhi }{\partial E^{a}}=\delta _{ab}I^{b}. \end{aligned}$$
(4)

The first of these equations corresponds to the first law of thermodynamics, whereas the second one is usually known as the condition for thermodynamic equilibrium [7].

Legendre invariance guarantees that the geometric properties of \(G\) do not depend on the thermodynamic potential used in its construction. Hernavo Quevedo [19] introduced the idea and constructed a general form for the Legendre invariant metric. The general choice of GTD metric is as follows

$$\begin{aligned} g=\phi ^*(G)= \left( E^{c}\frac{\partial {\varPhi }}{\partial {E^{c}}}\right) \left( \eta _{ab}\delta ^{bc}\frac{\partial ^{2}\varPhi }{\partial {E^{c}}\partial {E^{d}}} dE^a dE^d \right) . \end{aligned}$$
(5)

The thermodynamic geometry of a black hole is still a most fascinating subject and there are many unresolved issues in BHT. Using this we could solve a number of issues related to the abnormal behaviour of mass, temperature and heat capacity. The metric is built up from a Legendre invariant thermodynamic potential and from its first and second order partial derivatives with respect to the extensive variables. The earlier studies show that the thermodynamic stability of systems depends on the potential we have chosen. This contradiction has been removed by using new Legendre invariant metric introduced in the GTD. In this paper we describe the phase transition in terms of curvature singularities.

The main purpose of the present work is to show that the thermodynamic geometric methods can be used to explain the thermodynamics of RNdS black hole and MTZ black hole, in both cases we are taking the cosmological constant as an extensive variable. The organization of the manuscript is as follows, in Sect. 2 we study the usual thermodynamics of RNdS black hole. We analyze the thermodynamic geometry of RNdS as well. The extremal case of RNdS or the MTZ black hole has been studied in Sect. 3 followed by its thermodynamic geometry. Section 4 is devoted to conclusion and discussions.

2 RN de Sitter Black hole

2.1 Thermodynamics

The Reissner-Nordström-de Sitter solution describes a static, spherically symmetric black hole carrying mass \(M\), charge \(Q\) and a non vanishing cosmological constant \(\Lambda \).

The metric of the RNdS black hole is written as

$$\begin{aligned} ds^{2}=f(r)dt^{2}-f(r)^{-1}dr^{2}-r^{2}\left( d\Omega ^{2}\right) , \end{aligned}$$
(6)

where \(f(r)\) is equal to

$$\begin{aligned} f(r)= 1-\frac{2M}{r}+ \frac{Q^2}{r^2}-\frac{\Lambda r^2}{3}, \end{aligned}$$
(7)

here we could find the mass of the black hole \(M\), in terms of its entropy \(S\), charge \(Q\) and the radius of curvature of the de Sitter space \(\alpha \), where \(\alpha \) is connected to the cosmological constant \(\Lambda \) through the relation

$$\begin{aligned} \Lambda = \frac{(N-1)(N-2)}{2 \alpha ^2}, \end{aligned}$$
(8)

where \(N\) is the dimension of the space time. Using the relation between entropy \(S\) and event horizon radius \(r_{+}\), \(S= \pi r_+^2\) (from area law), we can write the mass term as,

$$\begin{aligned} M(S,Q,\alpha )=\frac{\pi ^2 Q^2 \alpha ^2 + \pi S \alpha ^2 - S^2}{2 \pi ^{\frac{3}{2}} \alpha ^2 S^{\frac{1}{2}}}. \end{aligned}$$
(9)

The other thermodynamic parameters can be identified using the above expression of mass as \(T=\frac{\partial M}{\partial S}, ~~~ C= T \frac{\partial S}{\partial T}\) and hence we can obtain the temperature as a function of \(S\) and \(Q\),

$$\begin{aligned} T= \frac{ \alpha ^2 \pi (S - \pi Q^2)- 3 S^2}{4 \alpha ^2 \pi ^{\frac{3}{2}}S^{\frac{3}{2}}}. \end{aligned}$$
(10)

The heat capacity is also obtained as

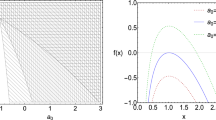
$$\begin{aligned} C=\frac{2S[\alpha ^2 \pi ( \pi Q^2 -S) + 3 S^2 ]}{3 S^2 + \alpha ^2 \pi (S- 3 \pi Q^2)}. \end{aligned}$$
(11)

Here we have obtained three thermodynamic quantities: mass\((M)\), temperature\((T)\) and specific heat\((C)\) and we have plotted all of them in terms of horizon radius \(r_+\) (Figs. 1, 2, 3). We could easily identify the abnormal behaviors in each of these quantities from their plots. In Fig. 1, we could see that mass of the black hole becomes zero at two places and reaches a maximum value at a particular value of \(r_+\). Temperature is positive only in between a certain range of horizon radius \(r_+\), which is shown in Fig. 2; the negative temperature is one of the issues we need to find a satisfactory explanation. Finally, the heat capacity changes from negative (unstable) phase to positive (stable) phase through an infinite discontinuity, as in Fig. 3. It refers to a second order thermodynamic phase transition in BHT. Thus the black hole will be thermodynamically stable for only a certain range of values of mass, temperature and heat capacity.

Fig. 1
figure 1

Variation of mass with respect to horizon radius \(r_+\). We set \(\alpha =\sqrt{3}\) and \(Q=0.4\)

Full size image
Fig. 2
figure 2

Variation of temperature with respect to horizon radius \(r_+\). We set \(\alpha =\sqrt{3}\) and \(Q=0.4\). The dashed portion is the negative—unphysical regime of temerature

Full size image
Fig. 3
figure 3

Variation of heat capacity with respect to horizon radius \(r_+\). We set \(\alpha =\sqrt{3}\) and \(Q=0.4\)

Full size image

On a close examination of Fig. 1 we can see that mass becomes zero at two points, viz, \(r_{+} = 0.446\) and \(r_+=1.739\). The maximum value for mass is for \(r_{+} = 0.872\). Temperature is positive only for the range of points \(r_{+} \ge 0.872\) and \(r_{+} \le 0.446\). Heat capacity becomes zero at \(r_{+} = 0.446\) and \(r_{+} = 0.872\), and suffers an infinite discontinuity at \(r_{+} = 0.59\).

While plotting the temperature and heat capacity verses the horizon radius we could find the so called abnormal behaviours of the RNdS black hole.

2.2 Thermodynamic geometry

Now we will apply the geometric techniques of Weinhold and Ruppeiner metrics of the system as well as the GTD. In this case the extensive variables are \(N^r =(\alpha , Q)\). Weinhold metric can be written from the above Eq. (1) as,

$$\begin{aligned} g^{W}_{ij}&= \partial _i \partial _j M(S,Q,\alpha ),\end{aligned}$$
(12)
$$\begin{aligned} dS^{2}_{W}&= M_{SS} dS^2 + M_{QQ} dQ^2 + M_{\alpha \alpha } d\alpha ^2 \nonumber \\&+2 M_{SQ} dS dQ + 2 M_{S \alpha } dS d\alpha + 2 M_{ \alpha Q} d\alpha dQ, \end{aligned}$$
(13)

and therefore,

$$\begin{aligned} g^{W}= \left[ {\begin{array}{c@{\quad }c@{\quad }c} M_{SS} &{} M_{SQ} &{} M_{S \alpha } \\ M_{QS} &{} M_{QQ} &{} 0 \\ M_{\alpha S} &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] . \end{aligned}$$

The second order partial derivatives can be found using the expression of \(M\) given in Eq. 9, in which \(M_{ \alpha Q}\) term will become zero while calculating. So there exists 5 independent elements in the metric.

We could calculate the curvature scalar of the Weinhold metric as,

$$\begin{aligned} R^{W}= \frac{\sqrt{S} \alpha ^2 \pi ^{\frac{3}{2}}(\alpha ^2 \pi ^2 Q^2+ \alpha ^2 \pi S- 9 S^2)}{(\alpha ^2 \pi ^2 Q^2-\alpha ^2 \pi S+ 3 S^2)^2}. \end{aligned}$$
(14)

The numerator is of little physical interest and we are interested in the denominator function. The denominator makes the \(R^{W}\) singular at \(S=\frac{\pi }{6}[\alpha ^2\mp \sqrt{\alpha ^4 - 12\alpha ^2 Q^2}]\). For each solution of \(S\) there exists a pair of \(r_+\), which can explain the singularities and zero points in the thermodynamic systems. We will avoid the negative values of the solution as it gives imaginary and negative roots. For the appropriate choices of the values of the parameter, we can see that it could explain the zero points of heat capacity, temperature and the peak value of mass at the value \(S=2.39\) or \(r_{+} = 0.872\) and zeros of temperature and heat capacity at the value \(S=0.636\) or \(r_{ +} = 0.45\).

Now we will go for the Ruppiner metric which can be conformaly transformed to Weinhold metric. Ruppiner metric is given by

$$\begin{aligned} g^{R}=\left( \frac{1}{T}\right) \left[ {\begin{array}{c@{\quad }c@{\quad }c} M_{SS} &{} M_{SQ} &{} M_{S \alpha } \\ M_{QS} &{} M_{QQ} &{} 0 \\ M_{\alpha S} &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] , \end{aligned}$$

which is equal to

$$\begin{aligned} g^{R}=\left( \frac{4 \alpha ^2 \pi ^{\frac{3}{2}}S^{\frac{3}{2}}}{\alpha ^2 \pi (S - \pi Q^2)- 3 S^2}\right) \left[ {\begin{array}{c@{\quad }c@{\quad }c} M_{SS} &{} M_{SQ} &{} M_{S \alpha } \\ M_{QS} &{} M_{QQ} &{} 0 \\ M_{\alpha S} &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] \end{aligned}$$

Now the curvature of the Ruppeiner metric is obtained as,

$$\begin{aligned} R^{R}= \frac{\alpha ^2 \pi (2 \pi Q^2-S)}{S(3S^2 - \pi \alpha ^2 S+ \pi ^2 Q^2 \alpha ^2) }. \end{aligned}$$
(15)

Here also the numerator is of less physical importance. We can see that the denominator throws light on the singularities. In addition to the singularities obtained from the Weinhold metric, we can see \(S=0\) or \(r_{+}=0\) is also a singular point in the Ruppiner method.

We can also use the Legendre invariant transformation of either Weinhold or Ruppiner metric to make further studies. In GTD it is possible to derive, in principle, an infinite number of metrics which preserve Legendre invariance, according to Eq. 5. The simplest way to attain the Legendre invariance for \(g^{W}\) is to apply a conformal transformation, with the thermodynamic potential as the conformal factor, which may unfold other hidden singularities in the present thermodynamic system of black hole. Here we are taking the conformal transformation which keeps the Legendre invariance as

$$\begin{aligned} g^{W'}= M \otimes g^W. \end{aligned}$$
(16)

Thus we could get the GTD metric as

$$\begin{aligned} g^{W'}=(M) \left[ {\begin{array}{c@{\quad }c@{\quad }c} M_{SS} &{} M_{SQ} &{} M_{S \alpha } \\ M_{QS} &{} M_{QQ} &{} 0 \\ M_{\alpha S} &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] , \end{aligned}$$

which is equal to

$$\begin{aligned} g^{W'}=\left( \frac{1}{2} \sqrt{\frac{S}{\pi }} + \frac{Q^2}{2}\sqrt{\frac{\pi }{S}} - \frac{1}{2 \alpha ^2} \left( \frac{S}{\pi }\right) ^{\frac{3}{2}}\right) \left[ {\begin{array}{c@{\quad }c@{\quad }c} M_{SS} &{} M_{SQ} &{} M_{S \alpha } \\ M_{QS} &{} M_{QQ} &{} 0 \\ M_{\alpha S} &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] . \end{aligned}$$

The curvature in the GTD is given by

$$\begin{aligned} R^{W'}= \frac{\mathcal {N}}{3 (-S^2+\pi ^2 Q^2 \alpha ^2 + S \alpha ^2 \pi )^3 (3S^2+\pi ^2 Q^2 \alpha ^2 - S \alpha ^2 \pi )^2}. \end{aligned}$$
(17)

Here the numerator \((\mathcal {N})\) is a lengthy expression and of little physical importance. We will get an extra term in the denominator apart from what we obtained in the Weinhold and Ruppeiner cases. That term makes the \(R^{W'}\) singular at \(S = \frac{\pi }{2} [\alpha ^{2} \mp \sqrt{\alpha ^{4} + 4\alpha ^{2} Q^{2}}]\). This can give an extra information about the zero point of mass at the value \(S = 2.39\) or \(r_{+} = 0.872\). The singularity in the heat capacity is not explained here by the curvature.

Finally we will do the most important GTD calculations in which the choice of thermodynamic potential does not affect the answer. In this method we could see the metric using Eq. 5 as follows,

$$\begin{aligned} g^{GTD}=(S M_S + Q M_Q + \alpha M_\alpha ) \left[ {\begin{array}{c@{\quad }c@{\quad }c} -M_{SS} &{} 0 &{} 0 \\ 0 &{} M_{QQ} &{} 0 \\ 0 &{} 0 &{} M_{\alpha \alpha } \\ \end{array} } \right] . \end{aligned}$$
(18)

The corresponding curvature is obtained as

$$\begin{aligned} R^{GTD}= \frac{\mathcal {N}}{(3S^2 + \pi \alpha ^2 S- 3 \pi ^2 Q^2 \alpha ^2)^2(S^2 + \pi \alpha ^2 S+ 3 \pi ^2 Q^2 \alpha ^2)^3 }. \end{aligned}$$
(19)

Here also the numerator \((\mathcal {N})\) is a lengthy expression and of little physical importance. We obtain an extra term in the denominator, and that makes \(R^{GTD}\) singular at \(S = \frac{\pi }{6} [-\alpha ^{2} \mp \sqrt{\alpha ^{4} + 36\alpha ^{2} Q^{2}}]\). This extra singularity arose here could explain the divergence of heat capacity at \(S = 1.1\) or \(r_{+} = 0.59\).

Hence the geometric methods we have elaborated above could give the singularities in the thermodynamic space. The metric which we used above could be transformed to Legendre invariant metric. The importance of GTD is that it won’t change the results even if we change the choice of thermodynamic potential choosen to obtain the metric. Here in our results we got the singular and zero points repeatedly in different methods, but the points were unique. And they are absolutely independent of the choice of thermodynamic potential we used to write the metric.

Thus we could plot a most generic curvature scalar with the horizon radius as in Fig. 4. From the figure, it is easy to find all the singular points and zeros of the curvature, which uncover the thermodynamic abnormalities in the system. Here the maxima, minima and zeros of the curvature actually correspond to the thermodynamic behaviour.

Fig. 4
figure 4

Variation of most generic curvature scalar of RNdS black hole with respect to horizon radius \(r_+\). We set \(\alpha =\sqrt{3}\) and \(Q=0.4\)

Full size image

Now we are interested in the extremal case of RNdS black hole we discussed above, known as MTZ black hole.

3 de Sitter black hole coupled with a scalar field

Now we study the thermodynamics and GTD of dS black hole coupled with a scalar field, which we shall refer to as the MTZ black hole [13]. MTZ black hole is the solution of the field equations arising from the action

$$\begin{aligned} I_L&= \int \limits _\mathcal {M} d^4 x \sqrt{-g}[\frac{1}{16 \pi }(R-2 \Lambda ) - \frac{1}{2} g^{ab} \partial _a \phi \partial _b \phi \nonumber \\&-\frac{1}{12} R \phi ^2 -\zeta \phi ^4 -\frac{1}{16 \pi } F^{ab}F_{ab}, \end{aligned}$$
(20)

where \(\zeta \) is the coupling constant. The metric of MTZ black hole is written as

$$\begin{aligned} ds^2 = -N(r) dt^2 + N(r)^{-1} dr^2 + r^2 (d\Omega ^2), \end{aligned}$$
(21)

where

$$\begin{aligned} N(r)= \left( 1-\frac{M}{r}\right) ^2 -\frac{\Lambda }{3} r^2. \end{aligned}$$
(22)

This black hole has inner, event and outer horizons at the values of the radial coordinate \(r\) given by

$$\begin{aligned} r_{-}&= \frac{\alpha }{2}\left[ -1+ \sqrt{1+\frac{4 M}{\alpha }}\right] , \\ r_{+}&= \frac{\alpha }{2}\left[ 1- \sqrt{1-\frac{4 M}{\alpha }}\right] ; \hbox { and } \\ r_{++}&= \frac{\alpha }{2}\left[ 1+ \sqrt{1-\frac{4 M}{\alpha }}\right] , \end{aligned}$$

where \(\alpha = \sqrt{\frac{3}{\Lambda }}\). From the above equation it is clear that, the solution is defined only for \(0<M<M_{max}=\frac{\alpha }{4}\). When \(M=0\) the metric reduces to the de Sitter space and there is only a cosmological horizon. In the other limit, \(M=M_{max}=\frac{\alpha }{4}\), the event and the cosmological horizons coincide, leaving the charge at the Nariai limit. Now we can do the usual thermodynamics of the event horizon at \(r_+\).

3.1 Thermodynamics

The usual thermodynamics of MTZ black hole is explained below. Using area law, we can express entropy as a function of \(M\) and \(\alpha \) as,

$$\begin{aligned} S(M,\alpha )=\frac{\pi \alpha ^2}{4} \left[ 1-\sqrt{1-\frac{4 M}{\alpha }}\right] ^2. \end{aligned}$$
(23)

We can now deduce the mass as,

$$\begin{aligned} M= \frac{S}{\alpha \pi }-\sqrt{\frac{S}{\pi }} \end{aligned}$$
(24)

Now we can straightforwardly write the temperature as

$$\begin{aligned} T= \frac{1}{\alpha \pi }-{\frac{1}{2\sqrt{\pi S}}}, \end{aligned}$$
(25)

while the heat capacity is

$$\begin{aligned} C=-2S+ \frac{4 S^{\frac{3}{2}}}{\alpha \sqrt{\pi }}. \end{aligned}$$
(26)

Here we have plotted all the three thermodynamic parameters as a function of horizon radius \((r_{+})\). In Fig. 5, we find that mass of the black hole is positive only for a particular range of \(r_+\). In the case of temperature also, in Fig. 6, it goes to the negative range after a particular value of \(r_+\). For heat capacity, here there is no infinite discontinuity, but it also falls to the negative(unstable) phase after a particular value of \(r_+\), as in Fig. 7.

Fig. 5
figure 5

Variation of mass with respect to horizon radius \(r_+\). We set \(\alpha =4\). The dashed portion is the negative—unphysical regime of mass

Full size image
Fig. 6
figure 6

Variation of temperature with respect to horizon radius \(r_+\). We set \(\alpha =4\). The dashed portion is the negative—unphysical regime of temerature

Full size image
Fig. 7
figure 7

Variation of heat capacity with respect to horizon radius \(r_+\). We set \(\alpha =4\)

Full size image

Thus we see that the thermodynamic parameters of the MTZ black hole also shows abnormal behaviours. The particular point about the present system is the validity of the choice of \(r_+\), which has been used to find the horizon thermodynamics here. The value of \(r_+\) lies in the range, \(M<r_+<\frac{\alpha }{2}\).

Mass of the black hole becomes zero at \(r_+=0\) and at \(r_+=4\). \(r_+=2\) corresponds to the maxima of the curve in Fig. 5. Temperature of the black hole becomes negative after reaching zero at \(r_+=2\). Heat capacity also reaches zero at \(r_+=2\) and then falls to the unstable phase.

3.2 Thermodynamic geometry

Now we construct the thermodynamic geometry of the MTZ black hole using Weinhold metric. In this case the extensive variable is \(N^r =[\alpha ]\) so that the general Weinhold metric becomes,

$$\begin{aligned} g^{W}= \left[ {\begin{array}{c@{\quad }c} M_{SS} &{} M_{S \alpha } \\ M_{\alpha S} &{} M_{\alpha \alpha }\\ \end{array} } \right] . \end{aligned}$$
(27)

We could easily find the metric elements from the expression of mass given by Eq. 23 and the corresponding scalar curvature becomes

$$\begin{aligned} R^W=\frac{\alpha ^2 \pi ^{\frac{3}{2}}}{\left[ 2\sqrt{S}(\alpha \sqrt{\pi }- 2 \sqrt{S})^2 \right] }. \end{aligned}$$
(28)

This curvature could explain two singularities in the thermodynamics of MTZ black hole. One at which \(S=0\) and the other at which \(S=\frac{\alpha ^2 \pi }{4}\). The latter brings the information of zeros in both heat capacity and temperature.

Now we construct the Ruppeiner metric,

$$\begin{aligned} g^{R}= \left( -\frac{1}{T}\right) \left[ {\begin{array}{c@{\quad }c} M_{SS} &{} M_{S \alpha } \\ M_{\alpha S} &{} M_{\alpha \alpha }\\ \end{array} } \right] , \end{aligned}$$
(29)

while calculating the curvature scalar, we can see that it is zero. So we can’t explain any of the singular behavior of the thermodynamic system under consideration using Ruppeiner method. Now we apply the GTD approach and we can find the GTD metric in a couple of ways by Legendre invariant conformal transformations,

$$\begin{aligned} g^{GTD}= \left( SM_S + \alpha M_\alpha \right) \left[ {\begin{array}{c@{\quad }c} - M_{SS} &{} 0 \\ 0&{} M_{\alpha \alpha }\\ \end{array} } \right] \end{aligned}$$
(30)

and the corresponding curvature is

$$\begin{aligned} R^{GTD}=\frac{- 3 \pi }{S}, \end{aligned}$$
(31)

which obviously gives only one singularity.

Another Legendre transform of this as \(g\rightarrow \Lambda ^{-1} g\) gives

$$\begin{aligned} g^{GTD*}= (SM_S + \alpha M_\alpha )^{-1} \left[ {\begin{array}{c@{\quad }c} - M_{SS} &{} 0 \\ 0&{} M_{\alpha \alpha }\\ \end{array} } \right] \end{aligned}$$
(32)

Here the curvature gives

$$\begin{aligned} R^{GTD*}= -\frac{1}{4}. \end{aligned}$$
(33)

It’s merely a scalar and independent of any of the parameters. So in this case, the Weinhold metric gives more good results regarding the thermodynamic abnormalities of MTZ black hole. Thus we consider a generalized Weinhold metric as in Eq. 16 as,

$$\begin{aligned} g^{W}=(M) \left[ {\begin{array}{c@{\quad }c} M_{SS} &{} M_{S \alpha } \\ M_{\alpha S} &{} M_{\alpha \alpha }\\ \end{array} } \right] . \end{aligned}$$
(34)

Following the previous steps, we could see that the curvature scalar gets the form,

$$\begin{aligned} R^{W*}=\frac{\alpha ^3 \pi ^{\frac{5}{2}}(3 \alpha ^2 \pi - 9 \alpha \sqrt{\pi S}+ 8S)}{4S(\alpha \sqrt{\pi }- 2 \sqrt{S})^2 (\sqrt{S}-\alpha \sqrt{\pi })^3}. \end{aligned}$$
(35)

Here the generalized Weinhold metric reveals the remaining zeros and singularities of the present thermodynamic system. One singularity is obviously at \(S = 0\) or \(r_{ +} = 0\); where the mass and heat capacity have zero values. Second singularity is at \(S = \frac{\alpha ^{2} \pi }{4}\) or \(r_{+} =2\); where the temperature and heat capacity have zero value, and mass has the maximum value. The final singularity is at \(S = \pi \alpha ^{2}\) which in turn gives \(r_{+} = 4\) and this corresponds to the second point in Fig. 5, where mass becomes zero. Thus, this metric provides us almost all of the thermodynamic singular and zero points. In general, the geometric methods uniquely determine the points of the thermodynamic parameters of MTZ black hole at which the thermodynamic quantities become singular. The generic scalar curvature can be plotted with horizon radius as in Fig. 8, and all the thermodynamic behaviours are revealed in this calculation.

Fig. 8
figure 8

Variation of most generic curvature scalar of MTZ black hole with respect to horizon radius \(r_+\). We set \(\alpha =4\)

Full size image

4 Conclusion

In this work we have analyzed the thermodynamics and thermodynamic geometry of RNdS black hole and its extremal case. First we have found the thermodynamics of RNdS black hole. The thermodynamics showed abnormalities in temperature, mass and heat capacity. The heat capacity exhibits a second order phase transition as well. So our aim is to express these abnormalities with the geometric tools available in thermodynamics. We have used three different thermodynamic geometric techniques to analyze these abnormalities.

We have found that in the case of RNdS black hole, the geometric methods of Weinhold, Ruppeiner and Quevedo (GTD), combined together give the singularities which could explain the abnormal behaviours of the system whereas in the case of MTZ black hole, the generalized Weinhold method only gives the correct results.