The collapse of the wave function in the joint metric-matter quantization for inflation

Abstract

It has been argued that the standard inflationary scenario suffers from a serious deficiency as a model for the origin of the seeds of cosmic structure: it can not truly account for the transition from an early homogeneous and isotropic stage to another one lacking such symmetries. The issue has often been thought as a standard instance of the “quantum measurement problem”, but as has been recently argued by some of us, that quagmire reaches a critical level in the cosmological context of interest here. This has lead to a proposal in which the standard paradigm is supplemented by a hypothesis concerning the self-induced dynamical collapse of the wave function, as representing the physical mechanism through which such change of symmetry is brought forth. This proposal was originally formulated within the context of semiclassical gravity. Here we investigate an alternative realization of such idea implemented directly within the standard analysis in terms of a quantum field jointly describing the inflaton and metric perturbations, the so called Mukhanov–Sasaki variable. We show that even though the prescription is quite different, the theoretical predictions include some deviations from the standard ones, which are indeed very similar to those found in the early studies. We briefly discuss the differences between the two prescriptions, at both, the conceptual and practical levels.

1 Introduction

Inflation represents one of the central cornerstones of modern cosmology. It was initially proposed as a solution to the classical naturalness problems of the the big bang model, but its impact became even more significant when it came to be regarded as a natural mechanism to account for the seeds of cosmic structure. However, as discussed in [1] (see also [2]), these claims are not fully justified. The point is that there is nothing that could account for the transmutation of the homogeneous and isotropic vacuum characterizing the quantum properties of the early universe, into something that might be identified with the inhomogeneous and anisotropic state characterizing the universe at, say, the last scattering surface, from which the cosmic microwave background (CMB) photons were emitted. At this point we should warn the reader that our posture in this regard is not shared by all the people working in the field, and thus we invite him/her to consider the arguments on the two sides of the issue by him/her-selves. For a sample of works expressing views contrary to ours, please see the references given in [3–19]. (Note however that different authors in the sample point to—slightly—different schemes, indicating that each author does not find the schemes espoused by other colleagues to be fully satisfactory.)

The problem was noted early on in [20] by Padmanabhan, but the issue was highlighted in [1], where the first proposal to address it was put forward. More recently, some books in which the standard picture is presented have mentioned the problem explicitly (see for instance [21–23] and [24]), while other researchers still claim that there is no outstanding issue [19]. The detailed analysis of such postures and the remaining shortcomings have been discussed in [2], and the arguments will not be reproduced here. However, let us note that most researchers in the field, including those who acknowledge that there is something missing in the standard picture, are convinced that this is in a sense “just the standard interpretational problem of quantum mechanics”, and as such, the issue is one of “pure philosophy” without any possible impact on the predictions of the theory. In fact, the issue is sometimes presented as that of the “quantum to classical transition”, but this, in our view, hides the seriousness of the real problem. We need some physical process to account for the passage from a state with a certain symmetry (homogeneity and isotropy) to another one lacking those symmetries, in a situation were we can find no physical mechanism that might account for that. The point is that by labelling this issue as just philosophy, what is meant by most physicists is the belief that the final results do not depend on the details of whatever one envisions as being behind the process that leads to the emergence of the primordial inhomogeneities out of the quantum “fluctuations” (or, more precisely, uncertainties). However, as we have shown in previous works [1], this is not the case, and particular aspects of the process could have left some imprints in the distribution of matter and the CMB.

The idea that has been considered in previous works as a possibility to deal with that problem involves adding to the standard model the hypothesis that the collapse of the wave function is an actual physical process that occurs independently of external observers. It was initially proposed in [1], and developed further in [25–31] (see also [2, 32, 33]). As discussed in [2], something that effectively might be described in terms of such a collapse of the wave function could have its origins in the passage from the atemporal regime of quantum gravity to the classical space-time description underlining the general theory of relativity. That is, in going from one description to the other, we might be forced to characterize some aspects of the underlying physics in terms of sudden jumps which are not compatible with the unitary Schrödinger evolution, and which modify the state of the universe in an stochastic way, being therefore capable of transforming a condition that was initially homogeneous and isotropic into another one that is not (the interested reader can consult the above mentioned works as those issues are not the focus of this paper).

The point we want to analyze here is to what extend do the general aspects and details of the results obtained in previous works depend on the specific approach to deal with the quantum aspects of the problem. The fact is that in all previous treatments we have relied on what is known as semiclassical gravity. That is, a classical description for the space-time metric (including its perturbations) coupled to a quantum treatment of the inflaton field. We considered a quantum field evolving in a space-time background, together with the assumption that the expectation value of the energy momentum tensor acts as the source of gravity in Einstein’s theory. The collapse has been assumed to occur at the level of the quantum description of the inflaton field, while the metric would simply respond to the modification in the expectation value of the energy momentum tensor leading to a geometry that is no longer homogeneous and isotropic. We have found in that case that the details of the model of collapse and the times assumed for the collapse of the various modes have an impact on the details of the CMB power spectrum [25].

In this work we will consider a similar analysis but implemented within a treatment that considers simultaneously the metric and the scalar field perturbations (both treated at the quantum level), while the space-time and inflaton homogeneous and isotropic background will be treated classically. That is, we will describe the system of interest in terms of the so called Mukhanov–Sasaki variable [34, 35], which will be quantized in the standard way, as it is now customary on the literature on the subject. However, we will modify the standard treatment with the inclusion of what we believe is the missing element, which at the phenomenological level would correspond to a dynamical collapse of the wave function, postulated as reflecting a yet undiscovered aspect of Nature, perhaps related to quantum gravity as suggested by Penrose [36] and Diósi [37].

Our motivation for this paper is twofold. On the one hand we will present the “self-collapsing” universe within what today is considered the standard approach to inflation. We believe this could made our ideas more accessible to the community. On the other hand, we will show that some important conclusions regarding the modification of the power spectrum are present in the two different manners of incorporating the collapse hypothesis into the formalism. The exact form of the modifications will differ from one approach to the other, so, in principle, we could use the cosmological observations to infer which one of the two pictures provides an appropriate effective description for the gravitational interaction at the quantum-classical interplay: semiclassical gravity or that proposed by Mukhanov and Sasaki. At this point it is important to emphasize that the issue of which is the variable that one should quantize is one with physical consequences. Thus the Mukhanov–Sasaki approach is more than a particular formalism, as it leads to the quantization of a particular combination of metric and scalar field perturbations. This contrast with the approach based on semiclassical gravity where only the scalar filed is quantized, and of course this can lead to differences between the results obtained in this paper and those obtained in previous works by our group.

The manuscript is organized as follows: In Sect. 2 we briefly review the standard description of cosmological perturbations (both at the quantum and classical level) in the inflationary scenario. After that, in Sect. 3 we proceed to make the quantum-mechanical treatment of the field and metric perturbations within the setting of our proposal, and compare our predictions with the observational results. Finally we discuss our findings in Sect. 4.

The conventions we will be using include a $(-,+,+,+)$ signature for the space-time metric and natural units with $c=1$. We will use the Planck mass $M_p^2\equiv \hbar ^2/8\pi G$ and the Planck time $t_p^2\equiv 8\pi G\hbar$, and follow the notation in Ref. [22]. However, we will work in the “conformal Newtonian gauge” from the beginning (see the expression (1) bellow). The reader should recall that the corresponding equations coincide (in form) with those obtained for their “gauge invariant counterparts” in [22] (for a detailed discussion on our motivation for choosing this particular gauge see the Ref. [26]).

2 The standard approach: a review

At the classical level the inflationary universe is described by Einstein’s theory $G_{\mu \nu }=8\pi G T_{\mu \nu }$ together with the equations of motion for the matter fields. We shall restrict ourselves to the simplest inflationary model, with a single scalar field with the standard kinetic and potential terms, the inflaton $\phi$. We will be only interested in those configurations very close to a homogeneous and isotropic Robertson–Walker cosmology.

The study of the seeds of cosmic structure depends essentially on the scalar sector of the perturbations. Ignoring for simplicity the so called vector and tensor modes, we can choose a coordinate system in which the space-time metric simplifies to

$$\begin{aligned} ds^{2}=a^{2}(\eta )\left[-(1+2\psi )d\eta ^{2}+(1-2\psi )\delta _{ij}dx^{i} dx^{j}\right],\quad \mathrm{{with}} \; \psi (\eta ,\mathbf{{x}})\ll 1. \end{aligned}$$

(1)

This choice corresponds to the “conformal Newtonian gauge”, with $\psi$ an analogue to the Newtonian potential and $\eta$ the cosmological time in conformal coordinates. The spatial coordinates $x^i$ are the usual “co-moving spatial coordinates”. Note that $\psi =0$ corresponds to a spatially flat homogeneous and isotropic Robertson–Walker universe. We shall restrict our attention to a universe that is very close to a de Sitter solution, and we will not concern ourselves with the question of how this concrete realization was obtained from a particular potential term. One then focuses on the background universe ($\psi =0$), which is characterized in terms of the conformal expansion rate $\mathcal{H }\equiv \dot{a}/a$ (related to the standard Hubble parameter through $\mathcal{H } = aH$) and the so-called slow-roll parameter $\epsilon \equiv 1-\dot{\mathcal{H}/\mathcal{H}}^2$. Here the “dot” denotes a derivative with respect to the conformal time. For practical reasons we will often work up to the lowest non-vanishing order in $\epsilon$, taken it as a small positive constant, i.e. $0\le \epsilon \ll 1$. For $\epsilon =0$ we recover a de Sitter universe, $a_{dS}(\eta )=-1/H \eta$, with $-\infty <\eta < 0$ and $H$ constant.

In order to proceed one decomposes the scalar field into a homogeneous and isotropic part $\phi _0(\eta )$ plus a small perturbation, $\phi (x)=\phi _0(\eta )+\delta \phi (\eta ,\mathbf{{x}})$. Working up to the first order in $\psi$ and $\delta \phi$ and defining the new fields

$$\begin{aligned} u\equiv \frac{a\psi }{4\pi G \dot{\phi }_0},\quad v\equiv a\left(\delta \phi +\frac{\dot{\phi }_0}{\mathcal{H}}\psi \right), \end{aligned}$$

(2)

the $00$ and the $0i$ components of the Einstein equations (the Hamiltonian and momentum constraints) can be casted in the form:

$$\begin{aligned} \Delta u=z\left(\frac{v}{z}\right)^{\cdot }\; \mathrm{{and}} \quad v=\frac{1}{z}\left(zu\right)^{\cdot }\!,\quad \mathrm{{with}} \quad z\equiv \frac{a\dot{\phi }_0}{\mathcal{H}}. \end{aligned}$$

(3)

These two constraints can be combined with the dynamical equations resulting in a single equation involving only the field $v$ and the (given) background universe:

$$\begin{aligned} \ddot{v}-\nabla ^2 v -\frac{\ddot{z}}{z}v=0. \end{aligned}$$

(4)

Using Friedmann’s equation $\mathcal{H }^2 - \dot{\mathcal{H}} = 4\pi G \dot{\phi }_0^2$ and the definition of $\epsilon$ we can re-express $z$ as $z=a\sqrt{\epsilon /4\pi G}$, thus $\ddot{z}/z\simeq \ddot{a}/a$ provided we are in the slow-roll regime. At this level the new field $v(\eta ,\mathbf{{x}})$ contains all the information about the perturbed universe: the perturbations in the metric and the scalar field can be read from that field using the constraints (3) and the definitions given in (2). For practical reasons it will be more convenient to work with periodic boundary conditions over a box of size $L$. We shall take the limit $L\rightarrow \infty$ at the end of the calculations. We can then use a Fourier decomposition and write

$$\begin{aligned} v(\eta ,\mathbf{{x}})=\frac{1}{L^{3/2}}\sum _{\mathbf{{k}}\ne 0} v_{\mathbf{{k}}}(\eta )\,e^{i\mathbf{{k}}\cdot \mathbf{{x}}}, \end{aligned}$$

(5)

where $k_n=2\pi j_n/L, j_n=0,\pm 1,\pm 2,\ldots$, and $n=1,2,3$. Note that the zero mode has been removed from the perturbed fields. Recall that we are working in co-moving coordinates, where the $\mathbf{{k}}$’s are fixed in time (and related to their physical values through $\mathbf{{k}}/a$). In terms of this decomposition the dynamical equation for each mode $v_{\mathbf{{k}}}(\eta )$ takes the form

$$\begin{aligned} \ddot{v}_{\mathbf{{k}}}+\left(k^2-\frac{\ddot{z}}{z}\right)v_{\mathbf{{k}}}=0. \end{aligned}$$

(6)

In what follows, and as it is usual in the field, we will consider a classical description for the background universe. However, we shall quantize the field $v(x)$ characterizing the small perturbations around the previous symmetric solution. That field can be described in terms of the canonical (first order) action

$$\begin{aligned} S=\frac{1}{2}\int d\eta \, d^3\mathbf{{x}}\left(\dot{v}^2+v\Delta v +\frac{\ddot{z}}{z}v^2\right). \end{aligned}$$

(7)

(see Section 10 in Ref. [18] for more details.) Recall that we are working to the linear order in $\psi$ and $\delta \phi$, so the interaction terms have not been retained here. At the quantum level the field $v(x)$ and its conjugate momentum $\pi (x)=\dot{v}(x)$ should be promoted to field operators acting on a Hilbert space ${\fancyscript{H}}$. These operators must satisfy the standard equal time commutation relations

$$\begin{aligned}{}[\hat{v}(\eta ,\mathbf{{x}}),\hat{\pi }(\eta ,\mathbf{{y}})]=i\hbar \delta (\mathbf{{x}}-\mathbf{{y}}),\quad [\hat{v}(\eta ,\mathbf{{x}}),\hat{v}(\eta ,\mathbf{{y}})]= [\hat{\pi }(\eta ,\mathbf{{x}}),\hat{\pi }(\eta ,\mathbf{{y}})]=0.\qquad \end{aligned}$$

(8)

The standard way to proceed now is to decompose ${\hat{v}}(x)$ in terms of the time-independent creation and annihilation operators

$$\begin{aligned} \hat{v}(x)=\frac{1}{L^{3/2}}\sum _{\mathbf{{k}}\ne 0} \hat{v}_{\mathbf{{k}}}(\eta ) e^{i\mathbf{{k}}\cdot \mathbf{{x}}}, \end{aligned}$$

(9)

with $\hat{v}_{\mathbf{{k}}}(\eta )\equiv {\hat{a}}_{\mathbf{{k}}} v_k(\eta ) + {\hat{a}}^{\dag }_{-\mathbf{{k}}} v^*_{k}(\eta )$ belonging to a set of normal modes satisfying the classical equation of motion (6) and orthonormal with respect to the symplectic product

$$\begin{aligned} v_{k}(\eta )\dot{v}^{*}_{k}(\eta )-\dot{v}_{k}(\eta )v^*_{k}(\eta )=i\hbar . \end{aligned}$$

(10)

With these definitions the commutators (8) translate into

$$\begin{aligned}{}[{\hat{a}}_{\mathbf{{k}}},{\hat{a}}^{\dagger }_{\mathbf{{k}}^{\prime }}]=\delta _{\mathbf{{k}}\mathbf{{k}}^{\prime }},\quad [{\hat{a}}_{\mathbf{{k}}},{\hat{a}}_{\mathbf{{k}}^{\prime }}]=[{\hat{a}}^{\dagger }_{\mathbf{{k}}}, {\hat{a}}^{\dagger }_{\mathbf{{k}}^{\prime }}]=0, \end{aligned}$$

(11)

and the Fock space can be constructed in the standard way starting with the vacuum state (i.e. the state defined by ${\hat{a}}_{\mathbf{{k}}}\vert 0\rangle =0$ for all $\mathbf{{k}}$).

The quantum theory is specified by an appropriate choice for the set of functions $v_{\mathbf{{k}}}(\eta )$. However, the Eqs.  (6) and (10) do not fix that set unequivocally. Following the standard literature on the subject we will assume the Bunch–Davies (BD) construction, based on functions $v_{k}(\eta )$ that in the asymptotic past contain only “positive energy solutions”, i.e. for $-k\eta \rightarrow \infty$, $\dot{v}_{\mathbf{{k}}}=-i\omega _k v_{\mathbf{{k}}}$ with $\omega _k>0$. For a universe close to a de Sitter solution and working to the lowest non-vanishing order in the slow-roll parameter one obtains

$$\begin{aligned} v_{k}(\eta )=\sqrt{\frac{\hbar }{2k}}\left(1-\frac{i}{k\eta }\right) e^{-ik\eta }. \end{aligned}$$

(12)

For that simple construction the state $\vert 0\rangle$ is known as the BD vacuum.¹ After a few “e-folds” of inflation, this is expected to accurately characterize the state of the inflaton field, and its quantum fluctuations (uncertainties). As we have indicated these are supposed to represent the seeds of cosmic structure. However, it is easy to see that this state is perfectly homogeneous and isotropic.² Thus, a universe characterized by that state will be homogeneous and isotropic not only at the classical, but also at the quantum level. Indeed, this is not a surprising result: if the initial state have a symmetry, and the dynamical evolution preserves that symmetry,³ the state of the system will be symmetric at any time, and there is nothing (e.g., decoherence, horizon crossing, etc.) that the standard unitary evolution of the quantum theory could do to avoid that conclusion. Of course, the standard accounts need to bypass this no-go result in some way or another. However, as it has been argued in detail in [2], all those attempts fail to provide a satisfactory answer to the question: what is the physical mechanism whereby the initial symmetry was lost?

3 Beyond the standard quantum theory

We believe that something beyond the standard quantum theory, and which we have previously called “the collapse”,

$$\begin{aligned} \vert \mathrm{{symmetric}}\rangle \rightarrow \vert \mathrm{{non-symmetric}}\rangle , \end{aligned}$$

(13)

seems to be required in order to break the “initial” symmetry characterizing the BD vacuum. That process is thought to represent some novel aspect of physics, connected perhaps with otherwise unexpected properties of quantum gravity, as has been previously suggested by Diósi and Penrose (see also the discussion in Sect. 4). In fact, we should mention that there is a long history of studies about proposals involving something like a collapse of the wave function, emerging basically from the community working in foundations of quantum theory (see for instance [38] and references therein). However, those had never been considered in the present context before the work [1].

For the purposes of this paper we will concentrate on the simplest possible case, where there is only one collapse per mode $\mathbf{{k}}$ (of course there is no reason a priori to consider that there could not be more than one collapse per mode $\mathbf{{k}}$, but this is not going to affect our findings, as has been discussed in [27]). We want to consider each of the modes of the field individually, and will be assuming that at $\eta _{\mathbf{{k}}}^c$ the mode $\mathbf{{k}}$ suffers a collapse, $\vert 0_{\mathbf{{k}}}\rangle \rightarrow \vert \Xi _{\mathbf{{k}}}\rangle$, with $\vert \Xi _{\mathbf{{k}}}\rangle$, in principle, some arbitrary state chosen from a suitable subset of $\fancyscript{H}_{\mathbf{{k}}}$.⁴ That is, in principle, we will allow the collapsing time $\eta _{\mathbf{{k}}}^c$ to vary from mode to mode. These collapses will be assumed to take place according to certain specific rules which we will present in more detail shortly and which, as we will see, will depend on the particular “collapse scheme” considered. Each one of the collapses will thus induce a change in the expectation value of the operator $\hat{\psi }_{\mathbf{{k}}}(\eta )$. The point is that after the collapse of the mode $\mathbf{{k}}$, the universe will be no longer homogeneous and isotropic (in general) at that particular corresponding scale (or more precisely, in regards to that mode).

At this point we must face the relation between the quantum and classical descriptions. In this particular setting we will focus our attention to the Newtonian potential, that is, the scalar metric perturbation $\psi$ determining the small anisotropies in the temperature of the CMB radiation on the celestial two-sphere (see the expression (19) bellow). We must relate that perturbation with the field operator $\hat{\psi }$ provided by the quantum theory in the previous discussion.⁵ The connection will be made by taking the view that the classical description is only relevant for those particular states for which the quantity in question is sharply peaked, and that the classical description corresponds to the expectation value of said quantity. We can think for instance in the wave packet of a free particle where the wave function is sharply peaked around some position, and that in such a case we could naturally say that the particle’s position is well defined and corresponds to the expectation value of the position operator in that wave packet state. In other words, we will be using the identification

$$\begin{aligned} \psi (x) = \langle \Xi |\hat{\psi }(x) |\Xi \rangle , \end{aligned}$$

(14)

with $|\Xi \rangle$ a state of the quantum field $\hat{v}(x)$ characterizing jointly the metric and field perturbation, which of course will be meaningful only as long as the state corresponds to a sharply peaked one in the associated variable $\hat{\psi }(x)$. As we have noted, if we consider that the relevant state is the BD vacuum, as it is usually done, we would have a serious problem simply because $\langle 0 |\hat{\psi }(x) | 0 \rangle =0$. This illustrates why one is lead to introduce the collapse hypothesis. ay that is detailed enough to allow us to compute the above quantities. In order to emphasize the dependence of the Newtonian potential on the quantum state we will often write $\psi ^{\Xi }(x)$ (in fact, we will generalize this notation to any operator, $\mathcal{O }^\Xi \equiv \langle \Xi | \hat{\mathcal{O}} |\Xi \rangle$). From the first equation in (3) we obtain (in Fourier space):

$$\begin{aligned} {\psi }^\Xi _{\mathbf{{k}}} (\eta ) \equiv \langle \Xi | \hat{\psi }_{\mathbf{{k}}} (\eta ) |\Xi \rangle =-\frac{\sqrt{4\pi G\epsilon }H}{k^2}\left({\pi }^\Xi _{\mathbf{{k}}} (\eta ) -\frac{\dot{z}}{z}{v}^\Xi _{\mathbf{{k}}} (\eta ) \right). \end{aligned}$$

(15)

This is a relation between expectation values of mode operators. We will be assuming that at time $\eta _\mathbf{{k}}^c$ a collapse in the state of the mode $\mathbf{{k}}$ has occurred, resulting in a state characterized (in part) by the expectation values of the operators $\hat{v}_{\mathbf{{k}}} (\eta )$ and $\hat{\pi }_{\mathbf{{k}}} (\eta )$ at that particular time. We can then make use of the Ehrenfest’s theorem to relate those values to the expectation values of said operators at any future time (assuming there are no additional collapses for that mode). In the present case those relations take the form

$$\begin{aligned} {\pi }^\Xi _{\mathbf{{k}}} (\eta )&= A_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c) {\pi }^\Xi _{\mathbf{{k}}} (\eta _{\mathbf{{k}}}^c) +kB_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c) {v}^\Xi _{\mathbf{{k}}} (\eta _{\mathbf{{k}}}^c),\end{aligned}$$

(16a)

$$\begin{aligned} {v}^\Xi _{\mathbf{{k}}} (\eta )&= k^{-1}C_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c) {\pi }^\Xi _{\mathbf{{k}}} (\eta _{\mathbf{{k}}}^c) +D_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c) {v}^\Xi _{\mathbf{{k}}} (\eta _{\mathbf{{k}}}^c), \end{aligned}$$

(16b)

with $A_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c), B_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c), C_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c)$ and $D_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c)$ some dimensionless functions depending on $k\eta$ and $k\eta _{\mathbf{{k}}}^c$. They are not very revealing so we will not write them here explicitly. The interested reader can find these functions in “Appendix”. Using the expressions above and the fact that for the situation of interest $\dot{z}/z = -(1+\epsilon )/\eta$, we can re-express $\psi ^\Xi _{\mathbf{{k}}} (\eta )$ to the lowest non-vanishing order in $\epsilon$ in the relatively simple form

$$\begin{aligned} {\psi }^\Xi _{\mathbf{{k}}}(\eta )&= -\frac{\sqrt{4\pi G\epsilon }H}{k^2}\left\{ \pi ^{\Xi }_{\mathbf{{k}}}(s_{\mathbf{{k}}}^c)\left[\cos \Delta _{\mathbf{{k}}}^c +\frac{\sin \Delta _{\mathbf{{k}}}^c}{s_{\mathbf{{k}}}^c}\right]\right.\nonumber \\&\left.+v^{\Xi }_{\mathbf{{k}}}(s_{\mathbf{{k}}}^c)k\left[\frac{\cos \Delta _{\mathbf{{k}}}^c}{s_{\mathbf{{k}}}^c}+\left(\frac{1}{(s_{\mathbf{{k}}}^{c})^2}-1\right) \sin \Delta _{\mathbf{{k}}}^c\right]\right\} . \end{aligned}$$

(17)

Here we have defined $s\equiv k\eta$, $s_{\mathbf{{k}}}^c\equiv k\eta _{\mathbf{{k}}}^c$ and $\Delta _{\mathbf{{k}}}^c\equiv s-s_{\mathbf{{k}}}^c$. Note that, by definition $-\infty <s,s_{\mathbf{{k}}}^c < 0$, with $s_{\mathbf{{k}}}^c < s$, and then $\Delta _{\mathbf{{k}}}^c$ positive definite.

In order to make contact with the observations we shall relate the expression (17) for the Newtonian potential (only valid during inflation) to the small anisotropies observed in the temperature of the CMB radiation, $\delta T(\theta ,\varphi )/T_0$. They are considered as the fingerprints of the small perturbations pervading the universe at the time of decoupling, and undoubtedly any model for the origin of the seeds of cosmic structure should account for them. These data can be described in terms the coefficients $\alpha _{lm}$ of the multipolar series expansion

$$\begin{aligned} \frac{\delta T}{T_0}(\theta ,\varphi )=\sum _{lm}\alpha _{lm}Y_{lm}(\theta ,\varphi ), \quad \alpha _{lm}=\int \frac{\delta T}{T_0}(\theta ,\varphi )Y^*_{lm}(\theta ,\varphi )d\Omega . \end{aligned}$$

(18)

Here $\theta$ and $\varphi$ are the coordinates on the celestial two-sphere, with $Y_{lm}(\theta ,\varphi )$ the spherical harmonics ($l=0,1,2\ldots$ and $-l\le m\le l$), and $T_0\simeq 2.725 K$ the temperature average. The different multipole numbers $l$ correspond to different angular scales; low $l$ to large scales and high $l$ to small scales. At large angular scales ($l \le 20$) the Sachs–Wolfe effect is the predominant source to the anisotropies in the CMB. That effect relates the anisotropies in the temperature observed today on the celestial two-sphere to the inhomogeneities in the Newtonian potential on the last scattering surface,

$$\begin{aligned} \frac{\delta T}{T_0} (\theta ,\varphi ) = \frac{1}{3} \psi (\eta _D, \mathbf{{x}}_D). \end{aligned}$$

(19)

Here $\mathbf{{x}}_D = R_D (\sin \theta \sin \varphi , \sin \theta \cos \varphi , \cos \theta )$, with $R_D$ the radius of the last scattering surface, $R_D \simeq 4000$ Mpc, and $\eta _D$ is the conformal time of decoupling. The Newtonian potential can be expanded in Fourier modes leading to $\psi ^{} (\eta _D, \mathbf{{x}}_D) = \sum _{\mathbf{{k}} } \psi ^{}_{\mathbf{{k}}} (\eta _D)\,e^{i \mathbf{{k}} \cdot \mathbf{{x}}_D}/L^{3/2}$. Furthermore, using that $e^{i \mathbf{{k}} \cdot \mathbf{{x}}_D} = 4 \pi \sum _{lm} i^l j_l (kR_D) Y_{lm} (\theta , \varphi ) Y_{lm}^* (\hat{k})$, the expression (18) for $\alpha _{lm}$ can be rewritten in the form

$$\begin{aligned} \alpha _{lm} = \frac{4 \pi i^l }{3L^{3/2}} \sum _{\mathbf{{k}}} j_l (kR_D) Y_{lm}^* (\hat{k})T_{{k}}(\eta _R,\eta _D) \psi ^{\Xi }_{\mathbf{{k}}} (\eta _R), \end{aligned}$$

(20)

with $j_l (kR_D)$ the spherical Bessel function of order $l$. Here we have included the transfer function $T_{{k}}(\eta _R,\eta _D)$ in order to evolve the perturbation in the Newtonian potential from the end of inflation to the last scattering surface, $\psi _{\mathbf{{k}}}(\eta _D)=T_{k}(\eta _R,\eta _D) \psi ^{\Xi }_{\mathbf{{k}}} (\eta _R)$, with $\eta _R$ the reheating time. We will be ignoring this aspect from this point onward, despite the fact that this transfer function is behind the famous acoustic peaks, the most noteworthy feature of the CMB power spectrum. The point is that they relate to aspects of plasma physics that are well understood and thus uninteresting for our purposes here. This will mean that the observational power spectrum would have such features removed before comparing with our results (this is in the same spirit that one removes the imprint of our galaxy, or the dipole associated with our peculiar motion). This would be equivalent to assume that the observations fits well with a nearly flat Harrison–Zel’dovich spectrum.

Note that the expression (20) has no analogue in the usual treatments of the subject, providing us with a clear identification of the aspects of the analysis where the “randomness” is located. In this case it resides in the randomly selected values for $\psi _{\mathbf{{k}}} (\eta _D)$, i.e. in the randomly selected values for $\psi ^{\Xi }_{\mathbf{{k}}}$ at the collapsing time, see (16) above. Here we also find a clarification of how, in spite of the intrinsic randomness, we can make any prediction at all. The individual complex quantities $\alpha _{lm}$ correspond to large sums of complex contributions, each one having a certain randomness, but leading in combination to a characteristic value in just the same way as a random walk made of multiple steps. Nothing like this can be found in the most popular accounts, in which the issues we have been focusing on here are hidden in a maze of often unspecified assumptions and unjustified identifications [2]. More precisely, all the modes $\psi _{\mathbf{{k}}} (\eta _D)$ contribute to $\alpha _{lm}$ with a complex number, leading to what is in effect a sort of “two-dimensional random walk” whose total displacement corresponds to the interesting aspect of the observational quantity (this will be more evident next when we specify the collapse scheme). It is therefore clear that, as in the case of any random walk, such quantity can not be evaluated, and the only thing that can be done is to calculate the most likely (ML) value for such total displacement, with the expectation that the observed quantity will be close to that value. That is, we need to estimate the ML value of

$$\begin{aligned} |\alpha _{lm} |^2= \frac{16 \pi ^2}{9L^{3}} \sum _{\mathbf{{k}}, \mathbf{{k}}^{\prime }} j_l (kR_D) j_l (k^{\prime }R_D) Y_{lm}^* (\hat{k}) Y_{lm} (\hat{k^{\prime }})\psi ^{\Xi }_{\mathbf{{k}}} (\eta _R){\psi ^{\Xi }_{\mathbf{{k}}^{\prime }}}^* (\eta _R). \end{aligned}$$

(21)

As it is now standard in our treatments, we do this with the help of an imaginary ensemble of universes (each one corresponding to a possible realization of the collapse), and the identification of the ML value $|\alpha _{lm}|_\mathrm{{ML}}^2$ with the ensemble’s mean value. The spread of the corresponding values within such ensemble corresponds to what is usually known as the cosmic variance.⁶ It is precisely at this point where there appears the link between the statistics of the quantum theory (we will be assuming that the collapses are guided by the quantum uncertainties) and the statistics over an ensamble of classical inhomogeneous universes. (In the standard approach all the evolution is unitary and then deterministic.) Under this assumption we obtain that all the information regarding the “self-collapsing” universe will be codified in the quantity⁷

$$\begin{aligned} \overline{\psi ^{\Xi }_{\mathbf{{k}}}(\eta _R)\psi ^{\Xi *}_{\mathbf{{k}}^{\prime }}(\eta _R)}, \end{aligned}$$

(23)

with the over-bar making reference to the ensemble average: the relevant quantities for the analysis of the seeds of cosmic structure are those characterizing the statistics of the collapse. We will further identify this quantity with the value of the corresponding limit $-k\eta _R \rightarrow 0$, which can be expected to be appropriate when restricting interest on the modes that are “outside the horizon” at the end of inflation, since these are the modes that give a major contribution to the quantities of observational interest. Let us note that the function $\psi ^{\Xi }_{\mathbf{{k}}}(\eta )$ in (17) depends on the time of collapse, so it is expected that the expression (23) will also depend (in general) on the values of $s_{\mathbf{{k}}}^c$. As we shall see that will affect the theoretical values of the quantities of interest, and in particular the form of the power spectrum (see for instance the expression (31) bellow). A simple and direct connection with the form of the standard results would be obtained if we had

$$\begin{aligned} \lim _{-k\eta _R\rightarrow 0}\overline{\psi ^{\Xi }_{\mathbf{{k}}}(\eta _R)\psi ^{\Xi *}_{\mathbf{{k}}^{\prime }}(\eta _R)}=\frac{2\pi ^2}{k^3}\mathcal{P }_{\psi }(k)\delta _{\mathbf{{k}} \mathbf{{k}}^{\prime }}, \quad \mathrm{{with}} \; \mathcal{P }_{\psi }(k)=\epsilon \frac{t_p^2H^2}{8\pi ^2}, \end{aligned}$$

(24)

(see Eq. (22) in footnote). Here $t_p$ is the Planck time, $H$ the scale of inflation, and $\mathcal{P }_{\psi }(k)$ the power spectrum for the Newtonian potential.⁸ However, in general, we will not obtain that simple relation. This is because the dependence of (23) on $s_{\mathbf{{k}}}^c$ will break the scale independence of the primordial perturbations, i.e. $\mathcal{P }_{\psi }(k)\ne \mathrm{{const.}}$

In order to see that, let us illustrate our findings with a very simple model for the collapse. As we want our collapse process to be closely related, or more precisely, to mimic the ordinary measurements in standard quantum mechanics, we describe the former in terms of hermitian operators. Thus, we decompose the operators $\hat{v}_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }_{\mathbf{{k}}}(\eta )$ in their real and imaginary parts, $\hat{v}_{\mathbf{{k}}}(\eta )=\hat{v}^\mathrm{{R}}_{\mathbf{{k}}}(\eta )+i\hat{v}^\mathrm{{I}}_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }_{\mathbf{{k}}}(\eta )=\hat{\pi }^\mathrm{{R}}_{\mathbf{{k}}}(\eta )+i\hat{\pi }^\mathrm{{I}}_{\mathbf{{k}}}(\eta )$, with $\hat{v}^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )=(v_{\mathbf{{k}}}(\eta ){\hat{a}}^ \mathrm{{R,I}}_{\mathbf{{k}}}+v^*_{\mathbf{{k}}}(\eta ){\hat{a}}^\mathrm{{ R,I}\dagger }_{\mathbf{{k}}})/\sqrt{2}$, $\hat{\pi }^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )=(\pi _{\mathbf{{k}}}(\eta ) {\hat{a}}^\mathrm{{R,I}}_{\mathbf{{k}}}+\pi ^*_{\mathbf{{k}}}(\eta ){\hat{a}}^ \mathrm{{R,I}\dagger }_{\mathbf{{k}}})/\sqrt{2}$, and

$$\begin{aligned} {\hat{a}}^\mathrm{{R}}_{\mathbf{{k}}}=\frac{1}{\sqrt{2}}\left({\hat{a}}_{\mathbf{{k}}}+ {\hat{a}}_{-\mathbf{{k}}}\right), \quad {\hat{a}}^\mathrm{{I}}_{\mathbf{{k}}}=\frac{-i}{\sqrt{2}}\left({\hat{a}}_{\mathbf{{k}}}-{\hat{a}}_ {-\mathbf{{k}}}\right). \end{aligned}$$

(25)

With these definitions $\hat{v}^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$ are Hermitian operators (i.e. $\hat{v}^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )=\hat{v}^\mathrm{{R,I} \dagger }_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )=\hat{\pi }^\mathrm{{R,I} \dagger }_{\mathbf{{k}}}(\eta )$), but the commutation relations between ${\hat{a}}^\mathrm{{R}}_{\mathbf{{k}}}$ and ${\hat{a}}^\mathrm{{I}}_{\mathbf{{k}}}$ are non-standard,

$$\begin{aligned} \left[{\hat{a}}^\mathrm{{R}}_{\mathbf{{k}}},{\hat{a}}^\mathrm{{R}\dagger }_{\mathbf{{k}}^{\prime }}\right]= (\delta _{\mathbf{{k}},\mathbf{{k}}^{\prime }}+\delta _{\mathbf{{k}},-\mathbf{{k}}^{\prime }}),\quad \left[{\hat{a}}^\mathrm{{I}}_{\mathbf{{k}}},{\hat{a}}^\mathrm{{I}\dagger }_{\mathbf{{k}}^{\prime }}\right]= (\delta _{\mathbf{{k}},\mathbf{{k}}^{\prime }}-\delta _{\mathbf{{k}},-\mathbf{{k}}^{\prime }}), \end{aligned}$$

(26)

with all the other commutators vanishing. Note that, according to (26), the modes $\mathbf{{k}}$ and $-\mathbf{{k}}$ in the previous decomposition are not independent. This will have important consequences later. Now, since $\hat{v}^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$ are Hermitian operators, they are susceptible of “being measured”: we will assume, in analogy with standard quantum mechanics, that the collapse is somehow analogous to an imprecise measurement of the operators $\hat{v}^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$ and $\hat{\pi }^\mathrm{{R,I}}_{\mathbf{{k}}}(\eta )$, and that the final result of the collapse will be guided by the quantum uncertainties,

$$\begin{aligned} \langle \hat{\pi }_{\mathbf{{k}}}^\mathrm{{R,I}}(\eta _\mathbf{{k}}^c)\rangle _\Xi&= \lambda _{\pi } x_{\mathbf{{k}},\pi }^\mathrm{{R,I}}\sqrt{\langle 0\vert \left[\Delta \hat{\pi }_{\mathbf{{k}}}(\eta _\mathbf{{k}}^c)\right]^2\vert 0\rangle }=\frac{\lambda _{\pi } x_{\mathbf{{k}},\pi }^\mathrm{{R,I}}}{\sqrt{2}}\left|\pi _k(\eta _\mathbf{{k}}^c)\right|,\end{aligned}$$

(27a)

$$\begin{aligned} \langle \hat{v}_{\mathbf{{k}}}^\mathrm{{R,I}}(\eta _\mathbf{{k}}^c)\rangle _\Xi&= \lambda _{v} x_{\mathbf{{k}},v}^\mathrm{{R,I}} \sqrt{\langle 0\vert \left[\Delta \hat{v}_{\mathbf{{k}}}(\eta _\mathbf{{k}}^c)\right]^2\vert 0\rangle }= \frac{\lambda _{v} x_{\mathbf{{k}},v}^\mathrm{{R,I}}}{\sqrt{2}}\left|v_k(\eta _\mathbf{{k}}^c)\right|, \end{aligned}$$

(27b)

with $x_{\mathbf{{k}},\pi }^\mathrm{{R,I}}$ and $x_{\mathbf{{k}},v}^\mathrm{{R,I}}$ taken to be a collection of independent random numbers selected from a Gaussian distribution centered at zero with unit-spread, and $\lambda _{\pi }$ and $\lambda _{v}$ two real numbers (usually $0$ or $1$) that allow us to specify the collapse proposal we want to consider. The mode $\mathbf{{k}}$ of any possible realization of the universe will be described in terms of the specific numerical values of $x_{\mathbf{{k}},\pi }^\mathrm{{R,I}}$ and $x_{\mathbf{{k}},v}^\mathrm{{R,I}}$. On the other hand, we will be using the values for $\lambda _{\pi }$ and $\lambda _{v}$ to characterize the different collapse schemes: (i) $\lambda _v=0$, $\lambda _\pi =1$ (corresponding to what was called the “Newtonian scheme” in the setting of semiclassical gravity), (ii) $\lambda _v=\lambda _\pi =1$ (which was called the “symmetric scheme”), or even (iii) $\lambda _v=1$, $\lambda _\pi =0$ (a scheme suggested to us by Prof. R. M. Wald). Introducing the expressions for $\langle \hat{\pi }_{\mathbf{{k}}}^\mathrm{{R,I}}(\eta _\mathbf{{k}}^c)\rangle _\Xi$ and $\langle \hat{v}_{\mathbf{{k}}}^\mathrm{{R,I}}(\eta _\mathbf{{k}}^c)\rangle _\Xi$ given in (27) into (17) and (23) and taking the limit when $-k\eta _R$ goes to zero we obtain

$$\begin{aligned} \frac{\epsilon t_p^2H^2 }{4k^{3/2}k^{\prime 3/2}}\left[ M_\mathbf{{k}} M_\mathbf{{k}^{\prime }} ( \overline{x_\mathbf{{k},v}^\mathrm{{R}} x_\mathbf{{k}^{\prime },v}^\mathrm{{R}}} + \overline{x_\mathbf{{k},v}^\mathrm{{I}} x_\mathbf{{k}^{\prime },v}^\mathrm{{I}}} ) + N_\mathbf{{k}} N_\mathbf{{k}^{\prime }} (\overline{x_\mathbf{{k},\pi }^\mathrm{{R}} x_\mathbf{{k}^{\prime },\pi }^\mathrm{{R}}} + \overline{x_\mathbf{{k},\pi }^\mathrm{{I}} x_\mathbf{{k}^{\prime },\pi }^\mathrm{{I}}} ) \right],\nonumber \\ \end{aligned}$$

(28)

with

$$\begin{aligned} M_\mathbf{{k}}&\equiv&\lambda _v \bigg [1 + \frac{1}{(s_\mathbf{{k}}^c)^2}\bigg ]^{\frac{1}{2}} \bigg [\frac{ \cos s_\mathbf{{k}}^c}{s_\mathbf{{k}}^c} - \bigg ( \frac{1}{(s_\mathbf{{k}}^c)^2} - 1 \bigg ) \sin s_\mathbf{{k}}^c \bigg ],\end{aligned}$$

(29a)

$$\begin{aligned} N_\mathbf{{k}}&\equiv&\lambda _\pi \bigg [ 1 - \frac{1}{(s_\mathbf{{k}}^c)^2} + \frac{1}{(s_\mathbf{{k}}^c)^4} \bigg ]^{\frac{1}{2}} \bigg [\cos s_\mathbf{{k}}^c - \frac{\sin s_\mathbf{{k}}^c}{s_\mathbf{{k}}^c} \bigg ]. \end{aligned}$$

(29b)

Here we have made use of the independence among the four sets of random variables $x_\mathbf{{k},v}^\mathrm{{R}}, x_\mathbf{{k},v}^\mathrm{{I}}, x_\mathbf{{k},\pi }^\mathrm{{R}}$ and $x_\mathbf{{k},\pi }^\mathrm{{I}}$. However, we need to recall that, within each set, the variables corresponding to $\mathbf {k}$ and $-\mathbf {k}$ are not independent. This will be reflected by setting $\overline{x_{\mathbf{{k}},i}^\mathrm{{R}}x_{\mathbf{{k}}^{\prime },i}^\mathrm{{R}}}= \delta _{\mathbf{{k}},\mathbf{{k}}^{\prime }}+\delta _{\mathbf{{k}},-\mathbf{{k}}^{\prime }}$ and $\overline{x_{\mathbf{{k}},i}^\mathrm{{I}}x_{\mathbf{{k}}^{\prime },i}^\mathrm{{I}}}= \delta _{\mathbf{{k}},\mathbf{{k}}^{\prime }}-\delta _{\mathbf{{k}},-\mathbf{{k}}^{\prime }}$ (here $i=\pi ,v$), in accordance with the commutators (26). Writing all these expressions together we conclude

$$\begin{aligned} \lim _{-k\eta _R\rightarrow 0}\overline{\psi ^{\Xi }_{\mathbf{{k}}}(\eta _R)\psi ^{\Xi *}_{\mathbf{{k}}^{\prime }}(\eta _R)} = \epsilon \frac{t_p^2 H^2}{4k^3} (M_\mathbf{{k}}^2 + N_\mathbf{{k}}^2) \delta _\mathbf{{k}\mathbf {k}^{\prime }}. \end{aligned}$$

(30)

Comparing (30) with (24) we obtain a power spectrum of the form

$$\begin{aligned} \mathcal{P }_{\psi }(k) \equiv \epsilon \frac{t_p^2H^2}{8\pi ^2} C(s_{\mathbf{{k}}}^c), \end{aligned}$$

(31a)

with the definition

$$\begin{aligned} C(s_{\mathbf{{k}}}^c)&\equiv\lambda _{\pi }^2 \left(1-\frac{1}{(s_{\mathbf{{k}}}^c)^2}+\frac{1}{(s_{\mathbf{{k}}}^c)^4}\right) \left[\cos s_{\mathbf{{k}}}^c-\frac{\sin s_{\mathbf{{k}}}^c}{s_{\mathbf{{k}}}^c}\right]^2\nonumber \\&+ \lambda _{v}^2 \left(1+\frac{1}{(s_{\mathbf{{k}}}^c)^2}\right)\left[\frac{\cos s_{\mathbf{{k}}}^c}{s_{\mathbf{{k}}}^c}-\left(\frac{1}{(s_{\mathbf{{k}}}^{c})^2}-1\right)\sin s_{\mathbf{{k}}}^c\right]^2. \end{aligned}$$

(31b)

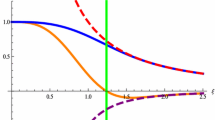
Note that, in general, the power spectrum is not flat, i.e. it depends on $\mathbf{{k}}$ through the previously defined quantity $s_{\mathbf{{k}}}^c \equiv k \eta _\mathbf{{k}}^c$. That is, the dependance on $\mathbf {k}$ in the spectrum is given by the function $C(s_\mathbf{{k}}^c)$ (see for instance Fig. 1 for the particular case with $\lambda _v=\lambda _\pi =1$). We will obtain a flat power spectrum if $s_{\mathbf{{k}}}^c=\mathrm{{const}}$, that is, if the times of collapse satisfy $\eta _\mathbf{{k}}^c= A k^{-1}$, with $A$ a (dimensionless) negative definite constant. This is a non-trivial relationship which could be taken as providing clues about the Nature of the mechanism behind the collapse. In Ref. [1], for instance, it was shown that a simple generalization of a proposal by R. Penrose (involving aspects of what he believes should be some features of quantum gravity) would lead exactly to this simple rule for the times of collapse. Without that, we do not obtain the standard Harrison–Zel’dovich shape of the power spectrum in any of the simple recipes for the collapse scheme considered, i) $\lambda _v=0$, $\lambda _\pi =1$, ii) $\lambda _v=\lambda _\pi =1$, or even iii) $\lambda _v=1$, $\lambda _\pi =0$. In fact, it is easy to see that in the absence of such specific pattern for the collapsing time, it is impossible to adjust $\lambda _v$ and $\lambda _\pi$ in order to recover an exactly flat power spectrum, i.e. to adjust those values in a way that the expression (31b) becomes independent of $s_{\mathbf{{k}}}^c$. In other words, a constant function (i.e. independent of $s_{\mathbf{{k}}}^c$) and the functions appearing as coefficients accompanying $\lambda _v^2$ and $\lambda _\pi ^2$ form a set of linearly independent functions. However, we will see that in certain cases a nearly flat power spectrum is possible, even with general patterns for the collapsing time, as long as they occur well outside the Hubble radius, see expressions (33) and (34) bellow.

Fig. 1

The function $C(s_\mathbf{{k}}^c)$ defined in (31b) for $s_\mathbf{{k}} \in [-20,0)$ using the symmetric scheme $\lambda _v=\lambda _\pi =1$

On the other hand, we do not presume that a collapse theory involving stochastic components will lead to decay times that precisely follow the pattern $\eta _\mathbf{{k}}^c = Ak^{-1}$, and therefore, it is natural to expect some deviations from the spectra found in standard treatments. In order to illustrate the nature of these deviations we will consider a simple modification from the above mentioned pattern which we parameterize here by $\eta _\mathbf{{k}}^c = A/k + \beta$, where $\beta$ a constant with dimensions of length such that $-\infty < s_{\mathbf{{k}}}^c < 0$. When $\beta =0$ we recover a flat spectrum. For the sake of exploring the dependance on $k$ in the power spectrum as given by (31), it is convenient to define the dimensionless quantity $x \equiv kR_D$ (recall that $R_D \simeq 4000$ Mpc). If we assume that the time of collapse of each mode is given by $\eta _\mathbf{{k}}^c = A/k + \beta$, then $s_\mathbf{{k}}^c (x) \equiv k \eta _\mathbf{{k}}^c = A + Bx$, with $B \equiv \beta /R_D$. In this way $A$, $B$ and $x$ are dimensionless quantities. It is important to note that the multipoles $l$ in the observed angular power spectrum cover the range $2 \le l \le 2600$, which corresponds to the modes with $10^{-3}$ Mpc$^{-1}$ $\le k \le$ 1 Mpc$^{-1}$, that is, the range of observational interest for $x$ is $1 \le x \le 10^{3}$. Furthermore, for the modes which the Sachs–Wolfe effect is dominant, the corresponding range of $x$ is given by $1 \le x \le 20$.

Once we have chosen a particular form for $\eta _\mathbf{{k}}^c$, we can compute the value of the scale factor at the collapse time $a^c_k \equiv a(\eta _\mathbf{{k}}^c)$, and compare it with the traditional value of the scale factor at the time of “horizon crossing” during the inflationary regime, $a^H_k \equiv a(\eta _\mathbf{{k}}^H)$, where $\eta _\mathbf{{k}}^H$ is the conformal time of horizon crossing for a mode $\mathbf {k}$ during inflation. The horizon crossing occurs when the length corresponding to the mode $k$ has the same value as the Hubble radius, $H_I^{-1}$, i.e. when $k=aH_I$ for comoving modes; therefore, $a_k^H =k/H_I$ (we recall that during the inflationary stage $H_I$ can be considered as a constant). Thus, the ratio of the value between the scale factor at horizon crossing for a mode $k$ (during the inflationary regime) and its value at the time of collapse for the same mode is

$$\begin{aligned} \frac{a_k^H}{a_k^c} \simeq \frac{k}{H_I} \bigg ( \frac{-1}{H_I \eta _\mathbf{{k}}^c} \bigg )^{-1} = k |\eta _\mathbf{{k}}^c| = |A + Bx| = |s_\mathbf{{k}}^c|. \end{aligned}$$

(32)

Thus, for every mode $\mathbf {k}$, we can read directly from this equation and our parametrization for the collapses (in terms of $A, B$ and $x$), the relationship between the scale factor at collapse and at horizon crossing.

It is interesting to note that we can recover a nearly flat power spectrum if we demand that, within the symmetric scheme $\lambda _v=\lambda _\pi =1$, the collapses take place at $s_{\mathbf{{k}}}^c\rightarrow -\infty$. In that case (and up to the first order in $1/s_{\mathbf{{k}}}^c$) the expression (31a) takes the form

$$\begin{aligned} \mathcal{P }_{\psi }(k)_{s_{\mathbf{{k}}}^c \rightarrow -\infty } \equiv \epsilon \frac{t_p^2H^2}{8\pi ^2} \left[1+\mathcal{O }^2 \left(\frac{1}{s_{\mathbf{{k}}}^c}\right)\right]. \end{aligned}$$

(33)

That is, in contrast to what is often assumed in the standard approach to the problem, this option would correspond to the collapses (the process that breaks the initial symmetry, usually considered as tied to the “the quantum to classical transition”) taking place when the modes are “well inside the Hubble radius” see (32) above. This situation is illustrated in Fig. 2 for some special values of the parameters $A$ and $B$, and assuming the symmetric collapse scheme. This is one case where no deviation from a flat power spectrum is observed.

Fig. 2

The function $C(x)$ in the interval $x \in [1,50]$, with $A=-0.01, B=-100$ and $\lambda _v = \lambda _{\pi } = 1$. In this case $a_k^H = |s_\mathbf{{k}}^c| a_k^c$ with $|s_\mathbf{{k}}^c| \in [100.01, 5000.01]$, i.e. $a_k^c \ll a_k^H$

It is also convenient to analyze the limit $s_{\mathbf{{k}}}^c \rightarrow 0$, corresponding to the opposite case in which the collapses take place well outside the Hubble radius (this could correspond, for instance, to the reheating time).⁹ In this case the expression (31a) takes the form

$$\begin{aligned} \mathcal{P }_{\psi }(k)_{s_{\mathbf{{k}}}^c \rightarrow 0} = \epsilon \frac{t_p^2H^2}{8\pi ^2} \left[ \lambda _{\pi }^2 \left(\frac{1}{9} + \mathcal{O }^2 (s_{\mathbf{{k}}}^{c}) \right) + \lambda _{v}^2 \left(\frac{2}{3} + \mathcal{O }^2 (s_{\mathbf{{k}}}^{c}) \right) \right]. \end{aligned}$$

(34)

This case is illustrated in Fig. 3, and corresponds to another case where no deviation from a flat power spectrum is observed. Thus, even though $s_{\mathbf{{k}}}^c$ may have a non-trivial $\mathbf{{k}}$ dependence, the spectrum becomes independent of $\mathbf{{k}}$, up to small corrections of order $s_{\mathbf{{k}}}^c \ll 1$.

Fig. 3

The function $C(x)$ in the interval $x \in [1,50]$, with $A=-0.01, B=-0.001$ and $\lambda _v = \lambda _{\pi } = 1$. In this case $a_k^H = |s_\mathbf{{k}}^c| a_k^c$ with $|s_\mathbf{{k}}^c| \in [0.011, 0.06]$, i.e. $a_k^c \gg a_k^H$

We also present the behavior of the function $C(x)$ within the symmetric scheme in some intermediate cases: Figs. 4, 5 and 6. It is interesting to point out that in Fig. 4, the function $C(x)$ would induce a pattern in the power spectrum similar to that usually described in terms of a spectral index   $n_s$, i.e. so that the power spectrum is proportional to $k^{n_s-1}$, with $n_s \ne 1$. Meanwhile, in Figs.  5 and 6, we observe that the collapse of the wave-function would affect only to the large scale modes $x = kR_D \le 20$ in both cases (a similar result, in a different context, was found in [30]). The door is clearly open for a more thorough investigation of the observationally allowed ranges, which requires direct comparison with data. In order to do that one must include the effects of the plasma acoustic oscillations, and a detailed analysis similar to that carried out in [31], which is beyond the scope of the present work.

Fig. 4

The function $C(x)$ in the interval $x \in [1,50]$, with $A=-0.01, B=-0.01$ and $\lambda _v = \lambda _{\pi } = 1$. In this case $a_k^H = |s_\mathbf{{k}}^c| a_k^c$ with $|s_\mathbf{{k}}^c| \in [0.02, 0.51]$, i.e. $a_k^c > a_k^H$

Fig. 5

The function $C(x)$ in the interval $x \in [1,50]$, with $A=-1, B=-0.1$ and $\lambda _v = \lambda _{\pi } = 1$. In this case $a_k^H = |s_\mathbf{{k}}^c| a_k^c$ with $|s_\mathbf{{k}}^c| \in [1.1, 6]$, i.e. $a_k^c < a_k^H$

Fig. 6

The function $C(x)$ in the interval $x \in [1,50]$, and $A=-1, B=-1$ and $\lambda _v = \lambda _{\pi } = 1$. In this case $a_k^H = |s_\mathbf{{k}}^c| a_k^c$ with $|s_\mathbf{{k}}^c| \in [2, 51]$, i.e. $a_k^c < a_k^H$

We should point out that the results we present here should be relevant irrespective of the views one takes on our collapse proposals. The point is that, even if one follows the standard views on the matter, but does so in a self-consistent way, one would come at the end to essentially the predictions above regarding the form of the spectrum. Let us assume that one chooses to ignore the shortcomings of the standard accounts and accepts that, say decoherence, addresses (somehow) the issue at hand (i.e. evades the conceptual problems discussed in Sect. 1 and the Refs. [1, 2]), and that the mystery lies only in the question concerning the precise mechanism that lies behind the fact that, from the “options” one finds in the decoherence analyses (i.e. those displayed in the reduced density matrix), a single particular one seems to be selected for “our branch”. Within this point of view, one would be assuming that the initial symmetry has been lost—at least for practical purposes (i.e. in our branch) as the relevant situation would not longer be described by the full fledged superposition of inhomogeneous and isotropic states (that make up the DB vacuum) but by the state corresponding to our branch, as presumably one would be advocating when adopting such position. That is, we would need to focus on a particular state that corresponds to the particular realization or actualization (represented by a particular element in the density matrix). Thus, it seems clear that for the sake of self-consistency, when studying aspects of the anisotropies in the CMB, one should consider that state corresponding to such “selected option”, and not the entire vacuum state which describes the homogeneous and isotropic state of affairs previous to the “selection”.¹⁰ In following such views, the discussion that we are presenting in this paper would have to be taken to represent the effective description corresponding to “our perceived universe” (in a context where one puts together something like the many-worlds interpretation with the arguments based on decoherence). Although we definitely do not adhere such view for the reasons explained in [2], it is clear that an effective description such as the one presented here is what would have to be contemplated when dealing with the issues within any view which pretends to allow one to deal with the details characterizing the inhomogeneities and anisotropies in the cosmic structure and its imprints in the CMB that we do observe.

Finally, it is worth mentioning that in the collapse model introduced in [1], where the collapse was considered within the framework of semiclassical gravity, one could also obtain a similar expression for the power spectrum to that given in Eq. (31). In that case only the matter fields were quantized, with the space-time metric considered to be an effective (classical) description of gravity. Using semiclassical gravity one obtains

$$\begin{aligned} \mathcal{P }_{\psi }(k) = \epsilon \frac{t_p^2H^2}{8\pi ^2} \left[ \lambda _{1}^2 \left(1+\frac{1}{(s_{\mathbf{{k}}}^c)^2}\right) \sin ^2 s_{\mathbf{{k}}}^c + \lambda _2^2 \left( \cos s_{\mathbf{{k}}}^c - \frac{\sin s_{\mathbf{{k}}}^c}{s_{\mathbf{{k}}}^c} \right)^2 \right], \end{aligned}$$

(35)

with $\lambda _1$ and $\lambda _2$ two real numbers analogous to those given in $\lambda _\pi$ and $\lambda _v$. Again, assuming $\lambda _1=\lambda _2=1$ and taking the limit when $s_{\mathbf{{k}}}^c \rightarrow -\infty$ we arrive to an expression of the form (33). However, taking the limit $s_{\mathbf{{k}}}^c \rightarrow 0$ in (35) we obtain

$$\begin{aligned} \mathcal{P }_{\psi }(k)_{s_{\mathbf{{k}}}^c \rightarrow 0} = \epsilon \frac{t_p^2H^2}{8\pi ^2} \left\{ \lambda _{1}^2 \left[ 1+\mathcal{O }^2 (s_{\mathbf{{k}}}^{c}) \right] + \lambda _2^2 \left[ \mathcal{O }^4 (s_{\mathbf{{k}}}^{c}) \right] \right\} . \end{aligned}$$

(36)

Note that expression (36) exhibits a distinct behaviour from (34). That is, if the collapse scheme is such that $\lambda _1=0$ and $\lambda _2=1$ (referred to as the Newtonian scheme in [1]), then the shape of the spectrum is not flat but proportional to terms of order $(s_{\mathbf{{k}}}^c)^4$. This contrasts with the behaviour of (34), where regardless of the values of $\lambda _v$ and $\lambda _\pi$, the spectrum is always flat plus small corrections of order $(s_{\mathbf{{k}}}^c)^2$.

In other words, the predictions regarding the shape of the spectrum depend strongly on what is the variable that characterizes the collapse, and the times at which the collapse of each mode takes place. The effect becomes substantially reduced if the collapse is tied to the Mukhanov–Sasaki variable, in the approach investigated in this work, or if it is tied to the field variable, in the approach studied in previous works, while the effects would be generically very large in the case where the collapse is tied to the momentum conjugate field variable in that approach. On the other hand, the spectrum would become close to the standard one if the collapse takes place always with very small values of $s_{\mathbf{{k}}}^c$.

The point is that, even if the appropriate treatment of the situation at hand involves either a collapse in the Mukhanov–Sasaki variables, or a collapse in the inflaton field, we face the prospect of important deviations (from the flat one) in the predictions of the primordial power spectrum. The fact is that in any scheme thought to be controlled by essentially stochastic rules, one would not expect any relationship—like that requiring the collapse to occur always for very small values of $s_{\mathbf{{k}}}^c$, or in a way that this quantity was always independent of $\mathbf{{k}}$—to hold exactly for all the modes involved, and thus interesting departures from the standard predictions are to be expected. Needless is to say that the effects might be much more important in the event that the collapse was more appropriately treated with the Newtonian scheme (in which the collapse occurs in the momentum conjugate to inflaton field modes). The discussion above shows how the parameters characterizing the different collapse schemes lead to predictions which can, in principle, be compared with the observational data, and are different from the standard ones even when we followed the standard approach in quantizing the gravitational sector of the cosmological perturbations.

4 Discussion

In this paper we have analyzed to what extend do the general properties and details of the results obtained in previous works (e.g. see [1, 25]) depend on the specific approach one takes to deal with the quantum aspects of the problem. In those original treatments the analysis of the collapse had relied on what is commonly known as semiclassical gravity: a classical description for the space-time metric (including its perturbations) coupled to a quantum treatment of the inflaton field. The collapse was assumed to affect the state of the inflaton field, while the metric simply “back-reacts” to the change in the expectation value of the energy-momentum tensor, leading to a geometry that is no longer homogeneous and isotropic. In the present work we implemented the collapse hypothesis on a variable that simultaneously characterizes the metric and the scalar field perturbations at the quantum level, the so called Mukhanov–Sasaki variable. That is, we simply incorporated the collapse hypothesis into the standard treatment found on the literature on the subject, as a way to deal with the basic issue of the transition from the homogeneous and isotropic situation to another one lacking those symmetries, and thus containing the seeds of cosmic structure. We have seen that confronting this issue leads one to results indicating that one can generically expect deviations from the flat primordial spectrum. We have also argued that even if one decides to ignore its shortcomings and adopt the standard posture in which decoherence plus the many world interpretation is taken to address the emergence of inhomogeneity and anisotropy, simple self-consistency would lead one to find essentially the same deviations in the form of the power spectrum as we have found here.

Going back to the present work, the point of view taken here a contrast with that of our previous studies in the specific variable one takes for the realization of the collapse hypothesis. In both types of treatments (the previous ones relying on semiclassical gravity and the present one relying on the joint quantization of metric and inflaton perturbations) we have found that the details of the specific model for the collapse do have an impact on the CMB power spectrum. We have found that similar results are obtained in both approaches if one assumes that the collapse occurs always for very small values of $s^c_{\mathbf{{k}}}$, and one avoids the purely Newtonian scheme of our previous works. On the other hand, it is easy to see that one of the most important differences between the two approaches refers to the predictions on the existence (or lack) of primordial tensor modes generated by the exact same mechanism (and thus at comparable magnitude level) as the scalar ones. This leaves an important open question: which one of the two is the most appropriate treatment of the subject?

We conclude by briefly discussing our current views on this issue (the interested reader is directed to Section 8 of Ref. [2]). Let us consider how can the “collapse of the wave function” fit into our general understanding of physical theory. The basic constituents of our world, as far as we understand them now, are the matter fields described by the standard model of particle physics (augmented to incorporate the masses of neutrinos and the inflaton), the still mysterious dark matter and dark energy, and the gravitational sector. Of these, the standard fields (including the electroweak and strong interactions, as well as the quarks and leptons, and the inflaton) seem to fit quite nicely into a framework incorporating quantum field theory on any reasonable background space-time. The dark matter is likely to be described by some other fields with a similar structure as that given for the ordinary matter (although perhaps involving distinct novel aspects like supersymmetry), and dark energy seems to be most economically described by a cosmological constant (although certainly naturalness and other kinds of issues are still outstanding). However, the component of our world which seems hardest to fit with the general paradigms offered by quantum theory is gravitation.

There exist a very extensive literature on this subject and we will not even attempt to describe all the problems, either technical or conceptual, found in this road. However, it seems quite clear that conceptually there is room for large differences from the usual cases to arise when considering the incorporation of the quantum aspects of Nature in the gravitational context. According to general relativity, gravitation reflects the structure of space-time itself, whereas quantum theory seems to fit most easily in contexts where this structure is a given one. That is, quantum states are associated with objects that “live” in space-times. For instance, the standard Schrödinger equation specifies the time evolution of a system, the quantum states of fields characterize the system in connection to algebras of observables associated with predetermined space-time regions, and so forth. It is clear that mayor conceptual modifications are in order if we want to describe the space-time itself in a quantum language. This issue appears in various guises in the different approaches now available to quantum gravity, most conspicuously as the problem of time which afflicts all attempts to deal with the subject following a canonical approach. It seems thus natural to speculate that it is precisely in this setting where something that departs as dramatically from the quantum orthodoxy as the dynamical collapse of the wave function might find its origin. That is, it seems plausible that in dealing with such conceptual problems, fundamental obstacles might prevent the emergence of the usual quantum theory as the full effective description when gravity is concerned. Lingering aspects of that more fundamental description would take the form of deviations from the standard unitary evolution that characterize quantum theory as we know it. In fact, there are already indications about such deviations in analysis that attempt to recover time, in a relational setting, by using some variables of the theory to play the role of physical clocks (see for instance the Refs. [39, 40]).

In other words, it seems natural to conjecture that the departure form the standard paradigm, that we have considered here as described effectively by the “collapse of the wave function”, corresponds to lingering features of the fundamental timeless (and probably spaceless) theory of quantum gravity. If that is the case, the emergence of space-time itself would be tied to the incorporation of such effective quantum description of matter fields living on space-time, and evolving approximately according to standard quantum field theory on curved spaces, with some small deviations which might include our hypothetical collapse. In that context it seems clear that space-time itself would be nothing but an effective description of the underlying quantum gravity reality. Ideas of this sort regarding emergent gravity have been indeed considered previously, for instance in [41, 42]. This suggests that in the context where we consider the collapse of the wave function the space-time itself must be regarded as an approximate phenomenological description, and thus as something that can not be subjected to quantization. Let us imagine for a moment that we want to consider the propagation of heat in a medium. It is well known that this can be described by the heat equation $\partial T/ \partial t - \nabla ^2 T = S$, where $S$ represents the heat sources. It is quite clear that despite the fact that this looks like a standard type of equation for some field, it would be meaningless to quantize it. Moreover, we can imagine some situation in which the source of heat requires a quantum mechanical treatment, so that $S$ becomes some quantum operator. Under such conditions it seems reasonable that to the extent that the temperature description is still relevant and of interest, the right hand side of the equation above should be replaced by something like $\langle \hat{S} \rangle$. Of course there will be situations that are so far removed from the context where the heat equation was derived that even the notion of temperature itself would become meaningless. We equally expect that in the quantum gravity theory we will be able to find many situations where the semiclassical Einstein’s equations would be completely inappropriate, but in following with our line of thought and simple analogy above, it seems quite likely that those would correspond to situations where the concept of space-time itself becomes meaningless.

Of course all these arguments above are filled with “educated” guesses and conjectures, and we can not take them as more than a guidance. Then, it is important to determine to what extent our predictions depend on the precise way to implement our ideas: semiclassical gravity or the Mukhanov–Sasaki approach. The study of this question was the main purpose of the analysis we have carried out in this manuscript. We have found that the predictions made by our proposal (i.e. the collapse) are generically different from the standard ones, and can be directly confronted with observations. (Indeed, as it has been argued in this paper, and was previously noticed in [1, 2], the standard treatment do not make any prediction at all). On the other hand, the predictions found in this paper (and which were obtained following the standard approach of quantizing the perturbations in the geometry but with the additional ingredient we called the self-induced collapse hypothesis) are very similar to those obtained in previous works (using the semiclassical approach) as far as the scalar perturbations are concerned. This strongly suggests that it is not the manner in which we treat the gravitational interaction (truly fundamental or as in an effective theory) that leads to predictions different to the standard ones, but the collapse hypothesis itself, which was introduced into the treatment in order to deal with the more fundamental issues we touched at the Introduction regarding the origins of the primordial perturbations.

Appendix: \(A_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}^c}), {B_{\mathbf{{k}}}}(\eta ,{\eta _{\mathbf{{k}}}}^c), {C_{\mathbf{{k}}}}(\eta ,{\eta _{\mathbf{{k}}}}^c)\) and  \({D_{\mathbf{{k}}}}(\eta ,{\eta _{\mathbf{{k}}}}^c)\)  in  Eq. (16)

In a universe close to de Sitter the functions $A_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c), B_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c), C_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c)$ and $D_{\mathbf{{k}}}(\eta ,\eta _{\mathbf{{k}}}^c)$ in Eq. (16) take the form

$$\begin{aligned} X_{\mathbf{{k}}} (\eta ,\eta _{\mathbf{{k}}}^c)&= X_{\mathbf{{k}}}^{(1)} (\eta ,\eta _{\mathbf{{k}}}^c)\cos \Delta _{\mathbf{{k}}}^c + X_{\mathbf{{k}}}^{(2)} (\eta ,\eta _{\mathbf{{k}}}^c)\sin \Delta _{\mathbf{{k}}}^c. \end{aligned}$$

(37)

Here $X$ denotes $A, B, C$ or $D$, with the different $X_{\mathbf{{k}}}^{(i)}(\eta ,\eta _{\mathbf{{k}}}^c)$ given by

$$\begin{aligned}&A_{\mathbf{{k}}}^{(1)} = 1-\frac{1}{s}\,C_{\mathbf{{k}}}^{(1)},\quad A_{\mathbf{{k}}}^{(2)} = \frac{1}{s_{\mathbf{{k}}}^c}-\frac{1}{s}\,C_{\mathbf{{k}}}^{(2)},\end{aligned}$$

(38a)

$$\begin{aligned}&B_{\mathbf{{k}}}^{(1)} =-C_{\mathbf{{k}}}^{(1)}C_{\mathbf{{k}}}^{(2)}, \quad B_{\mathbf{{k}}}^{(2)} =- 1+\frac{1}{s^2}+\frac{1}{s_{\mathbf{{k}}}^{c\,2}}-\frac{1}{ss_{\mathbf{{k}}}^c}C_{\mathbf{{k}}}^{(2)},\end{aligned}$$

(38b)

$$\begin{aligned}&C_{\mathbf{{k}}}^{(1)} = \frac{1}{s}-\frac{1}{s_{\mathbf{{k}}}^c},\quad \quad \; C_{\mathbf{{k}}}^{(2)} = 1+\frac{1}{ss_{\mathbf{{k}}}^c},\end{aligned}$$

(38c)

$$\begin{aligned}&D_{\mathbf{{k}}}^{(1)} = 1+\frac{1}{s_{\mathbf{{k}}}^c}\,C_k^{(1)}, \quad D_{\mathbf{{k}}}^{(2)} =-\frac{1}{s}\left(1-\frac{s}{s_{\mathbf{{k}}}^c}\,C_{\mathbf{{k}}}^{(2)}\right). \end{aligned}$$

(38d)

Remember that we are using $s\equiv k\eta , s_{\mathbf{{k}}}^c\equiv k\eta _{\mathbf{{k}}}^c$ and $\Delta _{\mathbf{{k}}}^c\equiv s-s_{\mathbf{{k}}}^c$.