1 Introduction

Surface waves travel along a “free” surface, such as the earth–air or the earth–water interface, and are usually characterized by relatively low velocity, low frequency, and high amplitude (Sheriff 2002). Rayleigh (1885) waves are the most fundamental of the surface waves, resulting from interfering P and SV waves, with strongest amplitudes in the neighborhood of the free surface of a planar elastic body (Aki and Richards 2002). For the case of a homogeneous medium, the velocity of propagation is 0.88–0.95 times the shear velocity, depending on Poisson’s ratio. In the case of one layer over a solid homogenous half-space, however, Rayleigh waves become dispersive when their wavelengths are in the range of 1–30 times the layer thickness (Stokoe et al. 1994). Longer wavelengths penetrate greater depths for a given mode, generally exhibit greater phase velocities, and are more sensitive to the elastic properties of the deeper layers (Babuska and Cara 1991). Conversely, shorter wavelengths are sensitive to the physical properties of surface layers. Therefore, a particular mode of surface wave will possess a unique phase velocity for each unique wavelength, leading to the dispersion of surface waves. In general, in case of a normally dispersive layered earth model, Rayleigh wave fundamental mode at the high frequency is approaching about 0.9 times S wave velocity of the top layer, while higher modes approach the S wave velocity of the top layer, and the fundamental mode at the low frequency approaches about 0.9 times S wave velocity of the half-space, while the higher modes reach the S wave velocity of the half-space (e.g., Xia 2014).

Love (1911) waves are another kind of surface waves, formed by constructive interference of multiple reflections of SH waves at the free surface (Bullen and Bolt 1985), and their particle motion is parallel to the surface but perpendicular to the direction of propagation. In order to exist, they require an increased velocity at some depth. They cannot, however, exist in a homogeneous half-space (Aki and Richards 2002). The dispersion characteristic of Love waves is independent of P wave velocity (Aki and Richards 2002). Moreover, generally for all the modes (whatever the fundamental or higher modes) of Love waves in case of a normally dispersive layered earth model, the asymptote of the phase velocity at high frequencies approaches the S wave velocity of the top layer and the asymptote at low frequencies approaches the S wave velocity of the half-space. Some works (e.g., Xia et al. 2012) suggested that Love wave dispersion curves are simpler than dispersion curves of Rayleigh waves. Numerical modeling results (Xia et al. 2012) also suggested that the independence of P wave velocity makes dispersion curves of Love wave energy have less chance possessing a complication of “Mode Kissing” or osculation, which is a phenomenon of a phase velocity of a lower mode being almost equal to that of a higher mode at some frequency (Xia et al. 2006a; Boaga et al. 2013; Gao et al. 2016). This phenomenon in Rayleigh wave analysis causes mode misidentification and results in that an inverted S wave velocity model possesses higher velocities than the true model (Zhang and Chan 2003).

Surface-wave analysis is nowadays widely adopted for building shear wave velocity profiles at a multiple scales—global seismology, exploration geophysics, near-surface geophysics (e.g., Kennett and Yoshizawa 2002; Yao et al. 2008; Snieder et al. 2009; Socco et al. 2010; Foti et al. 2011; Gabàs et al. 2016; Imposa et al. 2016). All of these applications share the same principles: they use the dispersive characteristic of surface waves to infer the properties of the medium by identifying the model parameters. In near-surface applications, the multichannel analysis of surface wave (MASW) and multichannel analysis of Love wave (MALW) methods have been given increasingly more attention and widely used to determine near-surface S wave velocities during the past two decades (e.g., Song et al. 1989; Miller et al. 1999; Park et al. 1999; Xia et al. 1999, 2006b, 2009, 2012, 2014; Ivanov et al. 2006; Mi et al. 2015, 2017; Fiore et al. 2016). Furthermore, with the aim of supplying the S wave velocity distribution in complex structures, some improvements have been proposed to account for lateral variations in recent years (e.g., Hayashi and Suzuki 2004; Strobbia and Foti 2006; Lin and Lin 2007; O’Neill et al. 2008; Socco et al. 2009; Vignoli and Cassiani 2010; Vignoli et al. 2011, 2016; Romdhane et al. 2011; Bergamo et al. 2012; Ikeda et al. 2013; Kaslilar et al. 2013; Bergamo and Socco 2014; Bignardi et al. 2012, 2014, 2015; Boiero and Socco 2014; Sloan et al. 2015; Schwenk et al. 2016; Pan et al. 2016; Yin et al. 2016; Groos et al. 2017).

Regardless of the type of surface waves used, the standard procedure for surface-wave analysis can be divided into three main steps: (I) acquire the experimental data, (II) process the data to obtain the experimental dispersion curves, and (III) invert the dispersion curves to estimate model parameters. Therefore, one of the key steps of using surface-wave methods to obtain S wave velocities is to pick correct phase velocities in dispersive images, especially when higher modes (e.g., Beaty et al. 2002; Beaty and Schmitt 2003; Xia et al. 2003; Ryden et al. 2004; Xu et al. 2006; Luo et al. 2007; Maraschini and Foti 2010; Ikeda et al. 2015; Bergamo and Socco 2016) are included in the inversion. It is essential to identify different modes in experimental data, and it is necessary to compare the experimental curve branches with specific theoretical modes. Hence, in most approaches to surface waves, the phase velocities need to be attributed to a specific propagation mode. This task is not straightforward because some modes may not be present in the experimental data and very smooth changes from one mode to another may occur (Forbriger 2003a, b; Boaga et al. 2013; Gao et al. 2016). The misidentification of modes may produce significant errors (e.g., Zhang and Chan 2003; Zhang et al. 2003; Maraschini et al. 2010; Gao et al. 2014).

In the real-world applications, the complexity of energy distribution on a dispersion image is exacerbated due to the complicated near-surface earth models. Previous studies about a low-velocity layer (LVL) among a layered earth model found that dispersive energy of such model “jumps” from the fundamental mode to higher modes and may not return to the fundamental mode at higher frequencies (Zhang et al. 2000, 2002; Nil 2005; O’Neill and Matsuoka 2005; Lu et al. 2007; Tsuji et al. 2012; Boaga et al. 2014), which leads to mode misidentification (O’Neill and Matsuoka 2005; Boaga et al. 2014; Dal Moro et al. 2015) and incorrect inversion outcomes (Zhang and Chan 2003; Liang et al. 2008; Tsuji et al. 2012; Boiero et al. 2013). Safani et al. (2006) also showed that it is difficult to identify Love wave mode if an LVL is bounded by equally stiff layers. The osculation points become more significant when the medium contains low-velocity layers. Sometimes the measured dispersion curve switches modes in the vicinity of osculation points (e.g., Zhang and Lu 2003a; Nil 2005; Liu and Fan 2012). Zhang and Lu (2003a) gave an explanation for the discontinuous dispersion curves by analyzing the surface displacement of each mode theoretically. They pointed out that the discontinuous dispersion curves are caused by the change of dominant modes with frequency. Ryden and Lowe (2004) also showed this discontinuous dispersion curves in stratified media with decreasing velocity with depth, and they called them fluctuating dispersion curves.

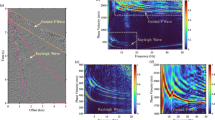
Here we give a real-world example about the Rayleigh wave dispersion energy jumping on a dispersion image (more field examples can be found in O’Neill and Matsuoka 2005; Safani et al. 2006; Socco et al. 2011; Tsuji et al. 2012; Boiero et al. 2013; Boaga et al. 2014; Dou and Ajofranklin 2014; Dal Moro et al. 2015). A 24-channel seismic record (Fig. 1a) was acquired with 24 vertical-component geophones at a location in Washington DC, USA. The borehole measurements at this site showed a very loose clayey sand layer at the depth of 2–4 m, which suggests there exists an LVL. The geophone spacing is 1.5 m, and the nearest offset is 6 m. The energy of Rayleigh waves is dominated in the data. A dispersion image in the frequency–phase velocity (f–v) domain (Fig. 1b) is generated from the multichannel record by the high-resolution linear Radon transformation (LRT, Luo et al. 2008) without any preprocessing. We can notice that dispersive energy of Rayleigh waves “jumps” from the fundamental mode to higher modes and the energy of the fundamental mode disappears at higher frequencies (Fig. 1b). In addition, the overall energy trends to higher phase velocities at higher frequencies.

Fig. 1
figure 1

a A real-world example of Rayleigh wave data, acquired from Washington DC, USA, with a 24-channel system. The geophone spacing is 1.5 m, and the nearest offset is 6 m. b A dispersive image in the f–v domain for the Rayleigh wave data in (a), calculated by the high-resolution LRT (Luo et al. 2008)

Full size image

What in essence causes the discontinuous dispersion energy distribution as shown in Fig. 1b? Although several papers have reported issues in picking and then inverting surface waves in the presence of low-velocity layers (e.g., Safani et al. 2006; Lu et al. 2007; Liang et al. 2008; Tsuji et al. 2012; Boiero et al. 2013; Boaga et al. 2014), it still remains unclear why the energy of each mode “jumps” or disappears at higher frequencies for an LVL model. Previous studies on the surface waves in an LVL model (e.g., Zhang et al. 2000, 2002; Nil 2005; Liu and Fan 2012) were based on computing the theoretical dispersion curves and their corresponding eigenfunctions with efficient algorithms (e.g., Thomson 1950; Haskell 1953; Schwab and Knopoff 1972; Abo-Zena 1979; Kennett 1983; Chen 1993; He et al. 2006). Few researchers focused on the dispersion energy characteristics based on surface-wave wavefield modeling.

In this paper, we analyze the dispersion energy of Rayleigh and Love waves based on finite-difference wavefield modeling (Virieux 1984, 1986; Xu et al. 2007; Luo et al. 2010; Zeng et al. 2011) and compare the energy with theoretical dispersion curves in near-surface layered models. For the accurate recognition of peak values of each mode energy concentration in the f–v domain, dispersion images are generated by the high-resolution LRT (Luo et al. 2008, 2009) from synthetic shot gathers to present energy distribution of Rayleigh and Love waves. We first compare three synthetic models to show the dispersion characteristics of Rayleigh and Love waves in an LVL model. Then, we introduce the guided waves generated in an LVL (LVL-guided waves) to clarify the complexity of the dispersion energy. We verify the energy of LVL-guided waves by analyzing the snapshots of SH and P–SV wavefield and comparing the dispersive energy with theoretical values of phase velocities calculated by the Knopoff method (Schwab and Knopoff 1972) and the generalized R/T coefficients algorithm (Chen 1993). Finally, we elaborate the effects of dispersion energy of LVL-guided waves in mode identification and discuss some properties of LVL-guided waves.

2 What are the Characteristics of Dispersion Energy for an LVL Model?

In order to study the propagation and dispersion characteristics of Rayleigh and Love waves, we first designed three three-layer models (Table 1) and performed dispersive analysis on the modeled Rayleigh and Love waves. In the finite-difference modeling of Rayleigh and Love waves, the source is a 20-Hz (peak frequency) Ricker wavelet with a 60-ms delay, located at the free surface. For the finite-difference implementation, the model is uniformly discretized into 0.1*0.1 m cells so that the grid sample density is sufficient (at least 20 points per wavelength). The time step size is chosen as 0.05 ms to ensure that the finite-difference algorithm is numerically stable. Seismic responses are recorded on the free surface with a 60-channel receiver array. The nearest offset is 30 m (for a more accurate image of dispersion energy, Pan et al. 2013a), with a subsequent 1-m receiver interval.

Table 1 Parameters of three-layer models
Full size table

The first model (Table 1) represents a “normal” layered model with P and S wave velocities increasing with depth. The dispersive images of Rayleigh and Love waves are shown in Fig. 2a, b, respectively. Rayleigh and Love wave energy dominates in two images. Dispersive energy concentrates for each mode distinctly and continuously, and it does not disappear at higher frequencies. Comparing Fig. 2a, b, it is worth mentioning that Love waves have a wider frequency band than Rayleigh waves. The crosses on all of the images in Fig. 2 represent the theoretical phase velocities calculated by the Knopoff method (Schwab and Knopoff 1972).

Fig. 2
figure 2

Dispersion images in the f–v domain for the three-layer models (Table 1). Rayleigh wave energy distribution is shown in a, c, and e for model 1, model 2, and model 3, respectively. Love wave energy distribution is shown in b, d, and f for model 1, model 2, and model 3, respectively. The crosses represent the theoretical dispersion curves calculated by the Knopoff method (Schwab and Knopoff 1972)

Full size image

The second model (Table 1) contains a high-velocity layer (HVL). Figure 2c, d shows the corresponding dispersive images of Rayleigh and Love waves, respectively. Rayleigh and Love wave energy dominates in two images. Dispersive energy concentrates for each mode distinctly and continuously, and it does not disappear at higher frequencies.

The third model (Table 1) contains an LVL. Figure 2e, f shows the corresponding dispersive images of Rayleigh and Love waves. However, there is almost no energy where the phase velocities are lower than 300 m/s either in Fig. 2e, f. The dispersive energy “jumps” from the fundamental mode to higher modes, and each mode of Rayleigh and Love waves (whatever the fundamental or higher modes) lacks energy in some high frequency range (different modes lack energy in different frequency ranges). The energy trends from low phase velocities to high phase velocities with the increasing frequencies.

Dispersion energy analysis of three-layer models (Fig. 2) reveals some critical characteristics of Rayleigh and Love wave propagation in an LVL model. Each mode of surface waves (whatever the fundamental or higher modes) lacks energy in some high frequency range so dispersion energy looks like “jumping” from the fundamental mode to higher modes.

3 Why Does the Dispersion Energy “Jump” for an LVL Model?

Guided waves are trapped in a waveguide by total reflections or bending of rays at the top and bottom boundaries (Aki and Richards 2002). If we consider the Earth’s surface as the top of a waveguide, surface waves, such as Rayleigh, Love, and their higher modes, are guided waves (e.g., Roth et al. 1998). If there is an LVL in an earth model, one kind of guided waves will be generated and propagate in that layer where most of the energy is trapped (Kennett 1983; Aki and Richards 2002; Zhang and Lu 2003b; Shen 2014). In order to facilitate the analysis, we call this kind of guided waves as LVL-guided waves, which is a trapped wave mode (Liu and Fan 2012), distinguished from other modes of surface waves. LVL-guided waves are also dispersive because longer wavelengths can penetrate out of the LVL for a given mode, generally exhibit greater phase velocities, and are more sensitive to the elastic properties of the top and bottom layers. Conversely, shorter wavelengths with lower phase velocities are trapped in the LVL. The penetrating depth/distance of LVL-guided waves is related to its wavelength, which is similar to the properties of other surface-wave modes (e.g., Sanchez-Salinero et al. 1987; Babuska and Cara 1991; Rix and Leipski 1991; Liu and Fan 2012; Yin et al. 2014).

We produce the P–SV and SH wavefield snapshots (Fig. 3) for the three three-layer models (Table 1). It shows that, for both of the P–SV and SH wavefield, there is strong energy trapped in the LVL (Fig. 3e, f), which is the LVL-guided wave. With LVL-guided waves, we can explain why the dispersion energy “jumps.” Shot gathers on the free surface can record all seismic waves that spread to the surface, and dispersive images generated from the shot gather contain full wavefield information. Therefore, dispersion energy contains the information of all kinds of guided waves. If there is an LVL in an earth model, LVL-guided waves will be generated and possess energy on dispersive images, which can interfere with the normal dispersion energy of Rayleigh or Love waves. Moreover, shorter wavelengths (generally with lower phase velocities and higher frequencies) of LVL-guided waves may not penetrate to the free surface, so each mode of LVL-guided waves at the free surface lacks energy in some high frequency range. As a consequence, the dispersive energy looks like “jumping” from the fundamental mode to higher modes.

Fig. 3
figure 3

Snapshots of P–SV and SH wavefield for the three-layer models (Table 1). a, c, and e show the vertical particle velocities (vz) of P–SV wavefield at t = 130 ms for model 1, model 2, and model 3, respectively. b, d, and f show the horizontal particle velocities (vy) of SH wavefield at t = 100 ms for model 1, model 2, and model 3, respectively. ‘R’ represents Rayleigh wave, ‘L’ represents Love wave, and ‘G’ in the LVL represents LVL-guided wave

Full size image

Different from Rayleigh waves, Love waves will not be generated in the top layer if the S wave velocity of the second layer is lower than that of the top layer. So there is no Love wave energy in the top layer of the third three-layer model with an LVL (Fig. 3f). While if the S wave velocity of the second layer is lower than that of the top and bottom layers, LVL-guided waves will be generated in that low-velocity layer (Fig. 3f). Therefore, the dispersive image of Love waves for the third three-layer model with an LVL (Fig. 2f) only contains the dispersion energy of LVL-guided waves.

In order to validate our explanation further, we designed a six-layer model with two LVLs (Table 2, modified from Xia et al. 1999) and performed dispersive analysis on the modeled Rayleigh and Love waves. In the finite-difference modeling, the source is a 20-Hz (peak frequency) Ricker wavelet with a 60-ms delay, located at the free surface. Seismic responses are recorded on the free surface with a 60-channel receiver array. The nearest offset is 30 m, with a subsequent 1-m receiver interval.

Table 2 Parameters of a six-layer model with two LVLs (modified from Xia et al. 1999)
Full size table

The six-layer model (Table 2) contains two LVLs (the second and fourth layers). As the analysis in previous paragraphs, two series of LVL-guided waves will be generated in the second and fourth layers, respectively. Figure 4a shows energy distribution of normal Rayleigh waves and guided waves generated in the two LVLs based on P–SV wave equations. R0, with the asymptote at the high frequency approaching about 0.9 times the S wave velocity of the top layer, represents the fundamental energy of normal Rayleigh waves. However, the higher mode energy of normal Rayleigh waves and the energy of LVL-guided waves are complicated and difficult to be identified. By contrast, the energy distribution image of Love waves (Fig. 4b) is simpler, which is the guided wave energy generated in the two LVLs based on SH wave equations. G2-0, G2-1, G2-2, and G2-3, lacking of energy in some high frequency range and not approaching the S wave velocity of the top layer, represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the second layer (the first LVL), respectively (we will confirm it further later); G4-0, G4-1, G4-2, and G4-3, having energy only in a greater wavelength range, represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the fourth layer (the second LVL), respectively.

Fig. 4
figure 4

Dispersion images in the f–v domain for the six-layer model with two LVLs (Table 2). a shows energy distribution of normal Rayleigh waves and guided waves generated in the two LVLs based on P–SV wave system. R0 represents the fundamental energy of Rayleigh waves; the higher mode energy of normal Rayleigh waves and the energy of LVL-guided waves are difficult to be identified. b shows energy distribution of the guided waves generated in the two LVLs based on SH wave system. G2-0, G2-1, G2-2, and G2-3 represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the second layer (the first LVL), respectively; G4-0, G4-1, G4-2, and G4-3 represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the fourth layer (the second LVL), respectively. The crosses represent the theoretical dispersion curves calculated by the Knopoff method (Schwab and Knopoff 1972)

Full size image

The theoretical dispersion curves calculated by the Knopoff method (marked with crosses in Fig. 4) become more complicated because of the existence of two LVLs. Some researchers (e.g., Lu et al. 2007; Pan et al. 2013b) have found that when the S wave velocity of the surface layer is higher than some of the layers below, the surface-wave phase velocity in a high frequency range calculated by existing algorithms based on solving dispersion equation (e.g., the Knopoff method) approaches a velocity related to the lowest S wave velocity among the layers, rather than a value related to the S wave velocity of the surface layer. Theoretically, trends of surface-wave dispersive energy approach a value related to the S wave velocity of the surface layer at a high frequency range when its wavelength is much shorter than the thickness of the surface layer. So they proposed methods to calculate the “correct” dispersion curve fitting the surface-wave dispersive energy (e.g., Pan et al. 2013b). According to our analysis previously, however, due to the existence of LVLs, theoretical dispersion curves calculated by the Knopoff method contain the phase velocity information of LVL-guided waves and they approach the LVL velocity in a high frequency range. Because shorter wavelengths of LVL-guided waves cannot penetrate to the free surface, there is no energy to fit the dispersion curve at a high frequency range. Therefore, the LVL-guided waves having lack of energy at a high frequency range leads to the misfit between the dispersion curve and dispersion energy, which looks that the dispersion curve is “wrong” calculated by the Knopoff method.

Shen et al. (2015) pointed out that the generalized reflection and transmission (R/T) coefficients method (Chen 1993) can calculate the roots of the dispersion equation that have displacements at the layer interface, which can be used to calculate theoretical dispersion curves to fit the dispersion energy of surface waves and guided waves generated in LVLs. In order to confirm different modes of guided waves generated in different LVLs, we will give the dispersion energy based on finite-difference modeling of SH wavefield and theoretical dispersion curves calculated by the generalized R/T coefficients algorithm at every layer interface for the six-layer model with two LVLs (Table 2). Figure 5 shows snapshots of SH wavefield for the six-layer model, and we can notice strong energy of LVL-guided waves in both of the two LVLs. The observation system (illustrated in Fig. 6) is used in the finite-difference modeling. Seismic responses are recorded on every layer interface with a 60-channel receiver array. The nearest offset is 30 m, with a subsequent 1-m receiver interval. The corresponding dispersive images are shown in Fig. 7.

Fig. 5
figure 5

Snapshots of SH wavefield for the six-layer model with two LVLs (Table 2). a, b, c, and d show the horizontal particle velocities (vy) at t = 100, 200, 300, and 400 ms, respectively. We can notice strong energy of guided waves in two LVLs

Full size image
Fig. 6
figure 6

An illustration of the observation system in the finite-difference modeling of SH wavefield for the six-layer model with two LVLs (Table 2). The source is a 20-Hz (peak frequency) Ricker wavelet with a 60-ms delay, located at the free surface. Seismic responses are recorded on every layer interface with a 60-channel receiver array. The nearest offset is 30 m, with a subsequent 1-m receiver interval

Full size image
Fig. 7
figure 7

Dispersion images of SH wavefield in the f–v domain at different layer interfaces for the six-layer model with two LVLs (Table 2). a–f show energy distribution of the LVL-guided waves at the top interfaces from the first to sixth layers, respectively. The crosses represent the corresponding roots of the dispersion equation at different layer interfaces calculated by the generalized reflection and transmission coefficients method (Chen 1993). G2-0, G2-1, G2-2, and G2-3 represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the second layer, respectively; G4-0, G4-1, G4-2, and G4-3 represent the energy of the fundamental and the first, second, and third higher modes of the LVL-guided waves generated in the fourth layer, respectively

Full size image

The crosses (Fig. 7) represent the corresponding roots of the dispersion equation that have displacements at different layer interfaces, calculated by the generalized R/T coefficients method (Chen 1993). The frequency range of energy distribution of the LVL-guided waves and roots of the dispersion equation changes at different layer interfaces because different wavelengths of LVL-guided waves can penetrate different depths to the LVL. By comparing Fig. 7a–f, we can notice that G2-0, G2-1, G2-2, and G2-3 have strong energy in the high frequency range at the top interface of the second layer (Fig. 7b), and roots of the dispersion equation also have a wider frequency range than that of other layer interfaces, which are confirmed as different modes of LVL-guided waves generated in the second layer. G4-0, G4-1, G4-2, and G4-3 have strong energy in the high frequency range at the top interface of the fourth layer (Fig. 7d), and roots of the dispersion equation also have a wider frequency range, which are confirmed as different modes of LVL-guided waves generated in the fourth layer.

The asymptotes of LVL-guided wave dispersion curves at the high frequency approach S wave velocity of the LVL. In the real world, however, the shot gather is recorded on the free surface and the LVL has a distance to the free surface. Thus, shorter wavelengths of LVL-guided waves may not penetrate to the free surface, and then each mode of LVL-guided waves (whatever the fundamental or higher modes) lacks energy in some high frequency range. This is different from the properties of normal Rayleigh and Love waves, whose shorter wavelengths travel around the free surface and they usually have energy in a high frequency range. This principle may be used to identify whether the energy on the dispersive image is surface wave or LVL-guided wave.

4 What Effects Does the Dispersion Energy of LVL-Guided Waves have on Mode Identification?

In the previous discussions about the near-surface LVL models, the S wave velocity of the LVL is acquiescently lower than that of the surface layer in the layered earth model (e.g., Zhang et al. 2000, 2002; Zhang and Chan 2003; Nil 2005; O’Neill and Matsuoka 2005; Lu et al. 2007; Liang et al. 2008; Pan et al. 2013b). LVL-guided waves are generated in a waveguide when the S wave velocity of this layer is lower than the neighboring top and bottom layers. So the S wave velocity of the LVL can be higher than that of the surface layer. In order to analyze the influence on the dispersion energy distribution of Rayleigh and Love waves with different S wave velocities of the LVL, we designed three six-layer models with different P and S wave velocities in one LVL (Table 3). In the finite-difference modeling, the source is a 20-Hz (peak frequency) Ricker wavelet with a 60-ms delay, and located at the free surface. Seismic responses are recorded at the free surface with a 60-channel receiver array. The nearest offset is 30 m, with a subsequent 1-m receiver interval.

Table 3 Parameters of three six-layer models (modified from Xia et al. 1999)
Full size table

The first six-layer model (Table 3) represents a “normal” layered model with P and S wave velocities increasing with depth. Rayleigh and Love wave energy dominates in Fig. 8a, b, respectively. Dispersive energy concentrates for each mode distinctly and continuously and agrees well with the theoretical dispersion curves calculated by the generalized R/T coefficients method (Chen 1993). R0 (Fig. 8a) represents the fundamental mode of Rayleigh waves. L0, L1, L2, and L3 (Fig. 8b) represent the fundamental, first higher, second higher, and third higher modes of Love waves, respectively. However, the higher mode energy of Rayleigh waves is weak and difficult to be identified. There is no LVL-guided wave energy both in the dispersive images of Rayleigh and Love waves.

Fig. 8
figure 8

Dispersion images in the f–v domain for the three six-layer models (Table 3). P–SV wavefield energy distribution is shown in a, c, and e for model 1, model 2, and model 3, respectively. SH wavefield energy distribution is shown in b, d, and f for model 1, model 2, and model 3, respectively. R0 represents the fundamental mode of Rayleigh waves. L0, L1, L2, and L3 represent the fundamental, first higher, second higher, and third higher modes of normal Love waves, respectively. G4-0 represents the energy of the fundamental mode of LVL-guided waves generated in the fourth layer. The crosses represent the theoretical dispersion curves calculated by the generalized R/T coefficients method (Chen 1993)

Full size image

The second model (Table 3) contains an LVL (the fourth layer), and the P and S wave velocities of the fourth layer are lower than those of the third and fifth layers, but higher than that of the first layer. Figure 8c, d shows the corresponding dispersive images of Rayleigh and Love waves. R0 (Fig. 8c) represents the fundamental mode of Rayleigh waves. L0 and L1 (Fig. 8d) represent the fundamental and first higher modes of normal Love waves, respectively. It is difficult to identify the higher modes of normal Rayleigh waves and the energy of LVL-guided waves (Fig. 8c). But it is obvious that G4-0 (Fig. 8d), possessing energy only in a low frequency range (a greater wavelength range) and lacking energy in a high frequency range, represents the energy of the fundamental mode of the LVL-guided waves generated in the fourth layer. There is no root for the dispersion curve G4-0 in the high frequencies with Chen’s method, and it intersects with the first higher mode of normal Love waves L1.

The third model (Table 3) contains an LVL (the fourth layer), and the P and S wave velocities of the fourth layer are lower than that of the first layer. Figure 8e, f shows the corresponding dispersive images of Rayleigh and Love waves. R0 (Fig. 8e) represents energy of the fundamental mode of Rayleigh waves, which looks discontinuous because of the existence of LVL-guided waves with strong energy (G4-0, the fundamental mode of the LVL-guided waves). And the fundamental mode dispersion curve of Rayleigh waves intersects with the fundamental mode of the LVL-guided waves. L0 and G4-0 (Fig. 8f) represent energy of the fundamental modes of Love waves and LVL-guided waves, respectively. With the interference of the fundamental mode energy (G4-0) of LVL-guided waves, the fundamental mode of Love waves (L0) appears broken at around 20 Hz and connects with the fundamental mode energy of LVL-guided waves. The osculation points become more significant for Love waves (Fig. 8f) than for Rayleigh waves (Fig. 8e) when the medium contains low-velocity layers. Liu and Fan (2012) found that nearby the osculation points, “coupled modes” that show the characteristics of two different modes simultaneously exist. In these areas, the two neighboring dispersion curves can exchange their corresponding modes of surface waves sometimes. The mode conversion can happen between LVL-guided waves and surface waves in the vicinity of osculation points (such as the point at around 20 Hz in Fig. 8f). And it is difficult to identify the higher modes of LVL-guided waves and surface waves (Fig. 8e, f) because of the complicated osculation points.

5 Discussion

Comparing the results of dispersion analysis for the three six-layer models (Fig. 8), we can conclude that LVL-guided waves will be generated if there is an LVL in an earth model, and the energy of LVL-guided waves at the free surface will contaminate the dispersion energy of surface waves. The interferential position and degree depend on the S wave velocity and depth of the LVL. If the S wave velocity of the LVL is higher than that of the surface layer, dispersion energy of LVL-guided waves approaches higher velocities (related to the S wave velocity of the LVL) at the high frequency than those of surface waves. So the energy of LVL-guided waves only contaminates higher mode energy of surface waves, and there is no interlacement with the fundamental mode of surface waves. While if the S wave velocity of the LVL is lower than that of the surface layer, dispersion energy of LVL-guided waves approaches lower velocities (related to the S wave velocity of the LVL) at the high frequency than those of surface waves. So the energy of LVL-guided waves may interlace with the fundamental mode of surface waves (as shown in Fig. 8f), which is the most important mode in inversion. Both of the interlacements with the fundamental mode or higher mode energy may cause misidentification for the dispersion curves of surface waves and produce errors in inversion.

Each mode of LVL-guided waves lacks energy in some high frequency range because shorter wavelengths of LVL-guided waves cannot penetrate to the free surface. If we refer to one-half-wavelength estimations (e.g., Sanchez-Salinero et al. 1987; Rix and Leipski 1991), the fundamental mode of LVL-guided waves can penetrate to the free surface (have energy on dispersive images) when its wavelengths are longer than 2 times of the LVL depth. Actually, however, longer wavelengths of LVL-guided waves are needed for penetrating to the free surface because most of the energy is trapped in the LVL, especially with strong Vs contrast between the LVL and its neighboring layers. What is more, by analyzing the energy distribution (Fig. 2f), we notice that the shortest wavelength that can penetrate to the free surface for each mode is becoming smaller for higher modes, which means with the same wavelength, higher modes of LVL-guided waves can penetrate to greater distances. This is also similar to the properties of normal Rayleigh and Love waves.

6 Conclusions

We have analyzed the dispersion energy of Rayleigh and Love waves based on finite-difference wavefield modeling in near-surface 2D isotropic elastic media with horizontally homogeneous layered models. Results demonstrate that if there is an LVL in a near-surface earth model, LVL-guided waves will be generated and may possess energy on dispersive images, which can interfere with the dispersion energy of normal Rayleigh or Love waves. We compared the dispersion energy with theoretical dispersion curves calculated by Knopoff’s and Chen’s algorithms. Each mode of LVL-guided waves having lack of energy at the free surface in some high frequency range causes the discontinuity of dispersive energy on dispersive images, which is because shorter wavelengths (generally with lower phase velocities and higher frequencies) of LVL-guided waves cannot penetrate to the free surface. If the S wave velocity of the LVL is higher than that of the surface layer, the energy of LVL-guided waves only contaminates higher mode energy of surface waves and there is no interlacement with the fundamental mode of surface waves. While if the S wave velocity of the LVL is lower than that of the surface layer, the energy of LVL-guided waves may interlace with the fundamental mode of surface waves. Both of the interlacements with the fundamental mode or higher mode energy may cause misidentification for the dispersion curves of surface waves.