Layer-Based Modelling of the Earth’s Gravitational Potential up to 10-km Scale in Spherical Harmonics in Spherical and Ellipsoidal Approximation

Abstract

Global forward modelling of the Earth’s gravitational potential, a classical problem in geophysics and geodesy, is relevant for a range of applications such as gravity interpretation, isostatic hypothesis testing or combined gravity field modelling with high and ultra-high resolution. This study presents spectral forward modelling with volumetric mass layers to degree 2190 for the first time based on two different levels of approximation. In spherical approximation, the mass layers are referred to a sphere, yielding the spherical topographic potential. In ellipsoidal approximation where an ellipsoid of revolution provides the reference, the ellipsoidal topographic potential (ETP) is obtained. For both types of approximation, we derive a mass layer concept and study it with layered data from the Earth2014 topography model at 5-arc-min resolution. We show that the layer concept can be applied with either actual layer density or density contrasts w.r.t. a reference density, without discernible differences in the computed gravity functionals. To avoid aliasing and truncation errors, we carefully account for increased sampling requirements due to the exponentiation of the boundary functions and consider all numerically relevant terms of the involved binominal series expansions. The main outcome of our work is a set of new spectral models of the Earth’s topographic potential relying on mass layer modelling in spherical and in ellipsoidal approximation. We compare both levels of approximations geometrically, spectrally and numerically and quantify the benefits over the frequently used rock-equivalent topography (RET) method. We show that by using the ETP it is possible to avoid any displacement of masses and quantify also the benefit of mapping-free modelling. The layer-based forward modelling is corroborated by GOCE satellite gradiometry, by in-situ gravity observations from recently released Antarctic gravity anomaly grids and degree correlations with spectral models of the Earth’s observed geopotential. As the main conclusion of this work, the mass layer approach allows more accurate modelling of the topographic potential because it avoids 10–20-mGal approximation errors associated with RET techniques. The spherical approximation is suited for a range of geophysical applications, while the ellipsoidal approximation is preferable for applications requiring high accuracy or high resolution.

1 Introduction

1.1 Motivation and Related Work

Global modelling of the Earth’s gravitational potential from its underlying mass distribution in spherical harmonics is a classical problem in geophysics and geodesy (e.g., Balmino et al. 1973; Rapp 1982; Rummel et al. 1988; Wieczorek 2007, 2015). The solution to this problem can be used for testing of topographic/isostatic hypothesis (Rummel et al. 1988; Göttl and Rummel 2009; Hirt et al. 2012; Grombein et al. 2014), modelling of Bouguer gravity (Balmino et al. 2012; Wieczorek 2015; Rexer et al. 2015), smoothing or reduction of the Earth’s gravity field and its observations [as, for example, needed for Stokes’ geodetic boundary value problem or improved interpolation/prediction with remove-compute-restore techniques (Grombein et al. 2014)], computation of fill-in gravity for combined gravity field models (Pavlis et al. 2007, 2012; Fecher et al. 2013), omission error modelling (Hirt et al. 2011; Rexer and Hirt 2015a) and the evaluation of digital elevation models (Rexer et al. 2015).

For some of the listed applications, a forward model that is as close as possible to the actual gravity field is desirable. Aiming at such a "perfect" synthetic gravitational model, an accurate mass model of the Earth is required. Mass models deliver information about the physical geometry of Earth along with density information about its interior. A perfect mass model would be able to describe the masses in terms of infinitesimal small bodies (such as rectangular prisms or tesseroids) at all 3D positions of Earth. Together with an adequate implementation of Newton’s law of gravitation, which means numerical integration over all masses (see, for example, Kuhn and Seitz 2005; Grombein et al. 2014), this mass model would allow to accurately determine the gravitational potential of Earth. However, such a mass model in reality is not practicable as the computational requirements are very challenging, and more prohibitively, because the required density and geometric information is neither available globally nor in 3D with adequate resolution. Today, globally consistent physical surface information (usually provided in terms of digital elevation models) at best is given with a resolution of ${\sim } 12\hbox { m}$ [TanDEM-X satellite mission: Bartusch et al. 2008] and a vertical accuracy of ${\sim } 4\hbox { m}$ (Rexer and Hirt 2016). At short scales $({\sim } 10\hbox { km}$ or less), it is mainly the masses of the crust—the upper part of the lithosphere—and hydrosphere that cause substantial anomalous gravitational signals. The anomalous potential that originates from the Earth’s interior (upper mantle or below) has long-wavelength character. Satellite-borne and terrestrial observation techniques result in complete (global) high-resolution models of the topographic elevation and to some extent also of the bathymetric depth, water bodies and ice sheets (Hirt and Rexer 2015), making forward modelling of short-scale (=crustal) gravity signals possible to ultra-high resolution, e.g., up to ${\sim } 2\hbox { km}$ scale (Balmino et al. 2012) and up to ${\sim } 200\hbox { m}$ scale (Hirt et al. 2013).

In contrast, available density information for the lithosphere (crust and upper mantle, down to about 30 km depth) is limited to a lateral resolution of about 110 km [CRUST1.0 (Laske et al. 2012) and LITHO1.0 (Pasyanos et al. 2014)]. Considering the density profile (vertical resolution), which is derived mainly from seismic tomography, presently available models only distinguish between 8 and 10 different layers, assuming that the density is not varying vertically within each layer. This short review of mass models already suggests that it is convenient and practicable to model Earth’s masses in terms of layers since layers are a natural way to describe the structure of the physical Earth.

Forward modelling can either be conducted by Newtonian integration over Earth’s masses in the space domain, e.g., by using rigorous analytical integration formulas for rectangular prisms (Nagy et al. 2000, 2002) or tesseroids (Grombein et al. 2013; Heck and Seitz 2007), or in the spectral domain, by using relations among surface spherical harmonic coefficients of the geometric boundary surfaces. Historically (Lee and Kaula 1967; Balmino et al. 1973; Rummel et al. 1988) and recently (Wieczorek 2007, 2015; Forsberg and Jensen 2015; Hirt et al. 2015) forward modelling approaches were often used in combination with "single-density” mass models, also known as rock-equivalent topography (RET) models. RET modelling involves a compression of all masses to a layer of constant (rock) density, resulting in approximation errors in the order of several dozens of mGal; see, for example, Grombein et al. (2016) and Kuhn and Hirt (2016). Therefore, it is very useful to have forward modelling approaches that are adapted to rigorous modelling of mass layers. These are available for spatial domain modelling in spherical (Kuhn and Seitz 2005) and ellipsoidal (Grombein et al. 2014) approximation. In spherical approximation, the topographic masses are forward modelled relative to a mass sphere. Correspondingly, in ellipsoidal approximation, a mass ellipsoid as a much closer approximation of the real Earth is used to provide the reference for the forward modelling. For spectral domain modelling a layer-based approach only was formulated in spherical approximation (Pavlis and Rapp 1990; Tenzer et al. 2010, 2015; Root et al. 2016). The spectral approach has mainly been used to create low resolution models, e.g., in

• Pavlis and Rapp (1990): to d/o 360, distinguishing between 6 different terrain types corresponding to the explicit modelling of 4 layers—topography, ocean, ice sheets/glaciers and lake water—as represented by the OSUJAN89 topographic database

• Tenzer et al. (2010): to d/o 90, only ice layer based on the CRUST2.0 model and the surface heights in GTOPO30 (US Geological Survey, released 1996)

• Tenzer et al. (2015): to d/o 180 based on the CRUST1.0 model as contained in the 9 layers—topography, ocean, polar ice sheets, sediments (3 layers) and consolidated crust (3 layers)—of Earth’s spectral crustal model (ESCM180: Chen and Tenzer 2014)

• Tenzer et al. (2016): to d/o 360 based on 4 layers—topography, ocean, inland lakes/seas and ice sheets– of the Earth2014 model (Hirt and Rexer 2015)

• Root et al. (2016): to d/o 1800 based on 2 layers—topography and ocean—of GTOPO30

and also for ultra-high-resolution modelling [Balmino et al. (2012): d/o 10800 based on four layers—topography, ocean, inland lakes/seas and ice sheets—of the ETOPO1 model (Amante and Eakins 2009)]. Note that in the work of Balmino et al. (2012), Tenzer et al. (2010) and Root et al. (2016) the integration is facilitated using a binominal series. In these cited works, the series expansion is evaluated only up to the third-order term resulting in (unknown) truncation errors (see Sect. 2.3), while Pavlis and Rapp (1990) present a rigorous integration which is more accurate but computationally more demanding, especially for high resolutions.

Recently, Claessens and Hirt (2013) have developed a spherical harmonic technique to model the Earth’s gravitational potential in ellipsoidal approximation, i.e. with respect to a reference ellipsoid. In contrast to the spherical concepts of Rummel et al. (1988); Pavlis and Rapp (1990); Balmino et al. (2012); Wieczorek (2015); Tenzer et al. (2015)—where the topograpdhic masses are considered relative to a reference sphere—the Harmonic Combination Method (HCM) (Claessens and Hirt 2013) models the topographic masses considered relative to a reference ellipsoid. Thus, the HCM provides the gravity spectrum to the same level of approximation (w.r.t. the same reference) as most spherical harmonic gravity field models based on observations available at IAG’s International Center for Global Earth Models (ICGEM: http://icgem.gfz-potsdam.de/ICGEM/). This, as will be shown, is a major advantage especially when it comes to combining and comparing the forward models with satellite data or other terrestrial data.

We may thus define—because of the underlying ellipsoidal approximation—Claessens and Hirt (2013) to provide a solution to the ellipsoidal topographic potential (ETP) while the methods based on a spherical approximation of the Earth’s masses provide a solution to the spherical topographic potential (STP).

Tenzer et al. (2015) and Root et al. (2016) provide the framework for layer-based modelling of the STP. For the ETP, such a framework is still missing. The HCM as formulated in Claessens and Hirt (2013) is designed for a single-density mass model, but it can be reformulated to adopt layer-based mass models, as will be shown in this contribution.

1.2 This Work: Contributions to Spectral Forward Modelling

In this contribution, we formulate a new spherical harmonic approach to compute the ETP from arbitrary volumetric layers having laterally varying density. The approach is based on the Harmonic Combination Method (Claessens and Hirt 2013) and allows the layers to be referenced to the surface of some reference ellipsoid. The new approach is then validated by modelling the Earth’s gravitational potential as implied by the masses of layers of the solid crust, ocean water, lake water and ice sheets up to spherical harmonic degree 2190 $({\sim } 10 \hbox { km})$.

First, we recapitulate known expressions for layer-based spherical harmonic modelling of the STP (with layers referenced to the sphere) (Sect. 2.1). In the next step, we make the transition from the spherical to the ellipsoidal case and formulate new expressions for layer-based spherical harmonic modelling of the ETP (with layers referenced to the ellipsoid) (Sect. 2.2). Then, a layer concept based on the layers of the Earth2014 (Hirt and Rexer 2015) data set (Sect. 3) and two ways of applying it within the previously introduced forward modelling approaches are defined (Sect. 3.1 and 3.2). The gravitational spectra and signals of the layer-based ETP are computed with 10-km spatial resolution (Sect. 4.1) and validated using GOCE satellite gradiometry (Sect. 4.2), other gravity field models (Sect. 4.3) and terrestrial observations (Sect. 4.4). Finally, differences between the ETP and the STP are elaborated in detail (Sect. 4.5) and conclusions are drawn (Sect. 5).

2 Spectral Forward Modelling of the Gravitational Potential Based on Volumetric Layers of Laterally Varying Density

Let V(P) be the gravitational potential at a point P exterior to the Earth’s body B. Following Newton’s law of gravitation and neglecting the presence of atmospheric masses, it may be written as the integral over the Earth’s mass distribution (see, for example, Heiskanen and Moritz 1967; Sanso and Sideris 2013)

$$\begin{aligned} V(P)= G\int _B \frac{\rho (Q)}{l_{PQ}} {\text {d}}B \end{aligned}$$

(1)

where G is the Newtonian gravitational constant, $\rho ~(>0)$ is the density value associated with the infinitesimal volume element ${\text {d}}B=r^2_B \sin {\theta } {\text {d}}r {\text {d}}\theta {\text {d}}\lambda$ at Q with $Q\in B$ and ${l_{PQ}}$ being the Euclidean distance between P and the respective mass element at Q. In order to get Eq. 1 in a spherical coordinate system (P and Q are then defined by the coordinate triplet: geocentric distance r, longitude $\lambda$, co-latitude $\theta$), the reciprocal distance ${1/l_{PQ}}$ has to be replaced by its spherical harmonic expansion. Rummel et al. (1988) show that Eq. 1 can then be represented as spherical harmonic series of the form

$$\begin{aligned} V(P)= & {} \frac{GM}{R} \sum _{n=0}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1}\nonumber \\&\times \left\{ \frac{1}{M(2n+1)} \int _B \left( \frac{r_Q}{R}\right) ^n \rho (Q) ~{\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \text{d} B \right\} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P) \end{aligned}$$

(2)

with the mass of Earth M, its mean radius R, the geocentric radii of the computation point $r_P$ and the source point $r_Q$, the spherical harmonic degree n and order m. ${\overline{Y}}_{\text {nm}}$ denote the well-known set of fully normalised Laplace’s surface spherical harmonic functions

$$\begin{aligned} {\overline{Y}}_{\text {nm}}(\theta ,\lambda )= {\overline{P}}_{\text {nm}}\left( \cos {\theta }\right) \left\{ \begin{array}{ll} \cos (m \lambda )&{\text{for}}\,m\le 0\\ \sin (m \lambda )&{\text{for}}\,m>0 \end{array} \right. \end{aligned}$$

(3)

with ${\overline{P}}_{\text {nm}}$ being the fully normalised ($4\pi$-normalised) associated Legendre functions of the first kind. The term in curly brackets in Eq. 2 now contains the integration over the Earth’s mass distribution and can alternatively be represented as a set of dimensionless fully normalised coefficients

$$\begin{aligned} {\overline{V}}_{\text {nm}}=\frac{3}{{\overline{\rho }} R^3(2n+1)} \frac{1}{4\pi } \int _B \left( \frac{r_Q}{R}\right) ^n \rho (Q) ~{\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) {\text {d}}B , \end{aligned}$$

(4)

that can be subdivided into their cosine- and sine-assigned equivalents, ${C}_{\text {nm}}$ and $S_{\text {nm}}$, according to Eq. 3, where M is replaced by ${\frac {4}{3}}\pi {\overline{\rho }}R^3$ and with ${\overline{\rho }}$ being the mean density of Earth. Then, Eq. 2 can be rewritten conveniently as

$$\begin{aligned} V(P)= \frac{GM}{R} \sum _{n}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1} {\overline{V}}_{\text {nm}} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P). \end{aligned}$$

(5)

Now, let’s consider an Earth that is subdivided into a set of volumetric mass layers $\varOmega _{\omega }$ $(\omega =[1,2,\ldots ,\omega _{\max }])$ fulfilling the following requirements:

• (i) $\rho$ varying only in the lateral direction in each layer ($\rho ^{(\varOmega _{\omega })}$ is radially invariant: $\rho ^{(\varOmega _{\omega })}(\theta ,\lambda )$),

• (ii) each layer having a defined upper bound (UB) and lower bound (LB) $\left( r_{{\text {LB}}}^{(\varOmega _{\omega })}\le r_{{\text {UB}}}^{(\varOmega _{\omega })}\right)$,

• (iii) the layer’s boundaries being entirely inside Earth’s body $\left( r_{{\text {UB}}}^{(\varOmega _{\omega })}\le r_{B}\right)$

• (iv) the layers being uniquely separated by their boundaries $\left( \varOmega _{\omega } \cap \varOmega _{\omega +1} \equiv 0\right)$

• (v) and the set of layers (including the remaining volumetric body inside the lower most layer boundary) forms a complete subset of Earth’s body $\left( \sum _{\omega } \varOmega _{\omega } \equiv B\right)$.

Then, the gravitational potential V(P) in Eq. 5 may be written as a sum of the gravitational potential of each layer $V(P)^{(\varOmega _{\omega })}$

$$\begin{aligned} V(P)= & {} \sum _{\omega } V(P)^{(\varOmega _{\omega })} = \frac{GM}{R} \sum _{n}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1} {\overline{V}}_{\text {nm}}^{(\varOmega _{1})} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P) \nonumber \\&+ \,\frac{GM}{R} \sum _{n}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1} {\overline{V}}_{\text {nm}}^{(\varOmega _{2})} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P) \nonumber \\&+\, \cdots + \frac{GM}{R} \sum _{n}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1} {\overline{V}}_{\text {nm}}^{(\varOmega _{max})} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P) \nonumber \\= & {} \frac{GM}{R} \sum _{n}^{\infty } \sum _{m=-m}^n \left( \frac{R}{r_p}\right) ^{n+1} \sum _{\omega } {\overline{V}}_{\text {nm}}^{(\varOmega _{\omega })} {\overline{Y}}_{\text {nm}}(\theta _P,\lambda _P). \end{aligned}$$

(6)

Thus, the fully normalised coefficients in Eqs. 4 and 9 are the sum of the respective coefficients of all layers

$$\begin{aligned} {\overline{V}}_{\text {nm}} = \sum _{\omega } {\overline{V}}_{\text {nm}}^{(\varOmega _{\omega })} \end{aligned}$$

(7)

The fully normalised potential coefficients of a layer ${\overline{V}}_{\text {nm}}^{(\varOmega _{\omega })}$ are given by the global radial integration of the layer’s masses

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{(\varOmega _{\omega })}= & {} \frac{3}{{\overline{\rho }} R^3(2n+1)}\frac{1}{4\pi } \int _{\varOmega _{\omega }} \left( \frac{r_Q}{R}\right) ^n \rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) {\text {d}} \varOmega _{{\omega }} \nonumber \\= & {} \frac{3}{{\overline{\rho }} R^3(2n+1)}\frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \int _{r_{{\text {LB}}}^{(\varOmega _{\omega })}}^{r_{{\text {UB}}}^{(\varOmega _{\omega })}} \left( \frac{r_Q}{R}\right) ^n\nonumber \\& \times \rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) r_Q^2 \sin {\theta } {\text {d}}r {\text {d}}\theta {\text {d}}\lambda \end{aligned}$$

(8)

where $\rho ^{(\varOmega _{\omega })}$ denotes the layers density distribution. With moving the reference radius outside the integrals, we then write (see Rummel et al. 1988)

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{(\varOmega _{\omega })} = \frac{3}{{\overline{\rho }} R(2n+1)} \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \varOmega ^{(\omega )} {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda \end{aligned}$$

(9)

where $\varOmega ^{(\omega )}$ denotes the radial integration of the layer’s masses

$$\begin{aligned} \varOmega ^{(\omega )} = \int _{r_{{\text {LB}}}^{(\varOmega _{\omega })}}^{r_{{\text {UB}}}^{(\varOmega _{\omega })}} \left( \frac{r_Q}{R}\right) ^{n+2} \rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q)~ {\text {d}}r. \end{aligned}$$

(10)

Since $\rho ^{(\varOmega _{\omega })}$ is assumed to be a function of $\lambda$ and $\theta$ only (and thus constant in radial direction within each layer), the solution of the integral in Eq. 10 yields

$$\begin{aligned} \varOmega ^{(\omega )} = \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) ~\frac{R}{n+3} \left[ \left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} \right] . \end{aligned}$$

(11)

Then, consider that the integral in Eq. 10 can also be defined with respect to the ellipsoidal radius by two separate integrals, e.g., by

$$\begin{aligned} \varOmega ^{(\omega )} = \int _{r=r_{{\text {LB}}}^{(\varOmega _\omega )}}^{r_{e}} \left( \frac{r_Q}{R}\right) ^{n+2} \rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q)~ {\text {d}}r + \int _{r=r_e}^{r_{{\text {UB}}}^{(\varOmega _{\omega })}} \left( \frac{r_Q}{R}\right) ^{n+2} \rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q)~ {\text {d}}r. \end{aligned}$$

(12)

The above (split) integral solution holds for all possible vertical arrangements of layer boundaries (where all, none or only a part of the masses of a layer are located within the reference ellipsoid), as shown in Claessens and Hirt (2013) for single-layer modelling. Then, with $\rho ^{(\varOmega _{\omega })}$ being radially invariant, the solution to the integral in Eq. 12 becomes

$$\begin{aligned} \varOmega ^{(\omega )}= & {} \,\rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q)~ \frac{R}{n+3}\nonumber \\&\times \left( \left[ \left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{r_e}{R}\right) ^{n+3} \right] - \left[ \left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{r_e}{R}\right) ^{n+3} \right] \right) , \end{aligned}$$

(13)

which essentially is the same as Eq. 11, since $\left( \frac{r_e}{R}\right) ^{n+3}$ cancels out in Eq. 13. Starting from this solution to the radial integral of the masses within a layer $\varOmega _{\omega }$—which will turn out to be of mathematically convenient form—we will derive the potential $V(P)^{(\varOmega _{\omega })}$ of a volumetric layer in spherical approximation in Sect. 2.1 and in ellipsoidal approximation in Sect. 2.2.

2.1 Layer-Based Modelling with Respect to a Reference Sphere

The potential based on volumetric layers of laterally variable density as given by Eq. 6 modelled with respect to a reference sphere means—in simple words—a spherical approximation of Earth’s masses and yields the spherical topographic potential $V^{{\text {STP}}}$. A solution to the layer-based STP was given already by Pavlis and Rapp (1990), Tenzer et al. (2015) and other works (see Sect. 1) and is recapitulated in own notation here.

The first spherical approximation that is introduced is setting

$$\begin{aligned} r_e=R \end{aligned}$$

(14)

in Eq. 13, which yields the spherical approximated mass of the layer

$$\begin{aligned} \varOmega ^{({\text {STP}},\omega )} = \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \left( \left[ \left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - 1 \right] - \left[ \left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - 1 \right] \right) . \end{aligned}$$

(15)

The second spherical approximation is made by describing the layer’s boundaries with respect to the reference sphere as

$$\begin{aligned} r_{{\text {UB}}}^{(\varOmega _\omega )}= & {} R + H_{{\text {UB}}}^{(\varOmega _\omega )}\nonumber \\ r_{{\text {LB}}}^{(\varOmega _\omega )}= & {} R + H_{{\text {LB}}}^{(\varOmega _\omega )} \end{aligned}$$

(16)

where $H_{{\text {UB}}}^{(\varOmega _\omega )}$ and $H_{{\text {LB}}}^{(\varOmega _\omega )}$ denote the orthometric height of the upper and the lower boundary of $\varOmega _{\omega }$, respectively. We may then introduce the well-known binominal expansion for both terms in square brackets in Eq. 15 (see Rummel et al. 1988)

$$\begin{aligned}&\left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - 1 = \sum \limits _{k=1}^{n+3}{ \left( \begin{array}{c} n+3\\ k \end{array}\right) \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k} = \sum \limits _{k=1}^{n+3} \frac{1}{k!} \prod \limits _{i=1}^{k} (n+4-i) \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k\nonumber \\&\left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - 1 = \sum \limits _{k=1}^{n+3}{ \left( \begin{array}{c} n+3\\ k \end{array}\right) \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^k}= \sum \limits _{k=1}^{n+3} \frac{1}{k!} \prod \limits _{i=1}^{k} (n+4-i) \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^k \end{aligned}$$

(17)

and yield

$$\begin{aligned} \varOmega ^{(STP,\omega )}= & {} \,\rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \left( \sum _{k=1}^{n+3} \left( \begin{array}{c} n+3\\ k\end{array}\right) \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k - \sum _{k=1}^{n+3} \left( \begin{array}{c} n+3\\ k\end{array}\right) \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R} \right) ^k \right) \nonumber \\= & {} \,\rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \sum _{k=1}^{n+3} \left( \begin{array}{c} n+3\\ k\end{array}\right) \left( \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k - \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R} \right) ^k \right) . \end{aligned}$$

(18)

Inserting Eq. 18 into Eq. 9 gives, after moving the double integral into the binominal series, the solution to the layer’s spherical topographic potential

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{({\text {STP}},\varOmega _{\omega })}= & {} \frac{3}{{\overline{\rho }} (2n+1) (n+3)}\sum _{k=1}^{n+3}\left( \begin{array}{c} n+3\\ k \end{array}\right) \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q)\nonumber \\&\times \left( \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k - \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R} \right) ^k \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda \end{aligned}$$

(19)

where the height function (HF) to the power k within the double integral, scaled by the density $\rho ^{(\varOmega _{\omega })}(\theta _Q,\lambda _Q)$ in each cell, can be expressed as a series of (fully normalised) surface spherical harmonic coefficients of the layer’s height density function (HDF)

$$\begin{aligned} {\overline{{\text {HDF}}}}_{{\text {knm}}}^{({\text {STP}}, \varOmega \omega )}= & {} \frac{1}{4\pi }\int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q)\nonumber \\&\quad \times \left( \left( \frac{H_{{\text {UB}}}^{(\varOmega _\omega )}}{R} \right) ^k - \left( \frac{H_{{\text {LB}}}^{(\varOmega _\omega )}}{R} \right) ^k \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda . \end{aligned}$$

(20)

Then, we arrive at a concise expression of the layer’s spherical topographic potential

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{({\text {STP}},\varOmega _{\omega })} = \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \sum _{k=1}^{n+3} \left( \begin{array}{c} n+3\\ k \end{array}\right) {\overline{{\text {HDF}}}}_{{\text {knm}}}^{({\text {STP}}, \varOmega \omega )}. \end{aligned}$$

(21)

Note that the radial integration (Eq. 10) can also be done rigorously (without using binominal series expansions), as shown, for example, by Pavlis and Rapp (1990). However, the rigorous integration is much less efficient compared to an integration based on binominal series expansions (Rummel et al. 1988). Therefore, especially for large $n_{\max }$, the rigorous approach may become excessively computationally demanding. The rigorous expressions in our notation are found in Appendix 1.

2.2 Layer-Based Modelling with Respect to a Reference Ellipsoid

Next, the potential based on volumetric layers of laterally variable density as given by Eq. 6 is modelled with respect to a reference ellipsoid. This procedure yields the ellipsoidal topographic potential $V^{{\text {ETP}}}$. In contrast to the spherical variant described in Sect. 2.1, this modelling technique defines the layered masses with respect to a reference ellipsoid. The Earth is thus not approximated by a sphere and the true physical shape of Earth can be preserved.

The solution to the layer-based ETP discussed next is based on the HC method derived in Claessens and Hirt (2013), who applied the HC method only to compute the ETP from a single-density (RET) model.

The starting point is Eq. 13 that is a solution to the radial integral of a layer’s masses (Eq. 10) with respect to an ellipsoid, which can also be written as follows:

$$\begin{aligned} \varOmega ^{({\text {ETP}},\omega )}= & {} \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \left( \frac{r_e}{R}\right) ^{n+3} \left( \left[ \left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - 1 \right] - \left[ \left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - 1 \right] \right) . \end{aligned}$$

(22)

The layer’s boundaries in the ellipsoidal case may be described by their pseudo-ellipsoidal heights $h'{}_{{\text {UB}}}^{(\varOmega _\omega )}$ and $h' {}_{{\text {LB}}}^{(\varOmega _\omega )}$ following

$$\begin{aligned} \begin{array}{c} r_{{\text {UB}}}^{(\varOmega _\omega )}=r'_e + h' {}_{{\text {UB}}}^{(\varOmega _\omega )}\\ r_{{\text {LB}}}^{(\varOmega _\omega )}=r'_e + h' {}_{{\text {LB}}}^{(\varOmega _\omega )} \end{array} \end{aligned}$$

(23)

measured along the direction towards the origin of the ellipsoid, akin to the geocentric coordinates needed for spherical harmonics [denoted approximate ellipsoidal height in Claessens and Hirt (2013)]. In approximation, the layer’s boundaries may be described by $d_{{\text {UB}}}^{(\varOmega _\omega )}$ and $d_{{\text {LB}}}^{(\varOmega _\omega )}$ denoting the ellipsoidal height h taken in the direction towards the geocenter and thus yields

$$\begin{aligned}&r_{{\text {UB}}}^{(\varOmega _\omega )}=r_e + d_{{\text {UB}}}^{(\varOmega _\omega )}\nonumber \\&r_{{\text {LB}}}^{(\varOmega _\omega )}=r_e + d_{{\text {LB}}}^{(\varOmega _\omega )}. \end{aligned}$$

(24)

The error of this ellipsoidal approximation, when $d_{{\text {UB}}}^{(\varOmega _\omega )}$ and $d_{{\text {LB}}}^{(\varOmega _\omega )}$ are used instead $h' {}_{{\text {UB}}}^{(\varOmega _\omega )}$ and $h' {}_{{\text {LB}}}^{(\varOmega _\omega )}$, is investigated in Sect. 4.5.

Both square brackets terms in Eq. 22 can—equivalent to the spherical case (Eq. 17)—be expressed by the binominal series expansions

$$\begin{aligned}&\left( \frac{r_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - 1 = \sum \limits _{k=1}^{n+3}{ \left( \begin{array}{c} n+3\\ k \end{array}\right) \left( \frac{d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k} = \sum \limits _{k=1}^{n+3} \frac{1}{k!} \prod \limits _{i=1}^{k} (n+4-i) \left( \frac{d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k\nonumber \\&\left( \frac{r_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - 1 = \sum \limits _{k=1}^{n+3}{ \left( \begin{array}{c} n+3\\ k \end{array} \right) \left( \frac{d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^k}= \sum \limits _{k=1}^{n+3} \frac{1}{k!} \prod \limits _{i=1}^{k} (n+4-i) \left( \frac{d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^k. \end{aligned}$$

(25)

Inserting Eq. 25 and Eq. 22 into Eq. 9 gives a preliminary solution to the ETP of a layer

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })}= & {} \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \sum _{k=1}^{n+3} \left( \begin{array}{c} n+3\\ k \end{array} \right) \nonumber \\&\times \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \left( \frac{r_e}{R}\right) ^{n+3} \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \left( \frac{d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k - \left( \frac{d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k \right) \nonumber \\&\times {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda . \end{aligned}$$

(26)

In order to get a practicable solution for the ETP that is independent of any term with degree n in the exponent, Claessens and Hirt (2013) have introduced a second (infinite) binominal series for $\left( \frac{r_e}{R}\right) ^{n+3}$ that has been derived in Claessens (2006):

$$\begin{aligned} \left( \frac{r_e}{R}\right) ^{n+3}= \left( \frac{b}{R}\right) ^{n+3} \left( 1-e^2\sin ^2{\theta }\right) ^{\left( -\frac{n+3}{2}\right) } = \left( \frac{b}{R}\right) ^{n+3} \sum _{j=0}^{\infty } \left( -1\right) ^j \left( \begin{array}{c} -\frac{n+3}{2} \\ j \end{array} \right) e^{2j} \sin ^{2j}\theta \end{aligned}$$

(27)

where b is the semi-minor axis of the ellipsoid and $e^2$ is the squared first numerical eccentricity. With the help of fully normalised sinusoidal Legendre weight functions ${\overline{K}}_{\text {nm}}^{2i,2j}$ [see, for example, Appendix 1 in Claessens and Hirt (2013) for more details on the recursion relations], it is evident that

$$\begin{aligned} \sin ^{2j}\theta {\overline{Y}}_{\text {nm}} = \sum _{i=-j}^{j}{\overline{K}}_{\text {nm}}^{2i,2j} {\overline{Y}}_{n+2i,m}. \end{aligned}$$

(28)

Inserting Eqs. 28 and 27 in 26 yields coefficients of the ellipsoidal topographic potential $V_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })}$ of the layer $\varOmega _{\omega }$:

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })}= & {} \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \left( \frac{b}{R}\right) ^{n+3} \sum _{k=1}^{n+3} \left( { \begin{array}{c} n+3\\ k \end{array}} \right) \sum _{j=0}^{\infty } \left( -1\right) ^j \left( \begin{array}{c} -\frac{n+3}{2} \\ j \end{array} \right) e^{2j} \sum _{i=-j}^{j} {\overline{K}}_{\text {nm}}^{2i,2j} \nonumber \\&\times \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \left( \frac{d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k - \left( \frac{d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k \right) \nonumber \\&\quad {\overline{Y}}_{n+2i,m}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda \end{aligned}$$

(29)

Again, the term within the double integral, scaled by the density $\rho (\theta _Q,\lambda _Q)$ in each cell, can be expressed as a series of (fully normalised) surface spherical harmonic coefficients of the layer’s (ellipsoidal) height density function

$$\begin{aligned} {\overline{{\text {HDF}}}}_{{\text {klm}}}^{(ETP, \varOmega \omega )}= & {} \frac{1}{4\pi }\int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \left( \frac{d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k - \left( \frac{d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e} \right) ^k \right) \nonumber \\&\times {\overline{Y}}_{{\text {lm}}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda \end{aligned}$$

(30)

where $l=n+2i$ and we arrive at a compact expression for the layer’s ellipsoidally approximated potential

$$\begin{aligned} {\overline{V}}_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })}= & {}\, \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \left( \frac{b}{R}\right) ^{n+3} \sum _{k=1}^{k_{\max }}{ \left( \begin{array}{c} n+3\\ k \end{array}\right) } \sum _{j=0}^{j_{\max }} \left( -1\right) ^j \left( \begin{array}{c} -\frac{n+3}{2} \\ j \end{array} \right) e^{2j} \\&\times \sum _{i=-j}^{j}\nonumber {\overline{K}}_{\text {nm}}^{2i,2j} {\overline{HDF}}_{{\text {klm}}}^{({\text {ETP}}, \varOmega \omega )} \end{aligned}$$

(31)

where $k_{\max }\le {n+3}$ and $j_{\max }<{\infty }$ denote the maximum orders of the binominal series expansions. While $k_{\max }$ and $j_{\max }$ are much smaller than the maximum harmonic degree of the model $n_{\max }$, generally, the number of binominal terms that are required to avoid truncation errors for different modelling parameters (e.g. spatial resolution) is discussed next. The rigorous expressions for the ETP of mass layers (devoid of binominal series expansions) are given in Appendix A.

Table 1 Order of truncation $k_{\max }$ of the first binominal series (Eq. 25) at various resolutions (harmonic degree n) and locations of the layer boundary required to reduce the relative error below the $1\,\%$-level, where $a=6{,}378{,}137\,\hbox {m} \ge r_e \ge b=6{,}356{,}752\,\hbox {m}$

Table 2 Order of truncation $j_{\max }$ of the second binominal series (Eq. 27) at various resolutions (harmonic degree n) and co-latitude $\theta$ required to reduce the relative error below the $1\,\%$-level, where $b=6{,}356{,}752\,\hbox {m}$ and $R=6{,}378{,}137\,\hbox {m}$

2.3 Convergence of Binominal Series Expansions

As shown above, Eq. 31 contains two binominal series expansions, one incrementing by k and one by j. The convergence of the first series (Eq. 25), which is also found in the solution of the STP for $r_e=R$ (Eq. 17), has been thoroughly studied, for example, by Sun and Sjöberg (2001) for various resolutions. Commonly, $k_{\max }=7$ is considered sufficient for degree 2160. We have studied the relative amplitudes in Eq. 17 since the series additionally depends on $r_e$ in case of the ETP. However, for $a=6{,}378{,}137\hbox { m}$ and $b=6{,}356{,}752\hbox { m}$ (where $a \ge r_e \ge b$), an identical number of terms were found to be required for different $r_e$. Our investigations show $k_{\max }=10$ is needed to achieve convergence at the $1\,\%$ level (i.e. less than $1\,\%$ truncation error) at degree 2160 (Table 1). Note that Root et al. (2016) showed that the convergence may be problematic for deep layers (e.g., upper mantle layers), with the boundaries’ lower bound $\ll R$. According to Root et al. (2016), the problem can be overcome by reducing the reference radius R during the forward modelling of the affected layer and a subsequent rescaling of the computed coefficients.

The second series (Eq. 27), a function of degree n and the co-latitude $\varTheta$, occurs in the ETP only. Despite its infinite summations, it was shown to always converge (Claessens 2006). Looking at the amplitudes of the series’s terms in a relative manner, at least $j_{\max }=18$ should be used to achieve convergence at the $1\,\%$ level for degree 2160 and $\theta \in \left[ 0;\frac{\pi }{2}\right]$ (Table 2).

2.4 Sampling Requirements of Height Density Functions

Special attention is required for the harmonic analysis of the layer’s height density functions [e.g., by means of quadrature (Rexer and Hirt 2015b)] that is needed to derive the surface spherical harmonic coefficients ${\overline{{\text {HDF}}}}_{{\text {knm}}}^{({\text {STP}}, \varOmega \omega )}$ or ${\overline{{\text {HDF}}}}_{{\text {klm}}}^{({\text {ETP}}, \varOmega \omega )}$. Due to the exponentiation of the height function by k, the bandwidth (expressed by the maximum degree N of the original height function) increases proportionally with k, following Hirt and Kuhn (2014),

$$\begin{aligned} N(k)=kN. \end{aligned}$$

(32)

Importantly, Eq. 32 implies that the gridded height functions need to be sampled according to $k_{\max }$ (see Sect. 2.3) in order to avoid any aliasing effects. Computing the STP to degree 2160 with $k_{\max }=7$ in an experiment (not shown here), with the grid sampling limiting the maximum degree to degree 2700, yields aliasing errors of up to ${\sim } 20\hbox { mGal}$ and a global root mean square (RMS) of $0.17\hbox { mGal}$. In all computations in this contribution, the increased sampling requirements are thus fully taken into account. A more detailed study of the aliasing effect is outside the scope of this paper.

3 Layer Concept Based on Earth2014

The mass layer concept using the STP and ETP framework presented in Sect. 2 can be applied with the four (geophysical) volumetric layers

$\varOmega _1$::

Ice

$\varOmega _1$::

Lakes

$\varOmega _1$::

Ocean

$\varOmega _1$::

Crust (solid rock)

while different rock types or sediment layers shall not be considered. It is of course possible to include more layers, but relevant global data sets at resolutions $<111\hbox { km}$ are not available (see Sect. 1.1). Note that vertical density functions (e.g., given by some polynomial) for the integration of ocean water columns (Tenzer et al. 2015) or radially varying mass density distributions in general (Root et al. 2016) were not integrated into the layer concept (although possible), as this is not the scope of this paper.

The layer’s boundaries are generated from the Earth2014 data set (Hirt and Rexer 2015) that provides a suite of self-consistent surface layers and masks which can be used to distinguish between ice, lake, ocean and solid Earth surface at $1'$ resolution $({\sim } 2 \hbox { km})$. Earth2014 is a freely available composite model combining up-to-date digital elevation data with other gridded surface data products from different sources in terms of mean-sea-level heights. As such Earth2014 can be considered an up-to-date, higher resolution and more detailed version of the OSUJAN89 (Pavlis and Rapp 1990), DTM2002 (Saleh and Pavlis 2002) and ETOPO1 (Amante and Eakins 2009) topographic databases that in principle provide the same terrain types (see, for example, Fig. 1 in Pavlis and Rapp 1990). We refer to Hirt and Rexer (2015) for a full account on Earth2014 data.

Fig. 1

Simplified scheme of the four geophysical layers extracted from the Earth2014 data set

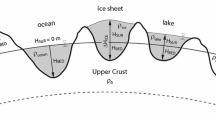
In Fig. 1, a scheme of the layer concept is given based on Earth2014 layers: bedrock layer (BED) describing the boundary of solid rock (green lines), surface layer (SUR) which is defined as the boundary between atmosphere and Earth (red lines) and the ice thickness layer (ICE). The difference between SUR and ICE describes an Earth free of ice cover/sheets and is indicated by the orange lines. Here, a total of ten different cases (A)–(J) are given showing the most common arrangement of layers w.r.t. mean sea level (MSL). Those cases and examples for occurrences on Earth are described in Table 3. Note that in both above described approaches the layer’s boundaries are subject to approximation since they are defined by the orthometric height w.r.t. the respective reference surface in a spherical harmonic frame. Effectively, thus, the geoid height is neglected and the reference surface conforms with the MSL line in Fig. 1. The geometry and approximation error due to height assumptions is further discussed in Sect. 4.5.

Table 3 Cases of layer arrangements shown in Fig. 1 and their occurrences on Earth

Two different possibilities exist for the choice of the densities, leading to the following two different approaches for layer-based forward modelling

• 1. LCA: layer correction approach with actual layer densities (c.f. Table 4)

• 2. LRA: layer reduction approach with density contrasts (c.f. Table 5)

which are described in the following.

3.1 Layer Correction Approach (LCA)

In this approach, the gravitational potential generated by each mass layer is modelled with its actual density. Each layer thus makes a (positive) contribution to the final model, i.e. the total topographic potential, that can be thought of as a correction in geodetic sense. Then, the total topographic potential is the sum of the potential contributions of all layers. In the LCA, the layer boundaries and densities for the four layers are selected from the Earth2014 database as listed in Table 4. The LCA can be best understood as bottom-up approach as each layer from the reference surface to the surface of Earth is modelled one after another. This is different from the approach described next.

Table 4 Description of layer boundaries and densities in the LCA approach using Earth2014 data

3.2 Layer Reduction Approach (LRA)

One can best imagine the LRA approach as a top-down approach: the crustal potential is modelled using the uppermost boundary layer (the physical surface of Earth) and is then reduced for the effect of mass density anomalies expressed by density contrasts (w.r.t. the assumed crustal density) that exist in each layer beneath the surface, down to the reference surface. The layer boundaries and density contrasts in the LRA approach are listed in Table 5. When using negative density contrasts for the layers, the total topographic potential is the sum of the gravitational effects of each layer.

Table 5 Description of layer boundaries and densities in the LRA approach using Earth2014 data

3.3 LRA Versus LCA

Theoretically, both approaches should yield the same potential and neither of the approaches is preferable in terms of computational expense. However, practically small differences may remain between the approaches, mainly due to spherical harmonic representation errors as will be shown (see Sect. 4.1). In the literature, often only the LRA approach based on density contrasts is considered. In Tenzer et al. (2015), for example, so-called striping corrections to the topographic correction are computed based on density contrasts, so their procedure corresponds to the LRA approach.

The cross-validation of the results of both approaches is a valuable tool for detecting inconsistencies of the used mass models. For example, consider

• (a) a layer A intersecting with another layer B (Fig. 2a)—then, the overlapping space would be modelled twice in the LCA approach and in the LRA approach, leading to different potentials: in case of LCA, the overlapping space would be corrected using both layers’ densities; in case of LRA, the overlapping space would be reduced for both layers’ density contrasts. In general, the error $\epsilon$ associated with this kind of inconsistency depends on $\rho _B$ if ${\text {UB}}_B$ is wrong and on $\rho _A$ if ${\text {LB}}_A$ is wrong. However, no error will occur in case of the LRA if ${\text {UB}}_B$ is wrong and layer B happens to be the crustal layer $(\rho _B = \rho _{{\text {crust}}})$.

• (b) a not modelled (volumetric) empty space between two layers A and B (Fig. 2b)—then, this space is not accounted for in the LCA approach at all, while the space is implicitly filled and modelled with crustal density in the LRA approach. Again, no error will occur in case of the LRA if ${\text {UB}}_B$ is wrong and layer B happens to be the crustal layer $(\rho _B = \rho _{crust})$.

Note that it is likewise possible (and associated with less computational costs) to detect inconsistencies in the mass models by applying the (purely) geometric conditions listed under (ii) to (v) in Sect. 2.

Fig. 2

Scheme and associated error of (a) intersecting layers or (b) empty space between layers in the LCA and the LRA approach

4 Results

This section presents a numerical study based on the ellipsoidal layer-based forward modelling technique (Sect. 2.2) using the volumetric layers defined in Sect. 3. It also shows the results of the layer-based forward modelling in spherical approximation (Sect. 2.1) for comparison purposes.

4.1 Global Gravitational Potential from Volumetric Layers in Ellipsoidal Approximation

The above presented techniques allow modelling the topographic gravitational potential of a single layer as well as the combined (total) effect of several layers via corrections or reductions. For the sake of clarity, an overview on the computed potential fields together with their approximation level and acronyms is given in Table 6.

Table 6 Acronyms of computed potential models in the numerical study together with used layers, type of approximation, layer approach and maximum spherical harmonic degree

The dimensionless degree variances

$$\begin{aligned} c_n=\sum _{m=-n}^n {\overline{V}}^2_{\text {nm}} \end{aligned}$$

(33)

of the ETP of all layers computed using the constants given in Table 7 are shown in Fig. 3. While the single layers’ potentials (coloured lines) are different (by a constant scale factor) for the LRA and the LCA approach, the sum of all layer’s potentials (black lines) yields similar spectra for both approaches. The difference is at least five orders of magnitude below the signal (Fig. 4, left plot), corresponding to a root mean square (RMS) of ${\sim } 0.001\hbox { mGal}$ in terms of gravity disturbances evaluated at the surface of Earth (Fig. 5). The largest differences are found above the inland lakes, which are accompanied by error patterns distributed approximately along great arcs. We believe those differences stem from spherical harmonic representation errors (Gibbs effect) that occur over small areas with large variations in height/depth (e.g., Lake Baikal). The corresponding coefficient differences are given in Fig. 4 (right plot).

We have computed a 5’ global grid of gravity disturbances from the new dV_ELL_Earth2014_lca model in spectral band of degrees 0 to 2190 at the Earth’s surface as represented by the Earth2014 SUR layer. This was done by using the isGrafLab software (Bucha and Janák 2014) along with the gradient approach for 3D harmonic synthesis (Hirt 2012). In Fig. 6, the gravity disturbances from the dV_ELL_Earth2014_LCA model vary approximately between −802 and 624 mGal with an average signal strength (RMS) of ${\sim } 350\hbox { mGal}$.

Table 7 Constants and modelling parameters used for the numerical study

Fig. 3

Degree variances of the ellipsoidal topographic potential models and their layers using the LCA approach (left) and the LRA approach (right)

Fig. 4

LCA versus LRA approach: difference between the respective spectra of layer-based ETP in terms of degree variances (left) and dimensionless coefficient differences (right)

Fig. 5

LCA versus LRA approach: difference of layer-based ETP (dV_ELL_Earth2014_lca - dV_ELL_Earth2014_lra) in terms of gravity disturbances evaluated at the surface of the Earth, d/o 0..2190 (unit is in mGal). ${\text {RMS}}=0.001\,\hbox {mGal}$; $\min =-0.06\,\hbox {mGal}$; $\max =0.07\,\hbox {mGal}$; ${\text {mean}}=0.00\,\hbox {mGal}$

Fig. 6

Gravity of layer-based ETP (dV_ELL_Earth2014_lca) in terms of gravity disturbances evaluated at the surface of the Earth, d/o 0..2190 (unit is in mGal). ${\text {RMS}}=349.45\,\hbox {mGal}$; $\min =-802.07\,\hbox {mGal}$; $\max =623.63\,\hbox {mGal}$; ${\text {mean}}=-283.58\,\hbox {mGal}$

The area of Antarctica has been selected to show the gravitational contribution of each layer to the total gravitational effect of the Earth2014 based mass model (Fig. 7), as each layer has a significant contribution over that region. The largest contributions are given by the crust layer and ocean layer, while the ice layer and lake layer have smaller (but still) significant contributions. Note especially that, for example, the ocean layer has significant contributions over continental Antarctica (and over other continents) which underlines the importance of explicitly modelling the ocean’s masses in order to retrieve a good approximation of the gravitational potential over land.

The benefit of layer-based modelling, as done here, compared to RET-based (single-density models) modelling obviously is largest over ice- and water-covered parts of Earth where discrepancies are of the order of ${\sim } 10{-}20\hbox { mGal}$ (Fig. 8). Especially over the mid-oceanic ridges and deep ocean trenches (but also over many other areas), notable differences are present which all can safely be interpreted as RET approximation errors (see Sect. 4.2). The discrepancies shown in Fig. 8 are in good agreement with the findings by Grombein et al. (2016) and Kuhn and Hirt (2016).

Fig. 7

Gravity contribution in terms of gravity disturbances (mGal) of the single layers, their combined effect and the difference between LCA and LRA approach over the area of Antarctica

Fig. 8

Layer-based modelling versus RET-based (single-density) modelling: difference between the layer-based ETP and the RET-based ETP in terms of gravity disturbances evaluated at the reference ellipsoid (unit is in mGal). ${\text {RMS}}=1.79\,\hbox {mGal}$; $\min =-45.67\,\hbox {mGal}$; $\max =65.91\,\hbox {mGal}$; ${\text {mean}}=-0.05\,\hbox {mGal}$

4.2 Validation of Layer-Based Modelling Using GOCE Satellite Gradiometry

The successful operation of a gradiometer on board of ESA satellite Gravity Field and steady-state Ocean Circulation Explorer (GOCE) resulted in global gravity gradient observations which currently are the most consistent and accurate source for Earth’s gravity at scales up to ${\sim } 70{-}80 \hbox { km}$. Its observations as incorporated in the GOCE-only gravity field model GO_CONS_GCF_2_TIM_R5 (EGM_TIM_R5) (Brockmann et al. 2014) are totally independent of any of the computed topographic potential models in this work and can therefore be used to quantify the benefits of layer-based modelling over RET-based modelling, thus corroborating our spectral layer approach. In this regard, we compute regional reduction rates (RR) (Hirt et al. 2012) from $1^\circ \times 1^\circ$ blocks of band-limited gravity disturbances $\delta g$ globally at the reference ellipsoid following

$$\begin{aligned} {\text {RR}}_{{\text {layer}}}= & {} 100 \cdot \left( 1 - \frac{RMS \left( \delta g_{dV\_ELL\_Earth2014} - \delta g_{EGM\_TIM\_R5} \right) }{ RMS\left( \delta g_{EGM\_TIM\_R5}\right) } \right) \nonumber \\ {\text {RR}}_{{\text {RET}}}= & {} 100 \cdot \left( 1 - \frac{RMS \left( \delta g_{dV\_ELL\_RET2014} - \delta g_{EGM\_TIM\_R5} \right) }{ RMS\left( \delta g_{EGM\_TIM\_R5}\right) } \right) \end{aligned}$$

(34)

and investigate their differences ${\text {RR}}_{{\text {layer}}}-{\text {RR}}_{{\text {RET}}}$ (Fig. 9). The limitation of the investigation to the spectral band $n=160\ldots 250$ is reasoned as follows: the GOCE gravity model contains the effects of isostatic compensation that are not modelled in this work. Since isostatic effects are predominantly of long-wavelength character, we exclude all degrees $n<160$. We further exclude all degrees $n>250$ since Brockmann et al. (2014) showed that this is where the signal-to-noise ratio of the gradiometer observations becomes 1. RMS denotes the root mean square operator, applied on the respective gravity disturbances. The RR visualise to what extend the forward modelled gravity in the ETP models can be reduced (i.e. explained) by the satellite’s observations. Blue areas in Fig. 9 thus are areas where the layer modelling—in simple words—agrees better with GOCE observations than RET-based modelling. Moreover, it is interesting to see that above the continents—predominantly above near-coastal land areas—significant improvement through the layer-based modelling was achieved, although the mass model over the continents is the same (except of lakes) in the case of RET-based and layer-based modelling. The reason for this behaviour of course is that the gravitational signal of a bounded density contrast (which in this case is the ocean) leaks over its physical boundaries.

Fig. 9

Layer-based modelling versus RET-based (single-density) modelling: reduction rate differences (Eq. 34) in $1^\circ \times 1^\circ$ blocks using gravity from the GOCE-only model GO_CONS_GCF_2_TIM_R5 in the band from degree 160 to 250. Positive values denote a better agreement between layer-based modelling and GOCE observations (unit is in percent). ${\text {RMS}}=+5.47 \;\%$; ${\text{average}}=+3.25 \;\%$

4.3 Corroboration of Layer-Based Modelling Using Other GGMs

Any existing global gravitational model (GGM) may be used to investigate the quality of the suggested layer-based forward modelling. We restrict our investigations to two models which are

• 1. EGM2008: the Earth Gravitational Model 2008 (Pavlis et al. 2012) which is a combined GGM using satellite observations, terrestrial observations and residual terrain fill-in gravity complete up to degree and order (d/o) 2190. EGM2008 incorporates the most complete (and up-to-date) set of terrestrial gravity observations of any available GGM and is therefore the best candidate to investigate the layer-based modelling at short scales with real observations.

• 2. RWI_TOPO_2015: the Rock–Water-Ice topographic model 2015 (Grombein et al. 2016) is a forward model based on layers of solid rock, water and ice derived from the same data set (Earth2014) as used for the layer-based ETP models in this work. Contrary to this work RWI_TOPO_2015 has been generated from an integration in the space domain using a tesseroid approach (see Grombein et al. 2013) and was transformed into the spectral domain by a subsequent spherical harmonic analysis. The model is also complete up to d/o 2190 and is perfectly suited for a cross-validation with the suggested spectral approach in this work.

Consequently, the comparison with EGM2008 will allow us to judge how closely the computed models approximate the observable gravity field at short scales while the comparison to RWI_TOPO_2015 will provide independent feedback on the modelling technique as such. The degree correlation (DC) $y_n$ (see, for example, Wieczorek 2007) of a GGM w.r.t. EGM2008 is given by

$$\begin{aligned} y_n=\frac{cx_n({\text {EGM2008, GGM}})}{\sqrt{c_n({\text {EGM2008}})~\cdot ~c_n({\text {GGM}})}} \end{aligned}$$

(35)

and indicates the degree of correlation $(\left[ -1;1\right] )$ between the signal contained in coefficients of equal degree of EGM2008 and the GGM under evaluation, where $cx_n$ is the cross-degree variance

$$\begin{aligned} cx_n({\text {EGM2008, GGM}})=\sum _{m=-n}^n {\overline{V}}_{\text {nm}}({\text {EGM2008}})~\cdot ~{\overline{V}}_{\text {nm}}({\text {GGM}}). \end{aligned}$$

(36)

As expected, the computed layer-based ETP models (dV_ELL_Earth2014_lca/lra) and RWI_TOPO_2015 show a higher correlation with EGM2008 than the RET-based model (Figs. 10, 11). However, the degree correlation computed from the (original) spherical harmonic models reaches a maximum correlation of 0.93 near degree ${\sim } 1000$, after which the correlations decrease again (and stay above 0.8). This is against all expectations, since the short-scale signals of the gravity field are driven by the topographic masses. Hence, an increase in the correlation is to be expected. The reason for this behaviour is that spherical harmonic models in ellipsoidal approximation (like EGM2008 and most other models found at ICGEM) cannot be used in small bands (band limited) because of dependencies among the coefficients that effect the ellipsoidal approximation. For instance, EGM2008 and other such models constructed in ellipsoidal approximation have to be synthesised up to degree 2190 to avoid erroneous striations increasing with latitude (also see Hirt et al. (2015), Fig. 13 ibid). However, by transforming the spherical harmonic models into truly ellipsoidal harmonic models using Jekeli’s transform (Jekeli 1988), a band-limited investigation of the GGMs becomes possible. Then, the degree correlations stay at a high level $({\sim } 0.92)$ even beyond degree ${\sim } 1000$ (c.f. Fig. 10, right panel), indicating that the computed layer-based ETP models agree well with the short-scale gravity as contained in EGM2008.

The difference of respective DCs reveals that the computed layer-based ETP models of this work show an increasingly higher correlation beyond degree 800 or so (up to $2\,\%$ near degree 2160) compared to the RWI_TOPO_2015 model (Fig. 11). Note that a higher correlation with EGM2008 is not necessarily a valid indicator for a better quality since EGM2008 itself (a) has incomplete observations over some areas (e.g., it contains only GRACE over Antarctica) and contains fill-in gravity and (b) is not error-free. However, we find the degree correlations in Fig. 10 together with the findings in the previous Sect. (4.2) to corroborate the layer-based modelling approach in this work, since the agreement with EGM2008 is at least as good as that of RWI_TOPO_2015.

Fig. 10

Degree correlation w.r.t. EGM2008 in terms of spherical harmonic models (left panel) and in terms of their ellipsoidal harmonic equivalents (right panel)

Fig. 11

Differences between the (spherical harmonic) degree correlation w.r.t. EGM2008 of RWI_TOPO_2015 (blue) and dV_ELL_RET2014 (black) versus the degree correlation of the layer model computed in this work (dV_ELL_Earth2014_lca) in per cent. Positive values denote a higher correlation of dV_ELL_Earth2014_lca

4.4 Combination with Satellite Data and Validation over Antarctica

For external validation with ground truth data, we have computed combination models with GOCE and GRACE gravity observation data. A combination is necessary to be able to directly compare the computed layer-based forward models (see Table 6) with ground truth data, particularly at short scales. Also, because isostatic effects have rather long-wavelength character (c.f. Grombein et al. 2014) and were not taken into account in the forward modelling, satellite observations are used here as an accurate source of such information. We use precomputed normal equation matrices for GRACE [ITG-Grace2010: Mayer-Gürr et al. (2010)] and GOCE [fifth release of time-wise method: Brockmann et al. (2014)] along with the combination strategy described in Hirt et al. (2015) (Eqs. 5–8) to create a combined model of (1) a layer-based ETP model and (2) GRACE and GOCE information that is optimal over the area of Antarctica (and to be used with care outside this area, since the ETP is likely to possess a too strong weight in some spectral bands there). The combination in principle means a regularisation of (non-regularised) GOCE and GRACE normal equations using ETP coefficients with empirically designed regularisation weights. We choose the weighting scheme A in Hirt et al. (2015), which was found superior especially within the polar gap region of GOCE. The combination of GRACE and GOCE with the model dV_ELL_RET2014 and dV_ELL_Earth2014_lca is named SatGravRet2014 and SatGravEarth2014, respectively. Importantly, a combination of this kind is not possible with spherically approximated (STP) models, since the levels of approximation of the satellite component and the topography component would not be consistent (see Sect. 4.5).

Table 8 Descriptive statistics of residual gravity between Antarctic gravity anomaly grid (AGAG) points and various gravitational models for four different AGAG gravity data subsets

Fig. 12

Antarctic gravity anomaly grid (upper left plot) and residuals with gravity anomalies synthesised from various GGMs (unit is in mGal)

We compared the combined models with gravity observations as contained in the newly released Antarctic gravity anomaly grids (AGAG) (Scheinert et al. 2016). The AGAG data set is based on 13 million observations and covers an area of $1\times 10^7 \hbox { km}^2$, corresponding to $73\,\%$ of the Antarctic continent (Fig. 12). We therefore synthesise the gravity anomaly at each AGAG point of height h above the reference surface from both combination models up to their maximum degree of resolution (d/o 2190). We also compute the gravity anomaly from the model EGM2008 (Pavlis et al. 2012) and the satellite-only model GOCO05s (Pail et al. 2011; Mayer-Gürr et al. 2015). The residuals—the differences between the AGAG data and the synthesised gravity—are taken here as an indicator of how close the observed potential (via AGAG) is represented by the different modelling variants. In case of the combination models, the differences between the AGAG gravity and modelled gravity can also be interpreted as short-scale Bouguer gravity: the AGAG observations are (more or less) completely reduced by the observed satellite gravity in the long wavelengths; in the short wavelengths, the AGAG gravity is reduced for the gravitational effect of the visible topographic masses (=Bouguer gravity).

For the entire AGAG data set (181,443 grid points) and a subset of the most accurate grid points (24,315 grid points with standard deviation $({\text {STD}}<2\hbox { mGal})$ the residuals reveal that the herein created combination model based on the layer approach (SatGravEarth2014) performs better than the other models under investigation (Table 8). The improvement in SatGravEarth2014 w.r.t. EGM2008 is $15\,\%$ using all AGAG points and $25\,\%$ using the more accurate subset of points, while it improves over GOCO05s with $8\,\%$ using all points and $18.5\,\%$ in the subset. The improvement in layer-based modelling w.r.t. RET modelling is about $2\,\%$ over both areas in Antarctica, which corresponds to an RMS/STD of ${\sim } 0.3\hbox { mGal}$. The improvement is not very large in absolute terms but still indicative, given the differences between SatGravRet2014 and SatGravEarth2014 gravity at the AGAG points (Fig. 12) have an RMS of ${\sim } 1\hbox { mGal}$ only. Further, the positive effect of layer-based modelling is more notable over the ocean $(5\,\%\hbox { improvement})$ than over land/continental Antarctica $(1\%\hbox { improvement})$. Globally, this tendency is shown already in Fig. 9. Note that EGM2008 shows a better performance over the ocean than the other investigated models. This is to be expected and reflects that AGAG data and EGM2008 are observation based down to short scales. EGM2008 has DTU altimetry data included over the oceans while AGAG over the oceans presumably relies on ship-track-based observations; hence, both data sets are observation based and thus in closer agreement than the AGAG observations with forward models. Also, this finding reveals limitations in currently available Antarctic bathymetry data.

The sum of (1) GOCO05s taken (from $n=0$) up to degree 280 and (2) ETP model (dV_ELL_RET2014 or dV_ELL_Earth2014) taken in the band $281\le n \le 2190$ shows less agreement with AGAG data (${\sim } 1\hbox { mGal}$ more in terms of RMS/STD, see Table 8) than the combination models that also comprise gravity from GRACE, GOCE and ETP model (SatGravRET2014 and SatGravEarth2014). Thus, a quite simple combination of the ETP and observed gravity, e.g., as done here by means of a regularisation, is better than omission error modelling, since the latter leads to higher residuals. Omission error modelling means the estimation of short-scale gravity signals that are not contained in a GGM (i.e. signals beyond the maximum degree N of the model) by band-limited information that can, for example, be computed from a residual terrain model (RTM modelling, c.f. Forsberg 1984) or taken from a (abrupt) truncation of a topographic potential model, as done here.

4.5 Modelling Differences Between the Spherical and Ellipsoidal Approach

The spherically approximated (see Sect. 2.1) and ellipsoidally approximated (see Sect. 2.2) layer-based forward modelling of the potential in spherical harmonics—leading to solutions of the STP and ETP, respectively—is to be treated and interpreted differently. The STP and ETP are inherently different regarding the spectral and spatial domain characteristics as will be shown next.

Fig. 13

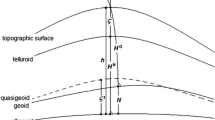
Scheme of mapping of the Earth’s physical surface in the investigated modelling techniques: mapping situation in STP modelling in spherical approximation (a), mapping situation in ETP modelling in ellipsoidal approximation (b) and mapping-free situation in ETP modelling without approximation by using pseudo-ellipsoidal heights $h'$ at their respective latitudes $\varphi '$ (c); $\varphi$: geocentric latitude; B: geodetic latitude; $r_e$: ellipsoidal radius to $P_o$; $r'_e$: ellipsoidal radius to $P'_o$; a, b: semi-major/minor axis of ellipsoid; R: spherical radius; H: orthometric height; h: ellipsoidal height; $D^{{\text {sph}}}$: mapped spherical height; d:mapped ellipsoidal height; $P_{{\text {s}}}$: surface point; $P_{\text {m}}$: mapped surface point; $t_{{\text {sm}}}$: distance ${\overline{P_{s}}P_{{\text {m}}}}$

Fig. 14

Mapping effects in the ETP in terms of height differences $h-h'$ (in metres, upper plot), latitude differences $\varphi -\varphi '$ (in arc-seconds, middle plot) and the resulting gravity disturbance differences $\delta _g-\delta _g'$ (in mGal, lower plot) of both geometric effects. Note, the effects are also contained in the mapping within the STP, but projected onto the sphere

4.5.1 Geometric Differences and Mapping of the Layer Boundaries

Essentially, both STP and ETP are different representations of the (same) potential that is generated by the same masses which are defined by volumetric layers (see Sects. 2, 3). The spherical approach assumes the boundaries of the layers to be referenced to some reference sphere. This is accomplished with the orthometric height serving as an approximation for the distance between sphere and surface point (referred to as mapped spherical height). The ellipsoidal approach assumes the layers to be referenced to some reference ellipsoid using the orthometric height as approximation for the distance between ellipsoid and surface point (referred to as mapped ellipsoidal height). See also Table 9 for an overview of the used heights, their definitions and use. Neither of the approaches thus takes into account the geoid–ellipsoid separation (i.e. the geoid height), which shall not be further looked at here, nor the fact that orthometric heights are not measured along the direction to the geocenter, which is implicitly assumed in the spherical harmonic framework.

Table 9 Definition of heights and their usage in this work (see also Fig. 13)

The result of the latter is a displacement (often referred to as mapping) of the Earth’s physical surface and of all layer boundaries (Fig. 13). In case of the spherical approximation (STP), the approximation error introduced by the mapping is hard to be determined/interpreted, since the masses and computation point $P_S$ are rearranged w.r.t. a spherical reference (Fig. 13a) and there is no workaround to avoid a displacement of masses. In case of the ellipsoidal approximation (ETP), the displacement due to mapping is largest at mid-latitudes and becomes zero at the poles and the equator (Fig. 13 B and Fig. 14). These displacements are also a part of the mapping within the STP, but (additionally) projected onto the sphere. At maximum, consider a point $P_{\text {s}}$ with extreme elevation of $h=9\hbox { km}$ above or $h=-10\hbox { km}$ below the ellipsoid and at a latitude of $B=45^{\circ }$, the displacement given by the distance $t_{{\text {sm}}}={\overline{P_{{\text {s}}}P_{{\text {m}}}}}$ between surface point $P_{\text {s}}$ and its mapped equivalent $P_{\text {m}}$ becomes ${\sim } 30\hbox { m}$ or $33\hbox { m}$, respectively (i.e. $\varphi -\varphi ' {\sim } 0.9''$ and $h-h'{\sim } 5\hbox { cm}$). This confirms similar the findings by Balmino et al. (2012). In view of 10-km resolution models as computed in this model, mass displacements of this order hardly play a role. Nevertheless, in case of the ETP, displacement can be avoided by working with what we denote pseudo-ellipsoidal heights $h'$ (c.f. Appendix 1 for their computation). They are given at their respective geocentric latitudes $\varphi '$ that are defined along the direction towards the geocenter (Fig. 13c). Working with the pseudo-ellipsoidal heights instead of mapped ellipsoidal heights within layer-based modelling to degree 2190 yields differences in the order of $\pm 3\hbox { mGal}$ or RMS=0.04 mGal (see Fig. 14). Accounting for the mapping is thus only required for applications of high accuracy or high resolution.

Fig. 15

Spectral characteristics of the spherically (dV_SPH_Earth2014_lca/lra) and the ellipsoidally (dV_ELL_Earth2014_lca/lra) approximated potential models in terms of degree variances, together with those of EGM2008 and Kaula’s rule of thumb

4.5.2 Differences in the Spectral Domain

The spherical harmonic coefficients of STP and ETP differ notably as can be seen from their degree variances (Fig. 15). The degree variances of the STP (dV_SPH_Earth2014_lca/lra) follow Kaula’s rule (Kaula 1966) closely, which itself is close to the truly ellipsoidal harmonic spectrum of the gravity field (Rexer and Hirt 2015a). The degree variances of the ETP (dV_ELL_Earth2014_lca/lra) run below those of STP. They are comparable to commonly used gravity field models (e.g., those listed at ICGEM). This has already been found by Rexer and Hirt (2015a), who empirically derived an approximate rule of thumb that allows to transform degree variances from a spherically approximated model (STP) into their ellipsoidally approximated equivalents (ETP) (and vice versa). All spherical harmonic GGMs $(\hbox {of }N> 2000)$ that (implicitly) assume an ellipsoidal Earth are accompanied by a “tail” of 30 degrees (from degree 2160 to 2190) with rapidly decreasing energy, which are needed for a proper representation of the potential. This is the very reason why band-limited investigation is not possible with this kind of models (see Sect. 4.3) without suffering from erroneous striations increasing with latitude (see also Claessens and Hirt 2013; Pavlis et al. 2012). Spherical harmonic models in spherical approximation allow band-limited investigations akin to truly ellipsoidal harmonic models (see Sect. 4.3).

Fig. 16

Gravity difference between the spherically (dV_SPH_Earth2014_lca/lra) and the ellipsoidally (dV_ELL_Earth2014_lca/lra) approximated potential models in terms of gravity disturbances evaluated at the respective reference surface (sphere and ellipsoid, respectively); ${\text {RMS}}=0.35\,\hbox {mGal}$; $\min =-4.66\,\hbox {mGal}$; $\max =2.84\,\hbox {mGal}$; ${\text {mean}}=-0.08\,\hbox {mGal}$ (unit is in mGal)

Fig. 17

Gravity difference between the spherically (dV_SPH_Earth2014_lca/lra) and the ellipsoidally (dV_ELL_Earth2014_lca/lra) approximated potential models in terms of gravity disturbances evaluated at the Earth’s surface; ${\text {RMS}}=0.36\,\hbox {mGal}$; $\min =-2.89\,\hbox {mGal}$; $\max =2.11\,\hbox {mGal}$; ${\text {mean}}=-0.08\,\hbox {mGal}$ (unit is in mGal)

4.5.3 Differences in the Space Domain

In the space domain, rather long-wavelength differences appear between the STP and the ETP at the level of few mGals (Fig. 16). Note that for a comparison of ETP and STP in the space domain, the ETP was evaluated on the surface of the reference ellipsoid while the STP was evaluated on the surface of the reference sphere. Similar differences were already found to reflect different mass arrangements between ETP and STP by Claessens and Hirt (2013) (ibid. Fig. 6a) who applied the HC method to a single-density mass model. At the Earth’s surface, the effect is almost of the same dimension with marginally smaller amplitudes and similar RMS (Fig. 17). The differences in Figs. 16 and 17 also contain the effect of mapping discussed above $(h\hbox { vs. }h'\hbox { and }\varphi \hbox { vs. }\varphi ')$, but they are dominated by the additional mapping of the masses from the ellipsoid onto the sphere.

The differences notably differ from the ellipsoidal correction (Fig. 12 in Balmino et al. 2012) which is thought to correct a STP model for the difference between integrating Earth’s masses w.r.t. spherical instead of an ellipsoidal reference. The range of the ellipsoidal correction in Balmino et al. (2012) is much smaller $({\sim }0.005\hbox { mGal}\hbox { vs. }{\sim }8\hbox { mGal})$—even when investigating the differences in Fig. 16 in the same spectral band $(0\le n \le 120)$—and is predominated by a zonal $J_{2}$ effect. Possibly, their correction, which is only computed to the second order, is a part of the true difference between a topographic forward model in spherical and ellipsoidal approximation.

5 Conclusions and Outlook

We presented spectral forward modelling based on volumetric mass layers to d/o 2190 at two different levels of approximation (spherical and ellipsoidal) and took full account of increased sampling requirements and all relevant terms of the involved binominal series expansions, avoiding aliasing and truncation errors due to early truncation of the series.

Based on the HCM method, we derived a new spherical harmonic approach that allows us to rigorously and efficiently compute the ellipsoidally approximated topographic potential based on volumetric layers of laterally varying density that are referenced to an ellipsoid. A layer concept has been established with the layers’ boundaries taken from the Earth2014 model, separating the masses of ice sheets, water in inland lakes/seas, ocean water and solid rock with $1'$ resolution. Applying the layer concept in two ways—in a correction approach with actual densities or in a reduction approach with density contrasts—leads to equivalent potentials, with negligible differences $(\hbox {RMS}\sim 0.001\hbox { mGal})$ that are caused by the spherical harmonic representation of the respective layer boundaries. The layer-based modelling approach reaches over $90 \%$ correlation with EGM2008 in the band $900 \le n \le 2150$ with significantly higher correlations compared to single-density (RET) modelling. Further, it was shown to be at least equivalent to state-of-the-art layer-based forward modelling in the space domain. A validation with ground truth gravity data over Antarctica shows that layer-based modelling improves over single-density modelling by ${\sim } 2\%$, with the improvement being largest over the ocean $({\sim } 5 \%)$. The latter was also confirmed globally by computing reduction rates with GOCE satellite observations as contained in GO_CONS_GCF_2_TIM_R5. For the validation, we computed a combination model, combining computed spherical harmonic coefficients in ellipsoidal approximation with satellite observations from GOCE and GRACE satellite, which is necessary in order to mitigate the problem of isostatically uncompensated masses in the forward models. The combination was done by means of an empirical regularisation of GOCE and GRACE normal equations. Using solely the most accurate ground truth observations $({\text {STD}}<2\hbox { mGal})$ available, the combination model was found superior to EGM2008 and the satellite-only model GOCO05s (by ${\sim } 25$ and ${\sim } 8\%$ in terms of RMS). The comparison with ground truth data also showed that a combination of satellite data with the topographic potential, e.g., by means of a regularisation, is to be preferred compared to omission error modelling in general.

Depending on the level of approximation—spherical or ellipsoidal—we provided the framework to the spherical topographic potential (STP) or the ellipsoidal topographic potential (ETP), which were found to have substantially different spectral characteristics, yet rather small differences in the space domain. Evaluated at the respective reference surface or at surface of Earth, the STP and ETP show differences at the level of ${\sim } \pm 5\hbox { mGal } ({\text {RMS}}=0.4\hbox { mGal})$ that mainly stem from a different arrangement of masses (mapping) due to different geometric assumptions in the approaches. In ellipsoidal approximation, the mapping, which was found to cause a rearrangement of masses by $30\hbox { m}$ at maximum, can completely be avoided by using pseudo-ellipsoidal heights that are measured towards the geocenter. The error introduced by the mapping is in the order of mGal and should be taken into account in applications requiring ultra-high-resolution or high accuracy topographic gravity.

In the spectral domain, the STP shows substantially larger energy at short scales (comparable to that predicted by Kaula’s rule of thumb or to the truly ellipsoidal harmonic spectrum of EGM2008) than the ETP. The ETP shows short-scale energy comparable to other spherical harmonic GGMs that make an (implicit) ellipsoidal assumption of Earth, e.g., EGM2008. This feature makes the ETP coefficients suitable for a combination with satellite data, e.g., as done in this work. The dependencies among the spherical harmonic coefficients in ellipsoidal approximation prevent application of the harmonic models in a band-limited manner (i.e. no truncations at $n<2190$). In contrast, spherical harmonic models in spherical approximation and truly ellipsoidal harmonic models are free of such dependencies and may be used in band-limited form (i.e. truncated at $n<2190$).

In conclusion, the choice between spherical and ellipsoidal approximation in spectral forward modelling depends on the application of the final models. While STP models may be good enough for a wide range of geophysical applications, ETP models are more accurate and needed for high-resolution applications. Current observation-based gravitational models conform spectrally with the ellipsoidal topographic potential which is inevitable for geodetic applications, such as a combination with satellite and terrestrial data by means of regularisation. The herein computed models are available at: http://ddfe.curtin.edu.au/models/Earth2014/potential_model/ .

Appendices

Appendix 1: Rigorous Expressions—Direct Solution to the Radial Integral in Modelling of the ETP and the STP

In contrast to the above presented solutions to the STP (Sect. 2.1) and ETP (Sect. 2.2) that rely on a binominal series expansion for the solution of the radial integral (Eq. 17), and in case of the ETP also on the binominal series expansion in Eq. 27, here the rigorous expressions are given.

The direct (rigorous) solution to the radial integral over the masses in a layer (Eq. 10) was given already in Eq. 11 or (in more generalised form) in Eq. 13, respectively.

1.1 Rigorous Solution to the STP of a Volumetric Mass Layer

In case of the STP, the direct integral solution to the radial integral from the lower to the upper layer bound in spherical approximation reads

$$\begin{aligned} \varOmega ^{({\text {STP}},\omega )} = \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \left( \left( \frac{R +H_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{R + H_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} \right) . \end{aligned}$$

(37)

Inserting Eq. 37 into Eq. 9 the rigorous expression of the STP of a volumetric mass layer is

$$\begin{aligned}{\hat{V}}_{\text {nm}}^{({\text {STP}},\varOmega _{\omega })} &= \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \times \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \left( \frac{R +H_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{R + H_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda , \end{aligned}$$

(38)

and with

$$\begin{aligned} {\overline{HDF}}_{\text {nnm}}^{({\text {STP}}, \varOmega \omega )}= \frac{1}{4\pi }\int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \left( \frac{R +H_{{\text {UB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} - \left( \frac{R + H_{{\text {LB}}}^{(\varOmega _\omega )}}{R}\right) ^{n+3} \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda . \end{aligned}$$

(39)

we arrive at the more concise form

$$\begin{aligned} {\hat{V}}_{\text {nm}}^{({\text {STP}},\varOmega _{\omega })} = \frac{3}{{\overline{\rho }} (2n+1) (n+3)} {\overline{HDF}}_{\text {nnm}}^{(STP, \varOmega \omega )}. \end{aligned}$$

(40)

As mentioned above, rigorous expressions for the STP of a layer in principle are known already in different notation, e.g., by Pavlis and Rapp (1990). The disadvantage of the rigorous expression in Eq. 40 is that it needs $n_{\max }$ spherical harmonic analyses of the surface function ${\overline{HDF}}_{\text {nnm}}^{({\text {STP}}, \varOmega \omega )}$, while the expression relying on a binominal series expansion (Eq. 21) only needs $k_{max}$ analyses, where $k_{\max }\ll n_{\max }$ in general (see Sect. 2.3 for convergency behaviour of the binominal series).

1.2 Rigorous Solution to the ETP of a Volumetric Mass Layer

In case of the ETP, the direct integral solution to the radial integral from the lower to the upper layer bound in ellipsoidal approximation reads

$$\begin{aligned} \varOmega ^{({\text {ETP}},\omega )} = \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \frac{R}{n+3} \left( \frac{r_e}{R}\right) ^{n+3} \left( \left( \frac{r_e + d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - \left( \frac{r_e + d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} \right) . \end{aligned}$$

(41)

Inserting Eq. 41 into Eq. 9, the rigorous expression of the ETP of a volumetric mass layer is

$$\begin{aligned}{\hat{V}}_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })} &= \frac{3}{{\overline{\rho }} (2n+1) (n+3)} \nonumber \\&\times \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \frac{r_e}{R} \right) ^{n+3} \left( \left( \frac{r_e +d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - \left( \frac{r_e + d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda , \end{aligned}$$

(42)

and with

$$\begin{aligned} {\overline{HDF}}_{\text {nnm}}^{({\text {ETP}}, \varOmega \omega )}= & {} \frac{1}{4\pi } \int _{\lambda =0}^{2\pi } \int _{\theta =0}^{\pi } \rho ^{(\varOmega _{\omega })} (\theta _Q,\lambda _Q) \left( \frac{r_e}{R} \right) ^{n+3}\nonumber \\&\times \left( \left( \frac{r_e +d_{{\text {UB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} - \left( \frac{r_e + d_{{\text {LB}}}^{(\varOmega _\omega )}}{r_e}\right) ^{n+3} \right) {\overline{Y}}_{\text {nm}}(\theta _Q,\lambda _Q) \sin {\theta } {\text {d}}\theta {\text {d}}\lambda . \end{aligned}$$

(43)

we arrive at the more concise form

$$\begin{aligned} {\hat{V}}_{\text {nm}}^{({\text {ETP}},\varOmega _{\omega })} = \frac{3}{{\overline{\rho }} (2n+1) (n+3)} {\overline{{\text {HDF}}}}_{\text {nnm}}^{({\text {ETP}}, \varOmega \omega )}. \end{aligned}$$

(44)

The disadvantage of the rigorous expression in Eq. 44 is that it needs $n_{\max }$ spherical harmonic analyses of the surface function ${\overline{HDF}}_{\text {nnm}}^{({\text {ETP}}, \varOmega \omega )}$, while the expression relying on binominal series expansions (Eq. 31) only needs $k_{\max }$ analyses, where $k_{\max }\ll n_{\max }$ in general (see Sect. 2.3 for convergency behaviour of the binominal series).

Appendix 2: Computation of the Pseudo-Ellipsoidal Height $h'$ and Its Latitude $\varphi '$ of the Surface Point $P_{\text{S}}$

Given a surface point $P_{\text {S}}$ with ellipsoidal height h, geodetic latitude B and geocentric distance r defined by

$$\begin{aligned} r^2=(r'_e+h')^2 \end{aligned}$$

(45)

the pseudo-ellipsoidal height $h'$ that is running along the direction towards the geocenter (Fig. 18) can be computed using the cosine rules

$$\begin{aligned} r^2= c^2 + ((N-e^2N)+h)^2 - 2c((N-e^2N)+h) \cdot \cos {(\pi -B)} \end{aligned}$$

(46)

where

$$\begin{aligned} c= & {} e^2N \cos {B},\end{aligned}$$

(47)

$$\begin{aligned} N= & {} \frac{a}{\sqrt{1-e^2\cdot \sin ^2{B}}} \end{aligned}$$

(48)

and

$$\begin{aligned} r_e^{'2} = a^2 \frac{1-e^2}{1 - e^2 \cdot \cos ^2{\varphi '}}. \end{aligned}$$

(49)

The (geocentric) latitude $\varphi '$ can be computed using the sine rule

$$\begin{aligned} \sin {\varphi '}=\left( \frac{((N-e^2N)+h)\cdot \sin {(\pi -B)}}{r}\right) . \end{aligned}$$

(50)

Then, the pseudo-ellipsoidal height is retrieved with

$$\begin{aligned} h'=r - r'_e. \end{aligned}$$

(51)

Fig. 18

Ellipsoidal height h and pseudo-ellipsoidal height $h'$