Global and Regional Gravity Field Determination from GOCE Kinematic Orbit by Means of Spherical Radial Basis Functions

Abstract

We present global and regional gravity field models to degree 130 based on the GOCE kinematic orbit from the period 01 November 2009 to 11 January 2010. The gravity field models are parameterized in terms of the Shannon and Kaula's spherical radial basis functions. The relation between the unknown expansion coefficients and the kinematic orbit of the satellite is established by the acceleration approach. We show that our global GOCE-only solutions free from prior information can compete with unconstrained spherical harmonic models in terms of accuracy. Furthermore, we utilize our low-degree global GOCE-based models to introduce prior information into the least-squares adjustment. This procedure substantially improves the zonal and near-zonal spherical harmonic coefficients, which are usually degraded due to the polar gap problem. As an unwanted side effect, low-pass filtering of the geopotential may occur, but this can be adjusted by the spectral content of the prior information. We show that the regional enhancement of the global solutions reduces noise in the final model between degrees 70 and 130 by ~10 % in terms of RMS error. In general, our Shannon-based solutions systematically outperform the Kaula-based ones. To validate our results, we use the EIGEN-6S model, which is superior to the solutions from kinematic orbits at least by one order of magnitude. Both the global and the regional models satisfy the GOCE-only strategy.

1 Introduction

Kinematic orbits of low Earth orbiters proved to be a useful source of information about the long-wavelength component of the geopotential. For instance, the orbit of the CHAMP (CHAllenging Minisatellite Payload, Reigber et al. 2002) satellite enabled to gain accuracy of the long-wavelength geopotential by one order of magnitude when compared with the pre-CHAMP era (Reigber et al. 2003). In addition to the static gravity field, the very long-wavelength time-variable gravity signal was also recovered from kinematic orbits (e.g., Weigelt et al. 2013). Recently, the need for the gravity information from satellite orbits was demonstrated by the dedicated satellite gravity mission GOCE (Gravity field and steady-state Ocean Circulation Explorer, ESA 1999). The key instrument on-board the GOCE satellite was the gravity gradiometer, which measured the second-order derivatives of the Earth’s gravitational potential. Due to the construction of the device, the low-degree part of the gravitational potential (say below 30) cannot be accurately determined solely from the gradiometric measurements (Pail et al. 2011). Within this spectral band, the GOCE-only models have to rely almost exclusively on the gravity information contained in the kinematic orbit of the satellite.

Regarding the current and the past satellite missions, the GOCE satellite seems to be an appropriate candidate to invert its kinematic orbit into a gravity field model. The reason is twofold. First, the satellite was orbiting the Earth at an extremely low altitude (~250 km above the Earth surface), thus being more sensitive to the fine structures of the gravity field. Second, it was equipped with a geodetic-quality GPS receiver enabling a precise satellite-to-satellite tracking in the high–low mode (SST-hl). A typical feature of the GOCE mission is the Sun-synchronous orbit inclined at 96.7°. Two spherical caps of the radius ~7° around the poles are therefore uncovered by the satellite ground tracks.

Gravity field models from satellite data are commonly produced on a global scale by means of spherical harmonics. Previous studies showed, however, that additional information may be extracted from these data when the gravity field is modelled on a regional scale (e.g., Eicker 2008; Eicker et al. 2014; Schmidt et al. 2007). In our opinion, there are two main reasons for this behaviour in the case of GOCE. The first reason is related to the downward continuation of satellite data. In general, downward continuation is an ill-posed inverse problem requiring a regularization to stabilize the solution. Spherical harmonic estimations are commonly stabilized by a single regularization parameter which may lead to an overall damping of the gravity signal (e.g., Eicker et al. 2014; Mayer-Gürr et al. 2005). It is not straightforward to add some spatially localized features to spherical harmonic approaches in order to properly account for the regionally varying gravity field. This is because spherical harmonics do not posses any localization in the space domain. Secondly, the lack of data within the polar caps results in a poor estimate of zonal and near-zonal spherical harmonic coefficients of medium- and high-resolution unconstrained GOCE-only models (Sneeuw and van Gelderen 1997). It seems to be therefore reasonable to seek for alternative approaches to the gravity field determination from the GOCE data. For instance, a regionally tailored stabilization technique, such as the spherical cap regularization (Metzler and Pail 2005), can be incorporated into the spherical harmonic approaches to mitigate the polar gap problem. Other regularization techniques, not necessarily based on a regional feature, can be used as well (e.g., Ditmar et al. 2003; Metzler and Pail 2005; Pail et al. 2011; Xiancai et al. 2011). Here we parameterize the gravity field by means of spatially localized basis functions, namely by spherical radial basis functions.

A spherical radial basis function (SRBF) is a function on a reference sphere depending only on the spherical distance between two points on this sphere. The harmonic upward continuation of SRBFs from the reference sphere into its exterior is of particular importance for the gravity field modelling. It enables us to establish observation equations for each relevant gravity field quantity taken on or above the Earth’s surface. Unlike spherical harmonics, SRBFs offer a trade-off between localization in both the space and the frequency domain; therefore, they can easily be regionally adapted.

In the context of the gravity field determination, theoretical studies on SRBFs go at least back to Weightman (1967). Therein, the point-masses located within the Earth’s interior are introduced as an alternative to spherical harmonics. Krarup (1969) developed the least-squares collocation. Freeden et al. (1998) and Freeden and Schneider (1998) presented a theory of wavelets on the unit sphere and of spherical harmonic wavelets, respectively. Another technique based on spherical wavelets is investigated in Holschneider et al. (2003). A typical feature of the wavelet-based methods is the decomposition of the signal into different spectral bands. Eicker (2008) introduced and applied splines constructed from the degree variances of the Earth’s gravitational potential and stabilized the estimation process by means of a regionally adapted regularization technique based on multiple regularization parameters. Ellipsoidal harmonic wavelets were introduced in Schmidt and Fabert (2008). Further references to other techniques based on SRBFs can be found, e.g., in Eicker (2008), Eicker et al. (2014) or Wittwer (2009).

Spherical radial basis functions have been applied to real satellite data of three types: (1) the SST in the high–low mode (e.g., Eicker 2008; Fengler et al. 2004; Schmidt et al. 2007); (2) the SST in the low–low mode (SST-ll; e.g., Eicker 2008; Schmidt et al. 2006, 2007; Wittwer 2009); (3) the satellite gravity gradiometry (SGG; e.g., Čunderlík 2013; Eicker et al. 2014; Lieb et al. 2013; Naeimi et al. 2015; Tscherning and Arabelos 2011; Yildiz 2012). Furthermore, Schmidt et al. (2006, 2007) and Wittwer (2009) made an attempt at spatio-temporal gravity field recovery from the GRACE (Gravity Recovery and Climate Experiment, Tapley et al. 2004) SST-ll data. From numerous simulation studies, we mention, e.g., Arabelos and Tscherning (2009), Bentel et al. (2013), Naeimi (2013) and Schmidt et al. (2005).

The aim of the present study is to deliver global and regional gravity field models from real GOCE kinematic orbit via the acceleration approach modified by Bezděk et al. (2014). We present two strategies of how to mitigate the impact of the polar gap problem, a global one and a regional one. Both approaches are based on SRBFs. In the global strategy, we stabilize the estimation of high-degree models (in our case of degree 130) by introducing prior information. The prior information is derived from a long-wavelength geopotential, e.g., up to degree 20, taken from our low-degree GOCE-based model estimated to degree 75. Such a low-degree model is only marginally affected by the polar gap problem; therefore, it can serve as prior information to which the high-degree model is, in a way, forced to be equal to. This significantly improves the zonal and near-zonal spherical harmonic coefficients of the high-degree GOCE-only models. In the second strategy, we apply the acceleration approach on a regional scale in a remove–compute–restore fashion, utilizing the long-wavelength geopotential from our global GOCE-based models. Both the global and the regional gravity field modelling, as presented in this paper, are based on the same orbital data and methodology. The present paper thus provides a consistent approach to gravity field determination from orbital data.

The outline of the paper is as follows. The underlying theory of spherical radial basis functions is briefly described in Sect. 2. In Sect. 3, we describe the modification of the acceleration approach developed by Bezděk et al. (2014). Section 4 presents the used orbital data and background models. In Sect. 5, we evaluate our global and regional gravity field models. Conclusions are drawn in Sect. 6.

2 Representation of the Gravity Field in Terms of Spherical Radial Basis Functions

A spherical radial basis function defined on a reference sphere $\Omega _{{\rm R}}$ is rotationally symmetric around the axis represented by the direction of the unit vector $\mathbf {r}_i / | \mathbf {r}_i |,\,\mathbf {r}_i \in \Omega _{{\rm R}}.$ Here, $\mathbf {r}_i$ is a nodal point at which the radial basis function is located and R is the radius of the sphere. Satellite data are taken at the exterior of the reference sphere $\Omega _{{\rm R}},$ which we shall denote as $\Omega _{{\rm R}}^{\mathrm {ext}}.$ The harmonic upward continuation of SRBFs into observational points is therefore of fundamental importance. It ensures that we can establish a relation between SRBFs and a gravity field quantity observed at a point $\mathbf {r}\in \overline{\Omega _{{\rm R}}^{\mathrm {ext}}},\,\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}= \Omega _{{\rm R}}\cup \Omega _{{\rm R}}^{\mathrm {ext}}.$ In this section, the gravity field modelling is understood in the global sense. The regional gravity field modelling will naturally follow from the global approach with only minor modifications.

The gravitational potential V at a point $\mathbf {r}\in \overline{\Omega _{{\rm R}}^{\mathrm {ext}}}$ expanded in a series of band-limited SRBFs reads (e.g., Freeden and Schneider 1998)

$$\begin{aligned} V(\mathbf {r}) = \sum _{i=1}^{I} a(\mathbf {r}_i) \, \Phi \left( \mathbf {r}, \mathbf {r}_i \right) , \end{aligned}$$

(1)

where $\Phi ( \mathbf {r}, \mathbf {r}_i)$ is a band-limited SRBF located at the nodal point $\mathbf {r}_i \in \Omega _{{\rm R}},\,a(\mathbf {r}_i)$ is the expansion coefficient of the ith SRBF to be determined and I is the total number of SRBFs. The gravitational potential V is to be understood as an approximation of the true gravitational potential $V^{\mathrm {true}}$ in the sense of the Runge–Krarup theorem (Krarup 1969; Freeden and Schneider 1998).

The band-limited SRBF in Eq. (1) is given as (Freeden and Schneider 1998)

$$\begin{aligned} \Phi \left( \mathbf {r}, \mathbf {r}_i \right) = \sum _{n=n_{\mathrm{min}}}^{n_{\mathrm{max}}} \frac{2n+1}{4\pi \, R^2} \, \phi _n \, \left( \frac{R^2}{|\mathbf {r}| \, |\mathbf {r}_i|} \right) ^{(n+1)} \, \, P_n \left( \frac{\mathbf {r}}{| \mathbf {r}|} \cdot \frac{\mathbf {r}_i}{| \mathbf {r}_i |} \right) , \end{aligned}$$

(2)

where $P_n$ is the (unnormalized) Legendre polynomial of degree $n,\,\phi _n$ are non-negative shape coefficients defining the spatial and the spectral properties of the SRBF and, finally, $n_{\mathrm{min}}$ and $n_{\mathrm{max}}$ are minimum and maximum degrees of the expansion, respectively. A SRBF is band-limited if the shape coefficients $\phi _n$ are zero for each degree beyond the maximum degree $n_{\mathrm{max}}.$ If the shape coefficients $\phi _n$ do not vanish for infinitely many degrees, the spherical radial basis function is referred to as non-band-limited. For various types of band-limited and non-band-limited SRBFs see, e.g., Freeden and Schneider (1998), Schmidt et al. (2007) or Wittwer (2009).

In this study, we prefer to work with band-limited SRBFs, since they allow a recovery of the geopotential signal in a given (finite) spectral band. In the corresponding bandwidth, the SRBF solution can thus be directly compared with its spherical harmonic counterpart. However, non-band-limited SRBFs can significantly reduce the computational load, owing to their analytical expressions which are frequently known or may be derived (Wittwer 2009). The closed expressions for non-band-limited SRBFs enable to omit the computationally demanding summation in Eq. (2).

We use two band-limited SRBFs shown in Fig. 1:

• (1) The Shannon SRBF defined by the shape coefficients $\phi _n = 1$ for all $n = n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}.$ The Shannon SRBF is the reproducing kernel of the space spanned by spherical harmonics of degrees $n_{\mathrm{min}},\ldots ,n_{\mathrm{max}}$ and all corresponding orders (Freeden and Schneider 1998). It is not difficult to prove (e.g., Bentel et al. 2013) that global gravity field modelling by means of the Shannon SRBF and of spherical harmonics leads to identical results. Therefore, on a global scale, we expect their comparable quality, but due to the reasons stated in Introduction, we anticipate a better performance of the regional models. In Sect. 5, these statements are confirmed by our results obtained from real orbital data.

• (2) SRBF based on Kaula’s rule of thumb for the degree variances of the Earth’s gravitational potential (Kaula 1966), in this paper referred to as Kaula’s SRBF. As commonly assumed, an incorporation of Kaula’s rule into the determination of models solely based on GOCE data does not contradict the GOCE-only strategy. Frequently, it enters the estimation in the form of the Kaula regularization (e.g., Metzler and Pail 2005; Pail et al. 2011). Nevertheless, such a solution is not entirely based on the data itself, as some prior knowledge of the gravity field is introduced, although empirical and rough. Unlike the Shannon-based models, the solutions based on Kaula’s SRBF are, to some extent, forced to follow the degree variances prescribed by Kaula’s rule. In Sect. 5, we therefore investigate the performance of both SRBFs. Here, all the shape coefficients $\phi _n$ of Kaula’s SRBF are normalized by its coefficient $\phi _2.$

Fig. 1

Spatial and spectral representations of the Shannon and Kaula’s SRBFs in the spectral bandwidth $n=70, \ldots , 130.$ In Sect. 5.3, these radial basis functions are used for regional gravity field determination. The slightly smaller oscillations of Kaula’s SRBF in the spatial domain are caused by the gradual attenuation of the shape coefficients $\phi _n$ prescribed by Kaula’s rule of thumb. For a better mutual comparison in the spatial domain, the spherical radial basis functions are normalized by their values at the spherical distance of 0°

Note that, in addition to Kaula’s rule, there are many other empirical rules by which SRBFs can be defined (see, e.g., Rexer and Hirt 2015 and the references therein). Also, an existing global gravity field model parameterized in spherical harmonics can readily be used to derive the degree variances and subsequently a SRBF. In our study, we aim at the GOCE-only gravity field modelling; therefore, we investigate only the performance of the Shannon and Kaula’s SRBFs.

2.1 Spatial Distribution of Nodal Points

The next important aspect is the total number of nodal points I and their spatial distribution on the reference sphere $\Omega _{{\rm R}}.$ Roughly speaking, the expansion coefficients $a(\mathbf {r}_i)$ of the gravitational potential V in Eq. (1) can be uniquely recovered provided that the nodal points $\mathbf {r}_i$ (or more precisely that some bounded linear functionals of the gravitational potential taken at these points) form a fundamental (or at least an admissible) system relative to the space spanned by all solid spherical harmonics of degrees $n=n_{\mathrm{min}},\ldots ,n_{\mathrm{max}}.$ A precise mathematical definition of fundamental and admissible systems can be found in the Appendix or in the literature provided therein.

Although the existence of fundamental systems can be proved (Freeden et al. 1998; Freeden and Schneider 1998), an algorithm generating positions of the points $\mathbf {r}_i$ of such systems is not available. In practice, we therefore work with admissible systems. An admissible system contains more functionals at the points $\mathbf {r}_i$ than the required minimum, but the uniqueness of the recovered gravitational potential is guaranteed. In other words, linearly dependent SRBFs occur in admissible systems. A drawback of admissible systems is that the design matrix has a rank deficiency, i.e. inversion of the resulting normal matrix is not defined.

There are many possible choices for the spatial distribution of the points $\mathbf {r}_i \in \Omega _{{\rm R}} ,$ e.g., Driscoll and Healy (1994), Eicker (2008), Freeden et al. (1998), Naeimi (2013), Reuter (1982) and Wittwer (2009). Here we use the Reuter grid (e.g., Eicker 2008; Reuter 1982; Wittwer 2009). For a given non-negative integer $\gamma ,$ the algorithm generates a system of points $\mathbf {r}_i$ here denoted as Reuter($\gamma$). Fortunately, there is a simple empirical rule saying that the functionals (for which the fundamental system exists) taken at the grid Reuter($n_{\mathrm{max}}+1$) form an admissible system relative to $\mathrm{Harm}_{0, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ (see Definition 1 in the Appendix). Due to the nature of the algorithm, the number of points I in the grid Reuter($\gamma$) can only be estimated by (Freeden et al. 1998)

$$\begin{aligned} I \le 2+\frac{4}{\pi } \, \gamma ^2. \end{aligned}$$

(3)

A fundamental system relative to $\mathrm{Harm}_{0, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ with, say, $n_{\mathrm{max}}= 130$ contains $I = (n_{\mathrm{max}}+1)^2 = 17{,}161$ functionals (see Appendix). By definition, this is also the total number of spherical harmonic coefficients for $n_{\mathrm{max}}=130.$ The number of expansion coefficients $a(\mathbf {r}_i)$ in an admissible system due to the grid Reuter($n_{\mathrm{max}}+1$) is $I=21{,}780.$ This shows that, in general, we deal with larger systems of linear equations compared to the spherical harmonic case. This drawback is related to the global gravity field modelling. When the gravity field is modelled on a regional scale, the number of expansion coefficients is usually greatly reduced, depending on the size of the recovery area. We prefer to work with Reuter grids for two reasons: (1) because of the simple empirical rule; (2) because the number of points in the Reuter grids increases quadratically with respect to the parameter $\gamma ,$ see Eq. (3). The latter rule is roughly in accordance with the rule $(n_{\mathrm{max}}+1)^2$ that holds for spherical harmonic coefficients.

3 Acceleration Approach

Several methods have been developed to invert SST-hl data into a gravity field model: (1) the energy balance approach, (2) the celestial mechanics approach, (3) the short-arc approach and (4) the acceleration approach. An overview and a comparison of these methods applied to the same GOCE orbital data are given in Baur et al. (2014), where also many references to these methods are listed. From these, we make use of the acceleration approach modified according to Bezděk et al. (2014). Other modifications can be found, e.g., in Baur et al. (2012), Ditmar and van der Sluijs (2004), Ditmar et al. (2006), Reubelt et al. (2003, 2014) and Weigelt et al. (2013).

The acceleration approach, which is based on Newton’s law of motion, links the unknown expansion coefficients to the accelerations acting on the satellite. The transition from kinematic orbit to accelerations domain is performed in an inertial reference frame by applying a second-order derivative filter to the kinematic orbit. The satellite is not, however, subject solely to the gravitational force generated by the Earth. In reality, its motion is also affected by perturbing forces that need to be properly accounted for. After removing all the perturbing accelerations that can be measured on-board (non-gravitational accelerations) or modelled (direct lunisolar perturbations, accelerations due to solid Earth and ocean tides, and correction due to general relativity), the resulting accelerations acting on the spacecraft are identified with the ones caused by the geopotential.

The gravitational vector $\mathbf {g}$ is obtained by applying the gradient operator to the series expansion in Eq. (1),

$$\begin{aligned} \mathbf {g}(\mathbf {r}) = \nabla V(\mathbf {r}) = \sum _{i=1}^{I} a(\mathbf {r}_i) \, \nabla \Phi \left( \mathbf {r}, \mathbf {r}_i \right) . \end{aligned}$$

(4)

After introducing random observation errors into Eq. (4), the following linear Gauss–Markov model can be established

$$\begin{aligned} \mathbf {y}= \mathbf {A}\, \mathbf {x}+ \mathbf {e}, \quad E\{ \mathbf {e}\} = \mathbf {0}, \quad D\left\{ \mathbf {y}\right\} = \sigma ^2 \, \mathbf {P}^{-1}, \end{aligned}$$

(5)

where $\mathbf {y}$ is the $N \times 1$ observation vector, $\mathbf {A}$ is the design matrix of dimensions $N \times I,\,\mathbf {x}$ is the $I \times 1$ vector of unknown expansion coefficients, $\mathbf {e}$ is the $N \times 1$ vector of stochastic observation errors, $\sigma ^2$ is the (unknown) variance factor, $\mathbf {P}$ is the $N \times N$ weight matrix of the observation vector $\mathbf {y}$ and, finally, E and D denote the expectation and the dispersion operators, respectively.

Due to the action of the second-order derivative filter on kinematic orbits which contain random errors, the errors in the obtained accelerations become autocorrelated. The correlation of the accelerations is reflected by a non-diagonal weight matrix $\mathbf {P},$ which has a Toeplitz structure. The Toeplitz structure stems from the assumption that, in the linear model (5), the noise in kinematic orbits is stationary and uncorrelated in time.¹ The elements of $\mathbf {P}$ are defined by the coefficients of the derivative filter. By means of the transformation matrix $\mathbf {W} = \mathbf {T}^{-1}$ obtained from the Cholesky decomposition of the matrix $\mathbf {P}^{-1} = \mathbf {T} \, \mathbf {T}^{\top },$ we linearly transform the model (5) into a new one

$$\begin{aligned} \mathbf {y}_1 = \mathbf {A}_1 \, \mathbf {x}+ \mathbf {e}_1, \quad E\left\{ \mathbf {e}_1 \right\} = \mathbf {0}, \quad D\{ \mathbf {y}_1 \} = \sigma _1^2 \, \mathbf {I} \end{aligned}$$

(6)

with $\mathbf {y}_1 = \mathbf {W}\,\mathbf {y},\,\mathbf {A}_1 = \mathbf {W}\,\mathbf {A},\,\mathbf {e}_1 = \mathbf {W}\,\mathbf {e}$ and with $\mathbf {I}$ being the $N \times N$ identity matrix. The models (5) and (6) lead to the same estimate of $\mathbf {x}.$ Further details can be found in Bezděk (2010) and Bezděk et al. (2014).

If the shape coefficients $\phi _n$ of the SRBF $\Phi$ in Eqs. (1) and (4) are nonzero only for $n=n_{\mathrm{min}}, \ldots , n_{\mathrm{max}},$ i.e. $\Phi \in \mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}),$ and if the functionals taken at the points $\mathbf {r}_i$ form an admissible system relative to $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}),$ then the design matrices $\mathbf {A}$ and $\mathbf {A}_1$ have a rank deficiency of $I - ((n_{\mathrm{max}}+1)^2 - n_{\mathrm{min}}^2),$ see Fig. 2. The number $(n_{\mathrm{max}}+1)^2 - n_{\mathrm{min}}^2$ is derived from the dimension of the space $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}),$ i.e. from the maximum number of linearly independent functions belonging to that space. In such a case, a unique least-squares solution minimizing the functional $\Vert \mathbf {A}_1 \, \hat{\mathbf {x}} - \mathbf {y}_1 \Vert _2^2$ does not exist. In other words, the rank deficiency of the design matrix results in a non-invertible normal matrix $\mathbf {N}= \frac{1}{\sigma _1^2}\,\mathbf {A}_1^{\top } \, \mathbf {A}_1.$ In order to find a unique least-squares solution of the system of linear equations (6), we can add some prior information to the model or an additional constraint to the functional to be minimized. For instance, instead of minimizing $\Vert \mathbf {A}_1 \, \hat{\mathbf {x}} - \mathbf {y}_1 \Vert _2^2,$ we can minimize the functional $\Vert \mathbf {A}_1 \, \hat{\mathbf {x}} - \mathbf {y}_1 \Vert _2^2 + \Vert \hat{\mathbf {x}} \Vert _2^2$ which means that the system is regularized. It can be shown (Aster et al. 2005) that, under this condition, a unique least-square solution can be found, e.g., by means of the truncated singular value decomposition (ibid.). Our experiments (not shown in the paper) with real GOCE SST-hl data revealed, however, that a better solution can be obtained by the variance components estimation (Koch and Kusche 2002). In the context of SRBFs, this approach is applied, e.g., in Eicker (2008), Eicker et al. (2014), Schmidt et al. (2007) and Wittwer (2009). Another techniques can be found, e.g., in Naeimi (2013).

Fig. 2

Singular values of the design matrices set up for all the three components of the gravitational vector in the satellite-fixed frame [along-track (A-T), cross-track (C-T) and radial (RAD), see Sect. 3.2]. Used is real GOCE kinematic orbit from the period 01 November 2009 to 11 January 2010. The minimum and the maximum degrees of the series expansion are 2 and 50, respectively. The SRBFs are located at the grid Reuter(51), yielding 3282 nodal points which is also the total number of the singular values. The extremely small singular values beyond the index $i= (n_{\mathrm{max}}+1)^2 - n_{\mathrm{min}}^2 = 2597$ indicate a linear dependence of $3282-2597=685$ columns of the design matrices. These singular values are different from zero, which is the value they should take by definition, due to the round-off errors. The linear dependence leads to a non-invertible normal matrix with the rank deficiency of 685. For a better scaling of the singular values, in this experiment we multiplied the design matrices by the factor of $R^2,$ see the denominator in Eq. (2)

Following the variance components estimation, we extend the linear model (6) by prior information on the unknown parameters. We thus obtain the linear model

$$\begin{aligned} \left( \begin{array}{ll} \mathbf {y}_1 \\ \varvec{\upmu } \end{array}\right) = \left( \begin{array}{ll} \mathbf {A}_1\\ \mathbf {I} \end{array}\right) \, \mathbf {x}+ \left( \begin{array}{ll} \mathbf {e}_1 \\ \mathbf {e}_{\varvec{\upmu }} \end{array}\right) ,\quad E\left\{ \left( \begin{array}{ll} \mathbf {e}_1 \\ \mathbf {e}_{\varvec{\upmu }} \end{array}\right) \right\} = \mathbf {0}, \quad D\left\{ \left( \begin{array}{ll} \mathbf {y}_1 \\ \varvec{\upmu } \end{array}\right) \right\} = \left( \begin{array}{ll} \sigma _1^2\, \mathbf {I} &{}\quad \mathbf {0} \\ \mathbf {0} &{}\quad \sigma _{\varvec{\upmu }}^2\, \mathbf {P}_{\varvec{\upmu }}^{-1} \end{array}\right) , \end{aligned}$$

(7)

where $\varvec{\upmu }$ is the $I \times 1$ vector of prior information on the vector of unknown parameters, $\mathbf {P}_{\varvec{\upmu }}$ is its $I \times I$ weight matrix known up to a variance factor $\sigma _{\varvec{\upmu }}^2,\,\mathbf {e}_{\varvec{\upmu }}$ is the $I \times 1$ error vector of prior information and I denotes the identity matrices of corresponding dimensions.

The least-squares estimator of the model (7) reads

$$\begin{aligned} \hat{\mathbf {x}}&= \left( \frac{1}{\sigma _1^2} \, \mathbf {A}_1^{\top } \, \mathbf {A}_1 + \frac{1}{\sigma _{\varvec{\upmu }}^2}\, \mathbf {P}_{\varvec{\upmu }} \right) ^{-1} \, \left( \frac{1}{\sigma _1^2}\, \mathbf {A}_1^{\top } \, \mathbf {y}_1 + \frac{1}{\sigma _{\varvec{\upmu }}^2}\, \mathbf {P}_{\varvec{\upmu }} \, \varvec{\upmu } \right) \nonumber \\&= \left( \mathbf {A}_1^{\top } \, \mathbf {A}_1 + \lambda _1 \, \mathbf {P}_{\varvec{\upmu }} \right) ^{-1} \, \left( \mathbf {A}_1^{\top } \, \mathbf {y}_1 + \lambda _1 \, \mathbf {P}_{\varvec{\upmu }} \, \varvec{\upmu } \right) \end{aligned}$$

(8)

with $\lambda _1 = \sigma _1^2 / \sigma _{\varvec{\upmu }}^2.$ The covariance matrix of the estimate $\hat{\mathbf {x}}$ is given as

$$\begin{aligned} D\{ \hat{\mathbf {x}} \} = \left( \mathbf {A}_1^{\top } \, \mathbf {A}_1 + \lambda _1\, \mathbf {P}_{\varvec{\upmu }} \right) ^{-1}. \end{aligned}$$

(9)

The expansion coefficients $\hat{\mathbf {x}}$ and the unknown variance factors $\hat{\sigma }_1^2$ and $\hat{\sigma }_{\varvec{\upmu }}^2$ are estimated iteratively using the variance components estimation (Koch and Kusche 2002). Equation (8) can be considered as a combined least-squares estimation based on the prior information $\varvec{\upmu }$ or as a biased estimation (Metzler and Pail 2005). In the latter case, the parameter $\lambda _1$ is interpreted as a regularization parameter. Furthermore, if $\varvec{\upmu } = \mathbf {0},$ then the estimator (8) is identical to the Tikhonov regularization (Koch and Kusche 2002). Eicker (2008) derived the elements of $\mathbf {P}_{\varvec{\upmu }}$ from inner products of SRBFs and compared such obtained solution with a simple case when $\mathbf {P}_{\varvec{\upmu }} = \mathbf {I}.$ This led to a conclusion that no significant loss of accuracy is produced by this simplified scenario. Therefore, we shall use $\mathbf {P}_{\varvec{\upmu }} = \mathbf {I}$ (e.g., Eicker et al. 2014; Schmidt et al. 2007; Wittwer 2009). The final solution is, however, sensitive to the choice of the parameter $\lambda _1.$ The discussion on the choice of the prior information $\varvec{\upmu }$ is postponed to Sect. 5.

When dealing with real data, analyses of the least-squares residuals $\hat{\mathbf {e}}_1,$ see Eq. (6), systematically imply a presence of strong correlation in time. This behaviour can be explained by the fact that the constellation of high orbiting satellites does not change much between two consecutive positions of the low orbiting satellite (for GOCE the interval is 1 s). This leads to similar measurement conditions and thus to a correlation of the errors in time. Therefore, by means of an autoregressive model (Brockwell and Davis 2002), we estimate an empirical covariance matrix of the least-squares residuals $\hat{\mathbf {e}}_1.$ Analogously, we compute the second linear transformation matrix $\mathbf {W}_1$ from the Cholesky factorization of this empirical covariance matrix and thus obtain a new linear model

$$\begin{aligned} \left( \begin{array}{ll} \mathbf {y}_2 \\ \varvec{\upmu } \end{array}\right) = \left( \begin{array}{ll} \mathbf {A}_2\\ \mathbf {I} \end{array}\right) \, \mathbf {x}+ \left( \begin{array}{ll} \mathbf {e}_2 \\ \mathbf {e}_{\varvec{\upmu }} \end{array}\right) ,\quad E\left\{ \left( \begin{array}{ll} \mathbf {e}_2 \\ \mathbf {e}_{\varvec{\upmu }} \end{array}\right) \right\} = \mathbf {0}, \quad D\left\{ \left( \begin{array}{ll} \mathbf {y}_2 \\ \varvec{\upmu } \end{array}\right) \right\} = \left( \begin{array}{ll} \sigma _2^2\, \mathbf {I} &{}\quad \mathbf {0} \\ \mathbf {0} &{}\quad \sigma _{\varvec{\upmu }}^2\, \mathbf {P}_{\varvec{\upmu }}^{-1} \end{array}\right) \end{aligned}$$

(10)

with $\mathbf {y}_2 = \mathbf {W}_1 \, \mathbf {y}_1,\,\mathbf {A}_2 = \mathbf {W}_1 \, \mathbf {A}_1,\,\mathbf {e}_2 = \mathbf {W}_1 \, \mathbf {e}_1.$ Again, this twice-transformed linear model is solved by means of the variance components estimation. Both the first and the second linear transformations are described in detail in Bezděk (2010) and Bezděk et al. (2014).

In the linear models (5), (6), (7) and (10), we neglect correlations between the individual components of the gravitational vector. For each direction, we separately establish a linear model, obtaining three independent solutions accompanied by their full covariance matrices. As mentioned in Ditmar et al. (2007), the impact of such an approximation on the final solution can be neglected. The three individual solutions along with their full covariance matrices are combined together in the least-squares sense, yielding a final solution. For further details, see Section 3.2 of Bezděk et al. (2014).

3.1 Regionally Tailored Regularization in Terms of SRBFs

A regionally tailored regularization in terms of SRBFs seems to be natural due to their localization in both the space and the frequency domain. In Eq. (8), we can easily account for the regionally varying gravity field by splitting up the weight matrix $\mathbf {P}_{\mathbf {\upmu }}$ into several matrices $\mathbf {P}_{\varvec{\upmu },\,j},\,j=1,\ldots ,J.$ Furthermore, each matrix $\mathbf {P}_{\varvec{\upmu },\,j}$ has its own individual regularization parameter estimated by means of the variance components estimation (Eicker 2008; Eicker et al. 2014).

First, the area in which the expansion coefficients $a(\mathbf {r}_i)$ are to be estimated is divided into J areas. Subsequently, the corresponding diagonal elements of the weight matrix $\mathbf {P}_{\varvec{\upmu },\,j}$ are set to 1 if the points $\mathbf {r}_i$ belong to the jth area. The rest of the elements of the weight matrix $\mathbf {P}_{\varvec{\upmu },\,j}$ is set to zero (the diagonal as well as the off-diagonal ones). Clearly, $\sum _{j=1}^{J} \mathbf {P}_{\varvec{\upmu },\,j} = \mathbf {I}.$ Equation (8) can thus be rewritten as

$$\begin{aligned} \hat{\mathbf {x}} = \left( \mathbf {A}_1^{\top } \, \mathbf {A}_1 + \sum _{j=1}^{J} \lambda _{1,\, j} \, \mathbf {P}_{\varvec{\upmu },\, j} \right) ^{-1} \, \left( \mathbf {A}_1^{\top } \, \mathbf {y}_1 + \sum _{j=1}^{J} \lambda _{1,\, j} \, \mathbf {P}_{\varvec{\upmu },\, j} \, \varvec{\upmu } \right) \end{aligned}$$

(11)

with $\lambda _{1,\,j} = \sigma _1^2 / \sigma _{\varvec{\upmu },\, j}^2.$ A formally similar estimator is obtained for the linear model (10).

In this way, the regularization parameters $\lambda _{1,\,j}$ can easily be regionally adapted allowing for the spatially varying structures of the gravity field. An optimum relative weighting of the variance factors $\sigma _{\varvec{\upmu },\,j}^2$ is obtained by the variance components estimation. A similar regional feature cannot be so straightforwardly introduced into spherical harmonic approaches, as spherical harmonics do not possess any localization in the space domain.

3.2 A Few Remarks on the Numerical Implementation

To approximate the second-order derivative of kinematic orbits, we use the Savitzky–Golay smoothing filters (Press et al. 1997). These filters are characterized by the length of the filter w and by the polynomial order k. Roughly speaking, the higher the order k, the higher the frequencies of the signal can be preserved, but with a less reduction of noise level; therefore, a compromise between the two has to be found. We tested the behaviour of many pairs of w’s and k’s when applied to the 1 s GOCE kinematic orbit. In all the experiments presented in this paper, we use the pair $w=25$ and $k=4.$ Using this pair, we systematically obtain slightly superior results compared to the preliminary pair $w=19,\,k=4$ used in Bezděk et al. (2014). Further discussion on the choice of the parameters w and k can be found in Bezděk et al. (2014).

In Eq. (4), we compute the partial derivatives of SRBFs in the local north-oriented frame (LNOF). The least-squares adjustment is performed in the satellite-fixed frame onto which they are rotated along with the gravitational vector (for the reasons, see Section 3.2 of Bezděk et al. 2014). We build the design matrix block-wise due to its enormous dimensions (see, e.g., Baur et al. 2012; Bezděk et al. 2014), setting the block size to a tenth of the orbital period. We work with band-limited SRBFs given by the Legendre series in Eq. (2), which can efficiently be computed by means of the Clenshaw summation (Press et al. 1997, Chapter 5.5). There are numerous applications of the Clenshaw summation in geodesy (see, e.g., Fantino and Casotto 2009 and the references therein). In order to assess its efficiency, we applied the Clenshaw summation to a test computation of a design matrix. The design matrix was built for the X-direction in the LNOF using $n_{\mathrm{max}}=130$ (i.e. 21,780 unknowns) and 43,200 points (one half of a day of GOCE data). Compared to the direct evaluation, we observed a speed-up factor of 4.5 in terms of the CPU time. Keeping the same settings, but computing only a block of the design matrix comprising 500 kinematic positions, we found the speed-up factor to be 2.1.

We solve the linear models (7) and (10) iteratively following the variance components estimation approach. The computation of the residuals² $\hat{\mathbf {e}} = \mathbf {A}\, \hat{\mathbf {x}} - \mathbf {y}$ is the most time-consuming operation of the iterations. The problem lies in the huge size of the design matrix $\mathbf {A}$ and in the computation of the product $\mathbf {A}\,\hat{\mathbf {x}}.$ The following approach is based on the fact that $\mathbf {A}\,\hat{\mathbf {x}}$ is nothing but a SRBF synthesis of the gravitational vector from the coefficients $\hat{\mathbf {x}}.$ First, we transform the expansion coefficients into the spherical harmonic coefficients (see the second paragraph in Sect. 5). After this transformation, we make use of the spherical harmonic coefficients to compute the product $\mathbf {A}\, \hat{\mathbf {x}},$ now, however, via the efficient spherical harmonic synthesis with Hotine’s equations (Sebera et al. 2013).

Besides the expansion coefficients, we co-estimate empirical parameters (biases) in all three directions. In the global gravity field modelling, these parameters are estimated once per day. In the regional gravity field modelling, we systematically obtain slightly better results with the biases modelled once per block of the design matrix. These settings were found by trial and error.

4 Data

Global and regional gravity field models to be presented in Sect. 5 are based on the GOCE kinematic orbit covering the period 01 November 2009 to 11 January 2010. Besides the two official ESA solutions, the time-wise and the space-wise (Pail et al. 2011), there is a number of other models derived over this period from the GOCE kinematic orbit (e.g., Baur et al. 2012, 2014; Bezděk et al. 2014; Jäggi et al. 2015).

Table 1 specifies the data and the background models that we employ. Furthermore, we assume that the non-gravitational accelerations in the along-track direction are to a large extent compensated by the drag-free control system. The non-gravitational accelerations in the cross-track and the radial directions are modelled, see Bezděk et al. (2014).

For the validation of our results, we made use of the EIGEN-6S model (Förste et al. 2011). It is based on a combination of (1) 6.5 years of the LAGEOS SLR (satellite laser ranging) data spanning the period 01 January 2003 to 30 June 2009, (2) the GRACE SST-hl and SST-ll data covering the same period (3) and 6.7 months of the GOCE SGG data (the diagonal components of the gravitational tensor) from 01 November 2009 till 30 June 2010. To account for the temporal variations of the gravity field, the model includes time-variable parameters for the spherical harmonic coefficients up to degree 50. In our validations, we utilize these coefficients due to the sensitivity of the SST-hl data to the very long-wavelength time-variable gravity field (e.g., Weigelt et al. 2013). As the epoch for the time-variable parameters, we use the mid-epoch of our data period. The EIGEN-6S model is expected to be superior to our models at least by one order of magnitude; therefore, we use it as a high-quality reference model. In fact, any recent model based on the GRACE SST-ll data from a sufficiently long time period might serve well for this purpose.

Table 1 Data and background models

5 Results

As is common in the global gravity field determination, the series expansion in Eq. (2) starts at degree $n_{\mathrm{min}}= 2.$ The maximum degrees of our global models vary from $n_{\mathrm{max}}=75$ to $n_{\mathrm{max}}=130.$ On the one hand, the low-degree solutions with $n_{\mathrm{max}}=75$ are only slightly affected by the absence of data within the polar areas. But, on the other hand, the frequencies beyond that degree, which are present in the signal but not modelled, cause a severe aliasing (here aliasing is understood as defined in Sneeuw and van Gelderen 1997). In addition to last, say, 3 or 4 degrees, aliasing noticeably deteriorates even the rest of the spectrum. To reduce this effect, we increase the maximum degree up to $n_{\mathrm{max}}=130.$ A poor recover of zonal and near-zonal spherical harmonic coefficients is inherent to unconstrained GOCE-only solutions of such a high degree (Sneeuw and van Gelderen 1997). Therefore, one of our goals is to derive GOCE-only models complete to degree 130 retaining the high quality of zonal and near-zonal coefficients from the low-degree solutions.

We evaluate our global SRBF models in both the spatial and the spectral domain, as they provide a mutually complementary information. For the analyses in the spectral domain, we make use of spherical harmonics. The spherical harmonic representation of a global SRBF solution is obtained via the transformation developed by Driscoll and Healy (1994). This quadrature provides an exact transformation of a properly sampled band-limited signal into spherical harmonic coefficients. The signal from our SRBF solutions is band-limited, see Sect. 2. All the results presented in Sects. 5.1 and 5.2 are based only on the Shannon SRBF which will be discussed at the end of Sect. 5.1.

In the regional gravity field determination, we locally refine global models in the spectral band 70–130, where we anticipate a superior performance of the regional approach. The gravity field up to degree 69 is taken from our global models, thus following the GOCE-only strategy even on the regional scale.

5.1 Global Solutions Free from Prior Information

In this section, we show that our global SRBF models can compete with unconstrained GOCE-only models based on spherical harmonics. The global models shown in this section are developed with prior information $\varvec{\upmu },$ see Eq. (8), derived from the $\bar{C}^{\mathrm {GRS80}}_{2,0}$ coefficient of the GRS80 reference ellipsoid (Moritz 2000). A similar step is common in global gravity field modelling (e.g., Metzler and Pail 2005); therefore, we shall use the label free from prior information. We use the $\bar{C}^{\mathrm {GRS80}}_{2,0}$ coefficient to compute the (normal) gravitational potential on the reference sphere R at the grid Reuter($n_{\mathrm{max}}+1$). Here the normal gravitational potential plays the role of pseudo-observations. The vector $\varvec{\upmu }$ is obtained by solving the established system of linear equations using the truncated singular value decomposition. This method is well-suited for the computation of $\varvec{\upmu },$ since we work with noise-free data and the number of linearly independent columns of the design matrix is known prior to the estimation, see the caption to Fig. 2. The rationale of the incorporation of the normal field is to reduce the total number of iterations needed to obtain a solution via the variance components estimation.

Fig. 3

Difference degree amplitudes (thick lines) and modified difference degree amplitudes (thin lines) of the global models complete to degrees $n_{\mathrm{max}}=75,$ 100 and 130. In the modified difference degree amplitudes, the zonal and near-zonal spherical harmonic coefficients are excluded according to the rule of thumb provided by Sneeuw and van Gelderen (1997). It is emphasized that this is done only to show the quality of the coefficients that are (almost) unaffected by the polar gap problem. Except for the modified difference degree amplitudes, we employ all the spherical harmonic coefficients throughout the paper. Reference model: EIGEN-6S

In Fig. 3, we show the difference degree amplitudes (the thick lines; see, e.g., Bezděk et al. 2014) of our global SRBF models recovered up to maximum degrees $n_{\mathrm{max}}=75,$ 100 and 130. Also, we show their modification (the thin lines) excluding the zonal and near-zonal coefficients according to the rule of thumb proposed by Sneeuw and van Gelderen (1997). We shall refer to these as the modified difference degree amplitudes. The highly degraded zonal and near-zonal spherical harmonic coefficients can be seen from the triangular scheme shown in Fig. 4. The inferiority of these coefficients significantly affects the difference degree amplitudes. The modified version therefore better reveals the quality of the coefficients that are almost unaffected by the polar gap problem. It is, however, emphasized that the modified version is shown only as a complementary information on the performance of our models. In most practical applications, all the coefficients are employed.

Fig. 4

Differences in spherical harmonic coefficients related to the solutions from Fig. 3: $n_{\mathrm{max}}=75$ (upper left panel), $n_{\mathrm{max}}=100$ (upper right panel) and $n_{\mathrm{max}}=130$ (bottom left panel). The bottom right panel provides a detail on the low-degree and order differences of the degree-130 solution. The colorbar is in a logarithmic scale. Reference model: EIGEN-6S

From Figs. 3 and 4, it is clear that the quality of zonal and near-zonal spherical harmonic coefficients gradually decreases with increasing maximum degree. However, at the same time, we can see an improvement in the rest of the spectrum, especially in the sectorial and near-sectorial coefficients. This is because the input accelerations possess spectral energy even beyond degrees 75 and 100, mainly due to the low altitude of the satellite. Omission of these high frequencies from the estimation process leads to a serious aliasing. The suppression of aliasing by increasing the maximum degree is also demonstrated by the reduced jump at the last, say, 3 or 4 degrees of the degree amplitudes. This effect is also seen in Fig. 4. Figures 3 and 4 (bottom right panel) further reveal that the degree-2 coefficients are determined weakly. We attribute this to the replacement of the real non-gravitational accelerations by the simulated ones, see Sect. 4. Such a behaviour is not surprising. A discussion on neglecting the non-gravitational accelerations acting on the GOCE satellite can be found in Section 7 of Baur et al. (2014).

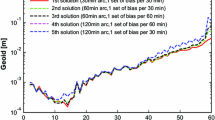
In Fig. 5, we evaluate the SRBF solution complete to degree 130 in terms of geoid height differences. The overall larger discrepancies over the southern hemisphere are caused by the orbit configuration of the GOCE satellite (Pail et al. 2011). The altitude of the satellite is higher over this region, thus making it more difficult to recover the fine structures of the gravity field.

Fig. 5

Geoid height difference (m) between the SRBF solution complete to degree 130 and the EIGEN-6S. The differences are computed with the grid step of 0.1° in both directions. Statistics of the whole data set: $\text {min} = -38.179\,\text {m},\,\text {max} = 83.391\,\text {m},\,\text {mean} = 0.778\,\text {m},\,\text {RMS} = 8.314\,\text {m}.$ Statistics of the data excluding the polar caps (10° radius): $\text {min} = -5.317\,\text {m},\,\text {max} = 5.176\,\text {m},\,\text {mean} = 0.001\,\text {m},\,\text {RMS} = 0.938\,\text {m}.$ The red rectangles bound the areas in which the regional gravity field modelling in Sect. 5.3 is performed

As a next assessment strategy, we validate our SRBF solutions against the traditional spherical harmonic approaches. We computed a solution complete to degree 75 using the same orbital data and the methodology, but parameterizing the gravity field by spherical harmonics (Bezděk et al. 2014). We found both the ordinary and the modified difference degree amplitudes of these solutions to be in a very good agreement. The degree amplitudes of the spherical harmonic solution are not shown in the paper, as at this scale, they virtually overlap the curves for the SRBF solution. This supports the statement from Sect. 2 that global gravity field modelling in terms of the Shannon SRBF and of spherical harmonics should provide the same results.

Next, we show a comparison between the SRBF solution complete to degree 130 and the models by Baur et al. (2014), kindly provided by Oliver Baur. These models are based on the same GOCE SST-hl data as we used, but rely on the spherical harmonic parameterization. The models are obtained by: (1) the celestial mechanics approach, (2) the short-arc approach, (3) the point-wise acceleration approach, (4) the averaged acceleration approach and (5) the energy balance approach. A detailed description as well as references to these methods can be found in Baur et al. (2014). All these models are complete to degree 130, except for the energy balance approach solution, which is estimated to degree 100. The degree amplitudes of all the models, including our SRBF solution, are shown in Fig. 6. The presence of the “zig-zag pattern” in the difference degree amplitudes, which is typical for GOCE-only models, is the strongest in our SRBF solution. In the spectral band 2–60, the even degrees are determined most weakly in the SRBF solution, while its odd degrees outperform the rest of the models nearly over all the frequencies. We assign this behaviour to the particular modification of the acceleration approach and not to the parameterization by SRBFs. The comparable quality of both parameterizations has already been pointed out. It is, however, acknowledged that the incorporation of the prior information from the $\bar{C}^{\mathrm {GRS80}}_{2,0}$ coefficient (i.e. the regularization) may also play some role, especially at the high frequencies. It is known that regularization may act as a low-pass filter suppressing errors and even signal at high frequencies. More importantly, the modified difference degree amplitudes imply that our SRBF approach is able to deliver global gravity field models of comparable quality with respect to the rest of the spherical harmonic approaches. This conclusion is supported by numerous other investigations (not shown in the paper) that we performed with real and with simulated orbits of the CHAMP, GRACE and GOCE satellites. In these experiments, we again found a very good agreement between both parameterizations.

Fig. 6

Difference degree amplitudes (thick lines) and modified difference degree amplitudes (thin lines) of the SRBF model to degree 130 and of the spherical harmonic models derived by: the celestial mechanics approach (CMA), the short-arc approach (SAA), the point-wise acceleration approach (PAA), the averaged acceleration approach (AAA) and the energy balance approach (EBA). Reference model: EIGEN-6S

We experimented with a global gravity field recovery using three regularization parameters, see Sect. 3.1, two for the polar gaps and one for the rest of the globe. In contrast to the regional gravity field determination, this resulted in a worse solution.

Finally, we mention that the global gravity field determination with Kaula’s SRBF is not shown in the paper, as it led to unsatisfactory results. Our global Kaula-based solutions are inferior to the Shannon-based solutions over the entire spectral band. Without attempting to draw general conclusions, it seems that Kaula’s SRBF pushes the gravity signal power towards the zero for degrees beyond ~60. This behaviour might be assigned to the fact that the degree variances derived from Kaula’s rule underestimate the power of the geopotential signal between degrees ~60 and 130 (we did not perform investigations beyond degree 130).

5.2 Global Solutions Based on Prior Information Pre-Computed from GOCE

In this section, we attempt to prevent the deterioration of zonal and near-zonal spherical harmonic coefficients of GOCE-only solutions. To this end, we derive the prior information $\varvec{\upmu }$ from our global GOCE-only model complete to degree 75 (see Sect. 5.1). Thanks to the low resolution of this model, its deterioration due to the polar gap problem is minor. It is therefore a suitable choice to stabilize the estimation of high-degree models. In a similar manner as in the previous section, we computed the prior information $\varvec{\upmu }$ from this model taking its coefficients up to degrees $n_{\mathrm{max},\mu }=10,$ 20, 30 and 70. Note that all the spherical harmonic coefficients up to the degree $n_{\mathrm{max},\mu }$ are used in these computations, not only the zonal and near-zonal ones.

Fig. 7

Difference degree amplitudes (thick lines) and modified difference degree amplitudes (thin lines) of the SRBF solutions complete to degree 100 with various prior information. Reference model: EIGEN-6S

Figure 7 shows the ordinary and the modified difference degree amplitudes of solutions complete to degree 100 obtained with $n_{\mathrm{max},\mu }=10,$ 20, 30 and 70. It is seen that the quality of the model, especially of the zonal and near-zonal spherical harmonic coefficients, highly depends on the choice of the cut-off degree $n_{\mathrm{max},\mu }.$ We observe the best results for $n_{\mathrm{max},\mu }=30.$ The two solutions with the smaller values of $n_{\mathrm{max},\mu }$ are characterized by a better, but still relatively weak recovery of low-order spherical harmonic coefficients. On the other hand, increasing $n_{\mathrm{max},\mu }$ beyond degree 30 gradually leads to a stronger damping of the recovered gravity field oscillations. This is demonstrated by the abrupt jump in the difference degree amplitudes of the solution with $n_{\mathrm{max},\mu }=70.$ The jump starts around degree 70 where the spectral content of the prior information ends. Around that degree, the signal power starts to attenuate. This implies that the prior information with a high cut-off degree $n_{\mathrm{max},\mu }$ leads to a low-pass filtering of the geopotential. This is not surprising, given that the prior information $\varvec{\upmu }$ plays the role of an individual observation group. A high value of the cut-off degree results in dominant prior information to which the solution is highly biased. This is supported by further computations that we performed with $n_{\mathrm{max},\mu }=25$ and 40. The impact of the cut-off degree $n_{\mathrm{max},\mu }$ on the rest of the spectrum seems to be negligible (except for the extreme case when $n_{\mathrm{max},\mu }=70$). This is indicated by the virtually untouched modified difference degree amplitudes in Fig. 7 and also by an inspection of the triangle spectra similar to those in Fig. 4 (not shown in the paper).

Table 2 Normalized variance factors of the prior information $\sigma _{\varvec{\upmu }}^2 / \sigma _{\varvec{\upmu },\mathrm{ref}}^2$ (unitless) related to the solutions from Fig. 7

Table 2 helps to further understand the impact of prior information on the final solution. For all three components of the gravitational vector, the variance factors $\sigma _{\varvec{\upmu }}^2$ decrease with increasing $n_{\mathrm{max},\mu }$ which is expected, since the prior information gradually better approximates the unknown estimating parameters. As a consequence, in the least-squares adjustment the weight of the prior information increases at the expense of the gravitational accelerations (in a relative sense), and the solution is biased to it. Or, in other words, the gravitational accelerations are down-weighted with respect to the prior information and, as a result, the high-frequency gravity field information, present only in the gravitational accelerations, is dampened.

Fig. 8

Difference degree amplitudes (thick lines) and signal amplitudes (thin lines) of the SRBF solutions complete to degree 130 with various prior information. In the bottom part of the spectrum, the red and the purple curves virtually overlap each other. Similarly, the red and the green curves closely follow each other for degrees beyond ~80. The bottom right plot shows a detail on the spectral band 90–130. Reference model: EIGEN-6S

Fig. 9

Differences in spherical harmonic coefficients related to the solutions from Fig. 8: free from prior information (upper left panel), $n_{\mathrm{max},\mu }=10$ (upper right panel), $n_{\mathrm{max},\mu }=20$ (bottom left panel) and $n_{\mathrm{max},\mu }=30$ (bottom right panel). The same logarithmic scale as in Fig. 4. Reference model: EIGEN-6S

Figures 8 and 9 evaluate solutions complete to degree 130 with incorporated prior information to degrees $n_{\mathrm{max},\mu }=10,$ 20 and 30. As a key finding of this section, we observe that the zonal and near-zonal spherical harmonic coefficients are distinctly superior to the solution free from prior information. Similarly as in the previous experiments, the cut-off degree $n_{\mathrm{max},\mu }$ noticeably influences the final solution. Its impact seems to be, however, slightly different as in the case of $n_{\mathrm{max}}=100.$ The “zig-zag pattern” is to a large extent suppressed even with $n_{\mathrm{max},\mu }=10$ and 20. But again, the solution with $n_{\mathrm{max},\mu }=30$ shows the smallest difference degree amplitudes. This is achieved, however, at the cost of unintended low-pass filtering of the geopotential starting near degree 80. This effect can be seen from the thin green curve (the signal from the solution with $n_{\mathrm{max},\mu }=30$) running below the black one (the signal from the EIGEN-6S reference model). It is known that regularization might suppress both signal and noise. This happens especially in that part of the spectrum where noise starts to dominate over signal (the signal-to-noise ratio is close to one). A similar behaviour can be seen in Fig. 8. Immediately as the noise (the thick green curve) approaches the signal (the thin green curve), the signal starts to attenuate and the noise curve is getting flat. As expected, the smoothing effect decreases with decreasing the cut-off degree $n_{\mathrm{max},\mu }.$ This statement is supported by Table 3, particularly by the statistics for the data excluding the polar gaps. While the RMS errors decrease with increasing $n_{\mathrm{max},\mu },$ the minimum and the maximum discrepancies show the opposite. The observed behaviour implies a presence of the low-pass filtering of the geopotential signal. This conclusion is supported by analyses of graphical representations of the discrepancies (not shown in the paper). For this particular case, we therefore consider the cut-off degree $n_{\mathrm{max},\mu }=10$ as a proper choice. We expect that to obtain optimum results with GOCE orbital data from a shorter/longer time period, a slightly different value of $n_{\mathrm{max},\mu }$ might be required.

It is worth mentioning that, in general, the entire spectrum is influenced by the introduction of prior information, even though its spectral content is limited to degree $n_{\mathrm{max},\mu }.$ From Fig. 9 it can be seen, however, that the prior information mostly affects the problematic coefficients of poor quality, i.e. the (near-)zonal ones and nearly all the coefficients beyond degree ~80. The remaining high-quality part of the spectrum stays almost untouched.

Table 3 Differences in terms of geoid heights between the SRBF solutions complete to degree 130 with various prior information and the EIGEN-6S

As far as the difference degree amplitudes are concerned, in the middle part of the spectrum, all these solutions outperform the models in Fig. 6 almost by one order of magnitude. Not shown in Fig. 8 for the sake of clarity, but within this spectral band, the modified difference degree amplitudes remain practically unchanged. The benefit of this approach is that the ratio between removing the “zig-zag pattern” and low-pass filtering of the geopotential can be well-controlled by the choice of the cut-off degree $n_{\mathrm{max},\mu }.$ In order to better understand the impact of prior information on the gravity field solutions from non-polar satellite orbits, further investigations should be carried out, especially under various conditions using synthetic data. This, however, is beyond the scope of the present paper.

Similarly as in the previous section, we attempted to derive a global solution to degree 100 with three regularization parameters. Despite using prior information this time ($n_{\mathrm{max},\mu }=30$), again, the solution was of poor quality over the entire spectrum. The zonal and near-zonal coefficients were degraded by ~1 order of magnitude when compared with the solution free from prior information. Furthermore, in the triangular scheme, we noticed blurred vertical strips, a few spherical harmonic orders wide, with coefficients of weaker quality. The strips were equally present for both the sine and the cosine coefficients and occurred each ~16 orders. We also derived a global solution to maximum degree 100 with prior information based on the global model ($n_{\mathrm{max},\mu }=30$) in the polar areas and on the $\bar{C}^{\mathrm {GRS80}}_{2,0}$ coefficient elsewhere. Again, the performance of such solution was unsatisfactory. Its quality was close to the ones shown in Fig. 7 (the prior information to degrees 10 and 20), except for the even zonal coefficients, which were, in fact, even worse than in the solution free from prior information (the same figure).

We expect that this approach based on the prior information might also be applicable in spherical harmonic approaches. In fact, a similar method in terms of spherical harmonics was successfully applied to simulated GOCE gradients in Xiancai et al. (2011). It should be, however, mentioned that, on the global scale, the GOCE-only gravity field modelling will never yield optimal results, simply because of the polar gaps. Regional approaches seem to be therefore a suitable alternative.

5.3 Regional Solutions

In the regional gravity field modelling, we neglect all the points in kinematic orbit with ground tracks outside a given region (the data area). We aim at a regional refinement of the global models over the bandwidth 70–130. We chose two study areas, depicted in Figs. 5 and 10, where the geoid features the strongest variations between positive and negative values. We anticipate that the regionally tailored gravity field recovery method might outperform the global approach and extract some additional information about the gravity field (i.e. reduce the noise). To prevent edge effects, the data areas are extended by 10° in each direction with respect to the study areas. The placing of the SRBFs is defined by the grid Reuter($n_{\mathrm{max}}+1$), $n_{\mathrm{max}}=130,$ considering only the points that fall inside the study areas extended by 20°. The long-wavelength gravity signal (degrees 0–69) is taken from our global model complete to degree 100 with $n_{\mathrm{max},\mu }=30,$ see Fig. 7. As the prior information, we always use the zero vector, i.e. $\varvec{\upmu } = \mathbf {0},$ which is common in regional gravity field recovery (e.g., Eicker 2008; Eicker et al. 2014; Koch and Kusche 2002; Schmidt and Fabert 2008; Wittwer 2009).

Fig. 10

Geoid undulations (m) over two regions to be regionally refined, here called Indonesia (left panel) and the Andes (right panel). Indonesia: $\text {min}=-12.069$ m, $\text {max}=9.447$ m; The Andes: $\text {min}=-6.916$ m, $\text {max}=8.629$ m. The geoid undulations are synthesized from the EIGEN-6S reference model in the spectral band 70–130 with the grid step of 0.1° in both directions. The red lines bound the areas where separate regularization parameters will be used

Evaluations of the regional solutions are provided in Fig. 11 and Table 4. The differences for the Kaula-based solutions (not depicted here) show virtually the same behaviour. We observe that the use of multiple regularization parameters noticeably improves the results. In particular, the RMS errors decreased by about 8–11 %. Importantly, in addition to the RMS errors, all the minimum and the maximum differences also dropped by about 10–25 %. This implies that instead of the smoothing effect achieved in Table 3, this time we observe an overall improvement. The regionally tailored regularization technique therefore indeed outperforms the use of a single regularization parameter. The slightly increased discrepancies in the north-west part of the Andes area (Fig. 11, right panels) indicate that a separate regularization parameter should be adapted for this subregion.

Table 4 Differences in terms of geoid heights between the regional SRBF solutions and the EIGEN-6S in the spectral band 70–130

Fig. 11

Geoid height differences (m) between the regional Shannon-based SRBF solutions and the EIGEN-6S in the spectral band 70–130. Upper row regional solutions with a single regularization parameter; bottom row regional solutions with multiple regularization parameters

In our experiments, the Shannon-based results systematically turn out to be slightly superior to the Kaula-based ones. Similarly as in Sect. 5.1, Kaula’s SRBF acts as a low-pass filter (note the larger minimum and maximum differences). This is not surprising, as Kaula’s rule itself suppresses certain frequencies of the gravity signal due to the underpowered geopotential within some spectral bands. Naturally, the smoothing effect mostly affects the high frequencies of the geopotential signal. This, however, contradicts one of the basic ideas upon which the regional gravity field modelling is based. That is, to regionally extract additional high-frequency gravity field features that may be difficult to detect on the global scale (see also Naeimi 2013; Naeimi et al. 2015). We therefore prefer the Shannon SRBF, which is free from prior assumptions on the behaviour of the degree variances of the geopotential.

A mutual comparison of the signal (Fig. 10) with the discrepancies (Fig. 11) indicates a smoothing even in the Shannon-based differences. To a large extent, we attribute this behaviour to the prior information $\varvec{\upmu } = \mathbf {0}.$ At first glance, this choice is natural, as the global residual gravity signal has a zero mean. But in this case, the impact of $\varvec{\upmu } = \mathbf {0}$ seems to be significant which results in a pushing the gravity signal towards the zero, i.e. the smoothing. A similar behaviour was observed in Sect. 5.2, where we used various values of the cut-off degree $n_{\mathrm{max},\mu }.$ The smoothing effect could be avoided or suppressed, e.g., by (1) using orbital data from a longer time period; (2) lowering the maximum degree $n_{\mathrm{max}}$; (3) choosing the prior information $\varvec{\upmu }$ more carefully. As for the last option, the prior information over the study area can be based, up to some cut-off degree $n_{\mathrm{max},\mu },$ on the global solutions presented in Sects. 5.1 and 5.2. In this way, the very crude prior information $\varvec{\upmu } = \mathbf {0}$ can be replaced by a better initial approximation of the unknown expansion coefficients. If one is willing to give up the GOCE-only strategy, some other global gravity field models can be used as well. Nevertheless, a study of this topic is needed to verify whether regional solutions can actually benefit from this step.

Over the Indonesia and the Andes regions, Fig. 12 and Table 5 evaluate the global solutions complete to degree 130 shown in Sect. 5.2. The four global models are developed with varying level of smoothing, from essentially un-smoothed (free from prior information) to significantly smoothed ($n_{\mathrm{max},\mu }=30$), see Fig. 8. From a cross-comparison of Tables 4 and 5, it is seen that the regional Shannon-based solutions with multiple regularization parameters provide the smallest RMS errors. Moreover, these regional solutions yield the second smallest minimum and maximum discrepancies. The results we obtained indirectly confirm the assumptions stated in the third paragraph of Introduction. We therefore believe that, at high frequencies, regional Shannon-based solutions may outperform global spherical harmonic models. Here, we again emphasize the superiority of the EIGEN-6S reference model, which provides us with a high-quality benchmark to reliably validate our gravity field models.

Table 5 Differences in terms of geoid heights between the global Shannon-based SRBF solutions (Figs. 8, 9) and the EIGEN-6S in the spectral band 70–130

Fig. 12

Geoid height differences (m) between the global Shannon-based SRBF solutions and the EIGEN-6S in the spectral band 70–130. Upper row global solution with $n_{\mathrm{max}}=130$ and $n_{\mathrm{max},\mu }=10$; bottom row global solution with $n_{\mathrm{max}}=130$ and $n_{\mathrm{max},\mu }=30$

6 Summary, Conclusions and Discussion

We have presented an approach to deliver both global and regional static gravity field models from kinematic orbit analysis. The core of the technique lies in the expansion of the gravity field in terms of band-limited spherical radial basis functions. We have demonstrated the comparable quality of our global GOCE-based models with respect to other spherical harmonic models derived from the same GOCE data. A key outcome of our global gravity field modelling is the approach improving the poor quality of zonal and near-zonal spherical harmonic coefficients of GOCE-only models. These coefficients tend to be degraded due to the inclined orbit of the GOCE satellite. Though so far not supported by numerical experiments, we expect that a similar improvement may also be achieved when applied to spherical harmonics. The present paper thus contributes to the wide variety of studies related to the polar gap issue (e.g., Albertella et al. 1999; Baur and Sneeuw 2007; Korte and Holme 2003; Metzler and Pail 2005; Pail et al. 2001; Rummel et al. 1993; Simons and Dahlen 2006; Sneeuw and van Gelderen 1997; Wieczorek and Simons 2005; Xiancai et al. 2011).

In addition to the static gravity field, its very long-wavelength temporal variations (up to degree ~10) can also be revealed from kinematic orbits. For a certain time period, kinematic orbits may become the only source of information about the time-variable gravity, given that the operational lifetime of the GRACE satellites might reach its end prior to the launch of the GRACE Follow-On mission. The results we achieved on the global scale imply that, in addition to spherical harmonics, temporal variations can also be studied in terms of SRBFs. It is, however, the opinion of the authors that, in this case, spherical harmonics are undoubtedly still the best choice.

Our experience implies that the fine high-frequency gravity information present in kinematic orbits can be better retrieved on a regional rather than on the global scale. Similar studies may turn out to be especially useful due to the possible gap between the GRACE and the GRACE Follow-On missions. In that case, non-dedicated gravity satellites equipped with a geodetic-quality GPS receiver might be the only source of information about the long-wavelength geopotential. The improvements we achieved on the regional scale agree well with recent studies coping with the regional gravity field refinement from satellite data (e.g., Eicker 2008; Eicker et al. 2014; Schmidt et al. 2007). Similarly as in these studies, we found the technique based on multiple regularization parameters to be one of the key ingredients to reach these improvements. We have also shown that the regional gravity field modelling from kinematic orbits is feasible without any need for using spherical harmonics. Although we obtained the prior information with the aid of spherical harmonics, they can easily be avoided by multi-resolution analysis (e.g., Freeden and Schneider 1998).

Some topics and issues still remain open and may be addressed in the future to achieve further improvements. (1) In this study, we relied on simulated non-gravitational accelerations. We expect that the non-gravitational accelerations measured on-board could improve our global models, in particular the low frequencies (mostly the degree-2 coefficients) (Baur et al. 2014). (2) We used the identity matrix to weight the prior information, but other choices are possible. For instance, when the prior information is derived from an existing gravity field model, its covariance matrix can be incorporated if available. (3) If deriving a SRBF from an empirical rule for the degree variances, different rules from Kaula’s could be examined (see, e.g., Rexer and Hirt 2015). This might reduce the low-pass filtering of the geopotential that we observed in the Kaula-based solutions. (4) In the regional gravity field modelling, we noticed a smoothing effect with both the Shannon and Kaula’s SRBF. To mitigate this issue, the regional prior information can be derived from a global SRBF solution up to a certain cut-off degree $n_{\mathrm{max},\mu }.$ In general, we expect a minor smoothing effect, but simultaneously a growth of the RMS error. But similarly as in the global solutions, a compromise may be found, leading to an overall better solution. (5) Regionally refined solutions covering the whole globe can be merged together and transformed into the traditional spherical harmonics as shown in Eicker (2008). Such a global solution may benefit from the regional refinement technique and may improve the high-frequency part of our global gravity field models.

Appendix: Fundamental and Admissible Systems

In order to formulate the conditions on the spatial distribution of nodal points, we borrow a few definitions from Freeden and Schneider (1998) and Freeden et al. (1998), where further details can be found.

Let $\{ Y_{nm} \}_{n=0,1,\ldots ;\, m=-n,\ldots ,n}$ be an orthonormal system of surface spherical harmonics on the unit sphere. Furthermore, let $\{ H_{nm} \}_{n=0,1,\ldots ;\, m=-n,\ldots ,n}$ be their harmonic continuation into the exterior of the unit sphere, called the solid spherical harmonics.

Definition 1

The span of all solid spherical harmonics of degrees $n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}$ defines the space $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}),$

$$\begin{aligned} \mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}) = \mathrm{span}\left\{ H_{nm} \ | \ n=n_{\mathrm{min}},\ldots ,n_{\mathrm{max}};\, m=-n,\ldots ,n\right\} . \end{aligned}$$

(12)

The dimension of the space $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ is $\sum _{n=n_{\mathrm{min}}}^{n_{\mathrm{max}}} (2n+1).$

Definition 2

A set $\{ L_i \}_{i=1, \ldots , M},\,M= \sum _{n=n_{\mathrm{min}}}^{n_{\mathrm{max}}} (2n+1),$ of M linearly independent bounded linear functionals on $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ is called a fundamental system relative to $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ if the matrix

$$\begin{aligned} \left( \begin{array}{lll} L_1 H_{n_{\mathrm{min}},-n_{\mathrm{min}}} &{}\quad \ldots &{}\quad L_M H_{n_{\mathrm{min}},-n_{\mathrm{min}}}\\ \vdots &{}\quad \ddots &{}\quad \vdots \\ L_1 H_{n_{\mathrm{max}},n_{\mathrm{max}}} &{}\quad \ldots &{}\quad L_M H_{n_{\mathrm{max}},n_{\mathrm{max}}}\\ \end{array}\right) \end{aligned}$$

(13)

is regular.

Definition 3

A set $\{ L_i \}_{i=1, \ldots , P},\,P > M = \sum _{n=n_{\mathrm{min}}}^{n_{\mathrm{max}}} (2n+1),$ of P bounded linear functionals on $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ is called an admissible system relative to $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}})$ if it contains a fundamental system relative to $\mathrm{Harm}_{n_{\mathrm{min}}, \ldots , n_{\mathrm{max}}}(\overline{\Omega _{{\rm R}}^{\mathrm {ext}}}).$

Some geodetically relevant fundamental and admissible systems are described in Freeden and Schneider (1998).