Higher dimensional Apollonian packings, revisited

Abstract

The Apollonian circle and sphere packings are well known objects that have attracted the attention of mathematicians throughout the ages. The historically natural generalization of the procedure for generating the packing breaks down in higher dimensions, as it leads to overlapping hyperspheres. There is, however, an alternative interpretation that allows one to extend the concept to higher dimensions and in a unique way. For relatively small dimensions (2 through at least 8), those packings can be thought of as ample cones for classes of K3 surfaces. We describe the packings in some detail for dimensions 4 (with plenty of pictures), 5, and 6.

The Apollonian circle packing is generated as follows: begin with four mutually tangent circles. In the resulting curvilinear triangles, we inscribe a circle tangent to the three sides, thereby producing new curvilinear triangles. We continue the procedure indefinitely, as shown in Fig. 1. The points left over, the residual set, is a set of measure zero. It is a fractal of dimension $\approx 1.305688$ [9, 16].

Fig. 1

Generating the Apollonian packing

The procedure can be done in three dimensions as well: Begin with five mutually tangent spheres. For each of the five subsets of four mutually tangent spheres, it is possible to inscribe a new sphere that is tangent to the four. Again, continue indefinitely. In two dimensions, it is clear that none of the newly generated circles will overlap any of the earlier generations (other than tangentially), as the curvilinear triangles are separated. In three dimensions, the space between the initial four mutually tangent spheres is connected, so it is not a priori clear that the procedure will not lead to overlapping spheres. This does not happen, and the resulting packing fills the space, except for a residual set of measure zero (with fractal dimension $\approx 2.42$ [8]).

In higher dimensions, this procedure in fact leads to overlapping hyperspheres, as was observed by Boyd [8]. This has led many to conclude there is no canonical way of generalizing the Apollonian packing to higher dimensions. Boyd gives alternative Apollonian-like packings whose initial configuration is a set of $N+2$ spheres of dimension $N{-}1$ in $\mathbb {R}^N$ but with gaps or separation (i.e. not mutually tangent) [8]. These packings are described via separation matrices.

In a recent work [6], we show that the Apollonian circle and spherical packings can be realized as the ample cone for classes of K3 surfaces. Given a K3 surface X with Picard group $\mathrm{Pic}(X)=\mathbf e_1\mathbb {Z}\oplus \cdots \oplus \mathbf e_{\rho }\mathbb {Z}$, the intersection matrix $J_{X}=[\mathbf e_i\cdot \mathbf e_j]$ uniquely determines the ample cone for X. Let $J_{\rho }$ be the $\rho \times \rho$ matrix with $-2$’s on the diagonal and 2’s off the diagonal. Then there are K3 surfaces with intersection matrix $J_{\rho }$ for $\rho \le 10$ [17], and the ample cone for $\rho =4$ and 5 generate the Apollonian circle and sphere packings, respectively [6]. Thus, it seems natural to suggest that the canonical Apollonian packing in 4 dimensions (for example) should be the ample cone generated by $J_6$. Ample cones can have edges, meaning the hyperspheres intersect, though the angle of intersection can only be $\pi /2$ or $2\pi /3$. (See [4] for an example.) Thus, the ample cone for $J_6$ a priori might not be what we expect or desire.

In this paper, using the above as our inspiration, we give a formal definition of the Apollonian packing in any dimension $N\ge 2$. This definition is consistent with the Apollonian circle and sphere packings, and with the ample cone for classes of K3 surfaces with Picard number $N+2=\rho \le 10$ (and possibly higher, though no larger than 20). Though arithmetic geometry played a role in our inspiration, this paper will not rely on any arithmetic geometry, except in the remarks. In each dimension, there is a unique Apollonian packing. For those familiar with multiple Apollonian circle packings (e.g. Figs. 2 and 3), we will take the point of view that these are the same packing but viewed from a different perspective.

For dimensions 4 through 6, we show that the Apollonian packing shares many of the familiar properties of the circle and sphere packings, and so are in a sense what we desire. These are:

• (a) The packings include a configuration of $N+2$ mutually tangent hyperspheres in $\mathbb {R}^N$.

• (b) Every hypersphere in the packing is a member of $N+2$ mutually tangent hyperspheres in the packing.

• (c) The hyperspheres do not intersect except tangentially.

• (d) The hyperspheres fill $\mathbb {R}^N$.

• (e) Given a perspective where a configuration of $N+2$ mutually tangent hyperspheres all have integer curvature, every hypersphere in the packing has integer curvature.

By “fill $\mathbb {R}^N$” in (d) we mean there is no space left where we can insert a hypersphere. By “curvature” we mean the inverse of the radius together with a sign, which is negative if the hypersphere contains the packing (e.g. the outside circle in Fig. 1) and positive otherwise. It is sometimes called bend.

We prove (a) and (e) for all N (see Lemmas 5.1 and 4.1). Because our definition is consistent with the description of ample cones for K3 surfaces, (d) for $2\le N\le 8$ follows from results due to Kovacs [14] and Morrison [17]. It is a priori possible that for some N, the packing has intersecting hyperspheres, though that intersection must be perpendicular. Assuming a variation of (d) we prove (c) (see Lemma 5.3), and in passing establish (b) (Corollary 5.4). The variation on property (d), which does not follow from the results of Kovacs and Morrison, is the main result in Sect. 6 and is established for $N=4$, 5, and 6.

Fig. 2

The circles of inversion (dotted lines) that generate the Apollonian packing. In this figure and figures throughout the paper, we will label a circle $H_{\mathbf n}$ with its normal vector $\mathbf n$

Fig. 3

The strip packing and its symmetries

Besides a mathematical/written description of the packings, we generate multiple two-dimensional cross sections of the four-dimensional Apollonian packing (see Figs. 5, 6, 7, 8, 9, 10, 11). We also explain the classical obstruction and how it does not fit in this description.

1 Definitions and background

It has long been known that the Apollonian circle and sphere packings have an underlying hyperbolic structure (e.g. [15]), an observation that was foreshadowed by René Descartes’ celebrated result a full two centuries before the discovery of hyperbolic geometry. We will model hyperbolic geometry with the pseudosphere embedded in Lorentz space. This is sometimes called the vector model. Boyd’s polyspherical coordinates [7] (attributed to Clifford [10] and Darboux [11] in the late nineteenth century) are essentially the same, though not interpreted that way. Suggested references for the pseudosphere in Lorentz space include [3, 18]. A nice summary appears in [12], who recommends the references [1, 2, 21]. (Dolgachev is also interested in the connection between Apollonian-like packings and arithmetic geometry; in particular the connection between the growth rate of orbits of curves on surfaces and the Hausdorff dimension of residual sets.)

1.1 The pseudosphere in Lorentz space

Lorentz space, $\mathbb {R}^{\rho -1,1}$, is the set of $\rho$-tuples over $\mathbb {R}$ equipped with the Lorentz product

$$\begin{aligned} \mathbf u\varvec{\circ }\mathbf v:=u_1v_1+u_2v_2+\cdots +u_{\rho -1}v_{\rho -1}-u_{\rho }v_{\rho }. \end{aligned}$$

The surface $\mathbf x\varvec{\circ }\mathbf x=-1$ is a hyperboloid of two sheets. Let us take the top sheet

$$\begin{aligned} {\mathcal H}: \qquad \mathbf x\varvec{\circ }\mathbf x=-1, \qquad x_{\rho }>0, \end{aligned}$$

which lies in the light cone

$$\begin{aligned} {\mathcal L}^+: \qquad \mathbf x\varvec{\circ }\mathbf x=0, \qquad x_{\rho }>0. \end{aligned}$$

We call ${\mathcal H}$ the pseudosphere, as it can be thought of as a sphere of radius i. Many of the properties we cite herein have analogous results on the sphere of radius r, where r is replaced with i and the dot product is replaced by the Lorentz product. We define the distance |AB| between two points on ${\mathcal H}$ by

$$\begin{aligned} \cosh (|AB|)= -A\varvec{\circ }B. \end{aligned}$$

(Compare this with the similar result for a sphere of radius r: $r^2\cos (|AB|/r)=A\cdot B$.) The pseudosphere ${\mathcal H}$ equipped with this metric is a model of $\mathbb {H}^{\rho -1}$.

Hyperplanes on ${\mathcal H}$ are the intersection of ${\mathcal H}$ with hyperplanes in $\mathbb {R}^{\rho -1,1}$ that go through the origin. That is, hyperplanes of the form $\mathbf n\varvec{\circ }\mathbf x=0$ with $\mathbf n\in \mathbb {R}^{\rho -1,1}$. The hyperplane intersects ${\mathcal H}$ if and only if $\mathbf n\varvec{\circ }\mathbf n>0$. Let us denote the hyperplane in $\mathbb {R}^{\rho -1,1}$ and its intersection with ${\mathcal H}$ by $H_{\mathbf n}$. The plane divides $\mathbb {R}^{\rho -1,1}$ and ${\mathcal H}$ into two halves, which we denote $H_{\mathbf n}^+$ and $H_{\mathbf n}^-$, where

$$\begin{aligned} H_{\mathbf n}^+=\{\mathbf x: \mathbf n\varvec{\circ }\mathbf x\ge 0\}. \end{aligned}$$

The angle $\theta$ between two hyperplanes $H_{\mathbf n}$ and $H_{\mathbf m}$ that intersect in ${\mathcal H}$ is given by

$$\begin{aligned} |\mathbf n||\mathbf m|\cos \theta = -\mathbf n\varvec{\circ }\mathbf m, \end{aligned}$$

(1)

where $|\mathbf n|=\sqrt{\mathbf n\varvec{\circ }\mathbf n}$, and $\theta$ is the angle in the region $H_{\mathbf m}^+\cap H_{\mathbf n}^+$. If the planes do not intersect, then

$$\begin{aligned} |\mathbf n\varvec{\circ }\mathbf m|=|\mathbf n||\mathbf m|\cosh \psi \end{aligned}$$

where $\psi$ is the shortest distance between the two planes $H_{\mathbf m}$ and $H_{\mathbf n}$. The sign of $\mathbf n\varvec{\circ }\mathbf m$ is negative if $H_{\mathbf m}^+\cap H_{\mathbf n}^+$ is the region between the two planes.

When $\mathbf u\varvec{\circ }\mathbf u<0$, our notation $|\mathbf u|=\sqrt{\mathbf u\varvec{\circ }\mathbf u}$ is the positive imaginary square root. The notation $||\mathbf u||$ represents the absolute value of $|\mathbf u|$.

We let

$$\begin{aligned} {\mathcal O}(\mathbb {R})&=\big \{T\in M_{\rho \times \rho }: T\mathbf u\varvec{\circ }T\mathbf v=\mathbf u\varvec{\circ }\mathbf v \hbox { for all } \mathbf u,\mathbf v\in \mathbb {R}^{\rho -1,1}\big \} \\ {\mathcal O}^+(\mathbb {R})&=\big \{T\in {\mathcal O}(\mathbb {R}): T{\mathcal L}^+={\mathcal L}^+\big \}. \end{aligned}$$

Reflection through the plane $H_{\mathbf n}$ is given by

$$\begin{aligned} R_{\mathbf n}(\mathbf x)=\mathbf x-2\mathrm{{proj}}_{\mathbf n}(\mathbf x) \frac{\mathbf n}{|\mathbf n|}=\mathbf x-2\frac{\mathbf n\varvec{\circ }\mathbf x}{\mathbf n\varvec{\circ }\mathbf n}\mathbf n, \end{aligned}$$

and is in ${\mathcal O}^+(\mathbb {R})$. Because all isometries (in any dimension and any geometry) are generated by reflections, the group ${\mathcal O}^+(\mathbb {R})$ is therefore the group of isometries of ${\mathcal H}$.

1.2 The Poincaré models

If we project ${\mathcal H}$ through the point $(0,\ldots ,0,-1)$ and onto the hyperplane $x_{\rho }=0$, then we get the Poincaré hyperball model of $\mathbb {H}^{\rho -1}$. (If we project ${\mathcal H}$ through the origin and onto $x_{\rho }=1$, then we get the Klein model.) Let $\partial \mathbb {H}^{\rho -1}$ be the usual compactification of $\mathbb {H}^{\rho -1}$, which is the spherical boundary of the hyperball model and is isomorphic to $\mathbb {S}^{\rho -2}$. For a point $E\in {\mathcal L}^+$, the set of planes that includes E and the origin generates a set of lines on ${\mathcal H}$, all with a common endpoint at infinity. In this way, we understand ${\mathcal L}^+/\mathbb {R}^+$ as representing $\partial {\mathcal H}\cong \partial \mathbb {H}^{\rho -1}$.

Let us use $E\in {\mathcal L}^+$ for our point at infinity for the Poincaré upper half hyperspace model, which we denote with ${\mathcal H}_E$. Let $\partial {\mathcal H}_E=\partial {\mathcal H}\setminus \{E\mathbb {R}^+\}$ be the bounding plane of ${\mathcal H}_E$. Then $\partial {\mathcal H}_E$ is isomorphic to $\mathbb {R}^{\rho -2}$. In [5], we give a direct map to this model, and prove that the metric

$$\begin{aligned} |PQ|_E^2=\frac{-2P\varvec{\circ }Q}{(P\varvec{\circ }E)(Q\varvec{\circ }E)} \end{aligned}$$

(2)

is a Euclidean metric on $\partial {\mathcal H}_E$. (In [5], there is no negative sign. This is because in that paper we use the intersection pairing, which is the negative of a Lorentz product.)

In the upper half space model ${\mathcal H}_E$, $H_{\mathbf n}$ is represented by a hemisphere or plane perpendicular to the boundary. Its intersection with $\partial {\mathcal H}_E$ is a $(\rho -3)$-sphere or plane, which we will represent with $H_{\mathbf n,E}$ or $H_{\mathbf n}$, depending on whether the choice of E is important.

Lemma 1.1

Let $H_{\mathbf n,E}$ be a $(\rho -3)$-sphere in $\partial {\mathcal H}_E$. Then the radius of $H_{\mathbf n,E}$ is given by

$$\begin{aligned} \frac{|\mathbf n|}{|\mathbf n\varvec{\circ }E|}, \end{aligned}$$

using the metric defined in Eq. (2).

Proof

The center of $H_{\mathbf n,E}$ is the reflection of E through the plane $H_{\mathbf n}$, so is $P=R_{\mathbf n}(E)=E-\frac{2\mathbf n\varvec{\circ }E}{\mathbf n\varvec{\circ }\mathbf n}\mathbf n$. Let Q be any point on the intersection of $H_{\mathbf n}$ with $\partial {\mathcal H}_E$, so $Q\varvec{\circ }Q=0$ and $Q\varvec{\circ }\mathbf n=0$. The radius of $H_{\mathbf n,E}$ therefore satisfies

$$\begin{aligned} r^2=|PQ|_E^2&=\frac{-2P\varvec{\circ }Q}{(P\varvec{\circ }E)(Q\varvec{\circ }E)} \\&=\frac{-2E\varvec{\circ }Q}{-\frac{2\mathbf n\varvec{\circ }E}{\mathbf n\varvec{\circ }\mathbf n}(\mathbf n\varvec{\circ }E)(Q\varvec{\circ }E)} \\&=\frac{\mathbf n\varvec{\circ }\mathbf n}{(\mathbf n\varvec{\circ }E)^2}, \end{aligned}$$

from which the result follows. $\square$

The sign of $\mathbf n\varvec{\circ }E$ depends on the orientations of $\mathbf n$ and E. In particular, once E is fixed, we can choose the orientation of $\mathbf n$ so that the curvature is $\mathbf n\varvec{\circ }E/|\mathbf n|$.

For $P\in {\mathcal H}$, the quantity $P\varvec{\circ }E$ can be thought of as a measure of how far away P is from $\partial H_E$ in the Poincaré model:

Lemma 1.2

Let $P\in {\mathcal H}$ and $E\in {\mathcal L}^+$. In the Poincaré upper half hyperspace model of ${\mathcal H}$, the image of P is a distance

$$\begin{aligned} \frac{||P||}{|P\varvec{\circ }E|} \end{aligned}$$

away from $\partial H_E$, using the Euclidean metric in Eq. (2).

Proof

Let us find the plane $H_{\mathbf n}$ through P with the property that the corresponding hypersphere $H_{\mathbf n,E}$ has minimal radius. The center of such a hypersphere is an endpoint of the line in ${\mathcal H}$ through P and E, so $\mathbf n$ is a linear combination of P and E:

$$\begin{aligned} \mathbf n=aE+P. \end{aligned}$$

Now

$$\begin{aligned} 0=\mathbf n\varvec{\circ }P&=aE\varvec{\circ }P+P\varvec{\circ }P \\ \mathbf n\varvec{\circ }E&=P\varvec{\circ }E \\ \mathbf n\varvec{\circ }\mathbf n&=2aE\varvec{\circ }P+P\varvec{\circ }P \\&=-2P\varvec{\circ }P+P\varvec{\circ }P=-P\varvec{\circ }P. \end{aligned}$$

Thus, the radius of the hypersphere $H_{\mathbf n,E}$ is

$$\begin{aligned} \frac{||P||}{|P\varvec{\circ }E|}, \end{aligned}$$

from which the result follows. $\square$

1.3 The Apollonian circle packing

To generate the Apollonian packing, we begin with four circles. Let us think of those circles as representing planes in the Poincaré upper half space model of $\mathbb {H}^3$. They can therefore be denoted with $H_{\mathbf e_i}$ for $i=1,\ldots ,4$ and vectors $\mathbf e_i$ in $\mathbb {R}^{3,1}$. Let us orient the vectors $\mathbf e_i$ so that the half space $H_{\mathbf e_i}^+$ includes the other circles $H_{\mathbf e_j}$, $j\ne i$. Note that with this choice of orientation, the curvature of $H_{\mathbf e_i}$ is positive if $E\in H_{\mathbf e_i}^+$, and negative otherwise. Let us also normalize their lengths so $\mathbf e_i\varvec{\circ }\mathbf e_i=1$. Since the circles are mutually tangent, the angle between them (in pairs) is zero, so $\mathbf e_i\varvec{\circ }\mathbf e_j=\pm 1$ for $i\ne j$. Because of the orientations we chose, and by Eq. (1), we get $\mathbf e_i\varvec{\circ }\mathbf e_j=-1$. If $\mathbf x$ and $\mathbf y$ are vectors in $\mathbb {R}^{3,1}$ expressed as linear combinations of the vectors $\mathbf e_i$, then $\mathbf x\varvec{\circ }\mathbf y=\mathbf x^tJ\mathbf y$ where

$$\begin{aligned} J=[\mathbf e_i\varvec{\circ }\mathbf e_j]=\begin{bmatrix}1&\quad -1&\quad -1&\quad -1 \\ -1&\quad 1&\quad -1&\quad -1 \\ -1&\quad -1&\quad 1&\quad -1 \\ -1&\quad -1&\quad -1&\quad 1\end{bmatrix}. \end{aligned}$$

Since $\det (J)\ne 0$, the set $\beta =\{\mathbf e_1,\mathbf e_2, \mathbf e_3, \mathbf e_4\}$ is a basis of $\mathbb {R}^{3,1}$.

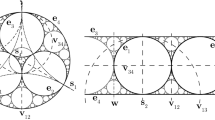
The next step in our generation of the packing is to inscribe circles in the curvilinear triangles formed by our initial four circles. We can think of this as inverting in the four circles shown in Fig. 2.

Let us denote these new circles as $H_{\mathbf s_i}$ for some vectors $\mathbf s_i\in \mathbb {R}^{3,1}$. The circle inscribed in the curvilinear triangle formed by $H_{\mathbf e_1}$, $H_{\mathbf e_2}$, and $H_{\mathbf e_3}$ is the image of $H_{\mathbf e_4}$ under inversion in the circle $H_{\mathbf s_4}$, etc.

Inversion in the circle $H_{\mathbf s_i}$ can be thought of as reflection in the plane $H_{\mathbf s_i}$ in $\mathbb {H}^3$. Since $H_{\mathbf s_i}$ is perpendicular to $H_{\mathbf e_j}$ for all $j\ne i$, we get the relations $\mathbf s_i\varvec{\circ }\mathbf e_j=0$, from which we can solve for $\mathbf s_i$ (up to a multiple): $\mathbf s_1=(-1,1,1,1)$, etc. (Note that $\mathbf s_i\varvec{\circ }\mathbf s_i=4$.) These inversions/reflections generate the Apollonian group

$$\begin{aligned} {\Gamma }_{Ap}=\langle R_{\mathbf s_1}, R_{\mathbf s_2}, R_{\mathbf s_3}, R_{\mathbf s_4}\rangle . \end{aligned}$$

The image of the circles $H_{\mathbf e_i}$ under the action of ${\Gamma }_{Ap}$ is the Apollonian packing.

What is often overlooked is that there is an underlying lattice, the lattice

$$\begin{aligned} \Lambda =\mathbf e_1\mathbb {Z}\oplus \mathbf e_2\mathbb {Z} \oplus \mathbf e_3\mathbb {Z} \oplus \mathbf e_4\mathbb {Z}. \end{aligned}$$

Let us consider the group

$$\begin{aligned} {\mathcal O}^+(\mathbb {Z})=\{T\in {\mathcal O}^+(\mathbb {R}): T\Lambda =\Lambda \}. \end{aligned}$$

Since $\mathbf s_i\varvec{\circ }\mathbf s_i=4$, it is not immediately obvious that $R_{\mathbf s_i}\in {\mathcal O}^+(\mathbb {Z})$, but it is easily verified. Thus ${\Gamma }_{Ap}\le {\mathcal O}^+(\mathbb {Z})$. Note that of our choices for $\mathbf s_i$, we chose $\mathbf s_i\in \Lambda$ and primitive, meaning its coefficients have no common factor.

Since we are viewing the Apollonian packing as the boundary at infinity of an object in $\mathbb {H}^3$, let us change our perspective and choose our point at infinity (for the upper half space model) to be a point of tangency, say where $H_{\mathbf e_3}$ and $H_{\mathbf e_4}$ meet. This gives us the familiar strip packing in Fig. 3. There are a lot of advantages to studying this version. It is in particular easier to visualize its analog in higher dimensions.

Let $H_{\mathbf v_{ij}}$ be the plane that is tangent to $H_{\mathbf e_i}$ and $H_{\mathbf e_j}$, and is perpendicular to $H_{\mathbf e_k}$ for $k\ne i, j$. Several are noted in Fig. 3. The reflection $R_{\mathbf v_{ij}}$ just switches the i-th and j-th component of vectors written in the basis $\beta$. Thus $R_{\mathbf v_{ij}}\in {\mathcal O}^+(\mathbb {Z})$. In [6], we prove

$$\begin{aligned} {\mathcal O}^+(\mathbb {Z})=\langle R_{\mathbf e_3}, R_{\mathbf s_2}, R_{\mathbf v_{12}}, R_{\mathbf v_{34}}, R_{\mathbf v_{14}}\rangle . \end{aligned}$$

The group

$$\begin{aligned} {\Gamma }=\langle R_{\mathbf s_2}, R_{\mathbf v_{12}}, R_{\mathbf v_{34}}, R_{\mathbf v_{14}}\rangle \end{aligned}$$

is the full group of symmetries of the packing.

1.4 Descartes’ theorem

Lemma 1.1 gives us a simple proof of Descartes theorem.

Theorem 1.3

(Descartes) Given four mutually tangent circles with curvatures $k_1$, $k_2$, $k_3$, and $k_4$, those curvatures satisfy

$$\begin{aligned} \mathbf k^tJ^{-1}\mathbf k=0, \end{aligned}$$

where $\mathbf k=(k_1,k_2,k_3,k_4)$.

Proof

Let $\mathbf e_i$ be as above. That is, let them represent the four circles. Recall that $\mathbf e_i\varvec{\circ }\mathbf e_i=1$, so $\mathbf e_i\varvec{\circ }E=k_i$, where E represents the point at infinity in the Poincaré upper half space model. Combining these four equalities, we get

$$\begin{aligned} JE&=\mathbf k \\ E&=J^{-1}\mathbf k. \end{aligned}$$

Since $E\varvec{\circ }E=0$, we get

$$\begin{aligned} (J^{-1}\mathbf k)^tJJ^{-1}\mathbf k&=0 \\ \mathbf k^{t}J^{-1}JJ^{-1}\mathbf k&=0, \end{aligned}$$

from which the result follows. $\square$

More generally, if $\mathbf k$ represents the curvatures of $\rho$ hyperspheres $H_{\mathbf e_i}$ in $\mathbb {R}^{\rho -2}$, and $J=[\mathbf e_i\varvec{\circ }\mathbf e_j]$ is not degenerate, then

$$\begin{aligned} \mathbf k^tJ^{-1}\mathbf k=0. \end{aligned}$$

This was observed by Boyd [8].

We also get the following classic result:

Lemma 1.4

Suppose $\rho$ hyperspheres $H_{\mathbf e_i}$ in $\mathbb {R}^{\rho -2}$ have integer curvatures $k_i$, that $J=[\mathbf e_i\varvec{\circ }\mathbf e_j]$ is not degenerate, and that $\mathbf e_i\varvec{\circ }\mathbf e_i$ are all equal. Suppose $\gamma \in {\mathcal O}^+(\mathbb {Z})$. Then the curvature of $H_{\gamma \mathbf e_i}$ is an integer.

Proof

As above, we note that $JE=\mathbf k|\mathbf e_i|$. The curvature of $H_{\gamma \mathbf e_i}$ is

$$\begin{aligned} \frac{\gamma \mathbf e_i \varvec{\circ }E}{|\gamma \mathbf e_i|}=\frac{\mathbf e_i^t\gamma ^t JE}{|\mathbf e_i|}=\mathbf e_i^t\gamma ^t \mathbf k. \end{aligned}$$

Since $\gamma$ and $\mathbf k$ have integer entries, this is an integer. $\square$

Remark 1

We get an integer packing if $E\in \Lambda$.

2 Intuition and the classical obstruction

In $\rho -2$ dimensions, it is possible to arrange $\rho$ mutually tangent $(\rho -3)$-spheres. As before, let us represent these spheres with $H_{\mathbf e_i}$ for $\rho$ vectors $\mathbf e_i\in \mathbb {R}^{\rho -1,1}$, normalized so that $\mathbf e_i\varvec{\circ }\mathbf e_i=1$, and oriented so that $H_{\mathbf e_i}^+$ is the half space that contains the other hyperplanes/hyperspheres. Then the tangency conditions and the orientations mean the matrix $J_{\rho }=[\mathbf e_i\varvec{\circ }\mathbf e_j]$ has 1’s along the diagonal and $-1$ off the diagonal. Note that J has eigenvalues $\lambda =2$ with multiplicity $\rho -1$, and $\lambda =2-\rho$ with multiplicity 1, so J has signature $(\rho -1,1)$ and hence yields a Lorentz product. (This is one way to show that it is possible to arrange $\rho$ mutually tangent hyperspheres in $\mathbb {R}^{\rho -2}$.)

2.1 The classical obstruction (part one)

The classical temptation is to invert $H_{\mathbf e_1}$ in the hypersphere $H_{\mathbf s_1}$ that is perpendicular to all the other hyperspheres $H_{\mathbf e_i}$ for $i\ne 1$. Solving for $\mathbf s_1$, we get

$$\begin{aligned} \mathbf s_1=(3-\rho )\mathbf e_1+\mathbf e_2+ \cdots +\mathbf e_\rho , \end{aligned}$$

and hence

$$\begin{aligned} R_{\mathbf s_1}(\mathbf x)=\mathbf x - 2\frac{\mathbf x\varvec{\circ }\mathbf s_1}{\mathbf s_1\varvec{\circ }\mathbf s_1}\mathbf s_1=\mathbf x - \frac{2x_1}{\rho -3}\mathbf s_1. \end{aligned}$$

For $\rho =4$ and 5, this is in ${\mathcal O}^+(\mathbb {Z})$, but not for $\rho \ge 6$, hence the perceived obstruction.

2.2 Intuition

We should think of the underlying lattice, $\Lambda _{\rho }=\mathbf e_1\mathbb {Z} \oplus \cdots \oplus \mathbf e_{\rho }\mathbb {Z}$, as a fundamental property of the packings. When we look at the strip version of the Apollonian packing (see Fig. 3), we see a Euclidean translational symmetry, which generates a one-dimensional sub-lattice of $\Lambda _4$. The strip version of the sphere packing has a similar symmetry. This is where we take three mutually tangent congruent spheres and sandwich them between two planes. The three spheres represent $H_{\mathbf e_1}$, $H_{\mathbf e_2}$, and $H_{\mathbf e_3}$, while the two planes represent $H_{\mathbf e_4}$ and $H_{\mathbf e_5}$. The two planes are tangent at the point at infinity, so we have a configuration of five mutually tangent spheres. The packing includes an infinite set of congruent spheres, laid out in a honeycomb pattern, and sandwiched between the planes $H_{\mathbf e_4}$ and $H_{\mathbf e_5}$. A cross section appears in Fig. 4. Again, we see a two-dimensional sub-lattice of $\Lambda _5$. Note that the reflection $R_{\mathbf s_1}$ is a symmetry of this two-dimensional sub-lattice.

Fig. 4

A cross section of the strip version of the sphere packing. The cross section goes through the centers of $H_{\mathbf e_1}$, $H_{\mathbf e_2}$, and $H_{\mathbf e_3}$, and is parallel to the planes $H_{\mathbf e_4}$ and $H_{\mathbf e_5}$. The dotted line represents $H_{\mathbf s_1}$, and $R_{\mathbf s_1}$ restricted to this cross section is reflection through the dotted line. The lower right inset is the inverse of this packing in the circle at that position. It is the cross section of the sphere packing that appears in Soddy’s paper [19, Figure 1]

By analogy, we should build the four-dimensional Apollonian packing as follows: Let us begin with four mutually tangent congruent spheres in $\mathbb {R}^3$, representing $H_{\mathbf e_1}$, ..., $H_{\mathbf e_4}$, which should be thought of as the analog of the three circles shown in Fig. 4. Let us use translations to extend this tetrahedral arrangement into a three-dimensional Euclidean lattice of congruent spheres in $\mathbb {R}^3$ arranged in a cannon-ball like packing. Let us think of this as a cross section of the (hypothetical) four-dimensional Apollonian packing. To get the four-dimensional packing, we thicken this configuration with a dimension and sandwich it between two hyperplanes, $H_{\mathbf e_5}$ and $H_{\mathbf e_6}$. To get the group of isometries, we first identify the isometries of the Euclidean lattice, lift these to isometries in $\mathbb {R}^{5,1}$, and then change our choice of point of tangency for the point at infinity, giving us more elements of the group of symmetries.

2.3 The classical obstruction (part two)

In the initial tetrahedral configuration of the spheres mentioned above, consider the bottom layer of three spheres $H_{\mathbf e_2}$, $H_{\mathbf e_3}$, and $H_{\mathbf e_4}$. These three spheres create a cradle on which we rest the fourth sphere, $H_{\mathbf e_1}$. Now let us extend the bottom layer into an infinite planar arrangement of spheres in a honeycomb pattern. In one of the infinitely many cradles created by this layer, we have nested $H_{\mathbf e_1}$. Note that the adjacent cradles now cannot be filled, as $H_{\mathbf e_1}$ is in the way. Filling in the second layer of spheres as prescribed by the lattice structure, we note that half of the cradles receive a sphere, while the other half remain empty. Now consider the layer below what we called the bottom layer, and in particular consider the other cradle formed by the spheres $H_{\mathbf e_2}$, $H_{\mathbf e_3}$, and $H_{\mathbf e_4}$. If we follow the pattern governed by our lattice, this cradle remains empty, and its adjacent cradles receive spheres. This requisite emptiness is the classical obstruction. The inversion $R_{\mathbf s_1}$ when restricted to this cross section, sends $H_{\mathbf e_1}$ into this cradle.

3 The Apollonian packing in four dimensions

As suggested in the previous section, we should begin with isometries of the cannon-ball sub-lattice in $\mathbb {R}^3$. There are of course the translations, but the fundamental building blocks are the $-1$ maps through the centers of the spheres, and through the points of tangency of pairs of tangential spheres. Such maps appear in [5]. Let $E, P\in {\mathcal L}^+$. Then the $-1$ map on $\partial {\mathcal H}_E$ through the point P is given by

$$\begin{aligned} \phi =\phi _{P,E}(\mathbf x)=\frac{2((P\varvec{\circ }\mathbf x)E +(E\varvec{\circ }\mathbf x)P)}{P\varvec{\circ }E}-\mathbf x. \end{aligned}$$

It is straight forward to verify that $\phi \in {\mathcal O}^+(\mathbb {R})$, $\phi ^2=id$, and that P and E are eigenvectors associated to the eigenvalue $\lambda =1$. The space perpendicular to E and P,

$$\begin{aligned} V^{\perp P,E}=\{\mathbf x\in \mathbb {R}^{\rho -1,1}: \mathbf x\varvec{\circ }E=\mathbf x\varvec{\circ }P=0\}, \end{aligned}$$

is the eigenspace associated to $\lambda =-1$. We would like to verify that $\phi \in {\mathcal O}^+(\mathbb {Z})$ for appropriate choices of P and E.

Note that $\mathbf e_i\varvec{\circ }(\mathbf e_i+\mathbf e_j)=0$, so $\mathbf e_i+\mathbf e_j$ is on both $H_{\mathbf e_i}$ and $H_{\mathbf e_j}$, and $(\mathbf e_i+\mathbf e_j)\varvec{\circ }(\mathbf e_i+\mathbf e_j)=0$. Thus, $\mathbf e_i+\mathbf e_j$ is the point of tangency between $H_{\mathbf e_i}$ and $H_{\mathbf e_j}$. Let

$$\begin{aligned} {\mathcal S}=\{\mathbf e_i+\mathbf e_j: i\ne j\}. \end{aligned}$$

For $E\in {\mathcal S}$ and $\mathbf e_i\varvec{\circ }E\ne 0$, let $P_{i,E}$ be the center of the sphere $H_{\mathbf e_i}$ in $\partial {\mathcal H}_E$:

$$\begin{aligned} P_{i,E}=R_{\mathbf e_i}(E)=E+4\mathbf e_i. \end{aligned}$$

Let

$$\begin{aligned} {\mathcal T}_E=\{\mathbf e_i+\mathbf e_j: \mathbf e_i\varvec{\circ }E\ne 0, \mathbf e_j\varvec{\circ }E\ne 0, i\ne j\} \cup \{P_{i,E}: \mathbf e_i\varvec{\circ }E\ne 0\}. \end{aligned}$$

Lemma 3.1

Suppose $\mathbf x\in \Lambda$ and $E=\mathbf e_i+\mathbf e_j\in {\mathcal S}$ for some fixed i and j. Then

$$\begin{aligned} \mathbf x\varvec{\circ }E \equiv 0 \pmod 2. \end{aligned}$$

Proof

It is enough to calculate $\mathbf e_k\varvec{\circ }E$ for all k. If $k\ne i, j$, then $\mathbf e_k\varvec{\circ }E=-2$. If $k=i$ or j, then $\mathbf e_k\varvec{\circ }E=0$. $\square$

Corollary 3.2

If $E\in {\mathcal S}$, and $P\in {\mathcal T}_E$, then $\phi _{P,E}\in {\mathcal O}^+(\mathbb {Z})$.

Proof

Case 1, $P=\mathbf e_i+\mathbf e_j\in {\mathcal T}_E$: Note that $E\varvec{\circ }P=-4$, so it is enough to verify that the numerator in the definition of $\phi _{P,E}$ is 0 modulo 4. This is straight forward, using the above lemma.

Case 2, $P=P_{i,E}$: Then $E\varvec{\circ }P=E\varvec{\circ }(E+4\mathbf e_i)=-8$, so we check the numerator modulo 8:

$$\begin{aligned} 2((P\varvec{\circ }\mathbf x)E+(E\varvec{\circ }\mathbf x)P)&\equiv 2(((E+4\mathbf e_i)\varvec{\circ }\mathbf x)E+(E\varvec{\circ }\mathbf x)(E+4\mathbf e_i)) \\&\equiv 2((E\varvec{\circ }\mathbf x)E+(E\varvec{\circ }\mathbf x)E) \equiv 0 \pmod 8. \end{aligned}$$

$\square$

Because of symmetry, ${\mathcal O}^+(\mathbb {Z})$ clearly includes the map that switches the i-th and j-th component of $\mathbf x$ when written in the basis $\beta$. Geometrically, this is the reflection $R_{\mathbf v_{ij}}$ where $\mathbf v_{ij}=\mathbf e_i-\mathbf e_j$. Composition of these maps gives us the group of permutations of the components of $\mathbf x$.

We now have a large group of isometries that preserves the lattice. Of course, ${\mathcal O}^+(\mathbb {Z})$ also includes the reflections $R_{\mathbf e_i}$, but we want to avoid these, as we did in our definition for ${\Gamma }$ in the circle packing case. Let ${\Gamma }'$ be the subgroup of ${\mathcal O}^+(\mathbb {Z})$ generated by the maps $\phi _{E,P}$ for $E\in {\mathcal S}$ and $P\in {\mathcal T}_E$, and the reflections $R_{\mathbf v_{ij}}$, and let us look at the image of the hyperspheres $H_{\mathbf e_i, E}$ under the action of this group (in $\partial H_E\cong \mathbb {R}^{\rho -2}$).

For $\rho =4$ and 5, it is clear that ${\Gamma }'$ is a subgroup of symmetries of the Apollonian circle packing, as we used those as inspiration to create ${\Gamma }'$. Thus, ${\Gamma }'\le {\Gamma }$. On the other hand, the packings are generated by the inversions $R_{\mathbf s_i}$, and the reflections $R_{\mathbf v_{ij}}$. For $\rho =4$, we have $R_{\mathbf s_2}=R_{\mathbf v_{34}}\circ \phi _{P_1,\mathbf e_3+\mathbf e_4}$, so ${\Gamma }'={\Gamma }$. For $\rho =5$, we have $R_{\mathbf s_1}=R_{\mathbf v_{23}}\circ R_{\mathbf v_{45}}\circ \phi _{\mathbf e_2+\mathbf e_3,\mathbf e_4+\mathbf e_5}$, so again ${\Gamma }'={\Gamma }$.

From here until the end of this section, we fix $\rho =6$ and $E=\mathbf e_5+\mathbf e_6$.

We use ${\Gamma }'$ to generate what we will call the Apollonian strip packing in four dimensions:

$$\begin{aligned} {\mathcal A}_{4,E}=\{H_{\gamma \mathbf e_1,E}\subset \partial {\mathcal H}_E\cong \mathbb {R}^4: \gamma \in {\Gamma }'\}. \end{aligned}$$

(3)

We will be more precise in the following sections, but for now, we have enough to see (sort of) what the packing looks like. Like we did in Fig. 4 for the sphere packing, we look at cross sections. If we let $x_1=x_2=0$ then we get the circle packing in Fig. 3. If we let $x_1=0$ then we get the sphere packing, and if we let $x_1=0$ and $x_5=x_6$ then we get the cross section in Fig. 4. Our first interesting cross section is shown in Fig. 5. This is the cross section with $x_2=x_3$ and $x_5=x_6$. The condition $x_5=x_6$ means we are looking at the cannon-ball packing in $\mathbb {R}^3$, the cross section parallel to and midway between the hyperplanes $H_{\mathbf e_5}$ and $H_{\mathbf e_6}$. In this 3-dimensional cross section, we are taking the plane that passes through the centers of $H_{\mathbf e_1}$ and $H_{\mathbf e_4}$, and through the point of tangency $\mathbf e_2+\mathbf e_3$.

Fig. 5

The cross section of the 4-dimensional strip version of the Apollonian packing (with $E=\mathbf e_5+\mathbf e_6$), corresponding to $x_2=x_3$ and $x_5=x_6$. The limit point of circles midway between $H_{\mathbf e_1}$ and $H_{\mathbf f_4}$ is the point $\mathbf e_2+\mathbf e_3$, which is where the hyperspheres $H_{\mathbf e_2}$ and $H_{\mathbf e_3}$ are tangent

Let $T_{ij}\in {\Gamma }'$ be translation from $P_i$ to $P_j$ (for $i,j\in \{1,\ldots ,4\}$), so

$$\begin{aligned} T_{ij}=\phi _{P_{i,E},E}\circ \phi _{\mathbf e_i+\mathbf e_j,E}. \end{aligned}$$

The translations $T_{12}$, $T_{13}$, and $T_{14}$ generate the three-dimensional sub-lattice of $\Lambda$ in $\partial {\mathcal H}_E$. We let $\mathbf f_i=T_{1j}\circ T_{1k} (\mathbf e_i)=T_{1k}\circ T_{1j} (\mathbf e_i)$, where i, j, k is a permutation of 2, 3, 4; and we let $f_1=T_{12}\circ T_{13}\circ T_{14}(\mathbf e_1)$. The canonical fundamental domain for the sub-lattice is the parallepiped with vertices the centers of the spheres $H_{\mathbf e_1}$, $H_{\mathbf e_2}$, $H_{\mathbf e_3}$, $H_{\mathbf e_4}$, $H_{\mathbf f_2}$, $H_{\mathbf f_3}$, $H_{\mathbf f_4}$, and $H_{\mathbf f_1}$. The cross section shown in Fig. 6 goes through the center of the parallelepiped, as well as $H_{\mathbf e_4}$ and $H_{\mathbf f_4}$, and is perpendicular to the hyperplanes $H_{\mathbf e_5}$ and $H_{\mathbf e_6}$. It is the cross section $x_2=x_3$ and $x_1+x_2=0$. As an Apollonian-like packing in two dimensions, it is Example 2.6 in Boyd’s paper [8]. It was also studied by Guettler and Mallows [13], who drew pictures, but seemed to be unaware of Boyd’s result.

Fig. 6

The cross section through the centers of $H_{\mathbf e_4}$ and $H_{\mathbf f_4}$, and in a plane perpendicular to $H_{\mathbf e_5}$ and $H_{\mathbf e_6}$

The strip cross section along the long diagonal of the parallepiped is shown in Fig. 7. This is the cross section $x_2=x_3=x_4$.

Fig. 7

The cross section along the long diagonal of the parallelepiped and perpendicular to $H_{\mathbf e_5}$ and $H_{\mathbf e_6}$

It is natural to consider the strip cross section through the centers of $H_{\mathbf e_1}$ and $H_{\mathbf f_4}$, and this is shown in Fig. 8. However, since $x_4=0$, this can also be thought of as a cross section of the sphere packing. In Fig. 4, our cross section is along the line perpendicular to $\mathbf s_1$ and through the center of $H_{\mathbf e_1}$. It is the cross section $x_2=x_3$.

Fig. 8

The strip cross section through the centers of $H_{\mathbf e_1}$ and $H_{\mathbf f_4}$. It is a cross section of the sphere packing

A couple more cross sections are shown in Figs. 9 and 10.

Fig. 9

The strip cross section through the tangent points $\mathbf e_1+\mathbf e_4$ and $\mathbf e_2+\mathbf e_3$. The constraints are $x_1=x_4$ and $x_2=x_3$

Fig. 10

The strip cross section through the tangent point $\mathbf e_2+\mathbf e_3$ and the center of the parallelepiped. The constraints are $x_2=x_3$ and $x_1+x_4=0$

In the caption of Fig. 5, we note that the limit point midway between $H_{\mathbf e_1}$ and $H_{\mathbf f_4}$ is the point of tangency of the two hyperspheres $H_{\mathbf e_2}$ and $H_{\mathbf e_3}$; it is the point $\mathbf e_2+\mathbf e_3$. The cross sections in Figs. 8, 9 and 10 all have points with the same type of feature, where one can imagine tangent spheres above and below the page. To better understand the packing near these points, we can invert (as we did with Fig. 4) so that these points are sent to infinity. If we do this to Fig. 8 then we get Fig. 4. If we do this to Fig. 9 then we get Fig. 5. If we do this to Fig. 10 then we get Fig. 11, which appears to be generated by a cross section of a square-based canon ball packing. Indeed, the triangular and square-based canon ball packings are the same. With a little imagination, this can be seen in Fig. 5: Four spheres creating a square base are $H_{\mathbf e_4}$; $H_{\mathbf f_4}$; the sphere $H_{\mathbf e_2}$, which is the sphere above the page at the point midway between $H_{\mathbf e_1}$ and $H_{\mathbf f_4}$; and the sphere $H_{\mathbf f_2}$, which is the sphere below the page and tangent to the page at the point midway between $H_{\mathbf e_4}$ and $H_{\mathbf f_1}$. One can also see it in the parallelpiped, which can be thought of as the union of an octahedron and two tetrahedrons (see Fig. 13 on page 22). The octahedron is the union of two square-based pyramids, and the vertices of that square are the centers of the four canon balls. The packing in Fig. 11 also appears in [20, Fig. 2].

Fig. 11

The cross section in Fig. 10, inverted in the point $\mathbf e_2+\mathbf e_3$

4 A formal definition of Apollonian packings

Let $\beta =\{\mathbf e_1, \ldots ,\mathbf e_{\rho }\}$ be a basis for a $\rho$-dimensional vector space. Define the bilinear form $\varvec{\circ }$ by

$$\begin{aligned} \mathbf e_i\varvec{\circ }\mathbf e_j=\left\{ \begin{array}{ll} 1 \qquad &{}\hbox {if } i=j \\ -1 &{}\hbox {if } i\ne j.\end{array} \right. \end{aligned}$$

As noted above, the set $\beta$ together with $\varvec{\circ }$ represent a configuration of $\rho$ mutually tangent hyperspheres in $\mathbb {R}^{\rho -2}$; the signature of $J=[\mathbf e_i\varvec{\circ }\mathbf e_j]$ is $(\rho -1,1)$; $\varvec{\circ }$ is a Lorentz product; and $\beta$ is a basis of $\mathbb {R}^{\rho -1,1}$. Let $\Lambda =\Lambda _\rho =\mathbf e_1\mathbb {Z} \oplus \cdots \oplus \mathbf e_{\rho }\mathbb {Z}$. Fix $D\in \Lambda$ such that $D\varvec{\circ }D<0$ and $D\varvec{\circ }\mathbf n\ne 0$ for any $\mathbf n\in \Lambda$ such that $\mathbf n\varvec{\circ }\mathbf n=1$. (Such a D exists, as we will see.) Let ${\mathcal L}^+$ be the cone that contains D:

$$\begin{aligned} {\mathcal L}^+=\{\mathbf x\in \mathbb {R}^{\rho -1,1}: \mathbf x\varvec{\circ }\mathbf x=0, \mathbf x\varvec{\circ }\mathbf D<0\}. \end{aligned}$$

Let

$$\begin{aligned} {\mathcal E}_1=\{\mathbf n\in \Lambda : \mathbf n\varvec{\circ }\mathbf n=1, \mathbf n\varvec{\circ }D<0\} \end{aligned}$$

and

$$\begin{aligned} {\mathcal K}=\bigcap _{\mathbf n\in {\mathcal E}_1} H_{\mathbf n}^-. \end{aligned}$$

That is, for every $\mathbf n\in \Lambda$ with $\mathbf n\varvec{\circ }\mathbf n=1$, we consider the half space that contains D and is bounded by $H_{\mathbf n}$, and take the intersection of all these half spaces. Thus ${\mathcal K}$ is a polyhedral cone with an infinite number of faces. For $\rho =4$ and 5, the faces do not intersect (the circles/spheres do not intersect except tangentially), but there is also no open space at infinity (the circles/spheres are space filling).

Let

$$\begin{aligned} {\mathcal E}^*_1=\{\mathbf n\in {\mathcal E}_1: H_{\mathbf n} \hbox { is a face of } {\mathcal K}\}. \end{aligned}$$

Then the Apollonian packing ${\mathcal A}_{\rho }$ is the set of hyperplanes

$$\begin{aligned} {\mathcal A}_{\rho }=\{H_{\mathbf n}\subset {\mathcal H}\cong \mathbb {H}^{\rho -1}: \mathbf n\in {\mathcal E}^*_1\}. \end{aligned}$$

Given a point $E\in {\mathcal L}^+$ and setting it as our point at infinity, we define the perspective with respect to E to be the set

$$\begin{aligned} {\mathcal A}_{\rho ,E}=\{H_{\mathbf n,E}\in \partial {\mathcal H}_E\cong \mathbb {R}^{\rho -2}: \mathbf n\in {\mathcal E}^*_1\}. \end{aligned}$$

So for example, the Apollonian circle packing shown in Fig. 3 is ${\mathcal A}_{4,\mathbf e_3+\mathbf e_4}={\mathcal A}_{4,(0,0,1,1)}$, while the one shown is Fig. 2 is $A_{4,(1,1,1,3+2\sqrt{3})}$. The strip version of the sphere packing is ${\mathcal A}_{5,\mathbf e_4+\mathbf e_5}$, while the model built by Soddy (see [19, Figure 2]) is ${\mathcal A}_{5,2\mathbf e_1+\mathbf e_5}$.

For fixed $\rho$, ${\mathcal A}_{\rho }$ exists and is unique. There are infinitely many perspectives ${\mathcal A}_{\rho ,E}$. It is a priori not clear that the spheres in ${\mathcal A}_{\rho , E}$ are space filling and do not intersect except tangentially, though it is clear that these properties are independent of the choice of E.

As we did for the Apollonian circle packing ($\rho =4$), let us define

$$\begin{aligned} {\mathcal O}^+(\mathbb {Z})={\mathcal O}^+_{\rho }(\mathbb {Z})=\{T\in {\mathcal O}^+(\mathbb {R}): T\Lambda =\Lambda \}, \end{aligned}$$

and define the group of symmetries of ${\mathcal K}$ to be

$$\begin{aligned} {\Gamma }={\Gamma }_{\rho }=\{T\in {\mathcal O}^+(\mathbb {Z}): T{\mathcal K}={\mathcal K}\}. \end{aligned}$$

To describe ${\mathcal A}_{\rho }$ for small values of $\rho$, we describe ${\Gamma }$ (or a sufficiently large subgroup of ${\Gamma }$).

We first establish property (e) (as outlined in the Introduction):

Lemma 4.1

Suppose we have a configuration of $\rho =N+2$ mutually tangent hyperspheres in ${\mathcal A}_{\rho }$ and suppose these $\rho$ hyperspheres all have integer curvature. Then every hypersphere in ${\mathcal A}_{\rho }$ has integer curvature.

Proof

Because the $\rho$ hyperspheres are in ${\mathcal A}_{\rho }$, they have normal vectors $\{\mathbf f_1,\ldots ,\mathbf f_{\rho }\}$ that are in $\Lambda$. Let us define $\Lambda '=\mathbf f_1\mathbb {Z}+ \cdots +\mathbf f_{\rho }\mathbb {Z}$, so $\Lambda '\subset \Lambda$. Note that both $\pm f_i\in \Lambda$, so let us choose the orientation so that $H^+_{\mathbf f_i}$ contains $H_{\mathbf f_j}$ for all $j\ne i$. This is how we chose the orientations of $\mathbf e_i$, so the matrix

$$\begin{aligned} J'=[\mathbf f_i\varvec{\circ }\mathbf f_j] \end{aligned}$$

is the same as J. In particular, $\det (J')=\det (J)$, so $\Lambda '=\Lambda$ and $\beta '=\{\mathbf f_1,\ldots ,\mathbf f_{\rho }\}$ is a basis of $\Lambda$. As in the proof of Theorem tDescartes, $J'E=\mathbf k$ where $\mathbf k$ is the vector of curvatures of the hyperspheres. If $H_{\mathbf n}\in {\mathcal A}_{\rho }$, then $\mathbf n\in {\mathcal E}_1^*$, so $\mathbf n\in \Lambda$ and $|\mathbf n|=1$. Thus the curvature of $H_{\mathbf n}$ is $\mathbf n\varvec{\circ }E=\mathbf n^tJ'E=\mathbf n^t \mathbf k$, so is an integer. $\square$

Remark 2

Given a different initial configuration of $\rho$ circles $H_{\mathbf e_1}$, ..., $H_{\mathbf e_\rho }$, we can define a $J=[\mathbf e_i\varvec{\circ }\mathbf e_j]$, where we again choose $\mathbf e_i\varvec{\circ }\mathbf e_i=1$, but $\mathbf e_i\varvec{\circ }\mathbf e_j$ is defined by the separation between the spheres $H_{\mathbf e_i}$ and $H_{\mathbf e_j}$. Boyd’s polyspherical coordinates yield the negative of J, which he calls a separation matrix [8]. For example, in Fig. 6, we can select the ordered basis $\beta =\{\mathbf e_5, \mathbf e_6, \mathbf e_4, \mathbf f_4\}$. We calculate $f_4=(-1,1,1,0,1,1)$ and $f_4\varvec{\circ }e_4=-3$, giving us the separation between $\mathbf e_4$ and $\mathbf f_4$. (Since the cross section goes through the centers of the hyperspheres $H_{\mathbf e_4}$ and $H_{\mathbf f_4}$, the curvatures of the circles are the same as the curvatures of the hyperspheres, so the separation in four dimensions is the same as in the two dimensional cross section.) We therefore get the matrix

$$\begin{aligned} J=\begin{bmatrix}1&\quad -1&\quad -1&\quad -1 \\ -1&\quad 1&\quad -1&\quad -1 \\ -1&\quad -1&\quad 1&\quad -3 \\ -1&\quad -1&\quad -3&\quad 1\end{bmatrix}, \end{aligned}$$

which is the negative of Boyd’s separation matrix in his Example 2.6.

Boyd also observed that the off diagonals can be half integers and still lead to Apollonian like packings, so it seems reasonable to look at $-2J$ instead. That is, require $\mathbf e_i$ to have square norm $\mathbf e_i\varvec{\circ }\mathbf e_i=-2$. (Note that $R_{\mathbf e_i}$ is still in ${\mathcal O}^+(\mathbb {Z})$, but this is not guaranteed if $\mathbf e_i\varvec{\circ }\mathbf e_i < -2$.) With this new Lorentz product, if $\mathbf e_i\varvec{\circ }\mathbf e_j\in \mathbb {Z}$ for all i and j, then the lattice $\Lambda$ is even, meaning for any $\mathbf x\in \Lambda$, $\mathbf x\varvec{\circ }\mathbf x$ is even. The set ${\mathcal E}_1$ is replaced with ${\mathcal E}_{-2}$ and yields the same ${\mathcal K}$.

If X is a K3 surface, then the Picard group for X is a lattice $\Lambda$ together with the intersection pairing. The lattice is even and the matrix J is the intersection matrix. If we choose D to be ample (so $\mathbf n\cdot D\ne 0$ for any $\mathbf n\in {\mathcal E}_{-2}$), then the set ${\mathcal E}_{-2}^*$ is the set of divisor classes of irreducible $-2$ curves on X, and ${\mathcal K}$ is the ample cone [14].

Given an even lattice $\Lambda$ of dimension $\rho \le 10$, there exists a K3 surface X with $\mathrm{Pic}(X)=\Lambda$ [17]. Thus, the Apollonian packing in dimensions two through 8 ($4\le \rho \le 10$) can be thought of as representing the ample cones for classes of K3 surfaces.

5 The details

In Sect. 3, we described a packing ${\mathcal A}_6$ by looking at the orbit of a hypersphere under the action of a group of isometries ${\Gamma }'$. In this section, we aim to justify what we did. We begin with a D and use that to define ${\mathcal K}$. We show that $R_{\mathbf v_{ij}}$ and $\phi _{P,E}$ are in ${\Gamma }$ so ${\Gamma }'\le {\Gamma }$. We use ${\Gamma }'$ to describe an a priori different cone ${\mathcal K}'$ and use ${\Gamma }'\le {\Gamma }$ to conclude ${\mathcal K}\subset {\mathcal K}'$. We then use a descent argument to show ${\mathcal K}'={\mathcal K}$. The descent argument is dimension specific, so in this section we state its main consequence (Statement 1), which we prove in Sect. 6 for $\rho =6$, 7, and 8.

Let us choose

$$\begin{aligned} D=\sum _{i=1}^\rho \mathbf e_i \end{aligned}$$

and use this to define ${\mathcal K}$. We need to know that $D\varvec{\circ }\mathbf n\ne 0$ for any $\mathbf n\in {\mathcal E}_1$.

For any $\mathbf n\in {\mathcal E}_1$, there exists an $E\in {\mathcal S}$ so that $\mathbf n\varvec{\circ }E\ne 0$, for otherwise, $\mathbf n\varvec{\circ }\mathbf e_i=0$ for all i, which has the unique solution $\mathbf n=\mathbf 0$. Let us use this E for our point at infinity. By Lemmas 1.1 and 3.1, the radius of the sphere $H_{\mathbf n,E}\in \partial {\mathcal H}_E$ is no more than 1 / 2. But D is too high in the Poincaré model ${\mathcal H}_E$, since by Lemma 1.2, its distance above $\partial {\mathcal H}_E$ is

$$\begin{aligned} \frac{||D||}{|D\varvec{\circ }E|}=\frac{\sqrt{\rho (\rho -2)}}{2(\rho -2)}=\frac{1}{2} \sqrt{\frac{\rho }{\rho -2}}>1/2. \end{aligned}$$

Thus $D\varvec{\circ }\mathbf n\ne 0$ for any $\mathbf n\in {\mathcal E}_1$. In the above calculation, and some that follow, it is useful to note that $D\varvec{\circ }\mathbf e_i=2-\rho$, so $D\varvec{\circ }D=\rho (2-\rho )$ and $D\varvec{\circ }E=2(2-\rho )$.

Suppose $\gamma \in {\mathcal O}^+(\mathbb {Z})$. Then by definition we have that if $\gamma {\mathcal K}={\mathcal K}$ then $\gamma \in {\Gamma }$. The condition that $\gamma {\mathcal K}={\mathcal K}$ is equivalent with $\gamma {\mathcal E}_1={\mathcal E}_1$, which is satisfied if and only if

$$\begin{aligned} \gamma {\mathcal E}_1^*={\mathcal E}_1^*. \end{aligned}$$

But

$$\begin{aligned} \gamma {\mathcal E}_1&=\{\gamma \mathbf n: \mathbf n\in \Lambda , \mathbf n\varvec{\circ }\mathbf n=1, \mathbf n\varvec{\circ }D< 0\} \\&=\{\mathbf m\in \Lambda : \mathbf m\varvec{\circ }\mathbf m=1, \gamma ^{-1}\mathbf m\varvec{\circ }D<0\} \\&=\{\mathbf m\in \Lambda : \mathbf m\varvec{\circ }\mathbf m=1, \mathbf m\varvec{\circ }\gamma D<0\}. \end{aligned}$$

Note that $R_{\mathbf v_{ij}}D=D$ (it switches the i-th and j-th component), so $R_{\mathbf v_{ij}}\in {\Gamma }$.

Lemma 5.1

The planes $H_{\mathbf e_i}$ are faces of ${\mathcal K}$.

Proof

Let $\mathbf n\in {\mathcal E}_1$ and let $\psi$ be the distance from $D/||D||\in {\mathcal H}$ to $H_{\mathbf n}$. Then $2\psi$ is the distance between D / ||D|| and its image $R_{\mathbf n}$ under reflection through $H_{\mathbf n}$, so

$$\begin{aligned} \cosh (2\psi )&=\frac{D\varvec{\circ }R_{\mathbf n}(D)}{D\varvec{\circ }D} \\&=\frac{1}{D\varvec{\circ }D}D\varvec{\circ }\left( D-\frac{2\mathbf n\varvec{\circ }D}{\mathbf n\varvec{\circ }\mathbf n}\mathbf n\right) \\&=1-\frac{2(\mathbf n\varvec{\circ }D)^2}{D\varvec{\circ }D} \\&=1+\frac{2(\rho -2)^2}{\rho (\rho -2)}\left( \sum _{i=1}^\rho n_i\right) ^2. \end{aligned}$$

Since $\mathbf n\varvec{\circ }D\ne 0$, this is minimal when the sum is one, which occurs when $\mathbf n=\mathbf e_i$. Thus, the planes $H_{\mathbf e_i}$ are all faces of ${\mathcal K}$, as there are no planes $H_{\mathbf n}$ with $\mathbf n\in {\mathcal E}_1$ that are closer to D / ||D||. $\square$

As a consequence, the initial configuration of $\rho$ mutually tangent hyperspheres represent faces of ${\mathcal K}$, so the packing ${\mathcal A}_{\rho }$ contains those hyperspheres. This establishes property (a) outlined in the Introduction.

Lemma 5.2

Suppose $E\in {\mathcal S}$ and $P\in {\mathcal T}_E$. Then $\phi _{P,E}\in {\Gamma }$.

Proof

Let $\mathbf n\in {\mathcal E}_1^*$, and let us first suppose that $\mathbf n\varvec{\circ }E\ne 0$. Then in the Poincaré model ${\mathcal H}_E$, the point D is above the highest point on $H_{\mathbf n,E}$, as we saw earlier. Now $\phi _{P,E}(D)\varvec{\circ }E=D\varvec{\circ }\phi _{P,E}^{-1}(E)=D\varvec{\circ }E$, so the image of D is at the same height and hence is still above $H_{\mathbf n, E}$. Thus, $\phi _{P,E}(\mathbf n)\in {\mathcal E}_1$.

The case when $\mathbf n\varvec{\circ }E=0$ is a bit more difficult. Without loss of generality, we may assume $E=e_{\rho -1}+e_\rho$. We first note that

$$\begin{aligned} 0=\mathbf n\varvec{\circ }E=-2\sum _{i=1}^{\rho -2} n_i, \end{aligned}$$

(4)

so

$$\begin{aligned} \mathbf n\varvec{\circ }\mathbf e_\rho =-\sum _{i=1}^\rho n_i+2n_\rho =n_\rho -n_{\rho -1}. \end{aligned}$$

Since both $H_{\mathbf n}$ and $H_{\mathbf e_\rho }$ contain E, the two intersect, so $\mathbf n\varvec{\circ }\mathbf e_\rho =0$ or $\pm 1$ (see Eq. 1). We note that

$$\begin{aligned} 1=\mathbf n\varvec{\circ }\mathbf n&=\sum _{i=1}^\rho n_i^2-2\sum _{i\ne j} n_in_j \\&\equiv \sum _{i=1}^{\rho } n_i^2 \pmod 2 \\&\equiv \left( \sum _{i=1}^{\rho }n_i\right) ^2 \pmod 2 \\&\equiv n_{\rho -1}^2+n_\rho ^2 \pmod 2 \qquad \qquad \hbox {(using Equation}~4). \end{aligned}$$

Thus $n_{\rho -1}\not \equiv n_\rho \pmod 2$, so $\mathbf n\varvec{\circ }\mathbf e_\rho =\pm 1$. That is, $H_{\mathbf n}$ and $H_{\mathbf e_\rho }$ are tangent at E. There are therefore at most two faces of ${\mathcal K}$ through E. Since $H_{\mathbf e_{\rho -1}}$ and $H_{\mathbf e_\rho }$ are two faces of ${\mathcal K}$ through E, we get that $\mathbf n=\mathbf e_{\rho -1}$ or $\mathbf e_\rho$.

Finally,

$$\begin{aligned} \phi _{P,E}(\mathbf e_\rho )=\frac{2(\mathbf e_\rho \varvec{\circ }P)E}{P\varvec{\circ }E}-\mathbf e_\rho = E-\mathbf e_{\rho }=\mathbf e_{\rho -1}, \end{aligned}$$

and $\phi _{P,E}(\mathbf e_{\rho -1})=\mathbf e_\rho$. Thus $\phi _{P,E}(\mathbf n)\in {\mathcal E}_1^*$ for all $\mathbf n\in {\mathcal E}_1^*$, so $\phi _{P,E}\in {\Gamma }$. $\square$

Let

$$\begin{aligned} {\Gamma }'=\langle \{R_{\mathbf v_{ij}}, \phi _{P,E}: i\ne j, E\in {\mathcal S}, P\in {\mathcal T}_E\}\rangle \end{aligned}$$

and define

$$\begin{aligned} {\mathcal K}'=\bigcap _{\mathbf n\in {\Gamma }'(\mathbf e_\rho )}H_{\mathbf n}^-. \end{aligned}$$

Then clearly ${\mathcal K}\subset {\mathcal K}'$, as ${\Gamma }'(\mathbf e_{\rho })\subset {\mathcal E}_1$. We wish to show that ${\mathcal K}'={\mathcal K}$. It is enough to show that the packing that corresponds to ${\mathcal K}'$ is space filling. If it is not, then there exists a gap in the packing where we can fit a sphere. This sphere represents a halfspace in ${\mathcal H}$ that is contained in ${\mathcal K}'$. Let us formalize this property with the following:

Statement 1

Let $\mathbf n\in \Lambda _{\rho }$ and suppose $D\in H_{\mathbf n}^-$. Then $H_{\mathbf n}^+\not \subset {\mathcal K}'$.

Establishing the veracity of this statement for $4\le \rho \le 8$ is the main result of the next section.

Lemma 5.3

Suppose Statement 1 is true for a given $\rho$. Then ${\mathcal K}'={\mathcal K}$. Furthermore, the hyperplanes in ${\mathcal A}_\rho$ do not intersect, so the hyperspheres in ${\mathcal A}_{\rho ,E}$ intersect tangentially or not at all.

Proof

Suppose there exists $\mathbf m\in {\mathcal E}_1^*$ that is not in ${\Gamma }'(\mathbf e_\rho )$. Then $H_{\mathbf m}$ is a face of ${\mathcal K}$ but is not a face of ${\mathcal K}'$. If $H_{\mathbf m}$ does not intersect any faces of ${\mathcal K}'$ except tangentially, then $H_{\mathbf m}^+\subset {\mathcal K}'$, contradicting Statement 1. Thus, $H_{\mathbf m}$ intersects $H_{\gamma \mathbf e_\rho }$ transversely for some $\gamma \in {\Gamma }'$. Consequently, $\mathbf m\varvec{\circ }\gamma \mathbf e_\rho =0$, as this product is an integer and is in the interval $(-1,1)$ (see Eq. 1). Hence, $\gamma ^{-1}\mathbf m\varvec{\circ }\mathbf e_{\rho }=0$. Note that $\gamma ^{-1}\mathbf m\in {\mathcal E}_1^*$, since $\gamma \in {\Gamma }'$. Let $\mathbf m'=\gamma ^{-1}\mathbf m$, so

$$\begin{aligned} 0=\mathbf m'\varvec{\circ }\mathbf e_{\rho }=m_{\rho }'-\sum _{i=1}^{\rho -1}m_i'. \end{aligned}$$

But then

$$\begin{aligned} 1=\mathbf m'\varvec{\circ }\mathbf m'&= \sum _{i=1}^\rho (m_i')^2-2\sum _{i\ne j}m_i'm_j' \\&\equiv \left( \sum _{i=1}^\rho m_i'\right) ^2 \pmod 2 \\&\equiv (\mathbf m'\varvec{\circ }\mathbf e_{\rho })^2 \equiv 0 \pmod 2, \end{aligned}$$

a contradiction. Thus no such $\mathbf m$ exists, so ${\mathcal K}'={\mathcal K}$. The same argument shows the hyperplanes in ${\mathcal A}_\rho$ do not intersect, so the hyperspheres in ${\mathcal A}_{\rho ,E}$ intersect tangentially or not at all. $\square$

This shows that the definition of ${\mathcal A}_{4,E}$ given in Eq. 3 is consistent with the formal definition given in Sect. 4. It also establishes properties (c) and (d) as outlined in the Introduction. Note that the proof of Lemma 5.3 depends on showing ${\mathcal K}'={\mathcal K}$, so does not follow from the results of Kovacs and Morrison. Finally, we have property (b):

Corollary 5.4

Suppose Statement 1 is true for a given $\rho$. Then every hypersphere in ${\mathcal A}_{\rho }$ is a member of $\rho$ mutually tangent hyperspheres in ${\mathcal A}_{\rho }$.

Proof

Let $H_{\mathbf n}$ be a hypersphere in ${\mathcal A}_{\rho }$. Then $\mathbf n=\gamma (\mathbf e_{\rho })$ for some $\gamma \in {\Gamma }'$. But then $H_{\mathbf n}$ is a member of the $\rho$ mutually tangent spheres $H_{\gamma \mathbf e_1}, \ldots , H_{\gamma \mathbf e_{\rho }}$. $\square$

6 The descent argument

In this section, we establish Statement 1 for $\rho =6$, 7, and 8. Our approach is a method of descent on curvature, which is roughly equivalent to establishing a fundamental domain for ${\Gamma }'$.

Suppose $H_{\mathbf n,E}$ is a hypersphere in $\partial {\mathcal H}_E$ with $E=\mathbf e_{\rho -1}+\mathbf e_{\rho }$. Its curvature is unchanged under the action of ${\Gamma }'_E$, the stabilizer of E in ${\Gamma }'$, as those maps are Euclidean isometries on $\partial {\mathcal H}_E$. In $\partial {\mathcal H}_E$, there are many points of tangency $E'$ between spheres (e.g. the set S), which are essentially no different than E. Our intuitive idea is to use ${\Gamma }'_E$ to move $H_{\mathbf n,E}$ close to one of these points $E'$, and check to see if the curvature of $H_{\mathbf n,E'}$ with respect to $E'$ is strictly smaller, thereby giving us a method of descent.

We will begin in three dimensions (the sphere packing, $\rho =5$), where our geometric intuition is strongest (and the packing is not too trivial), with a view to describing our geometric arguments algebraically, so that we may lift them to higher dimensions.

6.1 The case $\rho =5$ (the sphere packing)

Let $E=\mathbf e_4+\mathbf e_5$ be our point at infinity for the Poincaré model. Consider the cross section of ${\mathcal H}_E$ given by $x_4=x_5$. This is the cross section shown in Fig. 4. Recall, we define the translations $T_{ij}$ in ${\mathcal H}_E$ by

$$\begin{aligned} T_{ij}=\phi _{P_{i,E},E}\circ \phi _{\mathbf e_i+\mathbf e_j,E}. \end{aligned}$$

This is the translation that sends $P_{i,E}$ to $P_{j,E}$. The canonical fundamental domain for the group $G_1=\langle T_{12},T_{13}\rangle$ on this cross section is the parallelogram shown in Fig. 12, which we will use as a reference. Consider now the group $G_2=\langle R_{\mathbf v_{12}}, R_{\mathbf v_{23}}, \phi _{\mathbf e_2+\mathbf e_3,E}\rangle$, which includes $G_1$. The two reflections $R_{\mathbf v_{12}}$ and $R_{\mathbf v_{23}}$ give us two natural faces for a fundamental domain for $G_2$, namely the faces $H_{\mathbf v_{12}}$ and $H_{\mathbf v_{23}}$. Let $Q_1$ be the center of ${\Delta }P_{1,E}P_{2,E}P_{3,E}$, the point of intersection between these two faces and on this cross section. Then $Q_1$ has coordinates (x, x, x, y, y), satisfies $Q_1\varvec{\circ }Q_1=0$, and is oriented so that $Q_1\varvec{\circ }D<0$, from which we conclude $Q_1=(4,4,4,-1,-1)$. For the third face of a fundamental domain for $G_2$, let us use the plane

$$\begin{aligned} H_{\mathbf n}=\{\mathbf x\in \mathbb {R}^{4,1}: \mathbf x\varvec{\circ }Q_1=\mathbf x\varvec{\circ }\phi _{\mathbf e_2+\mathbf e_3,E}(Q_1)\}. \end{aligned}$$

Fig. 12

With $\rho =5$: A fundamental domain for $G_2$ (shaded triangle ${\Delta }Q_1Q_2Q_3$), inside a fundamental domain for $G_1$ (the parallelogram)

This is the plane midway between $Q_1$ and $\phi _{\mathbf e_2+\mathbf e_3,E}(Q_1)$, which has normal vector the difference of $Q_1$ and its image. Solving for $\mathbf n$, we find $\mathbf n=\mathbf s_1$ (up to a multiple). Using a method of descent (using distance from $Q_1$), we find every point in the cross section is the image of a point in the region bounded by these three planes and under the action of an element of $G_2$. Those familiar with Dirichlet domains (which I learned from [12]) may recognize this construction.

Note that we could have made the argument easier by using $R_{\mathbf s_1}=R_{\mathbf v_{23}}\circ \phi _{\mathbf e_2+\mathbf e_3,E}$ instead of $\phi _{\mathbf e_2+\mathbf e_3,E}$, but we want to stay away from $R_{\mathbf s_1}$, as its canonical analog for larger $\rho$ is not in ${\Gamma }'_\rho$.

The vertices of this region are the points $Q_i$ which satisfy the linear equations $x_4=x_5$, $Q_i\varvec{\circ }Q_i=0$, $Q_i\varvec{\circ }D<0$, and two of the three equations

$$\begin{aligned} x_1&=x_2 \qquad \hbox {(on}\,\, H_{\mathbf v_{12}})\nonumber \\ x_2&=x_3 \qquad \hbox {(on}\,\, H_{\mathbf v_{23}}) \nonumber \\ x_1&=0 \qquad \hbox {(on}\,\, H_{\mathbf s_1}). \end{aligned}$$

(5)

We get $Q_1$ (using the first two equations), $Q_2=\mathbf e_2+\mathbf e_3=(0,1,1,0,0)$ (using the first and third), and $Q_3=P_{3,E}=4\mathbf e_3+E=(0,0,4,1,1)$ (using the second and third equations).

Suppose there exists $\mathbf m\in \Lambda$ such that $\mathbf m\varvec{\circ }D<0$ and $H_{\mathbf m}^+\subset {\mathcal K}'$ (so contradicting Statement 1). Then the center of $H_{\mathbf m,E}$ lies between the planes $H_{\mathbf e_4}$ and $H_{\mathbf e_5}$. Using $G_3=\langle G_2, R_{\mathbf v_{45}}\rangle$, we can move this center to a point in the right prism bounded by the plane $H_{\mathbf e_5}$, $H_{\mathbf v_{45}}$, and the planes we found above: $H_{\mathbf v_{12}}$, $H_{\mathbf v_{23}}$, and $H_{\mathbf s_1}$. The prism has the vertices $Q_1$, $Q_2$, and $Q_3$, as well as the points $Q_i'$ which satisfies $Q_i'\varvec{\circ }\mathbf e_5=0$, and pairs of the equations in (5) (and of course, $Q_i'\varvec{\circ }Q_i'=0$ and $Q_i'\varvec{\circ }D<0$). We get the vertices

$$\begin{aligned} Q_1'&=(1,1,1,-1,2) \\ Q_2'&=(0,0,1,0,1)=\mathbf e_3+\mathbf e_5 \\ Q_3'&=(0,2,2,-1,3). \end{aligned}$$

Our intuition is that, once we have moved $H_{\mathbf m,E}$ so that its center is inside this prism, then the curvature of $H_{\mathbf m,E'}$ should be smaller for some $E'$. The intuitive choice is $E'=\mathbf e_3+\mathbf e_5$. We note that $R_{\mathbf v_{34}}(E')=E$ (it switches the third and fourth components). Thus, all we need to check is that the prism lies entirely within $H_{\mathbf v_{34},E}$, for if it does, then the center of this moved $H_{\mathbf m,E}$ will also be inside it. Its reflection through that plane, which is inversion in the sphere, will be a sphere with strictly smaller curvature, as desired.

Recall that $\mathbf v_{34}=\mathbf e_3-\mathbf e_4$, and note that $(\mathbf e_3-\mathbf e_4)\varvec{\circ }E=-2$, so the inside of $H_{\mathbf v_{34},E}$ is $H_{\mathbf v_{34},E}^+$. Thus, we need only check that $(\mathbf e_3-\mathbf e_4)\varvec{\circ }\mathbf x\ge 0$ for all $\mathbf x$ in the prism. Since the prism is convex, it is enough to check it for its vertices $Q_i$ and $Q_i'$, which just means checking the third component is larger than the fourth component. This is easily verified.

This gives us a fundamental domain for $\langle {\Gamma }', R_{\mathbf e_5}\rangle$ in ${\mathcal H}$, namely the region above the half hypersphere $H_{\mathbf v_{34}}$ (in the Poincaré model ${\mathcal H}_E$), and in the infinite prism in ${\mathcal H}_E$ that lies above the three dimensional prism in $\partial {\mathcal H}_E$ described above. This fundamental domain has finite hypervolume, so this group has finite index in ${\mathcal O}^+(\mathbb {Z})$. A fundamental domain for ${\Gamma }'$ is the region with the face $H_{\mathbf e_5}$ removed.

In terms of our descent argument for $H_{\mathbf m, E}$, since the property is preserved under the action of elements in ${\Gamma }'$, we have found an $\mathbf m'$ with the same property but such that $H_{\mathbf m',E}$ has strictly smaller curvature than $H_{\mathbf m,E}$. Since $\mathbf m\in \Lambda$, $\mathbf m\varvec{\circ }E$ and $\mathbf m'\varvec{\circ }E$ are integers. Therefore descent cannot continue indefinitely, so at some point we get an $\mathbf m'$ with curvature 0 (so $H_{\mathbf m',E}$ has no center), meaning $H_{\mathbf m'}$ goes through E. No such $\mathbf m'$ exists, as we cannot fit such a half space between the planes $H_{\mathbf e_4}$ and $H_{\mathbf e_5}$. Thus, Statement 1 holds for $\rho =5$.

6.2 The case $\rho =6$

Let $E=\mathbf e_5+\mathbf e_6$ be our point at infinity in the Poincaré model ${\mathcal H}_E$. Consider the cross section given by $x_5=x_6$, which has a lattice of congruent spheres in a canon-ball stacking. Let $G_1=\langle T_{12}, T_{13}, T_{14}\rangle$ and let its canonical fundamental domain be the parallelepiped shown in Fig. 13. Let $G_2=\langle R_{\mathbf v_{12}}, R_{\mathbf v_{23}}, R_{\mathbf v_{34}}, \phi _{\mathbf e_3+\mathbf e_4,E}\rangle$. As before, let $Q_1$ be the center of the tetrahedron, the point of intersection of $H_{\mathbf v_{12}}$, $H_{\mathbf v_{23}}$, $H_{\mathbf v_{34}}$ and $H_{\mathbf v_{56}}$. Solving (together with $Q_1\varvec{\circ }Q_1=0$ and $Q_1\varvec{\circ }D<0$), we get $Q_1=(2,2,2,2,-1,-1)$. We use this to get the plane

Fig. 13

With $\rho =6$: A parallelepiped that is the fundamental domain for $G_1$, together with the tetrahedron $Q_1Q_2Q_3Q_4$, which is a fundamental domain for $G_2$

$$\begin{aligned} H_{\mathbf n}=\{\mathbf x\in \mathbb {R}^{5,1}: \mathbf x\varvec{\circ }Q_1=\mathbf x\varvec{\circ }\phi _{\mathbf e_3+\mathbf e_4,E}(Q_1)\}, \end{aligned}$$

giving us $\mathbf n=(1,1,-1,-1,-1,-1)$ and the equation $x_1+x_2=0$. We therefore have, as an analog of Eq. (5), the following:

$$\begin{aligned} x_1&=x_2 \qquad \hbox {(from } R_{\mathbf v_{12}}) \nonumber \\ x_2&=x_3 \qquad \hbox {(from } R_{\mathbf v_{23}}) \nonumber \\ x_3&=x_4 \qquad \hbox {(from } R_{\mathbf v_{34}}) \nonumber \\ x_1+x_2&=0 \qquad \hbox {(from } \phi _{\mathbf e_3+\mathbf e_4,E} \hbox { and using } Q_1). \end{aligned}$$

(6)

The vertices are $Q_i$ where $Q_i$ is the solution to all but the $(4-i)$-th constraint (together with $Q_i\varvec{\circ }Q_i=0$ and $Q_i\varvec{\circ }D<0$). Solving, we get

$$\begin{aligned} Q_1&=(2,2,2,2,-1,-1) \\ Q_2&=(0,0,0,4,1,1)=P_{4,E} \\ Q_3&=(0,0,1,1,0,0)=\mathbf e_3+\mathbf e_4 \\ Q_4&=(-2,2,2,2,1,1). \end{aligned}$$

Note that $Q_4$ is the center of the parallelepiped. This gives us a tetrahedral fundamental domain for $G_2$, as pictured in Fig. 13.

Extending to $\partial {\mathcal H}_E$, we get a prism with vertices $Q_i$ and their corresponding points on $H_{\mathbf e_6}$:

$$\begin{aligned} Q_1'&=(2,2,2,2,-3,5) \\ Q_2'&=(0,0,0,1,0,1)=\mathbf e_4+\mathbf e_6 \\ Q_3'&=(0,0,2,2,-1,3) \\ Q_4'&=(-1,1,1,1,0,2). \end{aligned}$$

As before, we assume that $E'=\mathbf e_4+\mathbf e_6$ will be our best choice, so we consider the reflection $R_{\mathbf v_{45}}$. Again, $\mathbf v_{45}\varvec{\circ }E=(\mathbf e_4-\mathbf e_5)\varvec{\circ }E=-2$, so we wish to check that the vertices of the prism are in $H_{\mathbf v_{45}}^+$. That is, we verify that $\mathbf v_{45}\varvec{\circ }Q_i\ge 0$ and $\mathbf v_{45}\varvec{\circ }Q_i'\ge 0$ for all i, which again just means checking that the fourth component is larger than the fifth. We come to the same conclusions: Statement 1 is true for $\rho =6$; and we have fundamental domains for a subgroup with finite index in ${\mathcal O}^+(\mathbb {Z})$, and for ${\Gamma }'$. The fundamental domain for ${\Gamma }'$ is geometrically finite, which may be of interest to some.

6.3 The case $\rho =7$

We are ready to tackle a case without a picture. We let $E=\mathbf e_6+\mathbf e_7$. The parallelepiped will be important, but not at this step. We let $Q_1$ be the intersection of the planes $H_{\mathbf v_{12}}$, $H_{\mathbf v_{23}}$, $H_{\mathbf v_{34}}$, $H_{\mathbf v_{45}}$, and $H_{\mathbf v_{67}}$. As before, we require $Q_1\varvec{\circ }Q_1=0$ and $Q_1\varvec{\circ }D<0$. As before, we solve for $\mathbf n$ and find our set of equations is

$$\begin{aligned} x_1=x_2, \qquad x_2=x_3, \qquad x_3&=x_4, \qquad x_4=x_5 \nonumber \\ x_1+x_2+x_3&=0, \end{aligned}$$

(7)

giving us

$$\begin{aligned} Q_1&=(4,4,4,4,4,-3,-3)&\qquad&Q_1'=(1,1,1,1,1,-2,3)\\ Q_2&=(0,0,0,0,4,1,1)=P_{5,E}&\qquad&Q_2'=(0,0,0,0,1,0,1)=\mathbf e_5+\mathbf e_7 \\ Q_3&=(0,0,0,1,1,0,0)=\mathbf e_4+\mathbf e_5&\qquad&Q_3'=(0,0,0,2,2,-1,3)\\ Q_4&=(-4,-4,8,8,8,3,3)&\qquad&Q_4'=(-4,-4,8,8,8,-1,15)\\ Q_5&=(-4,2,2,2,2,3,3)&\qquad&Q_5'=(-2,1,1,1,1,1,3). \end{aligned}$$

Because we have no picture, we should give some thought as to whether these five vertices generate a four-dimensional polytope. This is easily verified by noting that the five equations in (7) together with $x_6=x_7$ yield the unique solution E. That means that each equation is a hyperplane in $\partial {\mathcal H}_E\cong \mathbb {R}^5$ and do not have a common point of intersection. That we could solve for the points $Q_i$ means no two hyperplanes are parallel, so they bound a polytope.

As before, our intuition is that the point is now close enough to $E'=\mathbf e_5+\mathbf e_7$, which is the image of E under $R_{\mathbf v_{56}}$. We check that all the vertices are in $H_{\mathbf v_{56}}^+$, which means the fifth component is greater than or equal to the sixth. This is true for all except $Q_5$.

This is where the parallelepiped comes in again. When $\rho =5$, the vertices of the parallelepiped (parallelogram) are $P_{1,E}$, $T_{12}(P_{1,E})=P_{2,E}$, $T_{13}(P_{1,E})=P_{3,E}$, and $T_{12}T_{13}(P_{1,E})=T_{13}T_{12}(P_{1,E})$. Notice the $1-2-1$ pattern (think binomial coefficients). When $\rho =6$, the endpoints of the long diagonal are $P_{1,E}$ and the center of $H_{\mathbf f_1}$; and the two rings of vertices $P_{i,E}$ for $i=2,3,4$, and the centers of $H_{\mathbf f_i}$ for $i=2,3,4$. Note again the $1-3-3-1$ pattern.

For $\rho =7$, we have the endpoints of the long diagonal $P_{1,E}$ and $T_{12}T_{13}T_{14}T_{15}(P_{1,E})$; the first ring of four vertices $T_{1i}(P_{1,E})=P_{i,E}$ for $i=2,3,4,5$; its complement at the other end; and the ring in the center, which are the six points $T_{1i}T_{1j}(P_{1,E})=T_{1j}T_{1i}(P_{1,E})$ for $\{i, j\} \subset \{2,3,4,5\}$. We found that $E'=\mathbf e_5+\mathbf e_7$ was not enough, as it is not close enough to $Q_5$, so we pick another point using a point of tangency between the hyperplane $H_{\mathbf e_7}$ and a sphere centered at a point on the middle ring. Intuition guides us to pick $E'=T_{14}T_{15}(\mathbf e_1)+\mathbf e_7=T_{14}\mathbf e_5+\mathbf e_7$. This leads us to consider reflection in the plane with normal vector $T_{14}\mathbf e_5-\mathbf e_6=T_{14}(\mathbf e_5-\mathbf e_6)$, which is $T_{14}R_{\mathbf v_{56}}T_{14}^{-1}$, so is in ${\Gamma }'$.

We now have two hyperballs $H_{\mathbf v_{56}}^+$ and $H_{T_{14}\mathbf v_{56}}^+$ that we hope together will cover the right prism. The edges of this right prism that include the vertex $Q_5$ are $Q_5Q_5'$ and the edges $Q_5Q_i$ for $i=1,\ldots ,4$. We can find the points where $H_{\mathbf v_{56}}$ cut these edges and if we can verify that they are in $H_{T_{14}\mathbf v_{56}}^+$, then we will be done. We note that $H_{T_{14}\mathbf v_{56}}^+$ includes $Q_5'$, $Q_3$, and $Q_4$, so we need only check the edges $Q_1Q_5$ and $Q_2Q_5$.

The line $Q_1Q_5$ is the intersection of the span of $\{Q_1,Q_5,E\}$ with $\partial {\mathcal H}$. We write $P=xQ_1+yQ_5+zE$, solve $P\varvec{\circ }\mathbf v_{56}=0$, $P\varvec{\circ }P=0$, orient P so that $P\varvec{\circ }D<0$, and verify that $P\varvec{\circ }T_{14}\mathbf v_{56}\ge 0$. We do the same for the line $Q_2Q_5$.

Since $H_{\mathbf v_{56}}^+$ and $H_{T_{14}\mathbf v_{56}}^+$ cover the prism, we conclude as before to get our method of descent and our fundamental domains.

6.4 The case $\rho =8$

Cutting to the chase: $E=\mathbf e_7+\mathbf e_8$; the equations are

$$\begin{aligned} x_1=x_2 \qquad x_2=x_3 \qquad x_3&=x_4 \qquad x_4=x_5 \qquad x_5=x_6 \\ x_1+x_2+x_3+x_4&=0, \end{aligned}$$

giving us

$$\begin{aligned} Q_1&=(1,1,1,1,1,1,-1,-1)&\qquad Q_1'&=(2,2,2,2,2,2,-5,7) \\ Q_2&=(0,0,0,0,0,4,1,1)=P_{6,E}&\qquad Q_2'&=(0,0,0,0,0,1,0,1)=\mathbf e_6+\mathbf e_8 \\ Q_3&=(0,0,0,0,1,1,0,0)=\mathbf e_5+\mathbf e_6&\qquad Q_3'&=(0,0,0,0,2,2,-1,3) \\ Q_4&=(-1,-1,-1,3,3,3,1,1)&Q_4'&=(-2,-2,-2,6,6,6,-1,11) \\ Q_5&=(-1,-1,1,1,1,1,1,1)&Q_5'&=(-2,-2,2,2,2,2,1,5) \\ Q_6&=(-3,1,1,1,1,1,3,3)&Q_6'&=(-6,2,2,2,2,2,5,9). \end{aligned}$$

This time there are two points not captured in $H_{\mathbf v_{67}}^+$, namely $Q_6$ and $Q_6'$. As before, we look at the reflection $R_{T_{15}\mathbf v_{67}}$. Only $Q_1$, $Q_2$, and $Q_1'$ are not in $H_{T_{15}\mathbf v_{67}}^+$, so we need only check the lines $Q_1Q_6$, $Q_2Q_6$, and $Q_1'Q_6'$. Again, we find the balls overlap on these line segments, so together they cover the prism.

6.5 The case $\rho =9$ (no conclusion)

The relative simplicity of the case $\rho =8$ is a bit deceptive, as this line of reasoning breaks down in the case $\rho =9$. We get the equations

$$\begin{aligned} x_1=x_2 \qquad x_2=x_3 \qquad x_3=x_4 \qquad x_4&=x_5 \qquad x_5=x_6 \qquad x_6=x_7\\ x_1+x_2+x_3+x_4+x_5&=0, \end{aligned}$$

giving us the vertices of the prism:

$$\begin{aligned} Q_1&=(4,4,4,4,4,4,4,-5,-5) \qquad&Q_1'&=(1,1,1,1,1,1,1,-3,4) \\ Q_2&=(0,0,0,0,0,0,4,1,1)=P_{7,E} \qquad&Q_2'&=(0,0,0,0,0,1,0,1)=\mathbf e_7+\mathbf e_9 \\ Q_3&=(0,0,0,0,0,1,1,0,0)=\mathbf e_6+\mathbf e_7 \qquad&Q_3'&=(0,0,0,0,0,2,2,-1,3) \\ Q_4&=(-4,-4,-4,-4,16,16,16,5,5)&Q_4'&=(-4,-4,-4,-4,16,16,16,-3,29) \\ Q_5&=(-4,-4,-4,6,6,6,6,5,5)&Q_5'&=(-2,-2,-2,3,3,3,3,1,7) \\ Q_6&=(-12,-12,8,8,8,8,8,15,15)&Q_6'&=(-12,-12,8,8,8,8,8,11,27) \\ Q_7&=(-4,1,1,1,1,1,1,5,5)&Q_7'&=(-8,2,2,2,2,2,2,9,13). \end{aligned}$$

The ball $H_{\mathbf v_{78}}^+$ covers all except $Q_6$, $Q_7$, $Q_6'$, and $Q_7'$. Since the parallelepiped now has seven rings, we do not expect to be able to cover the prism with just two balls. However, even when adding another ball from the middle ring, we still do not have enough to cover the prism. This case seems sufficiently different that we will leave its analysis for another time.