1 Introduction

Panmictic Evolutionary Algorithms [3], i.e., standard evolutionary algorithms characterized by a unique population and global recombination among all the possible individuals, are commonly used tools in optimization which have shown a high performance on various problems in applied science and engineering. On the other hand, these algorithms suffer from the well-known problems of stagnation and premature convergence caused by an improper balance of the population diversity, see e.g., [16]. In other words, the main drawback of a standard Evolutionary Algorithm (EA) is the fact that it may fail to generate new promising solutions and return a poorly performing suboptimal solutions.

In order to overcome this drawback, computer scientists and practitioners, since the earliest EA implementations, have attempted to enhance the EA performance by modifying the original ideas in various manners, e.g., proposing alternative search structures [52], developing adaptation models [45], hybridizing EAs with local search algorithms [33], or designing structured versions of EAs. The latter category, which is the focus of this paper, consists of a decentralization of the population into a set of sub-populations which have diverse roles and can somehow interact. Two most famous examples of structured EAs are Cellular Evolutionary Algorithms (CEAs), see [1, 5, 24, 25, 26, 58], and Distributed Evolutionary Algorithms (DEAs), see [2, 7, 22, 56, 62] and classification in Alba and Tomassini [3] and Alba and Troya [4]. In CEAs, the sub-populations are constructed on the basis of a neighborhood criterion and thus each sub-population has the role of exploring (and exploiting) a different region of the decision space. In DEAs, all the sub-populations explore the entire decision space and develop a parallel evolution for the solution of the same problem, usually cooperating in the search of the optimum by means of some information exchange.

Due to their nature, EAs (as well as other population based metaheuristics) are easy to be run in parallel over multiple machines or multiple core machines. The oldest, simplest and most straightforward EA parallelization is the so called Single-population Master-Slave Parallel Model (see [27, 43]). In this kind of parallelization, the EA runs with a single population and the fitness evaluations are distributed over several cores. Clearly, this parallelization does not influence the EA structure (since it is algorithmically equivalent to a standard EA) nor its performance.

Since structured EAs modify the normal EA by distributing the whole population into a set of many sub-populations, a parallelization can be naturally performed by assigning the management of a sub-population to each core. In this case, the distribution over several computational cores and the algorithmic modifications/enhancements are strictly connected issues. In literature several classifications of parallel EAs have been proposed, see e.g., [10, 11, 13].

In terms of parallelization, a popular classification, see [38], distinguishes between coarse-grained and fine-grained algorithms. Coarse-grained algorithms run on a limited amount of populations with a relatively high number of individuals while fine-grained algorithms run on many populations composed of only a few individuals. This classification often coincides with the one mentioned above (DEA and CEA) which sees the same issue from an alternative (according to the algorithmic structure) viewpoint.

Although the sub-populations evolve separately, they interact somehow and cooperate by exchanging information in order to pursue their common global optimization goal. In other words, the sub-populations copy, transfer, and exchange individuals according to various migration schemes, see e.g., [8, 11, 12, 14, 34].

Over the recent years, among the other EAs present in literature, Differential Evolution (DE see [15, 42, 49, 51]) stimulated the interest of computer scientists and practitioners. As many applications in engineering have proven, DE is a reliable and versatile function optimizer which is especially efficient in continuous problems. Thanks to, on one hand, its simplicity and ease of implementation, and on the other hand, its reliability and high performance, DE became a very popular solution for solving various real-world problems almost immediately after its original definition.

Although DE has a great potential, it has been clear to the scientific community that some modifications to the original structure were necessary in order to significantly improve its performance. A popular way, especially during the latest years, to enhance the DE is the integration of structured populations evolving in parallel. For example, in Lampinen [30] a distributed DE scheme employing a ring topology (the cores are interconnected in a circle and the migrations occur following the ring) has been proposed for the training of a neural network. In Salomon et al. [48], an example of DE parallelization is given for a medical imaging application. A few famous examples of distributed DE are presented in Refs.  [59, 60, 63]; in these papers the migration mechanism as well as the algorithmic parameters are adaptively coordinated on a criterion based on the genotypical diversity. In paper [61], a distributed DE for preserving the diversity in the niches is proposed in order to solve multi-modal optimization problems. In Tasoulis et al. [53], a distributed DE characterized by a ring topology and the migration of the individuals with the best performance, to replace random individuals of the neighbor sub-population, has been proposed. An application of the algorithm in Tasoulis et al. [53] for the training of a neural network has been presented in Pavlidis et al. [39]. Following a similar logic, paper [29] proposes a distributed DE where the computational cores are arranged according to a ring topology and, during the migration, the best individual of a sub-population replaces the oldest member of the neighbor population. In Refs. [17, 18, 19] a distributed DE has been designed for the image registration problem. In these papers, a computational core acts as a master by collecting the best individuals detected by the various sub-populations running in slave cores. The slave cores are connected in a grid and a migration is arranged among neighbor sub-populations. In Apolloni et al. [6], a distributed DE which modifies the scheme proposed in Tasoulis et al. [53] has been presented. In [6], the migration is based on a probabilistic criterion depending on five parameters. It is worthwhile to mention that also some parallel implementations of panmictic DE are available in literature, see [36]. An investigation about DE parallelization is given in Lampinen and Zelinka [31].

This paper deals with distributed versions of DE and proposes a novel implementation of distributed DE, namely Distributed Differential Evolution with Explorative–Exploitative Population Families (DDE-EEPF). The DDE-EEPF is a distributed algorithm composed of two families of sub-populations. In the first family the sub-populations have a fixed population size and employ a migration scheme. In the second family, the sub-populations have a different behavior depending on the generation number. During the beginning of the evolution, the sub-populations evolve independently by applying a population size reduction scheme. During the late stages of the evolution, the sub-populations belonging to the second family allow a migration of the individuals with the best performance to the sub-populations belonging to the first family. The distributed mechanism counts then on a family of sub-populations for exploring the decision space and performing the global search and on a family of sub-populations for exploiting the available search directions and thus detecting high quality solutions. The second family is then supposed to assist the first one by “injecting” high performance solutions within its explorative frameworks in the middle of their optimization process. This operation is supposed to enhance the overall algorithmic performance.

The remaining part of the paper is organized in the following way. Section 2 describes the working principles of DE and explains the reasons behind the parallelization. Section 3 gives a short description of recently presented distributed versions of DE and introduces the algorithms employed for comparison in the experimental section. Section 4 describes the proposed algorithm. Section 5 shows the experimental setup and numerical results of the present study. Section 6 gives the conclusions of this paper.

2 Standard differential evolution

In order to clarify the notation used throughout this chapter we refer to the minimization problem of an objective function f(x), where x is a vector of n design variables in a decision space D.

According to its original definition given in Storn and Price [51], the DE consists of the following steps. An initial sampling of S pop individuals is performed pseudo-randomly with a uniform distribution function within the decision space D. At each generation, for each individual x i of the S pop, three individuals x r , x s and x t are pseudo-randomly extracted from the population. According to the DE logic, a provisional offspring x′off is generated by mutation as:

$$ x'_{\rm off} = x_t + F(x_r - x_s) $$
(1)

where \(F\in [0,1+[\) is a scale factor which controls the length of the exploration vector (x r  − x s ) and thus determines how far from point x i the offspring should be generated. With \(F\in [0,1+[,\) it is meant here that the scale factor should be a positive value which cannot be much greater than 1, see [42]. While there is no theoretical upper limit for F, effective values are rarely greater than 1.0. The mutation scheme shown in Eq. (1) is also known as DE/rand/1. Other variants of the mutation rule have been subsequently proposed in literature, see [44]:

  • DE/best/1: x′off = x best + F(x s  − x t )

  • DE/cur-to-best/1: x′off = x i  + F(x best − x i ) + F(x s  − x t )

  • DE/best/2: x′off = x best + F(x s  − x t ) + F(x u  − x v )

  • DE/rand/2: x′off = x r  + F(x s  − x t ) + F(x u  − x v )

  • DE/cur-to-best/2: x′off = x i  + F(x best − x i ) + F(x r  − x s ) + F(x u − x v )

    where x best is the solution with the best performance among the individuals of the population, x u and x v are two additional pseudo-randomly selected individuals. It is worthwhile to mention the rotation invariant mutation shown in Price [41]:

  • DE/current-to-rand/1 x off = x i  + K(x t − x i ) + F′(x r  − x s )

    where K is the combination coefficient, which, as suggested in Price [41], should be chosen with a uniform random distribution from [0, 1] and F′ = K ·F. For this special mutation the mutated solution does not undergo the crossover operation described below.

Recently, in Price et al. [42], a new mutation strategy has been defined. This strategy, namely DE/rand/1/either-or, consists of the following:

$$ x^{\prime}_{\rm off}= \left\{ \begin{array}{lll} {x_t} + F\left( {{x_r} -{x_s}} \right)& \hbox{if} & \hbox{rand}\left( {0,1} \right)\,<\,{p_F}\cr {x_t} + K\left( {{x_r} + {x_s} - 2{x_t}} \right)&\hbox{otherwise} \end{array} \right. $$
(2)

where for a given value of F, the parameter K is set equal to 0.5(F + 1).

When the provisional offspring has been generated by mutation, each gene of the individual x′off is exchanged with the corresponding gene of x i with a uniform probability and the final offspring x off is generated:

$$ x_{{{\text{off}}}} = \left\{ {\begin{array}{*{20}c} {x_{{i,j}} \quad {\text{if}}\quad {\text{rand}}(0,1) < {\text{CR}}} \\ {x^{\prime}_{{{\text{off}},j}} \quad {\text{otherwise}}} \\ \end{array} } \right. $$
(3)

where rand(0, 1 ) is a random number between 0 and 1; j is the index of the gene under examination.

The resulting offspring x off is evaluated and, according to a one-to-one spawning strategy, it replaces x i if and only if f(x off) ≤ f(x i ); otherwise no replacement occurs. It must be remarked that although the replacement indexes are saved, one by one, during the generation, the actual replacements occur all at once at the end of the generation. For the sake of clarity, the pseudo-code highlighting the working principles of the DE is shown in Fig. 1.

Fig. 1
figure 1

DE pseudocode

Full size image

2.1 Why distribute differential evolution?

As shown in Sect. 2, DE is based on a very simple idea, i.e., the search by means of adding vectors and a one-to-one spawning for the survivor selection. Thus, DE is very simple to implement/code and contains a limited number of parameters to tune (only S pop, F, and CR). In addition, the fact that DE is rather robust and versatile has encouraged engineers and practitioners to employ it in various applications. For example, in Joshi and Sanderson [28], a DE application to the multisensor fusion problem is given. In Storn [50], a filter design is carried out by DE. In Tirronen et al. [54, 55], a DE based algorithm is implemented to design a digital filter for paper industry applications. A review of DE applications is presented in Plagianakos et al. [40].

From an algorithmic viewpoint, the reasons of the success of DE have been highlighted in Feoktistov [21]: the success of the DE is due to an implicit self-adaptation contained within the algorithmic structure. More specifically, since, for each candidate solution, the search rule depends on other solutions belonging to the population (e.g., x t , x r , and x s ), the capability of detecting new promising offspring solutions depends on the current distribution of the solutions within the decision space. During the early stages of the optimization process, the solutions tend to be spread out within the decision space. For a given scale factor value, this implies that the mutation appears to generate new solutions by exploring the space by means of a large step size (if x r and x s are distant solutions, F(x r  − x s ) is a vector characterized by a large modulus). During the optimization process, the solutions of the population tend to concentrate on specific parts of the decision space. Therefore, the step size in the mutation is progressively reduced and the search is performed in the neighborhood of the solutions. In other words, due to its structure, a DE scheme is highly explorative at the beginning of the evolution and subsequently becomes more exploitative during the optimization.

Although this mechanism seems at first glance very efficient, it hides a limitation. If for some reasons, the algorithm does not succeed in generating offspring solutions which outperform the corresponding parent, the search is repeated again with similar step size values and likely fails by falling into the undesired stagnation condition (see [32]). Stagnation is the undesired effect which occurs when a population-based algorithm does not converge to a solution (even suboptimal) and the population diversity is still high. In the case of the DE, stagnation occurs when the algorithm does not manage to improve upon any solution of its population for a prolonged number of generations. In other words, the main drawback of the DE is that the scheme has, for each stage of the optimization process, a limited amount of exploratory moves and if these moves are not enough for generating new promising solutions, the search can be heavily compromised.

Thus, in order to enhance the DE performance, alternative search moves should support the original scheme and promote a successful continuation of the optimization process. The use of multiple populations in distributed DE algorithms allows an observation of the decision space from various perspectives and, most importantly, decreases the risk of stagnation since each sub-population imposes a high exploitation pressure. In addition, the migration mechanism ensures that solutions with a high performance are included within the sub-populations during their evolution. This fact is equivalent to modifying the set of search moves. If the migration privileges the best solutions, the new search moves promote the detection of new promising search directions and thus allow the DE search structure to be periodically “refurbished”. Thus, the migration is supposed to mitigate the risk of stagnation of the DE (sub-)populations and to enhance the global algorithmic performance.

In addition, within a DE framework there is, with respect to the other EAs, a different relationship between algorithmic functioning and the population diversity. As it is well known, the concept of population diversity is very important in many EAs and, in order to obtain a proper algorithmic behavior, it is crucial to design a system to maintain the diversity high throughout the evolution. It might likely happen that a diversity loss in an EA can cause the premature convergence towards solutions characterized by a poor performance. In DE, as for swarm intelligence optimizers, there is not a quick diversity loss and the algorithm can perform the entire optimization process and still keep the diversity high. This fact can cause an excessively exploratory behavior and then the stagnation phenomenon mentioned above. Thus a successful DE, as explained above, is supposed to explore the entire decision space only during the early stage of the evolution and subsequently narrows its search in a small (and interesting) portion of the domain. In summary, DE is an atypical EA: operations which aim at maintaining the diversity high are beneficial to most of the EAs while being detrimental to DE.

On the other hand, it must be remarked that many population-based metaheuristics and not only the DE can greatly benefit from a proper parallelization. Generally speaking, a distributed population structure can offer an alternative search view to the algorithmic structures and generate compensation to the weak points of the chosen algorithm. In DE stagnation problems and the limited set of available moves have been highlighted. A classical example of the advantages of distribution can be the Distributed Evolution Strategies, see [46]. Evolution Strategies, especially those employing the “plus” strategy, suffer from premature convergence and diversity loss. The use of a distributed population with a proper migration mechanism can be an efficient countermeasure against diversity loss and thus an enhancement in the algorithmic performance.

In other words, the distribution of the population can be beneficial to DE (as well as to swarm intelligence algorithms) since it can generate extra moves in the search logic, thus mitigating the stagnation effect, and to other EAs since it can produce genotypes which increase the diversity, thus mitigating the premature convergence inconveniences.

The implementation of the parallelization e.g., occurrence of the migrations as well as the choice of migrating individuals, replacement rules, and choice of population involved in the migration events have been intensively discussed in literature and, in many cases, are still points of investigation for computer scientists. As a matter of fact, although the employment of structured populations can be beneficial to many meta-heuristics, each case must be, in our view, separately analyzed and the design of the distributed structure must be performed taking into account the nature and the limitation of each core algorithm.

The next section illustrates three successful, recently developed distributed DEs and highlights their differences and similarities.

3 Distributed differential evolution: recently developed algorithms

This section describes three distributed algorithm based on a DE structure recently proposed in literature. The algorithms described in this section are, according to our judgement, representative of the state of the art of structured DE algorithms and have been included in the benchmark in order to compare the performance of the proposed approach. Although the notation can generate some confusion, i.e., all the algorithms are distributed and can easily be parallelized, we decided to indicate them according to the original terminology defined by their respective authors.

3.1 Parallel differential evolution

In Tasoulis et al. [53], the problem of parallelization for DE schemes has been studied through an experimental analysis and an algorithm, namely Parallel Differential Evolution (here indicated with PDE) has been proposed.

The original PDE implementation uses the Parallel Virtual Machine (PVM), allowing multiple computers (called nodes) to be organized as a cluster and exchange arbitrary messages. PDE is organized around one master node and N sub-populations running each on one node, and organized as a unidirectional ring, as illustrated in Fig. 2. It must be noted that although the logical topology is a ring which does not contain the master node, the actual topology is a star, where all communications (i.e., the migrations of individuals) are passing through the master.

Fig. 2
figure 2

Unidirectional ring topology in the parallel differential evolution algorithm

Full size image

Each sub-population runs a regular DE algorithm while the master node coordinates the migration of individuals between the sub-populations. On each generation, the sub-population has a given probability to send a copy of its best individual to its next neighbor in the ring. Figure 3 describes the behaviors of both the master node and the sub-populations in more details.

Fig. 3
figure 3

Pseudo-code of the PDE algorithm

Full size image

The DE variant run by each sub-population is the same across all the sub-populations. In Tasoulis et al. [53], six mutation strategies have been compared, namely DE/best/1, DE/rand/1, DE/cur-to-best/1, DE/best/2, DE/rand/2 described in Sect. 2, as well as the trigonometric operator described in Fan and Lampinen [20]. Each strategy is used with different values of the migration constant ϕ and compared over seven test functions whose dimensions vary between 2 and 30. The results show that DE/best/1 is the most efficient mutation strategy and quite stable across different values of ϕ, whereas the results of DE/rand/1 are average and quite unstable when ϕ varies.

3.2 Island based distributed differential evolution

In Apolloni et al. [6] a distributed DE, namely Island Based Distributed Differential Evolution (IBDDE) has been proposed. The IBDDE is a modified version of the PDE described in Sect. 3.1. The algorithm is described in a generic way, presenting a population \({\mathcal{P}}\) structured in m sub-populations P p of n p individuals. The size of \({\mathcal{P}}\) is noted N = ∑ n i=1 n i . The migration policy is then defined as a five-tuple \({\mathcal{M}} = (\gamma, \rho, \phi_s, \phi_r, \tau).\) \(\gamma \in {\mathbb{N}}\) is the number of generations between two migrations, \(\rho \in {\mathbb{N}}\) is the number of individuals which are migrated from a sub-population during each migration, ϕ s is the selection function which, applied to a sub-population, returns the migrating individuals, ϕ r is the replacement function that selects the individuals to be replaced by the immigrants in the receiving sub-population, and \(\tau: {\mathcal{P}} \rightarrow 2^{{\mathcal{P}}}\) is the topological model, which selects what sub-population can send to (or receive from) what other sub-population. Figure 4 describes the algorithm as pseudo-code.

Fig. 4
figure 4

Pseudo-code of the IBDDE algorithm for sub-population P p

Full size image

For the actual experiments, the population size N is set to 20, and the population is divided into two sub-populations of 10 individuals in one experiment, and into four sub-populations of 5 individuals in a second experiment. The migration parameters are set to γ = 100, ρ = 1, the functions ϕ s and ϕ r are defined to randomly select an individual, and the topology τ is a unidirectional ring, very similar to the logical topology used by PDE (see Sect. 3.1). The mutation strategy for DE is DE/rand/1, and the algorithm is tested on 25 different test functions in 30 and 50 dimensions, for a total of 50 test functions.

3.3 Distributed differential evolution

In Falco et al. [17, 18, 19], in order to solve and image registration problem a distributed DE (here indicated with DDE) has been proposed. This algorithm differs from PDE and IBDDE by the topology it uses. Instead of a unidirectional ring, DDE uses a locally connected topology, where each node is connected to μ other nodes. Figure 5 represents such a topology where the nodes are arranged in a mesh folded into a torus.

Fig. 5
figure 5

Torus topology in the distributed differential evolution algorithm

Full size image

In this configuration μ = 4, i.e., each node (such as the black disc in the figure) has exactly four nearest neighbors (represented by the four grey discs). In DDE, each node represents one processor running a DE algorithm with a DE/rand/1 mutation strategy on a sub-population. Every M I generations (the migration interval), each sub-population is allowed to exchange S I (the migration rate) individuals with its nearest neighbors. In the experimental setup, each node sends a copy of its best individual to its neighbors. Figure 6 describes the algorithm as pseudo-code.

Fig. 6
figure 6

Pseudo-code of the DDE algorithm at a sub-population

Full size image

DDE also makes use of a master node, whose role is to collect the best solutions found in each sub-population and to present the results to the user.

4 Distributed differential evolution with explorative–exploitative population families

The proposed algorithm, namely distributed differential evolution with explorative–exploitative population families (DDE-EEPF), consists of the following steps.

An initial population of S pop individuals is pseudo-randomly sampled within the decision space D. These S pop individuals are distributed over m sub-populations; each sub-population has a size equal to \(S_{\rm s{\hbox{-}}pop}={\frac{S_{\rm pop}}{m}}.\) The m sub-populations are then divided into two families: α are assigned to the first family (hereafter named P p with p = 1, 2, ..., α) and β to the second (named Q q with q = 1, 2, ..., β); α + β = m.

The α sub-populations belonging to the first family are arranged according to a ring topology following the suggestions given in Tasoulis et al. [53]. In the first family, each sub-population P p evolves like a standard DE and employs the DE/rand/1 mutation strategy illustrated in Eq. (1) and the crossover described in Eq. (3). The replacements of the individuals are performed according to the one-to-one spawning shown in Sect. 2. These α sub-populations interact by means of a migration scheme. For each population P p , p = 1, ..., α, with a probability p mig, a copy of the best individual \(x_{\rm best}^{P_p}\) of sub-population P p is sent to the next sub-population in the ring. At that sub-population, the incoming \(x_{\rm best}^{P_p}\) replaces a pseudo-randomly selected (uniform distribution) solution, which is then discarded.

The behavior of the β sub-populations Q q composing the second family is divided into two ages. During the first age, the sub-populations evolve independently without the support of a migration scheme. Each sub-population employs the population size reduction strategy introduced in Brest and Maučec [9] (see also [23, 57]). This strategy requires that initial population size \(S_{\rm s{\hbox{-}}pop}^1\) (in our case \(S_{\rm s{\hbox{-}}pop}^1=S_{\rm s{\hbox{-}}pop}\)), duration of the first age in terms of fitness evaluations (time budget T b ), and number of stages N s (the number of population sizes employed during the algorithm’s run), are prearranged. Then, the first age (T b ) is divided into N s periods, each period being characterized by a population size value \(S_{\rm s{\hbox{-}}pop}^k\) (for k = 1 we obtain the initial population size). Each period is composed of N k g generations which are calculated in the following way:

$$ N_g^k = \left\lfloor {{\frac{T_b} {{N_s}S_{\rm s{\hbox{-}}pop}^k}}} \right\rfloor + {r_k} $$
(4)

where r k is a constant non-negative value which takes a positive value when T b is not divisible by N s . In this case r k extra generations are performed. The population reduction is simply carried out by halving the population size at the beginning of the new stage, see [9]. In other words, for k = 1, 2, ..., N s , the population size is halved \(S_{\rm s{\hbox{-}}pop}^{k+1}={\frac{S_{\rm s{\hbox{-}}pop}^k}{2}}.\) The selection of the survivors occurs by dividing into groups the sub-population according to their indexes and performing the one-to-one spawning to each corresponding pair of individuals. Finally, it should be remarked that in order to guarantee a proper functioning of the population reduction mechanism, populations should never undergo sorting of any kind.

In this way, the population size is progressively reduced during the optimization process until the budget of the first age (T b ) is reached. The concept behind this strategy is that of focusing the search in progressively smaller search spaces in order to inhibit the DE stagnation. During the early stages of the optimization process, the search requires a highly explorative search rule, i.e., a large population size, in order to explore a large portion of the decision space. During the optimization, the search space is progressively narrowed by decreasing the population size and thus exploiting the promising search directions previously detected. Although this strategy does not guarantee the detection of the global optimum, it allows quick improvements in the solution performance.

During the second age, the sub-populations composing the second family keep their size constant at their minimum and a migration scheme is employed. At each generation, for each sub-population belonging to the second family, its individual with the best performance migrates to a sub-population of the first family. As for the migration among sub-populations of the first family, individuals are copied and replace a pseudo-randomly selected individual of the target population. The choice of the target population is performed at pseudo-random with a uniform probability.

It is important to remark that a synchronization of the computational overhead has been implemented among the sub-populations belonging to the first and second family. In other words, the amount of fitness evaluations during a generation is kept constant for all the sub-populations. For example, if k = 2, the size of a sub-population belonging to the first family is twice bigger than the size of a sub-population of the second family. Under these conditions, for each generation in the first family two consecutive generations are performed in the second family.

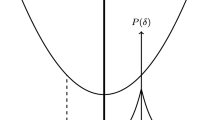
Figure 7 gives a graphical representation of the DDE-EEPF during both its ages of the evolution.

Fig. 7
figure 7

Operation scheme of the DDE-EEPF

Full size image

According to the idea proposed in this paper, the whole DE population is divided into sub-populations. These sub-populations are grouped into two families. Each family plays a different role on the optimization process. The sub-populations of the first family are supposed to explore the decision space and to attempt detecting the global optimum. The risk of stagnation is mitigated by the migration mechanism among the sub-populations of the first family. On the contrary, the sub-populations belonging to the second family have a completely different role and behavior. The sub-populations of the second family do not aim at exploring the entire decision space, but their role is focused on the greedy achievement of solutions with a high performance, despite the fact that these solutions can be suboptimal. There is no migration mechanism within the second family in order to allow a full exploitation of the available search directions. Migrations would slow down the search since they result in an increase of the exploration properties. When the sub-populations of the second family detected high quality solutions, the inter-family migration occurs. The introduction of high quality solutions into the exploratory search structure of the first family is supposed to further decrease the risk of stagnation and, most importantly, to assist the global search by proposing the exploration of promising search directions. Hence, during the second age, the sub-populations of the first family have the role to improve upon the immigrants coming from the second family and continue the search towards the optimum. In this sense, the first family is meant to be explorative while the second is to be exploitative.

5 Experimental results

The test problems listed in Table 1 have been considered in this study.

Table 1 Test problems
Full size table

The rotated version of some of the test problems listed in Table 1 have been included into the benchmark set. These rotated problems have been generated by means of the multiplication of the vector of variables by a randomly generated orthogonal rotation matrix. In total, 24 test problems have been considered in this study with both n = 500 and n = 1, 000. Each algorithm has been run for 500, 000 fitness evaluations in the case of n = 500 and for 1, 000, 000 fitness evaluations when n = 1, 000. Fifty independent runs have been performed for each algorithm involved in this paper.

The DDE-EEPF has been tested and compared with the PDE, IBDDE, DDE and one more algorithm designed by us for comparison (see below). Preliminary experiments related to the sequential DE have shown that DE is not at all competitive with the above distributed ones, and has therefore been left out from these result presentation.

The algorithms considered in this study have been run with the following parameter setting.

  • The DE used within the sub-populations of each of the distributed algorithms has been run with F = 0.7 and CR = 0.3, in accordance with the suggestions given in Zielinski and Laur [64] and Zielinski et al. [65].

  • The PDE has been run with populations of 200 or 400 individuals divided into 5 sub-populations of 40 or 80 individuals each, for the 500 and 1,000-dimensional problems, respectively. Despite [53] showing better performance for the DE/best/1 mutation strategy in 30 and 50 dimensions, it has proven excessively exploitative and has lead to premature convergence of the solutions when used on higher dimension problems. In order to perform a fair comparison, an analysis on mutations strategies has been made, leading to the choice of DE/rand/1 and setting the migration constant to ϕ = 0.2. These are the settings which have been chosen for the experiments described below.

  • Similarly to PDE, the IBDDE has been run with populations of 200 or 400 individuals divided into 5 sub-populations of 40 or 80 individuals each, depending on the dimensionality of the test problems. The other parameters have been chosen according to the values in Apolloni et al. [6]: the sub-populations exchange one individual (ρ = 1) every 100 generations (γ = 100). ϕ s and ϕ r have been defined so as to choose a uniformly random individual, and τ has been set to a unidirectional ring.

  • For the 500-dimensional problems, the DDE has been run with a population of 200 individuals divided into 16 sub-populations of alternatively 12 or 13 individuals. In the case of the 1,000-dimensional problems, the population has been set to 400 individuals divided into 16 sub-populations of 25 individuals. Following the suggestions in Falco et al. [18] the sub-populations have been organized into a 4 × 4 grid folded into a torus (μ = 4). Each sub-population migrated only its best individual (S I = 1) every M I = 5 generations.

  • The DDE-EEPF has been run with S pop = 200 or S pop = 400 (representing 5 populations of 40 or 80 individuals, for the 500 or 1,000-dimensional problems, respectively). The first family has been composed of α = 3 sub-populations while the second family has been made of β = 2 sub-populations. Although we do not have a theoretical explanation for the choice of α and β, it is worthwhile commenting the performed setting. Since in this algorithm α sub-populations are supposed to explore the decision space while β are supposed to exploit it, the choice of α and β should be made in order to efficiently balance the exploration and exploitation features of the algorithm. Our preliminary experiments have clearly shown that α should be greater than β. On the other hand, the role of the second family is very important and requires some computational effort. As a general guideline, on the basis of empirical observations, we suggest to set β about 20–40% of m. With both 500 and 1,000-dimensional problems, the migration constant has been set to p mig = 0.5, and the T b parameter for the population reduction algorithm has been set to 60% of the total budget, i.e., T b = 300, 000 and T b  = 600, 000 for 500 and 1,000 dimensions respectively. This proportion of the budget seems to guarantee a robust behavior of the algorithm: according to our interpretation, a too low value of T b implies a too short duration of the first age, which makes the algorithm too exploitative during the process, promoting quick improvements in the fitness values, but also causing premature convergence. Conversely, if T b is too high (e.g., the first age lasts for 80% of the duration of the optimization process), the algorithm is too explorative and the second age does not have the opportunity to exploit the promising search directions generated by the population size reduction algorithm. The other parameters of the population reduction algorithms have been set to r k  = 0 for all k values, and to N s  = 4 steps of reduction; see [9] for parameter setting.

  • In order to evaluate the impact, in DDE-EEPF, of the injection of individuals from the second family of sub-populations into the first family, a variant of DDE-EEPF named Parallel Differential Evolution With Random Injections (PDE-WRI) has been run, under the exact same conditions as DDE-EEPF. The only difference between DDE-EEPF and PDE-WRI is that, at the point when DDE-EEPF would send an individual from the second family to the first one, PDE-WRI introduces instead a new, randomly generated (uniform distribution) individual into the first family.

It is worthwhile commenting the choice of the population sizes S pop = 200 and S pop = 400. Although in Storn and Price [52] it is suggested to set the DE population size equal to about ten times the dimensionality of the problem, this indication is not confirmed by a recent study in Neri and Tirronen [35] where it is shown that a population size lower than the dimensionality of the problem can be optimal in many cases.

Table 2 shows the average of the final results detected by each algorithm ± the standard deviations, for the 500 dimension case, for the DE with additional components. Table 3 shows the results for the 1, 000 dimension case. The best results are highlighted in bold face.

Table 2 Average final fitness values ± standard deviations for 500 dimensions problems
Full size table
Table 3 Average final fitness values ± standard deviations for 1,000 dimensions problems
Full size table

Results in Tables 2 and 3 show that the proposed DDE-EEPF seems promising in terms of final result, since it detected (on average) the best performing solutions in fourteen cases out of the 24 considered in this study in 500 dimensions. PDE obtained the best results only in two cases, DDE is the best in three cases and PDE-WRI in five cases. In 1,000 dimensions, DDE-EEPF detected on average the best performing solutions in nine cases out of 24, DDE is the best in nine cases, and PDE and PDE-WRI win in three cases each.

In order to prove the statistical significance of the results, the two-tail unequal variance t-test has been applied according to the description given in Ruxton [47] (see also [37]) for a confidence level of 0.95. Tables 4 and 5 show the results of the test. A “+” indicates the case when the DDE-EEPF statistically outperforms, for the corresponding test problem, the algorithm mentioned in the column; a “=” indicates that the pairwise comparison leads to the success of the t-test, i.e., the two algorithms have the same performance; a “−” indicates that DDE-EEPF is outperformed.

Table 4 Results of the unequal variance t-test for 500 dimensions problems
Full size table
Table 5 Results of the unequal variance t-test for 1,000 dimensions problems
Full size table

In the case of 500-dimensional problems, the t-test results show that the DDE-EEPF outperforms PDE in 54.1% of the cases, IBDDE in 95.8%, DDE in 75.0% and PDE-WRI in 58.3% of the cases. On the opposite, DDE-EEPF is outperformed by PDE in 33.3% of the cases, by IBDDE in 4.17%, by DDE in 8.33% and by PDE-WRI in 25.0% of the cases. In the 1,000-dimensional problems, the t-test results show that DDE-EEPF wins against PDE, IBDDE, DDE and PDE-WRI in 79.1, 95.8, 50.0 and 41.7% of the cases, respectively. It loses in 4.17, 0.00, 25.0 and 12.5% of the cases against PDE, IBDDE, DDE and PDE-WRI, respectively.

In order to carry out a numerical comparison of the convergence speed performance, for each test problem, the average final fitness value returned by the best performing algorithm G has been considered. Subsequently, the average fitness value at the beginning of the optimization process J has also been computed. The threshold value THR  =  J − 0.95(G − J) has then been calculated. The value THR represents 95% of the decay in the fitness value of the algorithm with the best performance. If an algorithm succeeds during a certain run to reach the value THR, the run is said to be successful. For each test problem, the average amount of fitness evaluations \(\bar{ne}\) required, for each algorithm, to reach THR has been computed. Subsequently, the Q-test (Q stands for Quality) described in Feoktistov [21] has been applied. For each test problem and each algorithm, the Q measure is computed as:

$$ Q={\frac{\bar{ne}}{R}} $$
(5)

where the robustness R is the percentage of successful runs. It is clear that, for each test problem, the smallest value equals the best performance in terms of convergence speed. The value “∞” means that R = 0, i.e., the algorithm never reached the THR. It is important to remark that the Q-measure implicitly includes a piece of information on the computational time needed to reach a reasonably good performance. More explicitly, in order to determine the time that each algorithm requires in order to reach the threshold value it is enough to compute Q × number of runs (50) × time of a single fitness evaluation. The time of each fitness evaluation clearly depends on the test problem and on the hardware involved. The ∞ value means that the corresponding algorithm required an infinite time to reach the threshold.

Tables 6 and 7 show the Q values for 500-dimensional problems and 1,000-dimensional problems respectively. The best results are highlighted in bold face.

Table 6 Results of the Q-test for 500 dimensions problems
Full size table
Table 7 Results of the Q-test for 1,000 dimensions problems
Full size table

Regarding the Q-measures in Table 6, in 500 dimensions, the DDE-EEPF obtained the best results in 7 cases, while PDE, DDE and PDE-WRI obtained the best results in 4, 10 and 3 cases, respectively. In 1,000 dimensions (Table 7), DDE-EEPF obtained the best results in 8 cases, while PDE, DDE and PDE-WRI obtained the best results in 0, 12 and 4 cases, respectively. It is worthwhile commenting the DDE behavior: due to its grid structure, the DDE seems very fast in the early stages of the evolution but it tends to focus its search on not so promising areas of the decision space since it is often outperformed by PDE and DDE-EEPF in terms of quality of final solutions. Nevertheless, considering that the DDE was designed for a domain-specific application, it can be considered a rather robust algorithm.

Regarding the IBDDE, this study highlights that although the algorithm was very promising in 30 dimensions as showed in Apolloni et al. [6], it seems to suffer from the curse of dimensionality and to lose its high-quality performance.

It is important to remark that the proposed DDE-EEPF displays in Tables 6 and 7 the smallest number of ∞ values, which means that there is only one case in which it is not competitive with the best algorithm in 500 dimensions, and zero case in 1,000 dimensions. For the remaining test problems, the DDE-EEPF is either the best or a competitive algorithm. Thus, the DDE-EEPF demonstrated the best performance in terms of robustness.

Figure 8 shows average performance trends of the five considered algorithms over a selection of the test problems listed in Table 1 in 500 dimensions.

Fig. 8
figure 8

Performance trends in 500 dimensions

Full size image

Figure 8 a, c, d and f show that IBDDE improves only marginally. DDE, on the contrary, shows in those figures a very steep curve in the beginning of the optimization, outperforming at this point all the other algorithms, but quickly ceases to improve on its solutions. PDE’s start is less steep than DDE’s, but it continuously improves on its solutions and outperforms the algorithms above by a large margin. Finally, PDE-WRI and DDE-EEPF start with a steeper slope than PDE (although less steep than DDE’s), but show hints that their improvement rates will deteriorate more quickly than PDE’s. This can be explained by the fact that DDE-EEPF uses the same algorithm as PDE in the beginning, albeit with only three populations (instead of five for PDE) and with a higher migration constant which makes it more greedy and more prone to lose its ability to improve on its solutions. In Fig. 8, they are even slightly outperformed by PDE. However, at 300,000 fitness evaluations, PDE-WRI’s and DDE-EEPF’s first sub-population families start to be refreshed by individuals from the second sub-population family and by random new individuals, respectively. This shows on the curve as a “knee”, a sudden change in the slope, which becomes again much steeper. In these four examples, at the end of the run, PDE-WRI and DDE-EEPF clearly outperform PDE and the other two algorithms by a large margin, DDE-EEPF also outperforming PDE-WRI, albeit only slightly in Fig. 8a and f. Figure 8b shows the same behavior as described above, but PDE-WRI and DDE-EEPF lose very quickly their ability to make any improvement, until the time when the first family of sub-population is being refreshed. At this point, the slope of the curve becomes suddenly very much steeper. PDE-WRI is eventually outperformed by PDE, but DDE-EEPF outperforms PDE by a very large margin.

Figure 8e shows an example where PDE is on a par with DDE-EEPF and PDE-WRI: starting from 200,000 fitness evaluations, DDE-EEPF and PDE-WRI seem to become unable to improve on their solutions, while PDE continues improving. At 300,000 fitness evaluations, the sub-populations of the first family start receiving new individuals, causing DDE-EEPF and PDE-WRI to start improving again. DDE-EEPF eventually catches up with PDE around 500,000 fitness evaluations. One can also notice that on this function, IBDDE performs much better than on the other ones, without, however, being able to compete with the other algorithms.

In these six examples of 500-dimensional problems, IBDDE, DDE and PDE show similar behaviors whatever the test problem when one considers the general shape of their curves. PDE-WRI and DDE-EEPF behave identically during the first age of the algorithms, while the improvement in DDE-EEPF brought by the solutions of the second family of sub-populations, compared to the introduction of new, random individuals in PDE-WRI, ranges from very small in two cases to considerably large in one other case.

Figure 9 shows average performance trends of the five considered algorithms over a selection of the test problems listed in Table 1, in 1,000 dimensions.

Fig. 9
figure 9

Performance trends in 1,000 dimensions

Full size image

Similarly to the 500-dimensional problems, IBDDE in 1,000 dimensions improves on its solutions only marginally (see Fig. 9 d–f) or not at all (see Fig. 9a–c).

In Fig. 9b, PDE, DDE, PDE-WRI and DDE-EEPF present the same behavior as in 500 dimensions: DDE improves very quickly at first, but ceases to find any better solutions after about 200,000 fitness evaluations. DDE-EEPF and PDE-WRI seem to suffer from the same problem at first (although with a slower improvement rate than DDE), but at 600,000 fitness evaluations, the sub-populations of the first family start being refreshed, and the algorithms progress again, eventually finding better solutions than PDE. The difference between PDE-WRI and DDE-EEPF is unnoticeable on the graph.

In Fig. 9c–f, PDE, DDE, PDE-WRI and DDE-EEPF exhibit very similar behaviors across the different test problems: DDE improves very quickly at the beginning, faster than the other two algorithms, but improves only marginally on its solutions after about 400,000 fitness evaluations. PDE, PDE-WRI and DDE-EEPF both show a steady rate of improvement, PDE-WRI’s and DDE-EEPF’s being better than PDE’s, with a slight advantage for DDE-EEPF over PDE-WRI. Contrary to the 500-dimensional problems, DDE-EEPF’s second age is not marked by a sharp change in the slope of the curve although the figures do present a “knee” in the curve at 600,000 fitness evaluations, at the start of the second age. The absence of a sharp “knee” is explained by the fact that in 500 dimensions, PDE-WRI and DDE-EEPF are not anymore improving on their solutions near the end of the first age, while in 1,000 dimensions they still are.

Figure 9a, c and d show examples where DDE outperforms PDE and, in Fig. 9a, PDE-WRI as well: its sharper improvement rate in the beginning allows it to reach a better solution than the other algorithms, although all three reach similar solutions near the end. In Fig. 9a one can notice that the difference between DDE-EEPF and PDE-WRI is perceptibly larger than it is in Fig. 9c–f.

In these six examples of 1,000-dimensional problems, as was the case with the 500-dimensional problems, the shapes of the curves presented by IBDDE, DDE and PDE are very similar across the various test problems. Moreover, while PDE was outperforming DDE on the 500-dimensional problems, the latter is better than the former in 1,000 dimensions.

The comparison between DDE-EEPF and PDE-WRI shows that although the random injection leads to satisfactory results both in 500 and 1,000 dimensions, and thus requires further investigation in the future, DDE-EEPF shows better results on average. This fact confirms that the injection of proper, high quality solutions is beneficial. We believe that a proper selection of these high quality solutions to be injected might have a great potential on a various set of problems.

6 Conclusion

The DDE-EEPF algorithm proposed in this paper is compared against three state-of-the-art, distributed DE algorithms and one designed ad hoc in this study. DDE-EEPF is characterized in that it uses two families of sub-populations instead of only one, as is the case in the three distributed DE algorithms. The first family has sub-populations of constant size organized into a ring topology, where the best individuals of a sub-population can migrate to another sub-population. The second family has sub-populations with a dynamic population size, which is reduced progressively. This scheme allows the first family to explore the search space, while the second family independently attempts to detect high performance solutions. These solutions then migrate to the first family in order to direct the exploration towards better solutions.

Numerical results show that DDE-EEPF outperforms the other algorithms in the majority of the 24 high-dimensional test problems. The injection of individuals from the second family of sub-populations into the first family has, in most of the cases, a beneficial effect as it gives a “second breath” to the process and allows it to explore the search space further. The numerical results presented in this paper additionally show that the use of a structured population improves greatly the performance of the DE algorithm compared to its original, serial version, when applied to high-dimensional problems.

Future development of this work will consider a generalization and extension of the two-family mechanism. A first direction of the research could aim at testing the proposed distributed system for Particle Swarm Optimizers and Covariance Matrix Adaptation Evolution Strategy. A second could involve different algorithms operating on the sub-populations, or include local search algorithms instead of the second family of sub-populations in order to generate high quality solutions.