A polygon-based clustering and analysis framework for mining spatial datasets

Abstract

Polygons provide natural representations for many types of geospatial objects, such as countries, buildings, and pollution hotspots. Thus, polygon-based data mining techniques are particularly useful for mining geospatial datasets. In this paper, we propose a polygon-based clustering and analysis framework for mining multiple geospatial datasets that have inherently hidden relations. In this framework, polygons are first generated from multiple geospatial point datasets by using a density-based contouring algorithm called DCONTOUR. Next, a density-based clustering algorithm called Poly-SNN with novel dissimilarity functions is employed to cluster polygons to create meta-clusters of polygons. Finally, post-processing analysis techniques are proposed to extract interesting patterns and user-guided summarized knowledge from meta-clusters. These techniques employ plug-in reward functions that capture a domain expert’s notion of interestingness to guide the extraction of knowledge from meta-clusters. The effectiveness of our framework is tested in a real-world case study involving ozone pollution events in Texas. The experimental results show that our framework can reveal interesting relationships between different ozone hotspots represented by polygons; it can also identify interesting hidden relations between ozone hotspots and several meteorological variables, such as outdoor temperature, solar radiation, and wind speed.

1 Introduction

Tools that visualize and analyze geo-referenced datasets have gained importance in the last decade, as can be evidenced by the increased popularity of products, such as Google Earth, Microsoft Virtual Earth, and ArcGIS. Polygons play an important role in the analysis of geo-referenced data as they provide a natural representation of geographical objects, such as countries, buildings, and pollution hotspots. Polygons can also serve as models for geospatial clusters, and can model nested and overlapping clusters. Moreover, polygons have been studied thoroughly in geometry and they are mathematically well understood. Furthermore, powerful software libraries are available to manipulate, analyze, and quantify relationships between polygons. Spatial extensions of popular database systems, such as ORACLE, PostGIS, and Microsoft SQL Server, support polygon search and polygon manipulation in extended versions of SQL. However, past and current data mining research has mostly ignored the capabilities that polygon analysis can offer.

In general, polygon analysis is particularly useful to mine relationships among multiple geospatial datasets, as it provides a useful tool to analyze discrepancies, progression, change, and emergent events. Our work focus on clustering and analysis of polygons that have been generated from multiple geospatial point datasets. In particular, the scope of a spatial cluster is described by a polygon; point objects inside a polygon belong to the same spatial cluster, while point objects outside of a polygon do not. Our framework provides computational methods to create such spatial clusters from multiple geospatial point datasets. Multiple related geospatial datasets contain a lot of overlapping polygons. Traditional distance functions and clustering algorithms for data points would not work directly for such polygons. New distance functions and clustering algorithm are proposed in this paper to cluster polygons and generate meta-clusters. As there are usually a lot of meta-clusters containing multiple polygons, it is desirable to have automated screening procedures to help domain experts to select clusters and meta-clusters that they are interested in based on their domain-driven notion of “interestingness”. Therefore, our framework provides post-processing techniques which mine the obtained meta-clusters to extract interesting patterns and summarized knowledge based on a domain expert’s notion of interestingness. The architecture of our framework will be introduced in Section 2.

This paper’s main contributions include:

• A new polygon-based framework for clustering and analyzing multiple spatial datasets is presented.

• Novel distance functions to assess the similarity of overlapping polygons are proposed.

• A density-based clustering algorithm called Poly-SNN is introduced to cluster polygons.

• Two post-processing analysis techniques, which employ plug-in reward functions to capture a domain expert’s notion of interestingness, are introduced to extract interesting patterns and summarized knowledge from meta-clusters.

• Our work is evaluated in a challenging real-world case study involving ozone pollution events in Houston metropolitan area.

The rest of the paper is organized as follows. Section 2 introduces the architecture of our framework. Section 3 explains DCONTOUR algorithm. Distance functions and clustering algorithms for overlapping polygons are discussed in Section 4. Section 5 presents post-processing analysis techniques for finding interesting clusters. Section 6 evaluates our work with case studies on ozone pollution events in Houston metropolitan area. Section 7 discusses the related work. Section 8 concludes our study.

2 Polygon-based clustering and analysis framework for mining geospatial datasets

In our framework, we first generate spatial clusters represented by polygons from multiple geospatial point datasets. Both spatial clustering algorithms which directly derive polygon from point datasets and approaches that initially obtain spatial clusters as sets of objects and wrap a polygon around those objects can be used to obtain such spatial clusters. As the first type of algorithm is not very common, an algorithm called DCOUNTOUR will be introduced for this purpose. In the second step, we introduce new distance functions called Overlay distance and Hybrid distance to access the distance between overlapping polygons. The Shared Nearest Neighbor algorithm (SNN) is generalized to cluster polygons. In the third step, post-processing analysis techniques are provided to extract interesting patterns and to provide summaries from meta-clusters based on a domain expert’s notion of “interestingness”. A spatial cluster will be characterized by two things in our work: a polygon which described the scope of a spatial cluster and a statistical summary based on all the objects belonging to the same meta-clusters; the statistical summary usually contains mean values and standard deviations of various non-spatial variables for the objects in the same spatial cluster. Two particular post-processing techniques are proposed: First, a greedy algorithm is developed to automatically select a set of interesting polygons from meta-clusters to obtain a final clustering. Second, a screening procedure which uses plug-in reward functions is introduced to automatically identify interesting meta-clusters which has unexpected member distributions respect to a continuous non-spatial variable.

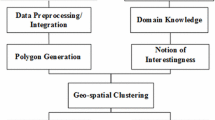
In summary, our framework is an integration of clustering algorithms, post-processing analysis techniques, and visualization. The architecture of our framework is summarized in Fig. 1. It consists of three steps:

Fig. 1

The polygon-based clustering and analysis framework for mining geospatial datasets

• Step 1: Apply DCONTOUR algorithm to collect/generate polygons which describe spatial clusters from multiple geospatial point datasets.

• Step 2: Use the Poly-SNN algorithm to create meta-clusters from the polygons that were generated in step1.

• Step 3: Extract interesting patterns and create summaries from the meta-clusters using post-processing analysis techniques.

We use multiple ozone concentration datasets downloaded from TCEQ (Texas Commission on Environmental Quality) website [20] as an example to further explain the three steps in our framework. TCEQ uses a network of 44 ozone-monitoring stations in the Houston-Galveston area which covers the geographical region within [−95.8070, -94.7870] longitude and [29.0108, 30.7440] latitude. It collects hourly ozone concentration data from each monitoring station and publishes the data on its website. In step 1, we first apply a standard Kriging interpolation method [8] to compute the ozone hourly concentrations on 20 × 27 grids that cover the Houston metropolitan area. Next, we feed the interpolation function into the DCONTOUR algorithm with a defined threshold to create sets of polygons. Such polygons describe ozone pollution hotspots at each hour—areas whose hourly ozone concentrations are above the input threshold. In step 2, we apply Poly-SNN with Hybrid distance functions to cluster polygons and create meta-clusters, which are clusters containing sets of similar polygons. In step 3, we propose several plug-in reward functions to capture a domain expert’s notion of interestingness to guide the extraction of knowledge from meta-clusters. In particular, an algorithm to generate a final clustering from meta-clusters is proposed. Such a final clustering could help domain experts to clearly capture the dominant ozone pollution hotspots and possible maximum range of ozone pollution events for Houston area. Moreover, automated screening procedures to identify unusual meta-clusters are introduced.

3 DCONTOUR

DCONTOUR [6] is the first density-based clustering algorithm that uses contour lines to determine cluster boundaries. Objects that are inside a contour polygon belong to the same cluster. DCONTOUR operates on the top of supervised density functions.

We assume that objects o∈O have the form ((x, y), z) where (x, y) is the location of object o, and z denoted as z(o) in the following is the value of interestingness of object o. In general, density estimation techniques employ influence functions that measure the influence of a point o with respect to another point v. The overall influence of all data objects o _i ∈O for 1 ≤ i ≤ n on a point v is measured by the density function ψ^O(v). Density estimation is called supervised because in addition to density information based on the locations of objects, we take the interestingness z(o) into consideration when measuring density. ψ^O(v) is defined as follows:

$$ {\psi}^{\mathrm{O}}\left(\mathrm{v}\right)={\displaystyle {\sum}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{f}}_{\mathrm{i}\mathrm{nfluence}}\left(\mathrm{v},{\mathrm{o}}_{\mathrm{i}}\right)={\displaystyle {\sum}_{\mathrm{i}=1}^{\mathrm{n}}\mathrm{z}\left({\mathrm{o}}_{\mathrm{i}}\right)\;{\mathrm{e}}^{-\frac{\mathrm{d}{\left(\mathrm{v},{\mathrm{o}}_{\mathrm{i}}\right)}^2}{2{\sigma}^2}}}\;} $$

The parameter σ determines how quickly the influence of o_i on v decreases as the distance between o _i and v increases.

The pseudo code of DCONTOUR is given in Fig. 2.

Fig. 2

Pseudocode of DCONTOUR

Figure 3 gives an illustration on how to construct contour intersection points based on density threshold equal to 4.5. For instance, when the right edge of the lower left cell is considered, because 4.5 is between 4.1 and 5.5, a contour intersection point exists on this edge; by interpolating between 4.1 and 5.5, a point on this edge is sampled and its density is computed as 4.8. Because 4.8 is larger than d, we continue the binary search by sampling a point south of this point. The binary search terminates if the density difference between a sampled point and d is less than a threshold. All the blue points on Fig. 3 are the contour intersection points b for density equal to 4.5. Finally, in step 4, we connect contour intersection points b found on cell edges and continue this process on its neighboring cells until a closed polygon is formed or both ends of the polyline reach the grid boundary. An algorithm proposed by Cottafava, and Moli [4] is used to compute contour polygons.

Fig. 3

Contour construction for density equal to 4.5

4 Distance functions and clustering algorithm for overlapping polygons

4.1 Distance functions for polygons

One unique characteristic of our work is that we have to cope with overlapping polygons. We believe that considering polygon overlap is of critical importance for polygon-based clustering of related geospatial datasets. Therefore, in addition to the Hausdorff distance, we propose two novel distance functions: Overlay and Hybrid distance functions. We define a polygon A as a sequence of points A = p ₁ ,…, p _n , with point p ₁ being connected to the point p _n to close the polygon. Moreover, we assume that the boundary of a polygon does not cross itself and polygons can have holes inside. Throughout the paper we use the term polygon to refer to such polygons.

4.1.1 Hausdorff distance

The Hausdorff distance measures the distance between two point sets. It is the maximum distance of a point in any set to the nearest point in the other set. Using the same notation as [23], let A and B be two point sets, the Hausdorff distance D_Hausdorff(A,B) for the two sets is defined as:

$$ {\mathrm{D}}_{\mathrm{Hausdorff}}\left(A,B\right)= \max \left\{{ \max}_{a\in A}{ \min}_{b\in B}d\left(a,b\right),{ \max}_{b\in B}{ \min}_{a\in A}d\left(a,b\right)\right\} $$

where d(a,b) is the Euclidean distance between points a and b.

In order to use the Hausdorff distance for polygons, we have to determine how to associate a point set with a polygon. One straight-forward solution is to define this point set as the points that lie on the boundary of a polygon. However, computing the distance between point sets that consist of unlimited number of points is considerably expensive. An algorithm that solves this problem for trajectories has been proposed [8] and the same technique can be applied to polygons.

4.1.2 Overlay distance

The overlay distance measures the distance between two polygons based on their degree of overlap. The overlay distance D_Overlay(A,B) between polygons A and B is defined as:

$$ {\mathrm{D}}_{\mathrm{overlay}}\left(A,B\right)=1-\frac{ area\left( Inter \sec tion\left(A,B\right)\right)}{ area\left( Union\left(A,B\right)\right)} $$

where the function area(X) returns the area a polygon X covers. The overlay distance subtracts the ratio of the size of intersection over size of union of two polygons from 1. The overlay distance is 1 for pairs of non-overlapping polygons.

4.1.3 Hybrid distance

The hybrid distance function uses a linear combination of the Hausdorff distance and the Overlay distance. Because the Overlay distance between two non-overlap polygons is always 1, regardless of the actual location in space, using the Hausdorff distance can provide more precise approximations of the distance between two non-overlap polygons. The hybrid distance function is defined as:

$$ {\mathrm{D}}_{\mathrm{Hybrid}}\left(A,B\right)=w\times {D}_{Overlay}\left(A,B\right)+\left(1-w\right)\times {D}_{Hausdorff}\left(A,B\right) $$

where w is the weight factor associated with the Overlay distance function (1 ≥ w ≥ 0).

There are several distance functions [4, 8, 13, 14] proposed in the literature for spatial polygons. However, none of them can cope with overlapping spatial polygons. Overlapping spatial polygons play a very important role in analyzing multiple related spatial datasets in many application domains. Failing to measure the degree of overlap will result in inadequate clustering results.

4.2 The Poly-SNN algorithm

The SNN (Shared Nearest Neighbors) algorithm [11] is a density-based clustering algorithm. SNN clusters data as DBSCAN does, except that the number of nearest neighbors that two points share is used to assess the similarity instead of the number of points being within the radius ε of a particular point. In SNN, similarity between two points p ₁ and p ₂ is the number of points they share among their k nearest neighbors as follows:

$$ similarity\ \left({p}_1,{p}_2\right)= size\_ of\left( NN\left({p}_1\right)\cap NN\left({p}_2\right)\right) $$

where NN(p _i ) is the set of the k nearest neighbors of point p _i.

SNN density of point p is defined as the sum of the similarities between point p and its k nearest neighbors as follows:

$$ density\;(p)={\displaystyle {\sum}_{\mathrm{i}=1}^{\mathrm{k}} similarity\;\left(p,{p}_i\right)} $$

where p _i is the i^th nearest neighbor of point p.

After assessing the density of each point, SNN algorithm finds the core points (points with an SNN density above an input threshold) and forms the clusters around the core points like DBSCAN. Similar to DBSCAN, SNN is able to find clusters of different sizes, shapes, and can handle noise in the dataset. Moreover, SNN copes better with high dimensional data and deals well with datasets having varying densities. SNN algorithm has the ability to discover clusters of arbitrary shapes and does not require the number of clusters to be determined in advance.

Our Poly-SNN algorithm extends SNN to cluster polygons. The key component of Poly-SNN is the calculation of polygon distances. We calculate the distances between all pairs of polygons using the Hybrid distance function. Next, we identify the k nearest neighbors for each polygon. Poly-SNN calculates the SNN density of each polygon using the k nearest neighbors, and clusters the polygons around core polygons as described above. Figure 4 lists the pseudocode of the Poly-SNN algorithm.

Fig. 4

Pseudocode for POLY-SNN

The proposed Poly-SNN algorithm is based on the well established density based clustering algorithm SNN [11]. There are several advantages of using SNN as our reference algorithm. First, it has the ability to find clusters in presence of outliers. Second, SNN is capable of finding clusters of different shape, size, and density. Third, it works well for high dimensional data. The experimental results and detail discussions in [11] show that SNN perform better than traditional methods, such as K-means, DBSCAN, and CURE on a variety of datasets.

5 Post-processing analysis techniques

5.1 Domain driven final clusterings generation methodology

In general, domain experts seek for clusters based on their domain-driven notion of “interestingness”. Usually, domain experts’ interestingness is different from generic characteristics used by traditional clustering algorithms; moreover, for a given dataset there usually are many plausible clusterings whose value really has to be determined by domain experts. Finally, even for the same domain expert, multiple clusterings are of value, e.g., clusterings at different levels of granularity. A key idea of this work is to collect a large number of frequently overlapping clusters organized in form of meta-clusters; final clusterings and other summaries are then created from those meta-clusters based on a domain expert’s notion of interestingness.

To reflect what was discussed above, we assume that our final clustering generation algorithms provide plug-in reward functions that capture a domain expert’s notion of interestingness. The reward functions will be maximized during the final clustering generation procedure. Our methodology provides an alternative approach to the traditional ensemble clustering by creating a more structured input for obtaining a final clustering, also reducing algorithm complexity by restricting choices. We propose algorithms that create a final clustering by selecting at most one cluster from each meta-cluster. Moreover, due to the fact that polygons originated from multiple related datasets usually overlap a lot, we provide an option for domain experts to restrict cluster overlap in the final clusterings. More specifically, we develop algorithms that create the final clusterings from meta-clusters by solving the following optimization problem:

Inputs:

• 1. A meta-clustering M = {X ₁ , …, X _k } —at most one object will be selected from each meta-cluster X _i (i = 1,…k).

• 2. The user provides the individual cluster reward function Reward _U whose values are in [0,∞).

• 3. A reward threshold θ _U —clusters with low rewards are not included in the final clusterings.

• 4. A cluster distance threshold θ _d , which expresses to what extent the user would like to tolerate cluster overlap.

• 5. A cluster distance function dist.

Find Z ⊆ X ₁ ∪…∪X _k that maximizes:

$$ q(Z)={\displaystyle {\sum}_{c\in Z}\; rewar{d}_{\kern0.1em U}(c)} $$

subject to:

• 1. ∀ x∈Z ∀ x’∈Z (x≠x’ ⇒ Dist(x, x’) > θ _d )

• 2. ∀ x∈Z (Reward _U (x) > θ _U )

• 3. ∀ x∈Z ∀ x’∈Z ((x∈ X _i ∧ x’∈ X _k ∧ x≠x’) ⇒ i ≠ k)

Our goal is to maximize the sum of the rewards of clusters represented by polygons that have been selected from meta-clusters. Constraint 1 prevents two clusters which are spatially too close to be included in the final clustering. Constraint 3 makes sure that at most one cluster from each meta-cluster is selected.

Assuming that we have n meta-clusters, each meta-cluster contains an average of m clusters (polygons), there are roughly (m + 1)ⁿ final clusterings; For each meta-cluster, we can either select one cluster for inclusion or we might decide not to take any cluster due to violations of constraints 1 and 2. Constraint 2 is easy to handle by removing clusters below reward threshold from the meta-clusters prior to running the final clusterings generation algorithm.

Many different algorithms can be developed to solve this optimization problem. We are currently investigating three algorithms:

• A greedy algorithm: A greedy algorithm that always selects the cluster with the highest reward from the unprocessed meta-clusters whose inclusion in the final clusterings does not violate constraints 1 and 2. If there are no such clusters left, no more clusters will be added from the remaining meta-clusters to the final clusterings.

• An anytime backtracking algorithm: An anytime backtracking algorithm that explores the choices in descending order of cluster rewards; every time a new final clustering is obtained, the best solution found so far is potentially updated. If runtime expires, the algorithm reports the best solution that have been identified.

• An evolutionary computing algorithm: It relies on integer chromosomal representations; e.g., (1, 2, 3, 0) represents a solution where cluster 1 is selected from meta-clustering 1, cluster 2 from meta-cluster 2,…, and no cluster is selected from meta-cluster 4. Traditional mutation and crossover operators are used to create new solutions, and a simple repair approach is used to deal with violations of constraint 1.

The greedy algorithm is very fast (O(m × n)) but far from optimal, the backtracking algorithm explores the complete search space (O(m ⁿ)) and—if not stopped earlier—finds the optimal solution if n and m are not very large; however, the anytime backtracking approach can be used for large values of m and n. Finally, the evolutionary computing algorithm covers a middle ground, providing acceptable solutions that are found in medium runtime. Figure 5 gives the pseudocode of the greedy algorithm.

Fig. 5

Pseudocode of the greedy algorithm

As an example, we use the reciprocal of the area of each ozone polygon as the reward function. This reward functions can help domain experts to identify potential ozone pollution point sources and to analyze patterns at different levels of granularity when different parameters are selected. First, all input meta-clusters generated by Poly-SNN are marked unprocessed. The final clustering F is initialized to empty. The reward for each polygon (the reciprocal of the area of the polygon) is computed. The user inputs reward threshold and distance threshold, e.g., reward threshold equal to 10 and distance threshold equal to 0.5. Next, polygon p with the highest reward from the unprocessed meta-clusters is selected, compute the distances between p and all polygons in F, if all distances are greater than distance threshold 0.5, put polygon p into F, and flag the meta-cluster X _i that polygon p belongs to as processed. Otherwise, remove polygon p from the meta-cluster X _i . The algorithm repeats until all the meta-clusters are flagged as processed. The output is the final clustering F containing all selected polygons.

5.2 Finding interesting meta-clusters with respect to a continuous variable v

Our second post processing technique allows automatic screening of the obtained meta-clusters for unexpected distributions. The main idea is to provide interestingness functions that automatically identify meta-clusters whose member distribution with respect to a non-spatial variable deviates significantly from its distribution in the whole dataset. We introduce such an interestingness function that measures interestingness of a meta-cluster based on its mean value and standard deviation of a non-spatial variable.

We assume a dataset D = (a ₁ ,…, a _n , v) and a meta-clustering M = {X ₁ , …, X _k } is given, where v is a continuous variable which has been normalized using z-scores. Our goal is to find contiguous clusters¹ in the A = {a ₁ ,…, a _n } - space² which maximize the following interestingness function:

• Let X _i ∈2 ^A be a cluster in the A-space

• Let σ be the variance of v with respect in dataset D

• Let σ(X _i ) be the variance of variable v in a cluster X _i

• Let mv(X _i ) the mean value of variable v in a cluster X _i

• Let t ₁  ≥ 0 a mean value reward threshold and t ₂  ≥ 1 be a variance reward threshold

We suggest using the following interestingness function φ to calculate the reward for each cluster:

$$ \varphi \left({X}_i\right)= max\left(0,\left| mv\left({X}_i\right)\right|-{t}_1\right)\times max\left(0,\sigma -\left(\sigma \left({X}_i\right)\times {t}_2\right)\right) $$

In general, only clusters, which satisfy |mv(c)| > t ₁ and σ(c) < σ/t ₂ , will receive a reward value; e.g., for t ₁  = 0.2 and t ₂  = 2 only clusters whose mean-value is below −0.2 or above +0.2 and whose variance is less than or equal to half of σ will receive a reward. In general clusters whose mean value is significantly different from 0 and variance is low will receive the highest rewards. We rank all clusters based on their reward and only report those whose rewards are higher than the reward threshold specified by the domain expert.

The proposed interestingness function is just an example for identifying unusual clusters with respect to a continuous variable—other useful interestingness functions can be proposed. Similar interestingness functions can also be proposed for categorical variables.

6 Experimental evaluation

6.1 The ozone datasets

It has been reported by the American Lung Association [1] that Houston Metropolitan area is the 7th worst ozone zone in the US. TCEQ is a state agency responsible for environmental issues including the monitoring of environmental pollution in the Texas. TCEQ uses a network of 44 ozone-monitoring stations in the Houston-Galveston area. The area covers the geographical region within [−95.8070, -94.7870] west longitude and [29.0108, 30.7440] north latitude. We downloaded hourly ozone concentration data between the timeframe of April 1, 2009 at 1 a.m. to November 30, 2009 at 11 p.m. from TCEQ’s website. In addition to the ozone concentrations, we also downloaded corresponding meteorology data including wind speed, solar radiation, and outdoor temperature.

Ozone formation is a complicated chemical reaction. There are several control factors involved:

• Sunlight measured by solar radiation is needed to produce ozone.

• High outdoor temperatures cause the ozone formation reaction to speed up.

• Wind transports ozone pollution from the source point.

• Time of Day: ozone levels can continue to rise all day long on a clear day, and then decrease after sunset.

Solar radiation is measured in langleys per minute. A langley is a unit of energy per unit area (1 gram-calorie/cm2) commonly employed in radiation measurements [20]. Outdoor temperature is measured in Fahrenheit. Wind Speed is measured in miles per hour.

Basically, we generate polygons from original point datasets to capture ozone hotspots for particular time slots in Houston area. Two polygon datasets are created by using DCONTOUR algorithm with two different density thresholds selected by domain experts. The use of the density threshold 180 creates 255 polygons. These polygons represent areas where the average one hour ozone concentration is above 80 ppb (parts per billion). The density threshold 200 generates 162 polygons that have one hour ozone concentrations more than 90 ppb. The current EAP ozone standard is based on an eight-hour average measurement. In order to meet the standard, the eight-hour average ozone concentration has to be less than 0.075 ppm (75 ppb). Therefore, we can consider these two polygon datasets represent areas where the ozone level exceeds the EPA standard during that hour.

We evaluate our methodology in three case studies. The goal of the first case study is to verify that our new distance functions and clustering algorithm for polygons can effectively cluster overlapping polygons generated from multiple geospatial datasets. By analyzing additional meteorological variables associated with polygons, such as outdoor temperature, solar radiation, wind speed, and time of day, we can characterize each cluster and identify interesting patterns associated with these hotspots.

In the second case study, we are interested in generating final clusterings that capture a domain expert’s notion of interestingness by plugging in different reward functions. For example, domain experts may interest in finding typical ozone pollution hotspots occurred when the outdoor temperatures are extremely high. In order to summarize final clusterings, the statistical results of three ozone pollution control variables are also provided.

In the third case study, we try to find interesting clusters with unexpected distributions respect to a continuous non-spatial variable. A screening procedure and interestingness function are proposed to assess the interestingness of the meta-clusters with respect to a continuous variable. Meta-clusters are evaluated with respect to different continuous variables, such as solar radiation, wind speed, and outdoor temperature, respectively.

6.2 Case study 1: polygon clustering and analysis

An ozone polygon is a hotspot area that has ozone concentration above a certain threshold. In order to generate polygons representing ozone pollution hotspots where ozone concentration is above 90 ppb from original ozone concentration point datasets downloaded from TCEQ’s website [20], we divide the Houston area into a 20 × 27 grid. The density function discussed in Section 3 is used to compute the ozone concentrations at each grid intersection point. Next, we compute contour intersection points b on grid cell edges where the density is equal to 90 using binary search and interpolation. Finally, we compute the contour polygons by connecting contour intersection points.

In this case study, we select the dataset with 162 polygons created by DCONTOUR with density threshold equal to 200. These polygons represent areas with 1 hour ozone concentration higher than 90 ppb. We then apply Poly-SNN clustering algorithm to find clusters of ozone hotspots called meta-clusters. Figure 6 displays the result of 30 meta-clusters generated by Poly-SNN using the hybrid distance function and the number of nearest neighbor k equal to 5. Out of 162 polygons, 30 % are considered as outliers by Poly-SNN. Polygons marked by the same color belong to the same meta-cluster.

Fig. 6

Meta-clusters generated by Poly-SNN using the Hybrid distance function

In general, by analyzing the meteorological characteristics of polygons domain experts may find some interesting phenomena that could lead to further scientific investigation. Therefore, we also compute some statistics of four meteorological variables involved in ozone pollution events. Table 1 lists the statistical results of four meteorological variables associated with the meta-clusterings displayed in Fig. 6.

Table 1 The statistical results for meta-clustering shown in Fig. 6

As expected, meta-clusters shown in Fig. 6 is characterized by high outdoor temperature (average of 90.6 and standard deviation of 5.3) and strong solar radiation (average of 0.8 and standard deviation of 0.4), which usually happens between 1 p.m. and 4 p.m.. Since the standard deviation of the wind speed (1.9) compared with the average wind speed (6.1) is nontrivial, the variance of the size of the polygons is significant in Fig. 6.

It is hard to visualize all meta-clusters in a single picture when clusters overlap a lot. Figures 7 and 8 display eight out of 30 mete-clusters shown in Fig. 6. As expected, the Hybrid distance function that employs both Overlay distance function and Hausdorff distance function creates clusters of polygons that are similar in terms of shape, size and location. Particularly, since we give more weights to the overlay distance function, the eight meta-clusters in Figs. 7 and 8 overlap significantly. This case study prove that our Poly-SNN clustering algorithm in conjunction with Hybrid distance function can effectively find clusters of overlapping polygons with similar size, shape, and location.

Fig. 7

Visualization of four meta-clusters (ID: 11, 12, 16, and 29) shown in Fig. 6

Fig. 8

Visualization of four meta-clusters (ID: 2, 4, 10, and 27) shown in Fig. 6

Tables 2 and 3 list the mean and standard deviation of outdoor temperature, solar radiation, wind speed, and time of day associated with eight meta-clusters shown in Figs. 7 and 8. The solar radiation information related to clusters 2 and 4 are not available from TCEQ’s website. Certainly, ozone formation is more complicated than only considering those four control factors. However, our polygon-based methodology does have the capability of handling more non-spatial variables.

Table 2 The statistical results of meta-clustering shown in Fig. 7

Table 3 The statistical results of meta-clustering shown in Fig. 8

Based on Table 2, we can see that polygons in meta-clusters 11 and 12 are characterized by high outdoor temperatures (98.8 and 99.1) compared with the entire dataset (90.6) and strong solar radiations (0.9 and 0.9) compared with the entire dataset (0.8). The wind speeds of cluster 11 and cluster 12 (5.2 and 4.9) are low compared with the mean value of entire meta-clustering (6.1) so that the average size of the polygons in cluster 11 and cluster 12 are relatively small compared with other polygons shown in Fig. 6. Also, Clusters 11 and 12 are captured around 2 p.m.. The statistical results associated with Cluster 16 are very close to the mean value of the entire dataset in Table 1.

Based on Table 3, cluster 10 has lower outdoor temperature (86.0), lower solar radiation (0.7), and lower wind speed (4.8) compared with the mean values of the entire dataset in Table 1. The average time of day for cluster 4 is about 4 p.m.. All those four lower meteorological values contribute to smaller polygon sizes inside meta-cluster 4 in Fig. 8.

6.3 Case study 2: generation of domain driven final clusterings

In this case study, the greedy algorithm introduced in Section 5 is used to generate the domain-driven final clusterings based on 30 meta-clusters shown in Fig. 6. We use several reward functions to capture domain experts’ different notions of interestingness. The final clusterings with statistical results of meteorological data can be used to summarize what characteristics the ozone hotspots in the same meta-clusters share.

The range of ozone pollution represented by the area of polygons is selected as the first cluster reward function, which will help domain experts recognize the possible maximal range of ozone pollution events in Houston area. By selecting different reward threshold and distance threshold, different final clusterings could be generated. Figure 9 shows one final clustering using reward threshold 0.04 and Hybrid distance threshold 0.5. There are 5 polygons in the final cluster. Table 4 shows the corresponding statistical results of meteorological data. Since the standard deviations of these four variables are relatively small, we will not discuss the standard deviation in this case study. Based on Table 4, polygons 21, 80, and 150 cover larger area with higher outdoor temperature, high wind speed, and strong solar radiation compared with polygons 13 and 125. Polygon 150 is interesting because it has a hole inside. Our methodology can handle polygons with holes inside. Further analysis could be done to help understand the formation of holes inside polygons.

Fig. 9

Final clustering for area of polygon reward threshold 0.04 and hybrid distance threshold 0.5

Table 4 The mean of four meteorological variables for the final clustering shown in Fig. 9

The reciprocal of the area of each polygon is selected as the second reward function for smaller granularity, which may be useful to identify the ozone pollution point sources and enable the domain experts to analyze patterns at different levels of granularity. By decreasing either the reward threshold or the distance threshold, we are able to get different final clusterings. Figure 10 shows the final clustering with reward threshold set to 10 and distance threshold set to 0.45. There are total 14 polygons in this final clustering. Table 5 lists the corresponding statistical results of four meteorological variables. Some of the values are not available in the original datasets downloaded from TCEQ’s website. All of those 14 polygons with relative smaller size occur either before 1 p.m. or after 4 p.m.. According to Table 1, the average time of day for the entire dataset is 2:30 p.m. with a standard deviation of 1.8. The time slot from 1 p.m. to 4 p.m. is definitely a major time period for ozone formation which could change the range and the concentration density of ozone pollution significantly. More analysis should be done specially for this time slot between 1 p.m. and 4 p.m..

Fig. 10

Final clustering for the reciprocal of area reward threshold 10 and hybrid distance threshold 0.45

Table 5 The mean of four meteorological variables for the final clustering shown in Fig. 10

Outdoor temperature, wind speed, and solar radiation also play very important roles in ozone formation. We use average outdoor temperature associated with each polygon as the third reward function. Figure 11 shows one final clustering with average outdoor temperature threshold equal to 90° F and hybrid distance threshold equal to 0.55. Figure 11 shows the final clustering. The corresponding statistical results of the meteorological variables are summarized in Table 6. Obviously, all the polygons with high temperatures occur during 2 p.m. to 4 p.m.. The lower the wind speed is, the smaller the area of the polygon is. For example, polygon 67 has the lowest wind speed of 4.1 compared with all the other four polygons in Fig. 11, relative high outdoor temperature, and strong solar radiation; the area of polygon 67 is still smaller than all the other four polygons shown in Fig. 11.

Fig. 11

Final clustering for average temperature reward threshold 90 and hybrid distance threshold 0.55

Table 6 The mean of four meteorological variables of the final clustering shown in Fig.  11

The solar radiation associated with each ozone hotspot is selected as the next reward function. Figure 12 shows the final clustering for solar radiation threshold equal to 0.9 and Hybrid distance threshold equal to 0.55. Table 7 lists the corresponding mean values of four meteorological variables. Based on Table 7, strong solar radiation happens between 11 a.m. and 1 p.m.. During that time period, the outdoor temperature is not relative high compared to the entire datasets (90.6). Polygon 107 is the smallest due to the smallest wind speed (4.6) even though it has the highest outdoor temperature (94.4) and stronger solar radiation (1.2). Polygon 21 has the relative strong solar radiation (1.3), high wind speed (6.1), and relative low outdoor temperature (86.4) compared with the other four polygons shown in Fig.  12 . However, the area of polygon 21 is still the largest one.

Fig. 12

Final clustering for solar radiation threshold 0.9 and hybrid distance threshold 0.55.

Table 7 The mean of four meteorological variables of the final clustering shown in Fig.  12

6.4 Case study 3: a screening procedure to identify interesting meta-clusters

For this case study, we use the dataset with 255 polygons generated by DCONTOUR with density threshold 180. 21 meta-clusters are created by using Poly-SNN with hybrid distance functions and k equal to four. 20 % of those polygons are considered as outliers by Poly-SNN. We evaluate these meta-clusters with respect to continuous meteorological variables, such as solar radiation, wind speed, and outdoor temperature, respectively. Meta-clusters with high rewards based on interestingness function φ discussed in Section 5.2 are identified.

The statistical summaries for three meteorological variables for all datasets are listed in Table 8. The average temperature is about 89 °F. The average solar radiation is about 0.8 langleys per minute. The average wind speed is about 5.9 miles per hour. Table 9 shows the statistical results after Z-score normalization. All mean values become 0; all variances become 1.

Table 8 Statistical results for meteorological variables

Table 9 Statistical results for meteorological variables after Z-score normalization

In this case study, the mean value threshold is set to 0.2, the variance threshold is set to 2, and the interestingness reward threshold is set to 0.4. We are interested in finding meta-clusters whose mean value is below −0.2 or above 0.2, whose variance is less than or equal to half of the variance of the entire dataset, and whose interestingness reward is above 0.4.

We first select outdoor temperature. Three meta-clusters (3, 15, and 16) depicted in Fig. 13 were selected by the post-processing procedure. Table 10 lists the normalized outdoor temperature associated with each meta-cluster. Table 13 at the end of this section lists the detail information of each polygon in the final meta-clusters. For example, Meta-cluster 15 has five polygons; two out of five polygons were monitored at 1 p.m. and 2 p.m. on May 4, 2009, the other three were monitored at 10 a.m., 11 a.m., and 12 p.m., respectively on June 7, 2009. Further investigation of meta-cluster 15 will help domain experts better understand how the ozone pollution change over time.

Fig. 13

Interesting meta-clusters with respect to the outdoor temperature

Table 10 Statistical results of outdoor temperature of the meta-clusters shown in Fig. 13

In general, the highest levels of ozone concentration appear a few hours after the maximum solar radiation. We pick solar radiation as our second continuous variable. Figure 14 shows three selected meta-clusters with respect to solar radiation. Table 11 lists the statistical results of the normalized solar radiation associated with each meta-cluster shown in Fig. 14. Meta-cluster 5 was picked due to the very low value of solar radiation. It contains five polygons monitored between 3 p.m. and 5 p.m. on five different dates (5/4/2009, 5/29/2009, 6/7/2009, 8/15/2009, and 9/4/2009). Meta-cluster 15, however, is picked up again in this case study due to its high value of solar radiation.

Fig. 14

Interesting meta-clusters with respect to solar radiation

Table 11 Statistical results of solar radiation of the meta-clusters shown in Fig. 14

The higher levels of ozone concentration are associated with the greatest magnitude of wind velocity. Figure 15 shows two final meta-clusters (2, 5) when the wind speed is selected as the next continuous variable in calculating the interestingness reward. Table 12 lists the statistical results of the normalized wind speed of each meta-cluster shown in Fig. 15. There are five polygons in meta-cluster 2; two out of five polygons were monitored at 2 p.m. and 3 p.m. on November 13, 2009; the other three were monitored at 2 p.m., 3 p.m., and 4 p.m. on June 6, 2009. Figure 15 clearly shows the progression of the ozone pollution events on those 2 days. Meta-cluster 5 is selected again due to high value of wind speed.

Fig. 15

Interesting meta-clusters with respect to wind speed

Table 12 Statistical results of wind speed of the meta-clusters shown in Fig. 15

Table 13 lists the summarized meterology data for all polygons in the final meta-clusters which were redflagged by our post-clustering analysis procedure in this case study. Some meterology data are not available in the original datasets from TCEQ noted as N/A in Table 13. Both meta-cluster 5 and meta-cluster 15 are reported twice in this case study with respect to different meterology variables. Meta-cluster 5 has very low mean value of solar radiation and relative high wind speed. Meta-cluster 15, however, has very high mean value of solar radiation and relative low temperature. They locate at the same area. Under different meterological conditions, the size of the ozone hotspots in meta-clusters 5 and 15 are different. Futher analysis of the polygons in meta-clusters 5 and 15 may help domain experts better understand how ozone hotspots change under different weather patterns over time.

Table 13 Meteorology information for polygons of selected meta-clusters

7 Related work

Polygon generation for point datasets has been a research area in computational geometry, computer graphics, computer vision, pattern recognition, and geographic information science for many years. Convex hulls are the simplest way to enclose a set of points in a convex polygon. However, convex hulls may contain large empty areas that are not desirable for good representative polygons. A commercial algorithm, called Concave Hull [17], generates tighter polygons by using a method that is similar to the “gift-wrapping algorithm” used for generating convex hulls. It employs a k-th nearest neighbors approach to find the next point in the polygon and creates a regular connected polygon unless the smoothness parameter k is too large. However, pre-processing the dataset to remove outliers and detect subregions is required for acceptable results. The Alpha shapes algorithm was introduced by Edelsbrunner et al. [10] in 1983 to address those short comings and since then has been the most widely used approach. The Alpha shapes algorithm uses Delaunay triangulation as the starting step and creates a hull by using edges of the Delaunay triangulation. However, this hull is not necessarily a closed polygon; most of the times the algorithm generates polylines, e.g. many straight lines that may or may not form closed polygons. Thus, the Alpha shapes algorithm requires post-processing for creating polygons out of the polylines. DCONTOUR [6] is the only known algorithm which uses density contouring for generating polygonal boundaries of a point set. DCONTOUR employs weighted influence function which uses a Gaussian Kernel density function. DCONTOUR can generate separate, non-overlapping polygons for each subregion in the dataset. It also works well in presence of outliers.

In [14], Joshi et al. propose a DBSCAN-style clustering algorithm for polygons. The algorithm works by replacing point objects in the original DBSCAN algorithm with the polygon objects. In [15], Joshi et al. introduce a dissimilarity function for clustering non-overlapping polygons that considers both spatial and non-spatial variables. However, the algorithms in [14, 15] do not cope with overlapping polgyons. Buchin et al. [4] propose a polygonal time algorithm to compute the Fréchet distance between two polygons. Several papers [2, 13] propose algorithms to compute the Hausdorff distance between polygons. Sander et al. [19] propose GDBSCAN, an algorithm generalizing DBSCAN in two directions: First, generic object neighborhoods are supported instead of distance-based neighborhoods. Second, it proposes other, more complicated measures to define the density of the neighborhood of an object instead of simply counting the number objects within a given radius of a query point.

Zeng et al. [22] propose a meta-clustering approach to obtain better clustering results by comparing and selectively combining results of different clustering techniques. In [12] Gionis et al. present clustering aggregation algorithms; the goal is to produce a single clustering that minimizes the total number of disagreements among input clusterings. The proposed algorithms apply the concept of correlation clustering [3]. Caruana et al. [5] propose a mean to automatically create many diversity clusterings and then measures the distance between the generated clusterings. Next, the hierarchical meta-clusters are created. Finally an interactive interface is provided to allow users to choose the most appropriate clustering from meta-clusters based on their preferences. In general, [5, 12, 22] perform meta-clustering on a single dataset, whereas our proposed methodology uses meta-clustering to analyze relationship between clusters from multiple related datasets.

Our work also relates to correspondence clustering, coupled clustering, and co-clustering which all mine related datasets. Coupled clustering [16] is introduced to discover relationships between two textual datasets by partitioning the datasets into corresponding clusters where each cluster in one dataset is matched with its counterpart in the other dataset. Co-clustering has been successfully used for applications in text mining [9], market-basket data analysis, and bioinformatics [7]. In general, the co-clustering clusters two datasets with different schemas by rearranging the datasets. The objects in two datasets are represented as rows and columns of a dataset. Then, the co-clustering partitions rows and columns of the data matrix and creates clusters which are subsets of the original matrix. Correspondence clustering [18] is introduced by Rinsurongkawong et al. to cluster two or more spatial datasets by maximizing cluster interestingness and correspondence between clusters. Cluster interestingness and correspondence interestingness are captured in plug-in reward functions and prototype-based clustering algorithms are proposed that cluster multiple datasets in parallel. In conclusion, coupled clustering [16] and co-clustering [7, 9] are not designed for spatial data and they cluster point objects using traditional clustering algorithms. The techniques introduced in correspondence clustering [18] are applicable to point objects in the spatial space whereas this paper focuses on clustering spatial clusters that originate from different, related datasets that are approximated using polygons.

We improve and extend previous work [6, 21] by introducing a new algorithm for finding interesting meta-clusters with respect to a continuous variable V that capture a domain expert’s interestingness. We integrate DCONTOUR [6] and Poly-SNN [21] into a polygonal meta-clustering methodology. A set of experiments are conducted to demonstrate the usefulness of these algorithms and to analyze some of their properties. We demonstrate how the clustering tools in our framework can be applied to multiple related spatial datasets and can help domain experts in answering interesting questions by visualizing and conducting a statistical analysis of polygonal meta-clusters.

8 Conclusion

Polygons are very useful to mine geospatial datasets as they provide a natural representation for particular types of geospatial objects and provide a useful tool to analyze discrepancies, progression, change, and emergent events. In this paper, we propose a novel polygon-based clustering and analysis framework for mining multiple geospatial datasets. We introduce a density-based contouring algorithm called DCONTOUR to generate polygons from multiple geospatial point datasets. Several novel similarity functions are proposed to assess the distances between overlapping polygons. A density-based polygonal clustering algorithm called Poly-SNN is developed to cluster polygons. A user-driven post-processing analysis procedure is introduced, which employ different plug-in reward functions capturing domain experts’ notion of interestingness to extract interesting patterns and summaries from meta-clusters. Experiments on multiple real-world geospatial datasets involving ozone pollution events in Houston show that our methodology is effective and can reveal interesting relationships between different ozone hotspots represented by polygons. Our framework can also identify interesting hidden relations between ozone hotspots and several meteorological variables, such as outdoor temperatures, solar radiation, and wind speed. Moreover, our framework has the capability for supporting various geospatial applications, such as water pollution and urban evolution.

In general, our work has the capability to cluster overlapping polygons, and polygons with holes inside. In today’s society, we are faced with analyzing an ever growing and changing amount of data. It should be highlighted that our framework tries to turn the information overload to our advantage by providing automated screening procedures. It allows for high level views of the data to facilitate data analysis. One key idea of our work is to use different plug-in reward functions to guide the knowledge extraction process, focusing on the extraction of interesting patterns and summaries with respect to a domain expert’s notion of interestingness. To the best of our knowledge, this is the first paper that proposes a comprehensive methodology that relies on polygon clustering and analysis techniques to mine multiple related geospatial datasets.

Our future work will focus on expanding the framework to incorporate additional novel clustering techniques for geospatial objects, investigating novel change analysis techniques that rely on spatial clustering to identify spatial and temporal changes with respect to spatial data, and to refine and optimize our methodology for a broad range of applications.