1 Introduction

Various studies expect the reaction of piles to the implemented axial load as discussed through the lectures with the aid of using relevant studies (Poulos 1989; Randolph 2003). The present knowledge of how piles reply beneath the load has improved many strategies researchers may utilize to estimate pile movement. Referred strategies were mentioned during the period by using many key researchers within the field, most notably by research (Stewart et al. 1994; Poulos 2006). These strategies vary from either easy-calculation methods via empirical and analytical strategies or finite element and finite difference numerical solutions. It is not always unusual while designing the basis for the pile to be based in a higher layer beneath the soil intensity accompanied by a much less compressible layer (Mishra et al. 2019; Kumar and Samui 2020).

This has been broadly acceptable with compressive sheets under the pile, which could significantly increase pile settlement, presenting a clear design challenge and risk. According to limited analysis, one research (Harry Poulos, 2017) proposes the incremental potential for subsidence due to the underlying layer, which can be significantly relevant to the geometry of the pile, soil, and its physical features. A study on this typical issue seems limited, and manual computational methods that looked analytical often seem unable to be considered for the existing distinct soil layers (Saggu 2022; Ma and Peng 2023).

Moreover, another research presented a way of analyzing the movement feasibility in a pile and introducing a theoretical function to study the coefficient of the pressure of the ground (Zhang et al. 2018a; b). The reference articles mainly evaluate pile motion, but none can be used directly without a ground reflection model. Further, solutions renowned as Artificial Neural Networks (ANN) and machine learning with proper ramifications through many types of research, Shanbeh et al. (Shanbeh et al. 2012), Che et al. (Che et al. 2003), Lee and Lee (Lee and Lee 1996), Liu et al. (Liu et al. 1997), and Hanna et al. (Hanna et al. 2004) used ways to predict some of the complex pile load problems. Present methods check parameters of pile settlement as well as pile friction and load capacity. Several studies have chosen the training data to complement and establish the predictive models to test the bearing capacity of piles and the motion. The data collection for the training set should be selected regarding the dynamic series in field investigations to provide modeling with a wide range of training data for an acceptable simulating process. A study (Goh 1996) that operated ANN attempted to form results on settlement characteristics of piles set up in rock. That data set related to the training stage was given through reports on actual piles in the field.

Regression techniques have been operated broadly, such as adaptive regression of multivariate splines, regression of Gaussian trend, and machine regression of minimax probability (Teodorescu and Sherwood 2008; Pal and Deswal 2010; Zhang and Goh 2013; Samui 2019; Benemaran and Esmaeili-Falak 2020; Momeni et al. 2020; Le and Le 2021). Strategies for some geotechnical problems are used via gene expression programming (GEP) (Teodorescu and Sherwood 2008; Alkroosh and Nikraz 2011; Mollahasani et al. 2011; Ozbek et al. 2013; Dindarloo 2015; Masoumi et al. 2020). Moodi et al. (2022) utilized MLP, RBFNN, and SVR models to estimate the compressive strength of concrete columns, and the correlation rates were calculated at 0.971, 0.973, and 0.901, respectively (Moodi et al. 2022). Chen et al. (2022) used 324 data sets with five independent input variables: water, cement, fine aggregate, coarse aggregate, and superplasticizer, to model the compressive strength with the conventional support vector regression (SVR) model. The results showed that SVR’s prediction accuracy and reliability were R2 = 0.973, RMSE = 1.595, MAE = 0.312, and MAPE = 2.469 (Chen et al. 2022). This technique to find a way for the axial capacity of the pile has been examined in many studies (Alkroosh and Nikraz 2011). A novel formulation based on GEP was developed (Mollahasani et al. 2011). Another study was handled using three algorithms containing a support vector machine, multilayer perceptron, and GEP to predict the UCS of rock (Dindarloo 2015). The capability of the support vector machine to simulate the motion of a stratified sedimentary rock mass is clearly acceptable (Alemdag et al. 2016).

The support vector machine method has proposed more accurate and dependable calculation results (Gao and Han 2020; Ma et al. 2021; Acosta et al. 2021, 2023). Also, one study used this technique to evaluate the bearing capacity of piles (Teh et al. 1997). The data inputs contain soil characteristics, footing size, and reinforcement specimens from empirical or in-situ data measured (Soleimanbeigi and Hataf 2006). Regarding primary literature, the parameters comprising UCS of rock, the ratio of pile length to its cross-section diameter, loading masses, and ratio relevant to the depth. of the pile length beneath the soil to rock, and \({N}_{SPT}\) to appraise the displacement of piles (Shahin et al. 2002).

This article aims to better understand the problem of pile settlement socketed in rock using the support vector regression (SVR) technique to design the practical model of pile movement. With this respect, this paper has attempted to join, promote, and investigate a coupled model as SVR machine learning with optimization algorithms. In light of referred purpose, two novel optimization algorithms, Arithmetic Optimization (AOA) and Grasshopper Optimization Algorithm (GOA), were operated by SVR to enhance modeling accuracy by finding optimum magnitudes of coefficients related to the machine learning process. The study novelties use novel algorithms to estimate the displacement of pillars socketed to rock with mentioned optimizers. The collection of experimental data to analyze pile motion and soil attributes was obtained from the Malaysia Transport Project in the Klang Valley Rapid Network (KVMRT) megacity of Kuala Lumpur.

The optimizers mentioned above, joined with the Support Vector Regressions (SVR), are productively examined for many complex issues because of their unique attributes, like being smart and straightforward. Both well-known techniques in the academic world have attracted much attention in the form of machine learning strategies used for many targets like biology, energy transformation analysis, and image processing (Alilou and Yaghmaee 2015; Bendu et al. 2016; Zendehboudi and Tatar 2017). The frameworks proposed as SVR-AOA and SVR-GOA provide the data gathered via penetrating the test and further static loading of on-ground indexes measured. Therefore, the pile loads, the parameters of the column length to the diameter ratio, the UCS parameter of rock, the length of the pillar beneath the soil to that rock ratio, as well as the NSPT parameters were chosen to investigate the pile settlement in KVMRT project (Shahin et al. 2002). Several studies have examined the use of SVR in various engineering fields, such as predicting precipitation rates by combining machine learning techniques and algorithms for optimization (Wu et al. 2015; Xu et al. 2016). That sought to compute the optimal number of neurons in the so-called hidden layer within the process.

The variables required for figuring out the pile movement are specialized as five parameters, including pile length to its crossed diameter, the length under the soil to that of under the rock sheets ratio, bearing capacity as being ultimate, the strength of uniaxial compressive, standard penetration test, and pile subsidence as output and models’ target. The main objective of the present research is to present a new way of coupling models with optimizers to estimate the optimum rate of model parameters for SVR. The present article has attempted to model the PS of pile samples by reproducing subsidence rates coupling with novel AOA and GOA optimization algorithms. Checking the dependability of the proposed model’s demands using the wide range of indexes for this research, R, MAE, OBJ, and RMSE were calculated to evaluate the modeling process. (Fig. 1).

Fig. 1
figure 1

KVMRT project as study area of research

Full size image

2 Methodology

2.1 Preparing Primitive Dataset

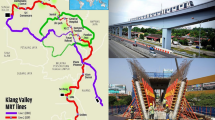
Kuala Lumpur’s most helpful transportation project to reduce traffic jams in Malaysia, called the Klang Valley Rapid Transit System (KVMRT), was the study area of the present research. Attention to the case study showed that thousands of bored piles were needed to support the transport stations in KVMRT. Same picture.1, presents the situation of Malaysia. Several stakes are driven on rocks, namely granite, phyllite, sandstone, and limestone.

Profiles of 96 granite-based piles were reviewed in this study. Within the region, the San Trias granite type was recorded. Subsurface information and materials were performed at the pile locations to verify common geological features. Based on the results, the structures of the underground subsoil are made up of residual rocks. Over the data collected, the depth of the bedrock ranges from 70 cm to more than 1400 m underground. With this respect, the sampling process among piles in the study area and relevant information and drilling log is described as follows:

  • Values of UCS upon the ISRM were recorded at 25 MPa to 68 MPa, respectively, for lowest and highest (Hatheway 2009).

  • Rock bulks were registered as moderately weathered to largely weathered.

  • Between 7.5 to 27 m in the region at ground depth level, subsoil materials were recorded with \({N}_{SPT}\) An index higher than 50 blows per 300 mm.

  • 16.5 MPa was considered highly weathered soil based on the bore log data down to the deep underground. Hard sandy mud, including a minimum and maximum \({N}_{SPT}\) Index of 4 and 167 blows per 300 mm, respectively, composed the predominant soil type.

The first stage in building a predictive model is organizing the best-fit data set with efficient state parameters. Identifying the important factors affecting model output is vital. The tests above were done using a tool of pile analyzing developed via Pile Dynamic Co manufacture. This was further mentioned earlier that pile diameter and length seem to be parameters affecting the estimated rate of pile settlement. Thus, two variables, the ratio of the length of the pile beneath the soil to that of under rock (Ls/Lr) and the ratio of the total length of the pile to the cross-section pile diameter (Lp/D), were chosen for the analysis of the influence on pile geometry. In addition, due to its effect, UCS is selected as the input model for pile settlement prediction. The NSPT, as input, is also taken to exhibit the status of the soil layers. In addition, the load on the pile has a direct forced effect on the subsidence. Therefore, the ultimate pile load capacity (Qu) is also taken as an input. Generally, five variables were selected as inputs to evaluate (PS) pile settlement. Table 1 introduces the target values of PS and inputs of the models accompanied by statistical reports. Figure 2 presents all of the inputs and outputs explained within Fig. 2.

Table 1 The statistical values of the input and output variables
Full size table
Fig. 2
figure 2

The input and target values and histograms of: a \({L}_{p}/D\), b \({L}_{s}/{L}_{r}\), c \({N}_{SPT}\), d \({Q}_{u}\), e UCS, and f PS

Full size image

2.2 Support Vector Regression (SVR)

A support vector machine was introduced for classifying and regression issues (Wang 2005). Support vector regression (SVR) was referred to as the regression sort of Support vector machine, which operates a tolerance area (ε) for regression outlining. The classifying and regression classes of the SVR approach are served for accomplishing a hyper-plane optimization. Support vector regression is owned by the supervised learning techniques to discover answers for regression issues via figuring out the following function (Vapnik 2013).

$$min_{{w,b}} = \frac{1}{2}\left\| w \right\|^{2} + C\sum _{{i = 1}}^{m} \left( {\xi _{i} + \xi _{i}^{*} } \right)$$
$$s.t. \left\{\begin{array}{c}{y}_{i}-\left({w}^{T}{x}_{i}+b\right)\le \varepsilon +{\xi }_{i}\\ \left({w}^{T}{x}_{i}+b\right)-{y}_{i}\le \varepsilon +{\xi }_{i}^{*}\\ {\xi }_{i}, {\xi }_{i}^{*}\ge 0\end{array}\right\}$$
(1)

wherein \(\xi\),\(w\),\(b\),\(\varepsilon\), and \(C\) denote the boundary violation amount, the weight factor, the bias, the deviation rate from the hyperplane, and the regularization parameter in the queue, respectively.

The fitness function contains two parts:

$$\frac{1}{2} {\| w\| }^{2}$$
(2)
$$C {\sum }_{i=1}^{m}({\xi }_{i}+{\xi }_{i}^{*})$$
(3)

Equation (2) was employed to enhance the area among the samples and hyperplane, and Eq. (3) plays the role of a modifier to preserve the interval among samples with the hyperplane via a unit. Over figuring out the function, the appropriate magnitudes of \(w\) and \(b\) are gathered, which as targets, seem a hyperplane. The quadratic objective function is used for this research to get better outcomes (Al-Fugara et al. 2020). The main task of the SVR is to solve the optimal values of determinative parameters: \(\varepsilon\), \(sigma\), and \(C\). For finding them, various optimization algorithms could be employed, in which optimization algorithms, namely Grasshopper Optimization Algorithm and Arithmetic Optimization Algorithm, were coupled with support vector regression to find the parameters of \(\varepsilon\), \(sigma\), and \(C\) at optimal levels. Figure 3 tries to show the internal setting of SVR to model the pile settlement based on training data.

Fig. 3
figure 3

Pseudo code of support vector regression

Full size image

2.3 Grasshopper Optimization Algorithm (GOA)

The Grasshoppers are diagnosed as feeder bugs. It has to be cited that grasshoppers are home animals, inflicting critical harm to grasslands and crops (Simpson et al. 1999). They can be free-standing or swarm in the wild. The grasshopper optimization algorithm, which stems from the herbal treatments of grasshoppers, progressed to discover answers to optimize issues (Saremi et al. 2017). Similar to the formerly suggested techniques of optimization rules in the whale, ant-lion, and swarm rules, the first segment is named the exploration segment, and the second is referred to as the mining segment. Rules of the grasshopper optimization algorithm have been changed through locust treatments. The stated steps are considered to discover the meals. Over digging, the nearby motion of the hunt area is chargeable for the actors (Saremi et al. 2017). The conducts for certain degrees of positive parameters with the technique have been explored for bugs’ distant points. Excretion happens at some stage over time intervals (Mafarja et al. 2019). Thus, if the locust’s distance is beyond the range, it suggests that the insect under attention is getting into the consolation zone. Thus, the algorithm of the cumulative move is brought with Eq. (7), wherein \({x}_{i}\) shows the position of the \({i}^{th}\) bug.

$${x}_{i}={r}_{1}{S}_{i}+{r}_{2}{G}_{i}+{r}_{3}{A}_{i}$$
(4)

where, \({r}_{1}, {r}_{2}\) and \({r}_{3}\) exhibit the accidental magnitudes between 0 to 1. Also, the variables \({S}_{i}\),\({A}_{i}\), and \({G}_{i}\), denote society’s relationship, the population’s attraction, and gravity, respectively (Cao et al. 2020; Armaghani and Asteris 2021).

2.4 Arithmetic Optimization Algorithm (AOA)

The arithmetic optimization algorithm can be considered a candidate-based class with an algebraic concept involving arithmetic operators finding and upgrading the population’s novel location without calculating their derivatives (Abualigah et al. 2021). Arithmetic seems the vital section of present mathematics and looks at one numerical basis algorithm that begins by initializing the candidate solutions created randomly.

$$C=\left[\begin{array}{ccc}{c}_{\mathrm{1,1}}& \cdots & {c}_{1,j}\\ \vdots & \ddots & \vdots \\ {c}_{N,1}& \cdots & {c}_{N,j}\end{array}\right]$$
(5)

The algorithm includes two main parts of exploration and exploitation. The exploration or exploitation search area should be specified and implemented using the math optimizer accelerator function (MOA) to produce the initial candidate.

$$MOA=Min+iter\times (\frac{Max-Min}{{Max}_{iter}})$$
(6)

wherein variables of \(Max\) and \(Min\) represent the maximum and minimum values of MOA. The variable of \(iter\) denotes the current iteration and \({Max}_{iter}\) Shows the maximum iteration number.

The process of exploration search is conducted by highly distributed magnitudes employing multiplication (M) and division (D) arithmetic operators to the exploration search process. Operators D and M make a high dispersion that cannot assist in reaching the target, but using operators of subtraction (S) and addition (A) arithmetic in the exploitation phase causes reaching the optimum target value.

If \({r}_{1}>MOA\), the exploration phase of the algorithm is in process. The situation in the exploration phase is being updated using Eq. (7), which uses M and D operators.

$${c(iter+1)}_{i,j}=\left\{\begin{array}{c}best\left({c}_{j}\right)\div \left(MOP+\varepsilon \right)\times \left(\left(ub-lb\right)\times \mu +lb \right) {r}_{2}>0.5 \\ best\left({c}_{j}\right)\div \left(MOP\right)\times \left(\left(ub-lb\right)\times \mu +lb \right) otherwise\end{array}\right.$$
(7)

wherein, \(best\left({c}_{j}\right)\) denotes the best location, \(ub,\) and \(lb\) are the upper and lower boundary of the area for search.\(\varepsilon\) denotes a small value, and \(\mu\) adjusts the parameter for controlling the search and is set to 0.499 for the model.\(MOP\) is specified as math optimization probability and is calculated with Eq. (8).

$$MOP\left( {iter} \right) = 1 - \frac{{iter^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\alpha $}}}} }}{{Max_{{iter}} ^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 \alpha }}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$\alpha $}}}} }}$$
(8)

In which \(\alpha\) denotes the exploitation accuracy sensitivity over the iterations and is considered 5.

Notably, when \({r}_{1}<MOA\), the exploitation stage happens in this phase when operators of S and A are employed for a deep search of the dense area. This deep searching is modeled with Eq. (9).

$${c(iter+1)}_{i,j}=\left\{\begin{array}{c}best\left({c}_{j}\right)-\left(MOP\right)\times \left(\left(ub-lb\right)\times \mu +lb \right) {r}_{3}>0.5 \\ best\left({c}_{j}\right)+\left(MOP\right)\times \left(\left(ub-lb\right)\times \mu +lb \right) otherwise\end{array}\right.$$
(9)

Figure 4 shows the performance of the AOA optimizer in finding hyperparameters’ rate at an optimal level for SVR.

Fig. 4
figure 4

Pseudo code of archimedes optimization algorithm (AOA)

Full size image

The conceptual relation in a combination of optimizers with Support Vector Regression is presented in Figure 5.

Fig. 5
figure 5

Conceptual relation in a combination of support vector regression with optimizers

Full size image

2.5 Performance Evaluation via Special Criteria

Table 2 represents the indices that survey the hybrid SVR frameworks’ performance.

Table 2 The evaluation indices used for the models’ examination
Full size table

3 Result and Discussion

The hybrid SVR machine learning technique outcomes, SVR-AOA and SVR-GOA, to forecast the rate of pile settlement were produced, shown in the present part. The complexity and cost of modeling accompanied by increasing appraising accuracy are considered, and these factors must be smoothed via optimizers utilized in this research. A MATLAB environment implemented the simulations. The scattered plot of the measured pile settlement ranges within the KVMRT project has been shown in Fig. 6, wherein 70 and 30 percent of measured data have been considered for, alternatively, training and testing phases. The suitable magnitudes of \(\varepsilon\), \(sigma\), and \(C\) of SVR for the data set lead to maximum determination coefficient and RMSE at minimum for SVR-AOA have been calculated as 0.6 and 0.554, respectively. Moreover, these values for SVR-GOA were 0.65 and 0.597, alternatively.

Fig. 6
figure 6

In-situ pile settlement data within the KVMRT project

Full size image

The SVR-AOA modeling to predict the subsidence rate of each pile was done, and the results are shown in Fig. 7. Overall, the prediction process has been done in a desirable way defined by R, and RMSE acquired as 0.99 and 0.55 mm. Further, the best trend line shows the appropriate correctness of modeling placed adjacent to the dashed bisector line with the overestimation for settlement rates below 12 mm and underestimation for higher than this magnitude. The slope of the best-fit trend line with around 0.9 also implies a suitable simulation with the model coupled with the AOA optimizer.

Fig. 7
figure 7

The SVR-AOA plot of measurement and predicted settlement rates

Full size image

Similar to the SVR-AOA model, SVR-GOA results are brought up via Fig. 8. At first look, the prediction process has been done in a desirable way that is definite by R and RMSE calculated as 0.99 and 0.59 mm. Further, the best trend line shows the appropriate correctness of modeling placed adjacent to the dashed bisector line with the overestimation for settlement rates below 12 mm and underestimation for higher than this magnitude. The slope of the best-fit trend line with around 0.9 also implies suitable simulation with the model coupled with GOA optimizer.

Fig.8
figure 8

The SVR-GOA plot of measurement and predicted settlement rates

Full size image

As depicted in Figs. 7 and 8, by comparing both of them, SVR-AOA demonstrated higher appropriate magnitudes for RMSE and R than SVR-GOA of 0.10% and 7.66%, alternatively. AOA could fulfil well for optimizing modeling performance because the points scattered around the best-fit line seem adjacent compared with those in GOA. Especially the piles involving large numbers have been modeled close to the actual measurement with minimal error. This can be accounted for by applying 70% of the data to train in the neural network.

In continuous, Table 3 shows modeling functionality for every hybrid framework and the usage of the VAF, R, MAE, OBJ, and RMSE indices (within Table 2). Each level of the train and test stage presents the same result. In the train section, the optimization set of AOA has fulfilled higher with the aid of using evaluating indices as acceptable compared to the consequences of GOA. The index of MAE has been given the maximum discrepancy with approximately 7.10% for SVR-AOA. However, the results of VAF and R-value indexes have not attracted interest with moderate distinction by the same performance. Identically, all indices of R, OBJ, MAE, VAF, and RMSE associated with the test stage for SVR-AOA had been located an acceptable degree in assessment with SVR-GOA with the aid of using the RMSE as acquired 7.62%. Moreover, the OBJ index, including the R, RMSE, and MAE in each level of train and test, offers a higher accuracy of modeling process for SVR-AOA that serves with 0.54 mm mistake in modeling pile settlement.

Table 3 Evaluation of models’ performance
Full size table

For a clear sight of the correctness of modeling, Fig. 9 attempts to show modeling errors for each pile rather than measured target values. They use Fig. 9 in cases where the measurements and the model line do not coincide. Many of the modeling parts are correctly done, as seen in both sections of the test and train phases. This chart has shown the extent to which the deviations between the models and the actual measurements are significant.

Fig. 9
figure 9

Modeled PS and measured data for each pile in a SVR-AOA and b SVR-GOA

Full size image

The SVR-AOA (a) model was modeled closest to the in-situ measurements in the diagram. However, the gap between modeling and measurement for piles nine and ten becomes larger than for other parts. Similarly, for SVR-GOA (b), this story runs indeed that bypassing the dashed line as the border of test and train phases, modeling accuracy has been enhanced to a better rate.

Figure 10 shows the best sight for modeling performance analysis. The scheme in question refers to the mistakes in achieving the target for the piles modeled in terms of measured values of positive (overestimated) and negative (underestimated). Thus, according to Fig. 10, diagram (a), SVR-AOA shows that the error in the simulation of pile motion during the training period is close to a maximum of 14%. However, during the testing phase, the error rate increased slightly but was too close to a 14% error line. Moreover, SVR-GOA (b) has completed its defining task of modeling pile settlement with a larger error than SVR-AOA. Actually, for the training period, the error of SVR-GOA exceeds 14%. This border has exceeded the maximum error of the previous step in the test step.

Fig. 10
figure 10

The modeling error in a SVR-AOA and b SVR-GOA

Full size image

Next, the distribution of errors and the normal distribution of modeling errors for both hybrid models will be exhibited. Figure 11 shows the error distribution in frequency and the standard error distribution curve.

Fig. 11
figure 11

Error distribution in the SVR-AOA model

Full size image

Concentrating errors not around the center of zero magnitudes on the horizontal error axis has led to the flattened shape of the standard distribution error curve. Maximum frequency for the error as the high histogram is found for around 25 with about -0.05. Also, Fig. 12 shows a similar exhibition for the SVR-GOA framework. For this model, identically, the standard curve has been shaped flattened so that this matter stems from error concentration, not in the center of zero point. Compared to the SVR-AOA, the tall histogram of error around -0.05 has 26 frequencies, the same pattern in the modeling process.

Fig. 12
figure 12

Error distribution in the SVR-AOA model

Full size image

Although SVR via the AOA performed better in modeling the pile settlement with appropriate results, the SVR-GOA has had the same pattern error distribution. Based on the results, Arithmetic Optimization Algorithm was more mighty than Grasshopper Optimization Algorithm with the sign of accurate calculation of SVR parameters. The differences in correlation and error rates for the two hybrid models are derived from various AOA and GOA internal settings. However, both optimizers regulated the SVR model to generate PS rates with an average correlation of 0.99.

4 Conclusion

The goal of the current study is to simulate the pile settlement using the Support Vector Regression (SVR) neural network, in which two optimization algorithms, as Arithmetic Optimization Algorithm (AOA) and Grasshopper Optimization Algorithm (GOA), have been operated to predict the better regression to calculate the pile settlement rates that would reduce the cost and complexity of network computations. For using coupled frameworks of SVR-AOA and SVR-GOA, the pile tests, their measurements, and earth properties were obtained for the Klang Valley Mass Rapid Transit (KVMRT) transportation project in Kuala lumper city.

Each framework developed had the desirable capability to estimate the dependent pile settlement variable, where the R-value of the training step was obtained on average 0.993 and 0.996 in the testing step for both SVR-AOA and SVR-GOA. Alternatively, that shows a 0.3 percent difference.

Overall, SVR-AOA could be given the allowable results via the indices for evaluating each method. SVR-AOA framework, statistically, with the appropriate numbers of R, RMSE, MAE, and VAF at 0.994, 0.55, 0.525, and 99.806 had suitable performance compared to SVR-GOA with mentioned criteria of 0.993, 0.592, 0.561, and 99.734, respectively, in which the higher difference is for RMSE by 7.66%. In the training step, including 70 percent of data, SVR-AOA could get 0.993 for R 0.11% is higher than SVR-GOA modeling results. Also, RMSE, MAE, and VAF of SVR-AOA in the training step were calculated at 0.548, 0.522, and 99.789, which were better rates by 7.68%, 7.10%, respectively, and 0.06% improvement. The comprehensive OBJ index includes the R, RMSE, and MAE indexes of errors and correlation indices. SVR-GOA and SVR-AOA obtained values of 0.541 and 0.586 mm, respectively, with a difference of 8.26%. Generally, hybrid models and artificial intelligent-based models can increase the accuracy of estimating pile settlement to substitute actual practical experiments and reduce the time and cost.