Stress Analytical Solution for Shallow Buried Lined Circular Tunnel Under the Deformation of Surrounding Rock Inner Edge

Abstract

In this article, an analytical solution is presented for an elastic shallow buried lined tunnel, which consider a certain surrounding rock deformation at the inner boundary. Concrete lining and the surrounding rock was assumed as linearly elastic materials. The solution uses Muskhelishvili complex potential functions combined with conformal mapping method to determine stress components within concrete lining and the surrounding rock mass. The coefficient of Laurent series expansion of the stress functions is determined by a combination of analytical and numerical computations. As an example, the case of a uniform radial displacement of surrounding rock inner edge is considered in some detail. The solution was verified by FEM through an example, very good agreement was demonstrated between analytical solution and numerical solution. Through numerical examples, the effect of elasticity modular and the ratio of the diameter to buried depth on the stresses component were assessed.

1 Introduction

With the development of the urban underground traffic system and utilization of underground space, shallow tunnels are favored in engineering projects in order to low operational costs, and they inevitably lie near the ground surface. The excavation of the shallow tunnels not only causes settlement of ground surface but also leads to displacement and stress concentration at around rock hole. It is essential for engineers to control settlement at ground surface by calculating the stress of surrounding rock, and given the strength required for lining (Bobet 2003; Huang and Zhang 2016).

For elastic plane problems of multiplying connected region, it is difficult to get the analytical solution by general methods. One of the useful approaches implemented in two dimensional elastic theories is Muskhelishvili’s (1966) (Sokolnikoff and Specht 1956) complex variable method. The method investigated based on complex potential functions and conformal mapping method, and stress components and deformations can be determined within the materials. Based on this method, Exadaktylos and Stavropoulou (2002) presented a closed-form solution to stress and displacement of semicircular tunnels. Fu et al. (2015) used complex variables method presented the solutions for a buoyant tunnel in an elastic half-plane, which considered the resultant buoyancy forces acting on the tunnel by assuming two additional logarithmic terms with the potentials. Based on previous studies, Verruijt (1997, 1998) (Verruijt and Booker 1998; Verruijt and Strack 2008; Kargar et al. 2015) has achieved a lot of research results, and proposed a similar method for stress and displacement around a circular tunnel in an elastic half-plane. The deformations of shallow tunnels have been investigated under different boundary conditions. Recently, some works on the analytical solution of tunnel via complex variable method have been reported (Zhou and Cao 2017; Wang et al. 2018). Include the problem of a half plane with a circular cavity loaded by a uniform radial stress, and the problem in which a uniform radial displacement is imposed on the cavity boundary. Verruijt (2015) investigated on a complex variable solution for a deforming circular tunnel in an elastic half plane. Lu at al. (2016) given the Solution of a circular cavity in an elastic half plane under gravity and arbitrary lateral stress. However, the complex variable solution for shallow buried lined circular tunnel under the deformation of surrounding rock inner edge has been rarely considered in the above-mentioned literature.

The aim at this paper is to give a plane-strain elastic solution to shallow buried lined circular tunnel, under the deformation of surrounding rock inner edge. The solution employs complex potential functions and conformal mapping method, and is verified by a series of numerical simulations. Through numerical examples, the solution is adopted to study the elasticity modular influences on the stress distribution around a shallow.

2 General Consideration

2.1 Description of the Problem

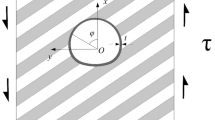
The problem deals with an elastic shallow buried lined circular tunnel in an elastic homogeneous material. The upper boundary of the half plane and lining inner boundary are considered to be free of stress, and the boundaries of the surrounding rock inner edge are assigned the displacement. The tunnel radius of lining and Surrounding rock is denoted by R and r, respectively. The tunnel axis is at a depth h from ground surface, and surrounding rock inner edge is at a depth d from ground surface (Fig. 1). Lining and Surrounding rock is assumed as isotropic and homogenous materials. It is supposed that liner is installed without any delay after tunnel excavation,and due to excavation produced deformation of the inner boundary is W. The infinite plate on complex plane is divided into two isotropic homogenous regions of S₁ and S₂ bounded by contours L₁ and L₂. The regions S₁ and S₂ referred to rock mass and concrete lining with Young modulus E₁, E₂ and Poisson ratio v₁, v₂, respectively. Assuming that the tunnel is infinitely long, the plane strain problem was analyzed. The shallow lining tunnel model established is shown in Fig. 1.

Fig. 1

The model of Lined tunnel at shallow depth

2.2 Conformal Mapping

Through two mapping functions, the region in the z-plane can be mapped conformally onto two circular rings (region γ₁ and γ₂) in the ζ-plane. Let w₁(ζ) be a conformal mapping function which maps boundaries L1 and the upper boundary of the half plane for two concentric circles (Fig. 2), bounded by the circles |ζ| = 1 and |ζ| = α. The conformal transformation is

Fig. 2

The mapping functions of surrounding rock

$$z = w_{1} \left( \zeta \right) = - ia\frac{1 + \zeta }{1 - \zeta }$$

(1)

where

$$a = h\frac{{1 - \alpha^{2} }}{{1 + \alpha^{2} }},\quad \alpha = \frac{1}{r}\left( {h - \sqrt {h^{2} - r^{2} } } \right)$$

(2)

Let w₂(η) be a conformal mapping function which maps boundaries L1 and L2 into two concentric circles (Fig. 3), bounded by the circles |η| = 1 and |η| = R₀, R₀ = R/r. The conformal transformation is

Fig. 3

The mapping functions of lining

$$z = w_{2} \left( \eta \right) = r\eta$$

(3)

2.3 Basic Equation

Two potential functions corresponding to the surrounding rock domain can be expressed by Laurent series (Sokolnikoff and Specht 1956)

$$\varphi_{1} \left( \zeta \right) = \sum\limits_{k = 0}^{\infty } {a_{k} } \zeta^{k} + \sum\limits_{k = 1}^{\infty } {b_{k} } \zeta^{ - k} \quad \psi_{1} \left( \zeta \right) = \sum\limits_{k = 0}^{\infty } {c_{k} \zeta^{k} } + \sum\limits_{k = 1}^{\infty } {d_{k} \zeta^{ - k} }$$

(4)

In the same way, two analytic functions corresponding to the lining can be expressed by Laurent series (Sokolnikoff and Specht 1956)

$$\varphi_{2} \left( \eta \right) = \sum\limits_{k = 0}^{\infty } {e_{k} } \eta^{k} + \sum\limits_{k = 1}^{\infty } {f_{k} } \eta^{ - k} \quad \psi_{2} \left( \zeta \right) = \sum\limits_{k = 0}^{\infty } {g_{k} \eta^{k} } + \sum\limits_{k = 1}^{\infty } {h_{k} \eta^{ - k} }$$

(5)

Stress components are determined based on these complex potential functions as follows:

$$\begin{aligned} & \sigma_{\rho j} + \sigma_{\theta j} = 2\left[ {\frac{{\varphi_{j}^{\prime } \left( t \right)}}{{\omega_{j}^{\prime } \left( t \right)}} + \frac{{\overline{{\varphi_{j}^{\prime } \left( t \right)}} }}{{\overline{{\omega_{j}^{\prime } \left( t \right)}} }}} \right] \\ & \sigma_{\theta j} - \sigma_{\rho j} + 2i\tau_{\rho \theta j} = \frac{{2e^{2i\theta } }}{{\omega_{j}^{\prime } \left( t \right)}}\left[ {\overline{{\omega_{j} \left( t \right)}} \frac{{\varphi_{j}^{\prime \prime } \left( t \right)\omega_{j}^{\prime } \left( t \right) - \varphi_{j}^{\prime } \left( t \right)\omega_{j}^{\prime \prime } \left( t \right)}}{{\left[ {\omega_{j}^{\prime } \left( t \right)} \right]^{2} }} + \psi_{j}^{\prime } \left( t \right)} \right],\;j = 1,2 \ldots \\ \end{aligned}$$

(6)

where $\sigma_{\rho j}$, $\sigma_{\theta j}$ and $\tau_{\rho \theta j}$ are radial, circumferential and tangential stress components, respectively. when j = 1, $t = \zeta$; j  = 2,$t = \eta$, represent surrounding rock and lining, respectively.

2.4 Boundary Condition

Stress functions $\varphi_{1}$, $\psi_{1}$ and $\varphi_{2}$, $\psi_{2}$ should satisfy boundary conditions. Under the mapping functions of surrounding rock, the upper boundary of the half plane are considered to be free of stress, and the deformation of the inner boundary is $W_{1} \left( \zeta \right)$, yields

$$\varphi_{1} \left( \zeta \right) + \frac{{\omega_{1} \left( \zeta \right)}}{{\overline{{\omega^{\prime}_{1} \left( \zeta \right)}} }}\overline{{\varphi_{1}^{\prime } \left( \zeta \right)}} + \overline{{\psi_{1} \left( \zeta \right)}} = 0$$

(7)

$$K_{1} \varphi_{1} \left( \zeta \right) - \frac{{\omega_{1} \left( \zeta \right)}}{{\overline{{\omega_{1}^{\prime } \left( \zeta \right)}} }}\overline{{\varphi_{1}^{\prime } \left( \zeta \right)}} - \overline{{\psi_{1} \left( \zeta \right)}} = 2G_{1} \left( {u_{x} + iu_{y} } \right) = W_{1} \left( \zeta \right)$$

(8)

where $u_{x}$ and $u_{y}$ are x and y direction displacement components. $G_{i} = \frac{{E_{i} }}{{2\left( {1 + \nu_{i} } \right)}}$, due to the analysis is a plane strain problem, so $K_{i} = 3 - 4\nu_{i}$. Under the mapping functions of lining, the inner boundary of the half plane is considered to be free of stress, and the deformation of the outer boundary is $W_{2} \left( \eta \right)$, yields

$$K_{2} \varphi_{2} \left( \eta \right) - \frac{{\omega_{2} \left( \eta \right)}}{{\overline{{\omega_{2}^{\prime } \left( \eta \right)}} }}\overline{{\varphi_{2}^{\prime } \left( \eta \right)}} - \overline{{\psi_{2} \left( \eta \right)}} = 2G_{2} \left( {u_{x} + iu_{y} } \right) = W_{2} \left( \eta \right)$$

(9)

$$\varphi_{2} \left( \eta \right) + \frac{{\omega_{2} \left( \eta \right)}}{{\overline{{\omega_{2}^{\prime } \left( \eta \right)}} }}\overline{{\varphi_{2}^{\prime } \left( \eta \right)}} + \overline{{\psi_{2} \left( \eta \right)}} = 0$$

(10)

3 Solution

3.1 The Solution for Surrounding Rock

Form (1), the following expressions can be obtained

$$\frac{\omega \left( \zeta \right)}{{\overline{{\omega^{\prime } \left( \zeta \right)}} }} = - \frac{{\left( {1 + \zeta } \right)\left( {1 - \bar{\zeta }} \right)^{2} }}{{2\left( {1 - \zeta } \right)}}$$

(11)

Along the outer boundary |ζ| = 1, the radiusρ = 1, so that $\zeta = \rho \sigma = \sigma = \exp (i\theta )$, $\bar{\zeta } = \sigma^{ - 1}$. Then Substituting (11) into (7), yields

$$\varphi_{1} \left( \sigma \right) + \frac{1}{2}\left( {1 - \sigma^{ - 2} } \right)\overline{{\varphi_{1}^{\prime } \left( \sigma \right)}} + \psi_{1} \left( \sigma \right) = 0$$

(12)

Substituting (4) into (12), by setting the coefficients of all powers of σ equal to zero. The following expressions can be obtained

$$c_{0} = - \bar{a}_{0} - \frac{1}{2}a_{1} - \frac{1}{2}b_{1}$$

(13a)

$$c_{k} = - \bar{b}_{k} + \frac{1}{2}\left( {k - 1} \right)a_{k - 1} - \frac{1}{2}\left( {k + 1} \right)a_{k + 1} \quad k = 1,\,2,\,3, \ldots$$

(13b)

$$d_{k} = - \bar{a}_{k} + \frac{1}{2}\left( {k - 1} \right)b_{k - 1} - \frac{1}{2}\left( {k + 1} \right)b_{k + 1} \quad k = 1,\,2,\,3, \ldots$$

(13c)

Along the inner boundary of surrounding rock |ζ| = $\alpha$, the radius ρ = $\alpha$, so that $\zeta = \rho \sigma = \alpha \sigma = \alpha \exp (i\theta )$, $\bar{\zeta } = \alpha \sigma^{ - 1}$. Then Substituting (11) into (8), yields

$$K_{1} \varphi_{1} \left( {\alpha \sigma } \right) - \frac{{ - \alpha \sigma - \left( {1 - 2\alpha^{2} } \right) + R_{0} \left( {2 - \alpha^{2} } \right)\sigma^{ - 1} - \alpha^{2} \sigma^{ - 2} }}{{2\left( {1 - \alpha \sigma } \right)}}\overline{{\varphi_{1}^{\prime } \left( {\alpha \sigma } \right)}} - \overline{{\psi_{1} \left( {\alpha \sigma } \right)}} = W_{1} \left( \zeta \right)$$

(14)

In order to the convenience of computation, for (14) multiplied by $\left( {1 - \alpha \sigma } \right)$ on both sides, yields

$$\left( {1 - \alpha \sigma } \right)\left[ {K_{1} \varphi_{1} \left( {\alpha \sigma } \right) - \frac{{ - \alpha \sigma - \left( {1 - 2\alpha^{2} } \right) + R_{0} \left( {2 - \alpha^{2} } \right)\sigma^{ - 1} - \alpha^{2} \sigma^{ - 2} }}{{2\left( {1 - \alpha \sigma } \right)}}\overline{{\varphi_{1}^{\prime } \left( {\alpha \sigma } \right)}} - \overline{{\psi_{1} \left( {\alpha \sigma } \right)}} } \right] = W^{\prime }_{1} \left( \zeta \right)$$

(15)

where

$${\text{W}}_{k}^{\prime } \left( \zeta \right) = {\text{W}}^{\prime }_{1} \left( {\alpha \sigma } \right) = \left( {1 - \alpha \sigma } \right)W_{1} \left( {\alpha \sigma } \right) = \sum\limits_{k = - \infty }^{k = \infty } {A_{k} } \sigma^{k}$$

(16)

Substitution of (4), (14) and (16) into (15) gives, In the same way, by setting the coefficients of all powers of σ equal to zero. The following expressions can be obtained

$$\left( {1 - \alpha^{2} } \right)\left( {k + 1} \right)\bar{a}_{k + 1} - \left( {\alpha^{2} + K_{1} \alpha^{ - 2k} } \right)b_{k + 1} = \left( {1 - \alpha^{2} } \right)K_{1} \bar{a}_{k} - \left( {1 + K_{1} \alpha^{ - 2k} } \right)b_{k} + A_{ - k} \alpha^{ - k} \quad k = 1,2,3 \ldots$$

(17)

$$\left( {1 + K_{1} \alpha^{2k + 2} } \right)\bar{a}_{k + 1} - \left( {1 - \alpha^{2} } \right)\left( {k + 1} \right)b_{k + 1} = \alpha^{2} \left( {1 + K_{1} \alpha^{2k} } \right)\bar{a}_{k} + \left( {1 - \alpha^{2} } \right)kb_{k} + \bar{A}_{k + 1} \alpha^{k + 1} \quad k = 1,2,3 \ldots$$

(18)

From these two Eqs. (20) and (21), the coefficients can be determined recursively. Thus, all the coefficients of the Laurent series for surrounding rock have been determined, except for a₀. As the system of equations is linear, the correct value of a₀ can be determined by first assuming a₀ = 0, then calculating the limiting value of a_k for k → ∞, repeating this calculation for an initial value a₀ = 1, and then determining the correct value of a₀ by linear interpolation such that a_k → 0 for k → ∞. It seems that this coefficient remains undetermined by the boundary conditions specified above. This part can refer to a complex variable solution for a deforming circular tunnel in an elastic half-plane by Verruijt (1997) If the boundary conditions are known, through (6) can give the stress component of surrounding rock.

3.2 The Solution for Lining

Along the outer boundary of lining |η| = 1, the radius ρ = 1, so that $\zeta = \rho \sigma = \sigma = \exp (i\theta )$, $\bar{\zeta } = \sigma^{ - 1}$, according to (3) can gives

$$w_{2} \left( \sigma \right) = r\sigma ,\quad w_{2}^{\prime } \left( \sigma \right) = r,\quad \overline{{w_{2}^{\prime } \left( \sigma \right)}} = r,\quad \frac{{w_{2} \left( \sigma \right)}}{{\overline{{w_{2}^{\prime } \left( \sigma \right)}} }} = \sigma$$

(19)

Through the mapping function z = w₂(η), the outer boundary displacement condition of the lining is

$${\text{W}}_{2} \left( \eta \right) = {\text{W}}_{2} \left( \sigma \right) = \sum\limits_{k = - \infty }^{k = \infty } {B_{k} } \sigma^{k}$$

(20)

Substitution of (19) and (20) into (9) gives

$$\begin{aligned} & K_{2} e_{0} + K_{2} e_{1} \sigma + K_{2} e_{2} \sigma^{2} + \sum\limits_{k = 3}^{\infty } {K_{2} e_{k} } \sigma^{k} + \sum\limits_{k = 1}^{\infty } {K_{2} f_{k} } \sigma^{ - k} - \bar{e}_{1} \sigma - 2\bar{e}_{2} - \sum\limits_{k = 1}^{\infty } {\left( {k + 2} \right)\bar{e}_{k + 2} } \sigma^{ - k} \\ & \quad + \sum\limits_{k = 3}^{\infty } {\left( {k - 2} \right)\bar{f}_{k - 2} } \sigma^{k} - \bar{g}_{0} - \sum\limits_{k = 1}^{\infty } {\bar{g}_{k} \sigma^{ - k} } - \bar{h}_{1} \sigma - \bar{h}_{2} \sigma^{2} - \sum\limits_{k = 1}^{\infty } {\bar{h}_{k} \sigma^{k} } = W_{2} \left( \sigma \right) \\ \end{aligned}$$

(21)

According to (21), by setting the coefficients of all powers of σ equal to zero. The following expressions can be obtained

$$g_{0} = K_{2} \bar{e}_{0} - 2e_{2} - \bar{B}_{0}$$

(22a)

$$h_{1} = K_{2} \bar{e}_{1} - e_{1} - \bar{B}_{1}$$

(22b)

$$h_{2} = K_{2} \bar{e}_{2} - \bar{B}_{2}$$

(22c)

$$h_{k} = K_{2} \bar{e}_{k} + \left( {k - 2} \right)f_{k - 2} - \bar{B}_{k} \quad k = 3,\,4,\,5, \ldots$$

(22d)

$$g_{k} = K_{2} \bar{f}_{k} - \left( {k + 2} \right)e_{k + 2} - \bar{B}_{ - k} \quad k = 1,\,2,\,3, \ldots$$

(22e)

Along the inner boundary of lining rock |η| = R₀, the radiusρ = R₀, so that $\zeta = \rho \sigma = R_{0} \sigma = R_{0} \exp (i\theta )$, $\bar{\zeta } = R_{0} \sigma^{ - 1}$. According to (3) can gives

$$w_{2} \left( {R_{0} \sigma } \right) = R\sigma ,\quad w_{2}^{\prime } \left( {R_{0} \sigma } \right) = R,\quad \overline{{w_{2}^{\prime } \left( {R_{0} \sigma } \right)}} = R,\quad \frac{{w_{2} \left( \sigma \right)}}{{\overline{{w_{2}^{\prime } \left( \sigma \right)}} }} = \sigma$$

(23)

Substituting (22) and (23) into (10), yields

$$\left( {K_{2} + 1} \right)\bar{e}_{0} + 2e_{2} \left( {R_{0}^{2} - 1} \right) = \bar{B}_{0}$$

(24a)

$$\left( {K_{2} + R_{0}^{2} } \right)\bar{e}_{1} + \left( {R_{0}^{2} - 1} \right)e_{1} = \bar{B}_{1}$$

(24b)

$$\left( {K_{2} + R_{0}^{4} } \right)\bar{e}_{2} = \bar{B}_{2}$$

(24c)

$$k\left( {1 - R_{0}^{2} } \right)\bar{f}_{k} + \left( {K_{2} + R_{0}^{2k + 4} } \right)e_{k + 2} = B_{k + 2} \quad k = 3,\,4,\,5, \ldots$$

(24d)

$$\left( {K_{2} + R_{0}^{ - 2k} } \right)\bar{f}_{k} + \left( {k + 2} \right)\left( {R_{0}^{2} - 1} \right)e_{k + 2} = \bar{B}_{ - k} \quad k = 1,\,2,\,3, \ldots$$

(24e)

According to (24) can give all the coefficients of the Laurent series for $\varphi_{2}$, Substituting (24) into (22) can give all the coefficients of the Laurent series for $\psi_{2}$. It seems that this coefficient remains undetermined by the boundary conditions specified above. If $\varphi_{2}$ and $\psi_{2}$ are known, by (6) gives the stress component of lining.

4 Solution of Uniform Radial Displacement

4.1 The Solution of Uniform Radial Displacement for Surrounding Rock

Considering a uniform radial deformation of magnitude u₀ at the inner boundary of surrounding rock. If the direction of displacement u₀ is considered in inward the displacement components at the inner boundary of surrounding rock face are

$$u_{x1} = - u_{0} \frac{x}{r},\quad u_{y1} = - u_{0} \frac{y + h}{r}$$

(25)

where $u_{x1}$ and $u_{y1}$ are the x and y displacements of surrounding rock face. According to (25), yields

$$2G_{1} \left( {u_{x1} + iu_{y1} } \right) = - 2G_{1} u_{0} \frac{z + ih}{r}$$

(26)

Through the mapping function z = w₁(ζ), along the inner boundary of surrounding rock ζ = $\alpha \sigma$, we can be obtained.

$$2G_{1} \left( {u_{x1} + iu_{y1} } \right) = - 2iG_{1} u_{0} \frac{\alpha - \sigma }{1 - \alpha \sigma }$$

(27)

Substituting (27) into (17), yields

$${\text{W}}_{1}^{\prime } \left( \zeta \right) = - 2iG_{1} u_{0} \left( {\alpha - \sigma } \right)$$

(28)

Form (28), the boundary function only contains two terms of order $\sigma^{0}$ and $\sigma^{1}$. The only two non-zero coefficients in the Fourier expansion (16) are

$$A_{0} = - 2iG_{1} u_{0} \alpha ,\quad A_{1} = 2iG_{1} u_{0}$$

(29)

The coefficients a_k and b_k can be determined from Eqs. (17) and (18). With (29) this gives

$$a_{1} = \frac{{2iG_{1} u_{0} \alpha }}{{1 + \left( {K_{0} - 1} \right)\alpha^{2} + \alpha^{4} }} + a_{0}$$

(30)

$$b_{1} = \frac{{2iG_{1} u_{0} \alpha^{3} }}{{1 + \left( {K_{0} - 1} \right)\alpha^{2} + \alpha^{4} }} + a_{0}$$

(31)

For Stress functions $\varphi_{1}$ and $\psi_{1}$, where it has been assumed, on the basis of a consideration of symmetry, that all the coefficients are purely imaginary. Now that the coefficients a₁ and b₁ have been determined, the other coefficients can be determined successively, using Eqs. (17) and (18). The value of the very Þrst constant a₀ can be determined from the condition that the coefficients tend towards zero if k → ∞.

4.2 The Solution of Uniform Radial Displacement for Lining

On the boundary between the surrounding rock and the lining, $u_{x1} + iu_{y1} = u_{x2} + iu_{y2}$. Through the mapping function z = w₂(ζ), along the outer boundary of ling ζ = $\sigma$,we can be obtained.

$$2G_{2} \left( {u_{x2} + iu_{y2} } \right) = - 2G_{2} u_{0} \left( {\sigma + i\frac{h}{r}} \right)$$

(32)

According to (32), yields

$$W_{2} \left( \sigma \right) = - 2G_{2} u_{0} \left( {\sigma + i\frac{h}{r}} \right)$$

(33)

Form (33), the boundary function only contains two terms of order $\sigma^{0}$ and $\sigma^{1}$. The only two non-zero coefficients in the Fourier expansion (16) are

$$B_{0} = - 2iG_{2} u_{0} \frac{h}{r},\quad B_{1} = - 2G_{2} u_{0}$$

(34)

The coefficients e_k and f_k can be determined from Eq. (24) gives

$$e_{0} = - \frac{{2iG_{1} u_{0} h}}{{r\left( {K_{2} + 1} \right)}},\quad e_{1} = - \frac{{2G_{1} u_{0} }}{{K_{2} + 2R_{0}^{2} - 1}},\quad e_{2} = \cdots = e_{k} = 0$$

(35a)

$$f_{1} = f_{2} = \cdots = f_{k} = 0$$

(35b)

Substituting (35) into (24), yields

$$g_{0} = - \frac{{2iG_{2} u_{0} h}}{{r\left( {K_{2} + 1} \right)}},\quad g_{1} = \cdots = g_{k} = 0$$

(36a)

$$h_{1} = \frac{{4G_{2} u_{0} R_{0}^{2} }}{{K_{2} + 2R_{0}^{2} - 1}},\quad h_{2} = \cdots = h_{k} = 0$$

(36b)

Substituting (36) into (5), yields

$$\varphi_{2} \left( \eta \right) = - \frac{{2iG_{2} u_{0} h}}{{r\left( {K_{2} + 1} \right)}} - \frac{{2G_{2} u_{0} }}{{K_{2} + 2R_{0}^{2} - 1}}\eta \quad \psi_{2} \left( \eta \right) = - \frac{{2i\mu_{2} u_{0} h}}{{r\left( {K_{2} + 1} \right)}} + \frac{{4\mu_{2} u_{0} R_{0}^{2} }}{{K_{2} + 2R_{0}^{2} - 1}}\frac{1}{\eta }$$

(37)

Substituting (37) into (6), yields

$$\sigma_{\rho 2} = \frac{1}{{r\rho^{2} }}\frac{{4G_{2} u_{0} R_{0}^{2} }}{{K_{2} + 2R_{0}^{2} - 1}} - \frac{1}{r}\frac{{4G_{2} u_{0} }}{{K_{2} + 2R_{0}^{2} - 1}}$$

(38a)

$$\sigma_{\theta 2} = - \frac{1}{{r\rho^{2} }}\frac{{4G_{2} u_{0} R_{0}^{2} }}{{K_{2} + 2R_{0}^{2} - 1}} - \frac{1}{r}\frac{{4G_{2} u_{0} }}{{K_{2} + 2R_{0}^{2} - 1}}$$

(38b)

$$\tau_{\rho \theta 2} = 0$$

(38c)

5 Discussion

5.1 Comparison of the Analytical Solution and ABAQUS Finite Element Code

In order to make a comparison, surrounding rock inner edge is at a depth d = 2.5 m from ground surface, the tunnel axis is at a depth h = 5 m depth from ground surface, the tunnel radius of lining and Surrounding rock are denoted by R = D/2 = 2.5 m and r = 2.8 m, respectively. The radial deformation u₀ = 0.05 m, input data are represented in Table 1. From equations (14), (20) and (21), all the coefficients of the Laurent series for surrounding rock have been determined. The coefficients of the Laurent series are presented in Table 2.

Table 1 Input date

Table 2 Coefficients of Laurent series

In this section, compressive stress is assumed a positive quantity for convenience. Figure 4 shows ABAQUS grid for tunnel cross-section. The magnitude of radial stress around tunnel is presented in Fig. 5. Figure 6 shows magnitude of circumferential stress along internal lining inner predicted by the analytical solution and ABAQUS finite element software. There’s a difference between the analytical solution and the ABAQUS solution, but the difference is very small, and it’s negligible.

Fig. 4

Finite element grid mesh

Fig. 5

The circumferential stress around tunnel in cylindrical coordinate system

Fig. 6

Circumferential stress along internal lining inner predicted by the analytical solution and ABAQUS

5.2 Parameter Analysis

In order to study the effect of elastic modulus E₁ and the ratio of the diameter to buried depth on the stress component, the stress around the tunnel is analyzed in this paper. Under different values of elastic modulus E₁, the radical stress component and the tangential stresses component of rock with E₂ = 45GPa is given in Figs. 7 and 8. With the increase of E₁, the radial stresses and tangential stress decrease from the edge of the tunnel to the ground surface. This is due to the stress concentration mainly occurs near the hole, and the less obvious the stress concentration with the increase of distance from the edge of the tunnel. In addition, with the increase of E₁, the radial stress and tangential stress is negative and the magnitude increase at the ground surface near.

Fig. 7

Radial stress with different values of elastic modulus at θ = 90°

Fig. 8

Tangential stress with different values of elastic modulus at θ = 90°

Under different values of elastic modulus E₁, the circumferential stress component of rock with E₂ = 45GPa is given in Fig. 9. We can find that the circumferential stress component of rock is negative, and the magnitude decrease from the edge of the tunnel to the ground surface. This is due to the ring is compressed under radial deformation, and the stress concentration gradually dissipates.

Fig. 9

Circumferential stress with different values of elastic modulus at θ = 90°

Under different values of the ratio of the diameter to buried depth D/h, the radical stress component and the tangential stresses component of rock with D = 2.5 m is given in Figs. 10 and 11. With the increase of D/h, the radial stresses and tangential stress decrease from the edge of the tunnel to the ground surface.

Fig. 10

Radial stress with different values D/h at θ = 90°

Fig. 11

Tangential stress with different values D/h at θ = 90°

Under different values of the ratio of the diameter to buried depth D/h, the circumferential stress component of rock with D = 2.5 m is given in Fig. 12. We can find the magnitude of the circumferential stress component of rock decrease with D/h decrease.

Fig. 12

Circumferential stress with different values D/h at θ = 90°

According to the strength theory, the failure is most likely to occur on the inner boundary of rock where the stress component is relatively large. Stress concentration mainly occurs near the hole, and with the increase of E₁, the phenomenon of stress concentration is more obvious. From Figs. 7, 8, 11 and 12, we also found the radical stress component and the tangential stresses component of rock are zero position around 0.8 m and 0.5 m from the ground surface, and it does not change with the elastic modulus of surrounding rock and the buried depth of tunnel.

6 Conclusions

The Stress analytical solution was presented for shallow buried lined circular tunnel under the deformation of surrounding rock inner edge. It was assumed that rock and concrete behaved as isotropic linear elastic materials, and surrounding rock and lining is contact completely. The stress components were predicted by employing complex potential functions and combined with conformal mapping method.

• (1) The numerical example result shows that by increasing elastic modulus of surrounding rock, the magnitude of stresses component decreases. With the increase of tunnel buried depth, the magnitude of stresses component decreases.

• (2) Stress concentration mainly occurs near the hole, and with the increase of E₁, the phenomenon of stress concentration is more obvious.

• (3) It was found that the stress concentration is gradually dissipating with the distance from the inner of tunnel, and with the increase of E₁, the stress concentration is more obvious.

• (4) We also found the radical stress component and the tangential stresses component of rock is zero position around 0.8 m and 0.5 m from the ground surface, and it does not change with the elastic modulus of surrounding rock and the buried depth of tunnel.