1 Introduction

Shallow foundations have been extensively used to support large onshore and offshore structures, such as wind turbines, platforms, transmission towers and masts. The bearing capacity of their shallow foundations under combined loadings is particularly important. For example, the horizontal loads on an offshore wind turbine caused by combined winds, waves and currents can be substantial, and a large tower height can lead to significant moment loading on the foundation. Traditional analytical methods for these types of foundations are based on classical solutions for the uniaxial vertical bearing capacity of shallow foundations. To account for the effects of load inclination and eccentricity, the load inclination factor and the effective foundation area are introduced, as recommended by some design guidelines (e.g. DNV 2016). However, this approach has been shown to be unconservative for some conditions (Ukritchon et al. 1998), and can be conservative for most cases under combined VHM loadings (Taiebat and Carter 2002).

A more recent design approach is the failure envelope method, which explicitly incorporates the load interaction effects of the various uniaxial loading components (Shen et al. 2017). API RP 2GEO (2011) and ISO 19901–4 (2016) recommend this approach as an alternative to conventional theories. Failure envelopes under undrained soil conditions for different foundation geometries, soil strength profiles, and interface conditions have been previously investigated [e.g. strip (Ganesh and Kumar 2021), rectangular (Gourvenec and Randolph 2003) and circular (Suryasentana et al. 2020) foundations; homogeneous strength (Taiebat and Carter 2010) and non-homogeneous strength (Ganesh and Kumar 2021) soils; and zero-tension interface (Shen et al. 2016; He and Newson 2019) and unlimited-tension interface (Wang et al. 2020) conditions] The currently available studies focus primarily on strip, rectangular and circular foundations. Recently, a number of onshore and offshore structures (e.g. wind turbines) have been constructed with foundations that have symmetrical polygon shapes (i.e. octagons) (Yilmaz et al. 2014). DNV (2016) recommends the design of these foundations as an equivalent inscribed circular foundation to accommodate for the octagonal shape. To date, there has been no verification of this assumption (particularly for the failure envelope method). Since the form of the failure envelope for shallow foundations has been found to be highly dependent upon the foundation shape (Gourvenec 2007), this simple approximation for the design of octagonal foundations should hence be rigorously assessed.

Therefore, the object of this study is to investigate the VHM failure envelope for octagonal foundations under a zero-tension interface for undrained soil conditions. The effects of soil strength heterogeneity and foundation embedment on the VHM failure envelope have been separately studied. A full 3-D VHM failure envelope is proposed using the finite element (FE) method.

2 Method – Finite Element Analysis

2.1 Material Models and Interface Conditions

A linear elastic perfectly plastic constitutive relationship with a Mohr–Coulomb (M–C) failure criterion was used to model the soil behavior. The M–C criterion devolves to the Tresca criterion under undrained soil conditions, which is defined by three soil parameters: the undrained Young’s modulus, Eu, the Poisson’s ratio, µ, and the undrained shear strength, su. In this study, the undrained soil shear strength was considered to linearly increase with depth (z) from the ground surface, as shown in Fig. 1:

$$s_{u} = s_{{{\text{u0}}}} + kz$$
(1)

where su0 is the undrained shear strength at foundation level; k is the strength increase per unit depth. In the analyses, su0 was held constant at 100 kPa, and the Poisson’s ratio of the undrained soil was taken to be 0.495. A sufficiently large Eu/su0 ratio of 10,000 was adopted to minimize mesh distortion (Abyaneh et al. 2015). The dimensionless soil strength heterogeneity ratio defined by κ = kD/su0 (D is the diameter of the inscribed circle) (Gourvenec and Randolph 2003) was taken as 0 (homogeneous), 2, 6 and 10. The foundation was assumed to act as a rigid body. A load reference point (LRP) attached to the center of the base of foundation was utilized to apply prescribed displacements or loads, as shown in Fig. 1.

Fig. 1
figure 1

LRP and soil strength profile

Full size image

A zero-tension rough base that allows separation of the foundation from the soil was considered. As demonstrated by Shen et al. (2016), the zero-tension rough base can be modelled using a Coulomb friction condition with a friction coefficient of 20. For embedded foundations, a reduced friction coefficient (i.e. partially rough interface) for side and top interfaces is recommended due to installation or in-service loading processes (Gourvenec and Mana 2011; Deshpande 2016). In this study, smooth side and top conditions (i.e. an interface adhesion factor α = 0 and the shear strength on the interface αsu = 0) for the embedded foundations were considered to provide more conservative predictions. The same consideration was made by Gourvenec and Mana (2011).

2.2 Geometry and Mesh

The 3D FE analysis was conducted using the software ABAQUS (Dassault Systèmes 2016). The diameter (D) (inscribed circle) and thickness (t) of the octagonal foundation used in this study are 19 and 3 m, representing typical dimensions for the onshore wind turbines used in North America. The embedment depth ratio, d/D (d refers to the foundation embedment depth), was taken to be 0, 0.08, 0.16, 0.23 and 0.30 to span cases of practical interest to the wind industry. To avoid the effects of the model boundaries, the mesh length, L, and mesh height, H, were taken as 120 and 50 m, following the recommendations of Deshpande (2016).

A number of mesh convergence studies were carried out for both surface and embedded foundations, and the result for the case of a surface foundation on a homogeneous soil is shown in Fig. 2. In Fig. 2 is the vertical load acting on the foundation; A is the soil-foundation contact area; and uv is the vertical displacement corresponding to V. The difference between the ultimate vertical loads using Mesh 2 (44,000 elements) and 3 (79,000 elements) is about 3%. However, the model solution with Mesh 3 takes about 2.5 times longer than that using Mesh 2. Therefore, Mesh 2 was adopted in the study. Figure 3 shows the three-dimensional half model using Mesh 2. The mesh was composed of around 44,000 8-noded brick elements (first-order). To capture the intense stress concentration close to the foundation edge and the large plastic shear strains at the interface, the soil regions in the vicinity of the foundation edge and the horizontal thin soil layer close to the interface were carefully refined (Gourvenec and Randolph 2003). The cylindrical circumference of the soil was constrained to prevent out-of-plane translations, and the bottom of the soil domain was fixed in the three orthogonal directions.

Fig. 2
figure 2

Mesh convergence study for a homogeneous soil

Full size image
Fig. 3
figure 3

Half-view of the FE mesh

Full size image

2.3 Sign Conventions and Loading Paths

In the analysis, the horizontal and moment loads were considered to be in the same plane. Unlike circular foundations, horizontal and moment loads acting on octagonal foundations can have different loading directions. Since a regular octagon can have planes of symmetry axes, viz. axes passing through the midpoints of two opposite sides (Case I) and axes passing through two opposite vertices (Case II), only these two special loading cases are required for investigations (more general cases lie in between these two extremes), as shown in Fig. 4. Preliminary analyses show that the difference in the failure envelopes between these two loading cases is rather small (less than 5%). Therefore, only Case I in Fig. 4 was considered for the majority of the analyses. The sign conventions for the loads are shown in Fig. 4.

Fig. 4
figure 4

Sign conventions

Full size image

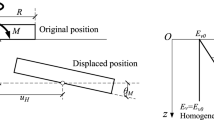
Probe tests were employed to detect the failure envelopes under various loading conditions. In a probe analysis, a vertical load is first applied at the LRP of the foundation and remains constant. A fixed-ratio displacement (see Fig. 5) is then imposed on the foundation to track the failure point on the failure envelope (Gourvenec and Randolph 2003). A probe test can only obtain a single point on a failure envelope. A typical failure envelope obtained using probe tests is shown in Fig. 5.

Fig. 5
figure 5

MH failure envelopes of a surface foundation for κ = 0 at V/Vult = 0.50

Full size image

3 Finite Element Results

This section presents the finite element (FE) results of the pure uniaxial capacities and the failure envelopes (i.e. Horizontal–Vertical, Moment–Vertical and Moment–Horizontal loading) for surface octagonal foundations on heterogenous soils and embedded octagonal foundations in homogeneous soils. The differences between the capacities for octagonal foundations and the corresponding circular foundations are presented.

3.1 Pure Uniaxial Capacity

The ultimate vertical and horizontal loads are referred to as the corresponding uniaxial load-carrying capacities in the absence of moment loading. As the foundation with a zero-tension interface cannot resist moment loading without vertical loads, the ultimate moment capacity is represented by the maximum moment load only under vertical loading (Shen et al. 2016). The uniaxial bearing capacity factors are defined as:

$$\begin{array}{*{20}c} {v_{0} = V_{{{\text{ult}}}} /\left( {A_{0} s_{{{\text{u0}}}} } \right)} \\ {h_{0} = H_{{{\text{ult}}}} /\left( {A_{0} s_{{{\text{u0}}}} } \right)} \\ {m_{0} = M_{{{\text{ult}}}} /\left( {A_{0} s_{{{\text{u0}}}} } \right)} \\ \end{array}$$
(2)

where Vult, Hult and Mult are the uniaxial vertical, horizontal and moment capacities, respectively; A0 is the area of the inscribed circle of the octagonal foundation, as recommended by DNV (2016).

The effects of the soil strength heterogeneity ratio and foundation embedment are shown in Figs. 6 and 7, respectively. Since h0 is affected only by su0 for surface foundations, h0 remains to be unity regardless of the value of κ. Figure 6 shows that the difference for v0 (around 8.5%) between octagonal and circular foundations is approximately the same, while the difference of m0 (around 11.4%) gradually increases with the value of κ. In Fig. 7, the embedded foundations in a homogeneous soil (i.e., κ = 0) have been considered. As can be seen from Fig. 7, octagonal foundations have larger uniaxial bearing capacity factors than circular foundations. In addition, the difference of h0 between octagonal and circular foundations appears to be smaller than that of v0 and m0. Relationships between the bearing capacity factors and κ and d/D are proposed in Eqs. (3) and (4). The comparison shown in Figs. 6 and 7 suggests good fits.

$$\begin{array}{*{20}c} {v_{0} = 6.45 + \frac{15.30\kappa }{{\kappa + 16.82}}} \\ {m_{0} = 0.68 + \frac{1.44\kappa }{{\kappa + 19.82}}} \\ \end{array}$$
(3)
$$\begin{array}{*{20}c} {v_{0} = 6.45 + \frac{4.17d/D}{{d/D + 0.49}}} \\ {h_{0} = 3.35d/D + 1.05} \\ {m_{0} = 0.68 - \frac{0.74d/D}{{d/D - 1.13}}} \\ \end{array}$$
(4)
Fig. 6
figure 6

Uniaxial bearing capacities for surface foundations: a Vult and b Mult

Full size image
Fig. 7
figure 7

Uniaxial bearing capacities for embedded foundations: a Vult; b Hult and c Mult

Full size image

3.2 Horizontal–Vertical Loading

The dimensionless and normalized HV failure envelopes for various soil heterogeneity ratios and foundation embedment ratios are depicted in Fig. 8. It can be seen from Fig. 8a and c that the absolute size of the envelope (i.e. dimensionless) increases with increasing κ and d/D. Since the size of the failure envelope is controlled by the uniaxial bearing capacities, octagonal foundations have larger dimensionless envelopes than the corresponding circular foundations. The normalized failure envelopes shown in Fig. 8b and d indicate that the HV envelopes normalized by the corresponding ultimate capacities collapse into a relatively narrow band, although a slight dependence on κ and d/D is observed.

Fig. 8
figure 8

HV failure envelopes: a Dimensionless, surface foundations; b Normalized, surface foundations; c Dimensionless, embedded foundations and d Normalized, embedded foundations

Full size image

A curve fit to Green’s exact solution (Green 1954) is widely used to characterize the HV failure envelopes, as shown by Eq. (5). The comparison shown in Fig. 8b and d indicates that Eq. (5) can provide conservative predictions of the FE results. For simplicity, Eq. (5) is used to model the current HV failure envelopes, ignoring the slight dependence on κ and d/D.

$$\begin{array}{*{20}l} {V/V_{{{\text{ult}}}} = 0.5 + 0.5\sqrt {1 - H/H_{{{\text{ult}}}} } , for V/V_{{{\text{ult}}}} \ge 0.5} \hfill \\ {H/H_{{{\text{ult}}}} = 1, for V/V_{{{\text{ult}}}} < 0.5} \hfill \\ \end{array}$$
(5)

3.3 Moment–Vertical Loading

Figure 9 shows the effects of κ and d/D on the MV failure envelopes. Significant expansion of the failure loci with increasing κ and d/D (see Fig. 9a and c) is observed. It can be seen that the dimensionless envelopes for octagonal foundations are consistently larger than those for the corresponding circular foundations. The comparison also shows that the difference between octagonal and circular foundations for various values of κ is larger than that for different values of d/D. In addition, the difference between octagonal and circular foundations slightly increases with κ.

Fig. 9
figure 9

MV failure envelopes: a Dimensionless, surface foundations; b Normalized, surface foundations; c Dimensionless, embedded foundations and d Normalized, embedded foundations

Full size image

As shown in Fig. 9b, the failure envelopes for the cases with different values of κ in terms of loads normalized by their ultimate values fall in a very tight band, with the shape following the parabolic function given by Eq. (6):

$$M/M_{{{\text{ult}}}} = 4\left[ {V/V_{{{\text{ult}}}} - \left( {V/V_{{{\text{ult}}}} } \right)^{2} } \right]$$
(6)

However, as can be seen from Fig. 9(d), the dependence of the MV failure envelopes on d/D cannot be directly eliminated by the normalization using the ultimate values, since an embedded foundation can still resist moment loads in the absence of vertical loads due to the side and top soils. In order to transform these failure envelopes with non-zero intercepts with the moment axis (i.e. at V/Vult = 0) into curves that pass through the origin, the failure envelopes shown in Fig. 9(d) are shifted to the right along the x axis (see Fig. 10(a)), which is equivalent to:

$$V\prime = V + \Delta V\;{\text{and}}\;V_{{{\text{ult}}}}^{\prime } = V_{{{\text{ult}}}} + \Delta V$$
(7)

where \(\Delta V\) represents the amount of offset and can be defined as \(\Delta V = V_{{{\text{ult}}}} \Delta f\left( {d/D} \right)\), where \(f\left( {d/D} \right)\) is a function of d/D. Curve fitting shows that \(f\left( {d/D} \right) = 4.95\left( {d/D} \right)^{3}\) can be a satisfactory prediction. As compared in Fig. 10(b), the modified normalized MV failure envelopes (i.e. \(M/M_{{{\text{ult}}}} \sim V\prime /V_{{{\text{ult}}}}^{\prime }\)) can still be approximated using Eq. (6).

Fig. 10
figure 10

Modified MV failure envelopes for embedded octagonal foundations: a Dimensionless and b Normalized

Full size image

The relationships between the contact area ratio (i.e. contact area / initial contact area) and load eccentricity predicted by the FE analyses and the equivalent effective area method of Hansen (1961), which is used by DNV (2016), are shown in Fig. 11. Typical contact areas for two values of load eccentricity are also presented; areas shown in black (sticking contact) and dark grey (slipping contact) are those predicted by the FE model, while the ellipse-shaped areas with red outlines and shaded with red stripes are estimated by the effective area method. It can be seen that the effective area method based on an inscribed circle consistently underestimates the contact area, resulting in the under-prediction of the moment capacity. Similar results were reported by Taiebat and Carter (2002) for eccentrically loaded circular surface foundations.

Fig. 11
figure 11

Relationship between contact area and load eccentricity

Full size image

3.4 Moment–Horizontal Loading

The dimensionless ultimate load-carrying capacities under combined moment and horizontal loadings for different values of κ and d/D are shown in Fig. 12. Only dimensionless failure envelopes at V/Vult = 0.50 are presented to show the evolution of the absolute size of the envelopes. As shown in Fig. 12, octagonal foundations consistently have larger MH envelopes than the corresponding circular foundations. Similar to the MV failure envelopes, the difference of the MH envelope between octagonal and circular foundations for different values of κ is larger than that for various values of d/D, and the difference slightly increases with κ (see Fig. 12a). Therefore, the approach of using an inscribed circle for octagonal foundations recommended by DNV (2016) tends to be more conservative for soils with larger strength heterogeneity. Figure 12 shows that the failure envelope for a surface foundation on a uniform soil is almost symmetrical about H = 0. However, the soil strength heterogeneity and foundation embedment gradually increase the degree of asymmetry (i.e. obliquity of the failure envelope) due to the cross-coupling effect between horizontal loads and moments. It should also be noted that the MH failure envelope tends to be right-skewed (i.e. positive skewness) with the increase of κ, while foundation embedment leads to left-skewed (i.e. negative skewness) MH failure envelopes.

Fig. 12
figure 12

Dimensionless MH failure envelopes at V/Vult = 0.50: a Surface foundations and b Embedded foundations

Full size image

Figure 13 shows the M–H failure loci (at V/Vult = 0.25, 0.50 and 0.75) normalized by the corresponding maximum horizontal load and moment (i.e. intersections of the failure envelopes with the horizontal load and moment axes). Since the shape of the failure envelope varies in a quite complex manner with κ and d/D, a general form of elliptic equation given by Eqs. (8) and (9) (accounting for the effects of κ and d/D, respectively) is used to approximate the FE results. The comparison presented in Fig. 13 shows reasonable predictions.

$$\left( {H/H_{\max } } \right)^{2} + \left( {M/M_{\max } } \right)^{2} + 0.22\left( {H/H_{\max } } \right) \cdot \left( {M/M_{\max } } \right) = 1$$
(8)
$$\left( {H/H_{\max } } \right)^{2} + \left( {M/M_{\max } } \right)^{2} - 0.082\left( {H/H_{\max } } \right) \cdot \left( {M/M_{\max } } \right) = 1$$
(9)
Fig. 13
figure 13

Fitting of MH failure envelopes: a Surface octagonal foundations on a non-homogeneous soil and b Embedded octagonal foundations in a uniform soil

Full size image

4 Full 3-D Failure Envelope in VHM Loading Space

This section derives a 3-D analytical expression for the failure envelope in VHM loading space. Based on the forms of the equations used in the previous sections, more general forms of the FE-derived equations are summarized in Eq. (10). In Eq. (10), the parameter c governs the tilt of the M–H failure envelope. According to Eqs. (8) and (9), the value of c is positive for the case of a surface foundation on a non-homogeneous soil and negative for the case of an embedded foundation in a homogeneous soil. Specific expressions of these failure envelopes for different soil and foundation conditions can be found in the previous sections.

$$\begin{array}{*{20}c} {M = 0: H_{\max } /H_{{{\text{ult}}}} = f_{h} \left( {V/V_{{{\text{ult}}}} } \right)} \\ {H = 0: M_{\max } /M_{{{\text{ult}}}} = f_{m} \left( {V/V_{{{\text{ult}}}} } \right)} \\ {V \ne 0: \left( {H/H_{\max } } \right)^{2} + \left( {M/M_{{{\text{max}}}} } \right)^{2} + c\left( {H/H_{\max } } \right)\left( {M/M_{\max } } \right) = 1} \\ \end{array}$$
(10)

Mathematical manipulations of Eq. (10) allow the formulation of a 3-D analytical expression for the failure envelope in VHM loading space in terms of \(V/V_{{{\text{ult}}}}\), \(H/H_{{{\text{ult}}}}\) and \(M/M_{{{\text{ult}}}}\):

$$\left( {\frac{{H/H_{{{\text{ult}}}} }}{{f_{h} \left( {V/V_{{{\text{ult}}}} } \right)}}} \right)^{2} + \left( {\frac{{M/M_{{{\text{ult}}}} }}{{f_{m} \left( {V/V_{{{\text{ult}}}} } \right)}}} \right)^{2} + c\left( {\frac{{H/H_{{{\text{ult}}}} }}{{f_{h} \left( {V/V_{{{\text{ult}}}} } \right)}}} \right)\left( {\frac{{M/M_{{{\text{ult}}}} }}{{f_{m} \left( {V/V_{{{\text{ult}}}} } \right)}}} \right) = 1$$
(11)

As an example, the full 3-D expression of the failure envelope for a circular surface foundation on non-homogeneous soils is shown in Fig. 14. The expressions for the HV, MV and MH failure envelopes can be found in the previous sections and are also shown for comparison.

Fig. 14
figure 14

3-D VHM failure surfaces for a circular surface foundation on non-homogeneous soils

Full size image

5 Conclusions

The general VHM failure envelopes of octagonal foundations under a zero-tension interface for undrained soils have been studied using finite element (FE) analyses. Two sets of FE cases, i.e. surface foundations on heterogeneous soils and embedded foundations in uniform soils, were considered to investigate the effects of soil strength heterogeneity and foundation embedment. Analytical formulas have been proposed to calculate the uniaxial capacities and the VH, VM and MH failure envelopes. The results indicate that the failure envelopes for octagonal foundations have similar shapes to those for the inscribed circular foundations. However, the size of the failure envelopes for octagonal foundations is larger, and the difference (about 10%) between them is not negligible. Therefore, the approximate method recommended for octagonal foundations by some design guidelines can be seen to be conservative. To facilitate the use of the developed method for the design of octagonal foundations, a full 3-D analytical expression for the VHM load failure envelope was derived based on the results provided herein. These approaches should aid the assessment of the ultimate limit state of shallow octagonal foundations under complex VHM loading conditions.