New Prediction Models for Mean Particle Size in Rock Blast Fragmentation

Abstract

The paper refers the reader to a blast data base developed in a previous study. The data base consists of blast design parameters, explosive parameters, modulus of elasticity and in situ block size. A hierarchical cluster analysis was used to separate the blast data into two different groups of similarity based on the intact rock stiffness. The group memberships were confirmed by the discriminant analysis. A part of this blast data was used to train a single-hidden layer back propagation neural network model to predict mean particle size resulting from blast fragmentation for each of the obtained similarity groups. The mean particle size was considered to be a function of seven independent parameters. An extensive analysis was performed to estimate the optimum value for the number of units for the hidden layer for each of the obtained similarity groups. The blast data that were not used for training were used to validate the trained neural network models. For the same two similarity groups, multivariate regression models were also developed to predict mean particle size. Capability of the developed neural network models as well as multivariate regression models was determined by comparing predictions with measured mean particle size values and predictions based on one of the most applied fragmentation prediction models appearing in the blasting literature. Prediction capability of the trained neural network models as well as multivariate regression models was found to be strong and better than the existing most applied fragmentation prediction model. Diversity of the blasts data used is one of the most important aspects of the developed models.

1 Introduction

Control of the particle size distribution of a muckpile after blasting is always an important subject for mining industry. Blasting has a significant impact on downstream processes of mining such as loading, crushing and grinding. Improvement of blasting results provides increase in loader and excavator productivity due to increased diggability capacity, and increased bucket and truck fill factors. Suitable and uniform particle size distribution results increase in crusher and mill throughput and decrease in energy consumption in size reduction process. Mckenzie (1966) found, in the studies at Quebec Cartier Mines, that the efficiency of all the subsystems of mining is dependent on the fragmentation (Chakraborty et al. 2004). Today, researchers suggest ‘mine to mill’ blasting approach that is defined as optimization of the blast design to maximize the overall profitability rather than individual operations (Kanchibotla et al. 1999; Grundstrom et al. 2001). Additionally, uniform particle size distribution also eliminates the need of the secondary blasting of the big boulders.

Several studies have been conducted on blastability and prediction of fragmentation. The term blastability refers to the ease with which a rock mass can be fragmented by blasting and is closely related to fragmentation. The parameters that determine fragmentation by blasting may be divided into four groups: (a) Blast design parameters; (b) Explosive parameters; (c) Rock mass structure parameters; (d) Intact rock and discontinuity physical and mechanical properties. Burden, spacing between boreholes, bench height, drill-hole diameter, hole length, charge depth, stem height, subdrilling, drilling pattern (square or staggered), hole inclination (vertical or inclined), blasting direction and blasting sequence (instantaneous or delayed) are all blast design parameters. All these parameters are controllable. Figure 1 shows most of the blast design parameters used in a bench blast. The diameter of the drill hole is the most important parameter for any blast design. It influences the selection of all other parameters. The hole is generally drilled slightly below the floor level to obtain a clean breakage. This total length of the hole is known as hole length. The extra length of the hole below the floor or the grade level is called the sub-drilling. The part of the drill hole at the top which is not filled with explosives is known as stemming height. Some inert material, such as drill cuttings, sand, crushed stone, etc., are used as stemming to contain the explosive gases in the hole for a slightly longer time to increase rock fracturing. The second group consists of explosive parameters. Explosive type (Anfo, water gel, emulsion or dynamite), its density (changes between 0.80 and 1.60 g/cm³), strength, resistivity and specific charge (kg Anfo/m³) are explosive parameters. All these parameters are also controllable. The third group consists of rock mass structure parameters. Number of discontinuity sets, orientation, size, spacing and intensity distributions of each discontinuity set belong to the third group. Physical and mechanical properties of the intact rock and discontinuities belong to the fourth group. Density, dynamic compressive strength, dynamic tensile strength, shear strength, dynamic elastic properties, hardness, durability, mineral composition and grain size of intact rock, and strength, deformability, roughness and infilling material properties of discontinuities belong to the fourth group. The parameters of the third and fourth groups are uncontrollable.

Fig. 1

Blast design parameter terminology (Ash 1973)

The parameters of the aforementioned 4 groups should be considered together to explain fragmentation process. Because a large number of parameters influence fragmentation distribution, it is obvious that the fragmentation process is extremely complex and thus it is an extremely challenging task to develop models to predict fragmentation distribution. Therefore, even though some of the fragmentation prediction models that appear in the literature have contributed to improving the state-of-the-art on the subject, none of them include all the important parameters. In some of the available prediction models crude, highly simplified or inappropriate procedures have been used in estimating rock mass fracture geometry parameters. Inappropriate distributions have been used to represent joint orientation. Corrections for sampling biases have not been applied in modeling joint size, joint orientation and joint intensity. Estimation of fracture spacing has been described in a highly vague manner. It is important to note that spacing of a fracture set changes with the direction and the correct spacing is obtained in the direction perpendicular to the fracture plane. In some of the blast fragmentation papers, RQD is used as a parameter. It is important to note that RQD changes with the direction and thus many values within a wide range exist for RQD for the same rock mass. In situ block size estimation has not been done in a comprehensive manner. Therefore, it is important to use better and accurate procedures in estimating rock mass fracture geometry parameters in developing rock blast fragmentation data bases in the future. Such quality data bases should then be used to improve the existing models or to develop new models to predict rock blast fragmentation distribution.

Because the blast fragmentation distribution depends on many parameters, and the process is highly complex due to the heterogeneity and anisotropy of a discontinuous rock mass system, it is impossible to derive an equation for fragmentation distribution purely from theoretical and mechanistic reasoning. In such situations, empirical approaches are used incorporating case history data along with statistical based procedures in developing prediction equations for complex geotechnical processes. Multivariate regression analysis has been used to develop fragmentation prediction models (Chakraborty et al. 2004; Hudaverdi et al. 2011). However, capturing of high non-linearity incorporating many parameters is a difficult task even with multivariate regression analysis.

Due to its excellent ability of non-linear pattern recognition, generalization, self-organization and self-learning, the Artificial Neural Network Approach (ANNA) has been proved to be of widespread utility in engineering and is steadily advancing into diverse areas as material sciences (Li et al. 2006), voice recognition, loan-risk assessment, stock market analysis, box office revenue forecasting (Zhang et al. 2009) and military target discrimination. In geosciences and geo-engineering, neural networks have been applied in rock mechanics and rock engineering (Zhang et al. 1991; Ghaboussi 1992; Lee and Sterling 1992), soil engineering (Kung et al. 2007), well-log and well-test interpretation (Rogers et al. 1992; Al-Kaabl and Lee 1993), seismic and satellite image processing (de Groot 1993; Penn et al. 1993), groundwater characterization and remediation (Rizzo and Doughery 1994; Rogers and Dowla 1994), earthquake intensity prediction (Tung et al. 1994), oil reservoir prediction (Yu et al. 2008) and conductive fracture identification (Thomas and La Pointe 1995). Neural network approach (NNA) is highly suitable for systems with highly non-linear complex relations between input and output parameters that are difficult to develop through physical reasoning and mathematical modeling. Linking between the rock blast mean fragment size and the blast design parameters, explosive parameters, rock mass structure parameters, and intact rock and discontinuity physical and mechanical properties is a very complex, non linear process. Therefore, NNA will be highly suitable to relate the mean fragment size to the aforementioned blast related parameters belonging to the four groups. Application of NNA to predict rock blast mean fragmentation size was dealt with in a previous paper (Kulatilake et al. 2010). A summarize account of it is given in this paper. Needed future research to improve the currently existing models are discussed in the paper.

2 Literature Review

A previous paper (Kulatilake et al. 2010) has covered the literature on the topic to an extensive level by referring to the following papers: Ghosh et al. (1990), Mojtabai et al. (1990), Ouchterlony et al. (1990), Chakraborty et al. (1994), Pal Roy (1995),Hagan (1995), Aler et al. (1996), Ozcelik (1998), Jhanwar et al. (2000), Castro et al. (1998), Latham and Lu (1999), Hamdi and Du Mouza (2005), Hall and Brunton (2002), Latham et al. (2003), Sanchidrian et al. (2007), Gheibie et al. (2009), and Rustan (1998). Kuznetsov (1973) has suggested the following empirical equation to predict the mean fragmentation size resulting from rock blasting:

$$ {\text{X}}_{50} = {\text{A}}({\text{V}}/{\text{Q}})^{0.8} {\text{Q}}^{0.167} $$

(1)

In Eq. 1: X₅₀ is the mean fragment size (cm); ‘A’ is a rock factor (7 for medium rock, 10 for hard highly fissured rock, and 13 for hard weakly fissured rocks); V is the rock volume (m³); Q is the mass of explosive per blast hole (kg). Kuznetsov also has suggested to use Rosin–Rammler equation (Rosin and Rammler 1933) given below to estimate the complete fragmentation distribution resulting from rock blasting:

$$ {\text{Y}} = \exp ({\text{X}}/{\text{X}}_{\text{c}} )^{\text{r}} $$

(2)

In Eq. 2, Y = Proportion of the material larger than X, X_c = characteristic size = X₅₀ and r = uniformity exponent. Even though Schumann Distribution (Schuhmann 1959) and Swebrec equation (Nie and Rustan 1987) are also suggested in the literature to predict the complete fragmentation distribution, Rosin–Rammler equation seems to be the most popular one.

It was experienced by many that the rock mass categories defined by Kuznetsov (1973) are very wide and need more precision (Chakraborty et al. 2004). Cunningham (1983, 1987) modified the Kuznetsov’s equation to estimate the mean fragment size and used the Rosin–Rammler distribution to describe the entire size distribution. The uniformity exponent of Rosin–Rammler distribution was estimated as a function of blast design parameters. Rock factor “A” in Kuznetsov’s equation was estimated incorporating Lilly’s blasting index, BI (1986). The final equation suggested by Cunningham, known as Kuz-Ram model, can be given as follows:

$$ {\text{X}}_{50} = {\text{A}} \times ({\text{V}}/{\text{Q}})^{0.8} \times {\text{Q}}^{0.167} \times ({\text{E}}/115)^{ - 0.633} $$

(3)

where

$$ {\text{A}} = 0.06 \times {\text{BI}} $$

(4)

and

$$ {\text{BI}} = 0.5 \times ({\text{RMD}} + {\text{JPS}} + {\text{JPO}} + {\text{RDI}} + {\text{S}}) $$

(5)

In Eq. 3, E is relative weight strength of explosive (Anfo = 100) and V = BSH where B = burden (m), S = blast hole spacing (m) and H = bench height (m). In Eq. 5: RMD is rock mass description (powdery or friable = 10, blocky = 20 and massive = 50); JPS is joint plane spacing (close < 0.1 m = 10, 0.1 − 1.0 = 20, > 1.0 = 50); JPO is joint plane orientation (horizontal = 10, dip out face = 20, strike normal to face = 30, dip into face = 40) and RDI is rock density influence equal to 25d-50, where d is density and S is rock strength, equal to 0.05 UCS, where UCS is uniaxial compressive strength. Even though a few other equations such as SveDefo’s fragmentation model (Hjelmberg 1983) and Kou and Rustan’s model (1993) are also available in the literature to estimate mean fragmentation size, Kuz-Ram model seems to be the most popular one.

Research at the JKMRC, Australia and elsewhere has demonstrated that the Kuz-Ram model underestimates the contribution of fines in the fragment size distribution. Hall and Brunton (2002) claim that the JKMRC model provides better prediction than Kuz-Ram model due to improved estimation of the fines to intermediate size (< 100 mm) of the fragmentation distribution (Chakraborty et al. 2004). The JKMRC model calculates the coarse and fines distributions independently. JKMRC uses Kuz-Ram model to calculate the course fraction.

3 Used Blast Database and Scope of Study

In a previous study conducted by the second and first authors of this paper (Hudaverdi et al. 2011), many blasts performed in different parts of the world and reported in the literature were carefully analyzed and put together to create a blast data base to develop fragmentation prediction models. A total of 109 blasts were used in this study. Ninety-seven blasts were used for model development and twelve blasts were used for model validation. For details of this blast data base, the reader is referred to Hudaverdi et al. (2011).

Five main blast design parameters are used in the developed multivariate and neural network models. They are the Burden (B, m), Spacing (S, m), Bench height (H, m), Stemming (T, m) and Hole diameter (D, m). Several blasting researchers have considered blast design parameters as ratios. In the conducted studies by the authors of this paper, the blast design parameters of all the blast data are also used as ratios. The ratio of bench height to drilled burden (H/B), ratio of spacing to burden (S/B), ratio of burden to hole diameter (B/D) and ratio of stemming to burden (T/B) are the blast design parameters used. All blasts in the database were performed using Anfo. Therefore, there was no need to use any parameter related to explosive type. The Powder factor (Pf) has been considered as an explosive parameter. The ratio of spacing to burden is determined based on energy coverage of the bench. For square pattern, S/B ratio is 1. The mean S/B ratio of the used blast data is 1.20. Generally, the ratio of stemming to burden applied is around 1. For the used data, the mean T/B ratio is 1.27 with a standard deviation of 0.69. Low T/B ratio may cause premature release of explosive gases and result in fly-rock and inefficient fragmentation. Conversely, excessive stemming length means low specific charge and may cause large boulders. Most of the blast design calculations start with burden determination. If the burden is too small, detonation gases escape to the atmosphere. Escape of the detonation gases cause noise and airblast. That means less energy is used for fragmentation. If the burden is too large, confined gases may cause ground vibrations and back-break. The particle size of the muckpile may be coarser than expected under such a situation. The ratio of burden to hole diameter (B/D) is one of the most important parameters. Ash (1973) suggested the ratio of burden to hole diameter (B/D) as 30 for average conditions. The B/D ratio is equal to 25 for low density explosives such as Anfo. For the used data, the mean B/D ratio is 27.21 with a standard deviation of 4.77. In this study, the ratio of the bench height to burden (H/B) is used instead of the ratio of hole length to burden (L/B) used by Ash. The ratio of bench height to burden indicates the stiffness of the rock beam under blast induced stress. Hustrulid (1999) indicated that the H/B ratio is 1.6 or more for most of the open-pit operations. The mean H/B ratio of the data used is 3.44 with a standard deviation of 1.64.

Because the data base was large and diverse, it turned out to be a difficult assignment to find common intact rock and rock mass parameters for all the selected blast data to use in developing fragmentation distribution models. On the other hand, it was possible to find in situ block size for all the blasts in the data base. Therefore, in situ block size which is accepted as one of the key parameters of the fragmentation process was used to represent rock mass structure in the data base. With respect to intact rock, the modulus of elasticity turned out to be the most common parameter available for all the blasts and was used to represent intact rock properties in the data base. Thus seven parameters were used to establish fragmentation prediction models based on multivariate analysis and NNA and incorporating the blast design parameters, powder factor, modulus of elasticity (E, GPa) and in situ block size (X_B, m). Table 1 shows the descriptive statistics of the parameters that were used to develop multivariate analysis and neural network based fragmentation prediction models.

Table 1 Descriptive statistics of the input parameters used to develop fragmentation prediction models

The cluster analysis was performed on this data to separate the blast data into two different similarity groups. The main difference between the two groups was found to be the modulus of elasticity value. The data belonging to the two groups are given in Tables 1 and 2 in Hudaverdi et al. (2011), respectively. The mean elastic modulus values are 51.14 and 17.99 for Groups 1 and 2, respectively. Group memberships were then analyzed and confirmed by the discriminant analysis. A part of the blast data was used to train neural network models for each of the obtained similarity groups. The blast data that were not used for training were used to validate the trained neural network models. Also, multivariate regression analysis was performed for each of the obtained similarity groups to develop prediction models for mean particle size.

Table 2 Summary of discriminant analysis

4 Application of Multivariate Analysis

The cluster analysis which is also called segmentation analysis or taxonomy analysis is used to create relatively homogeneous groups of variables or cases. The cluster analysis identifies a set of groups that minimize within group variation and maximize between-group variation. Several clustering techniques are available: the hierarchical clustering, Kmin clustering, two step clustering and fuzzy clustering (Kaufman and Rousseeuw 1990). The hierarchical clustering technique is the most common clustering technique that is applied in earth science. This technique creates relatively homogeneous groups of cases or objects (the blasts in the conducted research) based on selected variables or characteristics. Each object is identified as a separate cluster and then the clusters are combined until only one is left.

As the first step of the hierarchical cluster analysis, a data matrix (proximity matrix) is formed. If there are ‘n’ objects having ‘m’ measurable variables, ‘n × m’ data matrix, X, is formed as shown in Eq. 6:

$$ {\mathbf{X}} = \left[ {\begin{array}{*{20}c} {{\text{x}}_{11} } \hfill & \ldots \hfill & {{\text{x}}_{{1{\text{j}}}} } \hfill & \ldots \hfill & {{\text{x}}_{{1{\text{m}}}} } \hfill \\ \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill \\ {{\text{x}}_{{{\text{i}}1}} } \hfill & \ldots \hfill & {{\text{x}}_{\text{ij}} } \hfill & \ldots \hfill & {{\text{x}}_{\text{im}} } \hfill \\ \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill \\ {{\text{x}}_{{{\text{n}}1}} } \hfill & \ldots \hfill & {{\text{x}}_{\text{nj}} } \hfill & \ldots \hfill & {{\text{x}}_{\text{nm}} } \hfill \\ \end{array} } \right] $$

(6)

In matrix X, each row represents an object and each column shows data for a different variable (Kaufman and Rousseeuw 1990). For the conducted study, a data matrix of 97 blast data was formed. In the matrix, the objects are the blasts and the measurable variables are the 7 blast design and rock mass parameters.

In the data matrix, usually a standardization process is applied to weigh each measurable variable equally and to remove the effects of different units of measurement across the different variables. Each variable in the data matrix, x_ij, was standardized by subtracting the column mean, $\overline{{{\text{x}}_{\text{j}} }}$, and dividing by the column standard deviation, $\delta_{{{\text{x}}_{\text{j}} }}$, as shown in Eq. (7):

$$ {\mathbf{Z}}_{\text{ij}} = \frac{{{\text{x}}_{\text{ij}} - \overline{{{\text{x}}_{\text{j}} }} }}{{\delta_{{{\text{x}}_{\text{j}} }} }} $$

(7)

The above operation is also called z-score standardization and it produces the Z matrix given in Eq. 8.

$$ {\mathbf{Z}} = \left[ {\begin{array}{*{20}c} {{\text{z}}_{11} } \hfill & \ldots \hfill & {{\text{z}}_{{1{\text{j}}}} } \hfill & \ldots \hfill & {{\text{z}}_{{1{\text{m}}}} } \hfill \\ \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill \\ {{\text{z}}_{{{\text{i}}1}} } \hfill & \ldots \hfill & {{\text{z}}_{\text{ij}} } \hfill & \ldots \hfill & {{\text{z}}_{\text{im}} } \hfill \\ \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill & \ldots \hfill \\ {{\text{z}}_{{{\text{n}}1}} } \hfill & \ldots \hfill & {{\text{z}}_{\text{nj}} } \hfill & \ldots \hfill & {{\text{z}}_{\text{nm}} } \hfill \\ \end{array} } \right] $$

(8)

Several hierarchical clustering methods exist: the median clustering, Ward’s method, nearest neighbor, furthest neighbor, average linkage. The cluster method defines the rules for cluster objects. The basic criterion for any hierarchical clustering is the distance. The similarity between objects is determined based on the distance between each other. A small distance indicates the two objects are similar, whereas a large distance indicates dissimilarity. The objects that are similar should belong to the same cluster, and objects that are dissimilar should belong to different clusters. The distance (similarity) between two objects is some function of their measurable variables.

The distance between clusters may be computed using several functions: the Euclidian distance; Pearson correlation distance; Minkowski distance; Block distance; and Chebychev distance (SPSS 2008). The Pearson correlation distance (Pd) was used in this study to determine the distance between clusters. The Pearson correlation coefficient was calculated using z- score values given in matrix Z. The Pearson correlation coefficient between any two series of numbers (vectors) z _a  = {z_a1, … z_aj, … z_am} and z _b  = {z_b1, … z_bj, …, z_bm} is defined as:

$$ {\mathbf{r}}_{{{\mathbf{z}}_{{\mathbf{a}}} {\mathbf{z}}_{{\mathbf{b}}} }} = \frac{1}{\text{m}}\mathop \sum \limits_{{{\text{j}} = 1}}^{\text{m}} \left( {\frac{{{\text{z}}_{{{\text{aj}} - \overline{{{\text{z}}_{\text{a}} }} }} }}{{\delta_{{{\text{z}}_{\text{a}} }} }}} \right)\left( {\frac{{{\text{z}}_{{{\text{bj}} - \overline{{{\text{z}}_{\text{b}} }} }} }}{{\delta_{{{\text{z}}_{\text{b}} }} }}} \right) $$

(9)

where z_aj indicates the z-score of jth variable for object ‘a’; z_bj indicates the z-score of jth variable for object ‘b’; ‘m’ is the number of measured variables on each object. $\overline{{{\text{z}}_{\text{a}} }}$ is the average of the values in vector z _a ; $\overline{{{\text{z}}_{\text{b}} }}$ is the average of the values in vector z _b ; $\delta_{{{\text{z}}_{\text{a}} }}$ is the standard deviation of the values in vector z _a and $\delta_{{{\text{z}}_{\text{b}} }}$ is the standard deviation of the values in vector z _b and ${\mathbf{r}}_{{{\mathbf{z}}_{{\mathbf{a}}} {\mathbf{z}}_{{\mathbf{b}}} }}$ is the correlation coefficient between the vectors z _a and z _b . In this study, objects ‘a’ and ‘b’ are the blasts (for example, blasts Rc6 and Mg1). The vectors z _a  = {z_a1, … z_aj, … z_am} and z _b  = {z_b1, … z_bj, …, z_bm} are the z-scores of the blast design and rock mass parameters that belong to blasts ‘a’ and ‘b’, respectively. The Pearson correlation distance was computed as Pd = 1 − r and varies between 0 (when correlation coefficient is +1) and 2 (when correlation coefficient is −1). A small distance indicates the two objects are similar, whereas a large distance indicates dissimilarity (Garson 2009).

Computation of a similarity measurement using the pearson distance between all possible pairs of objects produces an n × n symmetrical matrix M. Each coefficient ${\text{m}}_{{{\text{z}}_{\text{a}} {\text{z}}_{\text{b}} }}$ in the matrix indicates the similarity level between the objects ‘a’ and ‘b’. Next, the objects are arranged into a hierarchy so that objects with the highest mutual similarity are placed together to form clusters. Then the groups having closest similarity to other groups are connected together until all of the objects are placed into a hierarchical tree diagram known as a Dendrogram (Kulatilake et al. 2007).

In this study, the average clustering technique was used to form the clusters. The linkage function that determines the distance between two clusters is computed as the distance between average values of the two clusters (Everitt 1993). Figure 2 shows the basic logic behind the average clustering technique. In Fig. 2, the clusters X and Y contain the blasts Rc6 and Mg6, and Mg1, Mg2, Mg3, respectively. ‘dn’ is the distance between individual blasts. The distance between the clusters X and Y (D_xy) is defined as the average of the distances between all pairs of individual blasts: D_xy = (d₁ + d₂ + d₃ + d₄ + d₅ + d₆)/6.

Fig. 2

Distances between blasts belonging to two clusters to calculate average distance between the two clusters

The dendrogram resulting from the performed hierarchical cluster analysis (SPSS 2008) is shown in Fig. 3. The dendrogram shows the relative size of the calculated distance coefficients at which the blasts and clusters were combined. The blasts that have smaller distance coefficients are combined. The X axis shows the blasts. The Y axis shows the rescaled version of the calculated distance. The blasts with low distance coefficient (high similarity) are close together.

Fig. 3

Dendrogram of the hierarchical classification for the examined blasts

As seen in the Dendrogram, the blasts are divided into two main clusters (groups) between rescaled distances of 22 and 25. The first group that appears on the right side of the dendrogram graphic is given in Table 1 in Hudaverdi et al. (2011). The second group of blasts that appears on the left side of the dendrogram is given in Table 2 in Hudaverdi et al. (2011). Group 1 contains 35 blasts and Group 2 contains 62 blasts.

The mean variable vectors of the groups may be examined to understand which parameters are effective on the occurrence of two different groups. Figure 4 shows the mean variable vectors of Groups 1 and 2 that are shown in Tables 1 and 2 of Hudaverdi et al. (2011), respectively. As seen in Fig. 4, the main difference between the two groups is the modulus of elasticity value. The mean elastic modulus values are 51.14 and 17.22 for Groups 1 and 2, respectively. Also, Pf and H/B values have some differences between the two groups. The mean Pf values for Groups 1 and 2 are respectively, 0.41 and 0.60. The mean H/B values for Groups 1 and 2 are respectively, 2.44 and 3.85.

Fig. 4

Mean vector variables for the two groups

The discriminant analysis technique was applied to make sure that the blasts are grouped (clustered) correctly. Also, the discriminant analysis enables one to investigate the differences between Groups 1 and 2 more precisely. The discriminant function used to classify the blasts can be presented based on the unstandardized discriminant function coefficients as SPSS (2008):

$$ {\text{L}} = 4.467({\text{S}}/{\text{B}}) - 0.551({\text{H}}/{\text{B}}) - 0.123({\text{B}}/{\text{D}}) + 1.642({\text{T}}/{\text{B}}) - 3.005({\text{Pf}}) + 0.309({\text{X}}_{\text{B}} ) + 0.208({\text{E}}) + 3.577 $$

(10)

The discriminant score is the value resulting from applying the discriminant function formula (Eq. 10) to the data belonging to a given blast. The histograms shown in Fig. 5 display the discriminant scores for the blasts of the Groups 1 and 2. The sharp difference between the discriminant scores of the two groups indicates strong discrimination of the discriminant function and the accuracy of the classification of the blasts into two groups. If there is a hesitation about group membership of a prospective blast, it is possible to assign the blast to Group 1 or 2 by the discriminant function.

Fig. 5

The discriminant scores of the blasts belonging to the two groups

A summary of the discriminant analysis is shown in Table 2. The second column in Table 2 shows the eigenvalue. Only one eigenvalue exists for each discriminant function. The eigenvalue, also called the characteristic root of each discriminant function, reflects the ratio of importance of the dimensions which classify objects (blasts) of the dependent variable (Garson 2009). The larger the eigenvalue, higher the variance in the dependent variable explained by the discriminant function. The third column displays the percent of variance explained by each function. The fourth column is the cumulative percent of variance explained. Thus a more general version of Table 2 can be used to understand the relative importance of discriminant functions if more than one function exists. Since we sorted the blasts into only two groups, only one discriminant function exists for the conducted study. Thus, the canonical correlation coefficient is the only important indicator in Table 2 for the conducted discriminant analysis. The canonical correlation is a measure of the association between the groups formed by the dependent variable and the given discriminant function. When the canonical correlation coefficient is zero, there is no relation between the groups and the function. When the canonical correlation is close to 1, there is a high correlation between the discriminant function and the groups. The canonical correlation is used to state to what extent the discrimination function is useful in determining group differences. For the conducted study, a canonical correlation of 0.973 was obtained. This indicates a highly successful discrimination.

Table 3 shows the tests of equality of group means. The tests of equality of group means measure each independent variable’s potential before the model is developed. Each test displays the results of a one-way analysis of variance (ANOVA) for the independent variable using the grouping variable as the factor. If the significance value (which is obtained through the F statistic, and the two degrees of freedom, df1 and df2, values) is larger than 0.10, it indicates that the parameter is not effective on occurrence of group (SPSS 2008). Accordingly, the S/B has no effect on occurrence of the groups. This finding agrees with the results appearing on Fig. 4. The effect of a parameter on the occurrence of the groups indicates only the discrimination ability of the selected parameter in cluster and discriminant analysis. It does not indicate the effect of the parameter on the fragmentation process. The discrimination ability of a parameter is highly related to its variance. For example, in our analysis, the range of the S/B parameter is relatively tight. On the other hand, the S/B is an important parameter for blasting and site engineers are very meticulous in selecting the value for the S/B parameter.

Table 3 Results of tests of equality of group means

Wilks’ lambda is another measure of a variable’s potential. Wilks’ lambda is a test statistic used in multivariate analysis of variance. It tests whether there are differences between the means of the groups of the subjects on a combination of dependent variables (Everitt and Dunn 1991; Huberty and Olejnik 2006). Smaller values indicate the variable is better at discriminating between groups. Wilks’ lambda test results show that the parameter that has a dominant effect on the occurrence of the two groups is the modulus of elasticity.

5 Application of Artificial Neural Network Approach (ANNA)

5.1 Setting Up and Training of ANNA

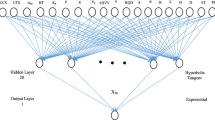
The back-propagation (BP) network, a multilayer feed-forward ANNA, is perhaps the most popular network architecture today as it contains the highlights of the neural network theory, simple in structure and clear in mathematical meaning. It has been proved that any continuous function can be uniformly approximated by BP network model with only one hidden layer (Cybenko 1989). So a single-hidden layer BP network is used in this paper to predict the mean particle size of rock fragmentation resulting from blasting. As stated previously, the mean particle size X₅₀ is considered to be a function of seven independent parameters. Consequently, the parameters S/B, H/B, B/D, T/B, Pf, XB and E are used as inputs and X₅₀ as the output in the BP network model. In the literature different opinions are expressed with respect to designing the neural network structure with respect to the number of nodes and the weights to obtain accurate performance from a trained network for a given number of training samples. This aspect was discussed in detail in Kulatilake et al. (2010). Research conducted in the past has shown that the number of hidden units has a great impact on the ANNA prediction results (John et al. 1995; Maier and Dandy 1998). Figure 6 shows the BP network configuration used in this study assuming the optimum number of hidden units as N. Section 5.2 deals with estimation of N in great detail.

Fig. 6

The structure of a 7-N-1 BP neural network

Kulatilake et al. (2010) covered in detail the equations associated with the information transfer between the input layer and the hidden layer as well as between the hidden layer and the output layer. In addition, the same paper covered in detail the equations associated with the training of the network.

As stated before, the blasting data have been divided into two groups by the value of elastic modulus. To increase the prediction precision, BP neural network was applied separately to each group. For group 1, thirty-five sets of data given in Table 1 were used to train the network and the five sets of data given in Table 4 were used to predict and validate the network. For group 2, sixty-two sets of data given in Table 2 were used to train the network and the seven sets of data given in Table 5 were used to predict and validate the network.

Table 4 Prediction results of the 8 simulations for Group 1 (for N = 9)

Table 5 Prediction results of the 8 simulations for Group 2 (for N = 7)

As their orders of magnitude are different, before running the neural networks, the original data were normalized using Eq. 11 given below:

$$ y_{i} = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }} $$

(11)

In Eq. 11, x is the vector before normalization; y is the vector after normalization; x _i and y _i are respectively the element of vector x and vector y; x _max and x _min are respectively, the maximum and minimum element of vector x.

Several algorithms are available in the literature to train a neural network. Each of them has its advantages and disadvantages. For a given problem, it is difficult to say which one works best. It depends on several factors, such as the complexity of the problem, the number of training samples, the structure of the network, error target and so on. The information flows through the network from the input layer to the output layer via the hidden layer. The objective of the training is to adjust the weights and thresholds that exist between the input layer and the hidden layer, and the hidden layer and the output layer to develop and estimate a complicated non-linear function between the output and input variables. The objective function given in Eq. 12 is used to obtain an optimized trained network.

$$ {\text{mse}} = \frac{1}{\text{T}}\sum\limits_{{{\text{t}} = 1}}^{\text{T}} {({\text{y}}_{\text{t}} - {\text{C}}_{\text{t}} )^{2} } $$

(12)

In Eq. 12, y_t is the expected output and C_t is the calculated output; T is the number of data sets used in the training sample. The weights and thresholds are adjusted using the gradient decreased learning method to minimize the objective function value given by Eq. 12 and thus to arrive at an optimized trained network. In a previous paper (Kulatilake et al. 2010), the best training method was decided by trying different methods and observing the performance of each method on a plot between mean square error (mse) value and number of training cycles. The training of the network was stopped after it has been trained for many cycles to reach a stable mse value. Four training methods were used to train the same selected network. The LM algorithm showed the highest stability among the four training algorithms. Also it reached the global minimum with the lowest number of training cycles. Therefore, only the LM algorithm was used for further modeling work with neural networks.

5.2 Procedure to Estimate Number of Units for the Hidden Layer

Choosing an appropriate number for the units in the hidden layer is not a straightforward task (Maier and Dandy 1998). The number of input parameters, number of output parameters, number of data sets available and the characteristics of the functional relation between the output and the input parameters may affect the optimum number for the units in the hidden layer. At present, the authors are not aware of any accepted procedure or formula available to determine the aforesaid optimum number. This optimum number may even change with different run (simulation) numbers for the same problem. Two empirical formulae available in the literature were used in Kulatilake et al. (2010) to estimate the optimum number for the hidden layer units.

Based on Kolmogorov’s theorem, Hecht-Nelson (1987) has suggested that 2n + 1 (where n is the number of input parameters) should be used as the upper bound for the number of hidden units for a one-hidden-layer back-propagation network. Because in our study n = 7, the number of hidden units for both Groups1 and 2 should be ≤15 according to Hecht-Nelson’s suggestion. According to the second empirical formula (Ge and Sun 2007), the number of hidden units, N, should satisfy the following inequality:

$$ \sum\limits_{i = 0}^{\text{n}} {{\text{C}}_{\text{N}}^{\text{i}} } > {\text{k}} $$

(13a)

where

$$ {\text{C}}_{\text{N}}^{\text{i}} = \frac{{{\text{N}}!}}{{{\text{i}}!({\text{N}} - {\text{i}})!}} $$

(13b)

In inequality Eq. 13a, n is the number of input parameters and k is the number of data sets used. Note that If i > N, ${\text{C}}_{\text{N}}^{\text{i}} = 0$. Application of inequality Eq. 13a to group 1 (n = 7, k = 35) and group 2 (n = 7, k = 62) results in N ≥ 6 for both groups. Therefore, use of the aforementioned two empirical criteria results in 6 ≤ N ≤ 15 for both Groups 1 and 2.

Accuracy of the network was considered to determine the optimum value for N. To evaluate the accuracy of the network for each N, two parameters were used. The Root Mean Square Error, RMSE, was used as the first parameter and it was defined by the following equation:

$$ {\text{RMSE}}_{\text{i}} = \sqrt {\frac{{\sum\nolimits_{{{\text{j}} = 1}}^{\text{J}} {{\text{error}}_{\text{ij}}^{2} } }}{\text{J}}} $$

(14a)

where

$$ {\text{error}}_{\text{ij}} = \left| {{\text{e}}_{\text{ij}} - {\text{r}}_{\text{ij}} } \right| $$

(14b)

In Eq. 14b, e_ij denotes the prediction result of the ith network under a certain N for the jth blast number, r_ij denotes the corresponding actual value for the same blast number. In Eq. 14a, J is the number of blast data used for prediction for a certain group. The correlation coefficient between the predicted value and the measured value for the aforementioned J blast data was used as the second parameter to evaluate the accuracy of each ith network under a certain N value. In evaluating the accuracy, several random simulations were performed for each ith network under a certain N value.

5.3 Results, Prediction and Validation

For group 1, five blasts were used for the prediction and validation. Note that under each N value, 8 simulations were made. As an example, the prediction obtained for each blast under N = 9 for each of the simulations made is shown in Table 4. En13 blast has the same values of S/B, H/B, B/D, T/B, Pf, X_B and E as for En4 blast. Therefore, the prediction result of X₅₀ for En13 blast is almost the same as the value for En4 blast. For RU7 & RU1, all the blasting parameter values are the same apart from the value for T/B. That has led to a large variation of the predicted value with respect to the simulation number. Table 4 also provides the predicted mean, μ, and coefficient of variation, δ, obtained for each blast from the 8 simulations.

The RMSE values and the coefficient of variations obtained for Group 1 for different N values are given in Table 6. High correlation coefficient values indicate predictions close to the measured values. The consistency of the correlation coefficient values shows high homogeneity of the Group 1 samples. N = 9 has resulted in the lowest RMSE and the highest correlation coefficient. That means for group 1, N = 9 is the optimum value. Table 4 shows a comparison between neural network predictions, measured values and predictions based on the Kuznetsov’s equation. All the blast data were examined carefully and the rock factor ‘A’ was estimated for each blast to apply the Kuznetsov’s equation. For all 5 blasts, neural network predictions are close to the measured values. This can be also seen from the regression analysis results given in Fig. 7a. For 4 out of the 5 blasts, predictions based on Kuznetsov’s equation are close to the measured values. This can be also seen from the regression analysis results given in Fig. 7b. Note that Group 1 blast data come from hard rocks that have high elastic modulus values.

Table 6 Prediction results of mean particle size from ANNA for Group 1 (for N = 6–15)

Fig. 7

Predicted mean particle size (m) versus measured mean particle size (m): a based on neural network models; b based on Kuznetsov’s equation; c based on developed regression models

For Group 2, seven blasts were used for the prediction and validation. Note that under each N value, 8 simulations were made. As an example, the prediction obtained for each blast under N = 7 for each of the simulations made is shown in Table 5. The same table also provides the predicted mean, μ, and coefficient of variation, δ, obtained for each blast from the 8 simulations. The RMSE values and the coefficient of variations obtained for Group 2 for different N values are given in Table 7. The results show high fluctuation of correlation coefficient values for Group 2 data. This shows that the homogeneity of Group 2 is weaker than that of Group 1. N = 7 has resulted in the lowest RMSE value and the highest correlation coefficient. That means for Group 2, N = 7 is the optimum value. Table 5 shows a comparison between neural network predictions, measured values and predictions based on the Kuznetsov’s equation. For all 7 blasts, neural network predictions are close to the measured values. This can be also seen from the regression analysis results given in Fig. 7a. Only for about 50% of the blasts, predictions based on Kuznetsov’s equation are close to the measured values. This can be also seen from the regression analysis results given in Fig. 7b. Note that group 2 blast data come from rocks that have relatively low elastic modulus values.

Table 7 Prediction results of mean particle size from ANNA for Group 2 (for N = 6–15)

Figure 7a shows the linear regression analysis performed between the predictions obtained from the neural network models developed for Groups 1 and 2 and the measured mean particle size. Figure 7b shows the linear regression analysis performed between the predictions based on Kuznetsov’s equation for Groups 1 and 2 and the measured mean particle size. In Fig. 7a, the prediction line has an intercept close to zero and a slope close to 1.0 with a R² value of 0.9407 (which indicates a strong regression fit). These results indicate that the matching between the neural network predictions and the measured values is very strong. In Fig. 7b, even though the prediction line has an intercept close to zero and a slope close to 1.0, the R² value is only 0.5697 (which indicates only a moderate level regression fit). In addition, the 95% confidence band in Fig. 7a is much narrower than that in Fig. 7b. These results clearly show that the neural network predictions are better than the predictions based on Kuznetsov’s equation.

6 Prediction of Mean Particle Size Based on Multivariate Regression Analysis

The multiple regression analysis (Draper and Smith 1981) was applied to develop a prediction equation for each group. The dependent variable of the multiple regression analysis is the mean particle size (x_50R) and the independent variables are the all blast design parameters, elastic modulus and in situ block size.

Equation 15 given below was developed for Group 1 that has high Young’s modulus values. Table 8 shows the obtained regression statistics.

$$ {\text{X}}_{50} = 208({\text{S}}/{\text{B}})^{2.788} ({\text{H}}/{\text{B}})^{0.112} ({\text{B}}/{\text{D}})^{0.027} ({\text{T}}/{\text{B}})^{ - 0.321} ({\text{Pf}})^{ - 0.360} ({\text{X}}_{\text{B}} )^{0.233} ({\text{E}})^{ - 1.802} $$

(15)

R, the multiple correlation coefficient, is the linear correlation between the observed and model-predicted values of the dependent variable. Its large value (close to 1) indicates a strong relation. R², the coefficient of determination, is the squared value of the multiple correlation coefficient. R² is the percent of variance in the dependent variable explained collectively by all of the independent variables. R² value close to 1 also indicates importance of regression. The regression row in Tables 8 and 9 provide information about the variation accounted by the regression model. The residual row displays information about the variation that is not explained by the regression model (Draper and Smith 1981; Montgomery et al. 2006). For example, the sum of squares values given in Table 8 show that over seventy percent of the variance in the mean particle size (x_50R) is explained by the regression model. The F test is applied to test the significance of the regression model. If the significance value of the F statistic is less than 0.05, it means that the variation explained by the model is not due to chance. In other words, the null hypothesis of no linear relationship of x_50R to the 7 independent variables is rejected. Table 8 shows a significance value of very close to zero based on the F and the degrees of freedom (df) value calculated. That indicates the importance of the developed regression equation for Group 1.

Table 8 Regression statistics obtained for Eq. 15

The equation given below was developed for Group 2 that has low elastic modulus values. Table 9 shows the regression statistics obtained for Eq. 16. Again a significance value of very close to zero was obtained under ANOVA results. All these values indicate that the regression is important and strong for Group 2.

$$ {\text{X}}_{50} = 0.60({\text{S}}/{\text{B}})^{0.547} ({\text{H}}/{\text{B}})^{0.535} ({\text{B}}/{\text{D}})^{0.427} ({\text{T}}/{\text{B}})^{ - 0.101} ({\text{Pf}})^{ - 0.115} ({\text{X}}_{\text{B}} )^{0.434} ({\text{E}})^{ - 1.202} $$

(16)

In Eqs. (15) and (16), the exponents obtained for S/B, B/D and X_B are positive. That means, the mean particle size increases with increasing S/B, B/D and X_B. The exponents obtained for T/B and PF are negative. That means, the mean particle size decreases with increasing T/B and PF. These results can be reasoned out easily intuitively. For both rock groups, the obtained exponent value for S/B is high in the regression models. It indicates that S/B is an important parameter for mean particle size prediction models. For the high modulus rock group, it has turned out to be the most important parameter. For the low modulus rock group, it has turned out to be the second most important parameter The coefficients associated with the modulus of elasticity are negative in Eqs. (15) and (16). This means increase of the elastic modulus results in decrease of the mean particle size. The modulus of elasticity is an indicator of rock stiffness. In the developed models, if the stiffness of rock increases the fragmentability of rock increases. The energy transmission velocity increases with increasing Young’s modulus. This in turn increases the fragmentability and results in lowering the mean particle size. In the developed model, H/B is positively correlated to mean particle size. This result may be explained as follows. H/B can be increased by increasing the H value and keeping the B value constant. The energy transmitted volume can be expected to increase with increasing H. If the same total energy is used under increasing H, it will result in decreasing the energy transmitted per unit volume. This will result in less fragmentability and higher mean particle size.

Table 9 Regression statistics obtained for Eq. 16

Equations 15 and 16 were applied respectively, to the 5 blasts shown in Table 4 and the 7 blasts shown in Table 5 to predict mean particle size based on the developed regression equations. The values obtained are shown in Tables 4 and 5, respectively. For all 5 blasts belonging to Group 1, the regression based predictions are close to the measured values. For the 7 blasts belonging to Group 2, apart from DB10, for the rest, the regression based predictions are close to the measured values. Figure 7c shows the regression analysis performed between the predictions based on the regression equation and the measured mean particle size. Even though the intercept of the prediction line is almost zero, the slope (equal to 0.86) is slightly off from 1.0. However, the R² value of 0.82 indicates a strong regression fit and the 95% confidence band is much tighter than the one appears in Fig. 7b. Comparison of Fig. 7b, c shows that the regression based predictions have better reliability than the predictions based on Kuznetsov’s equation. Comparison of Fig. 7a, c shows that the neural network predictions are better than the predictions based on developed multivariate regression models.

7 Discussion

Note that even though both the multivariate regression models and neural network models are non-linear models, the neural network models can be considered as more advanced non-linear models than multivariate regression models. It is important to note that neural network results do not provide a unique answer. The results depend on the factors such as network geometry, internal parameters of the learning algorithm and the simulation number. The deviation associated with the simulation number can be reduced by computing the mean value coming out of several simulations as done in this paper. For engineering and science problems, it is a difficult task to find large data bases that are suitable to use in neural network modeling. Therefore, as shown in this paper, attempts should be made to find the optimum network geometry and the best learning algorithm to obtain the best possible results for problems having a limited number of data. Best learning algorithms can be obtained as shown in the paper through numerical experimentation to minimize the mse between the predicted value and the expected value and to maximize the training speed and the stability of the calculated mse with number of training cycles. There is no universally accepted theoretical basis for choosing the network geometry. Therefore, in practical use, it should be obtained through numerical experimentation as shown in the paper to minimize the RMSE obtained between the prediction and the measured value. This will increase the workload when using the neural network approach. The learning and memory ability of a neural network depend on the training samples used. Therefore, if new data become available, to obtain accurate predictions, the network has to be rebuilt again from the very beginning.

Researchers use different procedures in estimating in situ block size. A wide variation is possible for the determination technique of the in situ block size. In the future, attempts should be made to provide uniformity in estimating the in situ block size to increase accuracy. At present, the developed models incorporate elastic modulus to represent the intact rock. In the future, attempts should be made to determine additional intact rock parameters such as uniaxial compressive strength, tensile strength, alteration and density, and discontinuity geometry parameters of the rock mass that would be subjected to blasting. It would be interesting to study whether the similarity groups emerging from the results of cluster and discriminant analyses change due to incorporation of additional parameters in the modeling procedure. This paper has looked into only the mean particle size resulting from blasting. In a future research, it is important to extend this research to cover the particle size distribution.

8 Summary and Conclusions

In a previous paper (Hudaverdi et al. 2011), many blasts performed in different parts of the world and reported in the literature were put together to create a blast data base to develop fragmentation distribution models. A hierarchical cluster analysis was used to separate the blasts data into two different groups of similarity based on the intact rock stiffness. The group memberships obtained from cluster analysis was confirmed by a discriminant analysis. A part of this blast data was used in another study (Kulatilake et al. 2010) to train a single-hidden layer back propagation neural network model to predict mean particle size resulting from blast fragmentation for each of the obtained similarity groups. The mean particle size was considered to be a function of seven independent parameters. It turned out to be a difficult assignment to find common intact rock and rock mass parameters for all the selected blast data to use in developing fragmentation distribution models. On the other hand, it was possible to find in situ block size for all the blasts in the data base. Therefore, in situ block size was used to represent rock mass structure in the developed models. With respect to intact rock, the modulus of elasticity turned out to be the most common parameter available for all the blasts and was used to represent intact rock properties in the developed models. It was possible to incorporate most of the important blast design parameters in the developed models.

Capability of the developed neural network models was determined by comparing neural network predictions with measured mean particle size and the predictions based on one of the most applied fragmentation prediction models appearing in the blasting literature. Prediction capability of the trained neural network models was found to be strong and better than the most applied fragmentation prediction model. For the same two similarity groups, multivariate regression models were also developed to predict mean particle size. The prediction capability of the multivariate regression models was also found to be strong and better than the most applied fragmentation prediction model. The prediction capability of the neural network models seems to be superior to that of multivariate regression models for the used data. No other study reported in the literature has used a large data base as that used in this study. Therefore, the diversity of the blasts data base is one of the strongest features of the developed models. The variety of the blasts is also an important element that increases the versatility and reliability of the developed models. The developed neural network models as well as multivariate regression models are not complex and are suitable for practical use at mines. As a result of this study, two different neural network models and two different multivariate regression models were developed to predict mean particle size resulting from blasting. This provides an opportunity to use a different prediction model in accordance with the value of modulus of elasticity of intact rock.

Application of the developed prediction models to new blasts will test the reliability of them. Attempts should be made to enlarge the blast database that will be used to develop fragmentation prediction models presented in this study. Neural network and multivariate statistical modeling procedures used in this paper have shown the capability of developing new fragmentation prediction models.