Seismic Passive Earth Pressure on Walls with Bilinear Backface Using Pseudo-Dynamic Approach

Abstract

By using pseudo-dynamic approach, a method has been proposed in this paper to compute the seismic passive earth pressure behind a rigid cantilever retaining wall with bilinear backface. The wall has sudden change in inclination along its depth and a planar failure surface has been considered behind the retaining wall. The effects of a wide range of parameters like soil friction angle, wall inclination, wall friction angle, amplification of vibration, variation of shear modulus and horizontal and vertical seismic accelerations on the passive earth pressure have been explored in the present study. For the sake of illustration, the computations have been exclusively carried out for constant wall friction through out the depth. Unlike the Mononobe-Okabe method, which incorporates pseudo-static analysis, the present analysis predicts a nonlinear variation of passive earth pressure along the wall.

1 Introduction

The determination of passive thrust on a retaining wall, under both static and seismic conditions, is very much essential as the damage of such earth retaining structures may lead to significant loss of life and wealth. Several investigations have been performed by different researchers to determine the passive earth pressure on a rigid retaining wall under seismic condition. Okabe (1926) and Mononobe and Matsuo (1929) provided data related to active and passive earth pressure using pseudo-static analysis. This analysis was later recognized as well known Mononobe-Okabe method (Kramer 1996) to compute the seismic earth pressure. Using upper bound limit analysis, Soubra (2000) determined both static and seismic passive earth pressure considering the multi-block mechanism. Kumar and Subba Rao (1997); and Zhu and Qian (2000) adopted the method of slices to predict the passive earth pressure coefficients. By considering the failure surface as a combination of a logarithmic spiral arc and a straight line, Kumar (2001) computed passive earth pressure coefficients for an inclined wall in the presence of horizontal pseudo-static earthquake body forces. Using the method of stress characteristics, Kumar and Chitikela (2002) reported the seismic passive earth pressure coefficients. Lancellotta (2007) determined the seismic passive resistance by using lower bound approach. In the pseudo-static analysis, the dynamic load induced by an earthquake is considered as time-independent, which eventually assumes that the magnitude and phase of acceleration are uniform throughout the backfill. Apart from this, pseudo-static analysis does not consider the variation of shear modulus throughout the backfill. To overcome this constraint, Steedman and Zeng (1990), Choudhary and Nimbalkar (2005) and Ghosh (2007) considered pseudo-dynamic approach to predict the seismic passive earth pressure behind a cantilever retaining wall. However, in practice, many a times a retaining wall does have sudden change in inclination of backface along the depth. Only a limited number of works have been carried out to estimate the thrust on such retaining walls with bilinear backface. Sokolovski (1960), Greco (2007) and Sadrekarimi et al. (2008) obtained active thrust on walls with bilinear backface. Using pseudo-static approach, Greco (2007) proposed a procedure to determine the active thrust on bilinear backface under seismic condition by simply modifying the friction angle of soil and that between soil and wall. Sadrekarimi et al. (2008) experimentally investigated the lateral pressure behind a hunched back gravity type quay walls under dynamic condition. However, considering pseudo-dynamic approach, the seismic passive thrust and pressure distribution behind a retaining wall with bilinear backface has not drawn much attention from the researchers.

This paper presents a study on the seismic passive earth pressure behind a bilinear rigid cantilever retaining wall using pseudo-dynamic analysis. The effect of non-uniform shear modulus distribution is also considered as it affects the amplification of acceleration and ultimately the magnitude of earth pressure. The present study explores the effects of soil friction angle (ϕ), angle of inclination of the upper part of wall backface (θ ₁), angle of inclination of the lower part of wall backface (θ ₂), interface friction angle between wall backface and soil medium (δ ₁ and δ ₂), horizontal earthquake acceleration coefficient (α _h ), vertical earthquake acceleration coefficient (α _v ), amplification factor (f _a ), depth exponent causing shear modulus variation (β), shear wave velocity (V _s ) and primary wave velocity (V _p ) on the seismic passive earth pressure using pseudo-dynamic approach. The limit equilibrium method, with a planar failure surface behind the retaining wall, has been considered to compute the passive resistance of the wall with bilinear backface. However, the present analysis has been performed based on the concept of small deformation, where the progressive yielding of material along the failure surface has not been considered.

2 Definition of the Problem

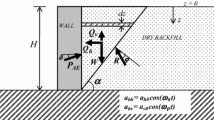
A rigid cantilever retaining wall of height H is placed with a dry, cohesionless, horizontal backfill as shown in Fig. 1. The upper (AB) and lower (BD) parts of wall face on the backfill side are inclined at an angle θ ₁ and θ ₂, respectively, with the horizontal. The wall friction angles along AB and BD are considered as δ ₁ and δ ₂, respectively. The objective is to determine the passive earth pressure coefficients and distribution by knowing the passive resistances on upper and lower parts of the wall P _pe1 and P _pe2, respectively, per unit length of the wall. The wall is subjected to a sinusoidal base shaking with linearly varying horizontal and vertical accelerations having the amplitudes of $\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right]\alpha_{h} g$ and $\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right]\alpha_{v} g$, respectively, where z is any depth below the ground surface and g is the acceleration due to gravity. The parameters shown in Fig. 1 are considered as positive and the unit weight of the soil is taken as γ.

Fig. 1

Failure mechanism and associated forces

3 Analysis

In line with the failure mechanism proposed by Greco (2007), the upper part of wall (AB in Fig. 1) experiences the passive thrust P _pe1 due to the failure wedge ABC bounded by a planar failure surface BC at an angle α _1, whereas a planar failure surface (DE) at an angle α ₂, has been considered to define the failure wedge (ABDE) for the whole wall. The passive thrusts P _pe1 and P _pe2 make angle δ ₁ and δ ₂ with the normal to the wall face AB and BD, respectively. The failure mechanism has been solved using pseudo-dynamic analysis to compute the passive resistance of the wall under seismic condition.

The pseudo-dynamic analysis, which considers finite shear and primary wave velocities, can be developed by assuming constant shear modulus G throughout the backfill and thus creating the variation in phase not in magnitude of horizontal and vertical accelerations. It is worth mentioning here that the shear modulus does not truly remain constant rather varies along the depth. However, the effect of variation in G on the lateral thrust for shallow retaining wall has been found to be not much significant and discussed later in detail. The present analysis considers both shear wave velocity $V_{s} = \sqrt {{\frac{G}{\rho }}}$ and primary wave velocity $V_{p} = \sqrt {{\frac{G(2 - 2\nu )}{\rho (1 - 2\nu )}}}$, where ρ and ν are the density and Poisson’s ratio of the soil medium, acting within the backfill during earthquake in the direction as shown in Fig. 1. The wave velocities remain constant throughout the analysis and their magnitudes in the failing wedge are assumed to be same as that in the backfill before failure. The analysis includes a period of lateral shaking T, which can be expressed as

$$ T = {\frac{{2{{\uppi}}}}{\omega }} $$

(1)

where ω is the angular frequency.

For a sinusoidal base shaking, the horizontal and vertical accelerations at any depth z below the ground surface and time t can be expressed as

$$ a_{h} (z,t) = \alpha_{h} g\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right]\sin \omega \left( {t - {\frac{H - z}{{V_{s} }}}} \right) $$

(2)

$$ a_{v} (z,t) = \alpha_{v} g\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right]\sin \omega \left( {t - {\frac{H - z}{{V_{p} }}}} \right) $$

(3)

3.1 Calculation of Passive Thrust on Upper Part (AB)

The mass of the small shaded part of thickness dz in the wedge ABC (Fig. 1) is given by

$$ m_{1} (z) = {\frac{\gamma }{g}}(H_{1} - z)(\cot \alpha_{1} - \cot {{\uptheta}}_{1} ){\text{d}}z $$

(4)

The total weight of the failure wedge W ₁ can then be derived from Eq. (4) and is given by

$$ W_{1} = {\frac{{\gamma H_{1}^{2} }}{2}}(\cot \alpha_{1} - \cot {{\uptheta}}_{1} ) $$

(5)

The horizontal inertia force exerted on the small element due to horizontal earthquake acceleration can be expressed as m ₁(z)a _h (z, t). Therefore, the total horizontal inertia force Q _h1(t) acting in the failure wedge ABC is given by the integral

$$ Q_{h1} (t) = \int\limits_{0}^{{H_{1} }} {m_{1} (z)a_{h} (z,t){\text{d}}z} $$

(6)

Similarly, the total vertical inertia force Q _v1(t) acting in the failure wedge ABC is given by

$$ Q_{v1} (t) = \int\limits_{0}^{{H_{1} }} {m_{1} (z)a_{v} (z,t){\text{d}}z} $$

(7)

The total passive resistance on the upper part P _pe1 can then be determined by considering the horizontal as well as vertical equilibrium of the wedge and is given by

$$ P_{pe1} (t) = {\frac{{W_{1} \sin (\alpha_{1} + \phi )}}{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{1} )}}} - \left[ {{\frac{{Q_{h1} \cos (\alpha_{1} + \phi ) + Q_{v1} \sin (\alpha_{1} + \phi )}}{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{1} )}}}} \right] $$

(8)

The first term on the right hand side gives the static passive thrust; whereas the last term predicts the dynamic passive thrust on the upper part of wall caused by the earthquake loading. The seismic passive earth pressure coefficient for the upper part of wall can then be obtained as

$$ K_{pe1} = {\frac{{2P_{pe1} (t)}}{{\gamma H_{1}^{2} }}} $$

(9)

It can be observed that K _pe1 is a function of α ₁, t/T, H/TV _s and H/TV _p . H/TV _s and H/TV _p are the ratio of time taken by the shear and primary wave velocity, respectively, to travel the full height H to the period of lateral shaking T. The optimization has been performed with respect to α ₁ and t/T to obtain the minimum value of K _pe1 . During optimization, the values of α ₁ and t/T have been varied in the range of 0–90° and 0–1, respectively.

3.2 Calculation of Passive Thrust on Lower Part (BD)

The mass of the small shaded part of thickness dz of the failure wedge ABDE (Fig. 1) is given by

$$ m(z) = m_{21} (z) + m_{22} (z) $$

(10a)

where

$$ m_{21} (z) = {\frac{{\gamma (H - z)(\cot \alpha_{2} - \cot {{\uptheta}}_{2} )}}{g}}\,{\text{d}}z - {\frac{{\gamma (H_{1} - z)(\cot {{\uptheta}}_{1} - \cot {{\uptheta}}_{2} )}}{g}}\,{\text{d}}z\quad 0 \le z \le H_{1} $$

(10b)

$$ m_{22} (z) = {\frac{{\gamma (H - z)(\cot \alpha_{2} - \cot {{\uptheta}}_{2} )}}{g}}\,{\text{d}}z\quad H_{1} \le z \le H $$

(10c)

The total weight of the failure wedge W can then be derived from Eq. (10) and is given by

$$ W = {\frac{\gamma }{2}}\left[ {H^{2} (\cot \alpha_{2} - \cot {{\uptheta}}_{2} ) - H_{1}^{2} (\cot {{\uptheta}}_{1} - \cot {{\uptheta}}_{2} )} \right] $$

(11)

The horizontal inertia force exerted on the small element due to horizontal earthquake acceleration can be expressed as m(z)a _h (z, t). Therefore, the total horizontal inertia force Q _h (t) acting in the failure wedge is given by

$$ Q_{h} (t) = \int\limits_{0}^{{H_{1} }} {m_{21} (z)a_{h} (z,t){\text{d}}z} + \int\limits_{{H_{1} }}^{H} {m_{22} (z)a_{h} (z,t){\text{d}}z} $$

(12)

Similarly, the total vertical inertia force Q _v (t) acting in the failure wedge is given by

$$ Q_{v} (t) = \int\limits_{0}^{{H_{1} }} {m_{21} (z)a_{v} (z,t){\text{d}}z} + \int\limits_{{H_{1} }}^{H} {m_{22} (z)a_{v} (z,t){\text{d}}z} $$

(13)

The total passive resistance on the lower part of wall P _pe2 can then be determined by taking the horizontal and vertical equilibrium of the whole wedge ABDE and is expressed as

$$ P_{pe2} (t) = {\frac{{W\sin (\alpha_{2} + \phi ) - Q_{h} \cos \left( {\alpha_{2} + \phi } \right) - Q_{v} \sin (\alpha_{2} + \phi )}}{{\sin (\theta_{2} - \delta_{2} - \phi - \alpha_{2} )}}} - P_{pe1} {\frac{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{2} )}}{{\sin (\theta_{2} - \delta_{2} - \phi - \alpha_{2} )}}} $$

(14)

In the passive state, the direction of both horizontal and vertical inertia force as shown in Fig. 1 generally causes the most critical effect on the wall under seismic condition. The seismic passive earth pressure coefficient for the lower part of wall can then be expressed as

$$ K_{pe2} = {\frac{{2P_{pe2} (t)}}{{\gamma H^{2} }}} $$

(15)

It can be observed that K _pe2 is a function of α ₂, t/T, H/TV _s and H/TV _p . Similar observation was also made earlier in case of K _pe1. The optimization has been done with respect to α ₂ and t/T to get the minimum value of K _pe2 . During optimization, the values of α ₂ and t/T have been varied in the ranges of 0–90° and 0–1, respectively. It is interesting to note, when θ ₁ becomes equal to θ ₂, the wall becomes linear and hence the points of application of the active thrust P _pe1 and P _pe2 converge into a single point and the total thrust acting on the wall can be determined from the expression provided by Ghosh (2007).

3.3 Estimation of Passive Earth Pressure

The passive earth pressure distribution behind the wall can be determined by taking partial derivative of passive thrust with respect to z. The pressure distribution along the upper part can be expressed as

$$ \begin{aligned} p_{pe1} (z,t) = \gamma z(\cot \alpha_{1} - \cot {{\uptheta}}_{1} ){\frac{{\sin (\alpha_{1} + \phi )}}{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{1} )}}} \\ & - \alpha_{h} \gamma z(\cot \alpha_{1} - \cot {{\uptheta}}_{1} )\left[ {1 + (f_{a} - 1)\frac{z}{H}} \right]\sin 2{{\uppi}}\left( {\frac{t}{T} - {\frac{z}{{TV_{s} }}}} \right){\frac{{\cos (\alpha_{1} + \phi )}}{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{1} )}}} \\ & - \alpha_{v} \gamma z(\cot \alpha_{1} - \cot {{\uptheta}}_{1} )\left[ {1 + (f_{a} - 1)\frac{z}{H}} \right]\sin 2{{\uppi}}\left( {\frac{t}{T} - {\frac{z}{{TV_{p} }}}} \right){\frac{{\sin (\alpha_{1} + \phi )}}{{\sin (\theta_{1} - \delta_{1} - \phi - \alpha_{1} )}}} \\ \end{aligned} $$

(16)

Similarly, for the lower part, the pressure distribution takes the following form

$$ \begin{aligned} p_{pe2} (z,t) = \gamma \{ z(\cot \alpha_{2} - \cot {{\uptheta}}_{2} ) - H_{1} (\cot {{\uptheta}}_{1} - \cot {{\uptheta}}_{2} )\} {\frac{{\sin (\alpha_{2} + \phi )}}{{\sin (\theta_{2} - \delta_{2} - \phi - \alpha_{2} )}}} \\ & - \alpha_{h} \gamma \{ z(\cot \alpha_{2} - \cot {{\uptheta}}_{2} ) - H_{1} (\cot {{\uptheta}}_{1} - \cot {{\uptheta}}_{2} )\} \left[ {1 + (f_{a} - 1)\frac{z}{H}} \right] \\ & & \sin 2{{\uppi}}\left( {\frac{t}{T} - {\frac{z}{{TV_{s} }}}} \right){\frac{{\cos (\alpha_{2} + \phi )}}{{\sin (\theta_{2} - \delta_{2} - \phi - \alpha_{2} )}}} \\ & - \alpha_{v} \gamma \{ z(\cot \alpha_{2} - \cot {{\uptheta}}_{2} ) - H_{1} (\cot {{\uptheta}}_{1} - \cot {{\uptheta}}_{2} )\} \left[ {1 + (f_{a} - 1)\frac{z}{H}} \right] \\ & & \sin 2{{\uppi}}\left( {\frac{t}{T} - {\frac{z}{{TV_{p} }}}} \right){\frac{{\sin (\alpha_{2} + \phi )}}{{\sin (\theta_{2} - \delta_{2} - \phi - \alpha_{2} )}}} \\ \end{aligned} $$

(17)

It can be observed from Eqs. (16) and (17) that the distribution of passive earth pressure behind the wall is nonlinear in nature which is not the case in pseudo-static analysis, which once again justifies the importance of the present study.

4 Results

The computations have been performed by writing a computer code in MATLAB. To find the minimum value of K _pe1 and K _pe2, the magnitudes of the variables α ₁, α ₂ and t/T have been varied independently at an interval of 0.01°, 0.01° and 0.001, respectively. It is worth noting here that the absolute minimum magnitudes of P _pe1 and P _pe2 do not occur at the same time rather it takes little higher time to obtain the minimum value of P _pe1 as compared to P _pe2. This time lag has been well observed during the analysis which is because of the transmission of waves from bottom to top. However, the absolute minimum magnitudes of P _pe1 and P _pe2 are obtained with a unique combination of α ₁ and t/T, and α ₂ and t/T; respectively. In the present analysis, the magnitudes of δ ₁ and δ ₂ have been kept equal (δ ₁ = δ ₂) since the variation of wall-soil interface friction along the depth is generally unlike to happen. However, if such situation arises, the passive thrust can be easily estimated from the above expressions. The results are presented for the following ranges of parameters: ϕ = 20°–50°; δ ₁ = 0 to ϕ; δ ₂ = 0 to ϕ; θ ₁ = 75°–90°; θ ₂ = 90°–120°; f _a  = 1.0–1.8; α _h  = 0–0.3; α _v  = 0.5α _h ; H/TV _s  = 0.3–0.6; and H/TV _p  = 0.16–0.32.

4.1 Seismic Passive Earth Pressure Coefficient

The variations of seismic passive earth pressure coefficients K _pe1 and K _pe2 with changes in α _h for different values of θ ₁ , θ ₂, δ ₁ and δ ₂ are shown in Fig. 2 for ϕ = 30°, H ₁/H = 1/3, α _v  = 0.5α _h , f _a  = 1.4, H/TV _s  = 0.3 and H/TV _p  = 0.16. It can be seen that the magnitude of earth pressure coefficient decreases continuously with an increase in α _h and increases with increase in the magnitude of wall friction. It can also be observed that the value of K _pe1 and K _pe2 decreases with increase in θ ₁ and θ ₂, respectively. It is important to note here that the variation of K _pe1 is unaffected with change in θ ₂, whereas the magnitude of K _pe2 changes marginally with change in θ ₁. The magnitude of seismic passive earth pressure coefficients K _pe1 and K _pe2 for different values of ϕ, δ ₁, δ ₂ and α _h with H ₁/H = 1/3, θ ₁ = 75°, θ ₂ = 100°, α _v  = 0.5α _h , f _a  = 1.4, H/TV _s  = 0.3 and H/TV _p  = 0.16 are presented in Table 1.

Fig. 2

Variation of passive pressure coefficients K _pe1 and K _pe2 with α _h for ϕ = 30°, H ₁/H = 1/3, α _v  = 0.5α _h , f _a  = 1.4, H/TV _s  = 0.3 and H/TV _p  = 0.16. (a) θ ₂ = 100° (b) θ ₁ = 75

Table 1 Values of passive earth pressure coefficients K _pe1 & K _pe2 for H ₁/H = 1/3, θ ₁ = 75°, θ ₂ = 100°, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4

4.2 Critical Collapse Mechanism

The values of the input parameters α ₁ and α ₂ associated with the critical collapse mechanisms are also presented in Table 1 for different values of ϕ, δ ₁, δ ₂ and α _h . It may be noted that the values of α ₁ and α ₂ remain generally different as the magnitudes of θ ₁ and θ ₂ differ. However, for the same value of θ ₁ and θ ₂, the α ₂ defines the failure surface and eventually forms a single triangular failure wedge (ADE). The critical values of α ₁ and α ₂ are found to decrease with increase in the magnitude of α _h .

4.3 Seismic Passive Earth Pressure Distribution

The normalized passive earth pressure distribution is shown in Fig. 3 for different values of amplification factor f _a with ϕ = 30°, δ ₁ = δ ₂ = 0.5ϕ, H ₁/H = 1/3, θ ₁ = 75°, θ ₂ = 100°, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3 and H/TV _p  = 0.16. It can be observed that for the upper part of wall the value of passive earth pressure decreases marginally with increase in the magnitude of f _a and eventually the difference in pressure becomes the maximum at the base of wall for different values of f _a . Due to sudden change in slope along the depth of wall, the point B becomes a singular point (Fig. 1) and a discontinuity occurs in the passive pressure distribution at point B, which happens at z/H = 1/3 in Fig. 3. In Fig. 4, the normalized passive pressure distribution is presented for different values of ϕ with δ ₁ = δ ₂ = 0.5ϕ, H ₁/H = 1/3, θ ₁ = 75°, θ ₂ = 100°, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4. It can be seen that the magnitude of passive earth pressure increases with increase in the value of ϕ and the discontinuity happens at the singular point (B) at z/H = 1/3 as discussed before. Figure 5 shows the normalized lateral passive pressure distribution for different values of θ ₁ and θ ₂ with ϕ = 30°, δ ₁ = δ ₂ = 0.5ϕ, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4. It is observed that the lateral passive earth pressure behind the wall decreases with increase in θ ₁ and θ ₂. The variation of passive pressure with changes in z/H for different values of wall friction and ϕ with θ ₁ = 75°, θ ₂ = 100°, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4 is presented in Fig. 6. It has been seen that for a particular value of ϕ, the magnitude of passive earth pressure increases with an increase in the value of wall friction (δ ₁ and δ ₂).

Fig. 3

Normalized passive earth pressure distribution for different values of f _a (ϕ = 30°, δ ₁ = δ ₂ = 0.5ϕ, θ ₁ = 75°, θ ₂ = 100°, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h, H/TV _s  = 0.3 and H/TV _p  = 0.16)

Fig. 4

Normalized passive earth pressure distribution for different values of ϕ (δ ₁ = δ ₂ = 0.5ϕ, θ ₁ = 75°, θ ₂ = 100°, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4)

Fig. 5

Normalized passive earth pressure distribution for different values of θ ₁ and θ ₂ (ϕ = 30°, δ ₁ = δ ₂ = 0.5ϕ, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4)

Fig. 6

Normalized passive earth pressure distribution for different magnitudes of wall friction and ϕ (θ ₁ = 75°, θ ₂ = 100°, H ₁/H = 1/3, α _h  = 0.2, α _v  = 0.5α _h , H/TV _s  = 0.3, H/TV _p  = 0.16 and f _a  = 1.4)

4.4 Influence of Shear Modulus Distribution

In the above sections, the analysis has been performed by assuming constant shear modulus in the backfill. However, in practice, shear modulus and thus both shear and primary wave velocities vary with depth, and generally in sands, the variation of shear modulus with depth can be expressed as (Steedman and Zeng 1990)

$$ G = G_{0} z^{\beta } \quad 0 \le \beta \le 1 $$

(18)

where G ₀ is a constant and z is the depth below the ground surface. The shear wave velocity may then be deduced as a function of depth z

$$ V_{s} = \left( {{\frac{{G_{0} }}{\rho }}} \right)^{1/2} z^{\beta /2} $$

(19)

where ρ is the mass density of backfill. Primary wave velocity V _p can be calculated as 1.87 V _s which is valid for most of the geological materials (Das 1993). The time increment for the passage of a shear wave from the base to a depth z will then be

$$ \Updelta t_{s} (z) = - \int\limits_{H}^{z} {{\frac{{{\text{d}}z}}{{V_{s} (z)}}}} = {\frac{{(\rho /G_{0} )^{1/2} }}{(1 - \beta /2)}}(H^{1 - \beta /2} - z^{1 - \beta /2} ) $$

(20)

Similarly, the time increment for the passage of a primary wave from the base to a depth z will be

$$ \Updelta t_{p} (z) = - \int\limits_{H}^{z} {{\frac{{{\text{d}}z}}{{V_{p} (z)}}}} = {\frac{{(\rho /G_{0} )^{1/2} }}{1.87(1 - \beta /2)}}(H^{1 - \beta /2} - z^{1 - \beta /2} ) $$

(21)

The variation of acceleration through a soil layer of reducing shear modulus also depends on damping and the interaction of reflected, refracted and surface waves in the vicinity of structure. However, assuming a constant magnitude of peak acceleration, the horizontal and vertical accelerations at depth z are given by

$$ a_{h} (z,t) = \alpha_{h} g\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right] \quad\sin \omega \left\{ {t - {\frac{{(\rho /G_{0} )^{1/2} }}{(1 - \beta /2)}}(H^{1 - \beta /2} - z^{1 - \beta /2} )} \right\} $$

(22)

$$ a_{v} (z,t) = \alpha_{v} g\left[ {1 + (f_{a} - 1){\frac{(H - z)}{H}}} \right]\quad\sin \omega \left\{ {t - {\frac{{(\rho /G_{0} )^{1/2} }}{1.87(1 - \beta /2)}}(H^{1 - \beta /2} - z^{1 - \beta /2} )} \right\} $$

(23)

By substituting a _h (z, t) from Eq. (22), the horizontal inertia force acting in wedge ABC and ABDE can then be determined from the integrals given in Eqs. (6) and (12), respectively. Similarly, the vertical inertia force acting in wedge ABC and ABDE can be obtained from Eqs. (7) and (13), respectively by substituting a _v (z, t) from Eq. (23). For values of β in the range of interest, these integrals can be solved analytically only for β = 0 and 1 and must be solved numerically for intermediate values of β. However, as the shear modulus varies with depth, it is necessary to define an average magnitude of shear and primary wave velocities as

$$ V_{savg} = {\frac{H}{{\Updelta t_{s} (z = 0)}}} = H^{\beta /2} (1 - \beta /2)\left( {{\frac{{G_{0} }}{\rho }}} \right)^{1/2} \,{\text{and}}\,V_{pavg} = 1.87V_{savg} $$

(24)

Optimizing the passive thrusts on upper and lower part of wall with respect to α ₁, α ₂ and t/T, it leads to the expression for K _pe1 and K _pe2 as a function of H/TV _savg , H/TV _pavg and β. The variation of K _pe1 and K _pe2 with α _h for different values of β are shown in Fig. 7 with ϕ = 30°, H ₁/H = 1/3, α _v  = 0.5α _h , θ ₁ = 75°, θ ₂ = 100°, f _a  = 1.4, H/TV _savg  = 0.3 and H/TV _pavg  = 0.16. It can be seen that there is not much significant difference in the values of K _pe1 and K _pe2 with change in β for lower values of α _h . However, for higher values of α _h , marginal difference can be observed in the magnitude of K _pe2. The same observation was also made by Steedman and Zeng (1990) for vertical wall and by Sreevalsa and Ghosh (2009) for non-vertical wall under active condition.

Fig. 7

Variation of passive pressure coefficients with α _h for different values of β (ϕ = 30°, θ ₁ = 75°, θ ₂ = 100°, δ ₁ = δ ₂ = 0.5ϕ, H ₁/H = 1/3, α _v  = 0.5α _h , f _a  = 1.4, H/TV _savg  = 0.3 and H/TV _pavg  = 0.16). a K _pe1 b K _pe2

5 Comparison

A limited number of investigations (Sokolovski 1960; Greco 2007; Sadrekarimi et al. 2008) have been carried out to obtain the active thrust on a retaining wall with bilinear backface. However, no significant research work is available in the literature to determine the passive thrust on wall with sudden change in slope. In Table 2, the present values of passive earth pressure coefficients for upper and lower part are compared for different values of H/TV _s and H/TV _p with H ₁/H = 1/3, δ ₁ = δ ₂ = 0.5ϕ, θ ₁ = 75°, θ ₂ = 100°, α _v  = 0.5α _h , and f _a  = 1.4. The magnitudes of K _pe1 and K _p2 obtained from the present analysis are found to decrease with increase in the values of H/TV _s and H/TV _p . As discussed earlier that for most of the geological materials V _p /V _s can be taken as 1.87 (Das 1993) and therefore, to satisfy this relationship the magnitudes of H/TV _s and H/TV _p have been decided accordingly in Table 2 (Ghosh 2008).

Table 2 Comparison of passive earth pressure coefficients K _pe1 and K _pe2 with H ₁/H = 1/3, ϕ = 30°, δ ₁ = δ ₂ = 0.5ϕ, θ ₁ = 75°, θ ₂ = 100°, α _v  = 0.5α _h and f _a  = 1.4

6 Conclusion

Using the pseudo-dynamic approach, the effects of the soil friction angle, wall inclination, wall friction angle, horizontal and vertical earthquake accelerations, amplification of vibration, variation of shear modulus, and shear and primary wave velocities on the seismic passive earth pressure behind a bilinear cantilever retaining wall have been explored. It has been found that the magnitude of seismic passive earth pressures for upper and lower parts of the wall decreases with an increase in the horizontal earthquake acceleration coefficient α _h and the wall inclinations θ ₁ and θ ₂ respectively. Unlike the pseudo-static analysis, where the passive pressure varies linearly, the seismic passive earth pressure distribution is found to be nonlinear behind the wall in pseudo-dynamic analysis. The nonlinearity of seismic passive earth pressure distribution increases with an increase in seismicity, which causes the point of application of the total passive thrust to be shifted. Both constant and varying magnitudes of shear modulus in the backfill have been considered in the present analysis. However, no significant difference in the passive thrust can be observed due to the variation of shear modulus through out the backfill. Due to the use of more rational pseudo-dynamic approach, the present values of K _pe1 and K _pe2 and pattern of passive earth pressure distribution could be used by the design engineers to design and assess the behavior of bilinear cantilever retaining wall under seismic condition.