The third Sandia Fracture Challenge: peridynamic blind prediction of ductile fracture characterization in additively manufactured metal

Abstract

In the context of the third Sandia Fracture Challenge (SFC3), the details of the blind predictions performed by the University of Texas team are provided in this article. Over the past two decades, the peridynamic theory has shown great promise in modeling autonomous crack nucleation and growth in materials. While peridynamics has been commonly applied to simulate failure of brittle materials, its ability in predicting ductile fracture has remained mostly untested. This fracture challenge was seen as an opportunity to assess the state of the art of the peridynamic theory in predicting the response of an additively manufactured 316L stainless steel bar with a complex geometry under the dynamic tensile experiments performed by Sandia National Laboratories. The performance of a recently proposed, generalized, ordinary finite deformation constitutive correspondence model, coupled with a recent state-based damage correspondence model was explored over this problem. For finite deformation material modeling, the classical elastoplastic framework of Simo was implemented within the ordinary correspondence theory. Damage modeling was achieved by incorporating the Johnson-Cook failure criterion using the damage correspondence framework. An iterative inverse technique was applied to calibrate the model parameters using the longitudinal and notched tensile tests data provided by Sandia National Laboratories. A blind prediction of the deformation and failure behavior of the SFC3 geometry was performed by embedding the calibrated model in a peridynamic simulation. Uncertainty was introduced into the model parameters to quantify material variability. The results are compared to the experiments conducted at Sandia National Laboratories. While our modeling approach led to qualitatively good results and a correctly predicted crack path, it underpredicted the load-carrying capacity of the structure and simulated an early fracture. Our post-experiment analysis identifies material instability issues associated with the model as the primary sources of error.

1 Introduction

Following the successful completion of the first two Sandia Fracture Challenges (Boyce 2014, 2016), the third of the series (SFC3) was issued by Sandia National Laboratories in January of 2017 providing an intriguing opportunity for the fracture mechanics community through a round robin format. An unbiased forum—by means of a truly blind prediction environment—was organized for the researchers to assess their current modeling capabilities in predicting ductile fracture and identify missing information necessary to improve prediction. The detailed description of the challenge input and objectives, and a comprehensive comparison and discussion on the results from all participants are provided in the leading article of SFC3 (Kramer et al. 2019). This international challenge invited volunteer participating teams to predict the deformations and failure behavior of a specially designed additively manufactured 316L stainless steel bar with a complex geometry, under dynamic tensile loading. The challenge geometry was developed to contain multiple through holes and internal cavities, which could have not been fabricated from conventional manufacturing, such that no obvious closed-form solution exists for the prediction of failure. Mechanical-test data from a set of experimental tensile tests were provided for the teams to facilitate calibration of their selected models. To ensure making purely blind predictions, without knowledge of the actual experiments, the organizers extracted experimental data from the actual testing of the challenge specimen only after the prediction submission due date in July 2017.

Participants were requested to include multiple quantities of interest, both macroscopic and local measures, in their report summarized here:

• load-displacement response of the challenge structure,

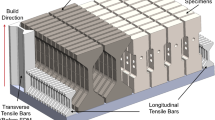
• Hencky (logarithmic) strains in the vertical direction (loading direction) at four points P1–P4 and along four lines H1–H4 on the surface, shown in Fig. 1,

• contours of vertical Hencky strains on the front view of surface at crack initiation and at complete failure.

Fig. 1

Schematic of the challenge geometry surface to denote the referenced locations in the challenge questions (P1–P4, H1–H4) and gage displacement measurement locations (P5–P10)

The University of Texas team found this challenge as an opportunity to explore the capabilities of the state of the art of the perdynamic theory in predicting ductile fracture. Peridynamics is a nonlocal reformulation of the classical solid mechanics and was initiated by Silling (2000) mainly to provide consistency in representing a mechanical system whether or not any discontinuity (e.g. cracks) is involved. Due to its capabilities in handling material failure without any complicated numerical treatments at discontinuities, the theory has been widely applied to a broad range of challenging problems, e.g. simulating nanostructures (Silling and Bobaru 2005), failure in concretes (Gerstle et al. 2007; Yaghoobi and Chorzepa 2017; Nikravesh and Gerstle 2018), crack branching phenomenon (Ha and Bobaru 2010), pitting corrosion damage (Jafarzadeh et al. 2018, 2019), intraply fracture in composites (Bobaru et al. 2018), damage in solder joints (Mehrmashhadi et al. 2019), homogenized modeling of porous materials (Chen et al. 2017), and meso-scale simulation of intra-granular fracture (Behzadinasab et al. 2018b).

This article presents a background on peridynamics and includes our reasoning in selection of appropriate material and failure models. Modeling and calibration efforts are detailed next, followed by a comparison between the blind predictions and the experimental data. Subsequently, sources of discrepancy between the results are discussed. The paper concludes with a summary and recommendations for future work.

2 Background on peridynamics

Silling (2000) introduced the peridynamic theory by extending the classical theory of solid mechanics and reformulating the balance of linear momentum in an integral form

$$\begin{aligned} \rho \frac{\partial ^{2} \mathbf {u}(\mathbf {x},t)}{\partial t^{2}} = \int _{\mathcal {H}(\mathbf {x})} \mathbf {f}\left( \mathbf {x'},\mathbf {x},t\right) \, \mathrm{d}V_{\mathbf {x'}} + \mathbf {b}(\mathbf {x},t), \end{aligned}$$

where $\rho$ is the mass density in the reference configuration, $\mathbf {u}$ is the displacement vector field, and $\mathbf {b}$ is a prescribed body force density field. $\mathbf {x}$ and t are dependent variables defining the position vector in the reference configuration and time, respectively. The integral functional on the right-hand side of the equation evaluates the internal state of a peridynamic body by relating pairwise forces between its material points.

Peridynamics, a nonlocal theory, states that the internal forces on a material point $\mathbf {x}$ is the result of its interactions with its neighbors$\mathbf {x'}$, within a finite distance, which exerts a pairwise vector-valued function $\mathbf {f}\left( \mathbf {x'},\mathbf {x},t\right)$ (with units of force per volume squared) on $\mathbf {x}$. $\mathcal {H}(\mathbf {x})$ constitutes a neighborhood set containing all the neighbors of $\mathbf {x}$ and is called the family of $\mathbf {x}$. In a 3-dimensional configuration, the neighborhood set is typically defined by a sphere with radius $\delta$, called the horizon. A peridynamic bond is a vector defined in the undeformed configuration from $\mathbf {x}$ to a neighbor $\mathbf {x'}$, typically given the symbol $\varvec{\xi }=\mathbf {x'}-\mathbf {x}$. An example of a peridynamic body is given in Fig. 2.

Fig. 2

A nonlocal peridynamic body in its reference, undeformed configuration with horizon $\delta$

The state-based peridynamics (Silling et al. 2007)—a generalized peridynamic framework and the most commonly one used today—expresses the pairwise force function in a general form

in which denotes the peridynamic force-vector state and maps a bond $\langle {\mathbf {x'}-\mathbf {x}} \rangle$ in its deformed configuration to its force state. is governed by constitutive relations and generally depends upon the deformation of the neighborhood set. In addition, it can be related to other parameters such as the history of deformation (plastic deformation), temperature, deformation rate, etc.

2.1 Finite deformation modeling

Silling et al. (2007) introduced a correspondence modeling framework by providing a bridge between local and peridynamic material models through kinematic variables to enable incorporating the well-established classical constitutive theories into peridynamics. Later, Tupek and Radovitzky (2014) identified some shortcomings associated with the model, such as the unphysical issue of matter interpenetration, which are allowed within the peridynamic formulation and would impose practical difficulties, especially in dealing with large deformations. As a remedy, they introduced the notion of non-linear bond strain measures in peridynamics and extended the original theory. Their model was recently generalized by Foster and Xu (2018), who presented a constitutive correspondence framework with kinematic variables (e.g. a nonlocal right Cauchy–Green deformation tensor) that can be applied directly to finite deformation plasticity and does not suffer from surface effects, a well-known issue in peridynamics. The generalized, ordinary, finite deformation correspondence theory of Foster and Xu (2018) uses the second Piola–Kirchhoff (P–K) stress as an intermediate quantity in determining the bond force. Suppose the mechanical response of a classical family of hyperelastic materials is described by the second P–K stress ($\mathbf {S}$) in a body as:

$$\begin{aligned} \mathbf {S}(\mathbf {x}) = \hat{\mathbf {S}}(\mathbf {C}(\mathbf {x})), \qquad \mathbf {C}(\mathbf {x}) = \mathbf {F}^T \mathbf {F} = \left( \frac{\partial \mathbf {y}}{\partial \mathbf {x}}\right) ^T \frac{\partial \mathbf {y}}{\partial \mathbf {x}}, \end{aligned}$$

where $\mathbf {C}$ is the right Cauchy–Green deformation tensor, rooted to the deformation gradient tensor $\mathbf {F}$. $\mathbf {C}$ is approximated by the peridynamic finite deformation correspondence theory as:

where is a positive-valued weight function called the influence state, describing the relative degree of interactions between material points; is the deformation state, mapping bonds onto their deformed images; and $\mathbb {L}$ is a super-symmetric fourth-order shape tensor defined by

(1)

Then the force state in a finite deformation correspondence material is given by

in which $\mathbf {S}=\mathbf {S}(\bar{\mathbf {C}})$.

The classical elastoplastic framework of Simo (1988a) has been widely accepted for finite deformations modeling. The theory is established upon a multiplicative decomposition of the deformation gradient into elastic and plastic parts; kinematically speaking,

$$\begin{aligned} \mathbf {F} = \mathbf {F^e} \mathbf {F^p} . \end{aligned}$$

Therefore, the right Cauchy–Green deformation tensor and its plastic part are related to the deformation gradient and its associated plastic part through the following relations:

$$\begin{aligned} \mathbf {C} = \mathbf {F}^T \mathbf {F}, \qquad \mathbf {C^p} = \mathbf {F^p}^{T} \mathbf {F^p} . \end{aligned}$$

To make the case suitable for metal plasticity, the deformation gradient is further split into a volumetric and a deviatoric response

$$\begin{aligned} \mathbf {F}&= J^{1/3}\; \bar{\mathbf {F}} , \\ \mathbf {C}&= J^{2/3}\; \bar{\mathbf {C}} , \end{aligned}$$

in which $J=det(\mathbf {F})=\sqrt{det(\mathbf {C})}$.

An uncoupled form of the free energy is introduced by Simo (1988a)

$$\begin{aligned} \hat{\varPsi }(\mathbf {C^p}^{-1},\mathbf {C}, \mathbf {Q}) = \mathrm{U}(J) + \hat{\varPsi }_{dev}(\bar{\mathbf {\mathbf {C}}},\mathbf {C}^{\mathbf {p}}) + \varXi (\mathbf {Q}) , \end{aligned}$$

(2)

where $\mathbf {Q}$ constitutes a set of internal plastic variables that characterizes the plastic response

$$\begin{aligned} \dot{\mathbf {Q}} = \dot{\gamma }\mathbf {H}(\mathbf {C}, \mathbf {C^p}, \mathbf {Q}) , \end{aligned}$$

in which $\mathbf {H}(\mathbf {C}, \mathbf {C^p}, \mathbf {Q})$ is a prescribed plastic hardening moduli.

Inspired by Ciarlet (1988), the following convex stored-energy function is considered:

$$\begin{aligned} \mathrm{U}(J) = k \frac{J^2-1}{4} - \frac{k}{2} ln\, J , \end{aligned}$$

(3)

where k is the bulk modulus. The deviatoric-energy function is adopted as (Simo and Hughes 2006):

$$\begin{aligned} \hat{\varPsi }_{dev}(\bar{\mathbf {C}},\mathbf {C}^{p}) = \mu \left( \mathbf {C^p}^{-1}:\bar{\mathbf {C}}-3\right) , \end{aligned}$$

(4)

in which $\mu$ is the shear modulus.

Using Eqs. (2)–(4) and the hyperelasticity relation $\mathbf {S} = 2 \dfrac{\partial \hat{\varPsi }}{\partial \mathbf {C}}$, the second P–K stress is governed by

$$\begin{aligned} \mathbf {S} = k \frac{J^2-1}{2} \, \mathbf {C}^{-1} + \mu \, J^{-2/3} \, \mathbf {DEV}\left[ \mathbf {C^p}^{-1}\right] , \end{aligned}$$

where $\mathbf {DEV}$ is the deviatoric function in the material frame

$$\begin{aligned} \mathbf {DEV}[\cdot ]:=(\cdot )-\frac{1}{3}\left[ \mathbf {C}:(\cdot )\right] \mathbf {C}^{-1} . \end{aligned}$$

Plastic deformation is described based on Von-Mises yield criterion

$$\begin{aligned} \phi (\mathbf {C}, \mathbf {C^p}) = \sigma _e - \sigma _y \le 0 , \end{aligned}$$

in which $\sigma _y$ and $\sigma _e$ are the yield and effective stresses, respectively.

$$\begin{aligned} \sigma _e&= \sqrt{\frac{3}{2} (\mathbf {DEV\; S})_{IJ} \,(\mathbf {DEV\; S})_{KL} \mathbf {C}_{IK} \mathbf {C}_{JL}} \, , \nonumber \\&= \mu \, \mathrm{J}^{-{\textstyle {\frac{2}{3}}}} \sqrt{\frac{3}{2}\left( \mathbf {C^p}^{-1} \mathbf {C}\right) :\left( \mathbf {C} \mathbf {C^p}^{-1}\right) - \frac{1}{2}\left( \mathbf {C^p}^{-1}:\mathbf {C}\right) ^2} . \end{aligned}$$

The principle of maximum plastic dissipation is invoked by Simo (1988a) to describe the plastic flow

$$\begin{aligned} \dfrac{\partial }{\partial t}\left( \mathbf {C^p}^{-1}\right) = -2\dot{\gamma } \left( \mathbf {C^p}^{-1}:\mathbf {C}\right) \mathbf {N} , \end{aligned}$$

where $\mathbf {N}$ is the yield surface normal direction

$$\begin{aligned} \mathbf {N} = \frac{3}{2}\frac{\mathbf {DEV \; S}}{\sigma _e}. \end{aligned}$$

A power-law hardening material is a generic model capable of capturing metal plasticity. Since the peridynamic finite deformation correspondence model is limited to isotropic materials, an isotropic power-law rule is used to model the hardening response of the material

$$\begin{aligned} \sigma _y = \sigma _0 \left( 1+\frac{\bar{\varepsilon }^p}{\varepsilon _0}\right) ^n , \end{aligned}$$

where $\varepsilon _0$, n, and $\sigma _0$ are the hardening parameters, and $\bar{\varepsilon }^p$ is the effective plastic strain

$$\begin{aligned} \dot{\bar{\varepsilon }}^p = \sqrt{\frac{2}{3}}\dot{\gamma } . \end{aligned}$$

A negligible strain rate dependency is assumed as the displacements are applied slowly. No temperature dependency is considered either.

The numerical integration scheme including the elastic trial step and plastic return mapping is similar to the one detailed in Simo (1988b) with slight modifications. For brevity, it is sufficed to refer the interested reader to the cited work.

2.2 Failure modeling

Irreversible bond breakage is typically employed in peridynamics to achieve damage modeling. Critical stretch failure criterion (Silling 2000) is a common approach for incorporating material failure. While this model was originally developed for bond-based peridynamics, it has been widely used in the state-based theory, which is arguable (Foster et al. 2011; Tupek et al. 2013). Although the application of the critical stretch failure criterion may be justifiable to simulating failure of brittle materials (Ha and Bobaru 2010; Behzadinasab et al. 2018a; Mehrmashhadi et al. 2019), it is certainly too simplistic to accurately predict ductile fracture.

Tupek et al. (2013) presented a state-based damage correspondence framework to embrace classical (local) failure models within the peridynamic formulation. In their theory, the influence state is decomposed into two parts

in which is the conventional (spherical) influence function, describing the relative degree of interaction between neighboring material points in the undamaged frame of material, and is a non-increasing function of the damage stateD. In this notation $D = D(\mathbf {x},t)$ and $D' = D(\mathbf {x'},t)$. This function is valued 1 for a virgin material and 0 for a completely damaged one. In this setting, the spherical part of the influence function is adopted as

which is a common approach in peridynamic modeling. The damage-based part of the influence function is chosen in a similar manner to element deletion in finite elements, i.e.,

In this manner a material point loses all its interactions with the body (except for the contact forces if a self-contact feature is considered) once its damage exceeds a critical value.

Influence of stress triaxiality and ductility on failure of metallic alloys are widely accepted. Therefore, the classical Johnson–Cook failure criterion (1985) was chosen to govern the evolution of damage

$$\begin{aligned} D = \int _0^t \dot{D} \, \mathrm{d}\tau , \qquad \dot{D} = \dfrac{\dot{\bar{\varepsilon }}^p}{\varepsilon _f} , \end{aligned}$$

with $\varepsilon _f$ defined as

$$\begin{aligned} \varepsilon _f = d_1 + d_2 \, \mathrm{exp}\left( -d_3 \frac{\sigma _m}{\sigma _e}\right) , \end{aligned}$$

where $d_1$, $d_2$, $d_3$ are material parameters, and $\sigma _m$ is the hydrostatic part of stress defined by

$$\begin{aligned} \sigma _m = \frac{1}{3} \mathbf {S}:\mathbf {C} . \end{aligned}$$

3 Modeling and calibration details

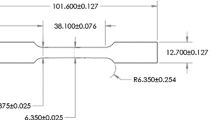
The material and damage models, formulated in the previous section, were implemented in Peridigm (Parks et al. 2012), which is an open-source, massively parallel peridynamic code, originated from Sandia National Laboratories. Because the material model was limited to isotropic materials, the transverse tensile data was neglected, and only the longitudinal and notched experimental data sets were utilized for calibrating the model parameters. With respect to the longitudinal tensile data, since no strain rate dependency was included, only the data initially provided by Sandia Labs were used: AM-finish longitudinal specimens pulled in tension at a rate of 0.05 mm/s. Notched tests were performed with a loading rate of 0.015 mm/s. To enhance computational efficiency, only the gage sections of the specimens were considered in our modeling. CUBIT Mesh Generation Toolkit (Blacker et al. 1994) was used to generate the geometries and their discretized forms. Each geometry was first discretized in a near uniform manner with tetrahedral elements of edge length 0.16 mm (this specific number was chosen such that 25 layers of peridynamic node exist along the thickness of the challenge geometry, which was believed to result in a refined enough particle discretization), then peridynamic nodes were placed on the centroid of each element. This procedure resulted in 7, 17, and 25 through-thickness layers of (peridynamic) nodes and 8859, 115,618, and 397,801 total number of nodes for the longitudinal, notched, and challenge specimens, respectively, with each node having 3 degrees of freedom. A typical horizon size in peridynamics equals 2.5 to 3 times the average node spacing. A horizon size of 0.43 mm was adopted in this work. As we were facing a time limit in this project, no effort was attempted to study the effect of different discretization schemes. Therefore, the same average mesh and horizon sizes were used for all three geometries.

Explicit dynamic time integration was used in the simulations. Direct displacement control was employed to apply boundary conditions, where the displacements were prescribed on 5 layers of peridynamic nodes at each end. To expedite the simulations, since no strain rate dependency was involved, boundary conditions were exerted at a faster rate than the experiments, 1 m/s in this case (an alternative approach would be to utilize mass scaling with a larger time step size). While the adopted loading rate sounds a lot higher than the experimental counterpart, the inertia effects are considered ignorable except for the early loading stage (part of the elastic region). This conclusion was made after comparing the simulation results of the longitudinal test with three different loading rates 1 m/s, 0.1 m/s, and 0.01 m/s. The higher applied rate was used throughout the simulations for efficiency. For the calibration tests, a time step size of 20 ns was used. The corresponding value for the prediction phase was 16 ns. All the simulations were performed on the Texas Advanced Computing Center (TACC) Stampede and Stampede2 clusters. 2040 processors were utilized to simulate the challenge problem in 2 h.

Fig. 3

Tetrahedral elements, with average edge of 0.16 mm, were used to discretize models of the gage sections of the a longitudinal and b notched test geometries. Peridynamic nodes were then placed at the centroid of each element and assigned with the associated cell volume. Units are in mm

Fig. 4

An iterative process to calibrate the model involving an inverse method. Multiple peridynamic simulations were initially performed with an engineering sense to find reasonable model constants (by comparing the simulation results with the experiments) and choose the specific range of parameters listed in the first block

The calibration geometry models in discretized form are shown in Fig. 3. Eight material and failure constants needed to be calibrated: two elasticity moduli (the Young’s modulus E and the Poisson’s ratio $\nu$), three hardening parameters ($\sigma _0$, $\varepsilon _0$, n), and three failure variables ($d_1$, $d_2$, $d_3$). The elasticity constants were determined first, where E was obtained by calculating the slope of the stress-strain curve from the longitudinal tensile data through fitting the best line to its elastic region. $\nu$ was decided to be 0.3, a typical value for stainless steel; the associated error was argued to be ignorable since the plastic behavior of the structure was expected to dominate its response. Then the Dakota project (Adams et al. 2014), an open-source, robust, and efficient optimization software, was utilized to select the other parameters through a genetic optimization algorithm engaging an inverse method illustrated in Fig. 4. The process involved peridynamic simulations of the calibration experiments with trial model constants, then comparison of the resulting load-displacement plots to the experimental results and computing the error. The objective was to minimize the following error function:

$$\begin{aligned} \varPsi = \psi _L + \psi _N , \qquad \psi = \sum _{j=1}^m \frac{\left| F_j^{sim} - F_j^{exp}\right| }{F_j^{exp}} , \end{aligned}$$

(5)

where $\psi _L$ and $\psi _N$ are the relative errors between the simulation and experiment for longitudinal and notched tests, respectively. In the definition of the relative error $\psi$, $F_j$ is the load at the jth level of elongation for m number of levels of elongation, which was taken to be 200. $F_j^{exp}$ was calculated by averaging the experimental loads for each strain data point.

Table 1 Tuned model parameters, extracted by the optimization procedure involving an inverse method

Fig. 5

Comparison of the load-displacement results from the model and experiments for the a longitudinal and b notched calibration tests. Gray color indicates the experimental data, and black shows our model results. A large variability in the bulk response of the structure is seen in the experimental data

In order to pursue an efficient optimization scheme, a reasonable range of values was assigned to each variable, then the best set (resulting in the least error defined in Eq. (5)) was found through the Efficient Global Optimization (EGO) method of Dakota. The hardening constants were calibrated by considering the range of data before the crack initiation—before the softening begins. Note that the failure model does not play any role before damage reaches a threshold value; thus, the damage model was turned off during the calibration of hardening rule. Finally, the failure parameters were tuned by simulating the whole range of the experiments. The calibrated variables are provided in Table 1, and the resulting load-displacement curves are plotted in Fig. 5. A good agreement is observed between the simulations and experiments. A comparison of the logarithmic strain contours at an instance of the notched tensile test is made between the experimental DIC measurements and peridynamic results, shown in Fig. 6.

Fig. 6

The strain contours for the notched tensile test are in qualitatively good agreement between a the peridynamic simulation and b the experimental DIC measurements. The snapshots correspond to Gage Displacement of 0.3 mm

4 Blind predictions

As described in the previous section and shown in Fig. 7, the gage section of the challenge geometry was modeled and meshed with tetrahedral elements in a semi-uniform way, then peridynamic nodes were placed on the centroid of each cell.

Fig. 7

Gage section of the challenge geometry was modeled and discretized using tetrahedral elements with average edge 0.16. Peridynamic nodes were then placed at each element centroids and assigned with the corresponding cell volumes. Units are in mm

Fig. 8

Contours of vertical Hencky strains compared between the experimental DIC measurements and prediction at a–b crack initiation and c–d complete failure

A considerable variability in the bulk response of the material was evident from the given calibration data—see Fig. 5. The variation were attributed to two main factors: small geometrical differences between the samples (imperfections from manufacturing) and material variations due to different thermal distributions during additive manufacturing. Due to a limited time frame, we sufficed to the nominal geometrical values and did not explicitly model each individual sample in our modeling. Instead, uncertainty was introduced into the material parameters. Corresponding to the evident scatter in the tensile load displacement data in the hardening regime, a range of $\sigma _0$ values from 5% lower to 5% higher than the nominal value was considered (510–562 MPa). To address the variability in the failure response, $d_1$ was varied from 0.02 to 0.08, $d_2$ from 2 to 3, and $d_3$ from 2.7 to 3.3. Blind simulations of the challenge problem over the range of material constants were performed next.

The correct crack path was captured from our blind predictions. As shown in Fig. 8, the failure initiated near the intersection between the through hole and the angled channels, then propagated along the channels. It is interesting to note that our model predicted that the crack nucleation did not exactly start at the intersection—see Fig. 9.

Fig. 9

Our simulations show that failure initiated near the inner corners of the intersection between the through hole and the angle channels. Damage contours shown in b correspond to the front view of the clipped blue segment of a zoomed along the yellow line. For the sake of visualization, peridynamic nodes are shown with spheres. The legend only applies to b

The macroscopic load-displacement response of the structure is compared between the blind predictions and experimental data in Fig. 10. The curves show an initial elastic behavior of the structure, followed by a nonlinear hardening response, and eventually a softening phenomenon due to crack initiation and growth. Evidently, our modeling approach underestimated the hardening behavior of the material and resulted in an early failure. The transition period from crack initiation to complete failure also took longer in our simulations.

Fig. 10

Macroscopic behavior of the challenge specimen compared between the simulations and experiments. The blind predictions resulted in an underestimation of the load-carrying capacity of the structure and an early prediction of crack initiation

Figure 11 illustrates histories of the vertical logarithmic strains at the points P1, P2, P3, and P4. For each plot, the strains initially increase with the loading and eventually reach a plateau. The strain values at P3 and P4 are much higher than P1 and P2, which is expected as we already know that the fracture initiated closer to the former points.

Figure 12 shows the vertical Hencky strains along the lines H1, H2, H3, and H4. The complex patterns are rooted to the existence of multiple holes and cavities. For example, strain values drop over the middle part of H2, which must be related to the channels and the spherical cavity underneath. H4 is the closest line to the location of failure initiation and has the largest strain values amongst all.

As shown in Fig. 8, the overall patterns of the predicted vertical Hencky strain contours qualitatively resemble the experimental DIC measurements; however, there are evident differences in the strain values, especially at the crack initiation instance. Similarly, our blind predictions were able to qualitatively capture the overall trend of the local strains but not quantitatively. As perceived from Figs. 11 and 12, our approach overpredicted the strains initially but underpredicted later (similar to the early crack initiation of our predictions).

5 Post-experiment analysis and sources of discrepancy

Fig. 11

Histories of the vertical logarithmic strains at a P1, b P2, c P3, and d P4 over the course of loading. Peridynamic blind simulations overpredicted the values earlier but underpredicted later

Fig. 12

Comparison of the simulation and experimental results of vertical logarithmic strains along 4 lines a H1, b H2, c H3, and d H4 at four instances of loading F1, F2, F3, and F4. Peridynamic blind simulations overpredicted the values earlier but underestimated later

Post-experiment analysis showed that the model could recover the load-displacement response of the challenge structure with different model parameters, shown in Fig. 13. Effect of the horizon size on the macroscopic behavior was also studied. As should be expected, keeping the material parameters constant, a smaller horizon size would reduce the non-locality and hence lead to a localization in plasticity and damage, i.e., a reduced plastic zone and an increased tendency to failure. Therefore, as shown in Fig. 14, a smaller horizon would result in a smaller load-carrying capacity and an earlier crack initiation. A similar study can also be carried out on the effect of different influence functions. In this work the spherical influence function takes only values of 1 and 0. Alternative choices include linear, exponential, and power-law degradations of with respect to $|\varvec{\xi }|$. It must be pointed out that the proper way to use a different horizon (or a different influence function) would be to recalibrate the model using the new horizon size (influence function). However, we did not conduct such study since our analysis identified some instability issues inherent in the model as described later in this section.

It is evident from the tension tests data that the yield stress is considerably higher (approximately 15%) in the transverse direction than the longitudinal. Hence, the lack of anisotropy in our model was initially speculated as a major origin of error. However, it was learned that some other participating teams (most notably teams E-K) did not consider anisotropy in their models, yet captured the hardening regime very well. Two factors were found later to be the main sources of discrepancy in our results.

Post-experiment assessment revealed that material instability issues (different from numerical instabilities) exist within the peridynamic generalized, ordinary, finite deformation constitutive correspondence model under compression loading (Behzadinasab and Foster 2019). Our analysis showed that while the model is superior to the previous peridynamic non-ordinary correspondence model (Silling et al. 2007) in dealing with tensile forces, even small compressions around a material point can lead to instabilities. The instability issue is in fact rooted to the application of the classical right Cauchy–Green deformation tensor (the peridynamic finite deformation model corresponds to this kinematic measure), which has a well-know compression issue such that large degrees of material compression lead to instabilities. The exposure of the nonlocal integral operator has exaggerated the problem to the extent that very small compressions (as little as 0.1%) can cause instability (Behzadinasab and Foster 2019). These material instabilities can manifest as premature material damage, thus undermine reliability of the results. Although this fracture challenge dealt mostly with tensile forces, there still exist compression states due to the existence of several holes and channels in the structure of the challenge material (and around the notches in the notched specimen), also because of the dynamic nature of loading through wave propagation. Nevertheless, due to the dominance of tensile forces in this challenge, our blind predictions yielded the correct crack path and captured the bulk response trend reasonably well. The mismatch would have been larger if more extensive compression was involved.

Fig. 13

Post-experiment analysis showed that the model could recover the macroscopic response with a different set of material parameters. Black line represents the peridynamic simulation and other colors indicate experimental data

Fig. 14

Effect of horizon size on the macroscopic response. Decreasing the horizon size leads to localization in damage, resulting in an earlier failure

Fig. 15

A large deformation scenario which the damage model cannot handle due to use of a Lagrangian framework. For simplicity a 2-D setup is considered where a circular neighborhood defines the family of the orange point in the undeformed configuration. The red color shows the points that are located near the crack surface in the current configuration, hence have reached the threshold damage and lost all their associated bonds. The green points are the only peridynamic nodes having unbroken bonds with the orange point in the Lagrangian, undeformed neighborhood. It is readily confirmed that these remaining bonds form a rank deficient, thus non-invertible shape tensor (Eq. (1)). The situation is similar in 3-D

We also attribute some of the errors after crack initiation to our failure modeling. Relying on a Lagrangian frame when extensive damage occurs around a material point under large deformations can induce additional errors. Suppose a peridynamic family becomes very distorted as it goes under large deformations, as shown in Fig. 15. In that case, if a crack passes through the neighborhood and breaks many of the bonds, the remaining unbroken bonds in the undeformed configuration may constitute a rank deficient, thus non-invertible shape tensor (defined in Eq. (1)). Due to numerical errors, a computer may not detect such tensor as singular (by calculating its determinant to be a small, yet non-zero value), hence continue with the simulation, leading to large errors afterwards. To remedy this problem, a Semi-Lagrangian framework can be effective in constructing family of peridynamic nodes in the current configuration, to ensure that every node has enough intact bonds in calculating its shape tensor (and the corresponding nonlocal kinematic variables). A study on the use of Semi-Lagrangian kernels for peridynamics is currently being undertaken.

6 Concluding remarks

The third Sandia Fracture Challenge was seen as an opportunity by the University of Texas team to assess the state of the art of the peridynamic modeling of ductile fracture. The details of our simulations in response to the challenge problem were presented in this article. Two recent material and damage correspondence models were used to leverage the well-developed local theories within the peridynamic framework. The classical elastoplastic theory of Simo (1988a) was used within the generalized, ordinary, finite deformation constitutive correspondence model of peridynamics (Foster and Xu 2018). The state-based damage correspondence framework (Tupek et al. 2013) also enabled the application of Johnson–Cook failure criterion (Johnson and Cook 1985) to this modeling. Our blind predictions correctly captured the location of crack initiation and its growth path. Overall, our results were in good qualitative agreement with the experiments—with many similarities in the patterns of local strain measurements and the trends of the macroscopic and microscopic measures. However, our modeling approach underestimated the load-carrying capacity of the structure and predicted an earlier fracture. Our post-experiment analysis revealed two major reasons behind the discrepancy. First, the peridynamic finite deformation correspondence model exhibits material instability issues in dealing with compression loading. The second source of error is attributed to the use of Lagrangian frames within the correspondence theory (in calculating a shape tensor and a nonlocal kinematic variable) that can induce large instability errors when severe damage occurs around a material point undergoing extremely large deformations—which is expected in ductile failure. Future work will seek to incorporate application of Semi-Lagrangian kernels to the peridynamic framework.