A state-based peridynamic model for quantitative fracture analysis

Abstract

A new state-based peridynamic model is proposed to quantitatively analyze fracture behavior (crack initiation and propagation) of materials. In this model, the general relationship of the critical stretch and the critical energy release rate is for the first time obtained for the state-based peridynamic model of linear elastic brittle materials, and the released energy density is defined to quantitatively track the energy released during crack propagation. The three-dimensional (3D) and two-dimensional (2D) (for both plane stress and plane strain) cases are all considered. As illustrations, the compact tension and double cantilever beam tests are analyzed using the proposed model, which is capable of successfully capturing fracture behaviors (e.g., crack path and concentration of strain energy density) of the considered fracture tests. The characteristic parameters (i.e., critical load, critical energy release rate, etc.) are calculated and compared with available experimental and numerical data in the literature to demonstrate validity of the proposed model.

1 Introduction

It is significant in engineering design to accurately predict fracture behavior of materials. Although experimental tests remain the best way to catch accurate results, numerical tools are much effective for complex structures with less cost. Thus, numerical prediction of crack growth has attracted much attention.

Most used numerical methods, e.g., finite element method (FEM), are naturally unsuitable to fracture analysis because of its requirement of displacement continuity for classical continuum mechanics. Various remedies, such as extended finite element method (Belytschko and Black 1999), were proposed to handle the shortcoming of FEM. Though the XFEM has been successfully applied for a number of fracture problems, the external criteria (Baydoun and Fries 2012) are still needed when it is employed to intricate problems. The theory of peridynamics was first proposed by Silling (2000) to overcome the limitations of classical continuum mechanics, particularly in dealing with discontinuity problems. Instead of partial differential equations used in the governing equations of continuum mechanics, the integral-differential equations are established in peridynamics to avoid the displacement derivatives, which are not defined in discontinuous field. Thus, the peridynamic model can effectively handle discontinuity problems, such as crack initiation and propagation.

The first proposed peridynamic (PD) model, so called “bond-based” (Silling 2000), assumes that points are connected with bonds through spring-like interactions and the response in a bond is independent of any other bonds. However, this assumption has constraints on material properties and restricts the types of materials. More general formulation was proposed as state-based peridynamic model (Silling et al. 2007), and the bond force density between points depends on the deformation of the points of whole family. In addition, a two-dimensional ordinary, state-based peridynamic model (Le et al. 2014) was proposed for linear elastic solids.

While peridynamics was primarily proposed to deal with the problems involving discontinuities, the suitable damage models are necessary and important for quantitative analysis of fracture problems. Silling and Askari (2005) first proposed the bond damage criterion for prototype microelastic brittle material and presented the relationship between the critical stretch for bond failure and the critical energy release rate of material. This model was used to analyze dynamic brittle fracture (Ha and Bobaru 2011), and it was later extened for damge predictions of concrete (Gerstle et al. 2007), composite material (Xu et al. 2007), orthtropic media (Ghajari et al. 2014), interface delamination (Hu et al. 2015), and bimaterial structures (Zhang and Qiao 2018). Furthermore, Hu et al. (2012) presented the formution of the J-intergral in the framework of bond-based peridynamics.

However, the aforementioned damage models for fracture analysis were all proposed using the bond-based peridynamic model. In the state-based peridynamic model, two connected points affect each other with collection of the deformation of the entire family. But the existing damage model in the framework of bond-based peridynamics model is not feasible for peridynamic state. Instead, Foster et al. (2011) proposed an energy-based failure criterion which can be used in peridynamic state, and the critical energy density for bond failure was defined and derived from the critical energy release rate of material. However, it is not easy to calculate the strain energy density stored in each neighboring bond in the state-based peridynamic model because of the nonlinear relationship between force scaler and extension scaler of the bond. Thus, it is necessary to develop state-based peridynamic model for fracture analysis and obtain new form of critical stretch in the context of state-based peridynamic model for potential quantitative fracture analysis.

In this paper, a peridynamic damage model for fracture analysis is proposed with the new form of critical stretch considering peridynamic state, and the fracture tests using the compact tension (CT) and double cantilever beam (DCB) specimens are quantitatively analyzed. First, the general state-based peridynamic model applicable for both the 3D and 2D cases is presented, and the relationship between the state-based and bond-based peridynamic models is introduced. A state-based peridynamic damage model for linear elastic brittle materials is proposed, and the new form of critical stretch considering peridynamic state is given. The parameter of energy release density is defined to quantitatively track the energy released during crack propagation. The quantitative fracture analysis and convergence study of the CT test are performed using the crack length (a) to specimen width (w) ratio $a{/}w = 0.5$, followed by the damage predictions of the CT specimens with different values of a / w. While fracture behavior of DCB test is analyzed with the proposed damage model, the critical load predictions of DCB specimens with different crack lengths are discussed. The characteristic parameters (e.g., critical load and critical energy release rate) are calculated and compared with available experimental and numerical data in the literature.

2 Review of peridynamic models

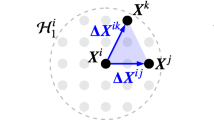
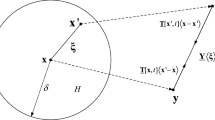
In the general state-based peridynamic model (Silling et al. 2007), the equation of motion of the material point x is:

$$\begin{aligned} \rho \left( {{\varvec{x}}} \right) \ddot{{\varvec{u}}}\left( {{\varvec{x}},t} \right)= & {} \int _{\mathrm{H}_x } \left\{ {{{{\underline{\varvec{T}}}}}}\left[ {{{\varvec{x}}},t} \right] \left\langle {{{{\varvec{x}}}}'-{{\varvec{x}}}} \right\rangle \right. \nonumber \\&\left. -\,{{{{\underline{\varvec{T}}}}}}\left[ {{{{\varvec{x}}}}',t} \right] \left\langle {{{\varvec{x}}}-{{{\varvec{x}}}}'} \right\rangle \right\} dV_{{{{\varvec{x}}}}'} +{{\varvec{b}}}\left( {{{\varvec{x}}},t} \right) \nonumber \\ \end{aligned}$$

(1)

where $\hbox {H}_{x}$ is the neighborhood of point x, $\rho$ is the density, and u is the displacement of x at time t. ${{{\varvec{x}}}}'$ is the material point in the neighborhood of x, and ${{\varvec{b}}}\left( {{{\varvec{x}}},t} \right)$ is the body force density of the point x. As shown in Fig. 1, ${{{{{\underline{\varvec{T}}}}}}}\left[ {{{\varvec{x}}},t} \right]$ and ${{{{{\underline{\varvec{T}}}}}}}\left[ {{{{\varvec{x}}}}',t} \right]$ are the force vector states that show the constitutive models of points x and ${{{\varvec{x}}}}'$, respectively.

Fig. 1

Ordinary state-based peridynamic model

In this section, a general state-based peridynamic model available for both the 3D and 2D cases is first presented. The relationship between the state-based and bond-based peridynamic models is discussed.

2.1 General peridynamic model

For the linear elastic isotropic material, the general strain energy density of material point x in the peridynamic model can be expressed as (Silling 2000):

$$\begin{aligned} W=\frac{a\theta ^{2}}{2}+\frac{b}{2}\left( {\underline{\omega }\underline{e}^{d}} \right) {\cdot }\underline{e}^{d} \end{aligned}$$

(2)

where a and b are the peridynamic constants, respectively. $\underline{\omega }$ is the influence function, $\theta$ is the volume dilatation, and $\underline{e}^{d}$ is the deviatoric extension state. The dot product $\left( {\cdot } \right)$ is defined in Silling (2010). As described in Silling (2010), those parameters in the case of 3D take forms of:

$$\begin{aligned} \theta =3\frac{\underline{\omega x}{\cdot }\underline{e}}{q},\quad \underline{e}^{d}=\underline{e}-{\theta \underline{x}}/3,\quad a=k,\quad b=\frac{15\mu }{q} \end{aligned}$$

(3)

where k and $\mu$ are the bulk and shear modulus, respectively. x is the scaler state whose value at the position ${\varvec{\xi }}$ is the scaler bond length $\left| {\varvec{\xi }} \right|$, e is the extension scalar state, and q is the weighted volume defined by $q=\left( {\underline{\omega x}} \right) {\cdot }\underline{x}$.

The scaler force state t of the 3D peridynamic model for elastic solid material is (Silling 2010):

$$\begin{aligned} \underline{t}=3k\theta \frac{\underline{\omega x}}{q}+\frac{15\mu }{q}\underline{\omega e}^{d} \end{aligned}$$

(4)

Unlike the definitions of the 2D peridynamic model in Le et al. (2014), the different forms of $\theta$ and $\underline{e}^{d}$ in this study are used as:

$$\begin{aligned} \theta =2\frac{\underline{\omega x}{\cdot }\underline{e}}{q},\quad \underline{e}^{d}=\underline{e}-{\theta \underline{x}}/2 \end{aligned}$$

(5)

Then, following the same deduction steps in Silling (2010), the expressions of a and b for 2D peridynamic model have different values as:

$$\begin{aligned} a={k}',\quad b=\frac{8\mu }{q} \end{aligned}$$

(6)

where ${k}'$ is the two-dimensional (2D) bulk modulus that can be expressed in terms of the elastic modulus E and the Poisson’s ratio v as:

$$\begin{aligned} {k}'=\left\{ {{\begin{array}{ll} {\frac{E}{2\left( {1-v} \right) }}&{}\quad \text {Plane stress} \\ {\frac{E}{2\left( {1+v} \right) \left( {1-2v} \right) }}&{}\quad \text {Plane strain} \\ \end{array} }} \right. \end{aligned}$$

(7)

And the form of scalar force state t for 2D peridynamic model can be expressed as:

$$\begin{aligned} \underline{t}=2{k}'\theta \frac{\underline{\omega x}}{q}+\frac{8\mu }{q}\underline{\omega e}^{d} \end{aligned}$$

(8)

Thus, in the 2D peridynamic model, by using the different definitions of $\theta$ and $\underline{e}^{d}$ in Eq. (5), the peridynamic energy density of Eq. (2) and the scalar force state of Eq. (8) have the different formations as those in Le et al. (2014). However, it can be proven that two kinds of forms are equal, and these forms in Eqs. (2) and (8) are much simple and easy to compute.

Generally, using the definitions of Eqs. (3) and (5), the strain energy density of peridynamic model in Eq. (2) can be rewritten as (Silling 2010):

$$\begin{aligned} W=\frac{1}{2}{a}'\theta ^{2}+\frac{b}{2}\left( {\underline{\omega }\underline{e}} \right) {\cdot }\underline{e} \end{aligned}$$

(9)

where ${a}'$ is defined as:

$$\begin{aligned} {a}'=\left\{ {{\begin{array}{ll} {a-\frac{bq}{9}}&{} \quad {3D}\\ {a-\frac{bq}{4}}&{} \quad {2D} \\ \end{array} }} \right. \end{aligned}$$

(10)

where a and b are given in Eqs. (3) and (6) for the cases of 3D and 2D, respectively. The form of scalar force state t can then be rewritten as:

$$\begin{aligned} \underline{t}=\left( {{a}'\theta } \right) \nabla _{\underline{e}} \theta +b\underline{\omega e} \end{aligned}$$

(11)

where $\nabla _{\underline{e}} \theta$ is the Frechet derivative of $\theta$ with respect to $\underline{e}$. According to the definition of the Frechet derivative (Silling et al. 2007) and using the forms of $\theta$ in Eqs. (3) and (5), $\nabla _{\underline{e}} \theta$ can be written as:

$$\begin{aligned} \nabla _{\underline{e}} \theta =\left\{ {{\begin{array}{ll} {3\frac{\underline{\omega x}}{q}}&{} {3\hbox {D}} \\ {2\frac{\underline{\omega x}}{q}}&{} {2\hbox {D}} \\ \end{array} }} \right. \end{aligned}$$

(12)

In summary, the general expressions of the strain energy density and scalar force state are given in Eqs. (9) and (11), respectively, and they are available for both the 3D and 2D cases with the respective parameters.

2.2 Relationship between the state-based and bond-based peridynamic models

For the bond-based peridynamic model, there are restrictions on the values of the Poisson’s ratio as (Silling 2000):

$$\begin{aligned} v=\left\{ {{\begin{array}{ll} {\frac{1}{3}}&{}\quad {\text {Plane stress}} \\ {\frac{1}{4}}&{}\quad {\text {3D or Plane strain}} \\ \end{array} }} \right. \end{aligned}$$

(13)

Substituting these constrained values of v into the definition of ${a}'$ in Eq. (10) leads to ${a}'$ equaling to 0. Then, the forms of strain energy density in Eq. (9) and scalar force state in Eq. (11) can be reduced as:

$$\begin{aligned} W=\frac{b}{2}\left( {\underline{\omega }\underline{e}} \right) {\cdot }\underline{e},\quad \underline{t}=b\underline{\omega e} \end{aligned}$$

(14)

Specially, if the influence function takes the form of $\underline{\omega }=\delta /{\underline{x}}$, which is then substituted in the forms of b, and the value of v in Eq. (13) is used, the forms in Eq. (14) can be rewritten as:

$$\begin{aligned} W= & {} \frac{1}{2}\int _{\mathrm {H}_x } {\frac{1}{2}C\underline{s}^{2}\underline{x}} dV_\xi =\frac{1}{2}\int _{\mathrm {H}_x } w _\xi dV_\xi ,\nonumber \\ \underline{t}= & {} \frac{1}{2}C\underline{s}=\frac{1}{2}f \end{aligned}$$

(15)

where the bond stretch scaler state s is defined as s = e / x, $w_\xi$ and f are the micropotential and scalar bond force of bond $\varvec{\xi }$ in the bond-based peridynamic model (Silling and Askari 2005), and C is the bond constant which has the values of:

$$\begin{aligned} C=\left\{ {{\begin{array}{ll} {\frac{18k}{\pi \delta ^{4}}}&{}\quad {3D}\\ {\frac{12{k}'}{\pi \delta ^{3}h}}&{}\quad {2D} \\ \end{array} }} \right. \end{aligned}$$

(16)

Until now, the forms of strain energy density and scalar force state are reduced to the expressions given in Eq. (15) with the constrained values of v and special form of influence function, and the forms of $w_\xi$ and f are totally equal to those of the bond-based peridynamic model in Silling and Askari (2005) and Ha and Bobaru (2011) for the cases of 3D and 2D, respectively. Thus, the bond-based model can be regarded as a special case of state-based model.

3 State-based peridynamic model for fracture analysis

In this section, a state-based peridynamic model for fracture analysis of linear elastic brittle materials is proposed, and more general relationship of the critical stretch for bond failure with the critical energy release rate of material commonly used in linear elastic fracture mechanics (LEFM) is for the first time established.

Unlike the bond-based peridynamic model, there is no real bond between pair points in the state-based peridynamics. The bond here is used loosely to describe the relationship between pair points and can be thought as an interaction potential (Foster et al. 2011), and the bond stretch criterion thus still works. When the deformation of bond between the two points grows beyond the critical stretch value, the bond permanently breaks and the crack will initiate and grow when a number of broken bonds coalesce into a surface and propagate.

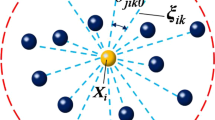
Similarly to Silling and Askari (2005), as shown in Fig. 2, the points x and ${{{\varvec{x}}}}'$ are connected with the bond ${\varvec{\xi }}$, and the $\hbox {H}_{1}$ domain is cut by the crack area from the whole horizon domain which is a sphere or circle in the cases of 3D or 2D, respectively. According to the form of peridynamic strain energy density in Eq. (9), the strain energy of point x gathers from other points in its horizon through those bonds. When the bond stretch s of ${\varvec{\xi }}$ grows beyond the critical stretch $s_{0}$, the bond ${\varvec{\xi }}$ is broken and the part of strain energy of point x gathering from point ${{{\varvec{x}}}}'$ is lost or released. As the crack grows or propagates, all bonds connecting the point x with the points ${{{\varvec{x}}}}'$ in $\hbox {H}_{1}$ are all broken, and the corresponding part of strain energy of the point x gathering from all points in the $\hbox {H}_{1}$ domain is thus released. Now, assume that the work requiring the point x to separate with all the neighboring points in $\hbox {H}_{1}$ is equal to the strain energy released as the crack grows.

Fig. 2

Computation of the total energy absorbed by point x in the domain $\hbox {H}_{1}$

To compute the released energy of point x, assuming that the bond stretch of all bonds ${\varvec{\xi }}$ across the crack area all arrives the critical stretch $s_{0}$, the extension scaler is $\underline{e}=s_0 \underline{x}$.

For 3D peridynamic model, according to the definition of $\theta$ in Eq. (3), the volume dilation caused by all broken bond is:

$$\begin{aligned} \widetilde{\theta }_s =3\frac{\underline{\omega }\underline{x}{\cdot }\underline{e}}{q}=3\frac{\int _{\mathrm{H}_1 } {\underline{\omega }} \underline{x}^{2}s_0 dV_\xi }{\int _\mathrm{H} {\underline{\omega }} \underline{x}^{2}dV_\xi }=3\lambda (z)s_0 \end{aligned}$$

(17)

where $\lambda$(z) is the ratio of the volume weight from the points in the $\hbox {H}_{1}$ domain to the volume weight from the points in the whole horizon, defined as:

$$\begin{aligned} \lambda (z)=\frac{\int _{\mathrm{H}_1 } {\underline{\omega }} \underline{x}^{2}dV_\xi }{\int _{\mathrm{H}_x } {\underline{\omega }} \underline{x}^{2}dV_\xi } \end{aligned}$$

(18)

Substituting Eq. (18) into the strain energy density of Eq. (9) leads to the released energy of a point x because of the crack growth as:

$$\begin{aligned} {{W}}_x= & {} \frac{{a}'}{2}\widetilde{\theta }_s ^{2}+\frac{b}{2}\int _{\mathrm{H}_1 } {\underline{\omega }} \underline{x}^{2}s_0^2 dV_\xi \nonumber \\= & {} \frac{1}{2}\left( {9{a}'\lambda (z)^{2}+bq\lambda (z)} \right) s_0 ^{2} \end{aligned}$$

(19)

Thus, the total released energy at unit area is:

$$\begin{aligned} d{{U}}_e= & {} 2\int _0^\delta {d{W}_x dz} =2\int _0^\delta {\frac{1}{2}\left( {9{a}'\lambda (z)^{2}+bq\lambda (z)} \right) s_0 ^{2}dz} \nonumber \\= & {} \left( {9{a}'{\beta }'+bq\beta } \right) s_0 ^{2} \end{aligned}$$

(20)

The first two multipliers of 2 in Eq. (20) is for the double side of the crack because of the homogeneous nature of the body, where $\beta$ and ${\beta }'$ are the certain parameters which are affected by the influence function, defined as:

$$\begin{aligned} \beta =\int _0^\delta {\lambda (z)dz},\quad {\beta }'=\int _0^\delta {\lambda (z)^{2}dz} \end{aligned}$$

(21)

The total released energy at unit area is equal to the critical energy release rate or fracture energy $G_{0}$, and it is expressed as:

$$\begin{aligned} G_0 =d{U}_e =\left( {9{a}'{\beta }'+bq\beta } \right) s_0 ^{2} \end{aligned}$$

(22)

So, the critical stretch ($s_{0})$ of state-based peridynamic model for 3D is uniquely obtained in term of the critical energy release rate ($G_{0})$ as:

$$\begin{aligned} s_0 =\sqrt{{G_0 }/{\left( {9{a}'{\beta }'+bq\beta } \right) }} \end{aligned}$$

(23)

In the cases of 2D, following the same deductions and using different peridynamic parameters in Eqs. (5) and (6), the released energy of point x and total released energy at unit area take the forms of:

$$\begin{aligned} {W}_x= & {} \frac{1}{2}\left( {4{a}'\lambda (z)^{2}+bq\lambda (z)} \right) s_0 ^{2},d{U}_e\nonumber \\= & {} \left( {4{a}'{\beta }'+bq\beta } \right) s_0 ^{2} \end{aligned}$$

(24)

Then, the critical stretch of state-based peridynamics model for 2D cases can be written as:

$$\begin{aligned} s_0 =\sqrt{{G_0 }/{\left( {4{a}'{\beta }'+bq\beta } \right) }} \end{aligned}$$

(25)

As a whole, substituting ${a}'$ in Eq. (10), a and b in Eqs. (3) and (5) into Eqs. (23) and (25) for the cases of 3D and 2D model, respectively, the critical stretch of state-based peridynamic model can totally be rewritten as:

$$\begin{aligned} s_0 =\left\{ {{\begin{array}{ll} {\sqrt{{G_0 }/{\left( {\left( {9k-15\mu } \right) {\beta }'+15\mu \beta } \right) }}}&{} {3D} \\ {\sqrt{{G_0 }/{\left( {\left( {4{k}'-8\mu } \right) {\beta }'+8\mu \beta } \right) }}}&{} {2D} \\ \end{array} }} \right. \end{aligned}$$

(26)

where $\beta$ and ${\beta }'$ are defined in Eq. (21), which are based on the definition of $\lambda$(z) in Eq. (18). The values of $\beta$ and ${\beta }'$ are the certain parameters which are decided by the horizon size $\delta$, the form of influence function, and the dimension of the model. Specifically, when the influence function takes the form of $\underline{\omega }=\delta /{\underline{x}}$ which is substituted to Eq. (21), the values of $\beta$ and ${\beta }'$ are computed using Matlab and then given as:

$$\begin{aligned} 3D:\left\{ {{\begin{array}{ll} {\beta =\frac{\delta }{5}}&{}\quad \\ {{\beta }'=\frac{26}{405}\delta }&{}\quad \\ \end{array} }} \right. , \quad 2D:\left\{ {{\begin{array}{ll} {\beta =\frac{3\delta }{4\pi }}&{}\quad \\ {{\beta }'=0.23873\delta }&{}\quad \\ \end{array} }} \right. \end{aligned}$$

(27)

For the bond-based peridynamic model, there are restrictions on the Poisson’s ratio. Substituting the values of v in Eq. (13) into Eq. (26) and using Eq. (27), the forms of critical stretch in the bond-based peridynamic model are recovered as:

$$\begin{aligned} s_0 =\left\{ {{\begin{array}{ll} {\sqrt{\frac{5G_0 }{9k\delta }}}&{}\quad {3D}\\ {\sqrt{\frac{\pi G_0 }{3{k}'\delta }}}&{}\quad {2D} \\ \end{array} }} \right. \end{aligned}$$

(28)

These forms of the critical stretch in Eq. (28) are just identical to the forms given in Silling and Askari (2005) and Ha and Bobaru (2011) for the cases of 3D and 2D, respectively, as typically proposed for the bond-based peridynamic model. Particularly, for the mode $\mathrm{I}$ type crack, the critical energy release rate $G_{IC}$ can be calculated from Sun and Jin (2013) as:

$$\begin{aligned} G_{IC} =\left\{ {{\begin{array}{ll} {\frac{\left( {1-v^{2}} \right) }{E}K_{IC}^2 }&{}\quad {\text {Plane strain}}\\ {\frac{1}{E}K_{IC}^2 }&{}\quad {\text {Plane stress}} \\ \end{array} }} \right. \end{aligned}$$

(29)

In summary, the general relationship of the critical stretch with respect to the critical energy release rate in LEFM is for the first time obtained in Eq. (26) for the state-based peridynamic model. The 3D, plane stress and plane strain cases are all considered. Unlike the fracture analysis for the bond-based model as given in Silling and Askari (2005) and Ha and Bobaru (2011), the critical stretch for the state-based model takes the varying values of the Poisson’s ratio into account. As a validation, the proposed state-based peridynamic model for fracture analysis can be further reduced to the bond-based damage model with the typical influence function and constrained values of the Poisson’s ratio. Also, unlike the critical stretch given in Madenci and Oterkus (2014) which is in the discrete form and with the special form of influence function, the new form in Eq. (26) developed in this study is in a general form for the state-based peridynamics and suitable to any reasonable influence function.

In addition, the forms of released energy of a point are given in Eqs. (19) and (24) for 3D and 2D cases, respectively. The variable parameter of point, i.e., released energy density, is defined to quantify the released energy as crack grows. The value of released energy density is equal to the released energy of a point, and the summation of the released energy density of system is equal to the total incremental surface energy. However, the released energy density is not a real physical energy, rather than the division of total released energy into the points around crack when crack propagates because of the non-local characteristic of peridynamic model.

Since the crack initiates and grows spontaneously in peridynamic fracture simulation, there is no explicit gap point of time between stable load before crack initiation and the increasing load as crack propagates. To track the zero time when the crack begins to grow, the critical time $t_{c}$ is defined. According to the forms of released energy density in Eqs. (19) and (24), the total released energy increases progressively with the increasing number of broken bonds. At the stage of the crack initiation, even some bonds around the pre-crack tip are broken, the system is stable to undertake the displacement load. Until the total released energy increases beyond a critical value, the crack starts to propagate. Thus, the critical released energy is defined as:

$$\begin{aligned} w_s =\frac{1}{2}G_0 B\Delta x \end{aligned}$$

(30)

where $\Delta x$ and B are the grid size and thickness of model ahead the crack tip, respectively. And the critical time $t_{c}$ is defined as

$$\begin{aligned} t_c =t_0, \quad if\quad W_S \left( {t_0 } \right) =w_s \end{aligned}$$

(31)

where $W_{S }(t_{0})$ is the total released energy (the incremental surface energy) of system in the time $t_{0}$. Thus, the critical time $t_{c}$ is recorded when $W_{S }(t_{0})$ increases to be equal to the critical released energy $w_{s}$, and it is proven to be the time when the crack starts to propagate.

4 Numerical implementation

Similarly to Silling and Askari (2005), the continuum system is discretized into the finite material nodes, and each node has a finite volume. The equation of motion in Eq. (1) can thus be rewritten as:

$$\begin{aligned} \rho _i {\ddot{u}}_i \left( {x_i,t} \right)= & {} \sum _{j\in \mathrm{H}_i } \{T[x_i,t]\left\langle {x_j -x_i } \right\rangle \nonumber \\&-\,T[x_j ,t]\left\langle {x_i -x_j} \right\rangle \}V_j+b_i \left( {x_i,t} \right) \nonumber \\ \end{aligned}$$

(32)

where i and j are the node numbers, and $V_{j}$ is the volume of node j. In all the examples followed, the uniform grid size $\Delta x$ is used. The summation of Eq. (32) is taken over the horizon $\hbox {H}_{i}$ of node i as $\left| {x_j -x_i } \right| \le \delta$, where $\delta$ is the horizon size as $\delta =m\Delta x$.

For the peridynamic simulations, the explicit (Silling and Askari 2005) and implicit (Zhang et al. 2016) time integration methods are usually used for dynamic and static analysis, respectively. In the following examples, the brittle damage process is simulated and the explicit time integration Velocity-Verlet algorithm (Hairer et al. 2003) is employed.

A paralleled C++ program has been developed to numerically solve the peridynamic equations. In the present work, all examples are run on a 24-core workstation running Linux.

5 Application to fracture specimens

In this section, the standard compact tension (CT) (ASTM E399-12 2013) and double cantilever beam (DCB) (ASTM D5528-01 2001) tests commonly for fracture characterization are considered to demonstrate and validate the proposed state-based peridynamic damage model.

5.1 Compact tension (CT) test

5.1.1 Problem setup and computational detail for CT test

The CT test (ASTM E399-12 2013) is usually used to determine the critical energy release rate of linear elastic isotropic metallic material. The CT specimen can be schematically shown in Fig. 3.

Fig. 3

The CT specimen

From the standard of test (ASTM E399-12 2013), the relationship of the critical stress intensity factor, $K_{IC}$, and the maximum crack propagation load, $P_{c}$, can be shown as:

$$\begin{aligned} K_{IC} =\frac{P_c }{Bw^{1/2}}f\left( {\frac{a}{w}} \right) , \end{aligned}$$

(33)

where

$$\begin{aligned}&f\left( {\frac{a}{w}} \right) =\nonumber \\ {}&\frac{\left( {2+\frac{a}{w}} \right) \left[ {0.886+4.46\frac{a}{w}-13.32\left( {\frac{a}{w}} \right) ^{2}+14.72\left( {\frac{a}{w}} \right) ^{3}-5.6\left( {\frac{a}{w}} \right) ^{4}} \right] }{\left( {1-\frac{a}{w}} \right) ^{3/2}} \end{aligned}$$

(34)

as shown in Fig. 3, a and w are the crack length and width of the specimen, respectively, and B is the thickness of the specimen. The crack mouth opening compliance is calculated as:

$$\begin{aligned} \frac{V_m }{P_c }=\frac{1}{{E}'B}q\left( {\frac{a}{w}} \right) \end{aligned}$$

(35)

where

$$\begin{aligned} q\left( {\frac{a}{w}} \right)= & {} \frac{19.75}{\left( {1-\frac{a}{w}} \right) ^{2}}\left[ 0.5+0.192\frac{a}{w}\right. \nonumber \\&+\,1.385\left( {\frac{a}{w}} \right) ^{2}-2.919\left( {\frac{a}{w}} \right) ^{3}\nonumber \\&\left. +\,1.842\left( {\frac{a}{w}} \right) ^{4} \right] \end{aligned}$$

(36)

for which $V_{m}$ is the crack mouth opening displacement at point o in Fig. 3, and:

$$\begin{aligned} {E}'=\left\{ {{\begin{array}{ll} {\frac{E}{\left( {1-v^{2}} \right) }}&{}\quad {\hbox {Plane strain}} \\ E&{}\quad {\hbox {Plane stress}} \\ \end{array} }} \right. \end{aligned}$$

(37)

In summary, the critical values of applied load and crack mouth opening compliance for the standard CT test can be obtained in Eqs. (33) and (35), respectively. Since the expressions for a / w in Eqs. (34) and (36) are considered to be accurate within 1% over the range 0.2 $\le a/w \le$ 1.0 (ASTM E399-12 2013), the equations can be used as the standard experimental results to compare with and validate the numerical peridynamic simulation results.

In this example, the material used is the 1CrMoV steel (Neale 1978), and the material properties are given in Table 1. The plane strain condition is considered, and uniform thickness of B = 1 mm is used. Damping is not considered in this example, and the energy balance condition is satisfied during the whole work.

The explicit time integration is utilized in this example. The uniform time step of 50 ns (nanosecond) is used, and it is proven to be the stable time step even for the finest grid size considered. The specimen is loaded by the linearly increasing displacement along the load line as shown in Fig. 3, with a constant speed of 20 mm/s. The total loading time is long enough to ensure that the dynamic effect is negligible before crack propagation. Unlike the standard CT specimen in ASTM E399-12 (2013), there is no physical holes simulated at the position of the loading pin on the CT specimen as shown in Fig. 3, and the displacement load is applied on the nodes located within 1 mm $\times$ 1 mm square centered at the position of the loading pin. Moreover, the no-damage zones are set in the loading areas to avoid the undesired damage because of local effect of loading conditions.

First, the fracture prediction of the CT test is performed with the proposed state-based peridynamic model as $a{/}w = 0.5$ (Fig. 3), followed by the convergence study (Bobaru et al. 2009). Then, the CT specimens with different values of a / w are considered to quantitatively validate the proposed model for predicting crack propagation problems with different pre-crack lengths.

Table 1 Material properties for 1CrMoV steel

5.1.2 Fracture behaviors of CT test with a/w = 0.5

In this section, a typical initial pre-crack length $a_{0} = 20\,\hbox {mm}$ and the specimen width $w = 40\,\hbox {mm}$ are used as shown in Fig. 3 which leads to $a{/}w = 0.5$.

For the numerical peridynamic simulation, the system is discretized into a finite number of nodes with uniform grid spacing. The values of $\delta$ = 1 mm and $m = 5$ are first considered to quantitatively analyze the fracture behavior of CT specimen.

The contours of y-direction displacement, damage (crack), and released energy density at the typical time of CT simulation are shown in Fig. 4, where the parameter of damage is defined as the volume weight of broken bonds in Silling and Askari (2005). As the displacement load increases, the y-direction displacement increases linearly and symmetrically (see Fig. 4a, b), and the crack starts to grow at the location of pre-crack tip around $6.0 \times 10^{-3}\,\hbox {s}$ (see Fig. 4c), and it grows along the pre-crack direction (see Fig. 4d) because of the symmetry of the geometry and loading condition. Meanwhile, the released energy density emerging at the location of crack starts to grow (see Fig. 4e), and it grows synchronously along with the crack path (see Fig. 4f). As shown in Fig. 4, the distribution of released energy density completely overlaps with the new damage map around both sides of pre-crack, because the released energy density is calculated from all the gathering broken bonds of point in Eq. (24), similar to the definition of damage given in Silling and Askari (2005).

Fig. 4

Contours of y-direction displacement distribution (a and b), damage (c and d), and released energy density (e and f) of CT specimen at crack propagation of $6 \times 10^{-3}\,\hbox {s}$ and $12 \times 10^{-3}\,\hbox {s}$, respectively. a AT $6 \times 10^{-3}\,\hbox {s}$, b At $12 \times 10^{-3}\,\hbox {s}$, c At $6 \times 10^{-3}\,\hbox {s}$, d At $12 \times 10^{-3}\,\hbox {s}$, e At $6 \times 10^{-3}\,\hbox {s}$, f At $12 \times 10^{-3}\,\hbox {s}$

Distributions of elastic strain energy density and released energy density around the crack tip before and after the pre-crack propagation are shown in Fig. 5. As shown in Fig. 5a, the strain energy density is first concentrated at the location of pre-crack tip, and the value of concentrated energy increases with the increasing displacement load before the crack starts to grow (see Fig. 5b, c). As the crack grows, the concentrated location of strain energy density moves with the crack tip, and the values of the concentrated strain energy density are nearly equal (see Fig. 5c, d). Meantime, the released energy density appears before the strain energy density arrives the maximum value (see and compare Fig. 5b, e), and it follows the same concentrated location as that of the strain energy density as the crack grows (see Fig. 5f, g). Comparing Fig. 5d and g, the concentrated location of strain energy density moves its front and overlaps with the head of the released energy density path, and the value and concentrated area size of the released energy density are much larger than those of the strain energy density.

Fig. 5

Distributions of elastic strain energy density (a–d) and released energy density (e– g) around the crack tip area before and after the pre-crack propagates. a $4.5 \times 10^{-3}\,\hbox {s}$, b $5 \times 10^{-3}\,\hbox {s}$, c $5.5 \times 10^{-3}\,\hbox {s}$, d $6 \times 10^{-3}\,\hbox {s}$, e $5 \times 10^{-3}\,\hbox {s}$, f $5.5 \times 10^{-3}\,\hbox {s}$, g $6 \times 10^{-3}\,\hbox {s}$

The plots of different energy components changing with the increasing displacement load are shown in Fig. 6. As shown in Fig. 6, the sum of $U_{e}$ (the strain elastic energy), $U_{k}$ (the kinetic energy), and $W_{S}$ (the incremental surface energy) is equal to $W_{e}$ (the work done by external forces) during the CT simulation. It thus perfectly matches the energy balance condition (Sun and Jin 2013):

$$\begin{aligned} dW_e =dU_e +dU_k +dW_S \end{aligned}$$

(38)

Also as shown in Fig. 6, the kinetic energy of the CT specimen is negligible as compared with the strain elastic energy before the crack starts to grow, which is consistent with the assumption of LEFM considered in the model.

The length of the crack increasing with the displacement load is shown in Fig. 7. As shown in Fig. 7, the velocity of crack propagation (i.e., the slope of the plot) decreases with time. Comparing this curve in Fig. 7 with the plot of incremental surface energy in Fig. 6, two curves have the similar trends. Though the released energy density appears at $4.71 \times 10^{-3}\,\hbox {s}$, the crack does not start to propagate until the total damage energy increases to $3.024 \times 10^{-3}\,\hbox {J}$ at the critical time $t_{c} = 5.26 \times 10^{-3}\,\hbox {s}$, which matches the released energy density distribution before the pre-crack starts to propagate (as shown in Fig. 5e). This means that even some bonds of point around the crack tip are broken, the system can still carry the displacement load, which thus confirms the definitions of critical released energy and critical time in Eqs. (30) and (31).

The relationship of $\Delta _{e}$ (the edge opening displacement) and $\Delta _{p}$ (the crack tip opening displacement) during CT simulation are shown in Fig. 8, where $\Delta _{e}$ is equal to $V_{m}$ in the standard test (ASTM E399-12 2013) and $\Delta _{p}$ is the displacement between two loading tips which is two times of $u_{y}$ (the displacement load). As shown in Fig. 8, $\Delta _{e}$ increases linearly with the increasing of $\Delta _{p}$ before the crack starts to propagate, and the slope of this region of plot is nearly 0.75. As the crack starts to grow, the slope of the curve decreases with time. The relationship between the edge opening displacement and tip opening displacement before the crack growth matches closely with that given in the experimental CT test (Neale 1978), i.e.,

$$\begin{aligned} \Delta _e =0.77\Delta _p \end{aligned}$$

(39)

The typical load-displacement is given in Fig. 9. As shown in Fig. 9, before crack initiation, the applied load increases linearly with the edge opening displacement, and the value of the reciprocal of slope of this region is 0.214 mm/KN. The value of critical applied load $P_{c}$ is 1.31 KN, peaked at the critical time $t_{c}$. After the critical time, the crack starts to grow and the load drops with the oscillations because of the explicit time integration in transient analysis.

The relationship between the total incremental surface energy $W_{S}$ and the crack length a as the crack grows is shown in Fig. 10, where $W_{S}$ is equal to the total released energy gathered from the released energy density of system. As a whole, $W_{S}$ increases linearly with the crack length but in the step-jump form. The value of a step in horizontal axis is the grid size $\Delta x$, while the value of a step in vertical axis is nearly equal to the value GB$\Delta x$. To trace the numerical energy release rate as crack propagates, the calculated critical energy release rate $G_{Q}$ is defined as:

$$\begin{aligned} G_Q =\frac{\Delta W_S }{B\Delta x} \end{aligned}$$

(40)

which means that the calculated critical energy release rate $G_{Q}/B$ is equal to the slope of the plot of $W_{S}$ vs. a. The value of $G_{Q}$ in Fig. 10 is 18.50 KJ, as reported in Table 2. Also, at the beginning of the plot, the crack length increases with the incremental surface energy beyond the critical released energy $w_{s}$, as defined in Eq. (30).

Fig. 6

Different energy components during CT test simulation

Fig. 7

Crack length versus displacement load during CT test simulation

Fig. 8

Edge opening displacement versus tip opening displacement during CT test simulation

Fig. 9

Applied load versus edge opening displacement during CT test simulation

Fig. 10

Incremental surface energy versus crack length as crack propagates

5.1.3 Convergence study of CT specimen with a/w = 0.5

Typical size $a_{0} = 20\,\hbox {mm}$ and $w = 40\,\hbox {mm}$ are still considered. The convergence study is performed with the horizons of $\delta$ = 1 and 2 mm, and $m = 4$, 5, 6, respectively.

First, a fixed horizon size $\delta$ = 1 mm and the varying values of m = 4, 5 and 6 are used for the m-convergence test. The plots of strain energy density and released energy density around the crack tip area with different values of m are shown in Fig. 11. As shown in Fig. 11, the plots for two different values of m have the same pattern, and for the larger value of m, the concentrated effect is much obvious. The typical load-displacement plots for different values of m are shown in Fig. 12. As shown in Fig. 12, the plots for different values of m are nearly coincided and have the similar values of slope and critical applied load, which are reported in Table 2. Furthermore, with the increasing value of m, the oscillation effect of curves is weakened when crack propagates.

Fig. 11

Strain energy density plots at $5.5 \times 10^{-3}$ s (a and b) and released energy density at $6 \times 10^{-3}$ s (c and d) around the crack tip area. a At $5.5 \times 10^{-3}\,\hbox {s}\,(m =4)$, b At $5.5 \times 10^{-3}\,\hbox {s}\,(m =5)$, c At $6.0 \times 10^{-3}\,\hbox {s}\,(m =4)$, d At $6.0 \times 10^{-3}\,\hbox {s}\,(m =5)$

Then, the fixed value of $m = 5$ is selected to perform the $\delta$-convergence test with the varying values of $\delta$ = 2 and 1 mm. The distributions of strain energy density and released energy density around the crack tip area with different values of $\delta$ are shown in Fig. 13. As shown in Fig. 13, the damage patterns and strain energy profiles for two different horizons are approximately same. For the smaller value of horizon $\delta$ = 1 mm, the concentrated effect of strain energy density and released energy density are more obvious, i.e., the sizes of concentrated area are much smaller and the maximum values are much bigger, which matches the local intensity in fracture mechanics. In addition, the plots of the total incremental surface energy $W_{S}$ with respect to the crack length a for different values of horizon are shown in Fig. 14. As demonstrated in Fig. 14, two plots with different horizons have the nearly same slope but with different increasing steps. For the smaller value of horizon, the value of a jump step in the plots of Fig. 14 is smaller, and the plot converges to a straight line. The values of slopes are also reported in Table 2.

Fig. 12

Applied load versus edge opening displacement for different values of m with $\delta$ = 1 mm

Fig. 13

Strain energy density plots (a and b) and released energy density (c and d). a $\delta =2\,\hbox {mm}\,\hbox {at}\,6.0 \times 10^{-3}\,\hbox {s}$, b $\delta =1\,\hbox {mm}\,\hbox {at}\,5.5 \times 10^{-3}\,\hbox {s}$, c $\delta =2\,\hbox {mm}\,\hbox {at}\,6.0 \times 10^{-3}\,\hbox {s}$, d $\delta =1\,\hbox {mm}\,\hbox {at}\,5.5 \times 10^{-3}\,\hbox {s}$

Fig. 14

Incremental surface energy versus crack length for different values of $\delta$ with $m = 5$

The simulation results of CT test for different values of $\delta$ and m are given in Table 2. As reported in Table 2, the characteristic parameters, i.e., ($\Delta _{p})_{c}$ (the critical load tip opening displacement), ($\Delta _{e})_{c}$ (the critical edge opening displacement), $P_{c}$ (the critical applied load), $\Delta _{e}/P$ (the crack mouth opening compliance), and $G_{Q}$ (the calculated critical energy release rate), are used in this study to quantify the crack initiation and propagation of CT test specimen, and the simulated results are then compared with and verified by those from the standard CT test (ASTM E399-12 2013), as given in Eqs. (33), (35) and (37).

From Table 2, the critical applied load $P_{c}$ matches closely with the standard values in Eq. (33) with the maximum difference of 3.0%, which means that the peridynamic simulation can successfully predict the critical applied load of CT test. The average value of compliance is less than that from Eq. (35); however, the maximum difference of crack mouth opening compliance between different values of $\delta$ and m is small (less than 4.7%), confirming that the model converges in the elastic region. Since the numerical peridynamic model in Fig. 3 does not exactly emulate the actual standard CT specimen in ASTM E399-12 (2013) which has the loading holes and notch and there is the stiffness enhancement of additional material in the simulation model, the crack mouth opening compliance by the peridynamic model is expectedly less than that of standard experimental model. In addition, the difference of compliance has no effect on the critical applied load which is much important in fracture analysis.

While the critical applied load and crack mouth opening compliance are used to capture the characteristic of CT test before the crack starts to propagate, the calculated critical energy release rate $G_{Q}$, as defined in Eq. (40), is employed to validate the effectiveness of the simulation during crack propagation. As shown in Table 2, the maximum difference of $G_{Q}$ in comparison with the critical energy release rate $G_{IC}$ is less than 3.6%.

Table 2 Peridynamic simulation results for CT test with a/w = 0.5

5.1.4 Analysis of CT test with different values of a/w

The CT test specimens with different values of a / w are considered to validate the proposed state-based peridynamic (PD) model for predicting the crack initiation and propagation with different pre-crack length.

A fixed specimen width of $w = 40$ mm and different crack length of $a_{0}$ increasing from 8 to 32 mm are considered for different values of a / w. According to the convergence study given above, the values of m = 5 and $\delta$ = 2 mm are used in the following analysis.

The critical applied load and crack mouth compliance for different values of a / w are presented in Figs. 15 and 16, respectively. The critical applied load decreases with the increasing value of a / w, as shown in Fig. 15. Except $a{/}w = 0.2$, the critical applied loads of peridynamic simulation are close to those from Eq. (33) within a maximum difference of 5.4%, and the difference increases as a / w approaching to 0.2 because of the local effect of the displacement load in the peridynamic model. Meanwhile, the value of crack mouth compliance increases exponentially with a / w, as shown in Fig. 16. The predicted values of crack mouth compliance from the peridynamic model are less than those in Eq. (35); however, the difference decreases as a / w increases, and it is less than 4.0% when a / w increases to 0.6.

As aforementioned, the stiffness in the peridynamic model (see Fig. 3) is higher than that in the experimental CT specimen (ASTM E399-12 2013) which has the loading holes and notch, and it thus leads to larger critical applied load and less crack mouth compliance in the peridynamic simulation. As the value of a / w increases (i.e., the crack length increases), the stiffening effect of material at the location of loading holes and notch on stiffness decreases and the simulation model can thus well capture the critical applied load and crack mouth compliance of CT test specimen.

Fig. 15

The critical applied load of CT specimens with different values of a / w

Fig. 16

The crack mouth compliance of CT specimens with different values of a / w

The quantitative values of simulation characteristic parameters of CT test for different values of a / w are given in Table 3. As shown in Table 3, the values of calculated critical energy release rate $G_{Q}$ for different a / w are close to the input value of $G_{IC}$ (= 17.856 N/mm), with a maximum difference of 3.1%.

Table 3 Peridynamic simulation results for CT test with different a/w

5.2 Double cantilever beam (DCB) test

5.2.1 Problem setup and computational detail for DCB test

Double cantilever beam (DCB) test is a common method to determinate the critical energy release rate of material under mode I fracture loading. As shown in Fig. 17, the special dimensions of DCB specimen are given as: $L = 240\,\hbox {mm}$, $h = 20\,\hbox {mm}$, and uniform thickness $B = 10\,\hbox {mm}$. The properties are chosen to replicate steel (Bidokhti et al. 2017), as reported in Table 4, and the plane stress condition is considered the same as the numerical model based on the finite element method (FEM) in Bidokhti et al. (2017).

The explicit time integration is utilized, and the uniform time step of 200 ns is used. The specimen is loaded with symmetrical and linearly increasing displacement at a constant speed of 20 mm/s, as shown in Fig. 17.

Fig. 17

The DCB specimen

In the DCB specimen simulation, the typical value of initial pre-crack length of $a_{0} = 100\,\hbox {mm}$ is first considered to analyze facture behavior under displacement loading. Then, the critical load analysis of DCB specimens with the different initial pre-crack length $a_{0}$ is performed.

Table 4 Material properties of steel

5.2.2 Fracture behavior of DCB test with initial pre-crack length a$_{0}$ = 100 mm

The typical initial pre-crack length $a_{0}\! =\! 100\,\hbox {mm}$ is first considered. In the peridynamic (PD) model, the system is discretized into uniform grids, and the values of $\delta$ = 2 mm and m = 5 are considered.

The displacements contours of DCB specimen in deformed shape are presented in Fig. 18. As shown in Fig. 18b, the two sub-beams move symmetrically upward and downward, respectively, with the value of displacement of about 1.2 mm. Meanwhile, the crack starts to grow along the pre-crack direction, and the contours of the crack path, strain energy density, and released energy density around the crack tip area are shown in Fig. 19. As expected, the strain energy density is concentrated at the location of initial pre-crack tip (see Fig. 19b), and the released energy density appears at the crack tip and follows the crack path (see Fig. 19c).

Fig. 18

Displacements contours of DCB specimen in deformed shape: a x component and b y component

Fig. 19

Simulation of DCB specimen: a crack path, b strain energy density, and c released energy density, around the crack tip at $60 \times 10^{-3}\,\hbox {s}$

The typical load-displacement plot of DCB test is shown in Fig. 20. As shown in Fig. 20, the peridynamic model successfully captures the load-displacement relationship of DCB test as compared with the FEM results given in Bidokhti et al. (2017). While the curve oscillation appears as the load drops and the crack grows because of the explicit time integration strategy. The values of critical load and displacement are reported in Table 5.

The normalized numerical critical energy release rate of DCB test is also shown in Fig. 21, where $G_{Q}$ (the calculated critical energy release rate) is calculated using Eq. (40) and normalized by the respective input value (i.e., $G_{IC} = 9.6278$ N/mm as given in Table 4). As shown in Fig. 21, the calculated critical energy release rate first increases quickly, and then stabilizes with further crack growth, indicating a great match (ASTM D5528-01 2001). The difference between the calculated and input critical energy release rates is less than 1.8% as the crack grows.

Fig. 20

Applied load versus displacement of DCB specimen with the initial crack $a_{0} = 100\,\hbox {mm}$

Fig. 21

Numerical critical energy release rate of DCB specimen estimated by the peridynamic model

Fig. 22

The critical applied load of DCB specimens with different initial crack length $a_{0}$

5.2.3 DCB test with different values of initial crack length a$_{0}$

The different values of initial crack length varying from $a_{0} = 100$ to 200 mm are considered. Again, the values of $\delta = 4\,\hbox {mm}$ and $m = 5$ are used in the peridynamic (PD) simulation.

The critical applied load and displacement for different values of initial crack length are presented in Figs. 22 and 23, respectively. As shown in Figs. 22 and 23, with the increasing value of the initial crack length, the critical load decreases and the critical displacement increases. Both the critical load and displacement from the peridynamic model greatly match those from the FEM data within maximum differences of 3.0 and 2.3%, respectively. The values of critical load and displacement of DCB specimens with different initial crack lengths are given in Table 5.

Fig. 23

The critical displacement of DCB specimens with different initial crack length $a_{0}$

Table 5 Peridynamic simulation results of DCB test with different initial crack length $a_{0}$

6 Conclusions

In this study, a state-based peridynamic model for fracture analysis is proposed, and the general relationship of the critical stretch and the critical energy release rate is for the first time obtained for the state-based peridynamic model of linear elastic brittle material. This model is utilized to predict the crack initiation and propagation. The commonly used fracture specimens, i.e., compact tension (CT) and double cantilever beam (DCB), are considered, and their fracture tests are investigated. First, the quantitative prediction of crack initiation and propagation and associated convergence study of the CT test are performed with an initial crack length of a / w = 0.5, followed by the CT specimen analysis with different values of a / w. Then, fracture behavior of DCB test is analyzed, and the critical load prediction of DCB specimens with different crack length is performed.

In the CT test case, the crack starts to grow at the location of pre-crack tip and grows symmetrically along the pre-crack direction, while the concentrated zones of strain energy moves along with the crack tip. The path of released energy density follows and overlaps the concentrated zones of strain energy. The crack initiation happens at the time of the incremental surface energy ahead of reaching the critical energy release rate, even some bonds around pre-crack tip are already broken. In the convergence study, the denser the grid size, the more obvious the concentrated effects, the smaller the size of concentrated area, the bigger the maximum value of energy density, and the weaker the oscillation of load-displacement curve as crack propagates.

With the increasing value of a / w, the simulated critical applied load decreases and is close to that from the standard equation of Eq. (33) within a maximum difference of 5.4%, except at a / w = 0.2, because of the local effect of the displacement load in the peridynamic model. While the simulated crack mouth compliance increases exponentially with the decreasing difference when compared to that from the standard equation of Eq. (35) because of the stiffness enhancement effect of material at the loading holes which is neglected in the peridynamic model. The calculated critical energy release rate also matches closely with the input critical energy release rate value.

In the DCB test case, the two sub-beams deform symmetrically upward and downward, and the crack starts to grow along the pre-crack direction while the strain energy density is concentrated at the location of crack tip. Comparing the simulated load-displacement curve with that from FEM, the peridynamic model successfully captures the load-displacement relationship; while the curve oscillation appears as the load drops and the crack grows because of the explicit time integration strategy. The numerical critical energy release rate of DCB from the peridynamic model also accurately matches the input critical value. With the increasing length of pre-crack, the critical load of DCB specimen decreases and the critical displacement increases, for which both match closely with FEM.

The proposed state-based peridynamic model for crack quantitatively captures the fracture behavior of the CT and DCB specimen tests. No special fracture criteria are required in the numerical prediction, and the only input parameter for fracture in the proposed state-based peridynamic model is the critical energy release rate of material. The general relationship of the critical stretch and the critical energy release rate Eq. (26) obtained in this study can be used in the framework of state-based peridynamic model to quantitatively analyze fracture behavior of linear elastic brittle materials.