Sandia fracture challenge 2: Sandia California’s modeling approach

Abstract

The second Sandia Fracture Challenge illustrates that predicting the ductile fracture of Ti-6Al-4V subjected to moderate and elevated rates of loading requires thermomechanical coupling, elasto-thermo-poro-viscoplastic constitutive models with the physics of anisotropy and regularized numerical methods for crack initiation and propagation. We detail our initial approach with an emphasis on iterative calibration and systematically increasing complexity to accommodate anisotropy in the context of an isotropic material model. Blind predictions illustrate strengths and weaknesses of our initial approach. We then revisit our findings to illustrate the importance of including anisotropy in the failure process. Mesh-independent solutions of continuum damage models having both isotropic and anisotropic yields surfaces are obtained through nonlocality and localization elements.

Through this work, we seek to illustrate Sandia California’s modeling approach to the Sandia Fracture Challenge 2 (SFC2). The first four sections of the paper, Initial approach, Constitutive modeling, Modeling the challenge geometry, and Blind predictions, attempt to encapsulate our values, intuition, and simulated understanding spanning the brief period of the competition. We then revisit our predictions in light of new physics and mesh-convergent (regularized) numerics in Revisiting the challenge problem and Regularization of the failure process, respectively. Finally, Conclusions and future work illustrates aspects of the physics, numerics, and processes needed for a team to model ductile fracture.

1 Initial approach

The material, time scale, and mode of loading dictated our approach to solving Sandia Fracture Challenge 2. Provided experimental data and literature advocate models that incorporate rate dependence (Follansbee and Gray 1989), temperature dependence (Administration 2013), and anisotropy in both the yield stress (Hammer 2012) and the hardening. Void evolution must include multi-axial nucleation, growth, and coalescence. The low thermal conductivity of titanium and the time scales for characterization and testing requires thermomechanical coupling and implicit time integration. Local material softening requires regularized methods for solution.

We used the Sierra multi-physics finite element analysis software suite to capture the required physics and numerics for solution. We modeled the solid mechanics response with an implicit solution scheme in the Sierra/SolidMechanics (SierraSM) application, a Lagrangian, 3D code (Sierra/SM Development Team 2015). SierraSM contains a versatile library of continuum and structural elements, and an extensive library of material models. For all SFC2 related simulations, we used eight-noded hexahedral elements with full integration of the deviatoric stress response and volume-averaging of the hydrostatic stress response. The baseline mesh had element side lengths on the order of 170 $\upmu$m in failure regions. To model crack initiation and propagation, we initially removed elements from the simulation according to a continuum damage model. Exploratory studies were also conducted with regularized methodologies (nonlocality, surface elements). Unstable modes of fracture were resolved with implicit dynamics (HHT time integration with numerical damping Hilber et al. 1977).

2 Constitutive modeling

In the absence of a model that could capture all of the desired physics, we used the SierraSM isotropic Elasto Viscoplastic (EV) material model for the simulations in our blind predictions because it contains most of the physics required to accurately model the SFC2 challenge problem, such as rate and temperature dependence, and damage evolution under stress states with and without positive triaxiality. However, since the EV model does not support anisotropic plastic behavior, the anisotropy evident in the provided data was included through other means, as described in detail in the following section. An anisotropic Hill plasticity model was later modified to include damage evolution. The new approach is described in the section devoted to revisiting the challenge problem.

The EV plasticity model, a variation of the model presented in Bammann et al. (1995), is an internal state variable model for describing the finite deformation behavior of metals. The EV model incorporates strain rate and temperature sensitivity, as well as damage, and tracks history dependence through the use of internal state variables. The kinematics and thermodynamics for the model are presented in Brown and Bammann (2012), which are based on the previous work by Kröner (1960), Lee and Liu (1967), Bammann and Aifantis (1987), and Coleman and Gurtin (1967). In its full form, the model has considerable complexity, but most of the material parameters and resulting behavior are optional. Although the full kinematics will not be presented, a multiplicative decomposition of the deformation gradient is used,

$$\begin{aligned} \varvec{F} = \varvec{F}^e\varvec{F}^p\varvec{F}^\theta \varvec{F}^\phi , \end{aligned}$$

(1)

where $\varvec{F}^e$ and $\varvec{F}^p$ represent the elastic and plastic portions of the deformation, and $\varvec{F}^\theta$ and $\varvec{F}^\phi$ represent the portions due to thermal expansion and porosity evolution, respectively.

Let $V_r$, and $V_\phi$ denote an elementary volume in the reference configuration and the voided configuration, and $V_v$ denote the volume of voids in the voided configuration. In what follows, we assume in the reference configuration, $V_r$ is fully dense, unloaded, and at room temperature. Then

$$\begin{aligned} V_\phi = V_r+V_v. \end{aligned}$$

(2)

The damage is then defined as

$$\begin{aligned} \phi = \frac{V_v}{V_\phi }. \end{aligned}$$

(3)

To simplify some of the derivations that follow, a damage measure relative to the reference configuration is defined as

$$\begin{aligned} \tilde{\phi } = \frac{V_v}{V_r}, \end{aligned}$$

(4)

from which it follows that

$$\begin{aligned} \tilde{\phi } = \frac{\phi }{1-\phi }. \end{aligned}$$

(5)

The damage can then be written as the product of the number of voids per volume $\eta =\frac{N}{V_r}$, and the average void volume $v_v$:

$$\begin{aligned} \tilde{\phi }=\eta v_v. \end{aligned}$$

(6)

The form of the material model specific to our use for SFC2 will now be outlined for the simplified case of uniaxial tension. For this simplified case, the stress evolves according to

$$\begin{aligned} \dot{\sigma } = \left( \frac{\dot{E}}{E}-\frac{\dot{\phi }}{1-\phi }\right) \sigma +E\left( 1-\phi \right) \left( \dot{\epsilon }-\dot{\epsilon }_p\right) \end{aligned}$$

(7)

where E is Young’s modulus, $\epsilon$ is the total strain, $\epsilon _p$ is the plastic strain, and $\phi$ is the damage, defined as the void volume fraction. The effective Young’s modulus $E_{\text {eff}}$ is assumed to be a function of temperature $\theta$ and damage, in the form

$$\begin{aligned} E_{\text {eff}} = E(\theta )(1-\phi ). \end{aligned}$$

(8)

The flow rule is defined by

$$\begin{aligned} \dot{\epsilon }_p = f\sinh ^n\left( \frac{\frac{\sigma _e}{1-\phi }-\kappa }{Y}-1\right) \end{aligned}$$

(9)

where $\sigma _e$ is the effective stress; Y is a material parameter representing the rate independent, initial yield stress; f and n are material parameters that govern the material rate dependence; and $\kappa$ is the isotropic hardening variable for the material, which evolves according to a hardening H minus dynamic recovery $R_{d}$ model originally proposed by Kocks and Mecking (1979):

$$\begin{aligned} \dot{\kappa }=\kappa \frac{\dot{\mu }}{\mu }+\left( H-R_d\kappa \right) \dot{\epsilon }_p. \end{aligned}$$

(10)

where $\mu$ represents the temperature-dependent shear modulus. Although the effective shear modulus in the homogenized material decreases with damage through a factor $1-\phi$, the isotropic hardening variable is defined in the matrix material. Although f, n, H, and $R_d$ can be temperature-dependent functions, they were treated as constants in all simulations performed in this work. Heat generation due to plastic work is calculated with

$$\begin{aligned} \dot{q}=\beta \sigma \dot{\epsilon }_p \end{aligned}$$

(11)

where the material parameter $\beta$ is the fraction of plastic work dissipated as heat.

Moving to a multiaxial formulation, the EV model accounts for damage evolution through two mechanisms, namely void nucleation and growth. Void growth is driven by stress triaxiality while void nucleation is dependent on $J_3$ and $J_2$ allowing for damage accumulation in pure shear stress states. Similar to Horstemeyer and Gokhale (1999), void nucleation is modeled according to

$$\begin{aligned} \dot{\eta }=\eta \dot{\epsilon }_pN_1\left[ \frac{4}{27}-\frac{J^2_3}{J^3_2}\right] \end{aligned}$$

(12)

where $N_1$ is a material parameter. The deviatoric stress $s_{ij}$ invariants are given by

$$\begin{aligned} J_2 = \frac{1}{2}s_{ij} s_{ij} \end{aligned}$$

(13)

and

$$\begin{aligned} J_3 = \frac{1}{3}s_{ij} s_{jk} s_{kl}. \end{aligned}$$

(14)

In the absence of nucleation, growth of existing voids is assumed to occur according to the relation proposed in Cocks and Ashby (1980) and subsequently used in Bammann et al. (1995):

$$\begin{aligned} \dot{\phi }=\sqrt{\frac{2}{3}}\dot{\epsilon }_p \frac{1-\left( 1-\phi \right) ^{m+1}}{\left( 1-\phi \right) ^{m}}\sinh \left[ \frac{2\left( 2m-1\right) }{2m+1}\frac{\langle p \rangle }{\sigma _{e}}\right] \end{aligned}$$

(15)

where m is the damage exponent, p is the trace of the Cauchy stress $\sigma _{ij}$ and $\sigma _{e} = \sqrt{3J_{2}}$. We can re-express damage evolution in terms of the average void volume $v_v$ and the void density $\eta$,

$$\begin{aligned} \dot{v_v}= & {} \sqrt{\frac{2}{3}}\dot{\epsilon }_p \frac{1}{\eta } \left( 1+\eta v_v\right) \left[ \left( 1+\eta v_v\right) ^{m+1}-1\right] \nonumber \\&\cdot \sinh \left[ \frac{2\left( 2m-1\right) }{2m+1}\frac{\langle p \rangle }{\sigma _{e}}\right] . \end{aligned}$$

(16)

By an argument analogous to the one derived in Brown and Bammann (2012), the effect on the average void volume of newly nucleated voids of volume $v_{vo}$ can be included in the following manner:

$$\begin{aligned} \dot{v_v}= & {} \sqrt{\frac{2}{3}}\dot{\epsilon }_p \frac{1}{\eta } \left( 1+\eta v_v\right) \left[ \left( 1+\eta v_v\right) ^{m+1}-1\right] \nonumber \\&\cdot \sinh \left[ \frac{2\left( 2m-1\right) }{2m+1}\frac{\langle p \rangle }{\sigma _{e}}\right] - \left( v_v-v_{vo}\right) \frac{\dot{\eta }}{\eta }. \end{aligned}$$

(17)

The first term accounts for growth under positive triaxiality, whereas the second term can reduce the average void volume due to addition of smaller voids into the population. This latter effect is neglected in Horstemeyer and Gokhale. Taking the time derivative of Eq. (6), we get

$$\begin{aligned} \dot{\tilde{\phi }}=\dot{\eta } v_v + \eta \dot{v_v} \end{aligned}$$

(18)

which, through combination with Eq. (17) leads to the evolution equation for damage under nucleation and growth:

$$\begin{aligned} \dot{\tilde{\phi }}= & {} \sqrt{\frac{2}{3}}\dot{\epsilon }_p \left( 1+\tilde{\phi }\right) \left[ \left( 1+\tilde{\phi }\right) ^{m+1}-1\right] \nonumber \\&\times \sinh \left[ \frac{2\left( 2m-1\right) }{2m+1}\frac{\langle p \rangle }{\sigma _{e}}\right] - \dot{\eta } v_{vo} \end{aligned}$$

(19)

or relative to the total volume,

$$\begin{aligned} \dot{\phi }= & {} \sqrt{\frac{2}{3}}\dot{\epsilon }_p\frac{1-\left( 1-\phi \right) ^{m+1}}{\left( 1-\phi \right) ^{m}} \nonumber \\&\times \sinh \left[ \frac{2\left( 2m-1\right) }{2m+1}\frac{\langle p \rangle }{\sigma _{e}}\right] + \left( 1-\phi \right) ^2 \dot{\eta } v_{vo}. \end{aligned}$$

(20)

Equations (12) and (20) must be solved in order to track the evolution of damage, whereas Eq. (17) is unnecessary since the average void volume can be post-processed at any given time step using Eqs. (5) and (6). The final form is very similar to the damage evolution in Nahshon and Hutchinson (2008), although they do not explicitly provide evolution equations for either average void volume or void density. The damage model requires the definition of the initial damage $\phi _0$, the initial size of newly-nucleated voids $v_{vo}$, and the initial void count per volume $\eta _{0}$.

Void coalescence is modeled through $\phi _{coal}$. The material point is unloaded for $\phi \ge \phi _{coal}$. In contrast to surface elements, elements are removed (element death) whenever any integration points satisfy the coalescence criterion, since stabilization of fully integrated formulations is problematic with loaded and unloaded integration points.

Although not used directly for our blind predictions, a rate and temperature independent, Hill plasticity (HP) material model (Hill 1948) was used to guide our choice of EV material model parameters. The HP model is an anisotropic material model where the yield criterion takes the form

$$\begin{aligned} f_Y^2\left( \sigma _{ij}\right)\equiv & {} F\left( \sigma _{22}-\sigma _{33}\right) ^2+G\left( \sigma _{33} -\sigma _{11}\right) ^2\nonumber \\&+\, H\left( \sigma _{11}-\sigma _{22}\right) ^2+2L\sigma _{23}^2 \nonumber \\&+\, 2M\sigma _{31}^2+2N\sigma _{12}^2={\bar{\sigma }_{e}}^2\left( \epsilon _p\right) \end{aligned}$$

(21)

where $\sigma _{ij}$ are the stress components in the principal material directions and the coefficients F, G, H, L, M and N relate the yield stresses of the material in each principal material direction to the Hill effective stress $\bar{\sigma }_{e}$. In SierraSM (2015), the yield coefficients are not explicitly specified. Instead the ratios of the yield stresses in each material direction are defined relative to a reference yield stress $\bar{\sigma }_Y$ such that

$$\begin{aligned} R_{ii} = \frac{\sigma _{ii}^y}{\bar{\sigma }_{Y}} \end{aligned}$$

(22)

and

$$\begin{aligned} R_{ij} = \sqrt{3}\frac{\tau _{ij}^y}{\bar{\sigma }_{Y}} \end{aligned}$$

(23)

where $\sigma _{ii}^y$ and $\tau _{ij}^y$ are the yields stresses in the normal and shear material directions, respectively. These ratios are then used to calculate the yield surface coefficients. During SFC2, the HP material model did not include the micromechanics of void nucleation and growth, and consequently, could not be used for blind predictions.

2.1 Iterative calibration

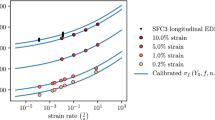
Since different material parameters often have a similar effect on the simulation load displacement curves, several simulations can be required to determine the appropriate parameter to elicit the desired effect from the models. To avoid this convolution of material parameters and physics, the calibration process involved an iterative approach where the complexity of the material model was increased as needed to capture characteristics evident in the available data. Initially, the yield (Y, f, and n) and hardening (H and $R_d$) parameters, as defined in Eqs. (9) and (10) respectively, were calibrated to the provided pre-peak load tensile data using a non-linear, least squares algorithm where the objective function consisted of the error between the provided experimental data and model data. Since the rate dependence for the initial yield stress is not uniquely constrained by two data points, we used rate dependence data from Follansbee and Gray (1989) to supplement the data at two rates provided for the challenge. As shown in Fig. 1, the isothermal tension test simulations with this initial parameter set matched the experimental data well before peak load, but did not yield structural softening sufficiently after peak load.

Fig. 1

Model calibrations of the provided a fast rate and b slow rate tensile experimental data. Black-outlined circles represent the experimental data and color circles represent the calibrated model data for various thermal boundary conditions. a Fast rate: 25.4 mm/s. b Slow rate: 0.0254 mm/s

Therefore, structural softening at higher plastic strains was incorporated through additional model parameters. Structural softening can be accomplished through increasing the dynamic recovery parameter or through thermal softening due to conversion of plastic work to heat. Since structural softening was more significant in the higher strain rate experiments, thermal effects were assumed to cause the observed post-peak load behavior. Using data available in MMPDS-08 (Administration 2013), temperature dependence was added to the initial yield stress and the elastic material properties. MMPDS-08 also provided data for adding temperature dependent thermal parameters such as thermal conductivity, thermal expansion and specific heat to the Ti-6Al-4V material model. Sources in the literature for the material parameter $\beta$ in Eq. (11) exhibit significant inconsistencies. Three of these sources presented $\beta$ as a function of plastic strain, each with differing trends and bounds (Macdougall and Harding 1999; Nemat-Nasser et al. 2001; Galan et al. 2013). Due to these inconsistencies and the inability of the material model to accommodate $\beta$ as a function of plastic strain, we chose $\beta = 0.8$ based on engineering judgment and simulation results.

The addition of thermal properties to the calibration simulations required the investigation of thermal boundary conditions. Figure 1 shows simulation results for four different thermal boundary conditions: (1) isothermal with no heating due to plastic work, (2) coupled thermomechanical with heating due to plastic work, conduction, radiation and natural convection, (3) coupled thermomechanical with heating due to plastic work and conduction, and (4) strictly mechanical with adiabatic heating due to plastic work. For condition (2), conservative approximations were made for the natural convection coefficient and emissivity to increase the effects of these boundary conditions on the simulations. An infinite plate model (Çengel 2007) provided the natural convection coefficient of 12.0 $\frac{W}{m^2K}$ and the emissivity was set at a constant value of 0.31. These simulation results demonstrate that the tension test simulations require a coupled thermo-mechanical model for both rates. Specifically, the adiabatic boundary condition is sufficient for the fast rate test but a coupled model with conduction is required to model the slow rate. These findings stem from the fact that a large region of the tensile specimen, the gauge section, deforms homogeneously prior to necking. Despite conduction into the grips for the slow rate, the temperature still increases ${\sim }$30 $^{\circ }$C. Since the shear test and challenge specimen simulations are much different thermal boundary value problems than the tension test, all further simulations using the EV material model were coupled with conduction.

After the plasticity material parameters were calibrated, damage was added to the material parameter set through the void growth damage model in Eq. (15). The damage parameters were chosen based on prior experience with the material model and a study of the model sensitivity to the damage exponent m. A value of $m=6$ caused the simulations to fail at a similar point as the experimental data; however, due to variability in the data, this parameter had high uncertainty. Adding the void growth damage model completed the material calibration to the provided tension test data. Figure 2a contains results from the calibrated tension simulations.

Fig. 2

Comparisons of the calibrated models to the tension and shear experiments for the fast and slow loading rates. a Tension data and calibrated model results. b Shear data and calibrated model results

The next calibration iteration focused on the shear test. Using the material parameters calibrated to the tension data, a model of the shear test did not accurately predict the yield behavior of the specimen thus indicating that the material exhibits an anisotropic yield surface. Since the material model does not support an anisotropic yield surface, a separate material parameter set was calibrated to the shear data. By reducing the initial yield parameter Y by $17\,\%$ to obtain a shear yield $Y^s=411$ MPa, the shear simulation results improved and compared well to the test data. Additionally, since the triaxiality driven void growth model cannot evolve damage in pure shear, sensitivity studies for the void nucleation parameters led to the selection of the appropriate $N_1$, $\phi _0^{\eta }$ and $\eta _0$ parameters needed to capture the shear test. Adding these void nucleation parameters to the damage model had no effect on the tension test simulations. Figure 2b contains the calibrated shear simulation results. Table 1 lists the material parameter values for both the tension and shear parameter sets where the only difference between the tension and shear parameters sets are the yield stresses $Y^{t}$ and $Y^{s}$, respectively. Through this iterative calibration process we span moderate triaxialities in the necked tensile specimen to nearly pure shear in the shear specimen. Although the components of the damage model have been partitioned into triaxiality-driven growth and shear-dominated nucleation, we seek to employ the model for void evolution under mixed-mode (tension–shear) loadings. The quality of our blind predictions will hinge on the extent to which our models are calibrated to experimental data that reflect the fields that evolve in the challenge geometry.

Table 1 Calibrated material parameters

Since a local damage model was initially used for both calibration and prediction, the same element size, approximately 170 $\upmu$m, was employed for the baseline challenge prediction. Although this does not remedy the mesh-dependence in the solution, a common element size attempts to establish a baseline discretization for field resolution. The bifurcation of the solution is fundamentally addressed in latter sections in which we eliminate the mesh dependence of the solution using nonlocality and surface elements that regulate the failure process to a plane.

3 Modeling the challenge geometry

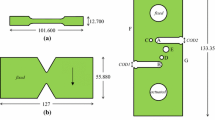
Modeling of the challenge specimen required careful attention to the geometry, mesh, boundary conditions, and material response. All simulations consisted of models constructed at the nominal dimensions according to the specimen drawings. For the mesh, the element type and size was previously described. A view of the mesh is shown in Fig. 3. The following focuses on our selection of the appropriate boundary conditions, incorporation of the aforementioned anisotropic yield response of the material, and failure representation.

Fig. 3

On the left, Block 2 is outlined in red on the undeformed model geometry. Hole and notch labels are included for designations of the crack path. On the right, the deformed geometry is shown after the crack has propagated into the upper hole in an unstable manner

The solid mechanics boundary conditions consisted of a symmetry boundary condition along the half-thickness plane of the specimen and approximations of the pin boundary conditions in the test. Frictional contact was not modeled in SierraSM due to the time constraints of the project conflicting with the significant computational overhead of solving contact. Instead, frictionless pins were approximated by a half-pin contiguously meshed into the specimen with the center node line having prescribed displacements. The top pin centerline was fixed and the bottom pin centerline was displaced downward with a rate corresponding to the test rates. As stated previously, the models for both rates were coupled and included heating due to plastic work. The thermal boundary conditions included symmetry at the half-thickness plane and conduction through the body.

After determining the appropriate boundary conditions, we incorporated the anisotropic yield surface into the challenge specimen model. Initial simulations using the EV material model using the tension calibrated yield stress $Y^t$ predicted that the specimen would fail in the upper notch through ligaments A–C–F. Since the material exhibits anisotropic yield behavior, we calibrated the HP material model to the data to determine where the challenge specimen would plastically localize and ultimately fail. The calibrated HP material model has identical hardening behavior to the EV material model and $\bar{\sigma }_Y$ is $Y^t$ scaled by the EV rate function depending on the plastic strain rates observed in the simulation. All yield stress ratios are set to 1 except for the shear yield ratio in the in-plane directions which is $R_{12}=0.87$. The challenge specimen simulations using the HP material model localized in the lower notch through ligaments B–D–E–A which illustrates the importance of the anisotropic yield surface in predicting the correct crack path for this problem. Without the HP material model, we would have predicted an incorrect crack path.

Fig. 4

Effect of $Y^{s*}$ on the challenge specimen simulation load versus COD1 curves and a comparison to the challenge specimen simulation using the HP material model

Since the EV material model cannot accommodate an anisotropic yield surface, the model of the specimen was split into two element blocks: Block 1 with a yield corresponding to the tension initial yield $Y^t$ and Block 2 with a lower yield $Y^{s*}=441$ MPa since that region is initially predominantly in shear. Figure 3 depicts Block 2 outlined in red with the remaining elements belonging to Block 1. Since the stress state in Block 2 does not directly correspond to that of the failure region in the shear model, a simulation of the challenge specimen at the slow rate using the HP material model influenced the selection of $Y^{s*}=441$ MPa. Due to the slow rate simulation being nearly isothermal, a direct comparison of challenge geometry simulations using the EV material model could be made to simulations using the HP material model. As a result, the correct $Y^{s*}$ was determined through a calibration process where $Y^{s*}$ was varied until the global load displacement curves between the two models agreed. Figure 4 shows the load versus COD1 curves for $Y^{s*}$ values corresponding to the shear test yield, the calibrated value used in the blind predictions, and 452 MPa. During the $Y^{s*}$ calibration, the HP material model was still in development and would not converge after peak load; therefore, the model results after peak load were ignored for the calibration process.

With all material parameters and boundary conditions determined, efforts shifted toward obtaining implicit solutions throughout the failure process. The initial attempt was to automatically apply element death to elements when damage reached $\phi _{coal}$. However, the nonlinear, implicit dynamics solution could not converge to acceptable residuals (${<}$10$^{-8}$ times the $L_{2}$ norm of the reaction forces) at the onset of element death. Therefore, an alternative approach was taken where blocks of elements were removed manually once the majority of elements in the blocks had damage near $\phi _{coal}$. In this manual element removal process, the simulations were stopped, the element blocks with the appropriate damage were removed, the new geometry was relaxed in a quasi-static simulation with artificially high numerical damping, and then the problem was restarted at the point previous to the element block removal. This process was used to obtain the blind predictions and suggested that the crack propagated unstably through ligaments B–D and D–E. To verify this unstable crack propagation, simulations using localization elements (described in section devoted to regularization) seeded along the crack path were used. The simulations with localization elements yielded implicit solutions through the entire crack propagation process without manual element removal and showed that the cracks propagated unstably. Since the thermal solution application in Sierra does not currently support localization elements, these simulations were only used to provide insight into the crack propagation process and were not used to provide our predictions for the challenge problem.

4 Blind predictions

Using the material model parameters and boundary conditions specified in the previous sections, the challenge specimen model predicted failure through crack path B–D–E–A for both rates. For both rates, the crack propagated unstably through B–D–E, as shown in Fig. 3, while the remaining ligament carried load until tensile failure occurred much further into the simulation (375 s for the slow rate and 0.36 s for the fast rate). More specifically, the crack initiated at the plane of symmetry in notch B and then propagated through ligament B–D and ligament D–E, respectively. The crack propagation took place over approximately 12 ms for the slow rate and approximately 60 $\upmu$s for the fast rate.

Table 2 Results predicted using the challenge specimen model

Fig. 5

The load versus COD1 predictions for the slow rate and the fast rate. Lower, median and upper correspond to our lower bound, nominal and upper bound predictions. a Fast rate COD1 predictions. b Slow rate COD1 predictions

Table 2 lists the maximum loads and CODs at crack initiation for each rate and Fig. 5 displays the predicted load versus COD1 for both rates. The upper and lower bounds were chosen using intuition gained from the calibration process. The only parameter change for the lower bound prediction was decreasing $Y^{s*}$ to $Y^s$. The parameter changes for the upper bound prediction included increasing $Y^{s*}$ to 451 MPa, decreasing $R_d$ to 12 and decreasing $\beta$ to 0.6. The method described in the previous section for obtaining an implicit solution through unstable crack propagation led to the gaps in the data for both the median and upper bound slow rate simulations.

Fig. 6

Comparison of temperatures predicted by the slow rate simulation to experimental results. Position 1 is on ligament B–D and position 2 on ligament A–C

Figure 6 compares temperatures predicted by the simulation to measurements taken at two locations on the challenge geometry for the slow rate. A similar comparison could not be made for the fast rate due to uncertainties in the experimental measurements. The experimental temperature data and information regarding its validity is reported in the main SFC2 article (Boyce et al. 2016). In summary, the temperatures were taken using thermocouples attached to the surface of the challenge geometry at two locations: position 1 and position 2. Position 1 is located approximately in the center of ligament B–D and position 2 is located near the center of ligament A–C.

Although the positions of the thermocouples were not precisely known, the results show strong agreement for the slow rate. The delayed onset of plastic deformation in our predictions causes the simulation temperature at position 1 to rise steadily until failure at approximately 150 s while the experimental temperature results increase abruptly at 108 s. This sharp increase in temperature is believed to coincide with a thermally driven localization process. A similar change in the heating rate is evident in the simulation results before failure; however, the temperature was sampled on, and not adjacent, to the element block removed for crack propagation.

5 Revisiting the challenge problem

As noted in the main article devoted to the Sandia Fracture Challenge (Boyce et al. 2016), boundary conditions, thermo-mechanical coupling, and plastic anisotropy differentiated team predictions. In that vein, we investigate the application of the pin loading, the conversion of plastic work to heat, and inclusion of both void nucleation and growth in the context of an anisotropic yield surface. For these post-challenge simulations, more robust implicit solver settings were used which allowed for implicit solutions with crack propagation through element death.

Fig. 7

Effect of modeling the pin boundary condition as fixed or frictionless for the challenge geometry simulations

5.1 Modeling the pin boundary condition

During discussions at the SFC2 Summit (Boyce et al. 2016), disagreement about the appropriate treatment of the pin boundary condition arose. Teams used contiguously meshed pins that were either fixed/free to rotate or they modeled the pins as separate bodies with frictional contact. Since no experimental data was taken relating to the pin boundary condition, simulations were employed to determine the effects of these different modeling approaches for the pins. Figure 7 shows results from simulations using fixed and free contiguously meshed pins. All other model parameters were identical to those used for the median blind prediction. The results from this investigation indicate that the free pin assumption was more appropriate for this problem since the more constrained pin boundary condition significantly increases the stiffness of the system. This increased system stiffness causes an increased slope in the elastic portion of the COD1 curves, a higher peak load for both rates and an earlier onset of crack initiation. An effort was made to investigate frictional contact for the problem; however, conclusive results could not be obtained due to the numerical difficulties associated with solving frictional contact in this problem.

Fig. 8

Effect of $\beta$ on plastic localization and failure for the fast rate challenge geometry simulation

5.2 Sensitivity to uncertain material parameters

A sensitivity study of the material parameters with the highest uncertainty (m, $N_1$ and $\beta$) was performed to determine if the predictions could be improved through improved material parameter calibration. The results of this study are shown in Figs. 8 and 9.

In Fig. 8, the fast rate simulation results are significantly affected by $\beta$. When $\beta =1$ the over prediction of COD1 at crack initiation is reduced 6 % and the adiabatic assumption causes the simulation to under predict COD1 at crack initiation by 10 %. Our calibrated value of $\beta =0.8$ and its uncertainty could have had a negative effect on our predictions for the fast rate; however, it does not account for all of the error in our predictions and had no effect on the nearly isothermal slow rate simulation.

Fig. 9

Effects of the void growth and void nucleation damage parameters on the challenge geometry simulations. a Effects of void growth parameter, $N_1$. b Effects of void nucleattion parameter, m

Figure 9 illustrates the substantial effect the damage parameters have on the simulation results. Increases in both damage parameters can cause the onset of crack initiation to occur at a lower COD1 for both simulations, but this can lead to early failures in the shear and tension simulations. For example, the nucleation parameter must be increased more than 100 % for the challenge geometry simulations to match the experiments, which causes the shear simulation to fail prematurely. For void growth, a damage exponent of 9 causes the challenge geometry simulations to initiate cracks at a COD1 approximately 0.1 mm greater than the maximum experimental value without negatively affecting the tension simulations results. Our calibrated value of $m=6$ for the blind predictions is near the lower bound for this parameter. An appropriate uncertainty quantification study for the calibrations likely would have identified this and resulted in improved predictions for COD1 at crack initiation for both rates. Such a study was not performed before submitting the predictions due to time constraints.

Fig. 10

Location of crack initiation in the slow rate challenge geometry simulation when using the EV material model (top) and the HP damage material model (bottom)

5.3 Incorporating an anisotropic yield surface with damage

The most apparent discrepancy in our approach to the problem was our use of an isotropic plasticity model to simulate a material with anisotropic yield and hardening behavior. After the challenge, we added the EV damage model to the existing Hill plasticity material model in SierraSM in an effort to improve our predictions. Implicit in this assumption is that we can decouple plastic anisotropy and void growth. In fact, prior efforts with the EV model adopt this construction. While the flow is rate and temperature dependent with internal variables that govern the hardening, the kinetics of void growth in the EV material model derive from power-law creep (Cocks and Ashby 1980). Although works have considered the effects of anisotropy and void shape on void growth (Benzerga et al. 2004a, b; Benzerga and Leblond 2010), we sought to incrementally increase complexity for this challenge problem. Focusing on the slow rate, we can ignore rate and temperature dependence. Consequently, the new formulation, Hill plasticity damage (HP Damage), retains the decoupled damage evolution and incorporates a Hill yield surface.

Initially, no additional recalibration was performed to populate the material parameters for the HP Damage model. The hardening parameters used were taken directly from the EV model hardening model and the Hill yield surface employed to calculate the appropriate value for $Y^{s*}$. The results for the updated yield surface with the original material parameters are shown in Figs. 10 and 11 in which the simulation results are in good agreement with the data. A discrepancy is the over-prediction of COD1 at crack initiation. In addition to improving the global load-COD1 behavior of the model, the addition of the Hill yield surface changes the location of crack initiation in the model as illustrated in Fig. 10. Experiments performed at UT Austin by Andrew Gross and Ravi Chandar have shown that for at least one test specimen the crack initiates in ligament D–E and then propagates through ligament B–D. The challenge geometry model with the HP Damage material model displays the same behavior, showing that the yield surface chosen to model ductile failure problems can significantly affect simulation results.

This delay in crack initiation for the slow rate simulation stemmed from the prior calibration of an isotropic yield surface. Since the anisotropic yield surface significantly affects the stress state after plastic localization for the shear simulation, the $N_1$ parameter required recalibration. The recalibration resulted in a revised value of $N_1=100$. Figure 11 also shows these improved results for the slow rate challenge geometry simulation using the HP Damage model and the revised $N_1$ parameter. With the correct material model and revised damage parameter, the simulation results lie within the experimental data.

Fig. 11

Improved results for the slow rate simulation using a material model incorporating a Hill anisotropic yield surface and a void growth and nucleation damage model

6 Regularization of failure processes

Calibration, initial predictions, and revised predictions were predicated on local damage using a baseline mesh size for field resolution. Although we did attempt to sufficiently capture the fields governing crack initiation, simulations in the post-bifurcation regime will exhibit mesh dependence in the solution (de Borst 2004). One needs to regularize the failure process through the addition of a length scale to yield a mesh-independent solution. Although the prior section focuses on anisotropy and targeted parameterization, the multiplicity of solutions was not addressed. The noted mesh dependence in the solution is illustrated for the fast and slow rates in Fig. 12. These findings indicate that neither a thermomechanical treatment nor the addition of rate-dependence into the constitutive model is sufficient to yield a mesh-independent solution.

To remedy matters, we introduce a length scale into the fracture process through multiple methods. For the fast rate, we examine a nonlocal method derived from a variational principle. For the slow rate, we employ surface elements for crack initiation and propagation. In both cases, we use bulk constitutive models with the dominant micromechanics to drive the failure process. We assert that developing cohesive models for surface separation that respect multiphysics, anisotropy, and relevant state variables such as the triaxiality can be quite difficult. Instead, we advocate general approaches that leverage local constitutive models with the appropriate micromechanics for fracture and failure.

Fig. 12

Mesh dependence that stems from local damage for the EV material model employing blind parameters. The number of elements spanning the half-thickness for the fast and slow rates are 9 (baseline) to 36 (fine) and 9 (baseline) to 18 (fine), respectively

6.1 Variational nonlocal method

In the vein of nonlocality (Pijaudier-Cabot and Bažant 1987; Bažant and Jirásek 2002), a variational nonlocal method was derived such that one can identify the state variable that controls softening Z and pose a variational principle such that the stored energy is dependent on a nonlocal state variable $\bar{Z}$. At a point, a Lagrange multiplier enforces $\bar{Z} = Z$. When we minimize and discretize, however, we derive an $L_{2}$ projection for the “coarser” $\bar{Z}$ and the balance of linear momentum for the “fine” scale. If we assume that the basis functions for the coarser discretization D are constant and discontinuous, we obtain the nonlocal $\bar{Z}$ as a simple volume average of Z.

$$\begin{aligned} \bar{Z} = \frac{1}{\int _{D} dV} \int _{D} Z dV \end{aligned}$$

(24)

In this particular case, less is more. We do not want to recover the mesh-dependent solution inherent in Z with a $\bar{Z}$. Instead, we seek to specify an additional discretization (length scale) independent of the discretization for Z. Because $\bar{Z}$ is just an average, we can consider a coarse domain to be a patch of fine scale elements having volume V that is consistent with a prescribed length scale l where $V = l^{3}$. For example, one might correlate the mesh dependence in the solution with scalar damage $\phi$. The variational nonlocal method would construct a $\bar{\phi }$ for each nonlocal domain D. The stress would then evolve from $\bar{\phi }$ and not $\phi$. Please refer to Sun and Mota (2014) for application to strain localization in 1D.

Domain decomposition algorithms (Devine et al. 2002) are invoked to construct coarse scale domains of common volume. For parallel execution, the mesh on each processor is partitioned into the requisite nonlocal domains during initialization. Nonlocal averages are calculated on the processor and no communication is necessary between processors. Initial findings employing geometric partitioning illustrated a sensitivity to domain shape. Although other researchers have developed methods for domain decomposition that focus on domain shape (Meyerhenke et al. 2009), we gravitated towards clustering algorithms and the resulting isotropy (Burkardt et al. 2002). Through Lloyd’s algorithm, a Centroidal Voronoi Tesselation (CVT) emerges through iterative K-means clustering of seeded points inside the body which are independent of the FE discretization. Details of the K-means algorithm and guidelines for usability can be found in the Sierra/SolidMechanics Capabilities in Development Manual (2015).

6.2 Localization elements

Localization elements (Yang et al. 2005) are planar elements that lie between bulk (volumetric) elements and can employ the same underlying bulk material model. Localization elements are topologically similar to cohesive surface elements (Klein et al. 2001; Foulk et al. 2007) with kinematic constructions that incorporate strong discontinuities (Armero and Garikipati 1996). In contrast to cohesive methods that only consider the displacement jump, the current approach also takes into account the in-plane stretching through the multiplicative decomposition of the deformation gradient ${\varvec{F}}$ such that ${\varvec{F}} = {\varvec{F}}^{\parallel } {\varvec{F}}^{\perp }$. Each portion of the decomposition can be expressed as

$$\begin{aligned} {{\varvec{F}}}^{\perp } = {{\varvec{I}}} + \frac{\llbracket {\varvec{\varPhi }} \rrbracket }{h} \otimes {{\varvec{N}}}, \quad {{\varvec{F}}}^{\parallel } = {\varvec{g}}_{i} \otimes \hat{{\varvec{G}}}^{i} \end{aligned}$$

(25)

where ${\varvec{F}}^{\parallel }$ encapsulates in-plane stretching and ${\varvec{F}}^{\perp }$ reflects the displacement jump $\llbracket {\varvec{\varPhi }} \rrbracket$ in the intermediate configuration which can be pushed to the current configuration through $\llbracket {\varvec{\varphi }} \rrbracket = {\varvec{F}}^{\parallel } \llbracket {\varvec{\varPhi }} \rrbracket$.

The jump is normalized by h which one can envision as an element thickness or a characteristic length scale governing separation. Quantities are considered to be constant through the thickness h. The curvilinear basis vectors in the reference and current configuration are ${\varvec{G}}_{A}$ and ${\varvec{g}}_{i}$, respectively. Given that ${\varvec{N}}$ is constructed to be normal to the in-plane basis vectors ${\varvec{G}}_{A}$ in the reference configuration, we can prove that the in-plane basis vectors in the intermediate configuration are equivalent to the in-plane basis vectors in the reference configuration ($\hat{{\varvec{G}}}_{A} = {\varvec{F}}^{\perp } {\varvec{G}}_{A} = {\varvec{G}}_{A}$). We can then express the multiplicative decomposition as an additive decomposition

$$\begin{aligned} {{\varvec{F}}} = {{\varvec{F}}}^{\parallel } + \frac{\llbracket {\varvec{\varphi }} \rrbracket }{h} \otimes {{\varvec{N}}} \end{aligned}$$

(26)

thus simplifying the initial formulation. We note that because the length scale h is independent of the discretization, the methodology is regularized and ideal for employing a local, softening material model to simulate the failure process. Currently, the crack path must be specified a priori. Details of the implementation and guidelines for usability can be found in the Sierra SolidMechanics Users’ Guide (2015).

6.3 Application to fast and slow rates

Prior sections focused the importance of thermomechanical coupling for the fast rate of loading and anisotropy for slow rate rate of loading. Although we have finalized both the theoretical development and implementation in our research environment, we do not have surface elements that can accommodate mulitphysics in our production environment (Sierra). Consequently, we apply thermomechanical coupling, EV material model, and the nonlocal method to the fast rate of loading and constant temperature, mechanics, HP Damage material model, and localization elements to the slow rate of loading.

The length scales introduced by the nonlocal method and localization elements generate the length scale governing the ductile failure process. We often refer to the region of the body providing resistance as the process zone. For the nonlocal method, the size of nonlocal volume l maps to the process zone size $l_{pz}$. For localization elements, the length scale that normalizes the displacement jump h indirectly yields a process zone size where $l_{pz}$ is some multiple of h. Provided the selected and generated process zone sizes are small compared to all the dimensions of the body, parameterization for specimen geometries may be transferable to the challenge geometry (Rice 1968).

Although one might hope to align the process zone size with experimental observations, initial scoping studies employing the EV material model yielded a process zone size of $l_{pz} = 300$ $\upmu$m. This resulted in a nonlocal domain size of $l = 300$ $\upmu$m and a smaller characteristic length scale for localization elements $h = 50$ $\upmu$m. Figure 13 illustrates both the nonlocal domains and the seeded surface elements employed to regularize damage evolution.

Fig. 13

Discretization of the nonlocal domains and the seeded surface elements employed to regularize the fast and slow rates, respectively

We have selected length scales that generate process zone sizes that permit resolution. Rather than tune the length scales to match experiments, we have instead chosen to select length scales that permit solution and re-examine the fitting process for damage evolution in light of the chosen method for regularization. We acknowledge that both the choice of length scale and the parameters governing damage evolution may not be unique. In this section, however, our goal is to illustrate mesh convergence for mixed-mode ductile failure processes. Future work might probe non-uniqueness in light of convergent solutions.

The application of the variational nonlocal method required a re-examination of the fitting process for damage evolution. In an effort to mitigate complexity, we only revisited the criteria for coalescence $\phi _{coal}$. For local damage, we selected $\phi _{coal} = 0.15$. Revised simulations of tensile tests revealed that selecting $\phi _{coal} = 0.05$ with a nonlocal length scale $l = 300$ $\upmu$m was in good agreement with experiments. A reduced value for coalescence reflects the fact that we now require an entire volume to reach $\phi _{coal}$ rather than a single element. As we refine the mesh, we still require the same nonlocal volume to reach the same criterion for coalescence. Because damage $\phi$ is the state variable that leads to bifurcation, we have regularized the failure process through an additional discretization (CVT) for damage evolution that is independent of the FE discretization. The resulting parameterization and nonlocal method applied to the challenge geometry is illustrated in Fig. 14.

Fig. 14

Convergence of the nonlocal method with a length scale of $l = 300$ $\upmu$m applied to the fast rate. The label blind* indicates that the criteria governing coalescence $\phi _{coal}$ was modified to account for nonlocality. The fine and finer designations correspond to 18 and 27 elements through the half-thickness of the specimen

Because the nonlocal region must be small compared to the ligaments, and the element size must resolve the nonlocal domain, the discretization required for the nonlocal method can be substantial. Although the baseline element size for local damage and the localization elements is ${\sim }172$ $\upmu$m, we consider a minimum element size employed in the nonlocal method to be 18 elements through the half-thickness of the specimen which results in a mesh size of ${\sim }86$ $\upmu$m and roughly 43 elements in each nonlocal domain. A finer mesh having 27 elements through the half thickness was also simulated with mesh sizes of ${\sim }58$ $\upmu$m and roughly 125 elements in each nonlocal domain. Although Fig. 14 does not illustrate global unloading, both discretizations are unloading with nonlocal volumes nearing the required damage for nonlocal coalescence. Fields for both the equivalent plastic strain $\epsilon _{p}$ and the nonlocal damage $\bar{\phi }$ at crack nucleation are illustrated in Fig. 15. We note that only the nonlocal damage evolves on the CVT discretization (through a volume average). Fields such as the equivalent plastic strain evolve smoothly throughout the domain. Although the current nonlocal method is less smooth than traditional methods that employ overlapping nonlocal kernels (Pijaudier-Cabot and Bažant 1987), the treatment of the boundaries is quite natural. In contrast, overlapping nonlocal kernels require rescaling at boundaries and necessarily contain a boundary layer. The details of boundaries are relevant for the current work and other geometries because cracks tend to nucleate at the boundaries of stress concentrations.

Fig. 15

Field evolution for the equivalent plastic strain $\epsilon _{p}$ and the nonlocal damage $\bar{\phi }$ at crack initiation in the challenge geometry. In contrast to the smoothness of $\epsilon _{p}$, $\bar{\phi }$ evolves on Centroidal Voronoi Tesselation (CVT) independent of the FE discretization

For the slow rate of loading, we employ localization elements to regularize the solution. Initial findings with the EV material model during blind predictions for cases employing both the adiabatic and isothermal assumption suggested that $h = 50$ $\upmu$m may be relevant. Following the work of the prior section on revisiting the challenge geometry, we incorporate anisotropy through the HP Damage material model and investigate both blind and revisited parameters. To ensure that hexahedral elements do not bifurcate, damage evolution is precluded in the bulk. Void nucleation, growth, and coalescence was only permitted in the localization elements. Paths were selected through the iterative process of determining the plane of strain localization via $\epsilon _{p}$ and then seeding that particular plane with localization elements (and thus dictating the crack path). After a couple of iterations, the localization elements were well-aligned with the plane of localization dictated by anisotropic plasticity. We note that the localization process is sensitive to the plane of the localization elements. Strain localization adjacent, but not on, the selected plane will retard damage evolution. One cannot obtain fields of physical significance and predict crack initiation if the seeded localization elements do not align with the plane of localization. Consequently, we believe the seeded plane to be accurate for this particular loading. Future work will generalize this capability through the adaptive insertion of localization elements.

Fig. 16

A comparison of experimental findings and simulations employing localization elements having a length scale of $h = 50$ $\upmu$m. Coarse, baseline, and fine discretizations reflect 3, 9, and 18 elements through the half-thickness of the specimen. Both the blind and the revisited parameters illustrate convergence for finer discretizations

Fig. 17

Convergence in the field of damage $\phi$ at crack initiation for both the blind and revisited parameters. The surface illustrated spans hole D to E in Figure 13. The criteria for coalescence is $\phi _{coal} = 0.15$. Localization elements provide a natural treatment for surface separation in which both void nucleation and growth dictate the physics of crack initiation and growth

The results of simulations for both the blind and revisited parameters are shown in Fig. 16 for the coarse, baseline, and fine meshes having 3, 9, and 18 elements through the half-thickness of the specimen, respectively. For both sets of parameters, we are able to achieve mesh convergence. In addition to examining far-field behavior, we can also investigate convergence in the local fields. Figure 17 not only illustrates convergence in the damage evolution at crack initiation, but also reflects the aforementioned physics regarding the role of void nucleation and growth. Because localization elements leverage the input micromechanics, the complexities of crack initiation within the interior ($N_1 = 54$) or on the surface ($N_1 = 100$) are both resolved and mesh convergent.

7 Conclusions and future work

Through this work, we sought to develop tools and approaches to predict the ductile fracture of Ti-6Al-4V subjected to mixed-mode loading in a thermomechanical environment.

• 1. Given observations regarding rate dependence, temperature dependence, anisotropy, and damage evolution under both tension and shear, we systematically increased complexity in the calibration process and included elements of anisotropy through the spatial modification of an isotropic yield surface.

• 2. Simulations revealed an intense competition between the upper and lower notches. Findings at slow rates revealed that an anisotropic yield surface would localize in the lower notches (B–D, D–E) while an isotropic yield surface would localize in the upper notch (A–C).

• 3. Our blind simulations confirmed the importance of thermomechanical coupling at elevated rates of loading and the need to include anisotropy in modeling the localization of rolled Ti-6Al-4V.

• 4. Subsequent investigations on the challenge geometry for fast and slow rates shed light on the importance of plastic work and plastic anisotropy on the localization of the deformation. For the fast rates of loading, thermomechanical coupling under increasing $\beta$ align computations and experiments. Slower rates of loading are insensitive to thermomechanical coupling and reflect the need to incorporate an anisotropic yield surface. For both cases, the localization of the deformation dictates crack path. Employing the same parameters for damage evolution, the predictions for the slow rate were not only more accurate capturing the plateau of the load-displacement curve but also confirmed experimental observations for crack initiation in ligament D–E rather than B–D.

• 5. Additional calibration and sensitivity studies illustrate that an increased emphasis on void nucleation rather than void growth aligns predictions with far-field measurements (load-COD1) and moves crack initiation from near the notch to the center of the second ligament.

• 6. A variational nonlocal method with a length scale of $l = 300$ $\upmu$m was applied to thermomechanical coupling and the EV material model to yield a mesh-independent solution. A recalibration of the criterion for coalescence $\phi _{coal}$ for tensile samples greatly increased the accuracy of prediction for the challenge geometry.

• 7. Surface elements with a 3D deformation gradient that accounts for both the displacement jump and in-plane stretching/rotations and a length scale of $h = 50$ $\upmu$m were applied to the HP Damage model to obtain mesh convergent solutions for both the blind and the revisited parameters.

Future work will seek to incorporate rate dependence, temperature dependence, and anisotropy in both the plasticity (yield, hardening) and the damage evolution (nucleation, growth, coalescence). One cannot understand the sensitivity of particular physics without an ability to model a particular physics. Just as one might find difficulty in decoupling the physics, the employment of local damage models and the ensuing conditions for bifurcation can obscure the physics with the numerics (mesh dependence) of localization. Both nonlocal and surface approaches included length scales to regularize the solution. Having regularized the solution, one can then begin to reliably investigate the sensitivity of boundary conditions, geometry, and the selected physics on the prediction. Rigorous studies that propagate uncertainty in the failure of metallic structures (or specimens) require the resolution of the dominant physics underpinned by regularized methods.