1 Introduction

Crack arrest length prediction is an important issue in the study of dynamic brittle fracture of industrial structures. It seems sensible to consolidate a conservative arrest estimate and to investigate complete crack kinematics during dynamic crack propagation. This analysis is made difficult, in particular because of wave reflections on the body boundaries. This paper attempts to tackle these difficulties using a dedicated fracture specimen. A commonly used laboratory test specimen to investigate dynamic crack arrest is the double cantilever beam (DCB) specimen, the geometry of which can be exploited to produce one-dimensional analysis models. Furthermore, the narrow width of the specimen geometry involves stress waves reflections, which can enhance the crack arrest length.

We focus here on the bimaterial DCB specimen, which has a high toughness in the part where the initial crack is blunted. This part is welded to a low toughness section where the crack enters with a high velocity, depending on the ratio of the the surface energies. This duplex specimen has been described by Kanninen (1985) using a special augmented model (Kanninen 1973), within the framework of a quasi-static analysis. Transient kinetic analyses may also be achieved with some analytical methods leading to hyperbolic equations being solved by a finite difference scheme applied to characteristic lines (Freund 1977; Hellan 1981).

The first quantitative prediction for the kinematics of a fast propagating crack, using energy balance, is due to Mott (1948). An original analysis, based on solving Lagrange’s equation for a DCB specimen motion, considered as a Bernoulli–Euler beam, has been initiated by Burns and Webb (1970), assuming that the kinetic energy would follow the expression of a specific constant loading rate. Freund (1989) has extended this approach to all loading conditions, using a Hamiltonian approach and introducing a modal decomposition, but his work is restricted to the mode \(N=0\), which is similar to Mott’s work. Wang and Williams (1996) applied this first mode truncation method to a tapered DCB and their results are in good accordance with finite element computations. From our knowledge, higher modes have only been considered as a small perturbation of a quasi-statically growing stable crack in a DCB, leading to natural frequencies and mode shapes Jagota et al. (2002). An extension to modal analysis is suggested here for higher vibration modes to investigate the dynamic crack growth and arrest in a bimaterial DCB specimen.

This paper is organized as follows. The general problem is first introduced, with the description of the crack growth modelling on a DCB specimen which presents a toughness discontinuity. Section 3 describes the modal decomposition of the beam deflection and the corresponding frequency eigenvalues. Then, a variational principle, using admissible fields expressed on the modal basis, leads to the local motion equations, including the crack kinematics governed by the Griffith law.

There are few available analytical solutions to dynamic crack growth problems in finite solids in literature. Whereas crack propagation problems with transient motion are often achieved with Finite Element Models, some analytical procedures are available for simple one-dimensional models such as the peeling of a thin film ( Freund 1989; Charlotte et al. 2008; Lazzaroni et al. 2012). In Sect. 5, the variational method associated to a modal analysis is validated on the peeling problem where an exact solution exists.

Section 6 is devoted to numerical experiments on the DCB with homogeneous fracture properties. A quasistatic method to capture the crack arrest length is suggested.

2 DCB motion approximation with a Bernoulli beam model

2.1 General description

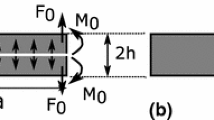
An elastic \(2h\) high DCB specimen, with an initial crack length \(\ell _{0} \), is illustrated Fig. 1. The specimen arms are slowly prescribed to a monotonic opening displacement \(W^{0}(t)\) which triggers a quasi-static mode I crack growth (marked by the current value \(\ell _{0} \le \ell <\ell _c )\) in a first part of the beam, which is made up of a \(2\Gamma _{0} \) fracture energy material. A second material with a lower toughness, referred to as the test section, is welded to the first one (the corresponding energy is \(2\Gamma _1 <2\Gamma _{0} )\). When the crack tip reaches the sections interface (\(x=\ell _c )\) where the toughness jump occurs, it runs rapidly throughout the test section, from time \(t=0\), while the displacement prescribed on the remote ends of the specimen arms is held fixed during the whole process (\(W^{0}(t)=W^{c},\quad \forall t, t\ge 0)\). The crack velocity \(\dot{\ell }\) (and the arrest length \(\ell _A )\) in this test section is governed by the energy ratio of the two sections (\(R=\Gamma _{0} /\Gamma _1 ,\;R>1)\). The aim of this paper is to investigate the crack kinematics during this stage, especially the crack arrest \(\ell _c \le x\le \ell _A \), under the assumption that the crack path is straight. Branching or kinking cracks are beyond scope of this paper.

Fig. 1
figure 1

Crack growth and arrest in a bimaterial DCB specimen

Full size image

The numerical model represents half of the specimen, and consequently half of the fracture energy (\(\Gamma _{0} ,\Gamma _1 )\). A Bernoulli–Euler model is used to simulate the beam (ratio \(h/\ell _c \) is considered small enough for the classical beam theory to hold). The motion is thus fully represented by the scalar beam deflection \(w(x,t)\). The general differential motion equation, associated with the boundary conditions may be written as follows, \(\forall \ell , \ell _{0} \le \ell \le \ell _A \) :

$$\begin{aligned} \left\{ {\begin{array}{l} EI\dfrac{\partial ^{4}w}{\partial x^{4}}+\rho A\dfrac{\partial ^{2}w}{\partial t^{2}}=0,\;\quad \forall x\;\in \;\left[ {0,\ell } \right] ,\;\forall t\; \\ w(0,t)=W^{0}(t),\;\dfrac{\partial ^{2}w}{\partial x^{2}}(0,t)=0, \\ w(\ell ,t)=0,\;\dfrac{\partial w}{\partial x}(\ell ,t)=0, \\ \end{array}} \right. \end{aligned}$$
(1)

where \(E,I,A,\rho \) are respectively the elastic modulus, the area moment of inertia, the area of the cross section, and the mass density of the material.

As it is the dynamic stage that is of interest, the initial conditions are those of the crack running onset time when \(\ell (t=0)=\ell _c \). Thus, the stage where \(w(x,t),\;t<0\;x\in [ {0,\ell _c } [\), is corresponding to the quasi-static propagation in the first beam section, which is not considered here. Nevertheless, this stage is detailed in the next paragraph, to determine what initial conditions should be prescribed.

2.2 Initial state of the dynamic process

The point where the crack tip reaches \(x=\ell _c \) (cf. Fig. 1) is the ultimate quasi-static stage where the deflection is denoted \(w^{stat}(x,t)\).

The equilibrium equation is the form of (1):

$$\begin{aligned} \left\{ {\begin{array}{l} \dfrac{\partial ^{4}w^{stat}}{\partial x^{4}}=0,\; \forall x\;\in \;\left[ {0,\ell } \right] ,\;\forall t\;< 0, \ell _{0} \le \ell <\ell _c \\ w^{stat}(0,t)=W^{0}(t),\;\dfrac{\partial ^{2}w^{stat}}{\partial x^{2}}(0,t)=0,\forall t\;< 0 \\ w^{stat}(\ell ,t)=0,\;\dfrac{\partial w^{stat}}{\partial x}(\ell ,t)=0,\;\ell _{0} \le \ell <\ell _c. \\ \end{array}} \right. \nonumber \\ \end{aligned}$$
(2)

The solution of the above system is readily written:

$$\begin{aligned} w^{stat}(x,t)=\frac{W^{0}(t)}{2}\frac{x}{\ell }\left( {\frac{x^{2}}{\ell ^2 }-3} \right) +W^{0}(t) \end{aligned}$$
(3)

The strain energy (which is also the potential energy without any prescribed forces along the specimen boundaries), associated to the above solution is therefore:

$$\begin{aligned} U=\frac{EI}{2}\int \limits _0^\ell {\left( {\frac{\partial ^{2} w^{stat}}{\partial x^{2}}} \right) ^{2}\;} dx_ =\frac{3}{2}EI\frac{\left( {W^{0}(t)} \right) ^{2}}{\ell ^3 } \end{aligned}$$
(4)

The energy release rate is then:

$$\begin{aligned} G(\ell (t))&= -\frac{\partial U(\ell )}{\partial \ell }=\frac{9}{2}EI\frac{\left( {W^{0}(t)} \right) ^{2}}{\ell ^4 },\nonumber \\&\ell _{0} \le \ell <\ell _c \end{aligned}$$
(5)

Assuming that the crack onset obeys the Griffith criterion:

$$\begin{aligned} G(\ell (t))\le \Gamma _{0} \end{aligned}$$
(6)

The critical length \(\ell _c \) is connected to the critical prescribed displacement and the surface energy through the relationship:

$$\begin{aligned} \ell \, _c^ =\root 4 \of {\frac{9}{2}EI\frac{\left( {w^{c}} \right) ^{2}}{\Gamma _{0} }} \end{aligned}$$
(7)

It may be noted that up to \(\ell =\ell _c\), the relation \(G(\ell )=\Gamma _{0} >\Gamma _1 \) holds true, because during this stage the crack propagation is stable. On the other hand, the Griffith criterion is violated when the crack tip reaches the interface bonding the starting and the test sections. Hence, the relation (7) is no longer relevant for \(\ell \ge \ell _c\). From now on, we will focus on the dynamic stage for \(\ell \ge \ell _c\) (disregarding the static stage \(\ell _{0} \le \ell <\ell _c)\).

3 Approximate equation of the DCB motion by modal decomposition

3.1 Natural frequencies and eigenmodes for a pinned-clamped beam

Considering a beam in free vibration, a separated solution of the deflection, in time and space, is assumed:

$$\begin{aligned} w(x,t)=w^{stat}(x)+\phi (x)f(t) \end{aligned}$$
(8)

where the static part \(w^{stat}\) fulfils the system (2).

The motion equation (1) may be written as:

$$\begin{aligned} \frac{EI}{\rho A}\frac{\phi ^{{\prime }{\prime }{\prime }{\prime }}(x)}{\phi _ (x)}=-\frac{f{^{\prime \prime }}(t)}{f(t)}=\omega ^{2} \end{aligned}$$
(9)

where \(\omega \) is the angular frequency, and which produces two differential equations:

$$\begin{aligned}&f{^{\prime \prime }}(t)+\omega ^{2}f(t)=0, \hbox { and } \phi ^{{\prime }{\prime }{\prime }{\prime }}(t)-\mu ^{4}\phi (t)=0\quad \end{aligned}$$
(10)
$$\begin{aligned}&\quad \hbox { with } \mu ^4 =\frac{\rho A\omega ^{2}}{EI} \end{aligned}$$
(11)

We only focus on the second equation, which provides the eigenmodes and the eigenvalues.

The general solution of this equation is:

$$\begin{aligned} \phi (x)&= A\cos (\mu x)+B\sin (\mu x)\nonumber \\&+\,Cch(\mu x)+Dsh(\mu x) \end{aligned}$$
(12)

with the boundary following conditions:

$$\begin{aligned} \left. {{\begin{array}{l} {\phi \left( 0 \right) =0\rightarrow A+C=0} \\ {\phi ^{{\prime \prime }}\left( 0 \right) =0\rightarrow -A+C=0} \\ {\phi \left( \ell \right) =0\rightarrow B\sin \left( {\mu \ell } \right) +Dsh\left( {\mu \ell } \right) =0} \\ {\phi ^{{\prime }}\left( \ell \right) =0\rightarrow B\cos \left( {\mu \ell } \right) +Dch\left( {\mu \ell } \right) =0} \\ \end{array} }} \right\} \end{aligned}$$
(13)

These conditions induce the following equation for the eigenvalue solution:

$$\begin{aligned} tg(\mu \ell )=th(\mu \ell ) \end{aligned}$$
(14)

This equation has an infinite number of solutions \(\mu _i , i\in \mathsf{N}\), which can be calculated numerically, or approximated for high frequencies (by noticing that for \(\mu _i \ell >>0, th(\mu _i \ell )\rightarrow 1)\) by:

$$\begin{aligned} \mu _i \ell =\frac{(4i+1)\pi }{4},\quad i\in \mathsf{N} \end{aligned}$$
(15)

The eigenmodes take the following form:

$$\begin{aligned} \phi _i \left( x \right) =B\left[ {\sin \left( {\mu _i x} \right) -\frac{cos \left( {\mu _i \ell } \right) }{ch\left( {\mu _i \ell } \right) }sh\left( {\mu _i x} \right) } \right] \end{aligned}$$
(16)

where the coefficient \(B\) is determined by the mode normality \(\left\| {\phi _i } \right\| =1\)

3.2 Approximate equation of motion

We focus now on the beam with the moving crack. The moving domain \(\left\{ {x,x\in \left[ {0,\ell (t)} \right] } \right\} \) will be normalized, with the variable change \(X=x/\ell ,\;X\in \left[ {0,1} \right] \), so that all expressions will be integrated over a stationary domain.

It is assumed that the deflection of the beam is given by the following approximation:

$$\begin{aligned} w\left( {X,t} \right) =w^{stat}\left( X \right) +\hat{{w}}\left( {X,t} \right) \end{aligned}$$
(17)

where \(\hat{{w}}\left( {X,t} \right) \)is the perturbation around the equilibrium solution \(w^{stat}\),corresponding to the expression (3). This perturbation can be decomposed for its eigenmodes, which provide an orthonormal basis:

$$\begin{aligned} \hat{{w}}\left( {X,t} \right) =a_i (t)\phi _i \left( X \right) ,\quad i=1,N \end{aligned}$$
(18)

where the Einstein summation convention is adopted. \(\phi _i \) is the ith normal mode shape for free vibration of the beam, and \(a_i \) the unknown deflection amplitude associated to \(\phi _i \) (which depends on the initial conditions).

The complete solution of the dynamic crack growth problem in the DCB is now restricted to the determination of the time dependent variables \(a_i (t),\ell (t)\)

4 General evolution of the system and local equations

The purpose of this section is to produce local equations of the general motion \(a_i (t),\ell (t)\) for the case of the DCB with a running crack, starting from a variational principle and the modal decomposition.

Let us consider the evolution of the total energy of the beam \(H(t)\) (the surface energy could be considered here as space dependent but for simplicity it is assumed that the fracture properties remain constant):

$$\begin{aligned} H(t)=U(t)+K(t)+\Gamma _1 (\ell (t)-\ell _c ) \end{aligned}$$
(19)

Between two mechanical states at time \(t=0\) (crack onset) and any time \(t_1 >0\), the energy balance states that \(H(t)\) keeps this initial value \(U_0 \) at any time:

$$\begin{aligned} H(t_1 )=U(t_1 )+K(t_1 )+\Gamma _1 (\ell (t_1 )-\ell _c )=U_0 \end{aligned}$$
(20)

The energy components may be written on the stationary spatial domain \(\left\{ {X=x/\ell ,\;X\in \left[ {0,1} \right] } \right\} \), with:

$$\begin{aligned} K(\ell (t),t)&= \frac{\rho A}{2}\int \limits _0^{\ell (t)} {\left( {\frac{\partial w(x,t)}{\partial t}} \right) } ^{2}\\ dx&= \frac{\rho A\ell }{2}\int \limits _0^1 {\left( {\frac{d\tilde{w}(X,t)}{dt}} \right) } ^{2}dX\\ U(\ell (t),t)&= \frac{EI}{2}\int \limits _0^\ell {\left( {\frac{\partial ^{2} w(x,t)}{\partial x^{2}}} \right) ^{2}\;}\\ dx&= \frac{EI}{2\ell ^{3}}\int \limits _0^1 {\left( {\frac{\partial ^{2} \tilde{w}(X,t)}{\partial X^{2}}} \right) ^{2}\;} dX \end{aligned}$$

Using the deflection modal decomposition on the eigenmodal basis \(\left\{ {\phi _i } \right\} \), the previous expressions are rewritten as:

$$\begin{aligned}&K(\ell (t),t) \nonumber \\&\quad =\frac{\rho A\dot{\ell }^{2}}{2\ell }\int \limits _0^1 \left( Xw^{stat\prime }\left( X \right) +Xa_i \left( t \right) {\phi }_i^{\prime } \left( X \right) \right. \nonumber \\&\qquad \left. -\frac{\ell }{\dot{\ell }}\dot{a}_i \left( t \right) \phi _i \left( X \right) \right) ^{2} dX \quad i=1,\ldots N \end{aligned}$$
(21)
$$\begin{aligned}&U=\frac{EI}{2\ell ^{3}}\int \limits _0^1 {\left( {w^{stat{^{\prime \prime }}}\left( X \right) +a_i \left( t \right) {\phi }_i^{{\prime \prime }} \left( X \right) } \right) } ^{2}dX \end{aligned}$$
(22)

Let \((q_i )\) denote the parameters of the energy terms \((q_i =a_i , i=1,N,\;q_{N+1} =\ell )\). The total energy is then a functional \(H(q_i ,\dot{q}_i )\) depending on the parameters and their time derivatives. Therefore, the following relation holds:

$$\begin{aligned} \frac{dH}{dt}=\frac{\partial H}{\partial q_i }\dot{q}_i +\frac{\partial H}{\partial \dot{q}_i }\ddot{q}_i =0 \end{aligned}$$
(23)

With a simple mathematical calculation, invoking the particular form of the kinetic energy (see “Appendix”), the \(N+1\) local motion equations hold:

$$\begin{aligned} \left\{ {\begin{array}{l} \dfrac{\partial (K-U)}{\partial q_i }-\dfrac{d}{dt}\dfrac{\partial (K-U)}{\partial \dot{q}_i }=0,\quad i=1,N \\ \dfrac{\partial (K-U)}{\partial \ell }-\dfrac{d}{dt}\dfrac{\partial (K-U)}{\partial \dot{\ell }}=\Gamma _1 \; \\ \end{array}} \right. \end{aligned}$$
(24)

To complete the problem statement, the constraints \(w\ge 0,\;\dot{\ell }\ge 0\), which describe respectively the crack lips non overlapping and the crack growth irreversibility, should be coupled to Eq. (24). These aspects will be henceforth disregarded, because the lips contact cannot be separately treated on each mode, and the irreversibility treatment, although it may be feasible, would increase the computation cost. These shortcomings do not greatly impact the final outcome.

That leads to the following second order differential equations governing the beam vibration coupled to the crack kinematics (see the details in “Appendix”):

$$\begin{aligned} \ddot{a}_i&= \frac{\ddot{\ell }}{\ell }\left( {C_3^i +a_j C_4^{ij} } \right) +\frac{2\dot{\ell }}{\ell }\dot{a}_j C_4^{ij}\nonumber \\&+\frac{\dot{\ell }^{2}}{\ell ^{2}}\left( {C_2^i +a_j C_1^{ij} } \right) \nonumber \\&-\frac{1}{\ell ^{4}}\frac{EI}{\rho A}a_i \mu _i ^{4},\quad i=1,N\end{aligned}$$
(25)
$$\begin{aligned} \ddot{\ell }&= \frac{\dot{\ell }^{2}}{2\ell }+\frac{\dot{\ell }}{\Delta }\left( {-2\dot{a}_i C_2^i -2\dot{a}_j a_i C_1^{ij} } \right) \nonumber \\&+\frac{3EI}{2\ell ^{3}\Delta \rho A}\left( {3(w^c )^{2}+a^{2}_i \mu ^{4}_i } \right) \nonumber \\&+\frac{\ell }{\Delta }\left( {\ddot{a}_i C_3^i +\ddot{a}_i a_j C_4^{ij} -\frac{\Gamma _1 }{\rho A}} \right) \end{aligned}$$
(26)

where the coefficients \(\left( {C_1^{ij} ,C_2^i ,C_3^i ,C_4^{ij} } \right) \) only depend on the mode shape of the beam (see “Appendix”), and \(\Delta =\frac{6(w^c )^{2}}{35}+a_i a_j C_1^{ij} +2a_i C_2^i \)

These two coupled systems are solved using a backward differentiation formula method, used for implicit equations. Once again, the above coupled system does not ensure the irreversibility of the crack growth (\(\dot{\ell }\ge 0)\), neither does it prevent the crack lips from interpenetrating (\(w\left( {x,t} \right) \ge 0\) should always be true). This does not affect the results but could be amended in future work, using corresponding constraints.

5 A one-dimension model for the peeling film process

Before solving the above equations, let us focus on a problem close to the running crack in the DCB, but more simple and having an exact solution.

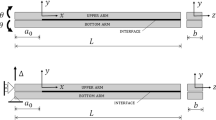
Let’s consider the peeling experiment of a thin film, inextensible and perfectly flexible, from a rigid surface. A vertical displacement \(W^{0}(t)\) is slowly prescribed at the origin \(x=0\), while the film is stretched by an axial force \(N\) and debonded from the surface, activating a surface energy \(\Gamma _{0} \) (cf. Fig. 2), for \(\ell _{0} \le x<\ell _c \) where \(\ell _{0} \ge 0\) is the initial length of the film. From \(x=\ell _c \), the bonding surface becomes weaker, having a lower surface energy \(\Gamma _1 \) with \(R=\Gamma _{0} /\Gamma _1 >1\). When \(\ell (t_c )=\ell _c \), the loading is frozen (\(W^{0}(t_c )=W^{0})\) and the peeling length is quickly increasing, up to the arrest length \(\ell (t_A )=\ell _A \). The aim is to determine the arrest length, and more generally the complete film kinematics during the dynamic stage, disregarding the trivial quasi-static peeling phase (\(t<0)\). This problem has been investigated by Freund (1989) and revisited by Marigo et. al. for a slightly different loading, Charlotte et al. (2008) and for heterogeneous debonding properties Lazzaroni et al. (2012). This problem, providing an exact solution, shares some similarities with the DCB problem and is a mockup for testing the approach defined above.

Fig. 2
figure 2

The peeling test with two surface energies

Full size image

5.1 Statement of the peeling test

Only the main outcome is presented here, the detailed analysis is presented in Freund (1989) and Charlotte et al. (2008), Lazzaroni et al. (2012). A specific property of this problem is that the peeling point carries a discontinuity of strain (\(w,_x )\) and velocity (\(w,_t )\), which propagates along the film at the wave speed \(c=\sqrt{N/\rho }\) where \(\rho \) is the wave celerity of the film. The motion and the peeling process involve the following energies (respectively kinetic, potential and dissipative part of the total energy):

$$\begin{aligned} K(\ell (t),t)&= \frac{\rho }{2}\int \limits _0^{\ell (t)} {\left( {\frac{\partial w}{\partial t}} \right) } ^{2}dx\end{aligned}$$
(27)
$$\begin{aligned} U(\ell (t),t)&= \frac{N}{2}\int \limits _0^{\ell (t)} {\left( {\frac{\partial w}{\partial x}} \right) ^{2}\;} dx\end{aligned}$$
(28)
$$\begin{aligned} D(\ell (t))&= \Gamma _1 (\ell (t)-\ell _c ) \end{aligned}$$
(29)

The boundary conditions are:

$$\begin{aligned} w(0,t_c )=W^{0}(t_c )=w^{c},w(\ell (t),t)=0,\quad \forall t, t\ge t_c \end{aligned}$$

while the initial conditions are: \(w(x,0)=w^{stat}(x,0)=w^{c}(1-x/\ell _c )\).

Furthermore, the velocities and strains jumps are expressed on the singular characteristic curves \(C_j =\left\{ {\left. {(x_j ,t_j )} \right\} } \right. \) in the space-time plane, as:

$$\begin{aligned} n_x \left| {\left[ {\frac{\partial w(x_j ,t_j )}{\partial t}} \right] } \right| =n_t \left| {\left[ {\frac{\partial w(x_j ,t_j )}{\partial x}} \right] } \right| \end{aligned}$$

where \(n\) is the unit normal of the characteristic curve.

The variational approach applied to this problem leads to the local equations:

$$\begin{aligned}&N\frac{\partial ^{2} w}{\partial x^{2}}-\rho \frac{\partial ^{2} w}{\partial t^{2}}=0,\quad \!on\!\quad \left[ {0,\ell (T)} \right] X\left[ {0,T} \right] {/}C_j \nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned}&Nn_t \left| {\left[ {\frac{\partial w(x_j ,t_j )}{\partial t}} \right] } \right| =\rho n_x \left| {\left[ {\frac{\partial w(x_j ,t_j )}{\partial x}} \right] } \right| \quad \!on\!\quad C_j \nonumber \\ \end{aligned}$$
(31)

These equations describe the film motion. Furthermore, the peeling point kinematics is depicted by a special characteristic curve and is expressed by the Griffith law:

$$\begin{aligned} \frac{1}{2}\left( {N\left[ {\frac{\partial w(\ell (t),t)}{\partial x}} \right] ^{2}-\rho \left[ {\frac{\partial w(\ell (t),t)}{\partial x}} \right] ^{2}} \right) =\Gamma _1 \nonumber \\ \end{aligned}$$
(32)

These equations may be solved by the characteristics method and lead to the exact solutions of the film deflection and kinematics. The main results may be summarized as follows:

$$\begin{aligned}&w(x ,t )=w^{c}\left( 1-\frac{x}{\ell _c }\right) \hbox { for } x\le \ell (t)-ct\nonumber \\ \end{aligned}$$
(33)
$$\begin{aligned}&w(x ,t )=w^{c}\left( 1-\frac{x}{\ell _c (1+\dot{\ell }/c)}\right) \hbox { for } x>\ell (t)-ct \nonumber \\ \end{aligned}$$
(34)
$$\begin{aligned}&\hbox { and } \dot{\ell }(t)/c=\frac{R-1}{R+1} \hbox { for } 0<t\le t_A \nonumber \\ \end{aligned}$$
(35)
$$\begin{aligned}&\ell _A =\ell (t_A )=R\ell _c \nonumber \\&K(\ell (t))=\left\{ {{\begin{array}{l} {U(\ell _c )\frac{R-1}{2R}(\frac{\ell }{\ell _c }-1),\quad 0\le t<\ell _c /c} \\ {U(\ell _c )\frac{(R-1)^{2}}{2R^{2}}-\frac{(R-1)}{2R^{2}}(\frac{\ell }{\ell _c }-1),}\\ \quad {\ell _c /t\le t<(\ell _c +\ell _A )/c} \\ \end{array} }} \right. \nonumber \\ \end{aligned}$$
(36)

It is worth noting that the kinetic energy is time dependent only through the peeling length, and obtains a zero value after the arrest point, making a substantial difference with the DCB test, as is discussed in Sect. 6.

5.2 Approximation of the peeling problem by a modal analysis

This problem may be also solved, by using a modal analysis and in disregarding the strain and velocity jumps, contrary to the characteristics method. Therefore, it provides only approximate results, although a reasonably accurate estimate can be obtained with a limited number of modes. As already stated for the beam, the film deflection can be expressed on the eigenmodal basis:

$$\begin{aligned} w\left( {X,t} \right)&= w^{stat}\left( X \right) +\hat{{w}}\left( {X,t} \right) \\&= w^{stat}\left( X \right) +a_i (t)\phi _i \left( X \right) ,\quad i=1,N \end{aligned}$$

where \(w^{stat}\left( X \right) =W^{0}\left[ {1-X} \right] \)

Unlike the DCB specimen, the eigenmodes and the angular frequencies are very simple and calculated crudely by hand. The local motion equation (30), associated to the boundary conditions leads to the following normalized eigenmode vector:

$$\begin{aligned}&\phi _i \left( X \right) =\sqrt{2}\sin (i\pi X),\\&\mu _i =i\pi , i=1,N,X\in \left[ {0,1} \right] , \end{aligned}$$

and the angular frequency: \(\omega _i ^{2}=\frac{\mu _i^2 c^{2}}{\ell ^{2}}=\frac{\mu _i^2 N}{\rho \ell ^{2}}\).

The potential and kinetic energy expressions, associated to \(N\) modes are:

\(U(w,t)=\frac{N}{2\ell (t)}(W^{0^{2}}+a_i a_j (i\pi )^{2}\delta _{ij} ),\) where \(\delta _{ij} \) is the Kronecker symbol.

$$\begin{aligned} K&= \frac{\rho \dot{\ell }^{2}}{2\ell ^{2}}\int \limits _0^1 {(W^{0}X+\frac{\ell }{\dot{\ell }}} \dot{a}_i (t)\phi _i (X)\\&-\,Xa_i (t)\phi ^{\prime }_i (X))^{2}dX \end{aligned}$$

In the same way as for the DCB test, assuming the stationarity of \(H(t)=U(t)+K(t)+\Gamma _1 (\ell (t)-\ell _c )\), the following equations hold:

$$\begin{aligned} \ddot{a}_i&= \frac{\ddot{\ell }}{\ell }\left( {-\int \limits _0^1 {XW^0 \phi _i } dX+a_j \int \limits _0^1 {X\phi ^{\prime }_j \phi _i } dX} \right) \nonumber \\&+\frac{2\dot{\ell }}{\ell }\dot{a}_j \int \limits _0^1 {X\phi _i \phi _j^{\prime } dX} \nonumber \\&-\frac{\dot{\ell }^{2}}{\ell ^{2}}\int \limits _0^1 {(W^{0}-a_j \phi _j^{\prime } )X^{2}\phi _i^{\prime } dX}\nonumber \\&-\frac{1}{\ell ^{2}}\frac{N}{\rho }a_i \mu _i ^{2},\quad i=1,N \nonumber \\ \end{aligned}$$
(37)
$$\begin{aligned} \ddot{\ell }&= \frac{\dot{\ell }^{2}}{2\ell }+\frac{\dot{\ell }\dot{a}_i }{\Delta }\left( {\int \limits _0^1 {2X^{2}(W^0 \phi ^{\prime }_i } -a_j \phi ^{\prime }_i \phi ^{\prime }_j )dX} \right) \nonumber \\&+\frac{N}{2\rho \ell \Delta }\left( {(W^0 )^{2}+a_i a_j \delta _{ij} \mu ^{2}_i } \right) \nonumber \\&+\frac{\ell }{\Delta }\left( {-\ddot{a}_i \int \limits _0^1 {XW^0 \phi _i } dX+\ddot{a}_i a_j \int \limits _0^1 {X\phi ^{\prime }_j \phi _i } dX-\frac{\Gamma _1 }{\rho }} \right) \nonumber \\ \end{aligned}$$
(38)

with : \(\Delta =(W^0 )^{2}/3+a_i a_j \int \nolimits _0^1 {X^{2}\phi ^{\prime }_j \phi ^{\prime }_i } dX-2a_i W^0 \int \nolimits _0^1 {X^{2}\phi ^{\prime }_i } dX\)

It can be seen that the above equations are very similar to those governing the DCB test (25,26).

5.3 Numerical application of the modal analysis

Selecting the following characteristics: c = 5,000 m/s, \(\rho = 7{,}800\) kg/m\(^{3}\) corresponding to steel properties, and a debonding energy ratio \(R=\Gamma _{0} /\Gamma _1 =2\), and with the initial length \(\ell _c =0.1\) m, the modal analysis is performed with a wide range of modes, and the results compared to the exact solution provided by the characteristics method. The peeling length versus the time process provided for different number of modes and compared to the exact solution is illustrated on the Fig. 3. For the basic mode (\(N=0)\), the kinematics are roughly designed but the arrest point is perfectly predicted because the energy balance is perfectly valid between the starting and the ending point. For \(N=2\), the kinematics is much better, oscillating around the analytical solution. Beyond \(N=10\), the results fit with the true solution (except some tiny oscillations which are invisible on the figure). Note that the arrest is established here when the peeling length decreases, which although not physically acceptable, is numerically possible because of the irreversibility not being taken in account.

Fig. 3
figure 3

Peeling length evolution

Full size image

The peeling point velocity is sketched in Fig. 4. The small oscillations noticed above for \(\ell (t)\) are increased for the velocity, but the magnitude oscillates around the exact value \(\dot{\ell }(t)=\frac{R-1}{R+1}c=\frac{c}{3}\), with a quasi jump for the debonding start and arrest.

Fig. 4
figure 4

Peeling velocity

Full size image

The kinetic energy (Fig. 5) increases up to the time \(t=\ell _c /c\) when the shock wave is reflected on the fixed point where the displacement \(w^{c}\) is prescribed. The energy then decreases and cancels at the time arrest. This process is correctly described with a sufficient number of modes but small perturbations remain (the solution is approximated by steps). Due to the lack of constraints concerning the peeling irreversibility, the numerical values increase again, after the definitive arrest (the film is “rebonding” as we can see on Fig. 3). The arrest is assumed at this point which fits with the theoretical one, corresponding to the round trip time delay for the wave (\((\ell _c +\ell _A )/c)\).

Fig. 5
figure 5

Kinetic energy evolution

Full size image

6 Application to the DCB test

The previous modal analysis is now applied to the DCB test, selecting the following characteristics: \(E=2 10^{11} \hbox {Pa},\;\;\rho =7800\,\hbox {kg/m}^{3}\) corresponding to steel properties, and with the initial length \(\ell _c =0.1\) m to be as close as possible to the previous test. The height of the beam is \(h=0.006\) m so that the initial slenderness ratio \(\lambda =\ell _c /h\approx 17\) is sufficiently large to make the Bernoulli model relevant, and a rectangular section is assumed with a unit width.

6.1 Modal analysis for R = 2 and R = 3

The Fig. 6 displays the crack length extension versus time for the surface energy ratio \(R=2\), and \(R=3\), assuming a zero initial crack velocity. Unlike the previous test, an analytical solution is no longer available. To obtain a point of reference, the modal analysis is compared with a 2D (plane strain) finite element investigation associated to a cohesive zone model Debruyne et al. (2012) (the cohesive zone is small enough to fit with the Griffith criterion). The crack kinematics are illustrated on Fig. 6 for \(R=2\) and for a range of mode from \(N=0\) to \(N=5\). By examining the figure, two initial comments can be made. First of all, the oscillations of the crack growth are more pronounced than those observed for the peeling test. Secondly, the average crack velocity is much lower than for the previous example, meaning that a number of backward and forwards travelling waves are possible. It can be assumed that these oscillations derive from two sources: the first is connected to the wave returns marked by transient short arrest (\(\dot{\ell }=0)\), depicted by short flat steps with the cohesive model, which are degenerated in oscillations with the modal analysis allowing crack growth reversibility. The second is most likely due to the mode shape, described by hyperbolic functions that are more complex to compute accurately than those related to the peeling film.

Fig. 6
figure 6

Crack kinematics for a modal decomposition up to 5 modes (R = 2)

Full size image

Nevertheless, the crack growth is in good agreement with the cohesive zone model for a modal analysis with \(N\ge 3\). For the basic mode \(N=0\), the complete kinematics is only very roughly approximated, but the crack arrest prediction is a rounded up value \((\ell _A /\ell _c \approx 1.45)\). Once again, this latter is assumed when there is a significant decrease of the crack length. Figure 7 sketches the crack kinematics for the ratio \(R=3\). The same conclusions can be drawn from observing the short transient arrests, the results fluctuations and the global agreement with the finite element analysis. The assumed definitive crack arrest is here \(\ell _A /\ell _c \approx 1.75\) and the basic modal analysis \((N=0)\) provides an upper bound of the solution \((\ell _A /\ell _c \approx 1.85)\).

Fig. 7
figure 7

Crack kinematics for a modal decomposition up to 5 modes (R = 3)

Full size image

6.2 Modal analysis for higher modes and higher ratios

The modal analysis correctly predicts the crack kinematics with a moderate number of modes \((N\le 5)\) and takes less than 1 min of computer time. Above the fifth mode (the analysis has been performed up to 10 modes), the curves related to each mode coincide almost perfectly, as represented by instance on Fig. 8, for the case \(R=2\). Above \(N=10\), the convergence is more difficult and the time significantly increases.

Fig. 8
figure 8

Crack kinematics for upper modes (\(5\le N\le 10)\) for R=2

Full size image

Below \(R=10\), no crack overlap has been detected, so that the lack of consideration of contact does not involve outliers. Beyond \(R=10\), a small crack overlap is observed in the earlier crack growth stage (cf. Fig. 9a) and the method reaches its limits.

Fig. 9
figure 9

a Beam deflection versus crack length At the crack onset,9b. Beam deflection versus crack length at the crack arrest

Full size image

6.3 Some comments about the kinetic energy role on the crack growth process

The kinetic energy can vary during a possible transient arrest and even for the definitive arrest, because some free vibrations remain \((K(\ell (t),t)_{\dot{\ell }=0} =\frac{\rho A\ell }{2}\int \nolimits _0^1 {\left( {\dot{a}_i \left( t \right) \phi _i \left( X \right) } \right) ^{2}} dX)\). Hence, unlike the peeling test where the kinetic energy only plays a transitory role and where the arrest is fully predicted by the total quasistatic energy balance (Lazzaroni et al. 2012), the kinetic energy evolution is more complex for the DCB test as it can been observed on Fig. 10 for \(R=3\). At the definitive crack arrest time, the kinetic energy does not vanish and yields a value slightly higher than its minimum, occurring during the second bounce corresponding to the beam vibration at the end of the crack propagation (cf. Fig. 10).

Fig. 10
figure 10

Kinetic energy versus time for R = 3

Full size image

As depicted on Fig. 11 (comparing kinetic energy evolution for \(R=2\) and \(R=3)\), the higher the ratio R, the greater the importance of the kinetic energy, including during the second bouncing stage.

Fig. 11
figure 11

Kinetic energy versus time for R = 2 and R = 3 (CZM solution)

Full size image

At certain moments, independent of the ratio, the energy evolution is disturbed probably by some wave deflection, long before the intended arrest time.

6.4 Crack arrest prediction with a quasistatic method and sensitivity of arrest to particular parameters

6.4.1 The approximate solution of Mott applied to the DCB specimen

Mott (1948) extended Griffith’s theory to dynamic crack propagation, including a contribution from the kinetic energy. Mott’s main assumptions are that the crack growth process is steady state and that in the energy balance relation (20), the kinetic energy is time dependent, but only throughout the crack velocity. For the case of the DCB, assuming that the displacement keeps its quasi-static shape, as related in (3), these assumptions lead to:

$$\begin{aligned} w(x ,t)=w^{stat}(x) \end{aligned}$$
(39)

and

$$\begin{aligned}&K(\ell (t),\dot{\ell }(t))=\frac{\rho A}{2}\dot{\ell }^{2}(t)\int \limits _0^{\ell (t)} {\left( {\frac{dw^{stat}}{d\ell }} \right) } ^{2}dx\nonumber \\&\quad =\frac{\rho A\left( {w^{c}} \right) ^{2}}{2}\dot{\ell }^{2}(t)\int \limits _0^{\ell (t)} {\frac{9}{4}\left( {-\frac{x^{3}}{\ell ^{4}(t)}+\frac{x}{\ell ^{2}(t)}} \right) } ^{2}dx\nonumber \\ \end{aligned}$$
(40)

which matches the expressions derived from the modal analysis with \(N=0\).

The energy balance is then written:

$$\begin{aligned} U_0 =\frac{3\rho A\left( {w^{c}} \right) ^{2}}{35\ell (t)}\dot{\ell }^{2}(t)+\frac{3}{2}\frac{EI\left( {w^{c}} \right) ^{2}}{\ell ^{3}(t)}+\Gamma _1 (\ell -\ell _c ) \nonumber \\ \end{aligned}$$
(41)

Considering \(\dot{\ell }_A =0\) and using the relations (4), (5) and (6), the following expression holds:

$$\begin{aligned} \frac{3}{2}\frac{EI\left( {w^{c}} \right) ^{2}}{\ell _c ^{3}}=\frac{\Gamma _{0}}{3}\ell _c =\frac{\Gamma _{0} }{3}\frac{\ell _c ^{4}}{\ell _A ^{3}}+\Gamma _1 (\ell _A -\ell _c ) \end{aligned}$$

which leads to a simple polynomial relation for predicting crack arrest:

$$\begin{aligned} 3\left( \frac{\ell _A }{\ell _c }\right) ^{4}-(R+3)\left( \frac{\ell _A }{\ell _c }\right) ^{3}+R=0 \end{aligned}$$
(42)

For the ratios \(R=2, R=3\), the relative arrest length are respectively \(\frac{\ell _A }{\ell _c }=1.45\) and \(\frac{\ell _A }{\ell _c }=1.84\), which is in good accordance with our previous investigations. It is expected that the prediction accuracy will be degraded for high ratios but will constitute an upper bound.

6.4.2 Sensitivity of arrest to initial crack velocity and beam slenderness

It is noteworthy that the expression (42) depends only on the ratio \(R\), and not on any beam geometry parameter. The following analysis is attempting to estimate the arrest length sensitivity to some parameters as the initial velocity, and the beam geometry.

The crack kinematics is affected by the initial crack velocity, as illustrated in Fig. 12:

Fig. 12
figure 12

Comparative crack kinematics for two different initial crack velocities

Full size image

The higher the initial velocity, the higher the average velocity and the sooner the arrest time. However the arrest length is not affected by this parameter. Note also that the kinetic energy behaviour (Fig. 13) is affected by the initial acceleration and only at the beginning of the crack growth. With respect to the beam geometry, the slenderness effect on the crack growth has also been investigated (see Fig. 14). The crack velocity decreases when the slenderness \(\lambda \approx \ell _c /h\) increases, which is as expected, but the result of great interest is the insensitivity of the crack arrest length to the slenderness. The more exceptional conclusion of these investigations is that the relative crack arrest length \(\ell _A /\ell _c \) is essentially governed by the fracture energy ratio.

Fig. 13
figure 13

Comparative kinetic energy for two different initial crack velocities

Full size image
Fig. 14
figure 14

Influence of the beam slenderness ratio on the crack kinematics

Full size image

7 Conclusions and outlines

The problem of an elastic DCB with a bi-toughness material, subjected to a slowly prescribed opening displacement has been investigated, focusing on the dynamic crack stage, which occurs in the test section with a lower fracture toughness while the prescribed displacement is suddenly stopped. The decomposition on the first \(N\) eigenmodes of a Bernoulli beam deflection associated to the total energy balance, leads to a system of \(N+1\) coupled differential equations of second order. The associated solution consists of \(N\) modal deflection amplitudes and to the crack length evolution.

The method has been applied to the dynamic peeling test of a thin film, where exact solutions are available (the equations derived from the DCB and the film are of course different but are structured in a similar way). The numerical prediction for the peeling test is in a very good accordance with the analytical solution, with only a few modes and a short computational time (a few seconds). Concerning the crack growth in the DCB specimen, the dynamic crack kinematics seem to be correctly described with a few modes, compared to a 2D finite element transient dynamic analysis using a cohesive zone model, but some problems remain. In particular, the numerical results are disturbed by some oscillations. These latter may be produced by a complex wave propagation which leads to transient short crack arrests (which are not present in the peeling test). But the failure to account the crack growth irreversibility \((\dot{\ell }\ge 0)\) in the method may magnify the difficulties. This shortcoming may be circumvented by adding the constraint inequality \(\dot{\ell }\ge 0\) to the motion equations, but with probably an increase in computational time (it takes only a few minutes for a complete analysis with the current method). If the aim is the prediction of the crack arrest length—which is of high interest for the engineer—the trivial mode \((N=0)\) is sufficient. Furthermore, the relative arrest length \(\ell _A /\ell _c \) is somewhat insensitive to parameters such as the beam geometry or the initial crack velocity, and is mainly governed by the ratio of the energy at the blunted crack onset over the surface energy of the running crack material. A simple method, based on an energy balance, has been suggested to predict the crack arrest length, disregarding the complex dynamic propagation stage, with a good estimation for moderate ratios. An extension of this method to a beam with variable section geometry (for instance tapered DCB), or a dynamic force loading, is straightforward. The next anticipated continuation of this work is to consider a complex toughness distribution, and in particular a layout of small flaws distributed on special sections of the beam. On the other hand, developments concerning the material behaviour such as the viscosity or plasticity, or the application to bidimensional geometries are possible but more complicated.