Atomistic and continuum modelling of temperature-dependent fracture of graphene

Abstract

This paper presents a comprehensive molecular dynamics study on the effects of nanocracks (a row of vacancies) on the fracture strength of graphene sheets at various temperatures. Comparison of the strength given by molecular dynamics simulations with Griffith’s criterion and quantized fracture mechanics theory demonstrates that quantized fracture mechanics is more accurate compared to Griffith’s criterion. A numerical model based on kinetic analysis and quantized fracture mechanics theory is proposed. The model is computationally very efficient and it quite accurately predicts the fracture strength of graphene with defects at various temperatures. Critical stress intensity factors in mode I fracture reduce as temperature increases. Molecular dynamics simulations are used to calculate the critical values of $J$ integral ($J_\mathrm{IC}$) of armchair graphene at various crack lengths. Results show that $J_\mathrm{IC}$ depends on the crack length. This length dependency of $J_\mathrm{IC}$ can be used to explain the deviation of the strength from Griffith’s criterion. The paper provides an in-depth understanding of fracture of graphene, and the findings are important in the design of graphene based nanomechanical systems and composite materials

1 Introduction

Extraordinary mechanical and electrical properties of graphene make it a candidate for novel applications ranging from medicine to electronics (Novoselov et al. 2012). Defects are unavoidable during the synthesis and fabrication of graphene-based devices (Hashimoto et al. 2004). Defects such as vacancies could cause stress concentrations and degrade the strength and stiffness. Graphene reinforcements remarkably improve the fracture toughness and fatigue crack propagation resistance of composite materials (Rafiee et al. 2010). A thorough understanding of the mechanical behavior of graphene is necessary for the design of advanced nanoelectromechanical systems such as graphene based resonators (Chen et al. 2009; Eichler et al. 2011). Fracture properties are one of the most important mechanical properties of graphene, which set a limit on the novel applications such as reinforcement in composite materials (Rafiee et al. 2010). It is very difficult to determine the fracture properties of graphene experimentally due to practical problems in designing experiments at the nanoscale (Kim et al. 2012). Therefore atomistic methods such as quantum mechanical (QM) models and molecular dynamics (MD) simulations play a key role in the investigation of fracture properties of graphene.

MD simulations have a profound advantage over QM models when considering the computational cost. Potential fields of MD simulations incorporate empirical data to evaluate the parameters of the potential field (Stuart et al. 2000; Brenner et al. 2002). Therefore the MD simulations are able to simulate the behaviour of atomic systems much closer to the physical behaviour compared to QM models, which are mostly theoretical compared to the empirical nature of MD simulations. MD ignores the electrons and assumes atoms as point particles whereas QM treats each electron of an atom separately. Therefore it is not possible in MD simulations to obtain the strain energy distribution between atoms and also at the crack tip, which may be important in the studies on crack propagation.

Omeltchenko et al. (1997) used MD simulations with reactive empirical bond order (REBO) potential to investigate the fracture of armchair graphene. They estimated the critical stress intensity factor in mode I fracture ($K_\mathrm{IC}$) using Griffith’s criterion and local stress distributions, and the corresponding values are 4.7 and 6 $\hbox {MPa m}^{1/2}$, respectively. Recently, some researchers have questioned the accuracy of these quantitative results due to the influence of the default cut-off function in REBO potential (Khare et al. 2007; Zhang et al. 2012a). However, the predicted values of $K_\mathrm{IC}$ by Omeltchenko et al. (1997) are within the same range as those reported in the recent literature (Xu et al. 2012; Zhang et al. 2012a).

Khare et al. (2007) studied the effects of large defects and cracks on the mechanical properties armchair graphene using a coupled quantum mechanical/molecular mechanical model. They found that the cross section of defects, perpendicular to loading direction, has a greater effect on the tensile strength of graphene compared to the shape of defects. Ansari et al. (2012), using MD simulations with REBO potential, showed that the presence of vacancy defects significantly reduces the ultimate strength of graphene, while it has a minor effect on the Young’s modulus. They also showed that defects have a higher effect on the strength along zigzag direction compared to that of armchair direction.

Wang et al. (2012) studied the effects of vacancy defects on the fracture strength of graphene sheets using MD with adaptive intermolecular reactive empirical bond order (AIREBO) potential. They found that vacancies can cause significant strength loss in graphene and concluded that temperature and loading directions affect the fracture strength. A recent work from Xu et al. (2012) revealed that the $K_{\mathrm{IC}}$ of graphene are 4.21 and 3.71 $\hbox {MPa m}^{1/2}$ for armchair and zigzag directions, respectively. They used a coupled quantum mechanical/continuum mechanics model for the study. Zhang et al. (2012a) calculated $K_\mathrm{IC}$ of armchair and zigzag graphene using MD simulations with REBO potential and the corresponding values are 3.38 and 3.05 $\hbox {MPa m}^{1/2}$, respectively. The values of $K_\mathrm{IC}$ by Zhang et al. (2012a) is different from the values obtained by Xu et al. (2012), which can be attributed to the two different modeling approaches pursued. It should also be noted that the simulation temperature in Zhang et al. (2012a) is 300 K, whereas Xu et al. (2012) did not include temperature effects in their model (i.e. 0 K). Temperature has a significant effect on the tensile strength of pristine graphene (Dewapriya et al. 2013). It is therefore important to understand the temperature dependent fracture properties of armchair and zigzag graphene.

In this work, we calculate stress intensity factors of graphene using proportionality between the strength and square root of crack length, as opposed to the $K$-field displacement used in the literature. Temperature dependence of the stress intensity factors is also investigated. We show that a recently proposed discrete fracture theory, called quantized fracture mechanics (QFM), is more accurate compared to Griffith’s energy balance criterion in predicting the fracture strength of graphene. Both QFM and Griffith’s criterion are linear elastic fracture theories, whereas stress–strain behavior of graphene shows a significant nonlinearity. Therefore we use $J$ integral, which can be used for nonlinear material, to model fracture of graphene. We present a new approach to calculate $J$ integral at the nanoscale using MD simulations. These calculations revealed, for the first time, that $J$ integral (and lattice trapping) of graphene depends on the crack length. This length-dependence of $J$ integral can be used to explain the deviation of the strength from Griffith’s criterion. A novel fracture model, based on QFM, Arrenhnius formula, and Bailey’s principle, is also proposed. This model can be used to predict the fracture strength of graphene at various temperatures. The model agrees quite well with MD simulations and it is computationally very efficient.

The paper is organized as follows. Section 2 describes the MD simulation parameters. Section 3 explains the calculation of $K_\mathrm{IC}$. In this section, Griffith’s criterion, quantized fracture mechanics theory, and kinetic analysis are used to obtain the ultimate strength. The calculation of $J_\mathrm{IC}$ of armchair graphene is also presented in Sect. 3. Conclusions are drawn in Sect. 4.

2 Method

Molecular dynamics simulations are performed using LAMMPS package (Plimpton 1995) with AIREBO potential (Stuart et al. 2000). AIREBO consists of three sub-potentials, which are REBO, Lennard-Jones, and torsional potentials. REBO potential gives the energy stored in a bond between two atoms. The Lennard-Jones potential considers the non-bonded interactions between atoms, and the torsional potential includes the energy from torsional interactions between atoms.

In REBO potential, the energy stored in a bond between atoms $i$ and $j$ is given as

$$\begin{aligned} E_{ij} ^{{\textit{REBO}}} = f\left( {r_{ij} } \right) \left[ {V_{ij}^R +b_{ij} V_{ij}^A } \right] \end{aligned}$$

(1)

where $V_{ij}^{R}$ and $V_{ij}^{A}$ are the repulsive and the attractive potentials, respectively; $b_{ij}$ is the bond order term, which modifies the bond strength depending on the local bonding environment; $r_{ij}$ is the distance between atoms $i$ and $j;\,f(r_{ij}$) is the cut-off function. The purpose of the cut-off function is to limit the interatomic interactions to the nearest neighbours (Brenner et al. 2002). The original cut-off function in REBO potential is given by

$$\begin{aligned} f(r_{ij} ) \!=\! \left\{ \begin{array}{l@{\quad }l} {1,}&{} {r_{ij} <R^{(1)}} \\ {1+\cos \left[ {\frac{\pi \left( {r_{ij} -R^{(1)}} \right) }{\left( {R^{(2)}-R^{(1)}} \right) }} \right] ,}&{} {R^{(1)}\!<\! r_{ij} \!<\! R^{(2)}} \\ {0,}&{} {R^{(2)}<r_{ij} } \\ \end{array} \right. \nonumber \\ \end{aligned}$$

(2)

where $R^{(1)}$ and $R^{(2)}$ are cut-off radii, which have the values of 1.7 and 2 Å, respectively. The values of cut-off radii are defined based on the first and the second nearest neighbouring distances of hydrocarbons.

It has been observed that the cut-off function could cause nonphysical strain hardening in stress–strain curves of carbon nanostructures (Shenderova et al. 2000). Therefore the researchers have modified the cut-off radii ranging from 1.9 to 2.2 Å to eliminate this non-physical strain hardening (Zhao and Aluru 2010; Zhang et al. (2012a, b); Cao and Qu 2013). In this study, we used a truncated cut-off function $f_{t}(r_{ij}$) given in Eq. (3) to eliminate the strain hardening ( Dewapriya 2012).

$$\begin{aligned} f_t (r_{ij} ) = \left\{ {{\begin{array}{l@{\quad }l} {1,}&{} {r_{ij} <R} \\ {0,}&{} {r_{ij} >R} \\ \end{array} }} \right. \end{aligned}$$

(3)

where the value of $R$ is 2 Å. Similar cut-off functions have been used by Zhao and Aluru (2010), Zhang et al. (2012a) and Zhang et al. (2012b), and Cao and Qu (2013) to simulate the fracture of graphene.

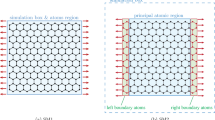
Length and width of the graphene sheets, used for MD simulations, are selected to be equal to 10 times the crack length in order to avoid the finite-size effects (Mattoni et al. 2005; Dewapriya 2012). Periodic boundary conditions (PBCs) are used along the in-plane directions for all the simulations to eliminate the effects of free edges. Strain rate and time step are $0.001\,\hbox {ps}^{-1}$ and 0.5 fs, respectively. The sheets are allowed to relax over a time period of 30 ps before applying strain. During the relaxation period, the pressure components along in-plane directions are kept at zero using NPT ensemble implemented in LAMMPS. The NPT ensemble uses Nośe–Hoover thermostat and barostat to control temperature and pressure, respectively (Nośe 1984; Hoover 1985). An initial random out-of-plane displacement perturbation ($\sim$0.05 Å) is induced to carbon atoms in order to eliminate the non-physical thermal expansion induced by Nośe–Hoover thermostat (Dewapriya et al. 2013). Strain is applied by pulling the graphene sheet in either armchair or zigzag direction. The pressure component perpendicular to the strain direction is kept at zero to simulate uniaxial tensile test conditions.

3 Results and discussion

3.1 Calculation of stress

Several studies reported in the literature use Cauchy stress (Zhao and Aluru 2010; Cao and Qu 2013), whereas some others use virial stress (Zhang et al. 2012b; Liu et al. 2012). One of the main advantages of Cauchy stress over virial stress is its computational efficiency. However, Cauchy stress induces nonphysical initial stress (at zero strain) in higher temperatures, whereas virial stress gives initial stress as zero (Dewapriya et al. 2013). Therefore we use virial stress in this work. However, we compare virial stress with Cauchy stress in this section to examine the influence of stress measure.

Virial stress, $\sigma _{ij}$, is defined as (Clausius 1870; Tsai 1979)

$$\begin{aligned} \sigma _{ij} = \frac{1}{V}\sum \limits _{\alpha } {\left[ {\frac{1}{2}\sum _{\beta =1}^N {\left( {R_i^\beta -R_i^\alpha } \right) F_j^{\alpha \beta } -m^{\alpha }v_i^\alpha v_j^\alpha } } \right] }\nonumber \\ \end{aligned}$$

(4)

where $i$ and $j$ are the directional indices (x, y, and z); $\beta$ is a number assigned to neighbouring atoms which varies from 1 to $N;\,R_{i}^{\beta }$ is the position of atom $\beta$ along direction $i;\,F_{j}^{\alpha \beta }$ is the force along direction $j$ on atom $\alpha$ due to atom $\beta ;\,m^{\alpha }$ is the mass of atom $\alpha ;\,v^{\alpha }$ is the velocity and $V$ is the total volume.

Cauchy stress is defined as the gradient of the potential energy per unit volume versus strain curve. Figure 1a compares virial stress ($\sigma _{v}$) and Cauchy stress $(\sigma _{c})$ of armchair and zigzag sheets of size 5 nm $\times$ 5 nm with PBCs along in-plane directions. Armchair and zigzag directions are demonstrated in Fig. 1b. The stresses are obtained from MD simulations at 1 K, where the contribution from the kinetic part of virial stress is negligible. Engineering strain $(\varepsilon$) is used as the strain measure. The initial volume is used in Cauchy stress calculation. It should be noted that there is an ambiguity in the definition of volume in virial stress. We used instantaneous volume in virial stress, which is suggested to be more appropriate and it has been used in previous studies (Khare et al. 2007). Thickness of graphene is taken as 3.4 Å. The two stress measures are almost equal except near the failure of zigzag sheets. Figure 2 shows the variations in virial stress and Cauchy stress at various temperatures. Graphene sheets at higher temperatures fail at lower strains, due to high kinetic energy of atoms. It can be seen in Fig.  2 that the $\sigma _{v}-\varepsilon$ curves at higher temperatures are slightly below the curves at low temperatures, which indicates a softening of the sheets at higher temperatures. This effect gradually increases with strain and becomes significant around the failure strain. This softening of the sheets occurs due to the expansion of carbon–carbon (C–C) bond at higher temperatures and the thermal contribution to virial stress, which is given by the term $m^{\alpha }v_{i}^{\alpha }v_{j}^{\alpha }$ in Eq. 4.

Fig. 1

a Comparison of virial stress ($\sigma _{v}$) and Cauchy stress ($\sigma _{c}$) of armchair (ac) and zigzag (zz) sheets at 1 K. b Armchair and zigzag edges of a graphene sheet. Arrows indicate the armchair and zigzag directions

Fig. 2

Comparison of virial stress ($\sigma _{v}$) and Cauchy stress ($\sigma _{c}$) of a zigzag sheet at various temperatures

It has been found, using MD simulations with AIREBO potential, that the coefficient of thermal expansion of a C–C bond is 7.9 $\times 10^{-6}\,\hbox {K}^{-1}$ (Dewapriya et al. 2013). This thermal expansion of C–C bonds does not cause an expansion in the graphene sheet, but it generates ripples. Amplitude of those ripples depends on the temperature. When strain is applied, those ripples are flattened out before graphene sheet experiences the applied strain. However, this thermal expansion of C–C bonds causes stress at zero strain, which is given by the first term in Eq. 4. This initial stress is canceled out by the stress given by the thermal contribution to the virial stress. The stress induced by thermal expansion of C–C bonds become negligible as the strain increases, where as the thermal contribution to the stress remain constant. This causes a slight softening in the $\sigma _{v}-\varepsilon$ curves at higher temperatures. The $\sigma _{c}-\varepsilon$ curves do not show noticeable changes in the shape as the temperature increases apart from giving non-zero initial stress at higher temperatures ($\sim$4  GPa at 700 K). This initial stress is due to neglecting the thermal contribution to the Cauchy stress.

3.2 Variation of strength with crack length and temperature

Molecular dynamics simulations are performed at 1 and 300 K for armchair and zigzag sheets with crack lengths ranging from 4 to 36 Å to investigate the effects of crack length and temperature on the ultimate tensile strength ($\sigma _{ult}$). The crack length $(2a$) in armchair and zigzag sheets are defined as shown in Fig.  3. The sheets are allowed to relax over a time period of 30  ps before applying the strain. It is noticed that the crack tips come out of the plane of sheet during relaxation. The crack tips are free edges. Deformation of free edges of graphene arises from the difference of the energy stored in edge atoms and interior atoms (Lu and Huang 2010). As shown in Fig. 4, the out-of-plane deformation of a crack tip at equilibrium configuration is localized around the tip. However, when the strain increases up to 0.018, the deformed shape of the crack tip changes to a localized ripple. As strain further increases up to 0.0235, this localized ripple spreads throughout the sheet. This behaviour prevails both at 1 and 300 K. Therefore temperature is not a significant factor in the observed rippling behaviour.

Fig. 3

Definition of the geometric parameters of a armchair and b zigzag cracks. The parameters $\rho$ and $a_{0}$ is defined in Sect. 3.3.2

Fig. 4

Ripples in a garphene sheet at various strain levels. Size of the sheet is 27 nm $\times$ 27 nm. Strain is applied along y-direction. Colours of the atoms indicate the out of plane (z) coordinate

Figure 5a compares the stress–strain curves of armchair sheets with various crack lengths. It shows a significant reduction in the ultimate stress as crack length increases. Figure 5b shows the stress–strain curves of zigzag sheets, which also indicate a significant reduction in the strength even at smaller crack lengths ($\sim$1.2 nm). It can be seen in Fig. 5 that the length of crack has not affected the stiffness of the sheets even at larger crack lengths ($\sim$3.5 nm). Ansari et al. (2012) observed a similar behavior in the stiffness at lower crack lengths ($\sim$0.7  nm).

Fig. 5

Stress–strain curves of a armchair and b zigzag sheets at 1 K with various crack lengths (2a)

Figure 6a compares $\sigma _{ult}$ of graphene sheets at 1 and 300  K. Zigzag sheets indicate a slightly higher drop in $\sigma _{ult}$ compared to the armchair sheets. $\sigma _{ult }$ at 300 K shows more fluctuations due to higher kinetic energy of atoms compared to the values at 1 K. Figure 6b presents a plot of $1/{\sqrt{2a}}$ versus $\sigma _{ult}$ at 1 K, and it clearly shows proportionality. This indicates a formal similarity with continuum fracture mechanics, which predicts a singular stress field. The critical stress intensity factor of graphene $(K^{\mathrm{g}}_{\mathrm{IC}} )$ can therefore be approximated as

$$\begin{aligned} K^{g} _\mathrm{IC} = \left( {\sigma _f - c} \right) \sqrt{2\pi a} \end{aligned}$$

(5)

where $c$ is a constant ($c$ is zero for a continuum) and $2a$ is the crack length.

The values of $K^\mathrm{g} _{\mathrm{IC}}$ and $c$ are given in Table 1. $K^\mathrm{g} _{\mathrm{IC}}$ decreases as temperature increases from 1 to 300 K, which reflects the reduction of $\sigma _{ult}$ at 300 K as shown in Fig. 6a. The reduction of $K^\mathrm{g} _{\mathrm{IC}}$ in zigzag sheets is greater than that of armchair. The calculated values of $K^\mathrm{{g}} _\mathrm{{IC}}$ are in good agreement with values reported in the literature as given in Table 1. It should be noted that (Xu et al. 2012) and (Zhang et al. 2012a) used the $K$-field displacements of a single crack to obtain $K^\mathrm{{g}} _\mathrm{{IC}}$. Considering the profound length- (size-) dependency at the nanoscale, it is necessary to investigate the influence of crack length on the value of $K^\mathrm{{g}}_\mathrm{{IC}}$. The value of $c$ is around 7.5 GPa at 1 K. We use a range of crack lengths from 4 to 36 Å to calculate $K^\mathrm{{g}} _\mathrm{{IC}}$. Therefore the values reported in this work take into account the effects of crack length on $K^\mathrm{{g}} _\mathrm{{IC}}$. The positive value of $c$ indicates that fracture toughness of graphene (i.e. $K^\mathrm{{g}} _\mathrm{{IC}}$) is less than that predicted by continuum fracture mechanics model as indicated by Eq. 5. This could be due to discrete nature of graphene.

Fig. 6

The ultimate tensile strength ($\sigma _{ult}$) of graphene with a crack length and b inverse of square root of crack length at 1 K

Table 1 Variation of $K^\mathrm{{g}} _\mathrm{{IC}}$ and $c$ of armchair (ac) and zigzag (zz) sheets with temperature.

The general agreement of MD simulation results with the continuum fracture mechanics concepts, as shown in Fig. 6b, motivates further investigation on the applicability of continuum fracture mechanics concepts to graphene. The ensuing sections explore the applicability of Griffith’s energy balance, quantized fracture mechanics concept, and $J$ integral to model the fracture of graphene.

3.3 Fracture mechanics models for graphene

3.3.1 Griffith’s energy balance

Griffith’s energy balance is a fundamental criterion for brittle fracture, which indicates that fracture occurs when the energy stored in a structure is sufficient to overcome the surface energy of the material (Griffith 1921). Failure stress of Griffith’s model can be expressed as

$$\begin{aligned} \sigma _f = \sqrt{\frac{2E_f \gamma _s }{\pi a}} \end{aligned}$$

(6)

where $E_{f}$ is the tangent modulus at failure; $\gamma _{s}$ is the surface energy and $a$ is the one-half crack length.

It should be noted that the original Griffith’s model in Eq. 6 is for linear elastic material and the value of $E_{f}$ is a constant. In this work, we use the tangent modulus at failure to reflect the nonlinear stress–strain behavior of graphene as observed in Fig. 1a.

The value of $\gamma _{s}$ can be calculated by dividing the difference in the energy of a graphene sheet before and after fracture by the area of newly created surface. The calculated value of $\gamma _{s}$ is 5.02 J/m$^{2}$ for both armchair and zigzag graphene since the distance between two broken C–C bonds is similar in both sheets. The tangent modulus at failure is obtained from the stress–strain curves of pristine graphene sheets at relevant temperature. The values at 1 K can be expressed as $E (\varepsilon ) =-5.89\varepsilon + 1.08$ TPa and $E (\varepsilon ) =-3.50\varepsilon + 0.89$ TPa for armchair and zigzag sheets, respectively. The value of $E_{f}$ is given by $E (\varepsilon _{f}),$ where $\varepsilon _{f}$ is the failure strain of a sheet with a particular crack length. The value of $\varepsilon _{f}$ can be obtained from MD simulations. However, the variation in the tangent modulus with temperature is negligible, whereas fracture strength significantly reduces with increasing temperature as shown in Fig. 2. Therefore the proposed tangent modulus approach does not capture the temperature dependent fracture of graphene as the originally proposed Griffith’s criteria.

3.3.2 Quantized fracture mechanics

A new energy based discrete fracture concept called quantized fracture mechanics has recently been developed (Pugno and Ruoff 2004). This novel concept can be used to model the fracture of graphene considering the discrete nature of the atomic structures.

Quantized fracture mechanics substitutes the differentials in Griffith’s criterion with corresponding finite differences (Pugno and Ruoff 2004). Considering the finite size of the sheets, fracture strength of a plate with width $w$, crack length $2a$, and crack tip radius $\rho$ can be written as

$$\begin{aligned} \sigma _f (2a) = \sigma _p \sqrt{\frac{1+\rho /2a_0 }{1+2a/a_0 }}\left[ {\frac{2w}{\pi a}\tan \left( {\frac{\pi a}{2w}} \right) } \right] ^{1/2} \end{aligned}$$

(7)

where $\sigma _{p}$ is the failure stress of a pristine structure; $a_{0 }$ is the fracture quantum, which is the extension of a crack by breaking one interatomic bond along the crack direction. Figure  3 demonstrates 2$a,\,a_{0}$, and $\rho$ for a typical armchair and zigzag cracks.

Figure 7 compares the ultimate tensile strength given by MD, Griffith, and QFM. In general, QFM predicts the ultimate strength more accurately compared to Griffith’s criterion. The ultimate strength of armchair sheets given by Griffith’s criterion is significantly higher than the MD values at larger crack lengths. This could arise from a high stress concentration at the tip of armchair crack compared to zigzag crack due to configuration of C–C bonds. As shown in Fig. 3a, there is a C–C bond perpendicular to the crack orientation in armchair crack. This bond at crack tip experiences higher stresses, which could initiate the failure at a much lower strain. This stress concentration could increase with the crack length so the failure occurs at much lower stresses compared to that predicted by Griffith’s criterion. Such a stress concentration does not prevail in zigzag sheets. Another important factor is the nonlinear stress–strain relation of graphene. The use of tangent modulus at failure to reflect the nonlinear stress–strain behavior of graphene significantly improves the results. But this modification of a linear elastic fracture theory may not be adequate to model fracture of graphene quite accurately. Therefore we use $J$ integral, which can be used for nonlinear material, in Sect. 3.5 to model fracture of graphene.

Fig. 7

Comparison of the ultimate strength of a armchair and b zigzag sheets given by MD, Griffith, and QFM

In view of the good agreement between MD and QFM results, it is required to estimate the ultimate tensile strength of pristine structure at different temperatures in order to apply QFM at various temperatures. By combining QFM with Arrhenius formula and Bailey’s principle, it is possible to estimate the fracture strength of graphene at various temperatures using only a stress–strain relationship at a certain temperature as explained in the ensuing section.

3.4 Kinetic model for temperature and crack length dependent fracture strength

Arrhenius formula and Bailey’s principle have been previously used to obtain the ultimate strength of pristine armchair and zigzag graphene at various temperatures and strain rates (Zhao and Aluru 2010; Dewapriya et al. 2013). However, these models cannot be used to predict the strength of defective graphene. In this work, we combine Arrhenius formula and Bailey’s principle with QFM concept, which can be used to predict the strength of graphene with a nanocrack (a row of vacancies) at various temperatures and strain rates.

The Arrhenius formula (Arrhenius 1889) express the lifetime $\tau$ as a function of tensile stress $\sigma ({t})$ and temperature ($T$) by equation

$$\begin{aligned} \tau \left( {T,t} \right) = \frac{\tau _0 }{ns}\exp \left( {\frac{U_0 -\gamma \sigma \left( t \right) }{kT}} \right) , \end{aligned}$$

(8)

where $\tau _{0}$ is the vibration period of atoms in solid; ns is the number of sites (bonds) available for state transition; $k$ is Boltzmann constant; $U_{0}$ is the interatomic bond dissociation energy which is 4.95 eV for a C–C bond; $\sigma (t)$ is the stress at time $t;\,\gamma =\alpha qv$ where $q$ and $v$ are the directional constant and activation volume, respectively. We define $\alpha$ as the coefficient of over stress, which is given as the reciprocal of the strength reduction factor in QFM (Eq. 7), where

$$\begin{aligned} \alpha = 1/ {\left\{ {\sqrt{\frac{1+\rho /2a_0 }{1+2a/a_0 }}\left[ {\frac{2w}{\pi a}\tan \left( {\frac{\pi a}{2w}} \right) } \right] ^{1/2}} \right\} }. \end{aligned}$$

(9)

It should be noted that the pre-exponential term in Arrenhnius formula (i.e. $\tau _{0}/ ns$) can be considered as temperature independent (Kuo et al. 2010).

Since the tensile stress, $\sigma (t)$, in MD simulations is time dependent, the rule of partial lifetime summation leads to Bailey’s principle (Zhao and Aluru 2010), which states that fracture initiates when

$$\begin{aligned} \int \limits _{0}^{t_f} {\frac{dt}{\tau \left( {T,t} \right) }} = 1, \end{aligned}$$

(10)

where $t_{f}$ is the time taken to fracture.

The stress ${\sigma }(t)$ can take any arbitrary form as long as it fits the stress–strain data at a particular temperature. The stress of a graphene sheet can be expressed in terms of strain rate $\dot{\varepsilon }$ and $t$ as

$$\begin{aligned} \sigma \left( t \right) =b\ln \left[ {c\left( {\dot{\varepsilon }t} \right) +d\left( {\dot{\varepsilon }t} \right) ^{2}+1} \right] , \end{aligned}$$

(11)

where $b,\,c$, and $d$ are constants, which can be calculated from stress–strain data.

The constant $b$ is $10^{12}$ Pa for both armchair and zigzag graphene. The values of $c$ and $d$ are 1.132, $-$3.139 for armchair sheet; the corresponding values for the zigzag sheet are 0.934 and $-$1.861, respectively. The constants $b$, $c$, and $d$ are obtained from a regression analysis of the stress–strain curves given by MD simulation at 300 K. Temperature dependency of the constants in Eq.  11 is negligible as seen in the stress–strain curves of Fig.  2.

We assumed $q$ (directional constant) as 1 for armchair sheets and 89.6/105.4 for zigzag sheets, where 89.6 and 105.4 are the ultimate tensile strengths (in GPa) of armchair and zigzag sheets at 300 K, respectively. The constant $q$ can also be viewed as a stress concentration factor, which depends on the direction of stress (i.e. armchair and zigzag). The source of stress concentration is the orientation of C–C bonds as explained in Sect. 3.3.2. $v$ is used as 8.25 Å$^{3}$, which is close to the representative volume of a carbon atom in graphene (8.6 Å$^{3});\,\tau _{0}$ is taken as 5 fs.

We obtain the life time of a graphene sheet with a nanocrack at various temperatures by substituting Eq. 11 into Eq.  8. Then the failure time $t_{f}$ is calculated by solving Eq. 10 numerically. The failure stress is the stress at $t=t_{f}$.

Figure 8 shows that the numerical model, outlined in Eq. 8 to Eq. 11, quite accurately predicts the ultimate tensile strength of graphene with various crack lengths. It can be seen in Fig. 8 that the model predicts the $\sigma _{ult }$ of zigzag sheets more accurately compared to armchair sheets. This is due to the ability of QFM to predict the $\sigma _{ult}$ of zigzag sheets accurately as observed in Fig. 7b.

Fig. 8

Comparison of the ultimate strength given by MD and the kinetic analysis for armchair (ac) and zigzag (zz) sheets. MD simulations are performed at 300 K

Figure 9 shows that the proposed kinetic model captures the temperature dependence of $\sigma _{ult}$ of pristine and defective graphene quite accurately. The crack lengths of defective armchair and zigzag graphene sheets are 7.3 and 5.6 Å, respectively.

Figures 8 and 9 show that the kinetic model estimates $\sigma _{ult }$ of graphene to a very high degree of accuracy. Therefore the model can be used to obtain the fracture strength of pre-cracked graphene at various temperatures, which saves a huge computational cost required by MD simulations. The proposed approach can be used to model graphene sheets with various defects such as random vacancies and Stone–Wales defects by modifying the parameters in Eqs. 8 and 11 appropriately.

Fig. 9

Comparison of the ultimate strength given by MD and the kinetic analysis for a armchair and b zigzag sheets

3.5 $J$ integral of armchair graphene sheets

Graphene shows a significant nonlinearity in the stress–strain relation as shown in Fig. 1a. Therefore $J$ integral could be a better continuum fracture mechanics theory to model fracture of graphene than Griffith’s criterion used in Sect.  3.3. In this section, we present a novel approach to calculate $J$ integral using MD simulations.

Crack propagation in armchair graphene occur perpendicular to loading direction, whereas propagation in zigzag sheets are at an angle to the loading direction with many crack branching (Omeltchenko et al. 1997). Therefore most of the crack propagation studies of graphene focus on armchair sheets due to its simplicity (Omeltchenko et al. 1997; Khare et al. 2007; Zhao and Aluru 2010; Le and Batra 2013).

Le and Batra (2013) calculated $J$ integral of armchair graphene by fitting a curve between crack length and potential energy obtained from MD simulations. However, the size of their graphene sheet is less than ten times the crack length, and it was as small as three times the crack length in some cases. This could have a significant effect on the numerical results (Mattoni et al. 2005; Dewapriya 2012). Le and Batra (2013) also defined the failure of graphene when the strain reaches 100 % (bond length becomes twice the initial length). Experimental observation (Lee et al. 2008) and many atomistic simulations (Khare et al. 2007; Zhang et al. 2012a; Dewapriya et al. 2013) have found that the failure strain of armchair graphene is around 15–20 %. Therefore the simulated failure of graphene at 100 % strain is not physically realistic.

In this work, we directly calculate $J$ integral using the data obtained from MD simulations. Size of the sheet is kept at ten times the crack length for MD simulations, and it is observed that failure of armchair graphene occurs around 15 % of strain. The critical value of $J$ integral ($J_\mathrm{IC}$) of armchair graphene is compared with twice the surface energy to evaluate the lattice trapping of graphene.

Figure 10 outlines the calculation procedure of $J_\mathrm{IC}$. Figure 10a shows the changes in potential energy with time (or applied strain) in an armchair graphene sheet with a size of 7.6  nm $\times$ 7.6 nm. A crack, length of $\sim$0.7 nm, is placed in the centre of the sheet. PBC are used along in plane directions. Simulation temperature is 1 K, and strain rate is 0.001 $\hbox {ps}^{-1}$. Figure 10b shows the variation in potential energy during the crack propagation. It can be seen that the potential energy increases just after the crack starts to propagate (around point d). This is due to the chemical potential energy release from C–C bond breaking overcomes the strain energy release by crack propagation. As more bonds break, the strain energy release due to crack propagation starts to govern the total strain energy release. The crack propagation at various stages (marked as d to g in Fig. 10b) is shown in Fig.  10d–g. The figures show that the crack propagates symmetrically. The out of plane deformation of the sheet, explained in Fig. 4, prevails.

Fig. 10

Calculation of energy release rate of graphene. a Variation of potential energy with time. b, c Variation of potential energy during the crack propagation. d–g The crack propagation in graphene. The corresponding positions of d–g in the potential energy-time curve are marked in b

The slope of the piece wise continuous curves in Fig. 10c is proportional to the $J$ integral, which is defined as (Anderson 1991) $J =-d \phi /dA; \phi$ is the potential energy given by $\phi = U-F$, where $U$ and $F$ are the strain energy stored in sheet and the work done by external forces, respectively; $A$ is the crack area.

In this work, we calculate the $J$ integral after each bond breaks. We define the critical value of $J$ integral after $i$th bond break ($J_{\mathrm{IC},i}$) as

$$\begin{aligned} J_{\hbox {IC},i} = -\frac{\left\{ {\left( {PE^{(2)}_i -PE_i ^{(1)}} \right) + \left[ {\left. {\frac{d(PE)}{dt}} \right| _{PE_i^{(1)} } \times \Delta t \left( {\frac{N-i}{N}} \right) } \right] } \right\} }{a_0 h}\nonumber \\ \end{aligned}$$

(12)

where $PE_{i}^{(1)}$ and $PE_{i}^{(2)}$ are the potential energies of the sheet just after $i$th bond break and just before $(i+1)$th bond break, respectively as shown in Fig.  10c; ${{d(PE)}/{dt}} |_{PE_i^{(1)} }$ is the rate of change of potential energy during the loading stage (before crack propagation starts) at a potential energy of $PE_{i}^{(1)};\,\Delta t$ is the time interval between $i$th bond break and $(i+1)$th bond break as shown in Fig. 10c; $a_{0 }$ is the fracture quantum as defined in Fig. 3; $h$ is the thickness of graphene, which is taken as 3.4 Å; $N$ is the total number of bonds that break during crack propagation. The factor $(N-i)/N$ takes into account the reduction in rate of change of potential energy due to bond breaking.

Figure 11 shows the variation of $J_\mathrm{IC}$ with the propagated crack length $(2a^{p})$ which has been normalized with respect to the width of the sheet ($w$). The value of $2a^{p}/w$ is approximately 0.1 when a crack starts to propagate since $w$ is kept around 10 times the initial crack length $(2a)$ to avoid the effects of finiteness. When $2a^{p}/w$ reaches 1, the periodic cracks start to interact with each other. Therefore Fig. 11 shows the value of $J_\mathrm{IC}$ up to 0.8 of $2a^{p}/w$, where the periodic cracks do not interact with each other for the smallest sheet considered (i.e. $w = 7.6\,\hbox {nm}$). Figure 11 indicates that crack length has a significant influence on the value of $J_\mathrm{IC}$. As the crack length increases, asymptotic value of $J_\mathrm{IC}$ decreases towards twice the surface energy $(2\gamma _{s})$. The average value of $J_\mathrm{IC}$ ($J_{\mathrm{IC,avg}}$) could be a reasonable measure to compare the fracture of graphene with well-established continuum concepts. Figure 11 shows that the ratio of $J_\mathrm{IC,avg }$ to 2$\gamma _{s}$ is $\sim$1 at small crack lengths (around 0.73 nm), and it is $\sim$0.9 at larger crack lengths. The Griffith’s energy balance criterion holds when $J_\mathrm{IC,avg}$ is equal to $2\gamma _{s}$ and it could over predicts the strength when $J_\mathrm{IC,avg }$ is less than $2\gamma _{s }$ (Thomson et al. 1971). According to Thomson et al. Fig. 11 indicates that the Griffith’s criterion accurately predicts the strength of armchair graphene at lower crack length, whereas it over predicts the strength at larger crack lengths, which is in fact confirmed by the MD simulations in Fig. 7a.

Fig. 11

Variation of $J_\mathrm{IC}$ of armchair graphene with propagated crack length ($2a^{p}$) for various initial crack lengths ($2a$). The solid symbols indicate the average value of $J_\mathrm{IC} (J_\mathrm{IC,avg})$ at various crack lengths. The left most solid symbol is the $J_\mathrm{IC,avg}$ for $2a = 0.73$ nm and other marks are in ascending order of initial crack lengths. The right most symbol is the $J_\mathrm{IC,avg}$ for $2a = 3.63$ nm

The fracture strength of graphene deviates from the Griffith’s criterion due to lattice trapping that is crack arrest by crystal lattice (Thomson et al. 1971). The ratio $J_\mathrm{IC,avg}/2\gamma _{s}$ of 0.9 indicates a moderate amount of lattice trapping. In the absence of lattice trapping, the ratio $J_\mathrm{IC,avg}/2\gamma _{s}$ is equal to 1 and the Griffith’s criterion holds. Khare et al. (2007) found the ratio of critical energy release rate ($J_\mathrm{IC}$) to 2$\gamma _{s}$ to be 1.1 using a coupled quantum mechanical/molecular mechanical method for an armchair graphene sheet with a fixed crack length ($\sim$2 nm). It is necessary to investigate the effects of crack length on the $J_\mathrm{IC}$ considering the length dependency at the nanoscale. Our result shows that lattice trapping in graphene increases as the crack length increases, which is indicated by deviating $J_\mathrm{IC,avg}$/2$\gamma _{s }$ from unity. However, it should be noted that this observation is based on the average value of $J_\mathrm{IC}$. The asymptotic value of $J_\mathrm{IC}$ indicates that lattice trapping disappears as crack length increases.

4 Summary and conclusions

Molecular dynamics simulations show that the strength of graphene is inversely proportional to the square root of crack length as seen in continuum fracture theories. QFM theory is more accurate compared to Griffith’s energy balance criterion in predicting the failure strength of graphene. The critical stress intensity factor of armchair and zigzag graphene reduces as the temperature increases, which reflects the reduction of the ultimate tensile strength of graphene at higher temperatures due to kinetic energy of atoms. A numerical model based on Arrhenius formula, Bailey’s principle, and QFM is proposed. The model can be used to predict the strength of pre-cracked graphene at various temperatures using only stress–strain data of a pristine sheet at a particular temperature. The model agrees quite well with MD simulations and it is computationally very efficient. A new approach is presented to calculate $J$ integral at the nanoscale using data obtained from MD simulations. Calculations show that $J$ integral (and lattice trapping) of armchair graphene depends on the crack length. These findings are critical in designing graphene based nanoelectromechanical systems and composite materials.