1 Introduction

In the Mössbauer effect, a nucleus emits or absorbs gamma rays without the expected loss of energy due to the recoil of the decaying or the absorbing nucleus [9, 24, 28]. It is extraordinarily sensitive and has found many uses in chemistry, condensed matter physics, and tests of relativity [3, 9,10,11, 17, 26, 27, 34]. The conventional explanation is that in the right circumstances a volume of a crystal in which the decaying nucleus is embedded can act effectively like a rigid body in response to the nuclear decay, and since the crystal’s mass is much larger than that of one nucleus alone, it can absorb the recoil momentum of a gamma ray without absorbing any appreciable amount of energy [2, 9, 24]. The same can happen on both emission and absorption. The probability of recoilless decay and resonant absorption depends on the temperature, on the phonon density of states, and on the detailed crystal structure [3, 9, 22, 24]. In classical relativity theory, it is generally conceded that a perfectly rigid body cannot exist because it would allow superluminal messages to be sent from one end of the body to another. There is some acknowledgement in the theoretical literature that the recoil may not, and perhaps cannot be instantaneous throughout a volume of the crystal. For example, Victor Weisskopf argued that the diffusion velocity of energy in a solid is limited by the sound velocity in that solid, and that consequently the effective radius of a rigid crystal would be given by the speed of sound times the lifetime of the excited isomer undergoing decay [38]. Fruaenfelder acquiesces to this viewpoint in his theoretical discussion in chapter 2 of [9]. Another viewpoint comes from particle physics. In the standard model, the energy–momentum density \(T^{\mu \nu }(x)\) is locally conserved in any Lorentz covariant classical field theory. Thus the maximum propagation is taken to be the speed of light, and therefore there is no reason why energy transport cannot occur up to this speed in a solid. Quantum electrodynamics is considered to be a local theory because the commutator of any two Bosonic fields separated by spacelike separation vanishes, although the precise statement of locality is somewhat problematical in this case since the Feynman propagators (for the photon for example) do not vanish outside of the light cone. The application of the standard model to a solid is not easy, and this issue of locality is not completely settled. In general, most theoretical physicists believe the rigid recoil picture to be incompatible with the perturbative picture of local quantum field theory and thus with the standard model, but non-perturbative rigid behaviour might be possible, as was argued by Preparata in his superradiance theory [2, 31]. The standard model, which includes QED, is believed to be the best fundamental theory of all matter at this time. So we have three possibilities in the theoretical literature

  1. 1.

    The recoil momentum is absorbed locally, and the added momentum diffuses throughout the crystal at the speed of sound

  2. 2.

    The recoil momentum is absorbed locally, and the momentum diffuses at the speed of light

  3. 3.

    The recoil momentum is absorbed non-locally and the whole crystal recoils instantaneously

So which case does nature choose? Or does this question even make any sense? Can an experiment be devised to answer it? Why does this matter even if it can be measured?

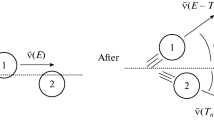
When a Mössbauer crystal recoils rigidly, it accelerates for a short time. In the rigid body picture, the acceleration is very large, but in a local field theory model the expected acceleration is much smaller, as the momentum injected into the crystal at the precise position of the decaying nucleus would need time to diffuse throughout the rest of the crystal. If the crystal has a net charge, then it will radiate electromagnetic radiation due to this acceleration. If the crystal is metallic, then the charge will reside on the outside surface. To a first approximation, Larmor’s radiation formula can be considered. This leads to a different radiation loss between instantaneous acceleration models and slower acceleration models, because the radiated power is proportional to the acceleration squared. Standard Mössbauer spectroscopy can be used then to try and measure the radiation loss with exquisite precision, and thus to determine which model for acceleration fits the data best.

The purpose of this paper is to examine this apparent contradiction between the three viewpoints regarding locality and diffusion rates after Mössbauer events, and to propose an experiment that might help to clarify the issue, and which might also provide new laboratory methods of practical use. We consider metallic nano-particles with an electromagnetic charge on their surface as either the source or the absorber in a Mössbauer experiment. When the nucleus either emits or absorbs a gamma ray, the crystal will recoil. It will experience acceleration for a short time, and there will be energy loss due to electromagnetic radiation. Using Larmor’s formula to estimate this radiation, we show that the amount of energy radiated depends on the charge squared, and also on how abruptly the crystal recoils. A perfectly rigid crystal which accelerated instantaneously would have a very large energy loss, and a slow diffusive recoil mediated by sound waves would have a much lower loss. If the diffusion occurred at near to the speed of light, the loss would be somewhere in between. The energy loss can be measured in the Mössbauer setup, and thus an experimental measurement can in principal be made of the recoil dynamics.

The Mössbauer effect is interesting for two fundamental reasons, aside from its many practical uses. First, it raises these fundamental question about locality, and second because it illustrates a system in which the chemical environment indisputably has a very large effect on the reaction rate of a nuclear process. There is another reason why this topic is important. In the perturbative standard model picture for the rigid recoil, all of the recoil momentum is absorbed by a single nucleus, and not by the whole crystal. But this nucleus must be off the mass shell, which is allowed in relativistic quantum field theory. This local explanation of the effect has not appeared in the literature prior to this paper, and it seems to me likely to be the true explanation for the effect. The instantaneous rigid recoil picture is thus very probably simply wrong. Solid state and condensed matter theory are entirely built upon on-mass-shell theories of quantum mechanics. Thus, they are incapable of describing the microscopic local interactions in the Mössbauer effect. What is needed is a covering theory of conventional many-body theory which allows for states of matter where the rest masses of particles in a solid are different from their usual values, ie. off the mass shell. This means that the Hilbert space of states must be enlarged to include off mass shell states as well. We discuss below theories which have this feature.

2 Textbook Theories of the Mössbauer Effect from Condensed Matter Physics

There are a number of theoretical approaches to describing the Mössbauer effect in the literature. Many historical papers can be found in Hans Frauenfelder’s excellent book [9]. The basic physical picture is that a region of a crystal recoils as a rigid body in response to a nuclear decay. The solid is typically approximated by the Debye model which treats it as a set of coupled oscillators. Quantization of these oscillators leads to a phonon spectrum with a non-zero energy gap between the ground state and the next excited state. When the recoil energy of the Mössbauer is comparable to this energy gap, then the probability for recoilless decay can become appreciable, depending on the Debye–Waller factor. Frauenfelder acknowledges the possible existence of a relaxation process of non-zero time duration after the nuclear decay but before the final state of the rigidly moving crystal is realized, but he does not go into details (see chapter 2 of [9]) of this transient possibility. His discussion of transient effects is influenced by a paper by Weisskopf [38]. Many papers simply treat the recoil as if it were an instaneous rigid recoil, and they judiciously avoid discussing any transient response of the system. The subject of rigid bodies and special relativity is discussed in some detail in [8], and the possibility of a rigid recoil of the whole crystal does not seem to be automatically ruled out. All of the early theories for the Mössbauer effect were developed before the standard model was known. An attempt was made to reconcile instantaneous recoil with the standard model in [2, 31] where the authors argued that the possibility of superradiant coherent oscillation of a group of nuclei at the plasma frequency might explain the rigidity of the crystal. I want to concentrate here on the rigid-recoil aspect of these theories, and so a simplified treatment is in order. The treatment by Lipkin [22, 23] is a good starting point to examine the locality of this process without getting into unnecessary complications. First of all, as in almost all theoretical models in solid state physics, the treatment is always done with non-relativistic quantum mechanics, the argument being that since the velocities of the nuclei remain non-relativistic after the decay, this is justified. This allows us to have a nice many-body Schrödinger picture with a local Hamiltonian description and a well defined Hilbert space of states. Most quantum mechanical discussions of the Mössbauer effect start by considering an isolated and free nucleus experiencing decay. The discussion typically proceeds something like this. Let \(\left| in\right\rangle \) and \(\left| out\right\rangle \) denote the nuclei’s wave function before and after the decay emission of a gamma ray, and we know that both that the total kinetic energy and momentum are conserved in the decay process. Furthermore, let us assume that the initial state is an eigenstate of momentum \(\left| in\right\rangle =\left| \mathbf {p_{in}}\right\rangle \). If we denote the momentum of the decay gamma ray as \(\mathbf {p}_{\gamma }\), then we have \(\left| out\right\rangle =\left| \mathbf {p}_{in}-\mathbf {p}_{\gamma }\right\rangle \). The rest mass of the decaying nucleus must change to the mass of the nuclear ground state that it decays into. Call these masses \(M_{in}\) and \(M_{out}\). These are known fixed values which can be found in standard nuclear databases. The kinetic energy of the nucleus before decay is \(E_{in}=\mathbf {p}_{in}^{2}/2M_{in}\), and the kinetic energy after the decay is \(E_{out}=\left( \mathbf {p}_{in}-\mathbf {p}_{\gamma }\right) ^{2}/2M_{out}\). Conservation of total energy requires that (c\(=\)1 here)

$$\begin{aligned} E_{in}+M_{in}= & {} \mathbf {p}_{in}^{2}/2M_{in}+M_{in}=E_{out}+M_{out}+E_{\gamma }\nonumber \\= & {} \left( \mathbf {p}_{in}-\mathbf {p}_{\gamma }\right) ^{2}/2M_{out}+M_{out}+\left| \mathbf {p}_{\gamma }\right| , \end{aligned}$$
(1)

where we have used the non-relativistic energy formula for the nuclei energies. This can be rewritten as

$$\begin{aligned} \frac{\mathbf {p}_{\gamma }^{2}}{2M_{out}}+\left( 1-\frac{\hat{\mathbf {k}}\cdot \mathbf {p}_{in}}{M_{out}}\right) \left| \mathbf {p}_{\gamma }\right| +\left( M_{out}-M_{in}\right) +\frac{\mathbf {p}_{in}^{2}}{2}\left( \frac{1}{M_{out}}-\frac{1}{M_{in}}\right) =0, \end{aligned}$$
(2)

where I have used the substitution \(\mathbf {p}_{\gamma }=\hat{\mathbf {k}}\left| \mathbf {p}_{\gamma }\right| \). The last term in this equation is usually extremely small and can be ignored. Solving for \(\left| \mathbf {p}_{\gamma }\right| \) then yields

$$\begin{aligned} \left| \mathbf {p}_{\gamma }\right| =\left| \frac{-\left( 1-\frac{\hat{\mathbf {k}}\cdot \mathbf {p}_{in}}{M_{out}}\right) +\sqrt{\left( 1-\frac{\hat{\mathbf {k}}\cdot \mathbf {p}_{in}}{M_{out}}\right) ^{2}-2\left( M_{out}-M_{in}\right) /M_{out}}}{1/M_{out}}\right| . \end{aligned}$$
(3)

In the case where \(\mathbf {p}_{in}=0\) we get

$$\begin{aligned} \left| \mathbf {p}_{\gamma }\right| =\left| -M_{out}+M_{out}\sqrt{1-2\left( M_{out}-M_{in}\right) /M_{out}}\right| , \end{aligned}$$
(4)

which, on expanding the square root in a Taylor series, yields

$$\begin{aligned} \left| \mathbf {p}_{\gamma }\right| =M_{in}-M_{out}-E_{\mathcal {R}}, \end{aligned}$$
(5)

where the recoil energy is \(E_{\mathcal {R}}=\left( M_{in}-M_{out}\right) ^{2}/2M_{out}\). Because the mass of the nucleus changes in the decay, the kinetic energy term changes to reflect this, and so does the Hamiltonian operator. So, in a strict sense, the \(\left| \mathbf {p}_{in}\right\rangle \) and \(\left| \mathbf {p}_{out}\right\rangle \) are states in two different Hilbert spaces such that for free particles we have

$$\begin{aligned} \frac{\mathbf {p}_{in}^{2}}{2M_{in}}\left| \mathbf {p}_{in}\right\rangle =E_{in}\left| \mathbf {p}_{in}\right\rangle ;\quad \frac{\mathbf {p}_{out}^{2}}{2M_{out}}\left| \mathbf {p}_{out}\right\rangle =E_{out}\left| \mathbf {p}_{out}\right\rangle . \end{aligned}$$
(6)

So, we must take the Hilbert space direct sum to construct one for the entire system. In systems where the Mössbauer effect is observed, the recoil energy is considerably larger than the decay width of the nuclear decay. Thus a gamma ray emitted from a free nucleus cannot be resonantly re-absorbed by a similar free nucleus in its ground state. But Mössbauer noticed that the measured resonant absorption in some circumstances where both source and absorber were in a solid crystal was in contradiction with the free particle model of nuclear decay, and in particular increased with temperature rather than decreased as one would expect in the free particle model, because the Doppler broadening of the gamma rays should tend to increase the likelihood that a gamma particle has the energy to be resonantly absorbed [23](see chapter 2.2). The idea that explained this was that the recoil momentum must be taken up by a crystal volume containing many atoms surrounding the decaying nucleus, and with a significant probability that no energy is lost to the lattice due to creation of phonons in this process.

For a bound nucleus decaying in a crystal, the dynamics of the crystal come into play. The mass change in the decaying nucleus is typically ignored because \(M_{in}-M_{out}\ll M_{in}\). The standard Lippmann-Schwinger scattering theory is typically used [25], where the S matrix satisfies the equation

$$\begin{aligned} S=U(\infty ,-\infty )=1-\left( i/\hbar \right) \int _{-\infty }^{\infty }H_{1}(t)U(t,-\infty )dt, \end{aligned}$$
(7)

where \(H_{1}\) is the interaction Hamiltonian, and U the time evolution operator in the interaction picture. When considering the decay of a radioactive particle, it is more appropriate to consider an approximate S operator for a finite time interval T which is small compared to the lifetime of the particle (\(9.8\times 10^{-8}\) s for the 14.4 keV excitation of iron-57 for example) but nevertheless assumed large compared to the relaxation time of the crystal holding the excited nucleus.

$$\begin{aligned} S(T)=U(T/2,-T/2). \end{aligned}$$
(8)

Considering just the crystal state vector, one can expand the initial state in terms of a complete set of momentum eigenstates for the decaying nucleus, denoted by index L. The Hilbert space of the whole crystal is a product space spanned by products of eigenstates for each particle in the solid. We concentrate on the momentum of the decaying nucleus and write

$$\begin{aligned} \left| in\right\rangle =\sum _{p_{L}\prime }\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \left. \mathbf {p}_{L}\prime \right| in\right\rangle , \end{aligned}$$
(9)

The out state is obtained by acting with the S matrix operator

$$\begin{aligned} \left| out\right\rangle =S\left| in\right\rangle =\sum _{p_{L}\prime ,p_{L}{\prime \prime }}\left| \mathbf {p_{L}}{\prime \prime }\right\rangle \left\langle \mathbf {p_{L}}{\prime \prime }\right| S\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \left. \mathbf {p_{L}}\prime \right| in\right\rangle . \end{aligned}$$
(10)

The \(\left| in\right\rangle \) state denotes the state of the crystal at \(t=-\infty \), and the \(\left| out\right\rangle \) state denotes the state of the crystal at \(t=+\infty \). This S matrix formalism does not address the issue of how long it takes for the solid to relax into the final state after the decay photon is detected. If we concern ourselves with the case that a single decay occurs, then momentum conservation requires

$$\begin{aligned} \mathbf {p}_{L}{\prime \prime }=\mathbf {p}_{L}\prime -\mathbf {p}_{\gamma }, \end{aligned}$$
(11)
$$\begin{aligned} \left| out\right\rangle =\sum _{p_{L}\prime }\left| \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right\rangle \left\langle \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right| S\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \left. \mathbf {p_{L}}\prime \right| in\right\rangle , \end{aligned}$$
(12)

but we can substitute the replacement \(\left| \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right\rangle =exp(-i{\hat{\mathbf p}}_{\gamma }\cdot {\hat{\mathbf x}}_{L})\left| \mathbf {p_{L}}\prime \right\rangle \) so that

$$\begin{aligned} \left| out\right\rangle =\sum _{p_{L}\prime }\left| \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right\rangle =\sum _{p_{L}\prime }exp(-i{\hat{\mathbf p}}_{\gamma }\cdot {\hat{\mathbf x}}_{L})\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right| S\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \left. \mathbf {p_{L}}\prime \right| in\right\rangle . \end{aligned}$$
(13)

Now if we assume that the initial state is such that \(\left\| \mathbf {p_{L}}\prime \right\| \ll \left\| \mathbf {p_{\gamma }}\right\| \), so that \(\left\langle \mathbf {p_{L}}\prime -\mathbf {p}_{\gamma }\right| S\left| \mathbf {p_{L}}\prime \right\rangle \approx \Bigl \langle -\mathbf {p}_{\gamma }\Bigr |S\Bigl |0\Bigr \rangle \), then we have

$$\begin{aligned} \left| out\right\rangle= & {} \Bigl \langle -\mathbf {p}_{\gamma }\Bigr |S\Bigl |0\Bigr \rangle exp(-i{\hat{\mathbf p}}_{\gamma }\cdot {\hat{\mathbf x}}_{L})\sum _{p_{L}\prime }\left| \mathbf {p_{L}}\prime \right\rangle \left\langle \left. \mathbf {p_{L}}\prime \right| in\right\rangle \nonumber \\= & {} \Bigl \langle -\mathbf {p}_{\gamma }\Bigr |S\Bigl |0\Bigr \rangle exp(-i{\hat{\mathbf p}}_{\gamma }\cdot {\hat{\mathbf x}}_{L})\biggl |in\biggr \rangle . \end{aligned}$$
(14)

The main effect on the crystal is an increase in the momentum due to the recoil of the decayed nucleus (see [23] equation 3.1 and following for a more complete discussion). Note that the recoil momentum is applied initially to the decaying nucleus only, but then over time it must be spread around the rest of the crystal.

3 A Non-perturbative Approach Based on Super-Radiance Theory in QED

In an effort to clarify the physical mechanisms which enable the Mössbauer effect to occur, Preparata together with others applied his “super-radiance” theory of coherent oscillation to the problem of the rigid recoil [2, 31]. They argued first off that a better explanation is required for the Mössbauer effect than the one physicists have developed. In fact the field was given over to chemists long ago, and not much attention has been paid to it by physicists for some time. They argued that in conventional solid state physics models, at very short distances, the presence of the solid can not have very much effect on the Mössbauer decay. They used the term “asymptotic freedom” for this expected decoupling, although this term is a bit confusing in this context since it has little to do with the asymptotic freedom of non-abelian guage theories. What they mean by “asymptotic freedom” is that when a system dominated by longer range forces is perturbed by a short range disturbance, it behaves as if it were free. Think of a bullet fired into a pendulum in equilibrium. At the instant of impact, the harmonic restoring force on the pendulum plays no role. He argues that the Mössbauer effect is just such a case, and that we should expect the recoil of the emitted (or absorbed) X-ray should be taken up entirely by the emitting nucleus if the conventional picture of a solid is correct. The rigid stiffness model of a volume of nuclei employed to explain the observed effect is clearly in contradiction to this intuitively expected asymptotic freedom. So they argued that conventional solid state physics really suggests that the Mössbauer effect is simply impossible, and something fundamentally different must be employed. They accuse mainstream physics of ignoring this logical conundrum by accepting the rigid theory, which does explain the experimental data, without questioning its logical consistency. Personally I think they were correct in this assessment. They argue that what is different is that the nuclei in a solid can undergo a collective and coherent low amplitude collective oscillation about their respective mean lattice sites, and that this collective motion gives a small volume of a solid the rigidity that is required to explain the recoil phenomenon. So Preparata et al. treat the set of nuclei in a metal as if it were a plasma, and they consider it quantum mechanically by introducing a wave-field for the nuclei \(\Psi (\overrightarrow{x},\overrightarrow{\xi })\), where \(\overrightarrow{x}\) denotes the mean position of a nucleus, and \(\overrightarrow{\xi }\) its deviation from this mean. These nuclei can oscillate collectively at the plasma frequency \(w_{p}=\frac{Ze}{\sqrt{M_{N}}}\sqrt{n}\), where \(Z,\,M_{N},\,and\,n\) are the atomic number, nuclear mass, and number density for the nuclei in the solid. This oscillation is not a phonon effect, but is a plasmon effect, and Preparata et al. argue that the quantization of this collective motion can lead to the rigidity observed in the Mössbauer phenomenon. They do not specifically calculate the time that it takes for the recoil to occur. As the region of the solid is perfectly rigid though, one might expect that this picture leads to an intantaneous recoil of a collective group of nuclei.

4 A Standard Model Picture Based on Perturbation Theory and Feynman Diagrams

The standard model of particle physics is considered at this time to be the best and only all-encompassing fundamental description of nuclear physics, atomic physics, and condensed matter physics known [29]. In condensed matter physics, it is for the most part equivalent to quantum electrodynamics because the electromagnetic interaction (via virtual photons) dominates the interactions. Since the primary tool for solving problems in QED is perturbation theory and Feynman diagrams, let’s assume to start off that such a description is suitable in this case, except that the nuclear decay dynamics themselves involve the weak and strong forces too. Let us therefore assume first that a perturbative approach, based on Feynman diagrams, can be used to describe the Mössbauer process. In any nuclear decay of an isomer which emits a photon, including a Mössbauer decay, the basic Feynman diagram for the decay is shown in in Fig. 1 on page 7. The effects of the weak and strong forces are summarized in vertex function for this diagram.

Fig. 1
figure 1

A zoom-in on the core Feynman diagram for the Mössbauer process

Full size image

In this elementary depiction of any nuclear decay by single photon emission, the 4-momentum is conserved, and the three legs of the vertex can in general be off the mass shell.

$$\begin{aligned} P_{in}^{\mu }=P_{out}^{\mu }+k_{\gamma }^{\mu }. \end{aligned}$$
(15)

The symbol \(P_{in}^{\mu }\) is the 4-momentum of the initial nuclear isomer which is decaying, and \(P_{out}^{\mu }\) is the 4-momentum of the final state. Now, if perturbation theory can be used, the ongoing interaction cannot influence the conservation of 4-momentum at the core decay vertex as shown in Fig. 1 on page 7. In Fig. 2 on page 7 we show an example of some of the other interactions which will occur between the decaying nucleus and the rest of the solid.

We must sum over all conceivable Feynman diagrams of this type to calculate the probability amplitude for arriving at any given final state. In these more complex diagrams, let’s assume that the X-ray photon with momentum \(k_{\gamma }\) is on-shell (\(k_{\gamma }^{\mu }k_{\gamma \mu }=0\)) since otherwise it could not travel very far out of the solid, and that it passes through the solid without scattering. Now the incoming and outgoing momenta for the decaying nucleus long before and long after the decay event can be changed by the interaction with the solid, and therefore

$$\begin{aligned} \widetilde{P^{\mu }}_{in}\ne P_{in}^{\mu }\quad and\quad \widetilde{P^{\mu }}_{out}\ne P_{out}^{\mu }. \end{aligned}$$
(16)

It is plausible to assume, however, that at least \(\widetilde{P^{\mu }}_{in}\) will be very close to the mass shell, and that the deviation in the kinetic energy will be on the order of the expected thermal fluctuations which are proportional to kT, where K is Boltzmann’s constant and T is temperature of the solid in Kelvin degrees. Let us define two rest masses for the two nuclear isomers. I use units such that \(c=\hbar =1\) and the metric signature is (\(+\),−,−,−). Let us define the following masses of the two nuclear states in a vacuum. These are just the standard mass values you find in a nuclear database.

$$\begin{aligned} M_{in}=rest\,mass\,of\,the\,unstable\,isomer\,of\,nucleus, \end{aligned}$$
(17)
$$\begin{aligned} M_{out}=rest\,mass\,of\,the\,ground\,state\,nucleus. \end{aligned}$$
(18)
Fig. 2
figure 2

Feynman diagram for the Mössbauer process showing multiple photon interactions that can diffuse the recoil momentum throughout the solid. The solid vertical lines represent charged particles in the solid including electrons and nuclei

Full size image

In order for the Mössbauer photon to be resonantly absorbed, its energy must satisfy the following equality with high accuracy.

$$\begin{aligned} k_{\gamma }^{0}=M_{in}-M_{out}. \end{aligned}$$
(19)

Let us consider Feynman diagrams such that the photon has this value, and working in the rest frame of the solid, let’s suppose that to a good approximation, especially at low temperatures, that we have the incoming mass on the mass shell so that

$$\begin{aligned} P_{in}^{\mu }P_{in\mu }=\widetilde{P^{\mu }}_{in}\widetilde{P}_{in\mu }=M_{in}^{2}, \end{aligned}$$
(20)

where I use the standard Einstein convention here, and repeated Greek indices are to be summed over the values (0, 1, 2, 3) where the zero index represents the time dimension. Therefore, if we ignore the thermal and zero-point agitation of the decaying nucleus in the solid for the time being, we can write

$$\begin{aligned} P_{in}^{\mu }=(M_{in},0,0,0);\quad k_{\gamma }^{\mu }=\left( \left( M_{in}-M_{out}\right) ,\,(M_{in}-M_{out})\hat{n}\right) , \end{aligned}$$
(21)

where \(\hat{n}\) denotes the unit 3-vector direction of the Mössbauer photon. Now we can calculate \(P_{out}^{\mu }\) from 4-momentum conservation.

$$\begin{aligned} P_{out}^{\mu }=P_{in}^{\mu }-k_{\gamma }^{\mu }=\left( M_{out},-(M_{in}-M_{out})\hat{n}\right) . \end{aligned}$$
(22)

Now we can calculate the mass of the nucleus that has resulted from the decay and emission of a Mössbauer photon (we use lower case \(m_{out}\) for this mass because it turns out to be off shell and therefore different from \(M_{out}\))

$$\begin{aligned} m_{out}=\sqrt{P_{out}^{\mu }P_{out\mu }}=\sqrt{M_{out}^{2}-(M_{in}-M_{out})^{2}}<M_{out}. \end{aligned}$$
(23)

For all examples of the Mössbauer effect the following is a good approximation \(M_{out}\gg M_{in}-M_{out}\) and consequently

$$\begin{aligned} m_{out}= & {} M_{out}\sqrt{1-\frac{(M_{in}-M_{out})^{2}}{\left( M_{out}\right) ^{2}}}\approx M_{out}\left( 1-\frac{(M_{in}-M_{out})^{2}}{2\left( M_{out}\right) ^{2}}\right) \nonumber \\= & {} M_{out}-\frac{1}{2}\frac{(M_{in}-M_{out})^{2}}{M_{out}}, \end{aligned}$$
(24)

and the amount that the nucleus is off-mass-shell is

$$\begin{aligned} \Delta m_{out}=m_{out}-M_{out}=-\frac{1}{2}\frac{(M_{in}-M_{out})^{2}}{M_{out}}=-\frac{1}{2}\frac{\overrightarrow{k_{\gamma }}{}^{2}}{M_{out}}. \end{aligned}$$
(25)

So the nuclear rest mass is off-mass-shell in the negative direction. We get the same formula for the absorption case. The mass of the final state isomer is slightly below the mass shell for that isomer when a Mössbauer photon is absorbed. For the case of \(^{57}Fe\) we have \(\left( M_{in}-M_{out}\right) \thickapprox 14.4\) keV, and \(\triangle m_{out}\thickapprox -0.002\) eV.

This off mass shell behavior is impossible to describe correctly within the framework of conventional solid state theory which is based almost exclusively on non-relativistic quantum mechanics, and on-mass-shell Schrödinger equations. It offers another explanation for the logical basis of the Mössbauer effect, but unlike the super-radiance theory, it uses a known property of conventional relativistic quantum field theory, namely the off shell behavior of virtual particles in a Feynman diagram. It’s surprising that this fact has not been pointed out before in the literature, which to my knowledge it hasn’t. Perhaps it is because the off mass shell behavior of virtual particles in Feynman diagrams has been considered a mathematical enigma since the on-mass-shell particle states are considered to be a complete set of states in the conventional picture of a solid.

At first, just after the decay, the recoil momentum is fully absorbed by a single nucleus, but then a transitory period of diffusion must occur. This momentum density that is concentrated at a single nucleus must be spread throughout the entire lattice, and result in a state corresponding to the common understanding of the Mössbauer effect - that of a rigid crystal moving with a small recoil velocity. After this diffusion occurs, the recoil momentum is described by this rigid motion of the crystal, and presumably all of the nuclei return to the mass shell (ie. their rest masses are the usual values). The excited isomer will eventually decay back to the ground state too. The mechanism for this diffusion presumably does not include any phonons since the solid is excited with an energy that is below the threshold for producing even one phonon. But it may include electromagnetic transport mediated by response of the electron gas in the solid to the motion of the recoil nucleus.

I think that this view of the Mössbauer effect would be preferred by particle physicists, but not by solid state physicists. Since there are many more solid state physicists, it is probably the case that the majority of physicists would reject the above description. In my view it is needed to reconcile locality and causality with the conventional interpretation of the Mössbauer effect. Since particle physics is the parent field for nuclear physics, I think that the standard model picture of the Mössbauer effect must be taken seriously. Of course, nature may not work this way, and the more non-local interpretation of solid state physicists could prevail if experiments could be devised to rule out the above standard model picture. I would personally bet on the standard model though.

We must sum over all the possible final states of the solid, where by final states I mean here states that have been reached some time after the decay has occurred, so that the crystal has had time to reach statistical equilibrium. I’m thinking in terms of just ordinary QED here, so the Mossbauer photon can be taken on the mass shell (ie. zero mass). Since the various configurations for the solid are not measured, or even measurable, I would sum over amplitudes, following Feynman’s dictum for indistinguishable outcomes, and therefore interference can occur. This is similar to the technique of summing over amplitudes for emssion of infra-red photons in order to deal the infrared divergences of QED. I think it will turn out if you do this that the final states which are very near to the whole solid moving with fixed velocity rigidly and with the proper recoil momentum will tend to be in phase and constructively interfere if the energy of the crystal is below the phonon gap for the crystal. Other final states would, I expect, interfere with random phases, and so tend to cancel out. Thus the Feynman paths in a path integral which resulted in the whole solid moving rigidly with the required recoil momentum would be singled out and have an enhanced amplitude, and this would enable one to calculate the decay probability and width for them. This is how the phonon density of states can enter the problem.

Obviously, if this argument is correct, then transient off-mass-shell behavior plays a critical role. Conventional solid state physics theory has difficulty with describing this phenomenon. The only course of action that I can see to remedy this situation is to modify solid state physics to incorporate off-mass-shell states into the Hilbert space of states. Such a possibility was long ago proposed by Greenberger [13,14,15,16]. One way to do this in a manifestly covariant way is to use the extensive machinery of the Fock–Steuckelberg–Horwitz–Piron covariant quantum mechanics [6, 7, 18, 20, 36, 37]. This theory is quite well developed, and seems well suited to study this phenomenon. So in summary, the perturbative picture of the standard model says the following about the Mössbauer effect:

  • All of the momentum of the emitted (absorbed) Mössbauer photon is accounted for by the recoil of a single decayed (or excited) nucleus immediately after the decay (absorption) has occurred.

  • If the initial nuclear state is on its mass shell, then the final nuclear state that results from and immediately after the Mössbauer decay/absorption is off the mass shell.

  • The subsequent diffusion following a decay or absorption can in theory propagate much faster than the speed of sound, up to the speed of light, and result in a rigidly recoiled final state.

4.1 Digression Into Off-Mass-Shell Covariant Relativistic Quantum Mechanics

The Feynman perturbation picture requires that either the final state of the nucleus (or possibly even the initial state) must be off the mass shell for a Mössbauer X-ray to be either emitted or absorbed as in 1. Thus, to handle this effect rigorously, some sort of off-mass-shell version of quantum mechanics must be used in which the on-mass-shell quantum states no longer form a complete set of states. The most well-developed set of such theories are of the Fock–Stueckelberg–Horwitz–Piron category. The recent very fine book by Horwitz [20] gives a detailed account of most of the current status of this field. Sometimes also referred to as the proper time formulation, the basic idea is to add a second Lorentz invariant time variable. All particles then move along trajectories in 4D Minkowski space which are parametrized by a common universal time which is both a Lorentz invariant and a common affine parameter for all trajectories, thus making the geometric arena for physics 5 dimensional. A point particle in this space is given a new name, and it’s called an event. The new time plays much the same role as Newtonian time in non-relativistic mechanics. The theory was extended to interacting many-body systems in a landmark paper by Horwitz and Piron in 1973 [18], and this theory introduced new and interesting possibilities for quantum mechanics. It’s basically a Schrödinger type of theory, the equation being first order in the new time but second order in the Minkowski time variable. The particle coordinates, functions of the universal time \(\tau \), are 4 dimensional vectors. It led to a generalization of electrodynamics called pre-Maxwell theory. The bibliography is extensive, and can largely be found in [20]. Methods for adding arbitrary spin have been worked out, and mechanisms for the mass to return the the standard rest mass have been partially explored. A recent paper by Land [21] has introduced a modification to pre-Maxwell theory that introduces a new constant into the theory that controls how close it is to conventional QED. These types of theories seem well suited for studying the relaxation of a crystal back to equilibrium after a Mössbauer decay or absorption has resulted in an off-mass-shell nucleus at a particular lattice site in the solid. I won’t attempt to give a thorough accounting of this subject here, but simply include the basic Horwitz–Piron wave equation for consideration:

$$\begin{aligned}&\sum _{i=1}^{N}\left[ \frac{\hbar ^{2}}{2M_{i}}\left( p_{i}^{\mu }-q_{i}A^{\mu }\right) \left( p_{i,\mu }-q_{i}A_{\mu }\right) +V(x_{1},x_{2},\ldots ,x_{N})\right] \Psi (x_{1},\ldots ,x_{N},\tau )\nonumber \\&\quad =i\hbar \frac{d\Psi (x_{1},\ldots ,x_{N},\tau )}{d\tau } \end{aligned}$$
(26)

where each \(x_{i}\) is a 4-vector in Minkowski space, and \(p_{i}^{\mu }=-i\hbar \partial /\partial x_{i,\mu }\), \(M_{i}\) the standard rest mass of each particle, \(q_{i}\) their charge, \(A^{\mu }\) an external electromagnetic potential, and V an arbitrary potential function. In general in this theory, even in a region of space time where \(A^{\mu }=0\), and \(V=0\), the particles can be off the mass shell so that \(p_{i}^{\mu }p_{i,\mu }\ne M_{i}^{2}\).

In a recent papers , Horwitz [19] and Land [21] have addressed the important issue of mass stability in these theories. Horwitz uses a statistical mechanics approach. His conclusion is that a second temperature controlling the mass, and different from the traditional temperature, is required. Land has developed a modification the the pre-Maxwell theory which contains a new parameter, he calls it \(C_{5}\), which controls how closely the theory agrees with standard QED, and also how quickly the masses of the particles return to their standard rest mass values, once all interactions have been off-mass-shell behavior. These two approaches might be related to one another. In a solid, one can imagine that Land’s \(C_{5}\) parameter might depend on the materials properties of the solid, in the way that the index of refraction does in conventional electromagnetic theory. The response of the crystal to a Mössbauer decay or absorption would then be controlled by this phenomenological parameter. These off-mass-shell theories, perhaps in combination, would seem to be superior to the standard Schrödinger equation for the many-body description of the solid in this circumstance.

5 Radiation from a Charged Metal Sphere Due to Recoil from the Emission of a Mössbauer X-ray—A Mechanism to Measure Response Time of Mössbauer Recoil

Rather than try to settle the theoretical debate about the rigidity of the Mössbauer crystal, I would like to propose an experiment for consideration which might shed light on the subject. Consider a small conducting sphere which consists of a material which is either undergoing Mössbauer decays or is resonantly absorbing Mössbauer X-rays. Let the sphere be charged with a total charge q. The charge will typically reside on the surface, but this is not fundamentally necessary for the effect. The effect that we will discuss is the same for either sign of the charge, however a positivelly charged sphere may be more stable to field emission than a negatively charged one, because of the much higher probability of electron tunneling than ion tunneling from a surface. If the entire sphere acts as a rigid body, as in the usual (and perhaps naive) solid state physics picture of the Mössbauer decay, then the conducting spherical shell of charge on the outer surface of the sphere will experience a pulse of acceleration. Consequently it will radiate electromagnetic energy away. The amount of radiated energy will depend on how large the acceleration is. A stiff crystal will lead to a short pulse of large acceleration, a diffusing crystal will lead to a longer pulse of smaller acceleration. The stiffer the acceleration, the more radiation is to be expected, because for the lower frequencies (\(\upsilon \ll R/c\)) we expect Larmor’s formula to hold, and this states that the radiated energy is proportional to the acceleration squared. The radiated power also varies as the square of the charge, and so the signal can be enhanced by increasing the charge up to the electrostatic breakdown limit. Whatever the amount of energy lost to radiation is, this energy must be subtracted from the energy available for either emission or absorption of of a Mössbauer photon Fig. 3.

Fig. 3
figure 3

Radiation emitted or absorbed by a charged sphere containing a decaying nucleus embedded in a metal crystal

Full size image

Let’s treat the recoiling crystal classically as a first approximation. Let its acceleration along the recoil direction be be a(t). Then the change in its velocity is

$$\begin{aligned} v_{f}-v_{i}=\int _{-\infty }^{+\infty }a(t)dt. \end{aligned}$$
(27)

If the direction and energy of the emitted or absorbed X-ray is known, then the change in the velocity of the recoiling crystal is determined by momentum conservation. As a first approximation to the energy radiated, we can use Larmor’s formula (in Gaussian cgs units)

$$\begin{aligned} P_{Larmor}(t)=\frac{2}{3}q^{2}a(t)^{2}/c^{3}. \end{aligned}$$
(28)

We see that in the limit of an infinite acceleration, we must have a(t) tending to a delta function in time, and so the radiated energy given by

$$\begin{aligned} E_{rad}=\int _{-\infty }^{+\infty }P_{Larmor}(t)dt=\frac{2}{3c^{3}}q^{2}\int _{-\infty }^{+\infty }a(t)^{2}dt, \end{aligned}$$
(29)

will become infinite. So we must limit the recoil time to a nonzero value. For simplicity, let’s assume that the acceleration is constant for a time T, and zero before and after this time, so that the aceleration is a simple step function.

$$\begin{aligned} \mathbf {a}(t)=\mathbf {a}_{0},\,-T/2<t<T/2,\,and\,0\,otherwise, \end{aligned}$$
(30)

or, in terms of the unit pulse function \(\Pi \),

$$\begin{aligned} \mathbf {a}(t)=\mathbf {a}_{0}\Pi \left( \frac{t}{T/2}\right) . \end{aligned}$$
(31)

We must require that the integral of the acceleration pulse over all time gives the change in the velocity of the crystal caused by the recoil of the Mössbauer event (here \(M_{\chi }\) is the mass of the stiff crystal, and \(k_{\gamma }\) is the wave number of the X-ray, either emitted or absorbed). Assuming that the initial momentum of the crystal is zero, the magnitude of its final recoil momentum is \(\pm \hbar k_{\gamma }\), an so its final velocity after recoil is given by

$$\begin{aligned} V_{M_{x}}=a_{0}T=\pm \hbar k_{\gamma }/M_{x} \end{aligned}$$
(32)

where the \(+\) sign if for absorption of a photon, and the − sign is for emission. Integrating over time we find the total energy radiated

$$\begin{aligned} E_{rad}= & {} E_{Larmor}=\int _{-T/2}^{T/2}P(t)dt=\frac{2}{3}q^{2}Ta_{0}^{2}/c^{3}=\frac{2q^{2}}{3c^{3}}\frac{V_{M_{x}}^{2}}{T}=\frac{2q^{2}\hbar ^{2}k_{\gamma }^{2}/M_{x}^{2}}{3c^{3}T}\nonumber \\= & {} \frac{2\hbar ^{2}k_{\gamma }^{2}}{3c^{3}T}\left( \frac{q}{M_{\chi }}\right) ^{2}. \end{aligned}$$
(33)

This energy must come from somewhere, implying that the energy of the Mössbauer event must be reduced by this amount. The linewidth of the Mössbauer decay in iron-57 is about \(1.0\times 10^{-8}\) eV, and this determines the sensitivity of energy measurements. If the radiative loss \(E_{rad}\) is comparable or larger than this linewidth, then the Mössbauer apparatus can in principle measure it. Let us calculate the energy radiated if T is the time it takes light to travel the diameter of the particle.

5.1 Calculation of the Energy Radiated for Speed of Light Recoil Response Using I-57 as the Mössbauer-Active Material with \(T=2R/c\)

To be specific, suppose the crystal consists of iron-57, the most common crystal used in the Mössbauer effect. We approximate the mass density iron-57 at room temperature by the corresponding value of natural iron, including all stable isotopes, which is about \(7.2\,\mathrm{gm/cm^{3}}\), and \(k_{\gamma }=14.4\) keV for \(^{57}\mathrm{Fe}\). The linewidth of the Mössbauer decay in iron-57 is about

$$\begin{aligned} \delta E=1.0\times 10^{-8}\,eV, \end{aligned}$$
(34)

and this determines the sensitivity of energy measurements. If the radiative loss \(E_{rad}\) is comparable or larger than this linewidth, then the Mössbauer apparatus can in principle measure it. If R is the radius of the sphere, we assume here that \(T=2R/c\), the time that it takes light to move the diameter of the crystal.

Then we obtain

$$\begin{aligned} E_{rad}=\frac{2}{3}\left( \frac{\hbar k_{\gamma }}{cM_{x}}\right) ^{2}\left. \frac{q^{2}}{cT}\right| _{T=2R/c}=\frac{2}{3}\left( \frac{\hbar k_{\gamma }}{cM_{x}}\right) ^{2}\frac{q^{2}}{2R}, \end{aligned}$$
(35)

but, the electrostatic energy of the charged sphere is just (in electrostatic cgs units)

$$\begin{aligned} E_{es}=\frac{q^{2}}{2R}, \end{aligned}$$
(36)

and therefore

$$\begin{aligned} E_{rad}=\frac{2}{3}\left( \frac{\hbar k_{\gamma }}{cM_{x}}\right) ^{2}E_{es}. \end{aligned}$$
(37)

Now the kinetic energy of the recoiling crystal must be less than \(\delta E\) in order for the Mössbauer effect to work. So, assuming this, we can write

$$\begin{aligned}&\left( \hbar k_{\gamma }\right) ^{2}/2M_{x}<\delta E,\end{aligned}$$
(38)
$$\begin{aligned}&E_{rad}<\frac{4}{3}\delta E\frac{E_{es}}{M_{x}c^{2}}. \end{aligned}$$
(39)

We can’t make R arbitrarily small, because we must statisfy the constraint (38). The crystal mass must therefore satisfy the condition:

$$\begin{aligned} M_{x}>\left( \hbar k_{\gamma }\right) ^{2}/2\delta E \end{aligned}$$
(40)

For Iron-57 we find

$$\begin{aligned} M_{x}>\left( 14.4\,\mathrm{keV}\right) ^{2}/\left( 2\times 10^{-8}\mathrm{eV}\right) =1.0368\times 10^{16}\mathrm{eV}=1.113\times 10^{7}AMU \end{aligned}$$
(41)

Each iron atom has a mass of about 56.9 amu, so the crystal must contain at least \(1.9\times 10^{5}\) iron atoms for the Mössbauer effect to work. We can calculate the radius from the formula

$$\begin{aligned}&M_{x}=\frac{4}{3}\pi R^{3}\left( 7.2\, \mathrm{gm/cm^{3}}\right) ,\end{aligned}$$
(42)
$$\begin{aligned}&R_{max}\approx 84.9{\AA }. \end{aligned}$$
(43)

The question then is, what is the maximum amount of (positive) charge that can be placed on an iron sphere of radius R before spontaneous emission of iron ions occurs? In order to estimate this, we make some crude assumptions. The threshold energy for sputtering of most metals is usually in the range of 10–30 eV. Let \(E_{th}\) be this energy for iron-57. We assume that the maximum electric field strength in the radial direction at the surface that can be withstood without iron-57 ions being spontaneously emitted is approximately determined by the condition

$$\begin{aligned} 2e\left| \mathbf {E}_{max}\right| a_{x}=E_{th}, \end{aligned}$$
(44)

where \(a_{x}\) is the lattice spacing of the crystal (\(\sim 2.87{\AA }for\,iron\)). We give the iron ion a charge of +2 because each iron atom contributes two electrons to the conduction band. So the maximum field strength is, taking 10eV for the sputtering threshold:

$$\begin{aligned} \left| \mathbf {E}_{max}\right| =\frac{E_{th}}{2ea_{x}}. \end{aligned}$$
(45)

Since we have spherical geometry, we have the relation just outside the surface of the sphere

$$\begin{aligned} E_{es}=\frac{1}{2}QR\left| \mathbf {E}\right| . \end{aligned}$$
(46)

the maximum value for Q is determined by

$$\begin{aligned} \left| \mathbf {E}_{max}\right| =\frac{Q_{max}}{4\pi \epsilon _{0}R_{max}^{2}}, \end{aligned}$$
(47)

and the voltage of the charged sphere is

$$\begin{aligned} V_{mzx}=R_{max}E_{max}, \end{aligned}$$
(48)

and therefore, the energy radiated is obtained from (39). The results are:

$$\begin{aligned}&\displaystyle R_{max}=85\,\mathrm{\mathring{A}};\;E_{th}=10\, \mathrm{eV};\;\left| \mathbf {E_{max}}\right| =34.8\, \mathrm{GV/m}\end{aligned}$$
(49)
$$\begin{aligned}&\displaystyle V_{max}=296V;\;Q_{max}=2.8\times 10^{-16}C,\end{aligned}$$
(50)
$$\begin{aligned}&\displaystyle E_{es}=258\,\mathrm{keV};\;M_{x}c^{2}=1.04\times 10^{7}\, \mathrm{GeV}, \end{aligned}$$
(51)

and from these results we have the maximum radiation energy loss

$$\begin{aligned} E_{rad}\approx \frac{4}{3}\delta E\frac{E_{es}}{M_{x}c^{2}}=3.3\times 10^{-19}\,\mathrm{eV}, \end{aligned}$$
(52)

and therefore

$$\begin{aligned} E_{rad}<<\delta E, \end{aligned}$$
(53)

which implies that the effect is too small to measure. So the only way that this effect could be measured is if the recoil is essentially instantaneous. There are two options available to increases the sensitivity. We can consider longer lifetime crystal materials which have smaller values of \(\delta E\), and we can consider using a volume of crystal which is below the mass needed for the Mössbauer effect, but which can still be resonant if moving with a precise velocity because of Doppler shifting. Both of these methods are discussed below.

5.2 Calculation of the Energy Radiated for Speed of Light Recoil Response Using Rhodium-103 as the Mössbauer-Active Material with T=2R/c

Rhodium-103 has a very long-lived isomer \(^{103m}Rh\) which is a candidate for precision Mössbauer research [4, 5]. Its linewidth is \(1.35\times 10^{-19}\) eV, which is eleven orders of magnitude narrower than the \(^{57}\)Fe isomer. The energy of the emitted photon is 39.8 keV, and the mass of \(^{103m}Rh\) is 102.9 amu. The density is \(12.45\, \mathrm{gm/cm^{3}}\). The lattice type is FCC, and the lattice spacing is \(3.8\,{\AA }\).The calculation is otherwise the same as for \(^{57}\)Fe. In order for the Mössbauer effect to work, the mass of the crystal in this case must be quite a bit larger then for iron-57, because of the much narrower linewidth for Rhodium-103. This larger mass then translates into a smaller radiation loss for a charged crystal due to acceleration. Consequently, if we go through the calculation done above for iron-57, but substituting the appropriate parameters for Rhodium-103, we find that the radiated power is actually smaller, so the reduced linewidth did not help. However, we shall now propose a way to utilize the full advantage a longer lived Mössbauer element such as Rhodium-103. We will consider an undersized Mössbauer crystal for the absorber, so that the kinetic energy is too large to allow for any Mössbauer absorption to occur. We propose to compensate for this energy loss by a Doppler shift applied to the absorber or source which would cancel the deficit in energy as far as the absorbed gamma ray energy was concerned. The reduced crystal mass makes the acceleration larger than it would be if the full Mössbauer crystal mass were used, and thus the energy loss due to radiation and Larmor’s formula will be greater. Let us consider a crystal consisting of N atoms of a Mössbauer active material, and let m denote the mass of a single nucleus, and \(q=N_{e}e\) .

$$\begin{aligned} M_{x}=Nm. \end{aligned}$$
(54)

R is determined by the condition

$$\begin{aligned} Nm=\rho _{\mu }\frac{4}{3}\pi R^{3}\rightarrow R=\left( \frac{3mN}{4\pi \varrho _{\mu }}\right) ^{1/3}, \end{aligned}$$
(55)

where \(\rho _{\mu }\) is the mass density. So we have

$$\begin{aligned} E_{rad}(N,N_{e})=\frac{2}{3}\left( \frac{\hbar k_{\gamma }}{cNm}\right) ^{2}\frac{N_{e}^{2}e^{2}}{2}\left( \frac{4\pi \varrho _{\mu }}{3mN}\right) ^{1/3}=\frac{N_{e}^{2}e^{2}}{N^{7/3}}\frac{1}{3}\left( \frac{\hbar k_{\gamma }}{cm}\right) ^{2}\left( \frac{4\pi \varrho _{\mu }}{3m}\right) ^{1/3}. \end{aligned}$$
(56)

Plugging in numbers for rhodium-103 we obtain the following formula

$$\begin{aligned} E_{rad}(N,N_{e})=\frac{N_{e}^{2}}{N^{7/3}}\left( 5.5680\times 10^{-13}eV\right) . \end{aligned}$$
(57)

As an exmple, suppose that \(N=10^{4}\), and \(N_{e}=10^{3}\), we calculate

$$\begin{aligned} E_{rad}(10000,1000)= & {} 2.584\times 10^{-16}\, \mathrm{eV},\quad R=32\,{\AA },\quad \nonumber \\ V= & {} 450V,\,v_{Doppler}=6.22mm/s \end{aligned}$$
(58)

where R is the radius of the sphere, V is the voltage at the outside of the spherical nanoparticle, and \(v_{Doppler}\) is the velocity required so that the Doppler shift compensates for the energy lost to kinetic energy of the recoil crystal, since we have intentionally considered and udersized Mössbauer crystal. This energy shift is over 3 orders of magnitude larger than the decay linewidth, and so it should be resolvable. Many other values of N and \(N_{e}\) give resolvable radiation results. There are some possible problems with this estimate though. One is that due to the small size of the crystal, the surface effects might be important. On the surface there may be isomer shifts on the energy levels of the rhodium-103 and rhodium-103m caused by the modified lattice at the surface of the sphere. Also at the surface, the outer several layers of atoms may experience a non-zero electric field due to the net charge on the sphere. This field could cause energy shifts in rhodium-103 and rhodium-103m because the electric quadrupole moment for these nucleii may not be zero, and such quadrupole moments are common among nucleii and cause energy shifts due to electric fields [35]. Other long-lived Mössbauer active isotopes which might be considered as alternatives to rhodium are \(^{45}\mathrm{Sc}\), \(^{107}\mathrm{Ag}\), and \(^{109}\mathrm{Ag}\) [4]. Although none of these have as narrow a linewidth, they are all more studied in the literature.

In this section we assumed that \(T=2R/c\), so that if the measured value of \(E_{rad}\) is greater than the estimated value here, the diffusion rate is faster than the speed of light, and if it is lower, then the diffusion rate is on average slower than the speed of light.

5.3 Gedanken Experiment for Testing These Ideas

I am a poor experimentalist, but I can never forego the temptation to design a thought experiment. Imagine a flat insulating disk, it could be a plastic, a glass, or a metal on which is deposited on one or both sides a layer of nano-particles of a controlled size of rhodium-103, or some other Mössbauer active element. Place this disk inside of a conducting tube which is held at some potential V above ground. The nano-particles are electromagnetically floating. Now shine a light source whose wavelength is short enough to allow electrons to leave the Mössbauer active nanoparticles and move to the concucting cylinder by means of the photoelectric effect. Eventually, when equilibrium is reached, the nano-particles will approach the voltage of the surrounding tube, and will then have a net positive charge on them. Multiple disks can be used to increase the absorption. Working in a non-ionizing atmosphere like helium might be simpler than working in a vacuum, provided the ionization levels could be kept to a low enough level. See Fig. 4. In order to have variable rates of Doppler shift, I would propose a precision linear 1 axis motorized stage. These are available with speeds up to about 300 mm/s with high repeatability and accuracy if cost is not an issue. They are routinely controlled by software. By varying the voltage on the outer cylinder, the charge on the nano-particles can be adjusted, and the energy shift caused by charging the nano-particles can be measured by adjusting the velocity of the stage to match the voltage on the cylinder.

Fig. 4
figure 4

Gedanken experiment for measuring the energy loss due to acceleration of charged micro-spheres undergoing Mössbauer recoil, and thereby gaining information about the rapidity of diffusion of momentum throughout the crystal

Full size image

6 Radiation from an Arbitrary Shaped Rigid Charged Body in Acceleration

The Larmor formula is for a point charge. There are corrections to it for an extended charge distribution which doesn’t change shape (ie. it moves rigidly) as it moves slowly along an arbitrary timelike trajectory. To analyze this, let the charge density be

$$\begin{aligned} \rho (\mathbf {x},t)=\rho _{0}(\mathbf {x}-\mathbf {\varvec{\xi }}(t)), \end{aligned}$$
(59)
$$\begin{aligned} \int \rho (x,t)d^{3}x=1, \end{aligned}$$
(60)

and where the current density is consequently

$$\begin{aligned} \mathbf {j}(\mathbf {x},t)=\mathbf {\varvec{\dot{\xi }}}(t)\rho (\mathbf {x},t). \end{aligned}$$
(61)

The retarded electromagnetic potentials are (in vacuum, in the Lorentz gauge, using Gaussian CGS units, and with c\(=\)1)

$$\begin{aligned} \varphi (\mathbf {x},t)=\int \frac{\rho (\mathbf {x}\prime -\varvec{\xi }(t_{r}))}{\left| \mathbf {x}-\mathbf {x\prime }\right| }d^{3}x\prime , \end{aligned}$$
(62)
$$\begin{aligned} A(\mathbf {x},t)=\int \frac{\mathbf {j}(\mathbf {x\prime },t_{r})}{\left| \mathbf {x}-\mathbf {x\prime }\right| }d^{3}x\prime , \end{aligned}$$
(63)

where the retarded time is given by \(t_{r}=t-\left| \mathbf {x}-\mathbf {x\prime }\right| /c\). We assume that the charge distribution is localized so that for large \(R=\left| \mathbf {x}-\varvec{\xi }(t-\left| \mathbf {x}\right| /c)\right| \) we have

$$\begin{aligned}&\displaystyle \varphi (\mathbf {\mathbf {x}},t)=\frac{1}{R}\int \rho (\mathbf {\mathbf {x\prime }}-\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime +O\left( \frac{1}{R^{2}}\right) =\frac{q}{R}+O\left( \frac{1}{R^{2}}\right) ,\end{aligned}$$
(64)
$$\begin{aligned}&\displaystyle A(\mathbf {x},t)=\frac{1}{R}\int \mathbf {\varvec{\dot{\xi }}}(t_{r})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime +O\left( \frac{1}{R^{2}}\right) , \end{aligned}$$
(65)

Note that \(t_{r}\) depends on \(\mathbf {x}^{\prime }\), and so in general it cannot be taken outside the integral. The radiation \(\mathbf {E}\) and \(\mathbf {B}\) fields fall off as 1 / R for large R. To calculate them we first can calculate the \(\mathbf {E}\) field, and then deduce the \(\mathbf {B}\) field from it. We see that \(\nabla \varphi \propto 1/R^{2}\), and so it cannot contribute to the radiation field. Since \(\mathbf {E}=-\mathbf {\nabla }\varphi -\partial \mathbf {A}/\partial t\), we can approximate \(\mathbf {E}=-\partial \mathbf {A}/\partial t+O(1/R^{2})\).

$$\begin{aligned} \mathbf {E}=-\partial /\partial t\left( \frac{1}{R}\int \mathbf {\varvec{\dot{\xi }}}(t_{r})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime \right) +O(1/R^{2}), \end{aligned}$$
(66)
$$\begin{aligned} \mathbf {E}=-\frac{1}{R}\int \left[ {\ddot{\mathbf \xi }}(t_{r})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))-\mathbf {\varvec{\dot{\xi }}}(t_{r})\left( \mathbf {\varvec{\dot{\xi }}}(t_{r})\cdot \mathbf {\nabla _{x\prime }}\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))\right) \right] d^{3}x\prime +O(1/R^{2}). \end{aligned}$$
(67)

Next we use the step function form for the acceleration which we assume for the rigid Mössbauer acceleration (31). We can take \(\dot{\xi }\) to be a constant inside the integrand since the recoil velocity of a Mössbauer crystal is very small. But in this case the second term vanishes, and so we have simply

$$\begin{aligned} \mathbf {E}(\mathbf {x},t)=-\frac{\mathbf {a_{0}}}{R}\int \Pi \big (\frac{t_{r}}{T/2}\big )\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime +O(1/R^{2}). \end{aligned}$$
(68)

The magnetic field may be calculated from this by using \(\mathbf {B}=\mathbf {\nabla }\times \mathbf {A}\) (\({\hat{\mathbf R}}\) is a unit vector pointing from the charge to the field point \(\mathbf {x}\))

$$\begin{aligned} \mathbf {B}=\hat{\mathbf {R}}\times \mathbf {E}. \end{aligned}$$
(69)

The Poynting vector in cgs units with c\(=\)1 is

$$\begin{aligned} \mathbf {S}=\frac{1}{4\pi }\mathbf {E}\times \mathbf {B}=\frac{1}{4\pi }\mathbf {E}\times \left( {\hat{\mathbf {R}}\times \mathbf {E}}\right) =\frac{1}{4\pi }\left[ \left( \mathbf {E\cdot E}\right) \hat{\mathbf {R}}-\left( \hat{\mathbf {R}}\cdot \mathbf {E}\right) \mathbf {E}\right] , \end{aligned}$$
(70)

and the power radiated per solid angle is

$$\begin{aligned} \begin{array}{l} d\mathcal {P}_{rad}=\left( \hat{\mathbf {R}}\cdot \mathbf {S}\right) \mathbf {R}^{2}d\varOmega =\left[ \mathbf {E}^{2}-\left( \hat{\mathbf {R}}\cdot \mathbf {E}\right) ^{2}\right] \mathbf {R}^{2}\frac{d\varOmega }{4\pi }\\ =\left[ \mathbf {a_{0}}^{2}-\left( \hat{\mathbf {R}}\cdot \mathbf {a_{0}}\right) ^{2}\right] \left( \int \Pi (\frac{t_{r}}{T/2})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime \right) ^{2}\frac{d\varOmega }{4\pi }+O(1/R^{2}). \end{array} \end{aligned}$$
(71)

Notice that this expression is never negative, so that the radiation into any solid angle is greater than or equal to zero, as causality requires. If we set the z axis to be parallel to \(\mathbf {a_{0}}\), we obtain

$$\begin{aligned} d\mathcal {P}_{rad}=\mathbf {a_{0}}^{2}sin^{2}(\theta )\left( \int \Pi (\frac{t_{r}}{T/2})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime \right) ^{2}\frac{d\varOmega }{4\pi }. \end{aligned}$$
(72)

If we let D be the maximum extent of the charge distribution, and then consider the limit cT>>D, we can replace \(\varPi \) by 1, and the integral just yields the total charge so in this case

$$\begin{aligned} d\mathcal {P}_{rad}=\mathbf {a_{0}}^{2}sin^{2}(\theta )q^{2}\frac{d\varOmega }{4\pi }, \end{aligned}$$
(73)

which on integration over the solid angle yields simply Larmor’s formula , with c=1. This result is independent of the shape of the charge distribution. We see that in general the radiation rate is a fraction of the Larmor rate, so that in general

$$\begin{aligned} d\mathcal {P}_{rad}=F(\Omega )\mathbf {a_{0}}^{2}sin^{2}(\theta )q^{2}\frac{d\varOmega }{4\pi }, \end{aligned}$$
(74)

where

$$\begin{aligned} F(\Omega )=\frac{\left( \int \Pi (\frac{t_{r}}{T/2})\rho (\mathbf {x}\prime -\varvec{\mathbf {\xi }}(t_{r}))d^{3}x\prime \right) ^{2}}{q^{2}}, \end{aligned}$$
(75)

if \(\rho (x)\) has the same sign for all positions, then \(F(\Omega )\) takes on values between 0 and 1. The total power radiated is then a fraction of the Larmor total power

$$\begin{aligned} P_{rad}(t)=\int F(\Omega )\mathbf {a_{0}}^{2}sin^{2}(\theta )q^{2}\frac{d\varOmega }{4\pi }=fP_{Larmor}(t),\;0\le f\le 1. \end{aligned}$$
(76)

We note that rigid non-radiating accelerations are possible for certain special classical systems as shown by multiple authors [1, 12, 30, 33].

We next consider the case of a spherical charged shell.

6.1 Radiation from a Rigid Thin Charged Spherical Shell

For the case of a charged metal nanosphere, the charge distribution is on the surface, and this can be approximated by a charged spherical shell. The calculation of the radiation from a charged hollow spherical shell has been studied extensively, as in [1, 32, 39, 40] and in references therein. The shell moves rigidly, and the charge density is radially symmetric in its rest frame. The vector coordinate for its center is \(\mathbf {\xi }(t)\). We need be concerned here with only non-relativistic velocities. The charge density and current for a general radial density, not necessarily a shell, are then given by

$$\begin{aligned} \rho (\mathbf {x},t)=qf(\left| \mathbf {x}-\mathbf {\xi }(t)\right| ),\quad \int d^{3}xf(\left| \mathbf {x}\right| )=1. \end{aligned}$$
(77)

For a shell we have

$$\begin{aligned} f(\mathbf {x})=\frac{\delta (\left| \mathbf {x}\right| -R)}{4\pi R^{2}}, \end{aligned}$$
(78)
$$\begin{aligned} j(x,t)=q\dot{\xi }(t)f(\left| \mathbf {x}-\mathbf {\xi }(t)\right| ). \end{aligned}$$
(79)

An approximate formula for the electromagnetic self force on the shell in the rest frame is given by Yaghjian [39, 40](see appendix A). His result is (in SI units)

$$\begin{aligned} \mathbf {F}_{self}(t)=\frac{-q^{2}}{6\pi \varepsilon _{0}Rc^{2}}\dot{\mathbf {u}}+\frac{q^{2}}{6\pi \epsilon _{0}c^{3}}\ddot{\mathbf {u}}+O(R),\;\mathbf {u}=0. \end{aligned}$$
(80)

He also calculates the power done on the shell by this self force to be

$$\begin{aligned} P_{el}=\frac{-5q^{2}}{24\pi \epsilon _{0}Rc^{2}}{\mathbf {u}\cdot \dot{\mathbf u}}+\frac{q^{2}}{6\pi \epsilon _{0}c^{3}}{\mathbf {u}\cdot \ddot{\mathbf u}}+O(R),\,\frac{\mathbf {u^{2}}}{c^{2}}\ll 1, \end{aligned}$$
(81)

where \(\mathbf {u}=d\mathbf {\mathbf {\xi }(t)}/dt\). Notice that \(P_{el}(t)\ne u\cdot \mathbf {F}_{self}(t)\). This discrepancy is explained carefully in [39, 40]. One needs to include Poincare stresses to eliminate it. If one does this, then the power equation is modified to (see [39], equation (5.5b), and taken to the small velocity limit)

$$\begin{aligned} P_{el}(t)=\frac{-q^{2}}{6\pi \epsilon _{0}Rc^{2}}{\mathbf {u}\cdot \dot{\mathbf u}}+\frac{q^{2}}{6\pi \epsilon _{0}c^{3}}{\mathbf {u}\cdot \ddot{\mathbf u}}+O(R),\mathrm{\,and\,for\,}\frac{\mathbf {u^{2}}}{c^{2}}\ll 1. \end{aligned}$$
(82)

If we integrate the second term in this expression, and assume that the acceleration vanishes in the distant future and distant past, then we find

$$\begin{aligned} \int _{-\infty }^{\infty }{\mathbf {u}\cdot \ddot{\mathbf u}}dt=-\int _{-\infty }^{\infty }{\dot{\mathbf u}^{2}}dt, \end{aligned}$$
(83)

so the second term just gives us the Larmor formula result for the energy radiated. The first term is a correction term which can be interpreted as a mass renormalization. It can bbe rewritten as

$$\begin{aligned}&\displaystyle \frac{-q^{2}}{6\pi \epsilon _{0}Rc^{2}}{\mathbf {u}\cdot \dot{\mathbf u}}=\frac{-q^{2}}{6\pi \epsilon _{0}Rc^{2}}\frac{1}{2}\frac{d}{dt}\left( \mathbf {u}^{2}\right) =-\frac{d}{dt}\left( \frac{1}{2}\left( \frac{4}{3}m_{es}\right) \mathbf {u}^{2}\right) ,\end{aligned}$$
(84)
$$\begin{aligned}&\displaystyle m_{es}=\frac{q^{2}}{8\pi \epsilon _{0}Rc^{2}}\text { in SI units, and }m_{es}=\frac{q^{2}}{2Rc^{2}}\text { in cgs Gaussian units}, \end{aligned}$$
(85)

This correction term to the Larmor formula varies as the charge squared, just as the radiation term does. This term cannot generally be ignored, since it can be larger than the Mössbauer linewidth. But in principle, the charge and the radius of the nanosphere can be known, and so it is straightforward to calculated the magnitude of this term and take its effect into account.

Of course the interior of the charged sphere is not empty in our case, and depending on the materials involved, there would be additional corrections which would require a numerical method to solve and are beyond the scope of the current paper. Moreover, there are higher terms in powers of R that might play a role.

The methods of Bohm and Weinstein [1] allow one to estimate higher order (in powers of R) corrections to the self force. Denote the \(k^{th}\) Fourier component of a function g(x, t) as

$$\begin{aligned} g(k,t)=\frac{1}{\left( 2\pi \right) ^{3/2}}\int g(x,t)exp(-i\mathbf {k\cdot x})d^{3}x,\;k=\left| \mathbf {k}\right| , \end{aligned}$$
(86)

and Defining f(k, t) by

$$\begin{aligned} f(k,t)=\frac{1}{\left( 2\pi \right) ^{3/2}}\int f(\left| \mathbf {x}\right| ,t)exp(-i\mathbf {k\cdot x})d^{3}x,\;k=\left| \mathbf {k}\right| . \end{aligned}$$
(87)

The self force for small velocities but arbitrarily large acceleration is found in [1] (in Gaussian units) to be

$$\begin{aligned} \mathbf {F}_{self}(t)=q^{2}\int _{0}^{\infty }d\tau G(\tau ){\ddot{\varvec{\xi }}}(t-\tau ), \end{aligned}$$
(88)

where

$$\begin{aligned} G(\tau )=\frac{-32\pi }{3c}\int _{0}^{\infty }dkk\left| f(k)\right| ^{2}sin(ck\tau ). \end{aligned}$$
(89)

For a spherical shell of radius R (from equation (17) and following in [1])

$$\begin{aligned} f(\mathbf {x})=\frac{\delta (\left| \mathbf {x}\right| -R)}{4\pi R^{2}},\;f(k)=\frac{1}{\left( 2\pi \right) ^{3/2}}\frac{sin(kR)}{kR} \end{aligned}$$
(90)

and it follows that

$$\begin{aligned} G(\tau )=\left\{ \begin{array}{ll} -1/(3R^{2}c),&{}\qquad \tau <2R/c\\ 0,&{}\qquad \tau >2R/c. \end{array}\right. \end{aligned}$$
(91)

Using (31)

$$\begin{aligned}&\displaystyle \mathbf {F}_{self}(t)=q^{2}G(0)\int _{0}^{2R/c}d\tau {\ddot{\varvec{\xi }}}(t-\tau )=q^{2}G(0)\int _{t-2R/c}^{t}dt\prime {\ddot{\varvec{\xi }}}(t\prime ),\end{aligned}$$
(92)
$$\begin{aligned}&\displaystyle \mathbf {F}_{self}(t)=-q^{2}\left( \dot{\mathbf {\xi }}(t)-\dot{\mathbf {\xi }}(t-2R/c)\right) /(3R^{2}c), \end{aligned}$$
(93)

one can calculate higher order powers of R corrections to the radiated power. Once again, it is wrong in general to equate the radiated power to the integrated work done by this self force. The power equation will have corrections as well, and these might have to be examined if a serious program to study this effect experimentally, but we leave this to future work.

7 Conclusion

This paper clearly shows the inadequacy of the current understanding of the Mössbauer effect at the microscopic level. The standard model of particle physics, which has been established as the basis for all of nuclear and condensed mattter phenomena, strongly suggests that a complete description of it must involve off-mass-shell particles–particles whose rest mass is not the standard value for that particle for a transient period of time after a Mössbauer event. Condensed matter theory currently does not have any way to incorporate this behavior convincingly and rigorously, since it is an effect of relativistic quantum field theory and the virtual off-mass-shell particles which appear in Feynman diagrams. What is needed is a covering theory for conventional quantum mechanics and associated many-body theory which allows off mass shell behavior. The most well-developed candidate for this is the proper-time formalism [20]. Off-mass-shell behavior is a relativistic effect which nonetheless cannot be ignored even though the velocities of all particles are moving non-relativistically. In the Mössbauer effect, all the particles are moving non-relativistically, but if the perturbation picture is correct, then off-mass-shell behavior is required to conserve energy and momentum, and this is the most plausible reconciliation of the effect with relativity theory. The problem or at least the mystery of crystal rigidity in the Mössbauer phenomenon has never been sufficiently clarified in the physics literature for this reason. The subject touches on fundamental questions for relativity and quantum mechanics. Part of the reason for the lack of resolution has been the absence of a direct experiment that could measure the intricacies of the diffusion of momentum inside the crystal immediately after a Mössbauer event (either decay or absorption). In order to address this, an experimental arrangement that utilizes the extreme precision of the Mössbauer effect itself has been proposed here to measure the time duration of the impulse given to a small Mössbauer crystal. This is achieved by measuring the amount of energy that is radiated away by bremsstrahlung of a charged particle undergoing a Mössbauer event. Besides helping to resolve the rigidity question, this experimental technique might prove useful for measuring some chemical or material properties, and thereby result in new analytical tools for chemistry and material science. The prediction is that the radiated energy, and consequently the associated Mössbauer energy shift, should vary in proportion to the charge squared divided by the diffusion time as in (33). If such an experimental effect can be observed, then subsequent more detailed theoretical and experimental analysis can zero in on the diffusion dynamics of a Mössbauer event, and hopefully clarify the underlying physical mechanism. The treatment of bremsstrahlung radiation here is strictly classical. There are undoubtedly quantum corrections to this, and if experiments reveal that the effect is indeed measurable, then it would justify plunging more deeply into a full quantum-mechanical description of the radiation.

The introduction of an off-mass-shell covering theory such as proper time, or SHP (for Stueckelberg, Horwitz, Piron) theory [20] into condensed matter physics, as is shown to be desirable if not necessary in this paper, would impact the foundations of all of condensed matter physics, not just the Mössbauer effect. The Hilbert space for condensed matter would need to include off-mass-shell states for completeness. Such a change could have far-reaching and unexpected consequences.