Duality for a class of fuzzy nonlinear optimization problem under generalized convexity

Abstract

In this paper, a Mond-Weir type dual program for a nonlinear primal problem under fuzzy environment is formulated. The solution concept of primal-dual problems is inspired by the nondominated solution. We have considered ordering among fuzzy numbers as a partial ordering and using the concept of Hukuhara difference between two fuzzy numbers and $H$-differentiability, appropriate duality theorems are established under pseudo/quasi-convexity assumptions. We have also illustrated a numerical example which satisfies the duality relations discussed in the paper.

1 Introduction

Fuzzy set theory was introduced by Prof. Lotfi Zadeh (1965). This has been applied in different areas such as topology, graph theory, algebra, logic etc. It can be applied to algorithms like clustering methods, control algorithms, mathematical programming and to transportation models, inventory control models, maintenance models, and others. Bellman and Zadeh (1970) considered the classical model of a decision and suggested a model for decision making in a fuzzy environment.

Zimmermann (1978) has first discussed fuzzy linear programming with several objective functions. Fuzzy linear programming problem (FLPP) in which the parameters are not fully known but only with some degree of precision was studied by Carlsson and Korhonen (1986). Fang et al. (1999) have solved linear programming problems with fuzzy coefficients in constraints. Gasimov and Yenilmez (2002) concentrated their work on linear programming problems with fuzzy technological coefficients in which both the right hand side and the technological coefficients are fuzzy numbers with linear membership functions. FLPP with fuzzy coefficients, also called robust programming was formulated by Negoita (1970). Tanaka and Asai (1984) proposed a formulation of FLPP with fuzzy constraints and gave a method for its solution which is based on inequality relations between fuzzy numbers.

The duality theory in FLPP was first studied by Rodder and Zimmermann (1977), who have also discussed the economic interpretation of the dual variables. Hamacher et al. (1978) have given some results on duality in fuzzy linear programming and mainly devoted to sensitivity analysis. Kabbara (1982) has also dealt with the problem of duality in a formal way. On the basis of fuzzification principle, the FLPP has been solved by Verdegay (1984). The author has also given a relationship of duality among fuzzy constraints and fuzzy objectives. Sergei Ovchinnikov (1991) characterized Zadeh’s extension principle in terms of the duality principle. Liu et al. (1995) have given a constructive approach in duality of fuzzy $MC^2$ linear programming.

Bector and Chandra (2002) have formulated a pair of fuzzy primal-dual problems and taking linear membership function, appropriate duality results have obtained. This work has modified the dual formulation and results of Rodder and Zimmermann (1977). Recently, Gupta and Mehlawat (2009) studied the same primal-dual pair as in Bector and Chandra (2002) and proved duality relations by taking exponential membership function. Wu (2003) has discussed the duality theory in FLPP by using the concept of fuzzy scalar (inner) product and in (2004), the author proved duality relations using partial ordering on the set of all fuzzy numbers in fuzzy optimization problems.

Vijay et al. (2004) introduced a dual for linear programming problems with fuzzy parameters and discussed two person zero sum matrix game with fuzzy pay-offs. Zhang et al. (2005) investigated the convex fuzzy mappings and discussed the duality theory in fuzzy mathematical programming problems with fuzzy coefficients. Later on, Ramik (2005) has given a new concept regarding the weak and strong duality theorems and then in (2006), the author proved duality theorems in fuzzy linear programming with possibility and necessity relations.

Beside the above mentioned papers, many researchers have proved results related to duality theory such as Amiri and Nasseri (2006) who have explored some duality results by using certain linear ranking function in fuzzy numbers. After that in (2007), they have established the dual of linear programming problems with trapezoidal fuzzy variables and hence developed the duality results based on certain linear ranking functions. Inuiguchi et al. (2003) defined the concept of duality and proved usual duality relations under fuzzy environment. Wu (2007) discussed the duality theory in a fuzzy optimization problem taking the concept of Hukuhara difference and $H$-differentiability for Wolfe’s primal and dual pair.

This paper is organized as follows. In the next section, we have discussed some notations and basic definitions about fuzzy numbers, their arithmetic operations, limit, continuity and differentiability of a fuzzy-valued function. In Sect. 3, we have given nondominated solution concept and definitions of pseudo/quasiconvex functions under fuzzy environment. Further, we have formulated a nonlinear fuzzy optimization problem, its Mond-Weir type dual and proved some duality results using the concept of Hukuhara difference and $H$-differentiability of a fuzzy-valued function. To verify our duality relations, a numerical example has also been illustrated in Sect. 4. In the final section, we have given conclusion of the present paper.

2 Notations and preliminaries

Throughout the paper, $\mathbb {R}^n$ denotes the $n$-dimensional Euclidean space, $\mathbb {R}$, the set of all real numbers and $\mathcal {F}(\mathbb {R})$, the set of all fuzzy numbers.

2.1 Basic definitions

Definition 2.1

Let $X$ be the universal set. $\tilde{A}$ is called a fuzzy set in $X$ if $\tilde{A}$ is a set of ordered pair

$$\begin{aligned} \tilde{A}=\{(x,\mu _{\tilde{A}}(x)):\,x\in X\}, \end{aligned}$$

where $\mu _{{\tilde{A}}{}_{}}:X\rightarrow [0,1]$ is the membership function of $x$ in $\tilde{A}$. We say that the fuzzy subset $\tilde{A}$ is crisp if $\mu _{\tilde{A}}$ is a characteristic function of ${\tilde{A}}$, i.e. $\mu _{\tilde{A}}:X\rightarrow \{0,1\}$. Fuzzy sets are an extension of the classical set theory used in Fuzzy logic.

Definition 2.2

Let $\tilde{A}$ be a fuzzy set in $X$ and $\alpha \in (0,1]$. The $\alpha$-level set of the fuzzy set $\tilde{A}$ is the crisp set, denoted as ${\tilde{A}}_\alpha$ and is defined as

$$\begin{aligned} {\tilde{A}}_\alpha =\{x\in X:\,\mu _{\tilde{A}}(x)\ge \alpha \}. \end{aligned}$$

The $0$-level set ${\tilde{A}}_0$ is defined as

$$\begin{aligned} {\tilde{A}}_0=cl(\{x\in X:\,\mu _{\tilde{A}}(x)>0\}), \end{aligned}$$

where $cl$ denotes the closure of a set in a given topological space.

Definition 2.3

A fuzzy set $\tilde{A}$ in $\mathbb {R}^n$ is said to be a convex fuzzy set if its $\alpha$-cuts $\tilde{A}_\alpha$ are (crisp) convex sets for all $\alpha \in (0,1].$ Alternatively, $\tilde{A}$ is convex if $\forall ~x_1,\,x_2\,\in \mathbb {R}^n,$

$$\begin{aligned} \mu _{\tilde{A}}(\lambda {x_1}+(1-\lambda ){x_2})\ge \min \{\mu _{\tilde{A}}({x_1}),\mu _{\tilde{A}}({x_2})\}, ~\hbox {for all}~\lambda \in [0,1]. \end{aligned}$$

Definition 2.4

(Bector and Chandra 2005) A fuzzy set $\tilde{A}$ in $X$ is said to be fuzzy number if it satisfies the following four properties:

• (a) ${\tilde{A}}$ is a normal fuzzy set, that is $\displaystyle \sup \nolimits _{x\in X}~\mu _{\tilde{A}}(x)=1,$

• (b) $\tilde{A}$ is convex,

• (c) $\,\mu _{\tilde{A}}$ is upper semicontinuous and

• (d) the  support  of  ${\tilde{A}}$ is  bounded   i.e.  the  set  $S({\tilde{A}})=\{x\in X:\,\mu _{\tilde{A}}(x)>0\}$  is bounded.

From Zadeh (1965), the $\alpha$-level set of the fuzzy set $\tilde{A}$ is a convex subset of $\mathbb {R}$ for all $\alpha \in {[0,1]{}{}}$ from condition $(b)$. Including this fact with conditions $(c)$ and $(d)$, the $\alpha$-level sets $\tilde{A}_\alpha$ of $\tilde{A}$ are compact and convex subset of $\mathbb {R}$ for all $\alpha \in [0,1]$. Therefore, we can also write $\tilde{A}_\alpha$ as

$$\begin{aligned} \tilde{A}_\alpha =[\tilde{a}_\alpha ^L,\,\tilde{a}_\alpha ^R]. \end{aligned}$$

We say that $\tilde{A}$ is a crisp number with value $n$ if its membership function is given by

$$\begin{aligned} \mu _{\tilde{A}}(m)=\left\{ \begin{array}{ll} \displaystyle 1 &{}\quad \mathrm {if}\quad m=n,\\ \nonumber \displaystyle 0 &{}\quad \text {otherwise}\nonumber \end{array} \right. \\ \nonumber \end{aligned}$$

We use the notation $\tilde{1}_{\{n\}}$ to represent a crisp number with value $n$.

Definition 2.5

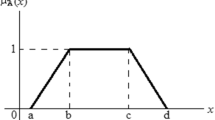
A fuzzy number $\tilde{a}$ is said to be a triangular fuzzy number if its membership function $\mu _{\tilde{a}}$ is defined as:

$$\begin{aligned} \mu _{\tilde{a}}(x) = \left\{ \begin{array}{ll} \displaystyle (x-{a}^l)/(a-{a}^l) &{}\quad \mathrm {if}\quad {a}^l \le x\le a,\\ \nonumber \displaystyle ({a}^u-x)/(a^u-{a})&{}\quad \mathrm {if}\quad a<x\le a^u,\\ \nonumber \displaystyle 0 &{}\quad \mathrm {otherwise},\nonumber \end{array} \right. \\ \nonumber \end{aligned}$$

where $\tilde{a}=(a^l,a,a^u)$. The $\alpha$-level set (a closed interval) of $\tilde{a}$ is then

$$\begin{aligned} \tilde{a}_\alpha =[\tilde{a}_\alpha ^l, \tilde{a}_\alpha ^u] \end{aligned}$$

where

$$\begin{aligned} \tilde{a}_\alpha ^l=(1-\alpha )a^l+\alpha a \quad \text {and}\quad \tilde{a}_\alpha ^u=(1-\alpha )a^u+\alpha a. \end{aligned}$$

2.2 Some arithmetic operations

Proposition 2.1

Let $\mathbb {R}$ be the universal set. Let $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers. Suppose $\tilde{A}_\alpha =[\tilde{a}_\alpha ^L,\,\tilde{a}_\alpha ^R]~$ and $~\tilde{B}_\alpha =[\tilde{b}_\alpha ^L,\,\tilde{b}_\alpha ^R]$ are the $\alpha -$level set of $\tilde{A}$ and $\tilde{B}$, respectively. Then, we have

$$\begin{aligned} (\tilde{A}(+)\tilde{B})_\alpha&= \tilde{A}_\alpha (+) \tilde{B}_\alpha =[\tilde{a}_\alpha ^L+\tilde{b}_\alpha ^L, \,\tilde{a}_\alpha ^R+\tilde{b}_\alpha ^R],\\ (\tilde{A}(+)\tilde{B})_\alpha ^L&= \tilde{a}_ \alpha ^L+\tilde{b}_\alpha ^L \quad \hbox {and}\quad \,(\tilde{A}(+)\tilde{B})_\alpha ^R=\tilde{a}_ \alpha ^R+\tilde{b}_\alpha ^R,\\ (\tilde{A}(-)\tilde{B})_\alpha&= \tilde{A}_ \alpha (-)\tilde{B}_\alpha =[\tilde{a}_\alpha ^L- \tilde{b}_\alpha ^R,\,\tilde{a}_\alpha ^R-\tilde{b}_\alpha ^L], \\ (\tilde{A}(.)\tilde{B})_\alpha&= \tilde{A}_\alpha (.) \tilde{B}_\alpha =\left[ \mathrm {min}\left\{ \tilde{a}_\alpha ^L\, \tilde{b}_\alpha ^L,\,\tilde{a}_\alpha ^L\, \tilde{b}_\alpha ^R,\,\tilde{a}_\alpha ^R\,\tilde{b}_ \alpha ^L,\tilde{a} _\alpha ^R\,\tilde{b}_\alpha ^R\right\} \right. ,\\&\qquad \qquad \qquad \qquad \times \left. \mathrm {max}\left\{ \tilde{a}_\alpha ^L\, \tilde{b}_\alpha ^L,\,\tilde{a}_\alpha ^L\,\tilde{b}_ \alpha ^R,\,\tilde{a}_\alpha ^R\,\tilde{b}_\alpha ^L,\tilde{a} _\alpha ^R\,\tilde{b}_\alpha ^R\right\} \right] , \end{aligned}$$

If $\tilde{A}$ is non-negative, then

$$\begin{aligned} (\tilde{A}(.)\tilde{B})_\alpha =\Big [\text {min} \left\{ \tilde{a}_\alpha ^L\, \tilde{b}_\alpha ^L,\,\tilde{a}_\alpha ^R\, \tilde{b}_\alpha ^L\right\} ,\,\text {max}\left\{ \tilde{a}_\alpha ^L\, \tilde{b}_\alpha ^R,\,\tilde{a}_\alpha ^R\, \tilde{b}_\alpha ^R\right\} \Big ]. \end{aligned}$$

Let $\tilde{A}=(\tilde{A}_1,\tilde{A}_2,\ldots ,\tilde{A}_n)^T$ and $\tilde{B}=(\tilde{B}_1,\tilde{B}_2,\ldots ,\tilde{B}_n)^T$ then $\tilde{A}(+)\tilde{B}$ is defined as

$$\begin{aligned} (\tilde{A}(+)\tilde{B})=\bigg (\tilde{A}_1(+) \tilde{B}_1,\tilde{A}_2(+)\tilde{B}_2,\ldots , \tilde{A}_n(+)\tilde{B}_n\bigg )^T. \end{aligned}$$

From above, we obtain

$$\begin{aligned} (\tilde{A}(+)\tilde{B})_\alpha ^L&= \bigg ((\tilde{A}_1(+)\tilde{B}_1)_\alpha ^L, (\tilde{A}_2(+)\tilde{B}_2)_\alpha ^L,\ldots , (\tilde{A}_n(+)\tilde{B}_n)_\alpha ^L\bigg )^T\\&= \bigg ((\tilde{A}_1)_\alpha ^L+(\tilde{B}_1)_\alpha ^L, (\tilde{A}_2)_\alpha ^L+(\tilde{B}_2)_\alpha ^L,\ldots , (\tilde{A}_n)_\alpha ^L+(\tilde{B}_n)_\alpha ^L\bigg )^T.\\ (\tilde{A}(+)\tilde{B})_\alpha ^R&= \bigg ((\tilde{A}_1(+) \tilde{B}_1)_\alpha ^R,(\tilde{A}_2(+)\tilde{B}_2)_\alpha ^R, \ldots , (\tilde{A}_n(+)\tilde{B}_n)_\alpha ^R\bigg )^T\\&= \bigg ((\tilde{A}_1)_\alpha ^R+(\tilde{B}_1)_\alpha ^R, (\tilde{A}_2)_\alpha ^R+(\tilde{B}_2)_\alpha ^R,\ldots , (\tilde{A}_n)_\alpha ^R+(\tilde{B}_n)_\alpha ^R\bigg )^T. \end{aligned}$$

We define $\bigoplus _{i=1}^m\tilde{A}_i$ as

$$\begin{aligned} \displaystyle \bigoplus _{i=1}^m \tilde{A}_i=\tilde{A}_1(+) \tilde{A}_2(+),\ldots ,(+)\tilde{A}_m. \end{aligned}$$

Let $\tilde{A}$ be a fuzzy number, then $\tilde{A}$ is said to be nonnegative fuzzy number if $\mu _{\tilde{A}}(x)=0$ for all $x<0$ and $\tilde{A}$ is called a nonpositive fuzzy number if $\mu _{\tilde{A}}(x)=0$ for all $x>0$. If $\tilde{A}$ is nonnegative then $\tilde{a}_\alpha ^L$ and $\tilde{a}_\alpha ^R$ are nonnegative real numbers for all $\alpha \in [0,1]$ and $\tilde{a}_\alpha ^L$ and $\tilde{a}_\alpha ^R$ are nonpositive real numbers for all $\alpha \in [0,1]$ if $\tilde{A}$ is nonpositive fuzzy number.

Let $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers and $\bigodot$ be any arithmetic operation between them. Then by using the Zadeh’s extension principle, the membership function of fuzzy number $\tilde{A}\bigodot \tilde{B}$ is defined as

$$\begin{aligned} \mu _{\tilde{A}\bigodot \tilde{B}}(z)=\displaystyle \sup _{z=x\cdot y}\,\min (\mu _{\tilde{A}}(x),\mu _{\tilde{B}}(y)). \end{aligned}$$

Suppose $A$ and $B$ are compact and convex subset of $\mathbb {R}^n$. If there exists a compact and convex subset of $\mathbb {R}^n$, say $C$, such that $A=B+C$, then $C$ is called the Hukuhara difference of $A$ and $B$. So $C$ can be written as $C=A\ominus B$ (Banks and Jacobs 1970). Using this concept, in fuzzy numbers we can also define the Hukuhara difference between two fuzzy numbers. Let $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers. If there exists a fuzzy number $\tilde{C}$ such that $\tilde{B}\oplus \tilde{C}=\tilde{A}$, then $\tilde{C}$ is unique and $\tilde{C}$ is called the Hukuhara difference of $\tilde{A}$ and $\tilde{B}$ and is denoted by $\tilde{A}\ominus _H \tilde{B}$.

Let $\tilde{f}:\mathbb {R}^n\rightarrow \mathcal {F}(\mathbb {R})$ be a fuzzy-valued function defined on $\mathbb {R}^n$. For any $x\in \mathbb {R}^n, \tilde{f}(x)\in \mathcal {F}(\mathbb {R})$ therefore for all $\alpha \in [0,1]$, we can define two real-valued functions $\tilde{f}_\alpha ^L(x)$ and $\tilde{f}_\alpha ^R(x)$ such that $\tilde{f}_\alpha ^L(x)=(\tilde{f}(x))_\alpha ^L$ and $\tilde{f}_\alpha ^R(x)=(\tilde{f}(x))_\alpha ^R$.

2.3 Limit and continuity of a fuzzy valued function

Let $L,M\subseteq \mathbb {R}^n$. The Hausdorff metric is defined by

$$\begin{aligned} d_H(L,M)=\text {max}\Bigg \{\displaystyle \sup _{l\in L}~\inf _{m\in M}~||l-m||,\,\sup _{m\in M}~\inf _{l\in L}~||l-m||\Bigg \} \end{aligned}$$

The metric $d_\mathcal {F}$ on $\mathcal {F}(\mathbb {R})$ for all $\tilde{l},\,\tilde{m}\,\in \mathcal {F}(\mathbb {R})$ is define by

$$\begin{aligned} d_\mathcal {F}(\tilde{l},\tilde{m})=\displaystyle \sup _{0\le \alpha \le 1}~d_H(\tilde{l}_\alpha ,\tilde{m}_\alpha ) \end{aligned}$$

Definition 2.6

(Wu 2007) Let $\tilde{A}$ be a fuzzy number. For $c\in \mathbb {R}^n$, we write

$$\begin{aligned} \displaystyle \lim \limits _{x \rightarrow c}\tilde{f}(x)=\tilde{A} \end{aligned}$$

if for every $\epsilon >0,$ there exists $\delta >0$ such that $||x-c||<\delta \Rightarrow \text {d}_\mathcal {F}(\tilde{f}(x),\tilde{A})<\epsilon .$

We say that $\tilde{f}$ is level-wise continuous at $c$ if and only if $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^R$ are continuous at $c$ for all $\alpha \in [0,1]$ and $\tilde{f}$ is continuous at $c$ if

$$\begin{aligned} \displaystyle \lim \limits _{x \rightarrow c}\tilde{f}(x)=\tilde{f}(c). \end{aligned}$$

Also, if $\tilde{f}$ is continuous at $c$, then $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^R$ are continuous at $c$ for all $\alpha \in [0,1]$.

Definition 2.7

Let $\tilde{A}$ be a fuzzy number, then $\tilde{A}$ is said to be canonical fuzzy number if the functions $\gamma _1(\alpha )=\tilde{a}_\alpha ^L$ and $\gamma _2(\alpha )=\tilde{a}_\alpha ^R$ are continuous on [0,1].

2.4 Differentiation of a fuzzy valued function

We can define the differentiation of fuzzy valued function following the concept of Hukuhara difference between two fuzzy numbers.

Definition 2.8

Let $X_0$ be a non-empty open subset of $\mathbb {R}$. A fuzzy-valued function $\tilde{f}:X_0\rightarrow \mathcal {F}(\mathbb {R})$ is called $H$-differentiable at $\overline{x}$ if and only if there exists a canonical fuzzy number $\tilde{A}(\overline{x})$ such that the limits

$$\begin{aligned} \displaystyle \lim \limits _{h \rightarrow 0^+}~\tilde{1}_{\{\frac{1}{h}\}}(.)\left[ \tilde{f} (\overline{x}+h)\ominus _H \tilde{f}(\overline{x})\right] \end{aligned}$$

and

$$\begin{aligned} \displaystyle \lim \limits _{h \rightarrow 0^+}~\tilde{1}_{\{\frac{1}{h}\}}(.)\left[ \tilde{f} (\overline{x})\ominus _H \tilde{f}(\overline{x}-h)\right] \end{aligned}$$

both exist and are equal to $\tilde{A}(\overline{x})$, where $\tilde{1}_{\{\frac{1}{h}\}}$ is a crisp number with value $\frac{1}{h}$. Here $\tilde{A}(\overline{x})$ is called the $H$-derivative of $\tilde{f}$ at $\overline{x}$.

Definition 2.9

(Wu 2009) Let $\tilde{f}:Y_0\rightarrow \mathcal {F}(\mathbb {R})$ be a fuzzy-valued function defined on an open subset $Y_0$ of $\mathbb {R}^n$ and $\overline{x}=(\overline{x}_1,\overline{x}_2,\ldots ,\overline{x}_n)\in Y_0$ be fixed. Then

• (i) $\tilde{f}$ is said to be level-wise differentiable at $\overline{x}$ if and only if the real valued functions $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^R$ are differentiable at $\overline{x}$ for all $\alpha \in [0,1]$ (which means that all the partial derivatives $\partial \tilde{f}_\alpha ^L/\partial x_i$ and $\partial \tilde{f}_\alpha ^R/\partial x_i$ exist at $\overline{x}$ for all $\alpha \in [0,1]$  and all  $i=1,2,\ldots ,n$).

• (ii) $\tilde{f}$ is said to have $i$th partial $H$-derivative $\tilde{A}^{(i)}(\overline{x})$ at $\overline{x}$ if the fuzzy-valued function $\tilde{h}(x_i)=\tilde{f}(\overline{x}_1,\overline{x}_2,\ldots , \overline{x}_{i-1},x_i,\overline{x}_{i+1},\ldots ,\overline{x}_n)$ is $H$-differentiable at $\overline{x}_i$ with $H$-derivative $\tilde{A}^{(i)}(\overline{x})$, that is,

  $$\begin{aligned} (\partial \tilde{f}/\partial x_i)(\overline{x})=\tilde{A}^{(i)}(\overline{x}). \end{aligned}$$

• (iii) $\tilde{f}$ is said to be $H$-differentiable at $\overline{x}$ if one of the partial $H$-derivatives $\partial \tilde{f}/\partial x_1,\partial \tilde{f}/\partial x_2,\ldots ,\partial \tilde{f}/\partial x_n$ exists at $\overline{x}$ and the remaining $n-1$ partial $H$-derivatives exist on some neighborhoods of $\overline{x}$ and are continuous at $\overline{x}$.

Clearly, if $\tilde{f}$ is $H$-differentiable at $x$, then $\tilde{f}$ is also level-wise differentiable at $x$. Let $\tilde{f}$ be $H$-differentiable at $x$. Then the $H$-gradient of $\tilde{f}$ at $x$ (Wu 2007) is defined as

$$\begin{aligned} \displaystyle \nabla \tilde{f}(x)=\left( \frac{\partial \tilde{f}}{\partial x_1}(x),\frac{\partial \tilde{f}}{\partial x_2}(x),\ldots ,\frac{\partial \tilde{f}}{\partial x_n}(x)\right) ^T \end{aligned}$$

where each $\frac{\partial \tilde{f}}{\partial x_i}(x),~i=1,2,\ldots ,n$ is a canonical fuzzy number. The $\alpha$-level set of $\nabla \tilde{f}(x)$ is defined as

$$\begin{aligned} \bigg (\nabla \tilde{f}(x)\bigg )_\alpha =\bigg (\displaystyle \bigg ( \frac{\partial \tilde{f}}{\partial x_1}(x)\bigg )_\alpha ,\bigg (\frac{\partial \tilde{f}}{\partial x_2}(x)\bigg )_\alpha ,\ldots ,\bigg (\frac{\partial \tilde{f}}{\partial x_n}(x)\bigg )_\alpha \bigg )^T, \end{aligned}$$

where

$$\begin{aligned} \displaystyle \bigg (\frac{\partial \tilde{f}}{\partial x_i}(x)\bigg )_\alpha {=}\left[ \bigg (\frac{\partial \tilde{f}}{\partial x_i}(x)\bigg )_\alpha ^L,\bigg (\frac{\partial \tilde{f}}{\partial x_i}(x)\bigg )_\alpha ^R\right] {=}\left[ \frac{\partial \tilde{f}_\alpha ^L}{\partial x_i}(x),\frac{\partial \tilde{f}_\alpha ^R}{\partial x_i}(x)\right] \quad \text{ for } \text{ all }~~\alpha \in [0,1]. \end{aligned}$$

From above it is clear that,

$$\begin{aligned} \bigg (\nabla \tilde{f}(x)\bigg )_\alpha ^L= \bigg (\displaystyle \bigg (\frac{\partial \tilde{f}}{\partial x_1}(x)\bigg )_\alpha ^L,\bigg (\frac{\partial \tilde{f}}{\partial x_2}(x)\bigg )_\alpha ^L,\ldots , \bigg (\frac{\partial \tilde{f}}{\partial x_n}(x)\bigg )_\alpha ^L \bigg )^T=\nabla \tilde{f}_\alpha ^L(x) \end{aligned}$$

and

$$\begin{aligned} \bigg (\nabla \tilde{f}(x)\bigg )_\alpha ^R=\bigg (\displaystyle \bigg (\frac{\partial \tilde{f}}{\partial x_1}(x)\bigg )_ \alpha ^R,\bigg (\frac{\partial \tilde{f}}{\partial x_2}(x)\bigg )_ \alpha ^R,\ldots ,\bigg (\frac{\partial \tilde{f}}{\partial x_n}(x) \bigg )_\alpha ^R\bigg )^T=\nabla \tilde{f}_\alpha ^R(x). \end{aligned}$$

3 Mond-Weir type duality

3.1 General optimization problem under crisp and fuzzy environment

Consider the following nonlinear optimization problem:

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} \mathbf{(NLP)} &{} \hbox {Minimize} &{} f(x)=f(x_1,x_2,\ldots ,x_n)\\ &{}\hbox {s.t.}&{} g_i(x)\le 0,~i=1,2,\ldots ,m\\ &{}&{} x\in X_0, \end{array} \end{aligned}$$

where $f:\mathbb {R}^n\rightarrow \mathbb {R}$, $g_i:\mathbb {R}^n\rightarrow \mathbb {R},~i=1,2,\ldots ,m$ are real valued functions and $X_0\subseteq \mathbb {R}^n$ with non empty open interior.

Let $\tilde{A}$ and $\tilde{B}$ be two fuzzy numbers. Then $\tilde{A}_\alpha =[\tilde{a}_\alpha ^L,\,\tilde{a}_\alpha ^R]$ and $\tilde{B}_\alpha =[\tilde{b}_\alpha ^L,\,\tilde{b}_\alpha ^R]$ are closed intervals in the real line for all $\alpha \in [0,\,1]$.

Consider $``\preceq$” as a partial ordering on $\mathcal {F}(\mathbb {R})$. Then $\tilde{B}\preceq \tilde{A}$ if and only if $\tilde{b}_\alpha \le \tilde{a}_\alpha$ for all $\alpha \in [0,\,1]$. Now we write $\tilde{A}\prec \tilde{B}$ if and only if $\tilde{a}_\alpha \le \tilde{b}_\alpha$ for all $\alpha \in [0,1]$ and there exists $\beta \in [0,1]$ such that $\tilde{a}_\beta < \tilde{b}_\beta$, i.e.,

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \tilde{a}\,_{\beta }^L<\tilde{b}\,_{\beta }^L~\\ \tilde{a}\,_{\beta }^U\le \tilde{b}\,_{\beta }^U~ \end{array}\right. } \quad \text {or}\quad {\left\{ \begin{array}{ll} \displaystyle \tilde{a}\,_{\beta }^L\le \tilde{b}\,_{\beta }^L~\\ \tilde{a}\,_{\beta }^U<\tilde{b}\,_{\beta }^U~ \end{array}\right. } \quad \text {or}\quad {\left\{ \begin{array}{ll} \displaystyle \tilde{a}\,_{\beta }^L<\tilde{b}\,_{\beta }^L~\\ \tilde{a}\,_{\beta }^U<\tilde{b}\,_{\beta }^U. \end{array}\right. } \end{aligned}$$

The fuzzy version of above (NLP) is as follows:

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} \mathbf{(FNP)}&{} \hbox {Minimize}&{} \tilde{f}(x)=\tilde{f}(x_1,x_2,\ldots ,x_n)\\ &{}\hbox {s.t.}&{}\tilde{g}_j(x)\preceq 0,~j=1,2,\ldots ,m\\ &{}&{}x\in X_0, \end{array} \end{aligned}$$

where $\tilde{f}:\mathbb {R}^n\rightarrow \mathcal {F}(\mathbb {R})$ and $\tilde{g}_j:\mathbb {R}^n\rightarrow \mathcal {F}(\mathbb {R})\,(j=1,2,\ldots ,m)$ are fuzzy valued functions with respect to objective functions and constraints of (FNP), repectively.

Let $X_1=\{x\in \mathbb {R}^n:\,x\in X_0\,$ and $\,\tilde{g}_j(x)\preceq 0$ for $j=1,2,\ldots ,m \}$ be the set of feasible points of (FNP) and let $\tilde{f}(X_1)=\{\tilde{f}(x):\,x\in X_1\}$ be the set of objective values of (FNP).

3.2 Nondominated solutions

Definition 3.1

A feasible solution $x^*$ of (FNP) is said to be a nondominated solution if there exists no $\overline{x}\,\,(\ne x^*)\in X_1$ such that $~\tilde{f}(\overline{x})\prec \tilde{f}(x^*).$

$\tilde{f}(x^*)$ is called the nondominated objective value of $\tilde{f}$. Let us denote $\textit{(NDP)}\tilde{f}(X_1)$, the set of all nondominated objective values of (FNP) i.e.

$$\begin{aligned} \textit{(NDP)}\tilde{f}(X_1)=\{\tilde{f}(x^*):\,x^* \hbox {is a nondominated solution of} \,\tilde{f} \,\hbox {in} \,\textit{(FNP)}\}. \end{aligned}$$

3.3 Convexity, pseudoconvexity and quasiconvexity

Suppose ${f}:Y\rightarrow \mathbb {R}$ is a differentiable function on a non-empty open convex subset $Y$ of $\mathbb {R}^n$. At $x_1\in Y$, the function ${f}$ is said to be

• convex if for all $x_2\in Y$, ${f}(x_2)- {f}(x_1)\ge \nabla {f}(x_1)^T(x_2-x_1)$.

• pseudoconvex, if for all $x_2\in Y$, $\nabla {f}(x_1)^T(x_2-x_1)\ge 0\Rightarrow {f}(x_2)\ge {f}(x_1);$ or equivalently if ${f}(x_2)<{f}(x_1)$ then $\nabla {f}(x_1)^T(x_2-x_1) < 0$.

• quasiconvex if for all $x_2$ $\in Y$, ${f}(x_2)\le {f}(x_1)$, then $\nabla {f}(x_1)^T(x_2-x_1)\le 0.$

Definition 3.2

(Wu 2009) Let $\tilde{f}:Y\rightarrow \mathcal {F}(\mathbb {R})$ be a fuzzy valued function on $Y$. The function $\tilde{f}$ is said to be convex at $x^*$ if and only if $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^U$ are convex at $x^*$ for all $\alpha \in [0,1].$

Definition 3.3

Let $\tilde{f}:Y\rightarrow \mathcal {F}(\mathbb {R})$ be a fuzzy valued function on $Y$. The function $\tilde{f}$ is said to be pseudoconvex at $x^*$ if and only if $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^U$ are pseudoconvex at $x^*$ for all $\alpha \in [0,1].$

Definition 3.4

Let $\tilde{f}:Y\rightarrow \mathcal {F}(\mathbb {R})$ be a fuzzy valued function on $Y$. Then $\tilde{f}$ is said to be quasiconvex at $x^*$ if and only if $\tilde{f}_\alpha ^L$ and $\tilde{f}_\alpha ^U,$ are quasiconvex at $x^*$ for all $\alpha \in [0,1].$

The function $\tilde{f}$ is convex/pseudoconvex/quasiconvex over $Y$ if $\tilde{f}$ is convex/pseudocon-vex/quasiconvex for all $x^*\in Y$.

3.4 Dual formulation

Mond-Weir (1981–1983) introduced the following dual to (NLP) (called as Mond-Weir dual):

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} \mathbf{(MWD)} &{} \hbox {Maximize} &{} f(y)=f(y_1,y_2,\ldots ,y_n)\\ &{}\hbox {s.t.} &{}\displaystyle \nabla f(y)+\sum _{i=1}^m u_i \nabla g_i(y)=0,\\ &{}&{}\displaystyle \,\sum _{i=1}^m u_i\,g_i(y)\ge 0,\\ &{}&{} y\in Y_0\subseteq \mathbb {R}^n,\,u_i\ge 0,\,i=1,2,\ldots ,m, \end{array} \end{aligned}$$

where $Y_0$ is a nonempty open subset of $\mathbb {R}^n$, and proved the duality theorems by weakening the convexity assumptions of $f$ to pseudoconvexity and $g$ to quasiconvexity of $g$. They also discussed duality results for the problems involving both equality and inequality constraints.

The dual of the (FNP), which is a fuzzy version of (MWD), is as follows

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} \mathbf{(FND)} &{} \hbox {Maximize} &{} \tilde{f}(y)=\tilde{f}(y_1,y_2,\ldots ,y_n)\\ &{}\hbox {s.t.} &{} \displaystyle ~~\nabla \tilde{f}(y)(+)\bigg (\bigoplus _{j=1}^m \tilde{1}_{\{u_j\}}(.)\nabla \tilde{g_j}(y)\bigg )=0,\\ &{}&{}\displaystyle \bigoplus _{j=1}^m \tilde{1}_{\{u_j\}}(.) \tilde{g_j}(y)\succeq 0,\\ &{}&{}y\in Y_0,\,u_j\ge 0,\,j=1,2,\ldots ,m. \\ \end{array} \end{aligned}$$

$$\begin{aligned} \text {Take}~ Y_1 = \left\{ \begin{array}{ll} (y,u)\in \mathbb {R}^n\times \mathbb {R}^m:&{}\nabla \tilde{f}(y)(+)\bigg (\bigoplus \nolimits _{j=1}^m \tilde{1}_{\{u_j\}}(.)\nabla \tilde{g_j}(y)\bigg )=0,\\ &{}\bigoplus \nolimits _{j=1}^m \tilde{1}_{\{u_j\}}(.) \tilde{g_j}(y)\succeq 0,\\ &{}y\in Y_0,\,u_j\ge 0,\,j=1,2,\ldots ,m, \end{array} \right\} \end{aligned}$$

where $\tilde{1}_{\{u_j\}}$ is a crisp number with the value $u_j,\, j=1,2,\ldots ,m.$ That is, $Y_1$ be the set of all feasible solutions of (FND). The set

$$\begin{aligned} \tilde{f}(Y_1)=\{\tilde{f}(y):\,y\in Y_1\}, \end{aligned}$$

contains all the objective values of (FND). Now, let $\textit{(NDD)}\tilde{f}(Y_1)$ is the set of all nondominated objective values of (FND) i.e.

$$\begin{aligned} \textit{(NDD)}\tilde{f}(Y_1)=\{\tilde{f}(y^*){:}\,(y^*,u^*)\, \hbox {is a nondominated solution of the problem}\,\textit{(FND)}\}. \end{aligned}$$

3.5 Duality results

Now, we will prove appropriate duality relations for dual pair (FNP) and (FND).

Theorem 3.1

Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on an open subset $Y_0$ of $R^n$. Suppose that $x$ is a feasible solution of primal problem (FNP) and $(y,u)$ is a feasible solution of dual problem (FND). If $\tilde{f}$ is pseudoconvex at $y$ and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ is quasiconvex at $y$. Then

$$\begin{aligned} \tilde{f}(x)\succeq \tilde{f}(y). \end{aligned}$$

Proof

Since $x$ and $(y,u)$ are feasible solutions of (FNP) and (FND), respectively, we see that

$$\begin{aligned} (\tilde{g_j})_\alpha ^L(x)&\le 0~\text {and}~(\tilde{g_j})_\alpha ^U(x)\le 0, \quad j=1,2,\ldots ,m\end{aligned}$$

(1)

$$\begin{aligned}&\nabla \tilde{f}_\alpha ^L(y)+\sum _{j=1}^m u_j \nabla (\tilde{g_j})_\alpha ^L(y)=0,\end{aligned}$$

(2)

$$\begin{aligned}&\nabla \tilde{f}_\alpha ^U(y)+\sum _{j=1}^m u_j \nabla (\tilde{g_j})_\alpha ^U(y)=0,\end{aligned}$$

(3)

$$\begin{aligned}&\displaystyle \sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^L(y)\ge 0,\end{aligned}$$

(4)

$$\begin{aligned}&\displaystyle \sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^U(y)\ge 0,\end{aligned}$$

(5)

$$\begin{aligned}&u_j\ge 0,\quad j=1,2,\ldots ,m. \end{aligned}$$

(6)

for all $\alpha \in [0,1]$. $\square$

Now, inequalities (1), (4) and (6) implies

$$\begin{aligned}&\sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^L(x)\le 0\le \sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^L(y)\\&\quad \text {i.e.}~\sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^L(x)\le \sum _{j=1}^m u_j (\tilde{g_j})_\alpha ^L(y). \end{aligned}$$

This follows from the quasiconvexity of $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ at $y$ that

$$\begin{aligned} \sum _{j=1}^m u_j \nabla (\tilde{g_j})_\alpha ^L(y)(x-y)\le 0 \end{aligned}$$

which using (2) yields

$$\begin{aligned} \nabla (\tilde{f})_\alpha ^L(y)(x-y)\ge 0. \end{aligned}$$

This further from the pseudoconvexity of $\tilde{f}$ at $y$ gives

$$\begin{aligned} (\tilde{f})_\alpha ^L(x)\ge (\tilde{f})_\alpha ^L(y). \end{aligned}$$

Similarly,

$$\begin{aligned} (\tilde{f})_\alpha ^U(x)\ge (\tilde{f})_\alpha ^U(y). \end{aligned}$$

Thus, we have

$$\begin{aligned} \tilde{f}(x)\succeq \tilde{f}(y). \end{aligned}$$

Hence the result.$\square$

Corollary 1

Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on $Y_0$. Let $\tilde{f}$ be pseudoconvex and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ be quasiconvex on $Y_0$. If $x^*$ is a feasible solution of primal problem (FNP) and $\tilde{f}(x^*)\in \tilde{f}(Y_1)$. Then $x^*$ solves (FNP) that is $\tilde{f}(x^*)\in \textit{(NDP)}\tilde{f}(X_1)$.

Proof

Suppose that $x^*$ is not a nondominated solution of the primal problem (FNP). Then, there exists an $\overline{x}~(\ne x^*)\in X_1$ such that

$$\begin{aligned} \tilde{f}(\overline{x})\prec \tilde{f}(x^*). \end{aligned}$$

i.e. $\tilde{f}_\alpha ^{\,L}(\overline{x})\le \tilde{f}_\alpha ^{\,L}(x^*)$ and $\tilde{f}_\alpha ^{\,\,U}(\overline{x})\le \tilde{f}_\alpha ^{\,\,U}(x^*)$ for all $\alpha \in [0,1]$ and there exists $\beta \in [0,1]$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \displaystyle \tilde{f}_{\beta }^{\,L}(\overline{x})<\tilde{f}_{\beta }^{\, L}(x^*)~\\ \tilde{f}_{\beta }^{\,\,U}(\overline{x})\le \tilde{f}_{\beta }^{\,\,U}(x^*) \end{array}\right. } \text {or}~ {\left\{ \begin{array}{ll} \displaystyle \tilde{f}_{\beta }^{\,L}(\overline{x}) \le \tilde{f}_{\beta }^L(x^*)~\\ \tilde{f}_{\beta }^{\,\,U}(\overline{x})<\tilde{f}_{\beta }^{\,\,U}(x^*) \end{array}\right. } \text {or}~ {\left\{ \begin{array}{ll} \displaystyle \tilde{f}_{\beta }^{\,L}(\overline{x})<\tilde{f}_{\beta }^{\, L}(x^*)~\\ \tilde{f}_{\beta }^{\,\,U}(\overline{x})<\tilde{f}_{\beta }^{\,\,U}(x^*). \end{array}\right. } \end{aligned}$$

Hence, either $~\tilde{f}_{\beta }^L(\overline{x})<\tilde{f}_{\beta }^L(x^*)$ or $\tilde{f}_{\beta }^U(\overline{x})<\tilde{f}_{\beta }^U(x^*)$.

Since $\tilde{f}(x^*)\in \tilde{f}(Y_1)$, there exists $(\overline{y},\overline{u})$, a feasible point of dual problem (FND) such that

$$\begin{aligned} \tilde{f}(x^*)=\tilde{f}(\overline{y}). \end{aligned}$$

(7)

Now, let $\tilde{f}_{\beta }^L(\overline{x})<\tilde{f}_{\beta }^L(x^*)$. Then from (7), we have

$$\begin{aligned}&\tilde{f}_{\beta }^L(\overline{y})=\tilde{f}_{\beta }^L(x^*)> \tilde{f}_{\beta }^L(\overline{x})\quad \hbox {or}\quad \tilde{f}_{\beta }^L(\overline{y})> \tilde{f}_{\beta }^L(\overline{x}) \end{aligned}$$

which contradicts Theorem 3.1. Similarly, a contradiction can be obtained when $\tilde{f}_{\beta }^{\,\,U}(\overline{x})<\tilde{f}_{\beta }^{\,\,U}(x^*)$. This completes the proof. $\square$

Corollary 2

Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on $Y_0$. Suppose that $\tilde{f}$ is pseudoconvex and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ is quasiconvex on $Y_0$. If $(y^*,u^*)$ is a feasible solution of dual problem (FND) and $\tilde{f}(y^*)\in \tilde{f}(X_1)$, then $(y^*,u^*)$ solves dual problem (FND) that is $\tilde{f}(y^*)\in (NDD)\tilde{f}(Y_1)$.

Proof

Suppose $(y^*,u^*)$ be not a nondominated solution of the dual problem (FND). Then, there exists $(y,u)\,(\ne (y^*,u^*))\in Y_1$ such that

$$\begin{aligned}&\tilde{f}(y^*)\prec \tilde{f}(y)\quad \hbox {i.e.}\, \tilde{f}_{\alpha }^L(y^*)\le \tilde{f}_{\alpha }^L(y)\,\quad \hbox {and}\, \tilde{f}_{\alpha }^{\,\,U}(y^*)\le \tilde{f}_{\alpha }^{\,\,U}(y)\,\quad \hbox {for all}\, \alpha \in [0,1] \end{aligned}$$

and there exists $\beta \in [0,1]$ such that

$$\begin{aligned} \tilde{f}_{\beta }^{\,L}(y^*)<\tilde{f}_{\beta }^{\,L}(y)\, \hbox {or}\, \tilde{f}_{\beta }^{\,\,U}(y^*)<\tilde{f}_{\beta }^{\,\,U}(y). \end{aligned}$$

Since $\tilde{f}(y^*)\in \tilde{f}(X_1)$ therefore there exists a feasible point $\overline{x}$ in (FNP) such that

$$\begin{aligned} \tilde{f}(\overline{x})=\tilde{f}(y^*). \end{aligned}$$

(8)

Now, if $\tilde{f}_{\beta }^L(y^*)<\tilde{f}_{\beta }^L(y)$, then from (8), we have

$$\begin{aligned} \tilde{f}_{\beta }^L(\overline{x})=\tilde{f}_ {\beta }^L(y^*)<\tilde{f}_{\beta }^L(y). \end{aligned}$$

This contradicts Theorem 3.1. Similarly, the proof can be obtained if $\tilde{f}_{\beta }^{\,\,U}(y^*)<\tilde{f}_{\beta }^{\,\,U}(y)$. Hence the result. $\square$

Corollary 3

Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on $Y_0$. Suppose that $\tilde{f}$ is pseudoconvex and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}} (\times )\tilde{g}_j$ is quasiconvex on $Y_0$. If $x^*$ is a feasible solution of the primal problem (FNP) and $(\overline{y},\overline{u})$ is a feasible solution of dual problem (FND) and $\tilde{f}(x^*)=\tilde{f}(\overline{y})$, then $x^*$ and $(\overline{y},\overline{u})$ solves primal and dual problems, respectively.

Proof

The proof can be obtained by contradiction. Suppose $x^*$ is not a nondominated solution of the primal problem (FNP). Therefore there exists a feasible point $x~(\ne x^*)$ of (FNP) such that

$$\begin{aligned} \tilde{f}(x)\prec \tilde{f}(x^*) \end{aligned}$$

i.e. $\tilde{f}_\alpha ^{\,L}(x)\le \tilde{f}_\alpha ^{\,L}(x^*)$ and $\tilde{f}_\alpha ^{\,\,U}(x)\le \tilde{f}_\alpha ^{\,\,U}(x^*)$ for all $\alpha \in [0,1]$ and there exists $\beta \in [0,1]$ such that

$$\begin{aligned} \tilde{f}_{\beta }^{\,L}(x)<\tilde{f}_{\beta }^{\,L}(x^*)\, \hbox {or}\, \tilde{f}_{\beta }^{\,\,U}(x)<\tilde{f}_{\beta }^{\,\,U}(x^*). \end{aligned}$$

Now, since $\tilde{f}(x^*)=\tilde{f}(\overline{y})$. Therefore, $\tilde{f}_{\beta }^L(\overline{y})=\tilde{f}_{\beta }^L(x^*)> \tilde{f}_{\beta }^L(x)$.

This contradicts Theorem 3.1. Similarly, the proof for the other case can be obtained. $\square$

Now, we present the strong duality theorem by taking $(NDP)\tilde{f}(X_1)$ and $(NDD)\tilde{f}(Y_1)$ have at least one point in common, that is, there exist $\tilde{f}(x^*)\in (NDP)\tilde{f}(X_1)$ and $\tilde{f}(\bar{x})\in (NDD)\tilde{f}(Y_1)$ such that $\tilde{f}(x^*)=\tilde{f}(\bar{x})$.

Definition 3.5

(Wu 2007) Two types of concepts about duality gap between primal and dual problems are discussed below:

• (i) We say that the primal problem (FNP) and the dual problem (FND) have no duality gap in the weak sense if and only if $(NDP)\tilde{f}(X_1)$ and $(NDD)\tilde{f}(Y_1)$ have at least one point in common.

• (ii) We say that the primal problem (FNP) and the dual problem (FND) have no duality gap in the strong sense if and only if there exists $\tilde{f}(x^*)\in (NDP)\tilde{f}(X_1)$ and $\tilde{f}(x^*)\in (NDD)\tilde{f}(Y_1)$.

It may be noted that in the above definition $(ii)$ implies $(i)$. But the converse will be true if $x^* = \bar{x}$.

Theorem 3.2

(Strong duality theorem in weak sense) Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on $Y_0$. Suppose that $\tilde{f}$ is pseudoconvex and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ is quasiconvex on $Y_0$. If one of the following conditions is satisfied:

• (i) there exists a feasible solution $x^*$ of primal problem (FNP) such that $\tilde{f}(x^*)\in \tilde{f}(Y_1)$.

• (ii) there exists a feasible solution $(x^*,u^*)$ of dual problem (FND) such that $\tilde{f}(x^*)\in \tilde{f}(X_1)$.

Then there will be no duality gap in the primal problem (FNP) and the dual problem (FND) in the weak sense.

Proof

Suppose the condition $(i)$ holds, then, after using Corollary 1 we just need to show that $\tilde{f}(x^*)\in (NDD)\tilde{f}(Y_1)$. Since $\tilde{f}(x^*)\in \tilde{f}(Y_1)$, there exists a feasible solution $(\overline{y},\overline{u})$ of dual problem (FND) such that

$$\begin{aligned} \tilde{f}(x^*)=\tilde{f}(\overline{y}). \end{aligned}$$

Now, we have to show that $\tilde{f}(\overline{y})\in (NDD)\tilde{f}(Y_1)$. As Corollary 1 gives $\tilde{f}(x^*)\in (NDP)\tilde{f}(X_1)$. Therefore, from above equation, we have

$$\begin{aligned} \tilde{f}(\overline{y})\in \textit{(NDP)}\tilde{f}(X_1) \end{aligned}$$

which implies $\tilde{f}(\overline{y})\in \tilde{f}(X_1).$ Hence, by using Corollary 2, we obtain that $\tilde{f}(\overline{y})\in \textit{(NDD)}\tilde{f}(Y_1)$.

Next, let condition $(ii)$ be true, then, from Corollary 2, it remains to show that $\tilde{f}(x^*)\in \textit{(NDP)}\tilde{f}(X_1)$. Since $\tilde{f}(x^*)\in \tilde{f}(X_1)$, there exists a feasible solution $\overline{x}$ of primal problem (FNP) such that

$$\begin{aligned} \tilde{f}(\overline{x})=\tilde{f}(x^*). \end{aligned}$$

Now, Corollary 2 gives

$$\begin{aligned} \tilde{f}(x^*)\in \textit{(NDP)}\tilde{f}(X_1). \end{aligned}$$

This follows from above equation that

$$\begin{aligned} \tilde{f}(\overline{x})\in \textit{(NDD)}\tilde{f}(Y_1)~~ \text {i.e.}~~ \tilde{f}(\overline{x})\in \tilde{f}(Y_1). \end{aligned}$$

Therefore, using the result of Corollary 1, we have

$$\begin{aligned} \tilde{f}(x^*)\in \textit{(NDP)}\tilde{f}(X_1) \end{aligned}$$

which completes the proof. $\square$

Theorem 3.3

(Strong duality theorem in strong sense) Let $\tilde{f}$ and $\tilde{g}_j$ $(j=1,2,\ldots ,m)$ be $H$-differentiable on $Y_0$. Suppose that $\tilde{f}$ is pseudoconvex and $\bigoplus _{j=1}^m{\tilde{1}_{\{u_j\}}}(\times )\tilde{g}_j$ is quasiconvex on $Y_0$. Suppose $x^*$ and $(x^*,u^*)$ are feasible solutions of primal (FNP) and dual (FND), respectively. Then $x^*$ and $(x^*,u^*)$ solves primal and the dual problems, respectively; or the primal problem (FNP) and the dual problem (FND) have no duality gap in the strong sense.

Proof

Proof follows immediately from Corollary 3. $\square$

4 Numerical illustration

Let $m=2$. Suppose that the fuzzy valued objective function $\tilde{f}:\mathbb {R}\rightarrow \mathcal {F}(\mathbb {R})$ and system constraints $\tilde{g}_j:\mathbb {R}\rightarrow \mathcal {F}(\mathbb {R})\,(j=1,2)$ are as follows:

$$\begin{aligned} \tilde{f}(x)&= \bigg (\tilde{3}(\times )\tilde{1}_ {\{x^2\}}\bigg )(+)\tilde{1},\\ \tilde{g}_1(x)&= \tilde{6}(\times )\tilde{1}_{\{x^3\}},~ \tilde{g}_2(x)= \bigg (\tilde{4}(\times )\tilde{1}_{\{x\}}\bigg )(+)(-\tilde{1}), \end{aligned}$$

where

$$\begin{aligned} \tilde{\mathbf{3}}&= (1,3,4),~\tilde{\mathbf{1}}=(0,1,3),~\tilde{\mathbf{6}}=(4,6,7),\\ -\tilde{\mathbf{1}}&= (-2,-1,0),~\tilde{\mathbf{4}}=(2,4,6). \end{aligned}$$

are triangular fuzzy numbers. The primal (FNP) and the dual (FND) become:

$$\begin{aligned} \begin{array}{l@{\quad }l@{\quad }l} \mathbf{(MP)}&{} \hbox {Minimize} &{} \tilde{f}(x)\\ &{}\hbox {subject to}&{} \tilde{g}_1(x)\preceq 0, \tilde{g}_2(x)\preceq 0,\\ \mathbf{(MD)}&{} \hbox {Maximize} &{} \tilde{f}(u)\\ &{}\hbox {subject to} &{} \displaystyle \nabla \tilde{f}(y)(+) \displaystyle \bigoplus _{j=1}^2\nabla \bigg (\tilde{1}_{\{u_j\}}(\times )\tilde{g}_j(y)\bigg )=0,\\ &{} &{}\displaystyle \bigoplus _{j=1}^2\tilde{1}_{\{u_j\}}(\times ) \tilde{g}_j(y)\succeq 0,\\ &{}&{} u_1,\,u_2\ge 0. \end{array} \end{aligned}$$

Using Proposition 2.1 and Definition 2.5, we obtain

$$\begin{aligned}&\displaystyle \tilde{f}_\alpha ^L(x)=(1+2\alpha )x^2+\alpha ,\quad \tilde{f}_\alpha ^U(x)=(4-\alpha )x^2+3-2\alpha ,\\&\displaystyle (\tilde{g_1})_\alpha ^L(x)=(4+2\alpha )x^3,\quad (\tilde{g_1})_ \alpha ^U(x)=(7-\alpha )x^3,\\&\displaystyle (\tilde{g_2})_\alpha ^L(x)=(2+2\alpha )x+\alpha -2,\quad (\tilde{g_2})_\alpha ^U(x)=(6-2\alpha )x-\alpha ,\\&\displaystyle \nabla \tilde{f}_\alpha ^L( x)=\bigg (\frac{d\tilde{f}(x)}{d x}\bigg )_\alpha ^L=2(1+2\alpha )x,\quad \nabla \tilde{f}_\alpha ^U(x)=\bigg (\frac{d\tilde{f}(x)}{d x}\bigg )_\alpha ^U=2(4-\alpha )x, \end{aligned}$$

$$\begin{aligned} \bigg (\nabla \tilde{g}(x)\bigg )_\alpha ^L&= \left( \displaystyle \bigg (\frac{d\tilde{g_1}(x)}{d x}\bigg )_\alpha ^L,\bigg (\frac{d\tilde{g_2}(x)}{d x}\bigg )_\alpha ^L\right) \quad \text {and}\quad \bigg (\nabla \tilde{g}(x)\bigg )_\alpha ^U\\&= \left( \displaystyle \bigg (\frac{d\tilde{g_1}(x)}{d x}\bigg )_\alpha ^U,\bigg (\frac{d\tilde{g_2}(x)}{d x}\bigg )_\alpha ^U\right) , \end{aligned}$$

where

$$\begin{aligned} \bigg (\frac{d\tilde{g_1}(x)}{d x}\bigg )_\alpha ^L&= 3(4+2\alpha )x^2,\quad \bigg (\frac{d\tilde{g_2}(x)}{d x}\bigg )_\alpha ^L=2+2\alpha , \\ \bigg (\frac{d\tilde{g_1}(x)}{d x}\bigg )_\alpha ^U&= 3(7-\alpha )x^2\quad \text {and}\quad \bigg (\frac{d\tilde{g_2}(x)}{d x}\bigg )_\alpha ^U=6-2\alpha . \end{aligned}$$

We first prove that the functions $\tilde{f}$ and $\tilde{g_j}$ $(j=1,2)$ defined above satisfy all the assumptions of weak duality theory (Theorem 3.1). For any real numbers $x_1$, $x_2$ and $\alpha \in [0,1]$, the expression $(\tilde{f})_\alpha ^L(x_1)<(\tilde{f})_\alpha ^L(x_2)$ yields $(1+2\alpha )x_1^2+\alpha < (1+2\alpha )x_2^2+\alpha$ and hence $x_1^2-x_2^2<0.$

Now,

$$\begin{aligned}&\nabla (\tilde{f})_\alpha ^L(x_2)(x_1-x_2) \\&\quad =2(1+2\alpha )(x_1x_2-x_2^2) \\&\quad \le (1+2\alpha )(x_1^2-x_2^2)~(\text {as}~2x_1x_2\le x_1^2+x_2^2) \\&\quad <0~~(\text {since}~x_1^2-x_2^2<0). \end{aligned}$$

Hence $(\tilde{f})_\alpha ^L$ is pseudoconvex for all $\alpha \in [0,1]$. Similarly, one can prove that $(\tilde{f})_\alpha ^U$ is pseudoconvex for all $\alpha \in [0,1]$. Therefore, the function $\tilde{f}$ is pseudoconvex.

Next, we will show that $u_1(\tilde{g_1})_\alpha ^L(x)+u_2(\tilde{g_2})_\alpha ^L(x)$ is quasiconvex. This holds trivially if $u_1= u_2=0$. If $(u_1, u_2)\ne (0,0)$, then from

$$\begin{aligned} u_1(\tilde{g_1})_\alpha ^L(x_1)+u_2(\tilde{g_2})_\alpha ^L(x_1)\le u_1(\tilde{g_1})_\alpha ^L(x_2)+u_2(\tilde{g_2})_\alpha ^L(x_2), \end{aligned}$$

we obtain

$$\begin{aligned} u_1(4+2\alpha )x_1^3+u_2(2+2\alpha )x_1\le u_1(4+2\alpha )x_2^3+u_2(2+2\alpha )x_2. \end{aligned}$$

This further yields

$$\begin{aligned} (x_1-x_2)\{u_1(4+2\alpha )((x_1+\dfrac{1}{2}x_2)^2+\dfrac{3}{4} x_2^2)+u_2(1+2\alpha )\}\le 0, \end{aligned}$$

Hence

$$\begin{aligned} x_1-x_2 \le 0. \end{aligned}$$

Therefore,

$$\begin{aligned}&\{u_1\nabla (\tilde{g_1})_ \alpha ^L(x_2)+u_2\nabla (\tilde{g_2})_\alpha ^L(x_2)\}(x_1-x_2) =\{3u_1(4+2\alpha )x_2^2 +u_2(1+2\alpha )\}\\&\quad \times \,(x_1-x_2) \le 0~(\text {as}~x_1-x_2\le 0). \end{aligned}$$

Hence $u_1(\tilde{g_1})_\alpha ^L(x)+u_2(\tilde{g_2})_\alpha ^L(x)$ is quasiconvex for all $\alpha \in [0,1]$. Similarly, one can prove that $u_1(\tilde{g_1})_\alpha ^U(x)+u_2(\tilde{g_2})_\alpha ^U(x)$ is quasiconvex for all $\alpha \in [0,1]$. Therefore, the function $\tilde{1}_{\{u_1\}}(\times )(\tilde{g_1})+ \tilde{1}_{\{u_2\}}(\times )(\tilde{g_2})$ is quasiconvex.

Hence, the assumptions of Theorem 3.1 has been verified.

Further, we will show that this example satisfy Theorem 3.1. Since $x$ and $(y,u)$ are feasible solutions of primal and dual problems, respectively. Then, we have

$$\begin{aligned}&\displaystyle (4+2\alpha )x^3\le 0,\end{aligned}$$

(9)

$$\begin{aligned}&\displaystyle (7-\alpha )x^3\le 0,\end{aligned}$$

(10)

$$\begin{aligned}&\displaystyle (2+2\alpha )x+\alpha -2\le 0,\end{aligned}$$

(11)

$$\begin{aligned}&\displaystyle (6-2\alpha )x-\alpha \le 0,\end{aligned}$$

(12)

$$\begin{aligned}&\displaystyle 2(1+2\alpha )y+3u_1(4+2\alpha )y^2+u_2(2+2\alpha )=0,\end{aligned}$$

(13)

$$\begin{aligned}&\displaystyle 2(4-\alpha )y+3u_1(7-\alpha )y^2+u_2(6-2\alpha )=0,\end{aligned}$$

(14)

$$\begin{aligned}&\displaystyle u_1(4+2\alpha )y^3+u_2\{(2+2\alpha )y+\alpha -2\}\ge 0,\end{aligned}$$

(15)

$$\begin{aligned}&\displaystyle u_1(7-\alpha )y^3+u_2\{(6-2\alpha )y-\alpha \}\ge 0,\end{aligned}$$

(16)

$$\begin{aligned}&\displaystyle u_1,\,u_2,\,\ge 0,\,\alpha \in [0,1]. \end{aligned}$$

(17)

If $(u_1,u_2)=(0,0)$, then (13) implies $y=0$ and hence obviously $\tilde{f}_\alpha ^L(x)\ge \tilde{f}_\alpha ^L(y)$. Now, if $(u_1,u_2)\ne (0,0)$, then from (9), (11), (15) and $u_1,\,u_2\ge 0$, we have

$$\begin{aligned}&(4+2\alpha )x^3u_1{+}\{(2+2\alpha )x+\alpha -2\}u_2\le u_1(4+2\alpha )y^3+u_2\{(2+2\alpha )y+\alpha -2\}\\&\quad \text {or} \quad u_1(4+2\alpha )(x^3-y^3)+u_2(2\alpha +2)(x-y)\le 0. \end{aligned}$$

This implies

$$\begin{aligned}&(x-y)\bigg \{(4+2\alpha )\bigg \{\bigg (x+\dfrac{y}{2}\bigg )^2+ \dfrac{3}{4}y^2\bigg \}u_1+(2\alpha +2)u_2\bigg \}\le 0\\ \end{aligned}$$

and hence using (17), we have $x\le y$.

This from (17) follows that

$$\begin{aligned} (x-y)\{3(4+2\alpha )y^2u_1+(2\alpha +2)u_2\}\le 0. \end{aligned}$$

(18)

Using (13) in (18), we get

$$\begin{aligned}&(x-y)[(1+2\alpha )y]\ge 0 \quad \text {or} \quad x^2-y^2\ge 0~(\text {since}~2xy\le (x^2+y^2)), \end{aligned}$$

which gives

$$\begin{aligned}&(1+2\alpha )x^2+\alpha \ge (1+2\alpha )y^2+\alpha \quad \text {or} \quad \tilde{f}_\alpha ^L(x)\ge \tilde{f}_\alpha ^L(y). \end{aligned}$$

Similarly, $\tilde{f}_\alpha ^U(x)\ge \tilde{f}_\alpha ^U(y)$. Hence the result.

Next, we will illustrate that the same example also justify the strong duality theory in strong sense (Theorem 3.3). Since $x^*=0$ and $(x^*,u^*)=(0,0)$ satisfied the constraints (9)–(12) and (13)–(17), respectively. Therefore these are the feasible solutions of the primal (MP) and dual (MD), respectively. We will prove that $x^*$ and $(x^*,u^*)$ are nondominated solutions of (MP) and (MD), respectively. On the contrary suppose $x^*=0$ is not a nondominated solution of (MP). Then there exists $\overline{x}$ $(\ne 0)\in X_1$ (the set of all feasible solutions of (MP)) such that

$$\begin{aligned} \begin{array}{c} \displaystyle \tilde{f}(\overline{x})\prec \tilde{f}(0).\\ \displaystyle \hbox {or}\quad \tilde{f}\,_\alpha ^L(\overline{x})\le \tilde{f}\,_\alpha ^L(0) \quad \hbox {and}\quad \tilde{f}\,_\alpha ^U(\overline{x})\le \tilde{f}\,_\alpha ^U(0) \hbox { for all } \alpha \in [0,1] \end{array} \end{aligned}$$

and there exists some $\beta \in [0,1]$ such that

$$\begin{aligned} \tilde{f}\,_\beta ^L(\overline{x})<\tilde{f}\,_\beta ^L(0)~\text {or}~ \tilde{f}\,_\beta ^U(\overline{x})<\tilde{f}\,_\beta ^U(0). \end{aligned}$$

Let $\tilde{f}\,_\beta ^L(\overline{x})<\tilde{f}\,_\beta ^L(0)$. Then, we have

$$\begin{aligned} (2\beta +1)\overline{x}^2<0 \end{aligned}$$

which is a contradiction as $\beta \in [0,1]$ and $\overline{x}^2\ge 0$ for all $\overline{x}$. Similarly, $\tilde{f}\,_\beta ^U(\overline{x})\nless \tilde{f}\,_\beta ^U(0)$. Hence $x^*=0$ is a nondominated solution of (MP).

Further, let $(x^*,u^*)=(0,0)$ is not a nondominated solution of (MD). Then there exists $(y,u)$ $(\ne (0,0))\in Y_1$ (the set of all feasible solutions of (MD)) such that

$$\begin{aligned} \begin{array}{c} \displaystyle \tilde{f}(0)\prec \tilde{f}(y) \\ \displaystyle \hbox {i.e.}\quad \tilde{f}\,_\alpha ^L(0)\le \tilde{f}\,_\alpha ^L(y) \hbox { and } \tilde{f}\,_\alpha ^U(0)\le \tilde{f}\,_\alpha ^U(y) \hbox { for all } \alpha \in [0,1] \end{array} \end{aligned}$$

and there exists some $\beta \in [0,1]$ such that

$$\begin{aligned} \tilde{f}\,_\beta ^L(0)<\tilde{f}\,_\beta ^L(y)~\text {or}~ \tilde{f}\,_\beta ^U(0)<\tilde{f}\,_\beta ^U(y). \end{aligned}$$

Let $\tilde{f}\,_\beta ^L(0)<\tilde{f}\,_\beta ^L(y)$. Therefore, we get

$$\begin{aligned} (2\beta +1) y^2>0. \end{aligned}$$

(19)

From (13) and (17), we have

$$\begin{aligned} y\le 0. \end{aligned}$$

Now, to contradict inequality (19), we just need to show that $y\nless 0$. Suppose $y<0$, then using (17), we have

$$\begin{aligned} u_1(4+2\alpha )y^3+u_2\{(2+2\alpha )y+\alpha -2\}\le 0 \end{aligned}$$

This further follows from (15) that

$$\begin{aligned} u_1(4+2\alpha )y^3+u_2\{(2+2\alpha )y+\alpha -2\}=0 \end{aligned}$$

with each term in the expression non-positive. This means $u_1(4+2\alpha )y^3=0$, $u_2(2+2\alpha )y=0$ and $u_2(\alpha -2)=0$. Hence, $u_1=u_2=0$. Therefore, (13) yields $y=0$, which contradicts our supposition. Similarly, $\tilde{f}\,_\beta ^U(0)\nless \tilde{f}\,_\beta ^U(y)$. Hence $(x^*,u^*)=(0,0)$ is a nondominated solution of (MD). $\square$

5 Conclusions

In this paper, we have formulated Mond-Weir type primal and dual problems with the fuzzy-valued objective function and system constraints. Further, usual duality theorems are established considering a partial ordering on the set of all fuzzy numbers and following the concept of $\alpha$-level set, Hukuhara difference and $H$-differentiability. We have also discussed a numerical example to verify duality relations obtained in the paper.